
Interactions of Gap Solitons in Coupled Bragg Gratings with
Cubic-quintic Nonlinearity and Dispersive Reflectivity
Afroja Akter and Javid Atai
Department of Electrical and Electronic Engineering, School of Electrical and Information Engineering,
The University of Sydney, NSW 2006, Australia
Keywords:
Fiber Bragg Gratings, Gap Solitons, Cubic-quintic Nonlinearity, Dispersive Reflectivity.
Abstract:
The interaction of quiescent gap solitons in coupled fiber Bragg gratings with dispersive reflectivity and cubic-
quintic nonlinearity in both cores is investigated. It has been found that with low to moderate dispersive
reflectivity the interactions have similar characteristics to the nonlinear Schrodinger solitons i.e. in-phase
solitons always attract each other and out-of-phase solitons repel. It is found that the interaction of in-phase
solitons may result in a number of outcomes such as formation of a quiescent soliton, generation of two
separating solitons and formation of a quiescent and two moving solitons. For strong dispersive reflectivity,
the interaction outcomes depend on the initial separation.
1 INTRODUCTION
Fiber Bragg gratings (FBG) have found many applica-
tions in optical signal processing, dispersion compe-
nation and sensing (Kashyap, 2010; Loh et al., 1996;
Cao et al., 2012; Cao et al., 2014). The periodic
variation in FBGs leads to linear resonant coupling
of counter-propagating waves which induces high ef-
fective dispersion. This dispersion can be six or-
der of magnitude greater than the chromatic disper-
sion of silica fiber (de Sterke and J.E.Sipe, 1994).
In the nonlinear regime, the balance between the
Kerr nonlinearity and the effective dispersion of the
FBG gives rise to the formation of gap solitons (GSs)
(Aceves and Wabnitz, 1989) (Christodoulides and
Joseph, 1989). The first observation of a GS was re-
ported in a 6-cm long FBG (Eggleton et al., 1996).
One of the properties of the GSs is that they can travel
at any velocity from zero to the speed of the light in
the medium. As a result, theoretical and experimen-
tal studies have focused on understanding of the fun-
damental properties of GSs and how they can be ex-
ploited to build novel optical devices (Eggleton et al.,
1996) (Barashenkov et al., 1998).
The formation of GSs have also been considered
in other nonlinear systems such as coupled FBGs
(Mak et al., 1998), semilinear coupled system (Atai
and A. Malomed, 2001), cubic-quintic nonlinear sys-
tem (Atai and Malomed, 2001; Dasanayaka and Atai,
2010), photonic crystal fibers(Skryabin, 2004; Neill
and Atai, 2007) and FBGs with dispersive reflectivity
(Atai and Malomed, 2005; Baratali and Atai, 2012).
In this paper, we consider the interactions of qui-
escent GSs in a dual-core system where each core has
a FBG with dispersive reflectivity and cubic-quintic
nonlinearity.
2 THE MODEL
Light propagation in a linearly coupled Bragg grat-
ings with dispersive reflectivity and cubic-quintic
nonlinearity can be described as the following equa-
tions (Akter et al., 2019):
iu
1t
+ iu
1x
+
1
2
|u
1
|
2
+ |v
1
|
2
u
1
−
η
1
4
|u
1
|
4
+
3
2
|u
1
|
2
|v
1
|
2
+
3
4
|v
1
|
4
u
1
+
v
1
+ λu
2
+ mv
1xx
= 0,
iv
1t
−iv
1x
+
1
2
|v
1
|
2
+ |u
1
|
2
v
1
−
η
1
4
|v
1
|
4
+
3
2
|v
1
|
2
|u
1
|
2
+
3
4
|u
1
|
4
v
1
+
u
1
+ λv
2
+ mu
1xx
= 0,
(...)
(1)
22
Akter, A. and Atai, J.
Interactions of Gap Solitons in Coupled Bragg Gratings with Cubic-quintic Nonlinearity and Dispersive Reflectivity.
DOI: 10.5220/0008909600220025
In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 22-25
ISBN: 978-989-758-401-5; ISSN: 2184-4364
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(...)
iu
2t
+ iu
2x
+
1
2
|u
2
|
2
+ |v
2
|
2
u
2
−
η
1
4
|u
2
|
4
+
3
2
|u
2
|
2
|v
2
|
2
+
3
4
|v
2
|
4
u
2
+
v
2
+ λu
1
+ mv
2xx
= 0,
iv
2t
−iv
2x
+
1
2
|v
2
|
2
+ |u
2
|
2
v
2
−
η
1
4
|v
2
|
4
+
3
2
|v
2
|
2
|u
2
|
2
+
3
4
|u
2
|
4
v
2
+
u
2
+ λv
1
+ mu
2xx
= 0.
(1)
Here, u
1,2
(x,t) and v
1,2
(x,t) are the amplitudes of the
forward and backward-propagating waves in core 1
and 2 respectively. η is a positive real parameter
that represents the strength of the quintic nonlinear-
ity, λ is the linear coupling between two cores, and the
strength of the dispersive reflectivity is represented by
m > 0. To determine the spectral gap, we substitute
u
1,2
,v
1,2
∼ exp(ikx−iwt) into the linearized Eqs. (1).
This leads to the following dispersion relation:
ω
2
=
1−mk
2
2
+ λ
2
+ k
2
±2λ
q
(1−mk
2
)
2
+ k
2
(2)
From Eq. 2 it is found that the bandgap is given by
ω
2
< (1−|λ|)
2
for m≤ 0.5 and ω
2
<
√
4m−1
2m
−|λ|
2
for m > 0.5.
3 SOLITON SOLUTIONS
Soliton solutions can be obtained by substituting
u(x,t) = U(x)e
−iωt
and v(x,t) = V(x)e
−iωt
into Eqs.
(1) which will result in the following system of cou-
pled equations (Akter et al., 2019):
−mU
1xx
= ωV
1
−iV
1x
+
1
2
|V
1
|
2
+ |U
1
|
2
V
1
−
η
1
4
|V
1
|
4
+
3
2
|V
1
|
2
|U
1
|
2
+
3
4
|U
1
|
4
V
1
+
U
1
+ λV
2
,
−mV
1xx
= ωU
1
+ iU
1x
+
1
2
|U
1
|
2
+ |V
1
|
2
U
1
−
η
1
4
|U
1
|
4
+
3
2
|U
1
|
2
|V
1
|
2
+
3
4
|V
1
|
4
U
1
+
V
1
+ λU
2
,
(...)
(3)
(...)
−mU
2xx
= ωV
2
−iV
2x
+
1
2
|V
2
|
2
+ |U
2
|
2
V
2
−
η
1
4
|V
2
|
4
+
3
2
|V
2
|
2
|U
2
|
2
+
3
4
|U
2
|
4
V
2
+
U
2
+ λV
1
,
−mV
2xx
= ωU
2
+ iU
2x
+
1
2
|U
2
|
2
+ |V
2
|
2
U
2
−
η
1
4
|U
2
|
4
+
3
2
|U
2
|
2
|V
2
|
2
+
3
4
|V
2
|
4
U
2
+
V
2
+ λU
1
.
(3)
Equations 3 do not have any analytical solution.
Hence, we have to solve Eqs. 3 by a relaxation
algorithm. There are two disjoint families of gap
solitons known as Type 1 and Type 2 solitons,
and each of the soliton families supports symmet-
ric (u
1
= u
2
, v
1
= v
2
) and asymmetric type solitons
(u
1
6= u
2
, v
1
6= v
2
). The difference between the soli-
ton families is in their amplitude, phase, and parities.
The two families are separated by a border that needs
to be determined numerically (Akter et al., 2019).
4 INTERACTION OF QUIESCENT
SOLITONS
To analyze the interaction of stable quiescent solitons
we have numerically solved Eqs. (1) subject to the
following initial conditions:
u
1,2
(x, 0) = u
1,2
x+
∆x
2
, 0
+
u
1,2
x−
∆x
2
, 0
exp(i∆φ)
v
1,2
(x, 0) = v
1,2
x+
∆x
2
, 0
+
v
1,2
x−
∆x
2
, 0
exp(i∆φ)
(4)
where ∆x and ∆φ denote the initial separation and
phase difference of the stable zero velocity gap soli-
tons respectively.
The interaction of two zero velocity gap soli-
tons is depends on the strength of the dispersive re-
flectivity. For lower values of dispersive reflectivity
(0 < m ≤ 0.3), the interaction outcomes behave sim-
ilar to Nonlinear Schr¨odinger (NLS) solitons, i.e. the
in-phase zero velocity solitons will initially attract
each other and out-of-phase solitons will always re-
pel. Interaction of in-phase asymmetric Type 1 may
Interactions of Gap Solitons in Coupled Bragg Gratings with Cubic-quintic Nonlinearity and Dispersive Reflectivity
23
-40 0 40
x
0
3000
t
(a)
-40 0 40
x
0
500
t
(b)
-40 0 40
x
0
1000
t
(c)
-40 0 40
x
0
1500
t
(d)
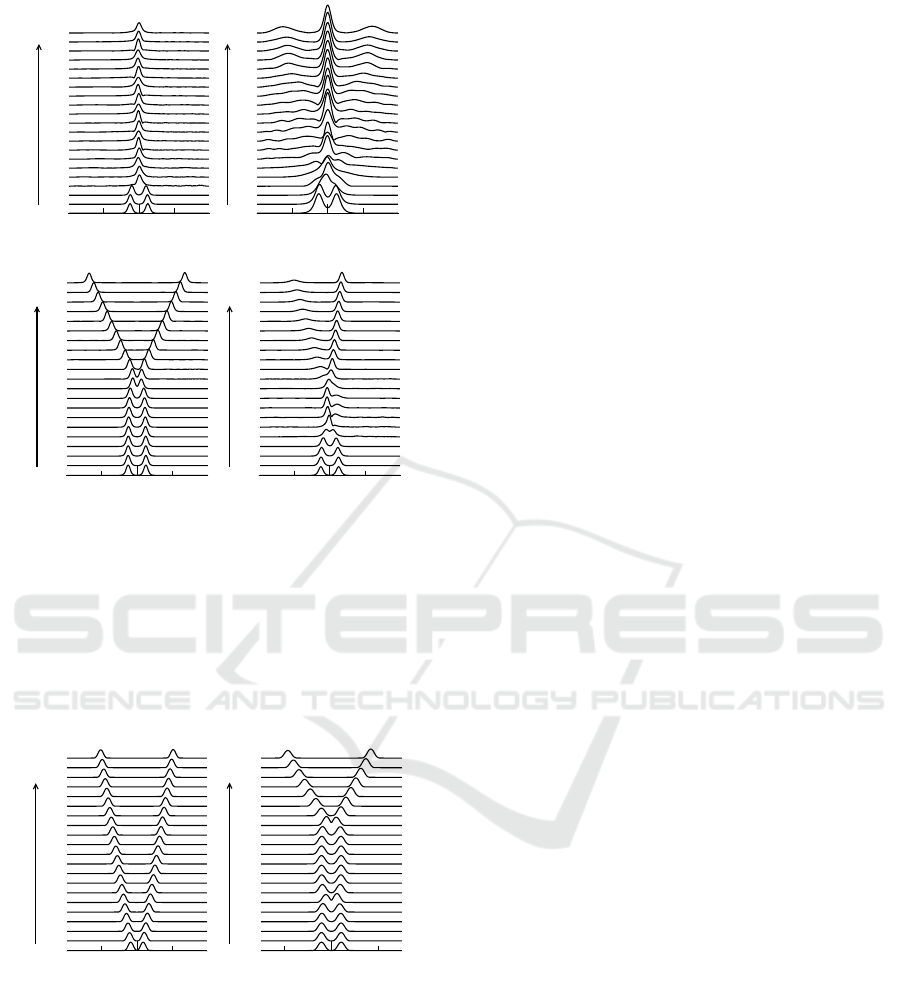
Figure 1: Interaction outcomes of Type 1 asymmetric qui-
escent solitons for m = 0.2, λ = 0.1, ∆x = 10.0. (a) Merger
into a quiescent soliton for ω = 0.3, η = 0.2, ∆φ = 0.0, (b)
generation of three solitons (one quiescent and two moving
solitons) for ω = 0.81, η = 0.77, ∆φ = 0.0, (c) symmetric
separation for ω = 0.2, η = 0.14, ∆φ = 0.0, and (d) asym-
metric separation after multiple collision for ω = 0.45, η =
0.21, ∆φ = 0.0. In this and other figures, only u
1
component
is shown.
-40 0 40
x
0
1000
t
(a)
-30 0 30
x
0
1000
t
(b)
Figure 2: Examples of interaction of Type 1 asymmetric
quiescent solitons for m = 0.4, λ = 0.1, ω = 0.40, η = 0.2;
(a) Repulsion of both solitons for ∆x = 7.0, ∆φ = 0; (b)
multiple collisions followed by formation of two separating
solitons for ∆φ = π and ∆x = 8.35.
lead to a variety of outcomes, namely formation of
a quiescent soliton Fig. 1(a), generation of three soli-
tons (one quiescent and two moving ones) (Fig. 1(b)),
generation of two symmetrically separating solitons
(Fig. 1(c)), two separating solitons with different ve-
locities (Fig. 1(d)) and repulsion of solitons.
For larger values of dispersive reflectivity
(i.e., 0.3 < m ≤ 0.5), the outcomes of the interac-
tions become dependent on the initial separation. As
is shown in Fig. 2(a), when ∆x = 7.0 the in-phase
asymmetric Type 1 solitons repel each other. How-
ever, when the phase difference between the solitons
is π, and ∆x = 7.75, the solitons undergo multiple
collisions and eventually two separating solitons are
generated. Similar behavior has also been observed
in the case of Type 2 solitons.
5 CONCLUSIONS
Interaction properties of stable quiescent Gap solitons
in a coupled Fiber Bragg gratings have been investi-
gated, where both cores have cubic-quintic nonlinear-
ity with dispersive reflectivity. A noteworthy result
is that for low to moderate dispersive reflectivity the
interactions have similar charactersitics of NLS soli-
tons, namely the in-phase solitons attract and π-out-
of-phase solitons repel. On the other hand, for strong
dispersive reflectivity, the outcomes are affected by
the initial separation of the solitons.
REFERENCES
Aceves, A. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodiedia.
Phys. Lett. A, 141(1):37 – 42.
Akter, A., Islam, M., and Atai, J. (2019). Effect of disper-
sive reflectivity on the stability of gap solitons in dual-
core bragg gratings with cubic-quintic nonlinearity. In
Proceedings of the 7th International Conference on
Photonics, Optics and Laser Technology - Volume 1:
PHOTOPTICS, pages 19–23. INSTICC, SciTePress.
Atai, J. and A. Malomed, B. (2001). Solitary waves in sys-
tems with separated bragg grating and nonlinearity.
Phys. Rev. E, 64:066617.
Atai, J. and Malomed, B. A. (2001). Families of bragg-
grating solitons in a cubic-quintic medium. Phys. Lett.
A, 284(6):247 – 252.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Phys. Lett. A,
342(5):404 – 412.
Barashenkov, I. V., Pelinovsky, D. E., and Zemlyanaya,
E. V. (1998). Vibrations and oscillatory instabilities
of gap solitons. Phys. Rev. Lett., 80:5117–5120.
Baratali, B. H. and Atai, J. (2012). Gap solitons in dual-core
bragg gratings with dispersive reflectivity. Journal of
Optics, 14(6):065202.
Cao, H., Atai, J., Shu, X., and Chen, G. (2012). Di-
rect design of high channel-count fiber Bragg grat-
ing filters with low index modulation. Opt. Express,
20(11):12095–12110.
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
24

Cao, H., Shu, X., Atai, J., Gbadebo, A., Xiong, B., Fan, T.,
Tang, H., Yang, W., and Yu, Y. (2014). Optimally-
designed single fiber Bragg grating filter scheme for
rz-ook/dpsk/dqpsk to nrz-ook/dpsk/dqpsk format con-
version. Opt. Express, 22(25):30442–30460.
Christodoulides, D. N. and Joseph, R. I. (1989). Slow bragg
solitons in nonlinear periodic structures. Phys. Rev.
Lett., 62:1746–1749.
Dasanayaka, S. and Atai, J. (2010). Stability of bragg grat-
ing solitons in a cubic-quintic nonlinear medium with
dispersive reflectivity. Phys. Lett. A, 375(2):225 – 229.
de Sterke, C. M. and J.E.Sipe (1994). Gap solitons.
Progress in Optics, XXXIII:203.
Eggleton, B. J., Slusher, R. E., de Sterke, C. M., Krug, P. A.,
and Sipe, J. E. (1996). Bragg grating solitons. Phys.
Rev. Lett., 76:1627–1630.
Kashyap, R. (2010). Fiber Bragg gratings. Academic Press,
Boston, second edition.
Loh, W., Laming, R., Robinson, N., Cavaciuti, A., Va-
ninetti, F., Anderson, C., Zervas, M., and Cole, M.
(1996). Dispersion compensation over distances in
excess of 500 km for 10-Gb/s systems using chirped
fiber gratings. IEEE Photon. Technol. Lett., 8(7):944–
946.
Mak, W. C. K., Chu, P. L., and Malomed, B. A. (1998).
Solitary waves in coupled nonlinear waveguides with
bragg gratings. J. Opt. Soc. Am. B, 15(6):1685–1692.
Neill, D. R. and Atai, J. (2007). Gap solitons in a hollow
optical fiber in the normal dispersion regime. Phys.
Lett. A, 367(1):73 – 82.
Skryabin, D. V. (2004). Coupled core-surface solitons in
photonic crystal fibers. Opt. Express, 12(20):4841–
4846.
Interactions of Gap Solitons in Coupled Bragg Gratings with Cubic-quintic Nonlinearity and Dispersive Reflectivity
25
