
Aerial Radar Target Classification using Artificial Neural Networks
Guy Ardon
1,2
, Or Simko
1,2
and Akiva Novoselsky
2
1
Department of Electrical & Computer Engineering, Ben-Gurion University of the Negev, Beersheba, Israel
2
ELTA Systems Ltd. Group & Subsidiary of Israel Aerospace Industries Ltd., Ashdod, 771020, Israel
Keywords: Aerial Radar Target Classification, Radar Cross Section (RCS), Time-Series Classification, Fully-Connected
Neural Networks, Empirical Mode Decomposition (EMD).
Abstract: In this paper, we propose a new algorithm for classification of aerial radar targets by using Radar Cross
Section (RCS) time-series corresponding to target detections of a given track. RCS values are obtained
directly from SNR values, according to the radar equation. The classification is based on analysing the
behaviour of the RCS time-series, which is the unique “fingerprint” of an aerial radar target. The classification
process proposed in this paper is based on training a fully-connected neural network on features extracted
from the RCS time-series and its corresponding Intrinsic Mode Functions (IMFs). The training is based on a
database containing RCS signatures of various aerial targets. The algorithm has been tested on a large and
diverse set of simulative flight trajectories, and its performance has been compared with that of several
different methods. We have found that the proposed neural network-based classifier performed better on our
database.
1 INTRODUCTION
Conventional uses of radar systems include detection
of targets through transmission of radio waves and re-
scattering of echoes from targets (Skolnik, 1962).
Radar systems, however, do not provide information
regarding the specific type of target which is detected.
In the past few decades, there has been an effort
to approach the problem of radar target recognition
(Herman & Moulin, 2002) – (Notkin et al., 2019).
Most of the works presented so far utilized Radar
Cross Section (RCS) of aerial targets for
classification. RCS values are not obtained directly
by the radar. In fact, the radar yields signal-to-noise
ratio (SNR) values, which can be transformed into
RCS values by using the radar equation. The RCS
signature of aerial targets depends on various factors,
such as the target’s unique geometry, size,
orientation, and reflectiveness, as well as on the
transmission frequency. RCS values can therefore
provide useful information regarding target
characteristics.
RCS measurements of aerial targets are strongly
dependent on the aspect angles (azimuth and
elevation), relative to the radar. These angles
determine where the radar beam hits the target. Since
different points on the target reflect the radar beam
differently, RCS values are characterized by large
variances, and even a slight change in one of the
aspect angles can cause large fluctuations.
Nevertheless, development of an aerial target
recognition capability is of great interest. There have
been several proposals to classify targets based on
various methods (Herman & Moulin, 2002),
(Molchanov et al., 2012), (Tian et al., 2015), (Notkin
et al., 2019).
The RCS time-series corresponding to an aerial
target track contains abundant information, which can
be used to characterise target types. However, RCS
time-series is non-stationary, which makes it difficult
to analyse. This calls for a comprehensive signal
processing analysis.
Empirical Mode Decomposition (EMD) is an
effective nonlinear signal processing technique for
adaptively representing non-stationary signals as a
sum of zero-mean components, known as Intrinsic
Mode Functions (IMF) (Huang et al., 1998). Since its
introduction, it has been used in various applications
(Colominas et al., 2014).
In this paper, we present a new method for
classifying aerial radar targets based on fully-
connected neural networks. Our algorithm utilizes a
database of RCS signatures of various types of aerial
targets, at a given resolution of aspect angles. Given
an observed flight track, and the corresponding RCS
136
Ardon, G., Simko, O. and Novoselsky, A.
Aerial Radar Target Classification using Artificial Neural Networks.
DOI: 10.5220/0008911701360141
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 136-141
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
time-series, we extract RCS signals corresponding to
the track, for all available targets in the database. RCS
signals are then decomposed into IMFs using EMD.
Features are then extracted from this set of RCS and
corresponding IMF signals. Finally, a fully-
connected neural network is trained with these
features to identify the observed target.
We compare the neural network-based classifier
with the K-Nearest Neighbour (KNN) classifier and
three classifiers that are based on time-series
similarity measures. In these types of classifiers, a
target can be identified by measuring the similarity
between the measured RCS signal, and RCS signals
of available targets in the database, corresponding to
the same flight track.
The paper is organized as follows: Section 2
describes the data preparation, and feature extraction
stages. Section 3 describes the proposed neural
network. Section 4 presents the results. Conclusions
are provided in section 5.
2 THE METHOD FOR
PREPARING RCS DATA FOR
THE CLASSIFIER
In this section, we present our method for preparing
the training and test data for the neural-network based
classifier.
In this work, we simulated a database that
contains RCS signatures for 8 different targets at two
aspect angles relative to the radar: azimuth ∈
0,360
∘
, and elevation ∈90
∘
,90
∘
at a given
resolution. The targets are indicated by the letters A,
B, C
1
, C
2
, C
3
, C
4
, D and E. Targets C
1-4
are four
different configurations of the same aircraft model,
which lead to mild changes in RCS signature.
In addition to the simulated database, we
simulated a radar tracker, and target trajectories. The
tracker provided us with the position and velocity of
the target, as well as the aspect angles (azimuth and
elevation), relative to the radar. Knowing these aspect
angles enabled us to extract the corresponding RCS
values by interpolating the database.
In each simulation of a target trajectory, we
obtained a time-series of RCS values. The RCS time-
series corresponding to the observed flight track is
given by
∈
, where is the number of
consecutive RCS measurements for a given
trajectory
.
Since aspect angles obtained by the radar are not
accurate, we generated RCS sequences for each pair
of possible aspect angles. This is done for all targets
in the database. The set of possible RCS time-
sequences for each of the targets form a “dynamic
bank”. The dynamic bank is denoted by
∈
.
is the number of RCS measurements for a given
trajectory. Since aspect angle estimation has inherent
error, we generate possible RCS sequences for
each target corresponding to a resolution of
possible aspect angles. is the number of targets in
the database.
The RCS time-series of a target-track is generally
composed of low-frequency and high-frequency
components. The assumption is that the low
frequencies correspond to the observation angle and
measurement errors, while the higher frequencies are
related to the target’s geometry and aspect angles
relative to the radar (Tian et al., 2015). Therefore, the
rapidly varying components in the RCS time-series
can characterize the targets well.
The RCS time-series is decomposed into
frequency components by using a signal processing
technique known as Empirical Mode Decomposition
(EMD). EMD decomposes a non-stationary signal
into stationary Intrinsic Mode Functions (IMFs)
(Huang et al., 1998; Rilling et al., 2003). The IMFs
are ordered according to their frequency components
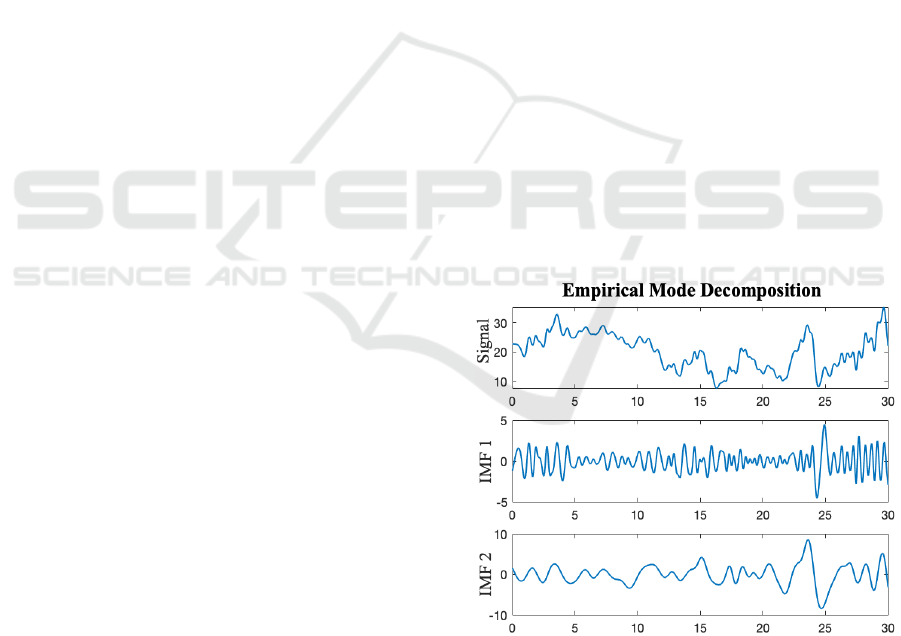
from high to low, as shown in figure 1. By using the
temporal RCS data in the dynamic bank, and the
RCS time-series of the observed track , we
implement EMD to decompose the RCS data into
IMFs.
Figure 1: EMD of a fluctuating signal into two intrinsic
mode functions.
At this stage, we extract ten features from the RCS
time-sequences in
, and ten features from their
corresponding IMFs. These features are later used as
training data for the neural network. The features are
chosen to characterize the statistical and spectral
Aerial Radar Target Classification using Artificial Neural Networks
137

nature of the time sequences well, while at the same
time enabling separation of targets. Classifying
targets based on noisy radar data using these features
can suppress the effect the noise, in comparison with
classification based on the raw RCS data.
The first and second features, minimum and
maximum values, are used as a measure of the range
of values that the time-series can take. The next
feature is the number of zero-crossings, which can
represent the oscillatory nature of the signal. The next
four features; the mean, variance, skewness and
kurtosis of the time-series are the 1
st
-4
th
standardized
moments, where the sample mean is the average of
the time-series values, variance indicates the spread
of data from the mean, skewness is a measure of the
asymmetry of the data around the mean, and kurtosis
is a measure of how outlier-prone the distribution of
values is. The next feature is the energy of the signal,
which is the squared
norm. The last two features
are Hjorth mobility and complexity (Hjorth, 1970).
Mobility represents the mean frequency, or the
portion of standard deviation of the power spectrum.
Hjorth complexity represents the change in frequency
of a signal.
The RCS and IMF features for each time-series in
the dynamic bank
are concatenated into the tensor:
∈
, where
is number of elements in
each feature vector, and
∙
is the number of
training examples. is the number of possible aspect
angles, and is the number of targets in the database.
Each component in the feature vector is standardized
using the z-score normalization. The feature-tensor
has a corresponding label tensor:
∈
. We denote
,
as the , element in
the matrix, where 0,1,…,1 , and
0,1, … , 1.
,
1 if training example
belongs to class , and 0 otherwise. The same feature
extraction process is applied to the signal ,
corresponding to the observed target, with
∈
the corresponding feature vector, which will be
used to test the network.
3 THE PROPOSED NEURAL
NETWORK CLASSIFIER
In this section, we will describe the proposed neural
network-based classifier, and how it uses the features
to classify the aerial targets. Artificial neural
networks are mathematical models for solving
complex problems, originally inspired by the way in
which the brain processes information (Theodoridis
& Koutroumbas, 2003). The network is composed of
several layers of neurons, where the first layer is the
input layer, and the last layer is the network decision,
or solution to the problem. Neurons are nodes in the
network that take in a weighted sum of values and
produce a single output value, which is then
processed by more neurons in the next layer.
In order to identify the observed target as one of
the targets in the database, we use a 2-layer fully-
connected neural network. The network has one
hidden layer, and a softmax output layer that
normalizes the outputs into probabilities for each
target. The neurons in the hidden layer are defined by
a hyperbolic tangent activation function, which take
in a weighted sum of the values from the input layer,
and map the results to [-1,1]. We have found that the
network performs best when using one hidden layer,
with 20 neurons. Using fewer neurons led to poor
results, by being a too general solution, and using
more neurons, or more hidden layers, caused
overfitting the data.
In figure 2, the neural network architecture is
presented. The input layer has
neurons,
corresponding to the number of features in each
feature-vector. The hidden layer’s neurons are
denoted by:
,
,…,
. The output layer has
neurons, denoted by
,
,…,
, which are
normalized in the softmax layer to obtain the final
outputs.
Figure 2: The proposed neural network architecture.
The neural network is trained on the feature
vectors in
and the corresponding labels in
, as denoted in section 2. Training a neural
network consists of two stages, feedforward, and
backpropagation. Feedforward is the stage at which
outputs at each layer are fed towards the final output
layer. During backpropagation, we minimize a cross-
entropy loss function defining the error between the
desired values in
, and the network outputs at
the final layer. During the training process, the
weights are adjusted accordingly to give a better
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
138
solution with each iteration. The weights and bias
values in each layer are optimized through scaled-
conjugate backpropagation (Møller, 1993).
The data was randomly split into training and
validation sets with a ratio of 80% - 20%
correspondingly. The training set was used to
compute the gradients, and update weights through
backpropagation. The validation set was used to
monitor the learning process. Both the training and
validation set errors are monitored during the training
process. At first, validation error decreases with the
training error, but after being presented with enough
data, the network starts to overfit to the training set,
the validation error begins to increase. We stop
updating the weights when the validation error is at a
minimum. In this way we make sure that the network
can generalize when presented with new examples.
Once the network is fully trained, we test the
network with
, the feature vector corresponding
to the RCS time-series of the observed target. The
network calculates probabilities for each target at the
output layer. Classification is defined as correct when
maximal probability corresponds to the correct target.
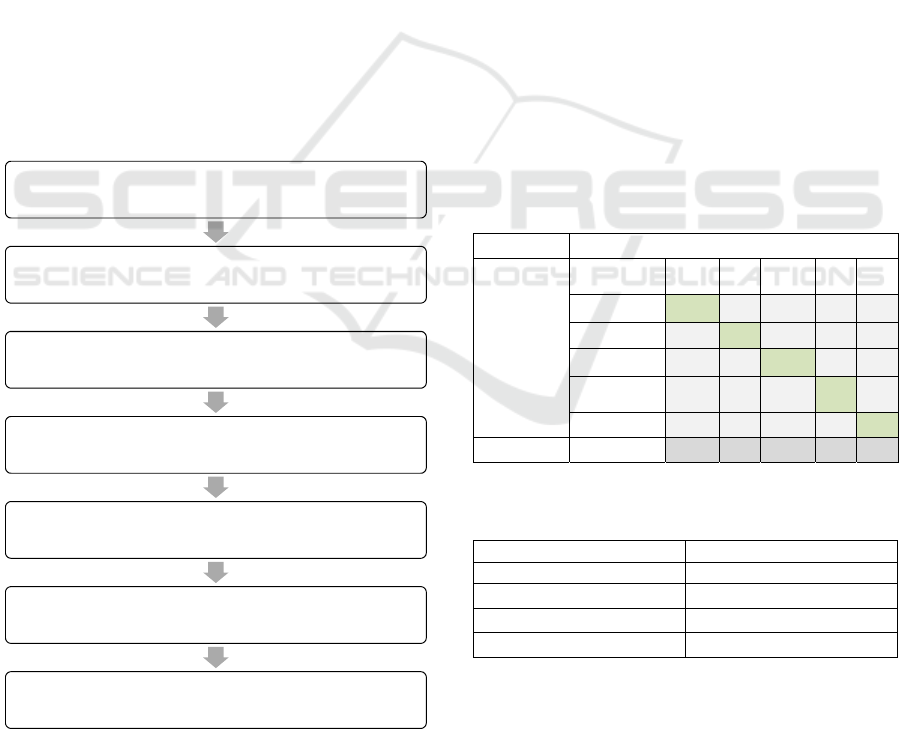
A pipeline figure for our algorithm is presented in
figure 3.
Figure 3: Dataflow and algorithm pipeline.
4 SIMULATION AND RESULTS
In this work, we simulated 640 target trajectories, 80
trajectories for each of the eight target types. The
classification accuracy of the neural network was
examined under various levels of noise. Additive
white Gaussian noise of up to 0.5
∘
was added to the
aspect angles of the target relative to the radar.
We defined a classification to be either be correct,
incorrect, or unknown. In order to reduce the false-
alarm rate, targets are defined to be ‘unknown’ when
there isn’t a good match in the database, or due to a
lack of data for a proper classification procedure. In
other words, it is better to define a target as
‘unknown’ than to classify it as an incorrect target.
For example, for a short flight track with few RCS
measurements, the features described in section 2
provide little value, and therefore we classify the
target as unknown.
Table 1 presents the confusion matrix for the 640
trajectories under 0.5
∘
of aspect angle noise. For this
amount of noise, we achieved an accuracy of 80.1%.
The accuracies of the network under various levels of
noise is presented in Table 2.
Table 1: Confusion matrix for the neural network-based
classifier. Results are shown for trajectories with additive
white Gaussian noise of 0.5
0
.
Actual Target
Predicted
Target
A B C D E
A
56
0 1 0 2
B
1
58
15 2 0
C
16 18
270
11 6
D
2 0 8
63
0
E
0 0 1 0
66
Unknown 5 4 25 4 6
Table 2: Final neural network classification results for the
simulated trajectories.
Aspect Angle Noise Accuracy
No Noise 93.3%
0.1
0
87.5%
0.3
0
82.7%
0.5
0
80.1%
We compared the results of the neural network-
based classifier with 5 other classifiers. The first
classifier is the K-Nearest Neighbours (KNN)
classifier (Covert & Hart, 1967). We implemented
KNN with the Mahalanobis distance metric, which
weights the distance by the inverse covariance of each
Radar Data
(Target Position, Target Velocity, SNR)
RCS Estimation
Generation of a dyanmic bank of possible RCS time-
sequences for targets in the database
Empirical Mode Decomposition of RCS time-series into
Intrinsic Mode Functions
Feature Extraction
Neural Network Training and Classification
Predicted Target Type
Aerial Radar Target Classification using Artificial Neural Networks
139

feature. We choose the target corresponding to the
minimum Mahalanobis distance as the correct target,
i.e. the first nearest neighbour.
The next three methods that we implemented take
a different approach, and rather than using features,
utilize time-series similarity measures between the
raw RCS signals in the dynamic bank and the RCS
signal of the observed target. The chosen target is the
target in the dynamic bank, with the most “similar”
RCS time-series. The first method used for time-
series similarity is the matched filter (Turin, 1960),
which correlates between signals by maximizing
SNR. The other two methods are Dynamic Time
Warping (Sakoe & Chiba, 1978), and Minimum
Jump-Cost (Serrà & Arcos, 2012), which work by
optimally aligning and stretching the time-series for
the best temporal match.
In figure 4, we compare the performance of the
proposed neural-network classifier with the other
methods. The performance of our proposed neural
network is better than the other methods.
Furthermore, the machine learning methods (neural
network and KNN) performed better under large
noise than the time-series similarity methods.
Figure 4: Classification accuracies for the compared
methods.
5 CONCLUSIONS
In this paper, we proposed a neural-network based
classifier for aerial radar targets. The classification is
based on features extracted from the RCS time-series
of an observed flight track and from its corresponding
IMFs. Comparison of the results have shown that our
classifier is better than other methods for the same
data. We conclude that the use of machine learning
can be effective for the task of aerial radar target
classification.
ACKNOWLEDGEMENTS
We would like to thank Ariel Rubanenko, Merav
Shomroni, Gregory Lukovsky, Nimrod Teneh, David
Feldman, and Or Livne for their useful discussion.
REFERENCES
Colominas, M.A., Schlotthauer, G. & Torres, M.E. (2014).
‘Improved complete ensemble EMD: A suitable tool for
biomedical signal processing’. Biomedical Signal
Processing and Control, 14, pp. 19-29.
Cover, T. & Hart, P. (1967). ‘Nearest Neighbor Pattern
Classification’. IEEE Transactions on Information
Theory, 13(1), pp.21-27.
Herman, S. & Moulin, P. (2002). ‘A particle filtering
approach to FM-band passive radar tracking and
automatic target recognition’, In: Proceedings, IEEE
Aerospace Conference, vol. 4, pp. 1789-1708.
Hjorth, B. (1970). ‘EEG analysis based on time domain
properties’. Electroencephalography and Clinical
Neurophysiology, 29(3), pp. 306-310.
Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H.,
Zheng, Q., Yen, N.C., Tung, C.C. & Liu, H.H. (1998).
‘The empirical mode decomposition and the Hilbert
spectrum for nonlinear and non-stationary time series
analysis’. In: Proceedings of the Royal Society of
London: Series A, 454(1971), pp. 903-995.
Molchanov, P, Totsky, A, Astola, J., Egiazarian, K.,
Leshchenko, S. & Rosa-Zurera, M. (2012). ‘Aerial
target classification by micro-Doppler signatures and
bicoherence-based features’. In: Proceedings of the 9th
European Radar Conference, pp. 214-217.
Møller, M.F. (1993). ‘A scaled conjugate gradient
algorithm for fast supervised learning’. In: Neural
Networks, 6(4), pp. 525-533.
Notkin, E. & Cohen, T. & Novoselsky, A. (2019).
‘Classification of Ground Moving Radar Targets with
RBF Neural Networks’. 8
th
International Conference
on Pattern Recognition Applications and Methods,
Prague.
Sakoe, H., & Chiba, S. (1978). ‘Dynamic programming
algorithm optimization for spoken word recognition.’
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
140

IEEE Transactions on Acoustics, Speech, and
Language Processing 26(1), pp. 43–50.
Serrà J. & Arcos J.L. (2012). ‘A Competitive Measure to
Assess the Similarity between Two Time Series’. In:
Agudo B.D., Watson I. (ed.), International Conference
on Case-Based Reasoning. Lecture Notes in Computer
Science, vol. 7466. Springer, Berlin, Heidelberg, pp.
414-427.
Rilling, G., Flandrin, P. & Goncalves, P. (2003). ‘On
empirical mode decomposition and its algorithms’.
In: IEEE-EURASIP Workshop on Nonlinear Signal and
Image Processing, 3(3), pp. 8-11.
Skolnik, M. I. (1962). Introduction to Radar Systems. New
York: McGraw-Hill.
Theodoridis, S. & Koutroumbas, K. (2003). Pattern
Recognition. 2
nd
Edition. San Diego: Elsevier.
Tian, X., Yiying, S. & Chengyu, H. (2015). ‘Target
Recognition Algorithm Based on RCS Time
Sequence’. International Journal of Signal Processing,
Image Processing and Pattern Recognition, 8(11), pp.
283-298).
Turin, G. (1960). ‘An Introduction to Matched Filters’. IRE
Transactions on Information Theory. 6(3), pp.311-329.
Aerial Radar Target Classification using Artificial Neural Networks
141
