Balancing Selfishness and Efficiency in Mobile Ad-hoc Networks:
An Agent-based Simulation
Marcin Korecki
1 a
, Malvin Gattinger
2 b
and Rineke Verbrugge
2 c
1
University of Edinburgh, Scotland, U.K.
2
Bernoulli Institute, University of Groningen, The Netherlands
Keywords:
Mesh-networks, Ad-hoc Networks, Agent-based Modelling, Wireless Networking.
Abstract:
We study wireless ad-hoc networks from an agent-based perspective. In our model agents with different
strategies such as being selfish, tit-for-tat or battery-based compete and cooperate. If only different levels of
selfishness are allowed then being selfish is clearly the dominant strategy. However, introduction of more
advanced strategies allows to some extent to combat selfishness. In particular we present a battery-based
approach and a hybrid of battery-based and tit-for-tat approaches. The findings give hope that the introduction
of widely available ad-hoc networks might at some point be possible. Even when users are given full control of
their devices, effective strategies allow for the networks overall to be effective and feasible.
1 INTRODUCTION
When browsing websites or accessing other Interenet
services, it is easy to forget about the vast infrastruc-
ture that allows us to do all this. However, the Inter-
net is in fact a highly centralised network based on
physical connections that have to be managed and con-
trolled. In this article we explore how a decentralised
physical architecture affects the efficiency and usage
of networks.
1.1 The Architecture of the Internet
Different technological solutions are employed in the
inner workings of the Internet, including different ca-
ble connections as well as wireless technologies. With
the increasing use of mobile devices, wireless tech-
nologies play an increasingly large role. Most wire-
less local area networks (WLAN) are based on the
IEEE 802.11 standards and operate in the infrastruc-
ture mode. This mode uses a central base station (for
example a router) through which connected devices
(nodes) communicate. The base station is most often
connected via a wire or fibre connection to a wider
network.
A single device first communicates with its base
a
https://orcid.org/0000-0002-2784-5172
b
https://orcid.org/0000-0002-2498-5073
c
https://orcid.org/0000-0003-3829-0106
station, which then relays the message to another de-
vice or the wider network. This system allows millions
of users to communicate with each other quickly and
efficiently. However, it is highly centralised and prone
to single point of failure mishaps. Any damage or
successful attack on the base station cuts off access for
all devices that rely on it. Another issue is the range
and capacity limitations of base stations.
1.2 Mesh Networks
A solution to some of the mentioned problems may
be mesh networks in place of the infrastructure mode.
A wireless mesh network (also referred to as ad-hoc
network) does not rely on central base stations. In-
stead, it is decentralised and the routing is done by all
individual connected devices (Hekmat, 2016). A sim-
plified model of an ad-hoc network is as follows: All
participating devices keep track of other participating
devices (often referred to as nodes); if data packets are
to be sent, a path is determined that can connect the
two communicating devices directly or via other nodes
on the network. Thus the message ‘jumps’ from one
device to the next, finally reaching its destination. Any
number of devices on such a network can at the same
time be connected to a conventional WLAN and thus
potentially relay the data over even larger distances. In
such a case, the ad-hoc network can still help to extend
the range of the base station.
Considering that as of 2019 there are three billion
Korecki, M., Gattinger, M. and Verbrugge, R.
Balancing Selfishness and Efficiency in Mobile Ad-hoc Networks: An Agent-based Simulation.
DOI: 10.5220/0008915101610168
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 161-168
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
161

smartphone users (Statista, 2019), it is easy to imagine
ad-hoc networks becoming feasible. The potential
of ad-hoc networks with the focus on smartphones
as primary nodes is of special interest. All modern
smartphones are equipped with bluetooth and WLAN
capabilities, both of which can be employed to create
an ad-hoc network. Taking into account the density of
population in the large urban areas of the world, one
could conclude that ad-hoc networks may be able to
provide access to the Internet (or any other network
for that matter) to vast numbers of people.
However, ad-hoc networks have their own prob-
lems. Firstly, for the network to be fully connected,
a certain minimum number of devices need to partic-
ipate. Moreover, those devices must remain within
one another’s range. If we consider that the devices
on the network can be in constant motion, it can be-
come quite difficult for the network to remain well
connected in its entirety. Secondly, ad-hoc networks
are prone to security issues which we will not dis-
cuss here. Lastly, the lack of a central node forces
all devices to take part in the routing process. There
exist many routing algorithms specifically designed
for the purpose of ad-hoc networks. Such algorithms
are usually designed with the focus on scalability, re-
liability, flexibility, throughput, load-balancing and
efficiency (Vijayakumar, Ganeshkumar, & Anandaraj,
2012).
Only recently another factor has started to be taken
into account when comparing different algorithms,
namely battery life (Sangwan & Pooja, 2016; Yoshi-
machi & Manabe, 2016). If smartphone devices are
the primary participants, then the success of a mesh
network is strongly related to how participation will
affect the battery life of individual devices. If the net-
work causes the battery life of devices to decrease
dramatically, the devices will turn off and thus the
network will start losing nodes until it eventually be-
comes disconnected. We thus focus on the willingness
of participants to volunteer part of their battery life of
their device to other participants.
1.3 Overview of the Study
We consider an ad-hoc network on an area of a square
in the centre of a densely populated city. All people
within the square are part of the network, but they can
choose whether to forward other people’s data packets
through their phones. The goal of each participant is to
send and receive data packets. We are then presented
with an interesting dilemma. Preventing other partici-
pants from using our device is beneficial for us, to save
battery life. But if all participants become selfish, the
network ceases to function and no one can send or re-
ceive data. If participants are in control of the amount
of ‘foreign’ data that goes through their phones, is
there a chance of achieving a stable network? We
believe that the success and more widespread adop-
tion of ad-hoc networks depends on the willingness of
the population to use it. Moreover, it is clear that for
the network to be appealing to new users, participants
should not be forced into forfeiting control over their
devices. Hence there is a need for investigation of
potential emergent behaviours in groups of users.
This leads to our first research question: “What
is the dominant strategy for participants in a mobile
ad-hoc network?”. It is our hypothesis that the domi-
nant strategy will be the selfish approach, since even
though selfish behaviour will ultimately lead to the
destruction of the network, affecting all participants
equally negatively, the selfish participant can profit
before the network ceases to function.
Our second research question is: “Is there a re-
ward/punishment system for participants that can im-
prove the longevity of a mobile ad-hoc network?”. We
hypothesise that there indeed exists a system that can
allow the voluntary ad-hoc network to be sustainable.
Our hypothesis is based on findings in many similar
game theory problems, such as the iterated prisoner’s
dilemma (or extensions such as public goods games).
In those games there usually exists a reward system
that can radically decrease the payoff of selfish be-
haviour and thereby limit or eradicate it (de Weerd &
Verbrugge, 2011; Juri
ˇ
si
´
c, Kermek, & Konecki, 2012).
We test our hypothesis with the help of a model of
the ad-hoc network. We model a densely populated
square in the city centre and we assume that the net-
work is functioning perfectly and without disruption;
it is only at the mercy of its participants.
The agents will have strategies ranging from fully
selfish to fully altruistic. The agents will use the net-
work at individually random intervals but the weight
of data packages introduced into the network by each
agent will be approximately the same. The effective-
ness of each agent will be measured in terms of data
packages it succeeded to send or receive. A genetic
algorithm will be used to determine the agents’ strate-
gies throughout subsequent days. We run the model
for 10 days, where a day is the time it takes for the
battery of half of the population to become empty.
2 METHODS
We now explain the design of the simulation appli-
cation used in this study and our design choices.
The simulation is written in C++ and all source
code is available at https://github.com/mbkorecki/
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
162

meshNetworkAgentModel. This repository also con-
tains all necessary scripts to reproduce our results.
We do not claim that our model provides a realis-
tic description of the network architecture. As long
as the relevant qualities of the network affecting the
behaviour of participants are well-defined, the model
should be sufficient for our purpose.
The success of an ad-hoc network correlates with
the number and spatial density of participants. The
larger the network, the longer distances we want our
data to travel, and the more participants we need. In
the same way, if participants may exhibit different lev-
els of participation, then the network requires a certain
minimum number of participants who are willing to
allow data of other nodes to be relayed through their
devices. This is the quality of the ad-hoc network that
we are mostly interested in and we will focus on im-
plementing it in our model. Subtleties such as signal
propagation and possibly radical heterogeneity of de-
vices participating in the network are of less concern
here. While it would certainly be interesting to inves-
tigate a highly realistic model of such a network, it
would not help us in answering our question and is
thus beyond the scope of this paper.
The main components of our model are: the agents
trying to communicate and moving around a grid-
shaped world; the routing algorithm deciding which
path a message can take; and the evolutionary algo-
rithm deciding which agents and thereby strategies
are kept or created. The model will be turn-based
and all of the actions will occur in a specific order, as
explained in the following subsections.
2.1 Agents and their World
The agents in our application will stand for the mobile
participants of an ad-hoc network. The function of the
agents will be to move in the simulation world and
to use the network. The movement of the agents will
be simulated with a very simple random-walk model.
We need the agents to be mobile but we do not need
their mobility patterns to be representative or realistic,
because we are more interested in how their strategic
choices affect the network. Each turn, the agents can
walk one step in each of the four cardinal directions or
stay in place with an equal chance of 20%.
The world of our agents is a rectangle of any in-
teger size and the agents always move by one unit of
size. For all results described in this article we used
a world of size 50 × 50 , populated with 80 agents. In
our implementation, these parameters can easily be
varied. If an agent walks over the border of our rect-
angle, it disappears from the network and with each
subsequent turn it has an increasing chance to return
from a random side. The chance of an agent returning
is 10% in the first turn, 20% in the second, up to the
agent returning with 100% chance in the tenth turn
after its disappearance. While the agent is gone from
the world, it does not take part in any of the network
activities (including message routing and receiving).
The part of the agents’ behaviour that we are most
interested in is their evolving strategies. For the first
iteration of our study, agents have a binary choice
space with two strategies possible: either completely
selfless (altruistic) or completely selfish. The former
will always route messages and the latter will never
route messages. This simple distinction is fitting for
a first step, a sort of preliminary testing of the waters.
In subsection 3.3 we propose and investigate more
complex and nuanced strategies.
2.2 Messages
Each turn, each agent has a 25% chance of deciding
to send a message to a randomly chosen agent that is
also present in the current world state. The message
is considered to be sent successfully if the sender and
the receiver are both connected through the network
(subsection 2.3). The agents store how many mes-
sages they wanted to send and how many they sent
successfully in order to calculate their effectiveness.
Each attempt at sending a message is associated
with a cost paid by the sender. Here we introduce the
battery life as a resource. Each agent starts a given
day with a fully charged battery of 1,000 points. Each
attempt at sending a message decreases the battery life
by 5 points. Similarly, routing a message of another
agent costs 3 points. The relation between the message
sending and routing costs affects how punitive the
routing is and therefore how costly it is for an agent to
be selfless. The costs can be tweaked and changed in
our implementation. We say that a day ends as soon
as half of the agents’ batteries are empty. Hence the
costs affect how many runs the simulation of each day
will take.
2.3 Routing
There is a wide variety of algorithms that can be used
in ad-hoc networks. Since we do not investigate the ef-
fectiveness of the algorithms, we are not bound to any
specific approach. The only requirement we pose is
that our routing algorithm always provides the agents
with optimal paths to the available receivers. In our
simulation we use a distance-vector routing proto-
col, which uses the Bellman-Ford algorithm (Bellman,
1958). This is certainly not optimal, but fast enough
for our purposes.
Balancing Selfishness and Efficiency in Mobile Ad-hoc Networks: An Agent-based Simulation
163

The algorithm as implemented in our simulation
works as follows. Each agent has a routing table which
lists all other agents in the simulation, the distance to
them (or infinity if they cannot be reached) and the
next agent via which messages should be sent (unless
the agent is reachable directly). At the beginning of
each run, after all agents have moved, each agent starts
with a new table where all its neighbours get distance
1 and all non-neighbours get infinity. What follows is
the crux of the algorithm: Each agent sends its table
to all its neighbours, which use it to update their own
tables. If they are offered a shorter route through the
currently advertising neighbour than the one they are
currently aware of, they will replace this line in their
table. This process is repeated until no agents will
make any more updates.
It is worth noting that when a selfish agent adver-
tises its table, it only provides the other agents with
routes to itself, as it disallows any other traffic to go
through its device. Another important point is that for
two agents to be considered neighbours, they must be
within 10 units of each other.
Now if an agent wants to send a message, it looks
up the receiver in its routing table. If the distance to
the receiver is finite, it is possible to reach the agent,
so the message is routed to the next node as provided
by the table. The next node then pays the routing costs
and repeats the process of looking up the receiver and
the next node in the table. The process continues until
the receiver node is reached.
2.4 Efficiency and Evolution
The efficiency of an agent is the ratio of the number
of messages successfully sent by it to the number of
messages it wanted to send. We use this value as the
fitness function for sorting agents in our evolutionary
algorithm. Hence, the maximum fitness is 1 and the
minimum fitness is 0. We keep track of the global effi-
ciency of the network, which is the average efficiency
of all participating agents.
Besides efficiency we also use the battery life of
each agent in our evolutionary algorithm. However,
we do not use the battery life in the fitness function,
but rather as a cut-off to mimic a real-world setting.
Agents whose battery life drops to 0 are considered
dead and removed from the world. Once half of the
initial population is dead, we say that a day has ended.
The dead half is discarded and the remaining survivors
are ordered by their fitness. The population for the
next day is then created on the basis of the surviving
half. The algorithm determining the other half of the
new population depends on the type of strategies and
is explained in the next section.
3 THREE SET-UPS
We have done three experiments, each with a different
choice of strategies. In each set-up, the model will
simulate 10 days. To make sure the results are rep-
resentative, 100 simulations of 10 days each will be
run and their results will be averaged. The standard
deviation values for selfishness and effectiveness will
also be calculated.
3.1 Set-up I: Binary Agents
Our first experiment focuses on running our simulation
with agents that can exhibit either a selfish or a selfless
approach. The selfish agents never allow any routing to
go through their devices and the selfless agents always
allow routing. The selfish agents seem to be privileged
in terms of the costs to their battery resources. At the
start of our simulation 1% of the agents are selfish, i.e.
1 out of 80. We keep track of the ratio of agent strate-
gies as well as the overall effectiveness of the network
over time. The evolutionary mechanism in this set-up
at the end of each day first allows the surviving half
of the population to pass to the next day. To fill up
the other half we iterate through the survivors one by
one and make copies of some of them, depending on
their fitness. For example, a surviving selfless agent
with a fitness of 0.78 , has a 78% chance to be cloned.
We stop as soon as the same total population size is
reached again and proceed to the next day.
3.2 Set-up II: Stochastic Agents
Our second experiment is based on the first set-up, but
now the strategies are not binary but stochastic. Each
agent is has a level of selfishness between 0 and 1 . An
agent with a selfishness of 0.45 has 45% chance of
refusing to route traffic through itself each turn.
This change also allows us to employ a more so-
phisticated evolution. In this set-up, again the surviv-
ing half of the population passes into the next day.
The remaining half however is now repopulated with
crossover agents that have the average selfishness of
two surviving agents. As in Set-up I, more effective
agents have a greater chance to reproduce. We also
add a small chance for mutation: Each new agent has
a 1% chance to change its selfishness by ±0.1.
3.3 Set-up III: Advanced Strategies
The third experiment addresses more advanced strate-
gies and a more heterogeneous environment. Besides
the stochastic strategy from subsection 3.2 we use the
following three strategies.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
164

The tit-for-tat strategy (TFT) inspired by Axelrod
(1980) keeps track of previous interactions. A TFT
agent will route a message if the original sender has
agreed to routing in their last interaction and disagree
if they disagreed. The decision is based only on the
previous interaction between the two agents in ques-
tion, if there was any. Otherwise, the TFT agent will
trustingly allow for routing to take place.
The battery-based strategy (BB) takes into consid-
eration energy usage. The BB agent will always route
if its battery is above 500 (half the initial amount). If
its battery is below 500, the BB agent will sometimes
refuse to route: the lower the battery, the greater the
chance of a BB agent refusing.
Finally, the hybrid strategy is a combination of
the TFT and BB agent. A hybrid agent’s decision is
made in two steps. The first step is the same as in a
TFT agent: if it is the first interaction or in previous
interaction the other agent cooperated, the hybrid agent
will go to step two, otherwise it will not route. The
second step is the same as in the BB agent, but the
battery cap is 400 instead of 500.
The evolutionary mechanism in this set-up is sim-
ilar to the one in Set-up II. The first half of the new
population again consists of the surviving half of the
population. The second half is formed by combining
two survivors, where those with higher efficiency are
more likely to get chosen. The selfishness of the child
is the average of the selfishness of the two parents.
Additionally, the selfishness has a 1% chance to mu-
tate by 0.1 in any direction. The type of the child will
be the same as one of the parents — each of the two
having 50% chance of passing its type. TFT, BB and
hybrid agents have a selfishness of 0.
4 RESULTS
We now give the results of our simulation described
in section 2, one set-up per section. The effectiveness
of the whole system shown in the results below is the
average effectiveness of all agents. The selfishness
of binary and stochastic agents is their willingness to
refuse routing, i.e. 0 or 1 for binary agents and a value
within [0, 1] for stochastic agents. The selfishness of
the whole system shown in the results is the average
selfishness of all agents. Entries of 0.000 mean that
the value is below 0.0005.
4.1 Set-up I: Binary Agents
The first part of Table 1 and the red plots in Figure 1,
show a clear relationship between effectiveness and
Table 1: Set-ups I and II (all standard deviations below 0.04).
Set-up I Set-up II
Day Effectiven. Selfishn. Effectiven. Selfishn.
1 0.878 0.031 0.858 0.034
2 0.805 0.078 0.802 0.062
3 0.673 0.172 0.727 0.105
4 0.470 0.370 0.630 0.162
5 0.229 0.753 0.515 0.232
6 0.052 0.979 0.413 0.312
7 0.004 0.997 0.317 0.396
8 0.000 1.000 0.241 0.478
9 0.000 1.000 0.176 0.553
10 0.000 1.000 0.132 0.619
1 2 3 4
5 6
7 8 9 10
0
0.25
0.5
0.75
1
day
Effectiveness Set-up I Selfishness Set-up I
Effectiveness Set-up II Selfishness Set-up II
Figure 1: Effectiveness and selfishness for Set-up I and II.
selfishness ratios. Namely, the increase in the self-
ishness ratio of individual agents correlates with the
decrease in the effectiveness of the network. Moreover,
as the days progress, the effectiveness of the system
decreases while the selfishness increases. The maxi-
mum system selfishness of 1 (meaning all agents are
selfish) is reached in day 8. This correlates with the
effectiveness of the system dropping to 0 . This is con-
sistent with the values of the effectiveness for a system
that is run with selfishness ratio 1 as initial condition.
Higher effectiveness of the system leads to fewer
runs per day. It takes on average 345.8 runs for half of
the agents to die when the effectiveness is 0.878 , but
821.920 runs when the effectiveness is below 0.001 .
This is because less or no messages get routed overall,
so less energy is used.
4.2 Set-up II: Stochastic Agents
As can be seen in the second half of Table 1 and the
blue plot in Figure 1, the trends occurring in Set-up
1 are apparent in Set-up II as well. Namely, the cor-
Balancing Selfishness and Efficiency in Mobile Ad-hoc Networks: An Agent-based Simulation
165

relation between the effectiveness and the selfishness
remains inversely proportional. However, the relation-
ship is weaker than in Set-up I. The fivefold increase
of selfishness over the first four days affects the effec-
tiveness less significantly than in Set-up I. However,
after the selfishness reaches the 0.3 mark, the decrease
in effectiveness becomes more rapid.
Even though the initial increase of the selfishness
is comparable in terms of the slope, the overall pattern
appears much less steep than in Set-up I. Nevertheless,
when the simulation is run for a sufficient number of
days, the selfishness increases to around 0.99 and the
effectiveness drops to around 0.14 . The number of
days needed to reach such a state is significantly larger
than in the case of Set-up I (around 50 days).
4.3 Set-up III: Advanced Strategies
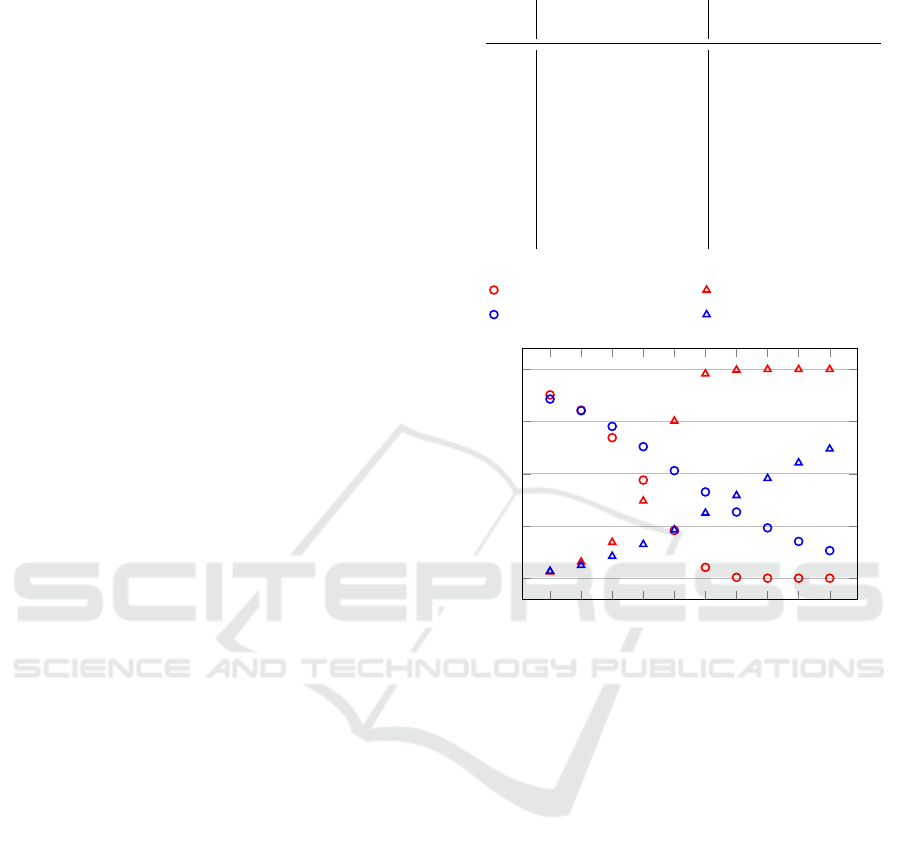
For each strategy we want to know if it survives against
selfish agents. Moreover, we want to compare all
strategies together in one setting. Hence we investigate
four different settings in Set-up III. In three settings
half of the agents are stochastic (with 0.01 selfishness)
and the others are TFT, BB and hybrid, respectively.
In a fourth “tournament” setting, we start with 25%
each of stochastic, TFT, BB and hybrid agents.
Tit-for-tat. The TFT agents are able to curtail the
stochastic agents — see the first part of Table 2 and
the orange plot in Figure 2. The stochastic agents still
exhibit (just like in Set-up II) a tendency to become
increasingly selfish, but the increase in selfishness and
the decrease in effectiveness are slower when com-
pared to Set-up II. The population of TFT diminishes
1 2 3 4
5 6
7 8 9 10
0
0.25
0.5
0.75
1
day
Eff. TFT Self. TFT
Eff. BB Self. BB
Eff. hybrid Self. hybrid
Eff. tournament Self. tournament
Figure 2: Effectiveness and selfishness for Set-up III.
slowly. The number of runs increases from around 350
to 400 over the course of the 10 days.
Battery based. Results of the second setting of Set-
up III are also shown in Table 2 and plotted in green
in Figure 2. The BB agents appear to have a similar
effect on the stochastic agents as the TFT agents. The
difference is that both initial and final effectiveness are
much lower. In the early days of the simulation, how-
ever, the BB agents are able to increase their number
well above the stochastic agents. The number of runs
increases over the days from 435 to 500.
Hybrid. In the third setting of Set-up III, the hybrid
agents dominate the stochastic agents, as shown in the
third part of Table 2 and by the red plot in Figure 2.
The selfishness remains stable, while the effectiveness
decreases slightly from 0.6 to around 0.45 — a value
consistent with a situation in which the world is pop-
ulated only by hybrid agents. The number of runs
needed for half of the agents to die increases over the
10 days from around 430 to 480.
Tournament.
For our last setting the results are shown
in the right-most part of Table 2 and plotted in blue in
Figure 2. Clearly, Hybrid and BB agents dominate the
rest. The number of BB agents increases from 20 to
39 and hybrid agents from 20 to 31. The selfishness
increases from 0.017 to 0.031 which is just a little bit
faster than in the Hybrid setting. The number of runs
increases from 440 to 490.
5 CONCLUSIONS
5.1 The First Research Question
The set-ups I and II can answer our first research ques-
tion, “What is the dominant strategy for participants in
an ad-hoc mobile network?” The dominant strategy is
a selfish one. Both in the run with binary agents and the
run with stochastic agents, the population became over-
run by the selfish element. This is especially striking
since only 1 selfish individual out of 80 or for Set-up
II a stochastic selfishness of 0.01 was enough for the
selfishness of the system as a whole to become 1. This
means the selfish behaviour is the dominant strategy
by far, confirming our hypothesis. This situation can
be understood by analysing the conditions in which
the agents operate. Each agent is rated based on the
number of messages it sent successfully related to the
total number of messages it wanted to send. However,
both sending and routing has a cost of depleting the
precious resource, namely, the battery life. Hence, an
agent who sends messages but does not route achieves
better results than an agent who both sends and routes.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
166

Table 2: Set-up III (all standard deviations below 0.05).
Stoch. vs. TFT Stoch. vs. BB Stoch. vs. Hybrid Tournament
Day Eff Self # TFT Eff Self # BB Eff Self # Hyb Eff Self # Stoch # TFT # BB # Hyb
1 0.880 0.017 40.00 0.579 0.024 40.00 0.595 0.017 40.00 0.569 0.017 20.00 20.00 20.00 20.00
2 0.857 0.022 36.65 0.560 0.035 43.57 0.591 0.020 43.03 0.579 0.019 19.61 18.82 22.44 19.13
3 0.843 0.028 35.55 0.512 0.050 50.25 0.555 0.022 50.00 0.544 0.021 16.32 15.64 27.22 20.82
4 0.818 0.036 35.11 0.469 0.050 50.25 0.524 0.024 50.74 0.518 0.023 13.27 12.70 30.03 24.00
5 0.787 0.045 35.16 0.438 0.085 56.79 0.502 0.024 60.40 0.494 0.024 10.77 10.37 33.09 25.77
6 0.766 0.058 35.32 0.410 0.108 56.79 0.487 0.024 64.46 0.478 0.025 8.43 8.13 35.21 28.23
7 0.733 0.072 33.79 0.387 0.137 55.50 0.478 0.023 67.16 0.460 0.027 6.80 6.27 37.72 29.21
8 0.691 0.087 33.21 0.359 0.173 52.96 0.470 0.022 69.49 0.456 0.029 6.72 5.02 38.64 29.62
9 0.659 0.106 32.00 0.333 0.221 48.61 0.462 0.022 71.75 0.447 0.030 6.59 3.94 38.84 30.63
10 0.619 0.126 31.07 0.308 0.272 43.07 0.459 0.020 73.38 0.445 0.031 6.31 2.96 39.31 31.42
The selfish agent abuses the selflessness of its less
selfish colleagues.
The situation quickly changes with more selfish
agents: the efficiency decreases as fewer agents are
willing to route. After a critical point is passed all
agents become selfish and the network becomes inef-
fective, allowing only direct messages. This situation
is similar to games such as Prisoner’s dilemma (de
Weerd & Verbrugge, 2011) and seems to reflect actual
human behaviour as described by Hardin (1968).
We sought to remedy this situation by introduc-
ing more advanced strategies, namely the TFT, BB
and hybrid agents. But the TFT agents did not stop
the selfish agents: after 10 days, the selfishness in-
creased ninefold. It did, however, significantly lower
the expansion of the selfish element, thus limiting the
decrease in effectiveness of the network. However, it
is likely that, as more days passed, the selfish element
would continue to increase.
The BB agents, while slowing down the expansion
of the selfish agents, were not able to keep them at bay.
After 10 days, the selfishness reached over 0.25 and
the effectiveness was just slightly above 0.25.
The hybrid agents exhibiting a combination of the
TFT and BB strategies showed an ability to combat
the selfish individuals. Over the course of 10 days, the
increase in selfishness was only 0.003 and the number
of stochastic agents decreased from 40 to around 7.
5.2 The Second Research Question
We can now answer our second research question: “Is
there a reward/punishment system for participants that
can improve the longevity of a mobile ad-hoc net-
work?”. The answer is yes, as we will now discuss.
The limited success of TFT can be explained if
we consider its interaction with selfish agents. A TFT
agent allows for routing at the first interaction with the
selfish one and then declines to route once the selfish
agent declines to route for the TFT agent. Hence self-
ish agents may abuse the trusting approach of the TFT
and get a slight advantage.
The limited success of BB agents lies in their abil-
ity to recognize the battery life as a valuable resource
and to base their decisions on its basis. Their behaviour
leads to a less efficient but more stable situation: Be-
cause agents with low battery life will not route, the
routing responsibilities are more distributed over the
system. However, since the BB behaviour is strictly
self preserving and not really punishing to the selfish
agents, the latter are still able to take advantage and
eventually dominate.
The success of the hybrid agents is a mixed bless-
ing. They are able to keep selfish agents away effi-
ciently. However, they also remove selfless and TFT
agents regardless of their beneficial behaviour. The
only agents that can potentially defeat hybrid agents
are BB agents and the resulting network exhibits an
effectiveness of around 0.45. This is far from optimal
but it is a definite improvement over Set-up I and II.
It is worthwhile to consider the results through the
lens of evolutionary game theory. We have a number
of groups of individuals exhibiting different survival
strategies, scarce resources, and a need for cooper-
ation. Of special interest would be to decide if the
strategies we discussed are evolutionarily stable. An
evolutionarily stable strategy is any strategy that can-
not be invaded by an initially rare, alternative strategy
(Easley & Kleinberg, 2017). Given the results of Set-
up III, the strategies that could be evolutionarily stable
are the BB and the hybrid strategy. The TFT strategy
becomes invaded by the selfish strategy. Note that for
a strategy to be evolutionarily stable, it does not need
to optimise the efficiency of the system. Therefore,
the BB agents, even though decreasing the effective-
ness of the system, cannot immediately be discarded
as candidates for being evolutionarily stable. However,
it is too early to say that the hybrid or BB strategy
is evolutionarily stable: we would need to test them
against a wider array of alternative strategies.
Balancing Selfishness and Efficiency in Mobile Ad-hoc Networks: An Agent-based Simulation
167

A recommendation to architects of mobile ad-hoc
networks based on our results is that users should be
allowed to control the routing done by their devices,
because there are non-selfish stable strategies. This
is also reasonable from both ethical and marketing
perspectives. Reporting the effectiveness of different
strategies to the users can easily be done and would
likely improve the overall effectiveness. Since strate-
gies such as our hybrid approach limit the effectiveness
of selfish users, selfishness would be naturally discour-
aged. More control over the use of the network would
lead to more users, which in turn allows for more
routing opportunities, larger range of the network and
overall robustness. Moreover, the network providers
would be able to build trust int the users by not enforc-
ing a global behaviour on all devices, thus recognising
different needs and abilities of different users.
5.3 Future Work
A natural next step to continue our research would be
to run simulations beyond 10 days. Another potential
extension is to consider other routing algorithms, in
particular taking into account the battery levels of the
users. Ideas to extend the battery life in mesh networks
have been discussed by Sangwan and Pooja (2016) and
Anastasi, Conti, Di Francesco, and Passarella (2009).
Another idea to make our model more realistic
would be to replace the square grid with a map of an
actual city and to use a realistic model of human mobil-
ity patterns (Serok & Blumenfeld-Lieberthal, 2015).
An improvement that we already hinted at could
be to test the BB and hybrid strategies against a larger
number of alternative strategies, in order to test their
potential evolutionary stability. Moreover, it seems
interesting to consider the dynamics of different strate-
gies and their evolution in mesh networks. It would
also be interesting to investigate how dynamic changes
of agents’ strategies, from day to day or maybe even
within one day, would work out in a mesh network.
Other researchers consider the importance of so-
cial learning, cooperation and individual reputation in
game theory considerations (Sigmund, 2016). While
those ideas have been taken into account in our study,
we think that our approach is still lacking realism. It
is difficult to predict the behaviour of groups of in-
dividuals in a reliable manner. Studies into crowd
psychology and the evolution of collective behaviour
could shed more light on the matter (Gordon, 2014).
Finally, models and simulations are great to design
and test new strategies, but should then also be tested
in real-life experiments. Running a study on actual
smartphones as done by Schejbal (2014), but then with
the additional strategy choice given to each user, could
provide us with more realistic data. Such experiments
can also take into account physical intricacies of ad-
hoc networks that we ignored in this study.
REFERENCES
Anastasi, G., Conti, M., Di Francesco, M., & Passarella,
A. (2009). Energy conservation in wireless sensor net-
works: A survey. Ad Hoc Networks, 7(3), 537–568.
doi:10.1016/j.adhoc.2008.06.003
Axelrod, R. (1980). Effective choice in the prisoner’s
dilemma. Journal of Conflict Resolution, 24(1), 3–25.
doi:10.1177/002200278002400101
Bellman, R. (1958). On a routing problem. Quarterly of
Applied Mathematics, 16(1), 87–90. doi:10.1090/qam/
102435
de Weerd, H., & Verbrugge, R. (2011). Evolution of altruistic
punishment in heterogeneous populations. Journal of
Theoretical Biology, 290, 88–103. doi:10.1016/j.jtbi.
2011.08.034
Easley, D., & Kleinberg, J. (2017). Networks, crowds, and
markets: Reasoning about a highly connected world.
Cambridge University Press.
Gordon, D. M. (2014). The ecology of collective behavior.
PLoS Biology, 12(3), e1001805. doi:10.1371/journal.
pbio.1001805
Hardin, G. (1968). The tragedy of the commons. Science,
162(3859), 1243–1248. doi:10.1126/science.162.3859.
1243
Hekmat, R. (2016). Ad-hoc networks: Fundamental proper-
ties and network topologies. Springer.
Juri
ˇ
si
´
c, M., Kermek, D., & Konecki, M. (2012). A review of
iterated prisoner’s dilemma strategies. In P. Biljanovic
(Ed.), Proceedings of the 35th international convention
MIPRO: Opatija, Croatia, 21-25 May 2012 (pp. 1093–
1097).
Sangwan, Y., & Pooja. (2016). A survey on battery conser-
vation approaches in MANET. International Journal
of Scientific Engineering Research, 7(12), 483–487.
Schejbal, J. (2014). A real-world study of mobile peer-to-
peer networking. TU Darmstadt. MSc thesis.
Serok, N., & Blumenfeld-Lieberthal, E. (2015). A simulation
model for intra-urban movements. PLOS ONE, 10(7).
doi:10.1371/journal.pone.0132576
Sigmund, K. (2016). The calculus of selfishness. Princeton
University Press.
Statista. (2019). Number of smartphone users worldwide
from 2014 to 2020 (in billions). Retrieved from https:
//www.statista.com / statistics/ 330695 / number - of -
smartphone-users-worldwide/
Vijayakumar, K. P., Ganeshkumar, P., & Anandaraj, M.
(2012). Review on routing algorithms in wireless mesh
networks. International Journal of Computer Science
and Telecommunication, 3(5), 87–92.
Yoshimachi, M., & Manabe, Y. (2016). Battery power man-
agement routing considering participation duration for
mobile ad hoc networks. Journal of Advances in Com-
puter Networks, 4(1), 13–18. doi:10.18178/JACN.2016.
4.1.196
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
168