
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic
Alternatives to Cancer Treatment
David F. Nettleton
1 a
, Vladimir Estivill-Castro
1,2 b
and Enrique Hern
´
andez Jim
´
enez
3 c
1
Department of Information and Communications Technology (DTIC), Universitat Pompeu Fabra, Spain
2
School of ICT, Griffith University, Brisbane, Australia
3
Institut d’Investigaci
´
o Biom
`
edica de Bellvitge, Barcelona, Spain
Keywords:
Simulation, Multi-agent Systems, Immunology, Cancer Cells.
Abstract:
There is exciting news in recent developments suggesting the potential to treat some human cancers by stim-
ulating the patients own immune system. However, there is still much to understand; therefore, modelling
the battle between those cells that are constituents of the human immune system against tumorous cells can
significantly provide insights as mathematical modelling has done regarding the immune system behaviour
against virus infections. In this paper we innovate in two directions. First, we move the modelling of immune
struggles from the sphere of ordinary-differential equation models to the modelling by multi-agent simula-
tions. We highlight the advantages of the multi-agent simulation, for example the consideration of elaborate
spatial proximity interactions. Secondly, we move away from the realm of infectious diseases to the complex
modelling of the stimulation of T-cells and their participation in fighting cancerous cell tumours.
1 INTRODUCTION
Recent developments in immunotherapy (ElSayed,
2018; Sun, 2017) indicate remarkable progress for
the treatment of some human cancers by stimulat-
ing the patient’s immune system (Chen and Mell-
man, 2013; Fern
´
andez et al., 2013; Pardoll, 2012;
Farag et al., 2002). Nevertheless, the high complex-
ity of the human immune system remains a challenge.
We require progressively more advanced and high
fidelity models for understanding the immune sys-
tem dynamics and mechanisms. In particular, mod-
elling the battle between those cells that are con-
stituents of the human immune system against tu-
morous cells can significantly provide insights as
mathematical modelling has already done regarding
the immune system behaviour against virus infec-
tions (Wodarz, 2006). We open the field in two direc-
tions. First, we move the modelling of immune strug-
gles from the realm of ordinary-differential equation
models (
´
Alvarez et al., 2017) to the modelling by
multi-agent simulations (B
˘
adic
˘
a et al., 2018; Karsai
et al., 2016; Zhao and Jin, 2005). We highlight that
a
https://orcid.org/0000-0002-5852-7716
b
https://orcid.org/0000-0001-7775-0780
c
https://orcid.org/0000-0002-8232-8151
the multi-agent simulation enables consideration of
elaborate spatial proximity interactions. Such inter-
actions are extremely important in the modelling of
competition and predator-prey scenarios in ecologi-
cal systems (Karsai et al., 2016). Secondly, we move
from the realm of infectious diseases to the complex
modelling of the stimulation of T-cells and their par-
ticipation in fighting cancerous cell tumours. Most
cancers are not caused by transmissible pathogens;
but, cancer immunotherapy suggests treatment anal-
ogous to infections (Chen and Mellman, 2013).
Adopting a system approach and modelling the
dynamics analogously to ecological systems (Wodarz,
2006) has enabled tremendous progress in the under-
standing of the interactions between pathogens and
the immune system. Such dynamics is modelled by
increasingly more complicated systems of ordinary
differential equations that abstract elements of what is
known by experimental means (
´
Alvarez et al., 2017;
Eftimie et al., 2016; Linderman et al., 2010).
The mathematical models of infections capture
population dynamic interactions of two types (Ada,
1997; Wodarz, 2006). One is predator-prey interac-
tions, where predators kill prey, and the predator pop-
ulation grows until much fewer prey results also in
a decrease of predator numbers. This is usually the
scenario of killer cells responding to a viral infec-
Nettleton, D., Estivill-Castro, V. and Jiménez, E.
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic Alternatives to Cancer Treatment.
DOI: 10.5220/0008915601690178
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 169-178
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
169

tion. Secondly, competition models abstract scenar-
ios where two species dispute a common resource (a
source of food). In the case of the immune system,
one immune cell type may expand more rapidly upon
exposure to infection, preventing another type of im-
mune cell from growing its numbers.
Such mathematical modelling stimulates the ex-
perimental agenda. In the realm of viral infections,
different models of how CTL (cytotoxic T lympho-
cytes or killer T cells) are assisted by CD4 T cell (T
cells that bear the CD4 marker of helper cells) in the
primary response and the resolution of an infection
as well as the memory phase prompted many experi-
ments (Wodarz, 2006, Chapter 4). In particular, im-
munological memory is the preservation of a much
larger number of specific CTL cells after a virus in-
fection than before the infection. This memory capac-
ity of the immune systems has delicate interactions
with the eradication of the infection. The mathemati-
cal models suggest that there is a trade-off. The virus
population is reduced by a high responsiveness and a
long life span of the memory CTL (Wodarz, 2006).
However, while there has been an extensive liter-
ature of the application of dynamic systems models
first to ecological systems (Chase et al., 2002; Kings-
land, 2015) and then to the immune systems (Wodarz,
2006), there is a recent opportunity in two directions.
First, to use the technology of multi-agent simula-
tion and second to apply it to the emerging promise
of the immune systems potential to fight cancer tu-
mours (Chen and Mellman, 2013). Therefore, in this
paper, we describe and test a modelling technique
based on multi-agent systems for simulating systemic
and inter-cellular behaviour for NK (natural killer)
and cancer cells. The clinical approach is to potentiate
the body’s own immune system, using reprogrammed
natural killers (NK is a type of lymphocyte; that is
a white-blood cell) to attack the cancer (or tumour)
cells. Therefore, no harm is caused to normal cells, in
contrast to widely used chemo-therapy approaches.
In order to be effective, NK cells require an opti-
mum programming against the particular cancer cell
adversary. This requires an individualized study of
the patient followed with a directed trial and error pro-
cess which typically is tested on mice with a 14-day
evolution period. Computer simulations could run
in just a few minutes, with a much lower economic
cost and could approach a realistic simulation perfor-
mance relative to the mouse and in-vitro experimen-
tation. Thus, multi-agent simulation could provide
an important step forward in accelerating the fight
against cancer-cell growth.
We incorporate medical know-how to build a
multi-agent simulation model with some degree of
realism. Every model is an abstraction, but we will
highlight the aspects that a multi-agent simulation of-
fers over the dynamic systems approach of using sets
of differential equations. We benchmark our simula-
tions against state of the art empirical in-vitro clinical
experiments, as described by Fern
´
andez et al. (2013).
Our results demonstrate that an agent system can ac-
curately model the in-vitro experiments in terms of
cytotoxicity, but without the need for defining a set
of differential equations as in dynamic system mod-
els nor a priori assumptions relative to the system, and
giving greater flexibility for trying many different sce-
narios. Our implementation uses random interaction
and cellular random movement in space.
2 THE CASE FOR MULTI-AGENT
SIMULATIONS
Purely clinical approaches to immunological treat-
ment of cancer rely heavily on the use of in vitro
trials with live mice requiring highly specialized pa-
rameterisations. Such parameterisations require deep
medical knowledge. A significant part of the chal-
lenge is to anticipate behaviour, and as we explained
before, so far in this field, the research has focused
on mathematical modelling in the realm of dynamic
systems abstracted as systems of differential equa-
tions (
´
Alvarez et al., 2017).
But, the techniques to formulate models of bi-
ological systems, and to solve them includes also
agent-based models, stochastic modelling techniques,
differential equations, spatial simulations, and direct
application of Gillespie’s stochastic simulation algo-
rithm (Barnes and Chu, 2015). Differential equa-
tions are suitable abstractions at the macro-level, but
multi-agent systems are suitable models at the micro-
level behaviour that can determine the macro-level
behaviour. Sets of ordinary differential equations
(ODEs) have limitations pertaining problems involv-
ing spatial interactions or emerging properties (Bor-
shchev and Filippov, 2004). Borshchev and Filippov
(2004) and others (Figueredo et al., 2014) argue ODE
methods exclude emergent and stochastic behaviour.
Louzoun (2007) consider ODE methods too nar-
row, using few reactive types focused on simple dy-
namics. Louzoun (2007) argues that immunological
modelling should incorporate genomic data and ex-
ploit computing power. His review (Louzoun, 2007)
suggests that applications of mathematical models in
immunology are shifting to immunomics: the con-
cepts of high–throughput measurements and system
immunology. Models of ODE systems for immunol-
ogy are categorised as deterministic compartmental
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
170
models (Figueredo et al., 2014) because continuous
values are used for all aspects of the modelling of
individuals in the environment; while multi-agent
systems explicitly represent the individuals. Strac-
quadanio et al. (2011) argue that agent-based mod-
els “seem to be the best suited abstraction to han-
dle the great complexity of the immune system”.
We acknowledge that the discrete-event scheduling of
Gillespie methods has been incorporated with multi-
agent simulation into mixed platforms (Montagna
et al., 2016). In particular, some variants of Gille-
spie’s discrete-event scheduling have been applied
to the simulation of the spatial interaction between
cells (Shimoni et al., 2011; Engblom, 2019).
The model accuracy is believed to be negatively
impacted by the exclusion of information on proxim-
ity (Stracquadanio et al., 2011) because most immune
interactions take place within local spatial regions of
the environment.
This advantage of multi-agent systems has been
illustrated in the field of ecology (B
˘
adic
˘
a et al., 2018)
and other specific disciplines (Montagna and Viroli,
2010; Montagna et al., 2010, 2016). Multi-agent sys-
tems have been used to explore what-if scenarios of
environments that combine cell proliferation and ran-
dom walks of cells on regular lattices, reactions for
nutrients and growth factors (Figueredo et al., 2013a).
Researchers use different modelling environ-
ments, but for multi-agent system modelling, the
Repast Simphony (North et al., 2013) is common.
In particular, Repast Simphony was used to illustrate
multi-agent systems simulations as an alternative to
dynamic systems of differential equations for the clas-
sical predator-prey scenario (Tatara et al., 2006).
3 RELATED WORK
The nearest work to our approach here is the appli-
cation of agent simulations of immune cell (effec-
tors) and tumour cell interactions (Figueredo et al.,
2013b, 2014). The focus of Figueredo et al. (2013b)
and Figueredo et al. (2014) is to compare a differen-
tial equation model (Gillespie) with an agent based
model. Figueredo et al. (2013b) and Figueredo et al.
(2014) find that the agent-based model effectively
simulates the system and also find patterns which
were unseen by the former. However, they do not
use distance based parameters, and as mentioned ear-
lier, spatial information (proximity) is considered cru-
cial (Stracquadanio et al., 2011). We do incorporate
proximity in our model. Figueredo et al. (2013b)
and Figueredo et al. (2014) do not relate the effector
and tumour cells to real biological equivalents; their
analysis is in-silico (Figueredo et al., 2014); that is,
pure simulation. Thus, Figueredo et al. (2013b) and
Figueredo et al. (2014) simulations were not matched
against any real experimental values. However, they
did include parameters for cell life and damage in-
curred to the effector cells by the tumour cells. In
terms of physical characteristics, IL2 is stimulatory
for the effector cells and TGF-beta suppresses the ef-
fectors and stimulates tumour growth.
An advantages of multi-agent systems is the dis-
crete event integration of the engagement within the
agents in a spatial sphere of influence. Other related
work incorporating spatial considerations into an eco-
logical model is in the area of computational epidemi-
ology (Jindal and Rao, 2017).
4 SIMULATION CASE STUDY
Firstly, we will define the following acronyms: IL15
(Interleukin-15), NKG2D (Natural Killer-gene 2D),
MICA (MHC class I polypeptide-related sequence
A), ULBP2 (UL16 binding protein 2) and HLA class
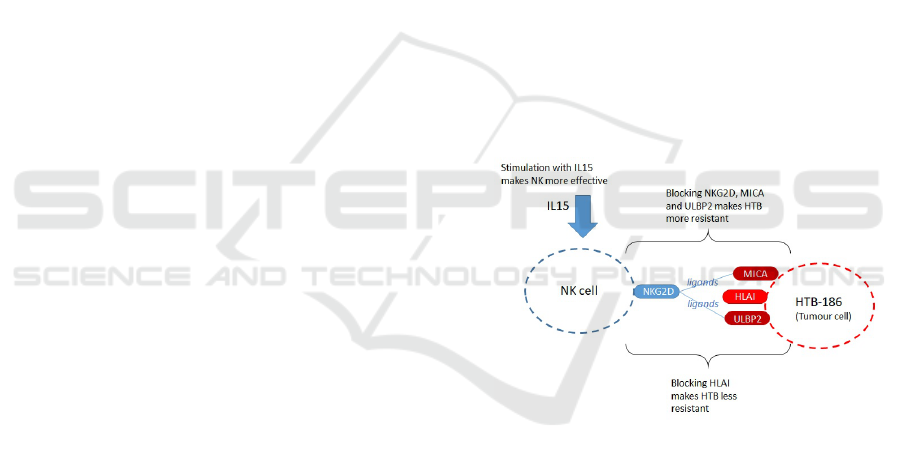
1 (Human Leukocyte Antigen).
Figure 1: Features on NK and Tumour cells (HTB-186).
We chose as our case study study the interac-
tion between tumour cells (HTB-186) and NK cells
under different conditions (Fern
´
andez et al., 2013).
Fern
´
andez et al. (2013) cultivated NK and HTB-186
tumour cells in vitro from 54 medulloblastoma pa-
tients. For the simulation we focus on the results
shown in (Fern
´
andez et al., 2013, Fig. 3), which
record the resulting cytotoxicity of NKs for differ-
ent blocking and stimulation conditions. Five con-
ditions are recorded: (i) Resting NK; (ii) IL15 stimu-
lated NK; (iii) Blocking of NKG2D (on NK), MICA
and ULBP2 (on HTB-186); (iv) HLA class 1 blocking
on HTB-186; (v) IL15 stimulated NK and HLA class
1 blocking on HTB-186. Note that (ii), (iv) and (v)
favour greater cytotoxicity of NK, whereas (iii) re-
duces cytotoxicity of NK. In the case of (iii), this is
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic Alternatives to Cancer Treatment
171

because NKG2D is the NK cell receptor and MICA
and ULBP2 are tumour (HTB-186) ligands for NK.
Refer to Figure 1 for an illustration of features on the
NK and tumour cells. Also note that, as the in-vitro
experiments have a duration of approximately three
hours, we do not consider proliferation or cell death.
4.1 Representation as a Dynamic
System Model
We now illustrate how the in-vitro experiment of our
case study ( Fern
´
andez et al. (2013)) would be mod-
elled as a “dynamic system model”.
Figure 2: Stock and flow diagram for NK and HTB-186
tumour.
A dynamic system model typically consists of a
stock and flow diagram (Figure 2), a set of differen-
tial equations to represent the behaviour of the stocks
(Figure 3), a set of algebraic equations to define the
flows (Figure 4), and a set of control parameters used
by the system (Figure 5). In Figure 2, the three stocks
are NKs, IL15 and Tumour cells. The flow on the top
right indicates the number of NK cells which are ef-
fective against the Tumour cells, and this is affected
positively by IL15 and the NKG2D activating recep-
tor (hence they are preceded by a +). The flow on
the bottom right indicates the number of Tumour cells
being killed by NKs, and this is positively affected
by MICA and ULDP2 ligands (+) and negatively by
HLA class I expression (-).
IL-15 is used as potential therapy to enhance NK
anti-tumoral activity. Additionally, IL-15 has been
shown to enhance the anti-tumor immunity of CD8+
T cells in pre-clinical models. In the current model
IL-15 is considered as a stimulator, but without local-
ization in the physical space, assuming it is homoge-
neously distributed and affects all NK’s equally. In
this sense, it’s considered in the same way as MICA,
NKG2D and ULBP. They are either present (or ac-
tive) or absent (or blocked). This also agrees with
the predator-prey model: NK are predators, HLA are
the prey, and IL-15 acts as a stimulator for NK. How-
ever, in future work the definition of IL-15 as an agent
could be considered.
Figure 3: Differential equations for stocks in Figure 2.
Figure 4: Differential equations for flows of Figure 2.
Figure 5: Control parameters for the dynamic system of
Figure 2.
5 AGENT MODEL
With reference to the simulation case study described
in Section 4, we will simulate two agent classes (us-
ing Repast Simphony (North et al., 2013)): agent-type
NK and agent-type Tumour. In our spatial environ-
ment, both classes are reactive agents (acting inde-
pendently, exhibiting control over their internal state).
Such individual agent behaviour is defined by global
rules as well as local rules.
NK-cells have short-term goal directed behaviour
for probabilistically aiming for a Tumour cell. We
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
172

Table 1: Agent control parameters.
Tumour cells NK-cells
speed of reproduction speed of reproduction range of range of distance kill dormant/activate
movement rate movement rate kill distance detection probability period
0.003 0.0 0.01 0.0 0.5 1.0 0.6 2
name Agent control parameters those values regulat-
ing the agents’ actions; these control parameters spec-
ify behaviour for the agents. A second set of param-
eters incorporates the experimental cellular informa-
tion.
The metric used to evaluate the fit of the simu-
lation to the in-vitro experiments is the number of
surviving Tumour cells when equilibrium is reached.
That is, the difference between the Tumour cell count
from Fernandez’s in-vitro experiments (Table 4) and
the Tumour cell count resulting from the agent model
(Table 5), which are shown in Figure 10.
The Repast source code of the system is available
at:github.com/dnettlet/AgentSim1.
In the first control parameter set (refer to Table 1),
for each agent type (NK or Tumour) we incorporate
the following control parameters (and their values)
based on experimental information ( Fern
´
andez et al.
(2013)): speed of movement of the agent instances in
the defined space; reproduction rate of the agents; dis-
tance at which a given agent type NK is able to detect
another agent type Tumour, and the distance at which
NK can kill (remove from participation in the simula-
tion) an agent of the class Tumour; and the probabil-
ity that, when NK is within distance to kill a Tumour
agent, it effectively eliminates the Tumour agent. The
dormant period is the number of cycles an NK-cell re-
quires to become dormant in the absence (within de-
tect distance) of Tumour cells. Likewise, the active
period is the number of cycles an NK-cell requires to
become active in the presence (within detect distance)
of Tumour cells.
Table 1 shows the initial value settings for the
control parameter set. Also, we use the values
by Fern
´
andez et al. (2013) to assign set-up values:
• Number of cycles without detecting tumour cells
for NK cells to become dormant (assigned as 2)
• Number of cycles having detected tumour cells
for NK cells to become active (assigned as 2)
• Initial number of tumour cells (assigned as 400)
• Initial number of NK cells (assigned as 400 for
ratio 1:1)
Each of the agent control parameters of Table 1 can
be related with a real biochemical process (e.g. kill
distance approximates the docking distance).
The second control parameter set (Table 2) consti-
tutes the experimental parameters of the real in-vitro
Table 2: Experiments, and their settings.
Experiment Resting IL15 ULBP2 MICA NKG2D HLAI
1 1 0 0 0 0 0
2 0 1 0 0 0 0
3 0 0 1 1 1 0
4 0 0 0 0 0 1
5 0 1 0 0 0 1
Table 3: Factors to incorporate stimulus or inhibition into
NK-cells behaviour.
Experiment Resting IL15 ULBP2 MICA NKG2D HLAI
1 1.1 0 0 0 0 0
2 0 1.1 0 0 0 0
3 0 0 0.9 0.9 0.9 0
4 0 0 0 0 0 1.1
5 0 1.1 0 0 0 1.1
experiments by Fern
´
andez et al. (2013). The original
labels for these experiments are 1 to 5 Fern
´
andez et al.
(2013). Each in-vitro experiment is defined by six test
conditions.
Table 2 indicates for each experiment, whether an
experimental feature is present or not. For example, in
Experiment 5, IL15 and HLAI are present, indicated
by a 1. When a feature is present, it acts as a stimulant
or inhibitor on the cytotoxicity (refer to Fern
´
andez
et al. (2013)).
We incorporate the experimental features into the
multi-agent simulation, as having either a stimulant
role or inhibitor role in the agents parameters (the val-
ues in Table 1). We apply them as multipliers that
either magnify or reduce the effect of the agents be-
havioural parameters. A magnifying multiplier will
be larger than 1 and a reducing multiplier will be less
than 1. Therefore, the conditions in Table 2 were cor-
rected to the multipliers in Table 3.
We apply this effect (which influences NK-cell be-
haviour) by affecting the behavioural parameters of
NK-cells of Table 1. For example, the IL15 and HLAI
features potentiate the cytotoxicity, (NKs kill a higher
percentage of Tumour cells) and they are both present
in Experiment 5, so the weights from Table 3 adjust
the NK-cell agent control parameters as follows:
kill distance =
number of features
∏
i=1
kill distance × w
i j
where j is fixed as the experiment number (5 in this
case). As an example, consider for Experiment 5 (Ta-
ble 3, Row 5) that the non-zero weights w are 1.1
(for IL15) and 1.1 (for HLAI), and the kill distance
is initially set to 0.5. Thus, the new kill distance in
the first iteration will be 0.5 × 1.1 = 0.55, and in the
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic Alternatives to Cancer Treatment
173

second iteration, 0.55 × 1.1 = 0.605. Similarly,
detect distance =
number of features
∏
i=1
detect distance × w
i j
On the other hand, in Experiment 3 (Table 3, Row 3)
the NKG2D feature dampens the cytotoxicity (re-
duces the NK kill rate on Tumour cells). This is a re-
duction weight of 0.9 that is multiplied with the agent
control parameters, so experiments with the presence
of NKG2D will see both “kill distance” and “detec-
tion distance” affected by the value 0.9.
We incorporated the effect of experimental fea-
tures to spatial behavioural features of the agents only
to three agent control parameters of only the NK-
cells. That is, we only affect the kill distance, de-
tection distance and kill probability of NK-cells. Be-
sides biological realism, initial simulations with our
agents showed only these behavioural components
had meaningful effects (number of Tumour cells re-
maining when system reaches equilibrium). Never-
Figure 6: State space definition for agent interactions.
theless, despite the incorporation of inhibitors and
stimulants to NK-cells, the interactions between NK-
cells and tumour cells is not magnified or reduced uni-
formly across all experiments. Thus, the interaction
of agent control parameter values (in Table 1) feature
weighting (in Table 3) requires further regulation. To
achieve such regulation, we used a third weight w
0
to
adjust all the NK-agents behavioural components uni-
formly but for each experiment and ratio. That is, the
weight w
0
adjusts the effect of the weights of Table 3
when applied to Table 1. Table 5 shows the optimised
weights w
0
resulting in high fidelity with simulations
achieving consistently the equilibrium point to the re-
quired cytotoxicity.
For example, consider that the optimizer weight
w
0
has been settled as the value 0.73 (see Table 5)
for Experiment 5 and NK to tumor cell ratio equal
to 1, then for all features i and Experiment j = 5, the
weights w in Table 3 are updated thus:
∀i, j ∈ I=1:6,J=1:5, w
i j
= w
i j
w
0
Figure 7: Agent simulation for Experiment 5, ratio 1:1.
Figure 8: Agent simulation for Experiment 5, ratio 4:1.
To illustrate the process, consider for Experiment 5
(Table 3, Row 5) that the non-zero weights w are 1.1
(for IL15) and 1.1 (for HLAI), and the kill distance is
initially set to 0.5. Thus, the new kill distance in the
first iteration will be 0.5 × 1.1 × 0.73 = 0.4015, and
in the second iteration, 0.55 × 1.1 × 0.4015 = 0.3224.
We repeat the experimental conditions (Table 2)
for the in-vitro experiments with real NK-cells and tu-
mour cells for four different initial ratios of NK-cells
and tumour cells, following exactly the ratio of NK-
cells to tumour cells suggested by Fern
´
andez et al.
(2013) and appearing in Table 4. Table 4 also shows
survival ratios in our experiments.
Each experiment was repeated several times to
verify that the same equilibrium point was reached
with the same weight. In some cases the result was
unstable (some runs did not stop at target) and this is
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
174

Table 4: Resulting cytotoxicity percentage for each ratio of
agent classes in in-vitro experiments.
Experiment Ratio
1 2 4 8
1 14 16 19 26
2 19 27 40 45
3 10 10 11 13
4 42 55 66 73
5 41 57 74 87
due to the stochastic nature of the agent system. In
this case, the weight value was varied slightly in up-
per and lower bound until a stable equilibrium was
found on repeats. In future work an automatic opti-
mization such as hill climbing with a fitness function
could be used.
In summary, in our simulation, NK-cell agents and
tumour-cell agents interact (refer to Figure 1) as per
the effects of inhibitors and stimulants (refer to Ta-
ble 3) that are tuned (by w
0
) to impact the behavioural
parameters (Table 1) in a two dimensional state space
(as illustrated by Figure 6). The kill distance and de-
tect distance represent the physical distance in the bi-
ological system for locking on (via ligands and recep-
tors) and detection of chemical substances by the NK
cell which signal the presence of a tumour cell. Note
that the predator (NK) agents perform a random walk
until a tumour cell falls within detect distance, then
the NK moves directly towards the tumour.
Figure 7 and Figure 8 show two scenes from
our multi-agent simulations using the Repast Sim-
phony (North et al., 2013). Both correspond to the
settings of Experiment 5, where Figure 7 has a ratio
of 1:1 NK-cell agents to tumour cell agents, with ini-
tial cell populations of 400 for each agent type. On
the other hand, Figure 8 is the case where the ratio
is 4:1, with initial cell populations of 1600 NK-cell
agents and 400 tumour cells. The tumour cells are
coloured red and the NKs are coloured blue. For Fig-
ure 7, the system has reached an equilibrium at 237
tumour cells, which matches the cytoxicity of 41%
obtained in the in-vitro experiment.
Figure 8 shows the situation where the system has
reached an equilibrium at 106 tumour cells, which
matches to the cytoxicity of 74% as obtained in the
in-vitro experiment.
6 EXPERIMENTS
We now detail the results of the experiments to
simulate the in-vitro clinical experiments presented
by Fern
´
andez et al. (2013). Table 5 shows a total
of 20 experiments given that we ran 4 ratios in 5 ex-
periments. Our results show that for all the ratios and
all of the experiments, we can successfully reproduce
the cytotoxicity percentage combinations. That is, in
each case, we achieve convergence to the target %
of tumour cells killed with error margin (%target vs
%real) of between -1.5% and +2.25% (last column
in Table 5). It can be seen that a lower weight (col-
umn 3) was found to be optimum for experiments 1,
2 and 4, whereas higher values were required for ex-
periments 3 and 5. This is due to the fact that the
experimental settings involve only one inhibitor (or
stimulant) in one set of experiments while the latter
experiments involve more factors.
Figures 9 to Figure 11 provide graphical illustra-
tions of the results of Table 5. In particular, Figure 9
shows the weight values w
0
we found for each exper-
iment and ratio. It can be seen that for each experi-
ment, the weights decrease inversely with respect to
the ratios. Also it can be seen that higher cytotox-
icity requires a higher weight but more overriding is
the combination of multiple factors (especially Exper-
iment 3). Figure 10 shows the simulated cytotoxic-
ity for each experiment and ratio. We obtain remark-
able similarity to the in-vitro results, our Figure 10
matches Fern
´
andez et al. (2013, Figure 3). Note that
Figure 11 shows the error margin (real in-vitro val-
ues (Fern
´
andez et al., 2013, Figure 3) vs our multi-
agent simulated cytotoxicity) for each experiment and
ratio. The relative errors are never more than 2.25%.
Figure 12 shows a benchmark of performance of
our simulations. We ran Repast Simphony 2.6 in
“batch mode” for environment with different num-
ber of cells. For this benchmark, we used Exper-
iment 5 with ratio 1:1 NK to tumour cells. We
used a Lenovo laptop with Intel Core i7-7500U, CPU
@2.7Ghz (64bit processor), 12GB RAM, Windows
10 64bit operating system. It can be seen that the pro-
cessing time fits to a third degree polynomial, where
9600 cells marks the saturation point of the com-
puter. The performance would of course be improved
using a GPU and/or multi core parallel processing,
which would allow for a much greater number of
cells, though for the current set of experiments this
was not considered necessary as the stochastic nature
and distance based interactions depend on density of
cells per square unit of space rather than pure quan-
tity. However, testing with greater quantities will be a
potential aspect for future work.
6.1 Discussion
From the results it can be seen that by manipulating
the control parameters we can accurately simulate the
real in-vitro experiments by Fern
´
andez et al. (2013).
The flexibility of the multi-agent simulation pays-off!
This promises to reduce the time needed for clinical
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic Alternatives to Cancer Treatment
175
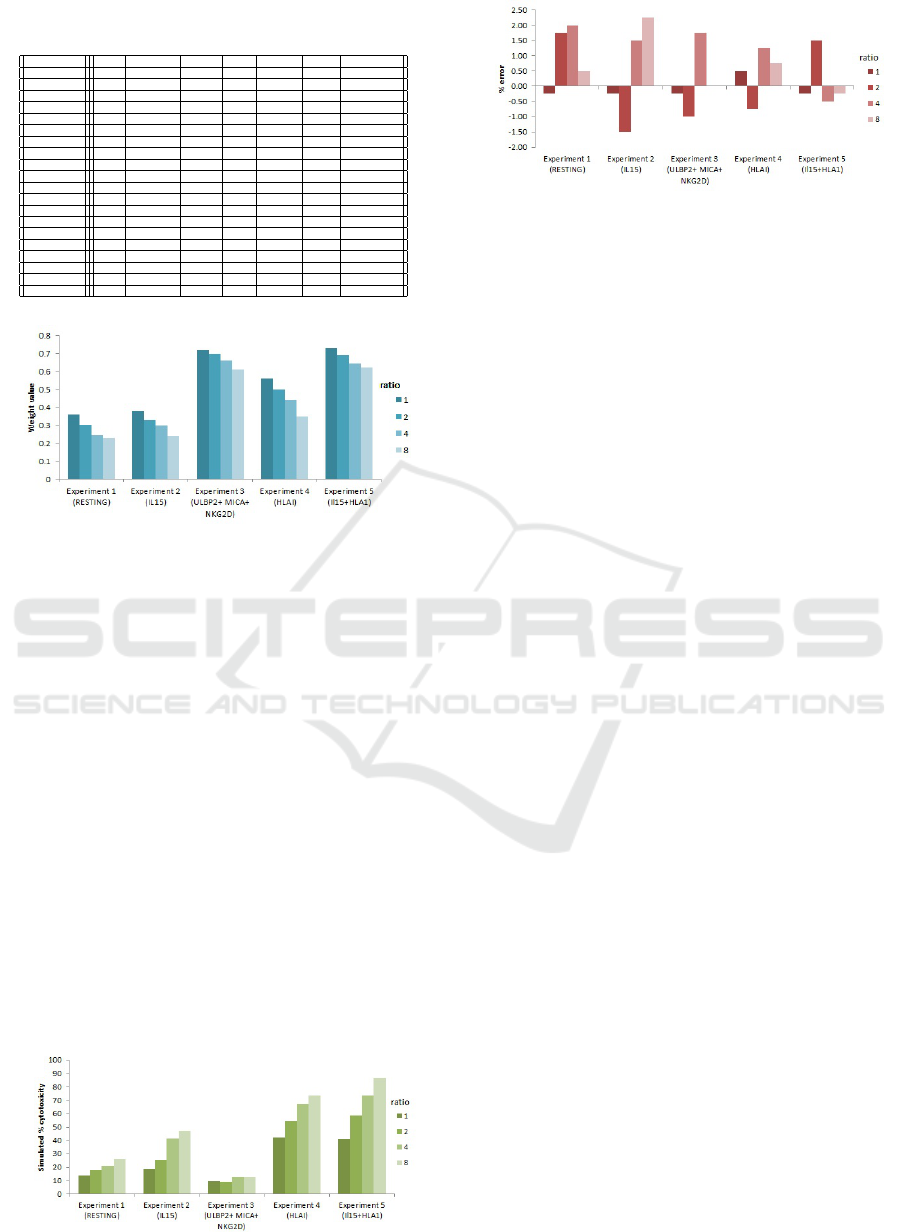
Table 5: Results of Experiments 1 to 5 for different ratios
of NK to Tumour cells.
Experiment Ratio Weight w’ #Target #Real %Target %Real %Deviation
1 1 0.36 344 345 14 13.75 - 0.25
1 2 0.3 336 329 16 17.75 + 1.75
1 4 0.245 324 316 19 21 + 2.0
1 8 0.228 296 294 26 26.5 + 0.5
2 1 0.38 324 325 19 18.75 - 0.25
2 2 0.33 293 298 27 25.5 - 1.5
2 4 0.297 240 234 40 41.5 + 1.5
2 8 0.24 220 211 45 47.25 + 2.25
3 1 0.72 360 361 10 9.75 - 0.25
3 2 0.70 360 364 10 9 - 1.00
3 4 0.66 356 349 11 12.75 + 1.75
3 8 0.61 348 348 13 13 0.0
4 1 0.56 232 230 42 42.5 + 0.5
4 2 0.5 180 183 55 54.25 - 0.75
4 4 0.439 136 131 66 67.25 + 1.25
4 8 0.347 108 105 73 73.75 + 0.75
5 1 0.73 236 237 41 40.75 - 0.25
5 2 0.693 172 166 57 58.5 + 1.5
5 4 0.645 104 106 74 73.5 - 0.5
5 8 0.62 52 53 87 86.75 - 0.25
Figure 9: Weight values for each experiment and ratio.
testing for customized patient treatment where every
day counts. The multi-agent system which allows
the creation of thousands of ‘virtual’ cells permits a
much closer stochastic type interaction, in contrast
to the typical differential equation approach. Also,
the agent simulation allows the definition of a virtual
space (a grid with N × M dimensions) in which the
agents move and interact. This, combined with the
kill distance and detection distance parameters allow
to approximate the real chemical detection between
cells, and the lock-on distance between receptors and
ligands. The approximation is due to the mapping
onto the two dimensional grid where the agents are
defined. The kill probability also reflects the stochas-
tic/probabilistic nature of the process: the probability
that an NK will realistically kill a Tumour cell when
within the kill distance. Whether the NK kills a Tu-
mour cell or not can depend on semi-random aspects
such as locking orientation, particularities of the indi-
Figure 10: Simulated cytotoxicity per experiment and ratio.
Figure 11: Error margin for each experiment and ratio.
vidual NK-cell and the Tumour cell in the encounter,
and probabilistic events such as movement of adjacent
cells. Finally, the steps with no tumour cells controls
the predator-prey interaction, which does happen in
the in-vitro environment. Here, we incorporate it as a
deactivation of the NK-cell; that is, if in N cycles no
tumour cell has entered into the detect distance of a
given NK-cell, then it becomes dormant. This param-
eter together with the detect distance are major pa-
rameters in steering the simulation: as more tumour
cells are killed and become less prevalent, more NK-
cells will become inactive. However, the NK-cells
reactivate again if the inverse happens: tumour cells
come within detect distance during at least N cycles.
For the in-vitro experiments, the activator for the
NK (IL15) and the ligands/receptors (NKG2D on the
NK cell, MICA, ULBP2 and HLAI on the tumour
cell) were pre-selected by clinical trials, as well as
the type of tumour cell (HTB-186 MB). Hence, in or-
der to build an even more accurate decision-support
system (DSS) for clinical trials, the agent simulation
would need to serve as a back-end to the DSS which
would, for a given combination of tumour type, NK-
cell type, activator and set of ligands/receptors, pro-
duce the expected result, that is the resulting kill rate
(cytotoxicity). It may be infeasible to expect to build
a general system for every cancer treatment, and it
would be likely that specialized systems (knowledge
bases) would be loaded for specific types of cancer.
One form of action could be the following: by
successfully simulating a diversity of in-vitro clini-
cal experiments, the optimum control parameters and
weights would be found for the corresponding cases.
This would build a knowledge-base of cases. Thus,
when a new case is presented, the closest historical
case would be retrieved and used as the basis for a
new simulation. Ideally, it would be possible not only
to find the optimum control parameter set of the agent
system, but also the combination of activator, lig-
ands/receptors to block or to potentiate maximal cy-
totoxicity. This would result in a system with just one
parameter as input (the tumour cell type) and a set of
parameters as output (immune system cell type, acti-
vators, ligands/receptors to block/potentiate, resulting
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
176
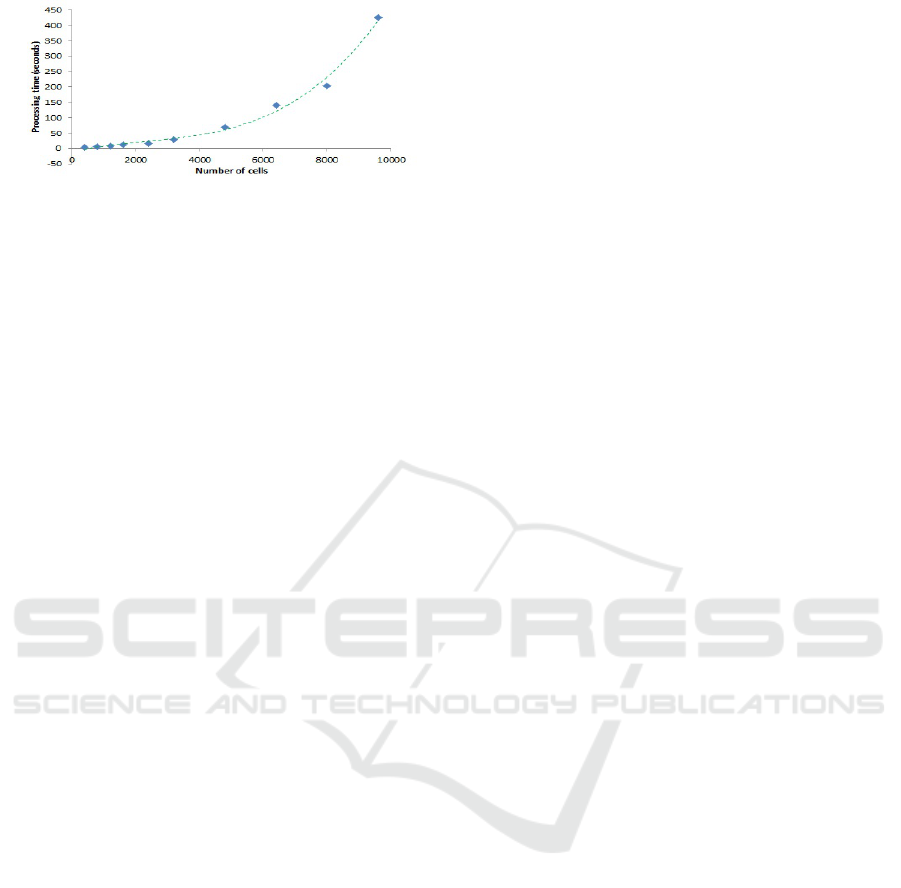
Figure 12: Number of cells vs processing time - Experi-
ment 5, ratio 1:1.
cytotoxicity). As a further enhancement, a DSS could
also answer questions such as: what would be the re-
sults if we use IL2 instead of IL15? If we block ligand
B instead of A, receptor Y instead of X, and so on. Is
it possible to reach 100% cytotoxicity? In general, we
could ask “what is the set of clinical parameters which
maximizes cytotoxicity?”
Returning to the current simulation, there remain
issues to evaluate: how close is the spatial represen-
tation to the real in-vitro physical environment. We
have used a 40 by 50 unit grid, where the agents them-
selves have no explicit dimension, but where the de-
tect distance value starts at 1.0 units and the kill dis-
tance starts at 0.5 units. How well does this map onto
the real physical space? Also, how many cells are
necessary to represent the in-vitro cell populations.
We have used a minimum of 400 and a maximum
of 3200 in the simulations. Is that enough to repre-
sent the stochastic behaviour? Also, the agent simu-
lation is defined on a two dimensional grid, whereas
the in-vitro is acting in a three dimensional space.
These aspects limit the scope of the simulation. How-
ever, even with these limitations, we would say that
the agent simulation is much more realistic than the
differential equation model, and follows similar lines
to agent simulations in general. As future work, we
could try to implement a 3D graph-data structure in-
stead of the 2D grid, in which graph nodes represent
the cells, which are in turn, linked to neighbourhoods
of adjacent cells.
Also, it could be said that the agent system per
se is somewhat limited to a detect/kill functionality
within a parameter-defined range. As a future step, in-
hibitors/stimulators could be modelled as entities in-
stead of modulators of parameter values, to account
for possible spatial effects, for example.
7 CONCLUSIONS
We have demonstrated the high flexibility of multi-
agent simulations in two aspects. First, modelling as-
pects of the real interaction between tumour cells and
the naturally existing NK-cells, as they are inhibited
or stimulated in real in-vitro environments. Secondly,
we can use the multi-agent system’s additional param-
eters to explore and optimise the best combinations
which influence the inhibitors and stimulatory com-
pounds on NK-agents to approximate the cytotoxicity.
Our results show that by manipulating the control pa-
rameters we can accurately simulate the real in-vitro
experiments of Fern
´
andez et al. (2013).
This is a promising step for assisting the need
for clinical testing for customized patient treatment
where every day counts. The multi-agent system
which allows the creation of thousands of “virtual”
cells permits a much closer stochastic type interac-
tion, in contrast to the typical ODE approach.
This research has resulted in new ideas for future
work, such as, how to build a true decision-support
system which can give the clinical trial set-up (im-
mune cell type, activator, which ligands and receptors
to inhibit/potentiate) to maximize cytotoxicity for a
given tumour cell type.
ACKNOWLEDGEMENTS
We are grateful to the anonymous reviewers for their
suggestions. We are also grateful to Sergio Nettle-
ton (Universitat Polit
`
ecnica de Catalunya, Barcelona,
Spain) for the Repast programming support.
REFERENCES
(1997). Adam, J. and Bellomo, N., eds., A Survey of Models
for Tumor-Immune System Dynamics, Modeling and
Simulation in Science, Engineering and Technology,
Boston. Birkh
¨
auser.
´
Alvarez, E., Toledano, V., Morilla, F., Hern
´
andez-Jim
´
enez,
E., Cubillos-Zapata, C., Varela-Serrano, A., Casas-
Mart
´
ın, J., Avenda
˜
no Ortiz, J., Aguirre, L. A., Ar-
nalich, F. Maroun-Eid, E., Mart
´
ın-Quir
´
os, A., Quin-
tana D
´
ıaz, M., and L
´
opez-Collazo, E. (2017). A sys-
tem dynamics model to predict the human monocyte
response to endotoxins. Frontiers in Immunology,
8:915.
Barnes, D. J. and Chu, D. (2015). Guide to Simulation and
Modeling for Biosciences. Simulation Foundations,
Methods and Applications. Springer.
Borshchev, A. and Filippov, A. (2004). From system dy-
namics and discrete event to practical agent based
modeling: Reasons, techniques, tools. 22nd Int. Conf.
of the System Dynamics Society.
B
˘
adic
˘
a, A., B
˘
adic
˘
a, C., Ivanovi
´
c, M., and D
´
anciulescu,
D. (2018). Multi-agent modelling and simulation of
graph-based predator–prey dynamic systems: A BDI
approach. Expert Systems, 35(5):e12263.
Multi-agent Modeling Simulation of In-vitro T-cells for Immunologic Alternatives to Cancer Treatment
177

Chase, J. M., Abrams, P. A., Grover, J. P., Diehl, S., Ches-
son, P., Holt, R. D., Richards, S. A., Nisbet, R. M., and
Case, T. J. (2002). The interaction between predation
and competition: a review and synthesis. Ecology Let-
ters, 5(2):302–315.
Chen, D. S. and Mellman, I. (2013). Oncology meets im-
munology: The cancer-immunity cycle. Immunity,
39(1):1–10.
Eftimie, R., Gillard, J. J., and Cantrell, D. A. (2016). Math-
ematical models for immunology: Current state of the
art and future research directions. Bulletin of Mathe-
matical Biology, 78(10):2091–2134.
ElSayed, Z. A. (2018). Recent advances in cancer im-
munotherapy. QJM: An Int. Journal of Medicine,
111(suppl 1).
Engblom, S. (2019). Stochastic simulation of pattern for-
mation in growing tissue: A multilevel approach. Bul-
letin of Mathematical Biology, 81(8):3010–3023.
Farag, S. S., Fehniger, T. A., Ruggeri, L., Velardi, A., and
Caligiuri, M. A. (2002). Natural killer cell recep-
tors: new biology and insights into the graft-versus-
leukemia effect. Blood, 100(6):1935–1947.
Fern
´
andez, L., Portugal, R., Valent
´
ın, J., Mart
´
ın, R.,
Maxwell, H., Gonz
´
alez-Vicent, M., and P
´
erez-
Mart
´
ınez, A. (2013). In vitro natural killer cell im-
munotherapy for medulloblastoma. Frontiers in on-
cology, 3(94).
Figueredo, G. P., Joshi, T. V., Osborne, J. M., Byrne, H. M.,
and Owen, M. R. (2013a). On-lattice agent-based sim-
ulation of populations of cells within the open-source
chaste framework. Interface focus, 3(2).
Figueredo, G. P., Siebers, P.-O., and Aickelin, U.
(2013b). Investigating mathematical models of
immuno-interactions with early-stage cancer under an
agent-based modelling perspective. BMC Bioinfor-
matics, 14(6):S6.
Figueredo, G. P., Siebers, P.-O., Owen, M. R., and Reps,
J. Aickelin, U. (2014). Comparing stochastic differ-
ential equations and agent-based modelling and simu-
lation for early-stage cancer. PLoS ONE, 9(4):e95150.
Jindal, A. and Rao, S. (2017). Agent-based modeling
and simulation of mosquito-borne disease transmis-
sion. 16th Conf. on Autonomous Agents and MultiA-
gent Systems, AAMAS ’17, pages 426–435, Richland,
SC. Int. Foundation for Autonomous Agents and Mul-
tiagent Systems.
Karsai, I., Montano, E., and Schmickl, T. (2016). Bottom-
up ecology: an agent-based model on the interac-
tions between competition and predation. Letters in
Biomathematics, 3(1):161–180.
Kingsland, S. (2015). Alfred J. Lotka and the origins of
theoretical population ecology. Proc. of the National
Academy of Sciences, 112(31):9493–9495.
Linderman, J. J., Riggs, T., Pande, M., Miller, M., Marino,
S., and Kirschner, D. E. (2010). Characterizing the dy-
namics of CID4+ T cell priming within a lymph node.
The Journal of Immunology, 184(6):2873–2885.
Louzoun, Y. (2007). The evolution of mathematical im-
munology. Immunological reviews, 216:9–20.
Montagna, S., Donati, S., and Omicini, A. (2010).
An agent-based model for the pattern formation in
drosophila melanogaster. Alife XII Conference.
Montagna, S., Omicini, A., and Pianini, D. (2016). Extend-
ing the Gillespie’s stochastic simulation algorithm for
integrating discrete-event and multi-agent based sim-
ulation. Multi-Agent Based Simulation XVI, volume
9568 of MABS 2015, pages 3–18, Cham. Springer.
Montagna, S. and Viroli, M. (2010). A framework for mod-
elling and simulating networks of cells. Electronic
Notes in Theoretical Computer Science, 268:115–129.
North, M. J., Collier, N. T., Ozik, J., Tatara, E. R., Macal,
C. M., Bragen, M., and Sydelko, P. (2013). Complex
adaptive systems modeling with Repast Simphony.
Complex Adaptive Systems Modeling, 1(1):3.
Pardoll, D. M. (2012). The blockade of immune check-
points in cancer immunotherapy. Nature reviews.
Cancer, 12(4):252–264.
Shimoni, Y., Nudelman, G., Hayot, F., and Sealfon, S.
(2011). Multi-scale stochastic simulation of diffusion-
coupled agents and its application to cell culture sim-
ulation. PloS one, 6:e29298.
Stracquadanio, G., Umeton, R., Costanza, J., Annibali,
V., Mechelli, R., Pavone, M., Zammataro, L., and
Nicosia, G. (2011). Large scale agent-based modeling
of the humoral and cellular immune response. Arti-
ficial Immune Systems, pages 15–29, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
Sun, W. (2017). Recent advances in cancer immunotherapy.
Journal of Hematology & Oncology, 10(1):96.
Tatara, E., North, M. J., Howe, T. R., Collier, N. T., and Vos,
J. R. (2006). An introduction to Repast modeling by
using a simple predator-prey example. 2006 Conf. on
Social Agents: Results and Prospects. Argonne Na-
tional Laboratory.
Wodarz, D. (2006). Killer Cell Dynamics: Mathemati-
cal and Computational Approaches to Immunology.
Springer, New York.
Zhao, D. and Jin, W. D. (2005). The study of coopera-
tive behavior in predator-prey problem of multi-agent
systems. Autonomous Decentralized Systems, 2005.
ISADS 2005., pages 90–96.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
178
