Surface Plasmons Phase Imaging Microscopy using Deep Learning

Suejit Pechprasarn

, Suvicha Sasivimolkul

, Chayanisa Sukkasem

Phitsini Suvarnaphaet

and Nuntachai Thongpance

College of Biomedical Engineering, Rangsit University, Phaholyothin Road, Pathum Thani, Thailand

Keywords: Surface Plasmon Resonance, Phase Imaging, Phase Retrieval Algorithm, Surface Plasmon Microscopy, Deep

Learning, Image Recognition.

Abstract: Surface Plasmon Resonance have been a gold standard for biosensing and chemical sensing over the past

decades. The surface plasmons are a confined electromagnetic wave mode propagating on surface of noble

metals. One of the key features of surface plasmons is that they are sensitive to its surrounding medium,

therefore the surface plasmons are usually applied in sensing applications. It has been very well established

that measuring the phase response of the surface plasmons is more sensitive and more robust compared to

intensity or amplitude measurements. To measure the phase, of course, an interferometer is required. This

will impose the complexity to the optical alignment. Moreover, the interferometric systems usually require a

well-controlled experimental condition, such as, vibration isolation system. Recently, there are some interest

of the research community to recover the surface plasmons phase through computational phase retrieval

algorithms, such as, Ptychography. Although these computational algorithms can recover the phase profile,

they do require many images or a lengthy computing time making them not suitable for real-time measurement.

Here, we propose a novel approach to perform surface plasmon phase retrieval using image recognition

though deep learning. We demonstrate the feasibility of using the deep learning to recover amplitude and

phase responses of simulated back focal plane images.

1 INTRODUCTION

Surface Plasmons (SPs) are a confined

electromagnetic wave phenomenon propagating on

surface of noble metals, such as, gold (Au), Silver

(Al) and Copper (Cu) (Somekh & Pechprasarn,

2016). Surface Plasmon Resonance (SPR) is a well-

known resonant effect of the SPs occurring when

there is a p-polarized light beam (TM polarization)

with a matching momentum to the resonant frequency

of the SPs illuminating on the noble metal surface.

The SPR is very sensitive to its local refractive index

change around the height of 200nm from the metal

surface due to the evanescent wave penetration depth

of the SPs (Shen, Learkthanakhachon, Pechprasarn,

Zhang, & Somekh, 2018). The SPs have been widely

utilized as a gold standard equipment for label-free

biosensing (Liedberg, Nylander, & Lundström,

1995), chemical sensing (Liedberg, Nylander, &

https://orcid.org/0000-0001-9105-8627

https://orcid.org/0000-0002-1459-8133

https://orcid.org/0000-0003-4057-7237

https://orcid.org/0000-0001-8195-1841

Lunström, 1983) and bioimaging (Pechprasarn &

Somekh, 2014; Somekh, Pechprasarn, Chow, Meng,

& Shen, 2016).

There are two standard approaches to excite the

SPs, which are (1) Kretschmann configuration

(Kretschmann & Raether, 1968) as shown in Figure

1a and (2) Otto configuration (Akowuah, Gorman, &

Haxha, 2009) as shown in Figure 1b. Both optical

configurations require high index prism coupling and

p-polarized incident illumination with the wavelength

in red to infrared regime. The main difference

between the two configurations is the thickness of the

metal and the position of the metal. On the reflectance

of both configurations, there will be a dark band in

the reflectance curve, so called ‘SP dip’ position and

the wave vector position that the SP dip occurs is the

surface plasmon’s wave vector or k

Pechprasarn, S., Sasivimolkul, S., Sukkasem, C., Suvarnaphaet, P. and Thongpance, N.

Surface Plasmons Phase Imaging Microscopy using Deep Learning.

DOI: 10.5220/0008917100330039

In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 33-39

ISBN: 978-989-758-401-5; ISSN: 2184-4364

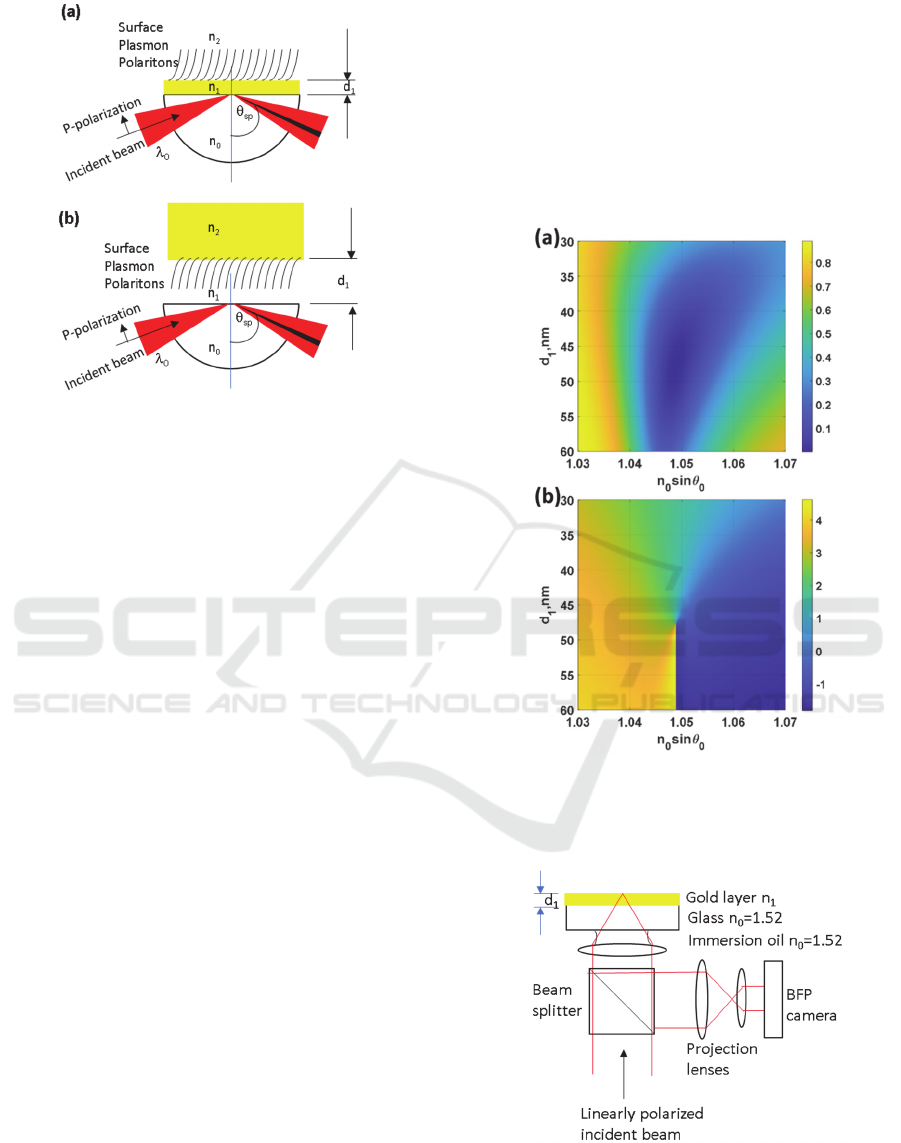
Figure 1: Shows conventional SPR optical setups (a)

Kretschmann configuration and (b) Otto configuration.

The SP dip occurs due to loss mechanisms of SP

coupling (Pechprasarn, Chow, & Somekh, 2018).

This is a strong evidence for SP excitation. Figure 2a

shows the simulated SP reflectance curves for

different thicknesses of gold between 60nm to 60nm

with the p-polarized incident wave of 633nm

wavelength (HeNe) and the gold complex refractive

index of 0.1834+3.4332i (Johnson & Christy, 1972)

for Kretschmann configuration. Fig.2b shows

corresponding phase responses. The phase responses

of reflection coefficient for p-polarized wave were

different for different thicknesses of the gold layer d

For the thicknesses lower than 47nm had 2π rad phase

transition over the SP dip, whereas the thicknesses

higher than 47nm had π rad phase transition. This can

be explained by coupling strength of the SPs and the

direct reflection from the gold surface, which is

explained in detail in the cited reference here

(Pechprasarn et al., 2018). The simulation results in

Figure 2 were calculated using Fresnel equations and

Transfer matrix approach (Suvarnaphaet &

Pechprasarn, 2018).

For Kretschmann configuration, the uniform

metal is usually very thin and attach to the glass prism

layer. The metal thickness (d

) for biosensing

depends

on the metal type and its application. For biosensing,

gold is usually used as the SPR sensor chip, since gold

is chemically stable and does not form an oxide layer

with its environment (Suvarnaphaet & Pechprasarn,

2018). The gold thickness is usually employed at

46nm to 50nm, since it gives the darkest |r

On the other hand, for the Otto configuration there

is a very thick metal layer positioned around one

wavelength of light away from the glass prism. The

Otto configuration to the best of author knowledge it

is not usually applied in a biosensing. Most of its

applications are in physics, like study of light-matter

interaction (Pechprasarn et al., 2016).

Thanks to high numerical aperture (NA) objective

lenses, which are becoming more affordable and

widely commercially available, they have made the

SPs excitation possible under a conventional

microscope configuration as shown in Figure 3.

Figure 2: Shows (a) Reflectance |r

and (b) phase of r

rad for 30nm to 60nm of uniform gold layer coated on BK7

glass with refractive index of 1.52. The incident wave was

p-polarized wave at 633nm wavelength.

Figure 3: Shows gold sensor under an oil immersion

objective lens and optical system to capture the back focal

plane (BFP) image.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

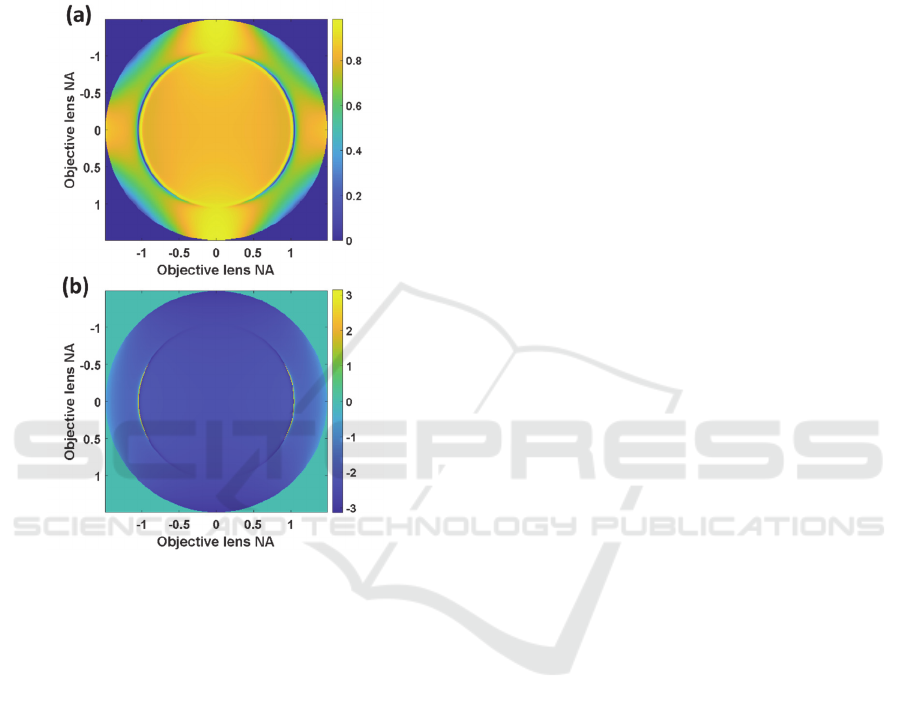
Figure 4a and Figure 4b show a simulated back

focal plane (BFP) of the 1.49 NA objective lens

microscope system in Figure 3a for a linearly

polarized coherent source of 633nm wavelength. The

pure p-polarization is along the x-axis of Figure 4 and

the pure s-polarization is along the y-axis of Figure

Figure 4: Shows (a) BFP intensity and (b) BFP phase in rad

for the electric field component along x-direction. n0=1.52,

n1=0.1834+3.4332i ,n2=1.00, d1=45nm λ0=633nm.

Although the SPR has been discovered and its

theory have been thoroughly studied and very well

established for a few decades, there are still new

findings and breakthroughs reported over the recent

years. One of the most exciting work in the field is

single protein molecule imaging (Taylor & Zijlstra,

2017) and quantitative bioimaging (Tan,

Pechprasarn, Zhang, Pitter, & Somekh, 2016). Most

of the ultra-sensitive SPR systems rely on phase SPR

phase measurement (Pechprasarn & Somekh, 2014).

It has been very well established that in measuring

SPR phase is more robust and more sensitive than

measuring SPR amplitude response (Kabashin,

Patskovsky, & Grigorenko, 2009). Of course, to

measure the phase response, an optical interferometer

is needed making the optical configuration more

sophisticated (Pechprasarn, Zhang, Albutt, Zhang, &

Somekh, 2014). There are several interferometric

configurations reported to improve SPR phase

measurement stability and repeatability, such as,

common path SPR interferometry (Pechprasarn et al.,

2014). Recently there is an interest in applying

computational phase retrieval algorithms, such as,

Ptychography (Somekh, Pechprasarn, Chen,

Pimonsakonwong, & Albutt, 2017), Transport of

intensity (Streibl, 1984) and Gerchberg and Saxton

(Zalevsky, Mendlovic, & Dorsch, 1996) to retrieve

the SPR phase with no requirement of an

interferometer system.

Although the phase retrieval algorithms can be

employed to recover the SPR phase, they still have

their own disadvantages for each of the algorithms.

For example, for the Ptychography and Gerchberg

and Saxton they are iterative therefore they are not

suitable for real time measurement. The transport of

intensity method is not an iterative method, it

recovers the phase by solving a Poison’s equation to

wave propagation to predict the phase of the

propagating wave. The method requires finite

element (FEM) calculation, computationally time

consuming and require relatively large computing

power compared to the other two methods.

Here, the mentioned issues will be addressed by

replacing the time-consuming phase retrieval

computations by a data driven technology deep

learning. Here a 3 layered U-shaped artificial neural

network (UNet) architecture was employed to learn

how to do image segmentation and regression to

predict the corresponding real part and imaginary part

of the back focal plane as the network output.

2 PROPOSED METHOD

In this section, an overview of relevant computational

methods and the deep learning are described in detail.

There are 3 major components to train the UNet

network (1) Input BFP intensity (2) the UNet network

and (3) the labelled output BPF. Once the UNet has

been trained and has reach its convergence. The

network can then be deployed to validate itself, by

predicting an output for a new BFP input. Validation

to test the robustness of the trained network will be

discussed in section 3.

2.1 Back Focal Plane Calculation

Here, 1,000 BFP images were computed with

different d

thicknesses ranging from 25nm to 65nm

serving as the training data for the UNet, which will

be described in detail in the later section. The d

thicknesses are randomly distributed as shown in

Surface Plasmons Phase Imaging Microscopy using Deep Learning

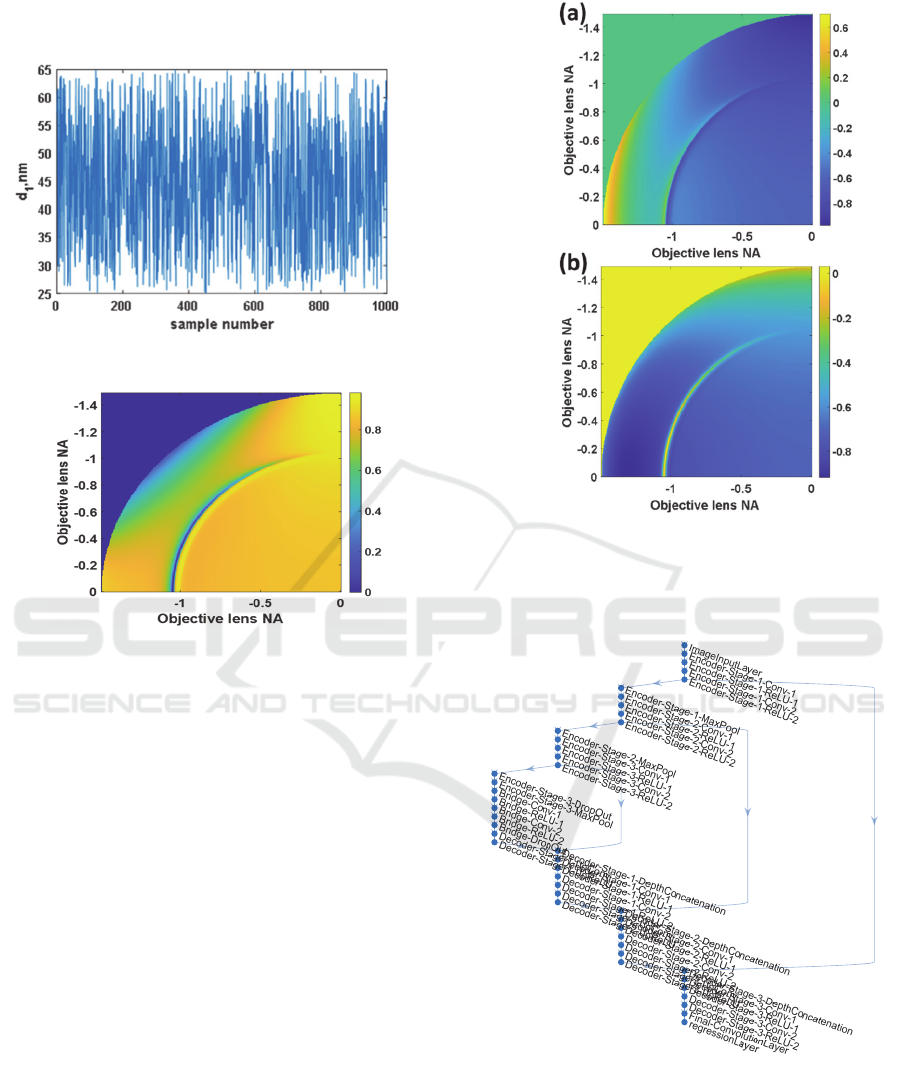
Figure 5. The mean value and the standard deviation

for the d

were 44.55nm and 11.33nm respectively.

Figure 5: Shows d1 thicknesses for all the 1,000 cases.

Figure 6: Shows one quadrant of the BFP intensity for the

500

sample with d

of 49.54nm.

BFPs for all the d

thicknesses were then

computed using Fresnel equations and the transfer

matrix approach (Suvarnaphaet & Pechprasarn,

2018). It is important to point out that only one

quadrant of the BFP was computed to reduce the size

of the training set since the other 3 quadrants contain

the exact same information. Figure 6 shows a

computed BFP intensity of the electric field pointing

along x direction for the case number 500 (d

49.54nm). This is the input for the neural network.

For the output from the neural network, the

labelled data was prepared as the real part and the

imaginary part of the BFP as shown in Figure 7a and

Figure 7b. The training dataset for the neural network

consisting of 1,000 images with 1 input (BFP

intensity with the size of 328 pixels x328 pixels) and

2 outputs (the real part of the BFP and the imaginary

part with the total size of 328 pixels x328 pixels x 2

dimensions). It is important to point out that one can

use only one output by taking the phase as the output,

but here the two outputs was implemented to avoid

the ambiguity of 2π rad phase wrapping. This will be

discussed in detail in discussion section later.

Figure 7: Shows (a) real part of the 500

sample BFP and

(b) imaginary part of the 500

sample BFP.

2.2 U-Network Shape Neural Network

Figure 8: Shows U-shaped artificial neural network

structure with 3 layers of encoders and 3 layers of decoders.

In this paper, U-shaped artificial neural network

structure with 3 layers of encoder and 3 layers of

decoder as shown in Figure 8 were employed. The

UNet has been found to one of the best artificial

neural networks (ANNs) for image segmentation and

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

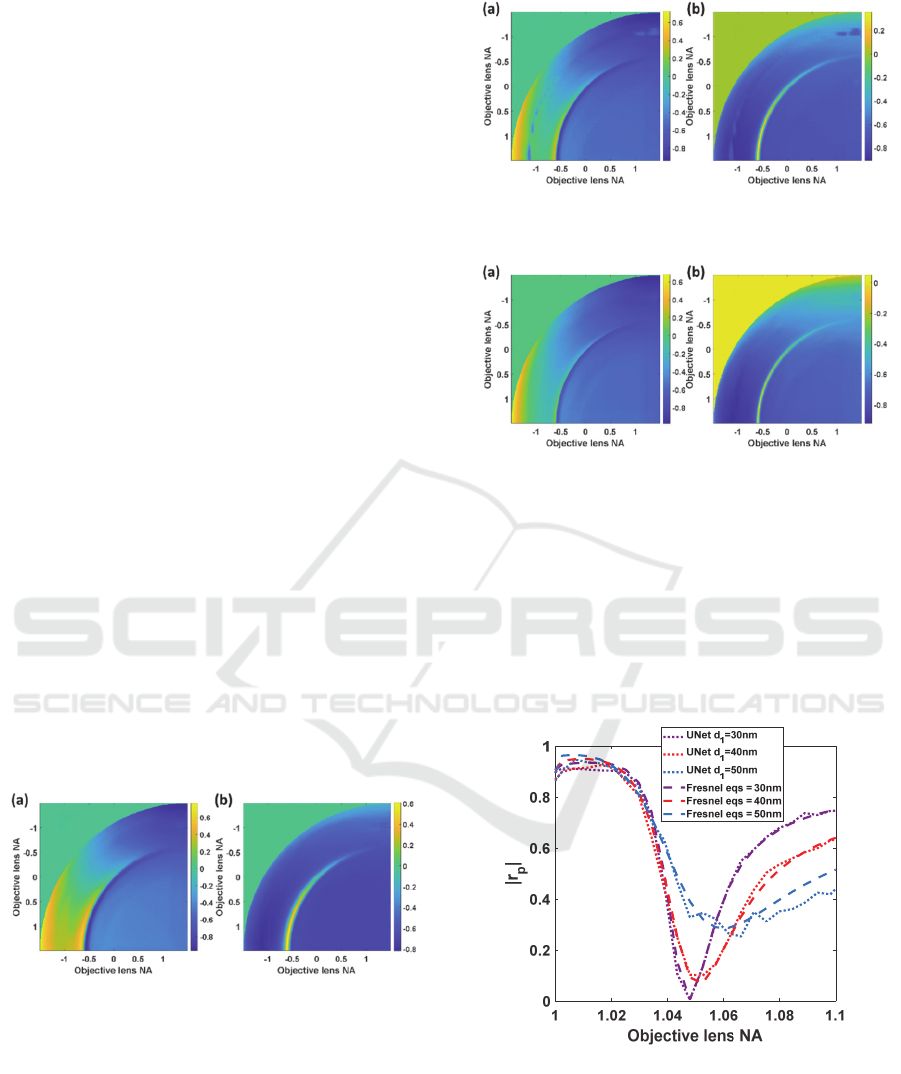
image regression. Predicting the phase values is, of

course, in the category of image regression. The

detailed functions for each network layer are omitted

they are all standard functions in deep learning. The

UNet is then trained with the BFP dataset described

in the section 2.1.

3 RESULTS AND DISCUSSION

3.1 Network Training

The UNet network was trained under

MATLAB2019a environment with a single graphic

processing unit (GPU) Nvidia GeForce GTX1060. It

took about 8 hours for 100 Epoches (100,000

iterations in total). The UNet is trained so that the

recovered outputs have reached the root mean square

error less than 0.0001 or 0.01%.

Once the UNet is trained, in the next section the

UNet will be tested with different thicknesses of d

validate the corresponding output results.

3.2 Network Testing with Simulated

Data

Here let us, see how well the network responses to the

simulated input BFP. It is interesting to point out that

the BFP phase responses do have different phase

gradient and transition levels depending on the d

sensor thickness. Three thicknesses of 30nm,40nm

and 50nm were chosen to be the test input to the

trained UNet.

Figure 9: Shows (a) real part for d

of 30nm and (b)

imaginary part for d

of 30nm.

The BFP images corresponding to the 3

thicknesses were then computed as discussed in

section 2.1. The 3 BFPs were employed as an input to

the trained UNet in turn. The output real part and

imaginary part images corresponding to the 3 inputs

are shown in Figure 9 to Figure 11 for d1 of 30nm,

40nm and 50nm respectively.

Figure 10: Shows (a) real part for d

of 40nm and (b)

imaginary part for d

of 40nm.

Figure 11: Shows (a) real part for d

of 50nm and (b)

imaginary part for d

of 50nm.

The UNet can recover the real and imaginary parts

for all the three inputs. However, for the 40nm case,

there were some noise artefacts at around the NA of

1.02 for both s and p polarizations.

From the results in Figure 9 to Figure 11, the

reflectance curve and the phase transition can be

calculated as shown in Figure 12. Figure 12 shows the

linescan reflectance |r

for the 3 thicknesses.

Figure 12: Shows linescan of recovered reflectance |r

calculated from the results in Figure 9 to Figure 11 in

comparison with the ideal BFPs calculated using Fresnel

equations.

It can be observed that the recovered intensity images

have the similar shape and intensity profiles

compared to the Fresnel calculations. However, they

did have some noise on the recovered SP dips

Surface Plasmons Phase Imaging Microscopy using Deep Learning

especially for 40nm case. The SP phase responses

could also be recovered from the results in Figure 9

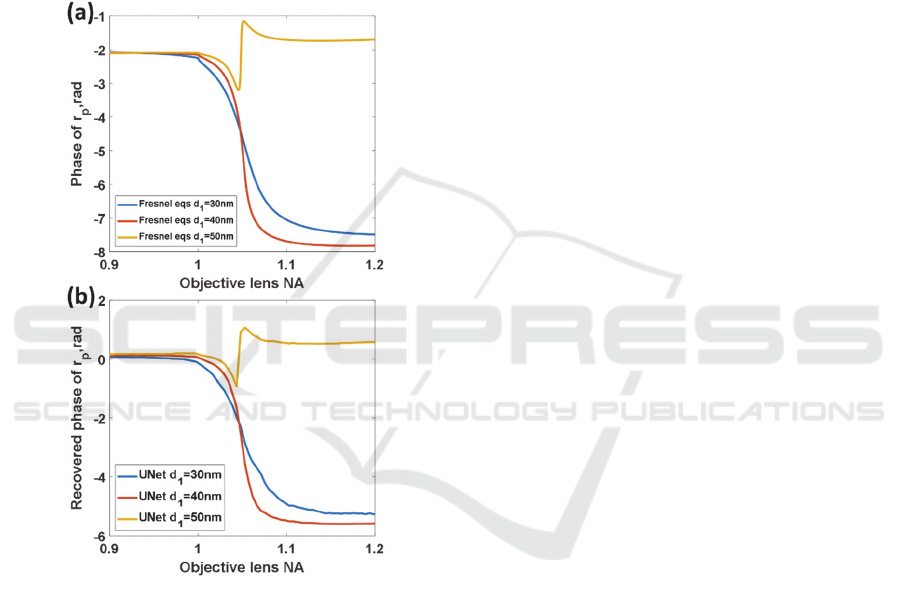
to Figure 11. The phase responses calculated from

Fresnel equations for the three gold thicknesses are

shown in Figure 13a in comparison with the phase

profiles recovered from the UNet as shown in Figure

13a. Like the intensity responses, the recovered phase

profiles using the UNet were like the phase profiles

from Fresnel calculation with some random noise on

the phase profile. These noises did not affect the

shape and gradient of the phase transition of the SPR

dip.

Figure 13: Shows (a) phase responses for the three

thicknesses of gold calculated using Fresnel equations and

(b) the recovered phase responses using the UNet.

The proposed image recognition using UNet

might be another promising candidate to get around

the issues of phase retrieval algorithms. There are still

several issues that need to be further investigated,

such as, how robust the network is at different input

noise levels and its performance compared to the

conventional interferometry and computational phase

retrieval algorithms.

4 CONCLUSION

In this paper, we have proposed a novel approach to

perform SPR phase measurement using U-shaped

artificial neural network through deep learning. The

UNet has been employed to replace the need for an

interferometer or a computational phase retrieval

algorithm. We have provided a theoretical analysis

showing that the trained UNet can correctly recover

different phase profiles. However, there are still some

noise artefacts on the recovered intensity and phase

profiles. There are still some room for further

improvement, such as, training the network with a

bigger dataset or including the image plane to the

training set. We are currently investigating these

possible improvements, which will be reported in

another separate publication.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the Research

Institute of Rangsit University, Thailand for research

funding and traveling grant.

REFERENCES

Akowuah, E. K., Gorman, T., & Haxha, S. (2009). Design

and optimization of a novel surface plasmon resonance

biosensor based on Otto configuration. Optics express,

17(26), 23511-23521.

Johnson, P. B., & Christy, R.-W. (1972). Optical constants

of the noble metals. Physical review B, 6(12), 4370.

Kabashin, A. V., Patskovsky, S., & Grigorenko, A. N.

(2009). Phase and amplitude sensitivities in surface

plasmon resonance bio and chemical sensing. Optics

express, 17(23), 21191-21204.

Kretschmann, E., & Raether, H. (1968). Radiative decay of

non radiative surface plasmons excited by light.

Zeitschrift für Naturforschung A, 23(12), 2135-2136.

Liedberg, B., Nylander, C., & Lundström, I. (1995).

Biosensing with surface plasmon resonance—how it all

started. Biosensors and Bioelectronics, 10(8), i-ix.

Liedberg, B., Nylander, C., & Lunström, I. (1983). Surface

plasmon resonance for gas detection and biosensing.

Sensors and actuators, 4, 299-304.

Pechprasarn, S., Chow, T. W., & Somekh, M. G. (2018).

Application of confocal surface wave microscope to

self-calibrated attenuation coefficient measurement by

goos-hänchen phase shift modulation. Scientific

reports, 8(1), 8547.

Pechprasarn, S., Learkthanakhachon, S., Zheng, G., Shen,

H., Lei, D. Y., & Somekh, M. G. (2016). Grating-

coupled otto configuration for hybridized surface

phonon polariton excitation for local refractive index

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

sensitivity enhancement. Optics express, 24(17),

19517-19530.

Pechprasarn, S., & Somekh, M. G. (2014). Detection limits

of confocal surface plasmon microscopy. Biomedical

optics express, 5(6), 1744-1756.

Pechprasarn, S., Zhang, B., Albutt, D., Zhang, J., &

Somekh, M. (2014). Ultrastable embedded surface

plasmon confocal interferometry. Light: Science &

Applications, 3(7), e187.

Shen, M., Learkthanakhachon, S., Pechprasarn, S., Zhang,

Y., & Somekh, M. G. (2018). Adjustable microscopic

measurement of nanogap waveguide and plasmonic

structures. Applied optics, 57(13), 3453-3462.

Somekh, M. G., & Pechprasarn, S. (2016). Surface

plasmon, surface wave, and enhanced evanescent wave

microscopy. Handbook of Photonics for Biomedical

Engineering, 1-41.

Somekh, M. G., Pechprasarn, S., Chen, W.,

Pimonsakonwong, P., & Albutt, N. (2017). Back Focal

Plane Confocal Ptychography. Paper presented at the

Applied Mechanics and Materials.

Somekh, M. G., Pechprasarn, S., Chow, W.-K., Meng, J., &

Shen, H. (2016). New avenues for confocal surface

plasmon microscopy. Paper presented at the Plasmonics

in Biology and Medicine XIII.

Streibl, N. (1984). Phase imaging by the transport equation

of intensity. Optics communications, 49(1), 6-10.

Suvarnaphaet, P., & Pechprasarn, S. (2018). Enhancement

of long-range surface plasmon excitation, dynamic

range and figure of merit using a dielectric resonant

cavity. Sensors, 18(9), 2757.

Tan, H.-M., Pechprasarn, S., Zhang, J., Pitter, M. C., &

Somekh, M. G. (2016). High resolution quantitative

angle-scanning widefield surface plasmon microscopy.

Scientific reports, 6, 20195.

Taylor, A. B., & Zijlstra, P. (2017). Single-molecule

plasmon sensing: current status and future prospects.

ACS sensors, 2(8), 1103-1122.

Zalevsky, Z., Mendlovic, D., & Dorsch, R. G. (1996).

Gerchberg–Saxton algorithm applied in the fractional

Fourier or the Fresnel domain. Optics Letters, 21(12),

842-844.

Surface Plasmons Phase Imaging Microscopy using Deep Learning