Improved Subspace Method for Supervised Anomaly Detection with

Minimal Anomalous Data

Fumito Ebuchi

, Aiga Suzuki

and Masahiro Murakawa

Graduate School of Systems and Information Engineering, University of Tsukuba, Japan

National Institute of Advanced Industrial Science and Technology (AIST), Japan

Keywords:

Subspace Method, Anomaly Detection, Optimization Problems.

Abstract:

In conventional anomaly detection methods, the classiﬁer is usually trained only with normal data. How-

ever, real-world problems may present a very small amount of anomalous data. In this paper, we propose

an improved subspace method for anomaly detection that has the ability to utilize a very small amount of

anomalous data. Our method introduces an objective function that minimizes the average projection length

of anomalous data into the conventional objective function for the subspace method. This formulation en-

ables a normal subspace that considers the distribution of anomalous data to be learned, thereby improving

the anomaly detection performance. Furthermore, because the information about anomalous data is provided

in the form of the average projection length, stable detection can be expected even when an extremely small

amount of anomalous data is used. We used MNIST and the CIFAR-10 dataset to evaluate the effectiveness

of the proposed method, which yielded a higher anomaly detection performance compared with the conven-

tional normal model or classiﬁer model under conditions in which very little anomalous data are obtainable.

The performance of our method on CIFAR-10 was assessed by imposing the constraint that only four or ﬁve

anomalous data samples could be used. In this test, our method achieved an average AUC of 0.263 points

higher than that of the state-of-the-art method using only normal data.

1 INTRODUCTION

The subspace method (SM)(Watanabe and Pakvasa,

1973; Oja, 1983), which is a pattern recognition tech-

nique, generates a low-dimensional subspace that rep-

resents the data distribution. In other words, the

subspace contains the maximum projection length of

data. Therefore, the optimization of SM entails the

maximization of the average projection length of data

onto its surface. In classiﬁcation problems, the in-

put data are classiﬁed into the class with the highest

similarity between the input data and the class sub-

space, which can be obtained from the data of one

class. Therefore, SM can also be applied to one-class

classiﬁcation problems and anomaly detection prob-

lems.

On the other hand, the decreasing cost of col-

lecting sensor data has prompted active research

on anomaly detection using machine-learning tech-

https://orcid.org/0000-0002-7982-0436

https://orcid.org/0000-0002-7794-1162

https://orcid.org/0000-0002-8406-7426

niques. This approach to anomaly detection has been

used for machine failure detection(Hasegawa et al.,

2018), fault detection in parts manufacturing(Moyne

and Iskandar, 2017), the detection of attacks in net-

work security(Barford et al., 2002), and the detec-

tion of anomalous echoes in infrastructure equipment

inspection(Ye et al., 2014). In general, in the ﬁeld

of anomaly detection, anomalous data are difﬁcult

to obtain compared to normal data, of which a large

amount is available. Therefore, most anomaly detec-

tion techniques using machine learning train a nor-

mal state using only normal data, and detect anoma-

lous data based on the dissimilarity from the normal

state(Wang et al., 2004)(An and Cho, 2015)(Zhou and

Paffenroth, 2017). Semi-Supervised Anomaly De-

tection (SSAD)(G

ornitz et al., 2013) is a valuable

anomaly detection method that can utilize anomaly

data based on Support Vector Data Description (Tax

and Duin, 2004). SSAD generates hyperspheres that

contain normal data and no anomalous data. SSAD

is effective when we have a large amount of anoma-

lous data, but is ineffective when very little anoma-

lous data are available. However, real-world problems

Ebuchi, F., Suzuki, A. and Murakawa, M.

Improved Subspace Method for Supervised Anomaly Detection with Minimal Anomalous Data.

DOI: 10.5220/0008918401510158

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 151-158

ISBN: 978-989-758-397-1; ISSN: 2184-4313

151

involve very small amounts of anomalous data in ad-

dition to a large amount of normal data. Therefore,

if we were to succeed in using these anomalous data

effectively, the anomaly detection performance could

be improved compared to the conventional anomaly

detection method.

In this paper, we propose a supervised SM with

a large amount of normal data and very little anoma-

lous data. The objective function of the conventional

SM is to maximize the average projection length of

normal data. The proposed method contains an addi-

tional term, which is added to minimize the average

projection length of very little anomalous data to the

objective function of the conventional SM. The eigen-

value problem is derived by applying the Lagrange

multiplier method to the optimization problem. Then,

we can obtain a basis vector of the normal class sub-

space by solving the eigenvalue problem. The pro-

posed method detects the anomalous data based on

the projection length when an unknown data value is

projected into the normal class subspace. Because

the normal class subspace of the proposed method

considers the distribution of anomalous data, it can

be expected to improve the anomaly detection per-

formance. Furthermore, even when extremely little

anomalous data are available, we expect to be able to

utilize these anomalous data to stably detect anoma-

lous data. This expectation considers that the pro-

posed method provides information on the anomalous

data using the average projection length.

In this paper, in Sect. 2, we discuss the necessi-

ties of anomaly detection with a large amount nor-

mal data and a small amount of anomalous data, and

describe the conventional SM. In Sect. 3, we present

the proposed method, and in Sect. 4, we describe the

effectiveness of the proposed method, which was as-

sessed by conducting computer experiments using the

MNIST and CIFAR-10 datasets. In Sect. 5, we deliver

the conclusion.

2 BACKGROUND AND RELATED

WORK

Anomaly detection has been studied for a long time,

and many anomaly detection methods have been pro-

posed. However, because anomalous data rarely ap-

pear in real-world problems, most anomaly detec-

tion methods are trained only with normal data. In

fact, it is rarely possible to obtain more than small

amounts of anomalous data. We could therefore ex-

pect to improve the anomaly detection performance

by utilizing the rare anomalous data instead of nor-

mal data. In such cases, we could use binary clas-

siﬁers such as neural networks, a support vector ma-

chine, and random forest without using an anomaly

detection method. However, a binary classiﬁer can-

not detect unknown data that are not contained in the

training dataset. Furthermore, it would not be pos-

sible to train the classiﬁer thoroughly because of the

data bias. Therefore, we would need to devise a way

to use the small amount of anomalous data effectively,

to enable the anomaly detection method to generate a

normal state.

Typical anomaly detection methods include a one-

class support vector machine, auto-encoder, and SM.

Among these methods, SM has been widely used be-

cause of its high generalization ability and easy im-

plementation. In this section, we describe the con-

ventional SM for anomaly detection in detail.

2.1 Subspace Method

In anomaly detection, we obtain the subspace for the

normal data by solving the following optimization

problem.

maximize

∑

i∈S

(1)

subject to v

v = 1, (2)

where x, v, and S

are the l-dimensional input vector,

l-dimensional weight vector, and subscript indicates

the subset of normal data, respectively. Introducing a

Lagrange multiplier λ enables equation (1) and (2) to

be transformed into the following optimization prob-

lem:

maximize

∑

i∈S

− λ(v

v − 1). (3)

The optimal condition for v can be obtained by the

following eigenvalue problem,

∑

i∈S

v = λv. (4)

We can obtain l eigenvalues λ

, λ

, ··· , λ

(λ

≥

≥ · · · ≥ λ

) and corresponding l eigenvectors

, v

, ··· , v

by solving the eigenvalue problem of

equation (4). Because these eigenvectors contain re-

dundant expressions, we select eigenvectors that sat-

isfy the following equation.

∑

i=1

∑

i=1

≥ η, (5)

where η is a hyperparameter less than 1, a so-called

cumulative contribution rate. Then, we ﬁnd the

smallest r that satisﬁes equation (5), and deﬁne V =

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

152

, v

, ··· , v

), where r < l as the normal class sub-

space.

The anomaly score of data z is calculated as the

distance between z and ˆz, which is reconstructed by

subspace V . In other words, the anomaly score is:

(z) = |sin θ|

kz − ˆzk

kzk

k(I

l×l

−VV

)zk

kzk

, (6)

where I

l×l

is an l × l identity matrix. Data z with a

relatively large D

(z) in equation (6) is classiﬁed as

anomalous data.

3 PROPOSED METHOD

In the conventional SM, the normal subspace is gen-

erated using normal data only. Therefore, even if we

were able to obtain anomalous data, we would not

be able to utilize these data. Thus, the effective use

of anomalous data would be expected to improve the

anomaly detection performance. Therefore, we de-

ﬁne a formulation by considering the anomalous data.

Speciﬁcally, we introduce a condition that minimizes

the average projection length of the anomalous data

to the objective function of the conventional equation

(1) as follows:

maximize

∑

i∈S

−

∑

i∈S

−

v) (7)

subject to v

v = 1, (8)

where C ∈ R

, and S

−

are the tradeoff hyperparame-

ters between the normal and anomalous data, and the

subscript subset of the anomalous data, respectively.

Especially, in the case of C = 0, equation (7) is equal

to equation (1). As in Sect. 2, we can obtain the

following eigenvalue problem by introducing the La-

grange multiplier λ into equation (7) and (8).



∑

i∈S+

−

∑

i∈S

−



v = λv (9)

By solving equation (9), we obtain eigenvectors

, v

, ··· , v

. Therefore, as in the conventional SM,

we obtain subspace V = (v

, v

, ··· , v

) using equa-

tion (5). In equation (7), because we use the infor-

mation on anomalous data by employing the average

projection length, it becomes possible to utilize very

little anomalous data in an effective manner.

The illustration in Figure 1 compares the conven-

tional subspace with the subspace of the proposed

method. Because the conventional subspace is deter-

mined only by normal data, anomalous data cannot be

considered. However, the proposed method considers

anomalous data, and designates an area away from the

data known to be anomalous as the normal subspace.

The generation of such a normal subspace enables the

anomaly detection performance to be improved.

ß?5

Conventional SM

Known anomalous data

Proposed method

€

Known normal data

move

Figure 1: Comparison of the proposed method and conven-

tional SM.

4 EXPERIMENTS AND RESULTS

We demonstrate the effectiveness of the proposed

method using the MNIST and CIFAR-10 datasets.

Because the proposed method uses very little anoma-

lous data, we compared the performance on both

of these datasets using both an anomaly detection

method and a binary classiﬁer.

4.1 Methods

We compare the proposed method with the conven-

tional SM with only normal data, and convolutional

neural network ResNet-50(He et al., 2016) as a binary

classiﬁer. In this section, we refer to the proposed

method as “ISM”, and ResNet-50 for a binary clas-

siﬁer as “BI-ResNet-50”. For SM and ISM, we used

the features of the fully connected layer of ResNet-

50 as the input features. In this section, we refer to

the feature extractor using ResNet-50 as “FE-ResNet-

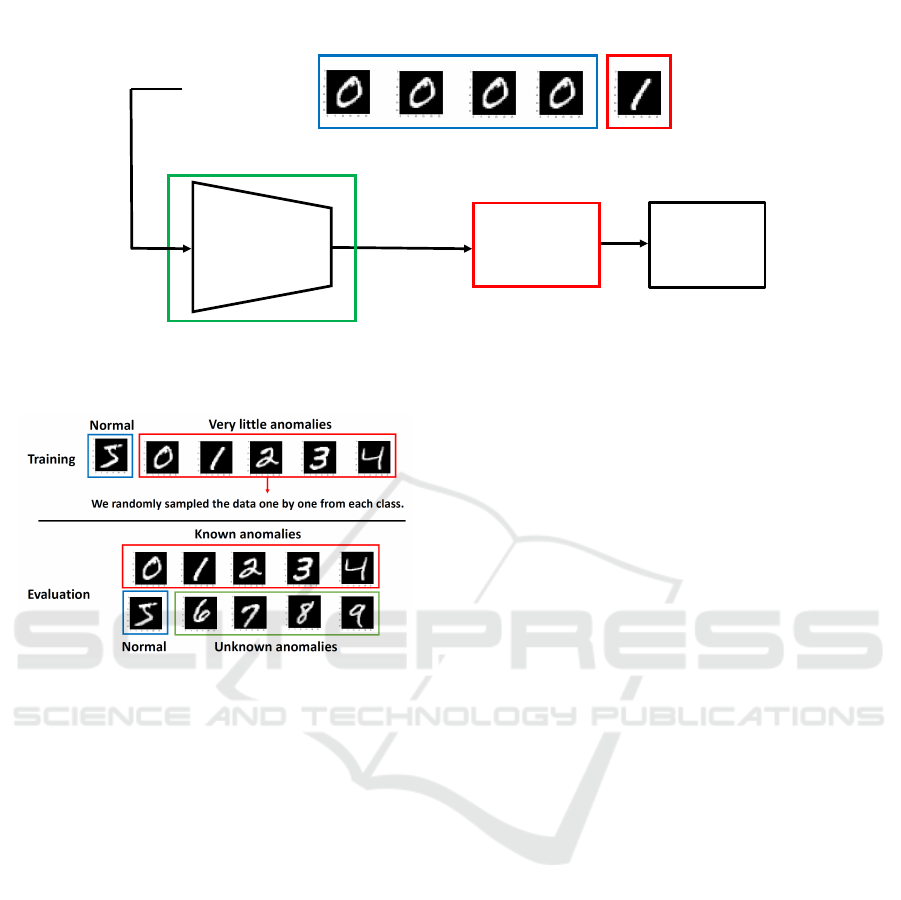
50”. Figure 2 shows the ﬂow of the proposed method.

In addition, we compare the proposed method and

SSAD(G

ornitz et al., 2013), which is trained with

both normal and anomalous data.

Furthermore, we compared the results of the

aforementioned methods with those of ISM, to

demonstrate the performance of our method relative

to the following recently proposed well-known meth-

ods that use only normal data.

Improved Subspace Method for Supervised Anomaly Detection with Minimal Anomalous Data

153

Pre-trained

CNN model

(ResNet50)

>rás?

Feature Extractor

Normalization

Proposed

Method

(ISM)

Anomaly

Score

:V;

Training data :

A large amount of normal data

Very little

anomalous data

Figure 2: Flow of the proposed method.

Figure 3: Experimental setting for training and test data

with anomalous data.

• Kernel Density Estimation (KDE) (Parzen,

1962)

• One-Class Support Vector Machine (OC-

SVM) (Scholkopf and Smola, 2001)

• Isolation Forest (IF) (Liu et al., 2008)

• Gaussian Mixture Model (GMM) (Fraley and

Raftery, 2002)

• Deep Convolutional Autoencoder (DCAE)

(Masci et al., 2011)

• Anomaly Detection with Generative Adversar-

ial Network (AnoGAN) (Schlegl et al., 2017)

• Variational Autoencoder (VAE) (Kingma and

Welling, 2013)

• Anomaly Detection with Generative Adversar-

ial Network (ADGAN) (Deecke et al., 2018)

The experimental results of each of these methods

were surveyed from (Deecke et al., 2018).

4.2 Setting Hyperparameters

We ﬁne-tuned all the layers of BI-ResNet-50 for 20

epochs using an Adam optimizer (α = 0.001, β

=0.9,

=0.999, ε = 10

−8

) and the weighted cross entropy

loss for considering class imbalance. The initial value

of BI-ResNet-50 is the weight and bias pre-trained

with ImageNET(Deng et al., 2009). FE-ResNet50

had pre-trained weights with ImageNET, and did not

require ﬁne-tuning.

The hyperparameters used in SSAD, SM, and

ISM were selected by 4-FOLD cross validation.

In our experiment, because there are only 4 or 5

anomalous data in the training data, we divided

the training data 3:1 for normal data and 1:3 for

anomalous data, and cross-validated with AUC as

the evaluation value. The hyperparameters were

selected every time the training dataset changed. We

selected η from {0.80, 0.85, 0.90, 0.95, 0.99}, C from

{0.5, 0.4, 0.3, 0.2, 0.1, 0.09, 0.08, 0.07, 0.06, 0.05, 0.04,

0.03, 0.02, 0.01}, the RBF kernel parameter

γ from {0.01, 0.1, 1, 10, 100}, and the trade-

off parameter for the error in SSAD from

{10

−2

, 10

−1

, 10

}. We set the trade-off

parameter for the margin κ = 1.0.

4.3 Datasets

We assessed the performance using the above-

mentioned two popular datasets. The ﬁrst, the MNIST

dataset, which contains grayscale images of handwrit-

ten digits, contains 60,000 training images and 10,000

test images with a 28 × 28 image size. The other,

the CIFAR-10 dataset, which contains RGB images

of real-world objects belonging to ten classes, con-

tains 50,000 training images and 10,000 test images

with an image size of 32 × 32.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

154

Table 1: Comparison of average AUC.

Normal Binary classiﬁcation Semi-Supervised Ours

Dataset class ResNet50 SM SSAD ISM

0 0.979±0.015 0.944±0.037 0.981±0.017 0.988±0.003

1 0.973±0.026 0.993±0.004 0.999±0.000 0.999±0.000

2 0.948±0.031 0.814±0.067 0.911±0.025 0.932±0.020

3 0.960±0.025 0.857±0.054 0.935±0.000 0.946±0.014

MNIST 4 0.983±0.007 0.928±0.038 0.960±0.019 0.983±0.006

5 0.953±0.021 0.831±0.048 0.926±0.000 0.937±0.015

6 0.994±0.003 0.837±0.064 0.932±0.000 0.956±0.011

7 0.967±0.024 0.874±0.069 0.940±0.023 0.975±0.006

8 0.969±0.023 0.903±0.062 0.974±0.000 0.977±0.006

9 0.924±0.037 0.858±0.055 0.890±0.034 0.958±0.008

Avg. 0.965±0.019 0.884±0.054 0.945±0.032 0.965±0.021

Airplane 0.700±0.074 0.790±0.088 0.880±0.034 0.895±0.005

Automobile 0.859±0.035 0.893±0.021 0.927±0.017 0.938±0.005

Bird 0.635±0.057 0.724±0.034 0.826±0.041 0.820±0.019

Cat 0.642±0.057 0.732±0.061 0.812±0.017 0.831±0.023

CIFAR-10 Deer 0.699±0.050 0.754±0.081 0.803±0.038 0.845±0.024

Dog 0.741±0.040 0.847±0.026 0.903±0.000 0.905±0.009

Frog 0.781±0.039 0.858±0.052 0.923±0.034 0.942±0.008

Horse 0.782±0.023 0.855±0.056 0.913±0.031 0.923±0.005

Ship 0.748±0.058 0.856±0.082 0.911±0.018 0.925±0.010

Truck 0.823±0.028 0.854±0.098 0.930±0.025 0.945±0.011

Avg. 0.741±0.069 0.816±0.058 0.883±0.047 0.897±0.045

4.4 Experimental Setting

Suppose we have a large amount of normal data and

very little anomalous data in the training dataset. In

our experiment, we assumed the data in each single

class to be normal. The training dataset contained a

large number of images from this single class. Addi-

tionally, we randomly sampled data one by one from

other class numbers as anomalous data. That is, the

number of anomalous data is very small compared to

the number of normal data in the training dataset.

Figure 3 shows the experimental setting for the

training and test data with anomalies for the MNIST

dataset. In this example, we take class5 as a normal

class, and one image of each of classes 0, 1, 2, 3, and

4 as anomalous data for the training dataset. The eval-

uation covered the data in all classes. In other words,

class 5, class 0, 1, 2, 3, and 4, and class 6, 7, 8, and 9

are a normal class, known anomaly classes, unknown

anomaly classes, respectively.

In the experiments, we deﬁne half of all classes

as known anomalies which are included in the train-

ing dataset. For the MNIST data set, we set known

anomalies as class 0, 1, 2, 3, and 4. For the CIFAR-

10 dataset, we set known anomalies as the airplane,

automobile, bird, cat, and deer classes. In the case

the normal class is included in the known anomalies

classes , the normal class is excepted from the anoma-

lies. Therefore, the training dataset included four or

ﬁve anomalous data and a large number of normal

data.

The random selection of anomalous data was

achieved by repeatedly evaluating the classiﬁer that

uses the anomalous data for training ten times under

the same experimental conditions, and comparing it

with the average value. The experiment was evalu-

ated using AUC for all test data.

4.5 Experimental Results

Table 1 lists the AUC for each problem for the con-

ventional and the proposed methods. The maximum

AUC for each problem is shown in bold. “Avg.”

means the average AUC for all classes. The experi-

ments were repeated ten times for the method using

the anomalous data, and the standard deviation is pro-

vided in the table.

For the MNIST dataset, the AUC for ISM is im-

proved by 0.081 points on average, compared with

the conventional SM. Because ISM minimizes the av-

erage projection length of anomalous data, a normal

subspace is generated away from the anomalous data.

A comparison of the AUC for ISM and ResNet-50

reveals that the average AUC for for the two meth-

ods is the same. Because the classiﬁcation of the data

in MNIST is a simple problem, it is possible to de-

Improved Subspace Method for Supervised Anomaly Detection with Minimal Anomalous Data

155

Table 2: Comparison of average AUC for known and unknown anomalies.

Normal All data vs. Known anomalies vs. Unknown anomalies

Dataset class SM ISM ISM ISM

0 0.944±0.037 0.988±0.003 0.995±0.002 0.98±0.004

1 0.993±0.004 0.999±0.000 0.999±0.000 0.999±0.001

2 0.814±0.067 0.932±0.020 0.940±0.017 0.935±0.023

3 0.857±0.054 0.946±0.014 0.962±0.013 0.958±0.012

MNIST 4 0.928±0.038 0.983±0.006 0.985±0.009 0.98±0.004

5 0.831±0.048 0.937±0.015 0.920±0.018 0.960±0.011

6 0.837±0.064 0.956±0.011 0.951±0.012 0.963±0.009

7 0.874±0.069 0.975±0.006 0.966±0.010 0.987±0.002

8 0.903±0.062 0.977±0.006 0.978±0.005 0.975±0.008

9 0.858±0.055 0.958±0.008 0.968±0.007 0.944±0.010

Avg. 0.884±0.054 0.965±0.021 0.966±0.023 0.968±0.019

Airplane 0.790±0.088 0.895±0.005 0.916±0.005 0.859±0.007

Automobile 0.893±0.021 0.938±0.005 0.976±0.005 0.888±0.006

Bird 0.724±0.034 0.820±0.019 0.819±0.020 0.823±0.016

Cat 0.732±0.061 0.831±0.023 0.874±0.017 0.835±0.028

CIFAR-10 Deer 0.754±0.081 0.845±0.024 0.883±0.021 0.806±0.027

Dog 0.847±0.026 0.905±0.009 0.901±0.008 0.911±0.011

Frog 0.858±0.052 0.942±0.008 0.926±0.008 0.961±0.007

Horse 0.855±0.056 0.923±0.005 0.916±0.004 0.933±0.007

Ship 0.856±0.082 0.925±0.01 0.912±0.011 0.94±0.009

Truck 0.854±0.098 0.945±0.011 0.933±0.010 0.96±0.012

Avg. 0.816±0.058 0.897±0.045 0.906±0.039 0.892±0.055

tect anomalous data sufﬁciently even when using bi-

nary classiﬁcation. A comparison of SSAD and ISM,

which are anomaly detection methods with normal

data and very little anomalous data, shows that AUC

for ISM is higher. In other words, ISM can effectively

utilize anomalous data stably.

For the CIFAR-10 dataset, the AUC for the pro-

posed method has the maximum value in all classes.

On average, the ISM improves the AUC by 0.081

points compared with the conventional SM. Further-

more, the AUC for ISM is signiﬁcantly higher than

the AUC for ResNet-50. Moreover, comparing SSAD

and ISM, the AUC for ISM is much higher than the

AUC for SSAD except for the bird class. On both the

MNIST and CIFAR-10 datasets, ISM improves the

AUC signiﬁcantly compared with the conventional

SM; thus, it is more effective when using very little

anomalous data when generating a normal subspace.

Table 2 shows the AUC of the test data for the

anomalous data included in the training dataset, and

the anomalies that are not included. “All data”, “vs.

Known anomalies”, and “vs. Unknown anomalies”

mean all test data, test anomalous data included in the

training dataset, and test anomalous data not included

in the training dataset, respectively. Because ISM

uses a small amount of anomalous data during train-

ing, the AUC for known anomalies of ISM is higher

than the AUC for SM. Table 2 reveals that the AUC

for unknown anomalies of ISM is higher than the

AUC for SM. This experimental result presents that

the proposed method is robust against known anoma-

lies as well as unknown anomalies.

Table 3 presents the result of applying the RO-

CAUC s with ISM when taking the experimental re-

sults from (Deecke et al., 2018)

. The maximum

AUC obtained for each problem is shown in bold.

For the MNIST dataset, the ISM AUC is the

largest of only three of the problems. Because

MNIST classiﬁcation is a simple problem, the ISM

AUC is 0.003 points lower than the ADGAN AUC,

but the AUC is not signiﬁcantly different.

For the CIFAR-10 dataset, the AUC for ISM is the

largest of all the problems; that is, the ROCAUCs for

ISM are much higher than the ROCAUCs for the other

methods. In particular, the AUC for ISM is 0.263

points higher than the AUC of ADGAN, which has

the best performance among the conventional meth-

ods. Furthermore, in the Automobile and Cat classes,

the conventional method is hardly able to distinguish

between anomalous and normal data, when perform-

ing the classiﬁcation. However, ISM classiﬁes the

anomalous and normal data from these problems as

effectively as the other problems. The experimen-

tal results show that, even if a very small amount of

anomalous data is available, we can expect to improve

The proposed method evaluates all the test data

(10,000). However, the surveyed data are the result of eval-

uating 5,000 randomly selected data values from all the test

data.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

156

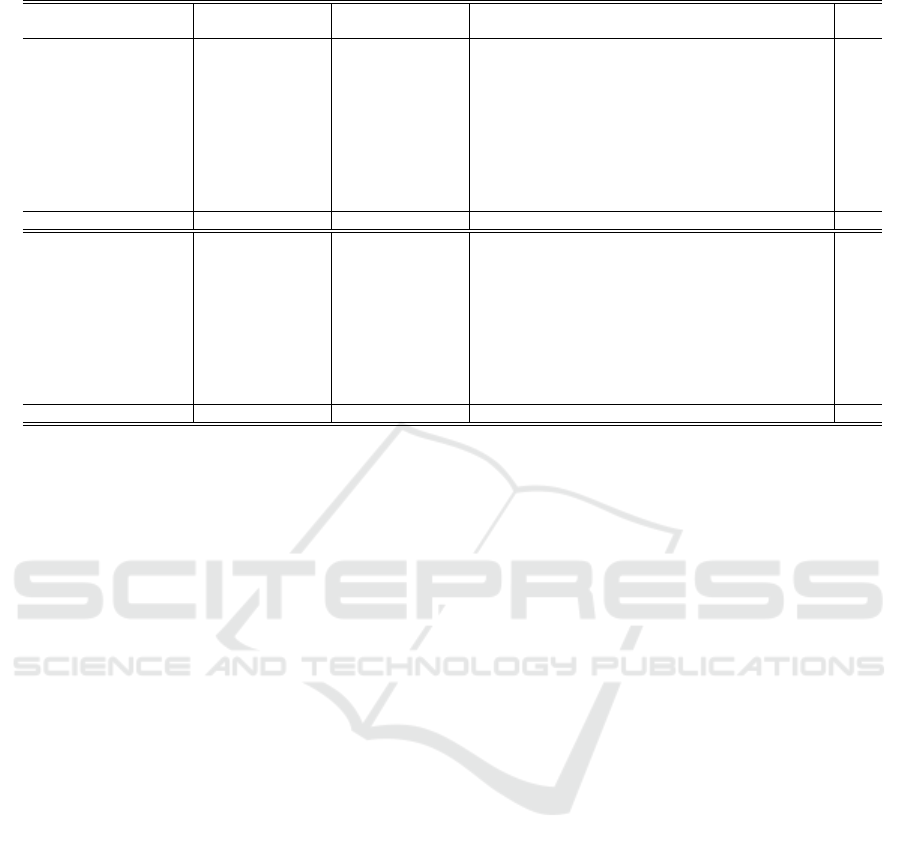
Table 3: Survey: Experimental results for AUC taken from (Deecke et al., 2018) (adapted for our proposed method).

Normal KDE OC-SVM Ours

Dataset class PCA ALEXNET PCA ALEXNET IF GMM DCAE AnoGAN VAE ADGAN ISM

0 0.982 0.634 0.993 0.962 0.957 0.970 0.988 0.990 0.884 0.999 0.988

1 0.999 0.922 1.000 0.999 1.000 0.999 0.993 0.998 0.998 0.992 0.999

2 0.888 0.654 0.881 0.925 0.822 0.931 0.917 0.888 0.762 0.968 0.932

3 0.898 0.639 0.931 0.950 0.924 0.951 0.885 0.913 0.789 0.953 0.946

4 0.943 0.676 0.962 0.982 0.922 0.968 0.862 0.944 0.858 0.960 0.983

MNIST 5 0.930 0.651 0.881 0.923 0.859 0.917 0.858 0.912 0.803 0.955 0.937

6 0.972 0.636 0.982 0.975 0.903 0.994 0.954 0.925 0.913 0.980 0.956

7 0.933 0.628 0.951 0.968 0.938 0.938 0.940 0.964 0.897 0.950 0.975

8 0.924 0.617 0.958 0.926 0.814 0.889 0.823 0.883 0.751 0.959 0.977

9 0.940 0.644 0.970 0.969 0.913 0.962 0.965 0.958 0.848 0.965 0.958

Avg. 0.941 0.670 0.951 0.958 0.905 0.952 0.919 0.937 0.85 0.968 0.965

Airplane 0.705 0.559 0.653 0.594 0.630 0.709 0.656 0.610 0.582 0.661 0.895

Automobile 0.493 0.487 0.400 0.540 0.379 0.443 0.435 0.565 0.608 0.435 0.938

Bird 0.734 0.582 0.617 0.588 0.630 0.697 0.381 0.648 0.485 0.636 0.820

Cat 0.522 0.531 0.522 0.575 0.408 0.445 0.545 0.528 0.667 0.488 0.831

Deer 0.691 0.651 0.715 0.753 0.764 0.761 0.288 0.670 0.344 0.794 0.845

CIFAR-10 Dog 0.439 0.551 0.517 0.558 0.514 0.505 0.643 0.592 0.493 0.640 0.905

Frog 0.771 0.613 0.727 0.692 0.666 0.766 0.509 0.625 0.391 0.685 0.942

Horse 0.458 0.593 0.522 0.547 0.480 0.496 0.690 0.576 0.516 0.559 0.923

Ship 0.595 0.600 0.719 0.630 0.651 0.646 0.698 0.723 0.522 0.798 0.925

Truck 0.490 0.529 0.475 0.530 0.459 0.384 0.705 0.582 0.633 0.643 0.945

Avg. 0.590 0.570 0.587 0.601 0.558 0.585 0.583 0.612 0.524 0.634 0.897

the anomaly detection performance greatly, using our

proposed method. In addition, the proposed method

generates the normal subspace; therefore, it is robust

against unknown anomalies.

5 CONCLUSION

This paper proposed a novel anomaly detection

method for supervised anomaly detection. The pro-

posed method, which utilizes very little anomalous

data, is based on the subspace method. Speciﬁcally,

our proposed method is able to generate a normal sub-

space using a large amount of normal data and very

little anomalous data. In particular, we deﬁned the op-

timization problem as being the maximization of the

projection length for normal data and minimization of

the projection length for anomalous data. Because the

proposed method uses the information of the anoma-

lous data using the average projection length, the nor-

mal subspace can be generated stably. Furthermore,

the proposed method can detect unknown anomalous

data because of its ability to generate a normal sub-

space.

In the experiments, we compared the AUC of

the proposed method with that of the state-of-the-

art method trained only with normal data. When

very little anomalous data were used, the anomaly de-

tection performance of the proposed method signiﬁ-

cantly exceeded the performance of the state-of-the-

art method. In particular, on the CIFAR-10 dataset,

our proposed method with a minimal amount of

anomalous data (four to ﬁve samples) achieved an av-

erage AUC that was 0.263 points higher than the state-

of-the art method with only normal data. The experi-

mental results conﬁrmed that the proposed method is

powerful when very little anomalous data are avail-

able.

In the future, we plan to evaluate the effective-

ness of the proposed method using a real-world prob-

lem. For example, we aim to evaluate the pro-

posed method with the MVTec anomaly detection

dataset (MVTec AD), which was previously proposed

(Bergmann et al., 2019).

REFERENCES

An, J. and Cho, S. (2015). Variational autoencoder based

anomaly detection using reconstruction probability.

Special Lecture on IE, 2(1).

Barford, P., Kline, J., Plonka, D., and Ron, A. (2002). A

signal analysis of network trafﬁc anomalies. In Pro-

ceedings of the 2nd ACM SIGCOMM Workshop on In-

ternet measurment, pages 71–82. ACM.

Belhumeur, P. N., Hespanha, J. P., and Kriegman, D. J.

(1997). Eigenfaces vs. ﬁsherfaces: Recognition us-

ing class speciﬁc linear projection. IEEE Transactions

on Pattern Analysis & Machine Intelligence, (7):711–

720.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger, C.

(2019). Mvtec ad–a comprehensive real-world dataset

for unsupervised anomaly detection. In Proceedings

of the IEEE Conference on Computer Vision and Pat-

tern Recognition, pages 9592–9600.

Bishop, C. M. (2006). Pattern recognition and machine

learning. springer.

Improved Subspace Method for Supervised Anomaly Detection with Minimal Anomalous Data

157

Deecke, L., Vandermeulen, R., Ruff, L., Mandt, S., and

Kloft, M. (2018). Image anomaly detection with gen-

erative adversarial networks. In Joint European Con-

ference on Machine Learning and Knowledge Discov-

ery in Databases, pages 3–17. Springer.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei,

L. (2009). Imagenet: A large-scale hierarchical image

database. In Proc. 2009 IEEE conference on computer

vision and pattern recognition, pages 248–255. Ieee.

Fraley, C. and Raftery, A. E. (2002). Model-based clus-

tering, discriminant analysis, and density estima-

tion. Journal of the American statistical Association,

97(458):611–631.

ornitz, N., Kloft, M., Rieck, K., and Brefeld, U. (2013).

Toward supervised anomaly detection. Journal of Ar-

tiﬁcial Intelligence Research, 46:235–262.

Hasegawa, T., Ogata, J., Murakawa, M., and Ogawa, T.

(2018). Tandem connectionist anomaly detection:

Use of faulty vibration signals in feature represen-

tation learning. In Proc. 2018 IEEE International

Conference on Prognostics and Health Management

(ICPHM), pages 1–7. IEEE.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-

ational bayes. arXiv preprint arXiv:1312.6114.

Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple

layers of features from tiny images. Technical report,

Citeseer.

Laskov, P., D

ussel, P., Sch

afer, C., and Rieck, K. (2005).

Learning intrusion detection: supervised or unsuper-

vised? In Proc. International Conference on Image

Analysis and Processing, pages 50–57. Springer.

LeCun, Y., Cortes, C., and Burges, C. J. (1998). The

mnist database of handwritten digits, 1998. URL

http://yann. lecun. com/exdb/mnist, 10:34.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation

forest. In 2008 Eighth IEEE International Conference

on Data Mining, pages 413–422. IEEE.

Masci, J., Meier, U., Cires¸an, D., and Schmidhuber, J.

(2011). Stacked convolutional auto-encoders for hi-

erarchical feature extraction. In International Con-

ference on Artiﬁcial Neural Networks, pages 52–59.

Springer.

Moyne, J. and Iskandar, J. (2017). Big data analytics for

smart manufacturing: Case studies in semiconductor

manufacturing. Processes, 5(3):39.

Oja, E. (1983). Subspace methods of pattern recognition,

volume 6. Research Studies Press.

Parzen, E. (1962). On estimation of a probability density

function and mode. The annals of mathematical statis-

tics, 33(3):1065–1076.

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Schmidt-Erfurth,

U., and Langs, G. (2017). Unsupervised anomaly de-

tection with generative adversarial networks to guide

marker discovery. In International Conference on In-

formation Processing in Medical Imaging, pages 146–

157. Springer.

Sch

olkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J.,

and Williamson, R. C. (2001). Estimating the support

of a high-dimensional distribution. Neural computa-

tion, 13(7):1443–1471.

Scholkopf, B. and Smola, A. J. (2001). Learning with ker-

nels: support vector machines, regularization, opti-

mization, and beyond. MIT press.

Tax, D. M. and Duin, R. P. (2004). Support vector data

description. Machine learning, 54(1):45–66.

Wang, Y., Wong, J., and Miner, A. (2004). Anomaly in-

trusion detection using one class svm. In Proceedings

from the Fifth Annual IEEE SMC Information Assur-

ance Workshop, 2004., pages 358–364. IEEE.

Watanabe, S. and Pakvasa, N. (1973). Subspace method of

pattern recognition. In Proc. 1st. IJCPR, pages 25–32.

Ye, J., Iwata, M., Takumi, K., Murakawa, M., Tetsuya, H.,

Kubota, Y., Yui, T., and Mori, K. (2014). Statistical

impact-echo analysis based on grassmann manifold

learning: Its preliminary results for concrete condition

assessment. In Proc. EWSHM - 7th European Work-

shop on Structural Health Monitoring.

Zhou, C. and Paffenroth, R. C. (2017). Anomaly detec-

tion with robust deep autoencoders. In Proceedings of

the 23rd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 665–

674. ACM.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

158