
Stable Feature Selection for Gene Expression using Enhanced Binary
Particle Swarm Optimization
Hassen Dhrif
a
and Stefan Wuchty
Computer Science, University of Miami, Coral Gables, FL, U.S.A.
Keywords:
Feature Selection, Stability, Scalability, Particle Swarm Optimization, Evolutionary Computation, Gene
Discovery.
Abstract:
Feature subset selection (FSS) is an intractable optimization problem in high-dimensional gene expression
datasets, leading to an explosion of local minima. While binary variants of particle swarm optimization
(BPSO) have been applied to solve the FSS problem, increasing dimensionality of the feature space pose
additional challenges to these techniques imparing their ability to select most relevant feature subsets in the
massive presence of uninformative features. Most FSS optimization techniques focus on maximizing classi-
fication performance while minimizing subset size but usually fail to account for solution stability or feature
relevance in their optimization process. In particular, stability in FSS is interpreted differently compared to
PSO. Although a large volume of published studies on each stability issue separately exists, wrapper models
that tackle both stability problems at the same time are still missing. Specifically, we introduce a novel ap-
praoch COMBPSO (COMBinatorial PSO) that features a novel fitness function, integrating feature relevance
and solution stability measures with classification performance and subset size as well as PSO adaptations to
enhance the algorithm’s convergence abilities. Applying our approach to real disease-specific gene expres-
sion data, we found that COMBPSO has similar classification performance compared to BPSO, but provides
reliable classification with considerably smaller and more stable gene subsets.
1 INTRODUCTION
Gene expression profiles have long been used to dis-
cover small numbers of features (biomarkers) that
are important for patient stratification, drug discov-
ery and the development of personalized medicine
strategies. However, genes that govern biological pro-
cesses are usually co-expressed, aggravating the dif-
ferentiation between features that are (ir)relevant for
the corresponding classification task (Perthame et al.,
2016). Therefore, the identification of independent
genes (features) whose expression patterns point to a
meaningful phenotype as well as the scaling to high
dimensional search spaces is a challenge for many
feature selection methods. Particle swarm optimiza-
tion (PSO) approaches (Eberhart and Kennedy, 1995),
its binary, single objective variant BPSO (Kennedy
and Eberhart, 1997) and its multi-objective variant
MOPSO (Zhang et al., 2017; Yong et al., 2016;
Xue et al., 2013; Chandra Sekhara Rao Annavarapu
and Banka, 2016) are evolutionary computation tech-
niques, that have been combined with different clas-
a
https://orcid.org/0000-0002-3842-1762
sification methods to select informative markers from
gene expression data (Han et al., 2017; Han et al.,
2014). In particular, such approaches aim to max-
imize classification performance, while keeping the
size of the gene subset as small as possible. As a
consequence, such approaches are supposed to find
all genes that are strongly relevant for the classifi-
cation process and ignore all irrelevant ones. While
the above-mentioned PSO methods select subsets of
predictive genes that allow reliable sample classifica-
tion, the size of the obtained gene subsets is usually
large. Furthermore, subsets tend to be highly variant,
limiting the stability of obtained results, a necessary
condition to scale to high dimensional feature space.
Such characteristics are putatively rooted in the ten-
dency of PSO algorithms to usually lose the diversity
of the swarm, leading to premature convergence and
leaving many areas of the search space unexplored.
While many solutions were suggested (Babu et al.,
2014) to tackle these drawback, previous work left the
integration of the relevance and stability of selected
feature subset and the stability of the PSO algorithm
untouched.
Dhrif, H. and Wuchty, S.
Stable Feature Selection for Gene Expression using Enhanced Binary Particle Swarm Optimization.
DOI: 10.5220/0008919004370444
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 437-444
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
437

Here, we introduce an extension of the BPSO vari-
ant proposed in (Dhrif et al., 2019b; Dhrif, 2019)
by introducing multiple algorithm modifications, that
maximizes (i) the performance of sample classifica-
tion, (ii) minimizes the underlying set size of infor-
mative (relevant) genes, and (iii) maintains stability
of the size of gene subsets in the massive presence
of uninformative (i.e. irrelevant) genes. As a con-
sequence, we expect that our algorithm scales with
datasets that have tens of thousands of genes, while
selecting relatively small subsets of informative (i.e.
relevant) genes. In more detail, we introduce (i) a
novel multi-objective optimization fitness function in-
tegration not only classification performance and sub-
set size but also the relevance of features to the class
label and the stability of the selected features sub-
set (subsection 3.1), (ii) an encoding technique that
enhances the diversity of the swarm to solve binary
optimization problems ( subsection 3.2), (iii) a novel
adaptive function that governs the inertia weight and
the acceleration coefficients, allowing the swarm to
explore and exploit the search space more thoroughly
(subsection 3.3), (iv) a dynamic population strategy to
faster discover new global best solutions (gbest) and
a turbulence operator, enabling the swarm to escape
a local optimum (subsection 3.3), (v) and asymmet-
ric position boundaries that control the divergence of
the swarm and increase the probability of sampling
candidate solutions with smallest number of selected
genes (subsection 3.4).
Applying our approach on real disease-specific
gene expression data, we observe that COMBPSO has
similar classification performance compared to BPSO
through considerably smaller and more stable gene
subsets.
2 BACKGROUND
2.1 Stability of Feature Subset Selection
The FSS problem revolves around the minimization
of selected feature subsets, while optimizing a given
performance measure. Generally, the solution to a
FSS problem features three steps (Kumar and Minz,
2014). In the Subset discovery step, approaches deter-
mine a subset of features that are subsequently eval-
uated. While many strategies to select feature sub-
sets have been proposed, we focus on the Particle
Swarm Optimization (PSO) algorithm. In the Sub-
set evaluation step, the performance of feature sub-
sets is tested according to given evaluation criteria.
While subsets are usually evaluated through diverse
machine learning procedures, we focus on supervised
learning only (i.e. classification), where a-priori class
labels are known. Furthermore, we evaluate the rel-
evance of features for the classification process (Ku-
mar and Minz, 2014) through metrics that consider
consistency, dependency, distance and information of
feature subsets. In (John et al., 1994), features were
classified as strongly relevant, weakly relevant, and
irrelevant. As a consequence, an optimal subset must
include all strongly relevant features, may account
for some weakly relevant ones, but no irrelevant fea-
tures. Subset discovery and subsequent subset evalu-
ation are repeated until a stopping condition such as
a predefined maximum number of iterations or a min-
imum classification error rate is met. In the Result
validation step the optimal feature subset is validated
using n-fold cross-validation.
Stability, defined as sensitivity of a FSS algorithm
to a small perturbation in the training data is as im-
portant as high classification performance when eval-
uating FSS performance (Khaire and Dhanalakshmi,
2019). Strong correlation between features frequently
lead to multiple equally performing feature subsets,
reducing the stability of traditional FSS methods and
our confidence in selected feature subsets.
2.2 Stability of Particle Swarm
Optimization
PSO, a simple mathematical model developed by
Kennedy and Eberhart in 1995 (Eberhart and
Kennedy, 1995), is a meta-heuristic algorithm that
uses a streamlined model of social conduct to solve
an optimization problem in a cooperative framework.
In particular, PSO has been combined with differ-
ent classification methods to select informative fea-
ture subsets. However, PSO algorithms are limited in
their abilities to converge (Bonyadi and Michalewicz,
2017). In particular, the convergence to a point prob-
lem the velocity vector of particles grows to infinity
for some values of the acceleration and inertia coeffi-
cients, an issue that is also known as swarm explosion.
Stability analysis focuses on the particles’ behavior to
find the reasons why the sequence of generated solu-
tions does not not converge. In particular, First-order
stability analysis investigates the expectation of the
position of particles to ensure that this expectation
converges. Second-order stability analysis focuses
on the variance of the particle’s position to ensure
convergence to zero. In (Cleghorn and Engelbrecht,
2014), first-order analysis has been conducted where
it was assumed that the personal best and global best
vectors can occupy an arbitrarily large finite num-
ber of unique locations in the search space. In (Poli,
2009), second-order analysis showed that particles do
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
438

not stop moving (convergence of the variance of the
particles’ positions) until their personal bests coincide
with the global best of the swarm. Furthermore, PSO
is not locally convergent (Bonyadi and Michalewicz,
2017). To solve local convergence issues, a mutation
operator replaces global/personal best vectors by a
randomly selected point around the global best vector
(Bonyadi and Michalewicz, 2014; Van den Bergh and
Engelbrecht, 2010). Furthermore, regeneration of ve-
locity vectors prevent particles from stagnating, solu-
tions that considerably slow the search process. While
the stability features of standard PSO have been thor-
oughly investigated convergence behavior of BPSO
remains unknown.
3 PROPOSED METHODS
3.1 Objective Function
Objective functions to solve a FSS problem usually
feature two conflicting objectives, maximizing the
classification performance and minimizing the size
of the selected feature subset. However, discarding
the features which are highly associated with the re-
sponse variable is one of the main causes of instabil-
ity. Therefore, we introduce a novel fitness function
that integrates feature relevance, subset stability and
classification performance in a weighted-sum multi-
objective optimization model.
To eliminate noise we introduce a measure of non-
linear correlation between features and response vari-
ables. In particular, we adopted the Randomized De-
pendence Coefficient (RDC) (Lopez-Paz et al., 2013)
that we implemented in (Dhrif et al., 2019a). RDC
is an empirical estimator of the Hirschfeld-Gebelein-
R
´
enyi (HGR) maximum correlation coefficient that
measures non-linear dependencies between random
variables X ∈ R
p
and Y ∈ R
q
, defined as
RDC(X,Y ) = max
α
α
α∈R
k
,β
β
β∈R
ρ
α
α
α
T
Φ
Φ
Φ
X
,β
β
β
T
Ψ
Ψ
Ψ
Y
. (1)
Given a dataset of m samples with n features and q re-
sponse variables, the individual association between
any feature f ∈ R
m×n
and the class C ∈ R
m×q
is de-
fined by RDC( f ,C) ∈ [0,1] where 1 indicates that the
feature f is strongly relevant. Indicating the relevance
of a subset S we average the RDC score over all fea-
tures by
R (S) =
1
|S|
∑
f ∈S
RDC( f ,C), (2)
suggesting that R = 1 when all features in S are
strongly relevant.
Accounting for subset stability in the FSS eval-
uation step, we calculate the amount of overlap be-
tween subsets of selected features (Mohammadi et al.,
2016). As multiple iterations of the algorithm provide
differing feature subsets, we define the consistency
C ( f ) of a feature f as
C ( f ) =
F
f
− F
min
F
max
− F
min
, (3)
where F
f
is the number of occurrences of feature
f in subsets obtained at iteration t, F
min
= 1 is the
global minimum number of occurrences and F
max
is
the global maximum number of occurrences of any
feature at iteration t. Furthermore, we defined the av-
erage consistency of the whole subset S by
C (S) =
1
|S|
∑
f ∈S
C ( f ). (4)
C (S) tends toward 1 if features appear repeatedly in
obtained feature subsets, indicating high stability.
Measuring classification performance of a feature
subset S, we considered recall defined as P (S) =
t p
t p+ f n
, where t p and f n refer to the number of true
positive and false negative predictions. Recall is con-
sidered a measure of a classifiers completeness, where
a low recall rate points to the presence of many false
negatives.
Based on the relevance R (S), consistency C (S)
and the classification performance P (S) that account
for the size of the feature subset S we define the fitness
function as
max F (S) = α
1
P (S) + α
2
R (S) + α
3
C (S)
subject to P (S) ≥ P (D),
(5)
where D is the set of all features, and α
1
+ α
2
+ α
3
=
1 are weight factors, balancing classification perfor-
mance, feature relevance and subset stability.
3.2 Improving Exploration and
Exploitation Capabilities
As our objective is the selection of a limited set of
features, we consider each particle as a binary vec-
tor where the presence (absence) of a feature is rep-
resented by a binary digit. BPSO handles this type
of representation by mapping particle positions to a
binary space where a particle moves by flipping its
bits. However, such a movement does not provide
an intuitive notion of velocity, direction and momen-
tum in a binary feature space. While BPSO under-
performs compared to PSO, Saberi et al. (Mohamad
et al., 2011) indicated that modelling velocity as a
Stable Feature Selection for Gene Expression using Enhanced Binary Particle Swarm Optimization
439
sigmoid function reduces the number of attributes to
roughly half the total number of features. As BPSO
suffers from poor scaling behavior Lee et al. (Lee
et al., 2008) introduced a velocity update that is based
on a binary encoding mechanism of the underlying
position. Here, we propose a novel encoding scheme
(Fig. 1) that maps particle positions to probabilities,
sustaining search in continuous space. In contrast to
(Lee et al., 2008), velocity vector v and position vec-
tor x are represented in continuous form by
v
t+1
i
=ωv
t
i
+ r
1
c
1
(p
i
−x
t
i
) + r
2
c
2
(g −x
t
i
)
x
t+1
i
=x
t
i
+v
t
i
.
(6)
where i indicates the i
th
particle, and t indicates the
t
th
iteration. Furthermore, we utilize a binary vector
b that maps the continuous space position to binary
digits by
b
i j
=
(
1, if rand() < S(x
i j
)
0, otherwise,
(7)
where
S(x
i j
) =
1
(1 + e
−x
i j
)
, (8)
indicating that feature (i.e. gene) j in particle i is ac-
counted for in a feature subset if b
i j
= 1.
Furthermore, dynamics of the particles in PSO
must be carefully controlled to avoid premature con-
vergence in the early stages of the search and enhance
convergence to the global optimum solution during
later stages of the search. Specifically, a high value of
the inertia component, ωv
i
(t) and cognitive compo-
nent, r
1
c
1
(p
i
−x
i
(t)) in Eq. (6), where p
i
is the parti-
cle specific best solution encountered so far will result
in particles explore the search space. In turn, a high
value of the social component, r
2
c
2
(g −x
i
(t)), where
g is the global best solution, rushes particles prema-
turely toward a local optimum. In the early stages
of a population-based optimization process, particles
are supposed to explore the search space thoroughly,
without being limited to local optima. In later stages,
particles are supposed to converge toward the global
optimum. Bansal et al. (Bansal et al., 2011) compared
multiple inertia weight functions for parameters ω, c
1
and c
2
, concluding that, despite its popularity, a lin-
ear time-variant function does not secure best perfor-
mance. Here, we propose to model coefficients c
1
,c
2
and ω as sigmoid functions that allow fast transitions
between search phases and extends the particles time
in the exploration and exploitation phase by
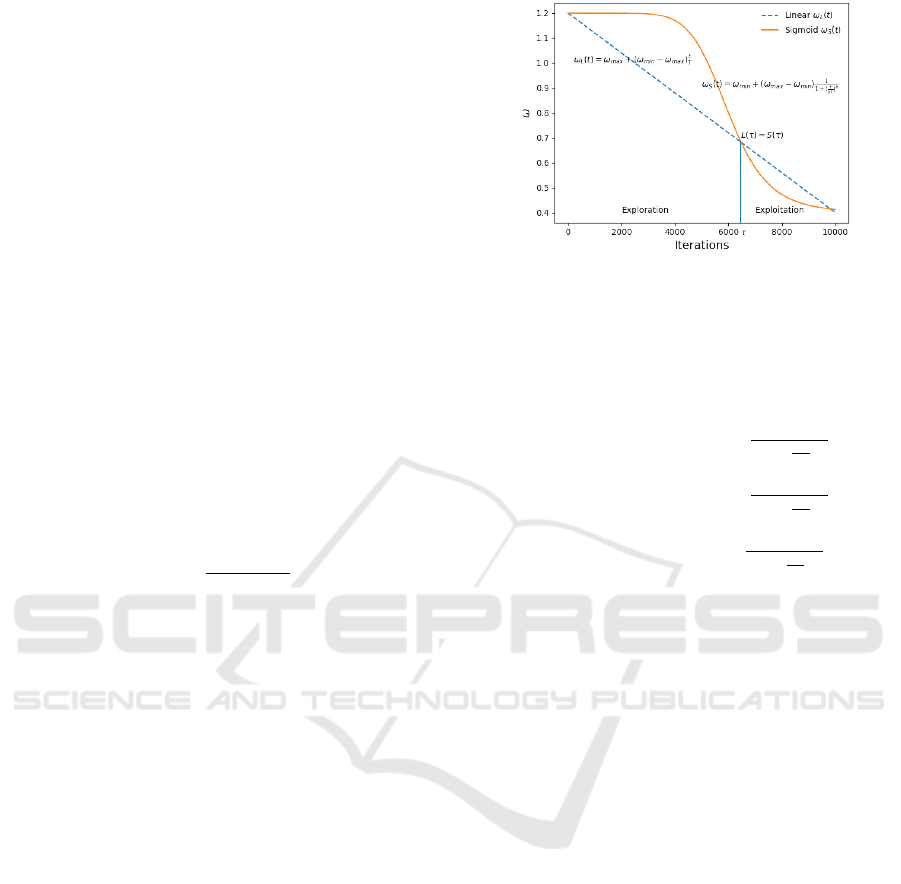
Figure 1: Example of inertia weight ω as a sigmoid func-
tion. Instead of a linear function COMBPSO applies a sig-
moid function to establish inertia weights, where ω
min
=
0.6, ω
max
= 0.9, a = 0.5 and b = 4. Compared to a linearly
decreasing function, our function maintains longer explo-
ration and exploitation phases.
ω = ω
min
+ (ω
max
− ω
min
)
1
1 + (
t
aT
)
b
c
1
= c
min
+ (c
max
− c
min
)
1
1 + (
t
aT
)
b
c
2
= c
max
+ (c
min
− c
max
)
1
1 + (
t
aT
)
b
,
(9)
where t is the iteration number, and T is the maxi-
mum number of iterations. Such a function is shown
in Fig. 1 where a governs the transition point, while b
determines the length of the exploration and exploita-
tion phase of the particles. Compared to a linearly
decreasing function, our proposed sigmoid function
maintains longer exploration and exploitation phases
and avoids premature convergence of the swarm.
3.3 Improving Convergence Rate and
Avoiding Premature Convergence
To solve the local convergence problem in PSO, we
introduce a dynamic population strategy. While pop-
ular approaches update global best solutions in each
step, our new strategy uses a heap data structure to
heapify all the previously identified best positions.
Each time a new global best position is found, the
one being replaced is pushed onto the heap. Then,
every time a particle’s best position stagnates, the
heap is checked for better solution which is eventu-
ally popped from the heap.
Furthermore, avoiding premature convergence, a
turbulence operator re-initializes the velocity of a
fraction γ ∈ [0,1] of particles, if the global best so-
lution was not updated after θ iterations.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
440

3.4 Reducing the Size of Gene Dubsets
Engelbrecht (Engelbrecht, 2012) indicated that parti-
cles tend to leave the boundaries of the search space
irrespective of the initialization approach. As such
characteristics result in wasted search efforts, parti-
cles therefore should be controlled by boundary con-
straints. However, the choice of the boundary values
of x
min
and x
max
is critical, affecting the balance be-
tween exploration and exploitation and the size of the
generated subsets. If x
max
is too large, many genes
that are irrelevant for the underlying classification
task will be selected. In turn, some critical genes will
be missed in the selection process if x
min
is too small.
While a vast majority of approaches adopts symmet-
ric boundaries, i.e. x
max
= −x
min
, we introduce an
asymmetric velocity boundary coefficient λ by
v
max
= −λv
min
,λ ∈ [0,1]. (10)
As a consequence, an elevated value of λ increases
the probability to obtain additional genes.
3.5 Design of COMBPSO
As outlined in Algorithm 1, COMBPSO first initial-
izes the particle population and subsequently solves
the optimization objective. Given a dataset of gene
expression profiles, the algorithm searches for the
most stable subset of genes with the highest predic-
tion performance. The identified subset S
i
is rep-
resented by a binary vector
b
i
where each element
points to a gene, such that S
i
= 1 when gene i is se-
lected, and 0 otherwise. Iteratively, velocities and po-
sitions of particles are updated according to Eqs. 6
and 7. In each step, the fitness function F is evalu-
ated while the personal best solution p
i
of each parti-
cle and global best solution g are updated accordingly.
The search and evaluation process keeps iterating un-
til a maximum number of iterations, T
max
, is reached.
After R independent runs (Alg. 1 Line 38) the final re-
sult is the most performing subset S
∗
out of R subsets
thus obtained.
4 EXPERIMENTAL RESULTS
4.1 Experimental Datasets
To verify the effectiveness and efficiency of the
proposed method for gene selection, we considered
public disease specific gene expression datasets (Ta-
ble II). The Leukemia (Armstrong et al., 2001) data
set contains 28 Acute Myeloid Leukemia (AML),
24 Acute Lymphoblastic Leukemia (ALL) and 20
Algorithm 1: The COMBPSO algorithm.
1: procedure COMBPSO
2: Initialize swarm sw
3: for t ← 1,T
max
do
4: ω ← ω
min
+ (ω
max
− ω
min
)
1
1+(
t
aT
)
b
5: c
1
← c
min
+ (c
max
− c
min
)
1
1+(
t
aT
)
b
6: c
2
← c
max
+ (c
min
− c
max
)
1
1+(
t
aT
)
b
7: for i ← 1,|sw| do |sw| swarm size
8: v
i
← wv
i
+ c
1
r
1
(p
i
− x
i
) +c
2
r
2
(g −x
i
)
9: Clip v
i
to velocity boundaries
10: x
i
← x
i
+ v
i
11: Clip x
i
to position boundaries
12: b
i
← sigmoid(x
i
) b
i
is feature subset i
13: F
i
← α
1
R (b
i
) +α
2
C (b
i
) +α
3
P (b
i
)
14: if F
i
> p
i
then
15: Push p
i
into heap
16: p
i
← F
i
17: else
18: p
i
← Pop from heap
19: end if
20: if F
i
> g then
21: Push g into heap
22: g ← F
i
23: else
24: if g stagnates then
25: Partial velocities reinitialized
26: end if
27: end if
28: end for
29: end for
30: S ← g
best
31: return S
32: end procedure
33: procedure MAIN
34: Load dataset D into X, y
35: for all f ∈ D do
36: R( f ) ← RDC( f ,y)
37: end for
38: for k ← 1,R do
39: S
k
← COMBPSO(D)
40: end for
41: S
∗
← Best of all S
k
42: return S
∗
43: end procedure
Mixed-Lineage Leukemia (MLL) samples, referring
to expression profiles of 11,225 human genes. The
Prostate Tumor (Singh et al., 2002) data set has
52 tumor and 50 non-disease control samples, each
consisting of expression profiles of 10,509 human
genes. The DLBCL data (Shipp et al., 2002) con-
tains 58 patient samples with Diffuse Large B-Cell
Lymphomas (DLBCL) and 14 patient samples with
Follicular Lymphomas where each sample has 5,469
human genes.
Stable Feature Selection for Gene Expression using Enhanced Binary Particle Swarm Optimization
441

Table 1: Characteristics of Cancer data sets.
#samples #features #classes
Leukemia 72 11,225 3
Prostate 102 10,509 2
Lymphoma 72 5,469 2
Table 2: Hyper parameters used in the experimental set-up.
Symbol ω is the inertia weight, c1 and c2 are the velocity
coefficients, and λ is the velocity boundary coefficient.
Parameters
BPSO COMBPSO
MIN MAX MIN MAX
ω 0.4 0.9 0.4 0.9
c
1
,c
2
2.05 1.7 2.1
(a,b) in Eq. 9 (0.6, 8)
velocity -6.0 6.0 -6.0 0.25
λ in Eq. 10 1/32
(θ,γ) in Subsec.3.3 (5, 20%)
α
1
0.8 0.8
α
2
0.1 0.1
α
3
0.1 0.1
swarm size 100 100
# iterations 300 300
4.2 Experimental Setup
The choices of appropriate values of hyper-
parameters for metaheuristic algorithms have
been strongly debated (Ye, 2017; Rezaee Jordehi
and Jasni, 2013). Here, simulations are carried out
with numerical benchmarks to find the best range
of values. Given the dynamic nature of c
1
and c
2
as introduced in subsection 3.3, we allow c
1
,c
2
to
vary between c
min
= 1.7 and c
max
= 2.1 while the
transition coefficients are set to a = 0.6 and b = 8.
Furthermore, we introduce an asymmetric boundaries
coefficient, as defined in Eq. 10, that we empirically
set to λ = 1/32. To control premature convergence
by avoiding stagnation of the swarm, we introduce
both a stagnation coefficient θ, representing the
number of iterations the globally best solution, gbest,
did not change before firing the turbulence operator.
Moreover, the turbulence coefficient γ,γ ∈ [0,1],
indicates the fraction of particles in the swarm that
reset their velocities (subsection 3.3). These two
coefficients are empirically set to θ = 5 and γ = 0.2,
respectively. Furthermore, swarm size impacts the
performance of PSO as a smaller swarm leads to
particles trapped in local optima while a larger swarm
slows the performance of the algorithm. In Eq. 5 we
set α
1
= 0.8, α
2
= 0.1, andα
3
= 0.1. Finally, we set
the swarm size to 100 particles while the number of
iterations is set to 300. All parameters are presented
in Table 2.
We use a wrapper approach, requiring a machine
learning estimator to evaluate the classification
performance of the selected features. Here, we use
Random Forest (RF), that shows excellent perfor-
mance when most predictive variables are noisy, and
when the number of variables is much larger than
the number of observations. Furthermore, RFs can
handle problems with more than two classes and
returns measures of variable importance (Breiman,
2001).
During the search process, we randomly sample
70% of instances as the training set and 30% as the
test set. A 10-fold cross-validation is employed to
evaluate the classification performance of the selected
feature subset on the training set, while the selected
features are evaluated on the test set to obtain testing
classification performance.
4.3 Results
The performance of COMBPSO is examined by con-
sidering three cancer specific gene expression sets. In
particular, we determined the performance of clas-
sification of COMBPSO and BPSO averaging over
10 independent executions (1,000 iterations each)
for each disease specific dataset individually. Con-
sidering all genes in the underlying data sets, we
obtained a 84.88% performance in the Leukemia
dataset, while we observed classification performance
of 81.36% and 84.58% in the Prostate tumor and
Lymphoma datasets. In Table 3, we observe that
both BPSO and COMBPSO provide similar classifi-
cation performance, outperforming the all-gene clas-
sification benchmark. Compared to BPSO, however,
COMBPSO provides significantly smaller gene sub-
sets that allow a reliable classification.
5 CONCLUSION
Combining stability of FSS with stability of PSO
and suggesting solutions to tackle both issues within
a wrapper model are the main contributions of our
work. Integrating feature relevance, we introduced
a non linear correlation measure between features
and response variables. Accounting for feature sub-
set stability, we integrated a consistency measure
as part of the fitness function. Enhancing PSO
stability, we introduced a variant of BPSO, called
COMBPSO, that allowed us to find feature subsets
that boosted classification performance when imple-
mented on datasets with tens of thousands of features.
In particular, we improved PSO’s stability and scala-
bility characteristics by introducing (i) a new encod-
ing scheme in the continuous space, (ii) fast varying
inertia weight and acceleration coefficients as well as
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
442

Table 3: Performance of COMBPSO and BPSO obtained with disease specific gene expression datasets. First column R:
represents run number. G in columns 2,4,6,8,10,12 represent the number of genes selected. R.(%) in columns 3,5,7,9,11,13
represents classification recall. µ,σ represent mean and standard deviation. Bold typeface represents the best average values
of performance (Recall) and size of gene subsets.
Leukemia Prostate Lymphoma
R COMBPSO BPSO COMBPSO BPSO COMBPSO BPSO
G A.(%) G A.(%) G A.(%) G A.(%) G A.(%) G A.(%)
1 15 97.82 198 95.65 8 92.09 169 92.09 9 94.25 91 93.75
2 16 97.80 202 95.71 13 91.18 181 92.09 9 96.25 92 92.50
3 18 98.21 208 96.07 15 95.18 193 93.18 10 96.25 93 92.50
4
18 98.89 211 97.50 16 91.27 193 91.18 12 95.50 95 93.75
5 11 98.23 212 96.90 17 92.18 196 93.09 13 96.75 95 94.58
6 11 97.64 214 95.89 17 95.18 200 90.27 13 96.07 97 92.08
7 12 97.89 217 97.32 17 91.18 204 93.09 14 96.32 97 93.75
8 12 97.57 217 98.57 19 94 204 92.09 8 96.32 99 93.75
9 13 97.85 221 96.07 19 94 205 93.09 9 95.90 100 93.57
10 14 97.75 221 98.57 19 95.09 205 93.09 9 95.50 100 95.00
µ 14 97.96 212 96.83 16 93.14 195 92.33 11 95.91 96 93.52
σ ±2.90 ±0.01 ±7.27 ±0.01 ±3.2 ±1.4 ±11.3 ±0.01 ±2.64 ±0.01 ±3.08 ±0.01
(iii) a novel diversity strategy. Notably, such algorith-
mic changes allowed us to identify subsets of consid-
erably smaller size and low classification error when
we compared their performance to the standard binary
variant BPSO.
Although our approach did not explicitly consider
redundancy of features, our method selected strongly
relevant features as indicated by an average SRF
cover close to 100% in most cases. As we applied
COMBPSO to cancer specific gene expression pro-
files, such a characteristic indicates the ability of our
approach to select smallest, yet robust gene subsets
that are highly relevant for the underlying disease sys-
tem. As a consequence of their stability, such small
gene subsets may well serve as consistent biomarkers
that allow a reliable diagnostic call, may point to dis-
ease relevant genes as well as drug targets.
Although our wrapper method that uses a ran-
dom forest classifier is highly cost effective at obtain-
ing high classification performance subsets, computa-
tional costs may not scale with large datasets. There-
fore, further research may need to focus on mitigat-
ing computation costs in the presence of ultra-high
dimensional search space with millions of features.
REFERENCES
Armstrong, S. A., Staunton, J. E., Silverman, L. B., Pieters,
R., den Boer, M. L., Minden, M. D., Sallan, S. E., Lan-
der, E. S., Golub, T. R., and Korsmeyer, S. J. (2001).
Mll translocations specify a distinct gene expression
profile that distinguishes a unique leukemia. Nature
Genetics, 30:41 EP –. Article.
Babu, S. H., Birajdhar, S. A., and Tambad, S. (2014). Face
recognition using entropy based face segregation as a
pre-processing technique and conservative bpso based
feature selection. In Proceedings of the 2014 Indian
Conference on Computer Vision Graphics and Image
Processing, page 46. ACM.
Bansal, J. C., Singh, P., Saraswat, M., Verma, A., Jadon,
S. S., and Abraham, A. (2011). Inertia weight strate-
gies in particle swarm optimization. In Nature and Bi-
ologically Inspired Computing (NaBIC), 2011 Third
World Congress on, pages 633–640. IEEE.
Bonyadi, M. R. and Michalewicz, Z. (2014). A locally
convergent rotationally invariant particle swarm op-
timization algorithm. Swarm intelligence, 8(3):159–
198.
Bonyadi, M. R. and Michalewicz, Z. (2017). Particle
swarm optimization for single objective continuous
space problems: a review.
Breiman, L. (2001). Random forests. Machine Learning,
45:5–32.
Chandra Sekhara Rao Annavarapu, S. D. and Banka, H.
(2016). Cancer microarray data feature selection using
multi-objective binary particle swarm optimization al-
gorithm. EXCLI journal, 15:460.
Cleghorn, C. W. and Engelbrecht, A. P. (2014). A gener-
alized theoretical deterministic particle swarm model.
Swarm intelligence, 8(1):35–59.
Dhrif, H. (2019). Stability and Scalability of Feature Subset
Selection using Particle Swarm Optimization in Bioin-
formatics. PhD thesis, University of Miami, FL.
Dhrif, H., Giraldo, L. G., Kubat, M., and Wuchty, S.
(2019a). A stable hybrid method for feature subset
selection using particle swarm optimization with local
search. In Proceedings of the Genetic and Evolution-
ary Computation Conference, pages 13–21. ACM.
Dhrif, H., Giraldo, L. G. S., Kubat, M., and Wuchty, S.
(2019b). A stable combinatorial particle swarm opti-
mization for scalable feature selection in gene expres-
sion data. arXiv preprint arXiv:1901.08619.
Eberhart, R. and Kennedy, J. (1995). Particle swarm opti-
mization, proceeding of ieee international conference
on neural network. Perth, Australia, pages 1942–
1948.
Stable Feature Selection for Gene Expression using Enhanced Binary Particle Swarm Optimization
443

Engelbrecht, A. (2012). Particle swarm optimization: Ve-
locity initialization. In Evolutionary Computation
(CEC), 2012 IEEE Congress on, pages 1–8. IEEE.
Han, F., Sun, W., and Ling, Q.-H. (2014). A novel
strategy for gene selection of microarray data based
on gene-to-class sensitivity information. PloS one,
9(5):e97530.
Han, F., Yang, C., Wu, Y.-Q., Zhu, J.-S., Ling, Q.-H.,
Song, Y.-Q., and Huang, D.-S. (2017). A gene se-
lection method for microarray data based on binary
pso encoding gene-to-class sensitivity information.
IEEE/ACM Transactions on Computational Biology
and Bioinformatics (TCBB), 14(1):85–96.
John, G. H., Kohavi, R., and Pfleger, K. (1994). Irrelevant
features and the subset selection problem. In Machine
Learning Proceedings 1994, pages 121–129. Elsevier.
Kennedy, J. and Eberhart, R. C. (1997). A discrete bi-
nary version of the particle swarm algorithm. In 1997
IEEE International Conference on Systems, Man, and
Cybernetics. Computational Cybernetics and Simula-
tion, volume 5, pages 4104–4108 vol.5.
Khaire, U. M. and Dhanalakshmi, R. (2019). Stability of
feature selection algorithm: A review. Journal of King
Saud University-Computer and Information Sciences.
Kumar, V. and Minz, S. (2014). Feature selection. SmartCR,
4(3):211–229.
Lee, S., Soak, S., Oh, S., Pedrycz, W., and Jeon, M.
(2008). Modified binary particle swarm optimization.
Progress in Natural Science, 18(9):1161–1166.
Lopez-Paz, D., Hennig, P., and Sch
¨
olkopf, B. (2013). The
randomized dependence coefficient. In Advances in
neural information processing systems, pages 1–9.
Mohamad, M. S., Omatu, S., Deris, S., and Yoshioka, M.
(2011). A modified binary particle swarm optimiza-
tion for selecting the small subset of informative genes
from gene expression data. IEEE Transactions on In-
formation Technology in Biomedicine, 15(6):813–822.
Mohammadi, M., Noghabi, H. S., Hodtani, G. A., and
Mashhadi, H. R. (2016). Robust and stable gene se-
lection via maximum–minimum correntropy criterion.
Genomics, 107(2-3):83–87.
Perthame, E., Friguet, C., and Causeur, D. (2016). Stability
of feature selection in classification issues for high-
dimensional correlated data. Statistics and Comput-
ing, 26(4):783–796.
Poli, R. (2009). Mean and variance of the sampling dis-
tribution of particle swarm optimizers during stagna-
tion. IEEE Transactions on Evolutionary Computa-
tion, 13(4):712–721.
Rezaee Jordehi, A. and Jasni, J. (2013). Parameter selec-
tion in particle swarm optimisation: a survey. Journal
of Experimental & Theoretical Artificial Intelligence,
25(4):527–542.
Shipp, M. A., Ross, K. N., Tamayo, P., Weng, A. P., Ku-
tok, J. L., Aguiar, R. C. T., Gaasenbeek, M., An-
gelo, M., Reich, M., Pinkus, G. S., Ray, T. S., Koval,
M. A., Last, K. W., Norton, A., Lister, T. A., Mesirov,
J., Neuberg, D. S., Lander, E. S., Aster, J. C., and
Golub, T. R. (2002). Diffuse large b-cell lymphoma
outcome prediction by gene-expression profiling and
supervised machine learning. Nature Medicine, 8:68
EP –. Article.
Singh, D., Febbo, P. G., Ross, K., Jackson, D. G., Manola,
J., Ladd, C., Tamayo, P., Renshaw, A. A., D’Amico,
A. V., Richie, J. P., Lander, E. S., Loda, M., Kantoff,
P. W., Golub, T. R., and Sellers, W. R. (2002). Gene
expression correlates of clinical prostate cancer be-
havior. Cancer Cell, 1(2):203 – 209.
Van den Bergh, F. and Engelbrecht, A. P. (2010). A conver-
gence proof for the particle swarm optimiser. Funda-
menta Informaticae, 105(4):341–374.
Xue, B., Zhang, M., and Browne, W. N. (2013). Particle
swarm optimization for feature selection in classifica-
tion: A multi-objective approach. IEEE transactions
on cybernetics, 43(6):1656–1671.
Ye, F. (2017). Particle swarm optimization-based automatic
parameter selection for deep neural networks and its
applications in large-scale and high-dimensional data.
PloS one, 12(12):e0188746.
Yong, Z., Dun-wei, G., and Wan-qiu, Z. (2016). Feature
selection of unreliable data using an improved multi-
objective pso algorithm. Neurocomputing, 171:1281–
1290.
Zhang, Y., Gong, D.-w., and Cheng, J. (2017). Multi-
objective particle swarm optimization approach
for cost-based feature selection in classification.
IEEE/ACM Transactions on Computational Biology
and Bioinformatics (TCBB), 14(1):64–75.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
444
