A Highly Constrained Integer Linear Program with Fuzzy Boundary

Conditions for Scheduling in Online Tutoring

Quoc Tien Au and Faiyaz Hasan

GradeSlam, Montreal, Canada

Keywords:

Scheduling, Online Tutoring, Integer Linear Programming, Heuristics, Staff Scheduling, Rostering,

Constraints, Objective Function, Adaptive Constraints, Constraint Relaxation, Robustness, Robust

Scheduling.

Abstract:

Scheduling personnel is an important aspect of many organizations and can rapidly become unsustainable to

perform manually. It is crucial that the automated algorithm consistently generates a high quality schedule.

This paper discusses a linear integer program with a set of constraints, developed in collaboration with a

scheduling expert, required to generate reliable schedules for a live online tutoring platform. The focus in

the algorithm is shifted away from the optimization of an objective function to adopting hard constraints that

guarantee any solution will be sufﬁciently good. Furthermore, a graceful degradation protocol to implement

fuzzy boundary conditions for the constraints ensure that appropriate compromises can be made in most cases

to ﬁnd a solution. Lastly, a comparison of the automated algorithm to a domain expert shows a 5% higher

topic coverage and 10% lower cost in favor of the former which has led to a rapid adoption of the automated

scheduler by the organization.

1 INTRODUCTION

Organizations that rely on scheduling experts and

skilled employees with multiple specializations to

meet the demand for their service face challenges re-

lated to scalability. To provide an excellent service, it

is necessary to create a schedule such that the person-

nel have the speciﬁc set of skills that the customers

require. As the number of employees and customers

grow, manually generating a schedule becomes in-

tractable while continuing to satisfy the various hard

and soft constraints imposed by the unique charac-

teristics of the organization. This type of rostering

problem, as demonstrated by the well studied Nurse

Scheduling Problem (NSP), is prevalent in hospitals,

airports and online tutoring companies.

GradeSlam is a chat-based online tutoring plat-

form that instantly connects a tutor to a student when

they request support for an academic topic. Students

can ask questions corresponding to any elementary to

high school level topic at any time of day throughout

the week. While the exact number of students and

when they will appear on the platform is impossible

to know apriori, an approximate number of tutors to

meet the demand for each topic can be determined

from the historical data. Each tutor has a different

set of specializations, times they are available to work

on the platform, level of seniority, and reliability, all

which must be taken into account to generate an ef-

fective and fair schedule.

Until recently, the schedules at GradeSlam were

created manually by an expert week after week. This

expert manages the entire tutor team and conse-

quently knows the topics they teach, the number of

students they can handle at a given time, and even

their shift preferences. She would manually create a

schedule by cross-referencing the required topic cov-

erage and the tutor availability calendar while factor-

ing in her nuanced knowledge of the staff. Initially,

this was possible to do in a reasonable amount of time,

but the growing tutor team made scheduling increas-

ingly time consuming and ultimately unscalable. The

implemented solution discussed in this paper takes

inspiration from the NSP, which is a closely related

problem in the context of healthcare.

In this paper, an integer linear program is used

to solve the scheduling problem in the context of a

live, online tutoring platform. A number of hard and

soft constraints have been identiﬁed and integrated

into the optimization problem formulation to ensure

the service quality, satisfaction of labor regulations,

and fairness in terms of the number of hours assigned

Au, Q. and Hasan, F.

A Highly Constrained Integer Linear Program with Fuzzy Boundary Conditions for Scheduling in Online Tutoring.

DOI: 10.5220/0008919303130320

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 313-320

ISBN: 978-989-758-396-4; ISSN: 2184-4372

313

to each tutor. The combination of all of these con-

straints, coupled with the fact that the tutor availabil-

ity is variable, often makes the automatic schedule

generation infeasible. However, similar to the expert,

a robust scheduling algorithm should be able to work

around such difﬁculties to ﬁnd a solution despite the

highly complex problem setup. In this paper, we dis-

cuss an effective strategy of creating a more robust

algorithm by integrating the notion of graceful degra-

dation and strategically relaxing the constraints and

relevant parameters.

The paper is organised as follows. Section 2 pro-

vides a literature review of real world applications of

the employee scheduling problem. Section 3 deﬁnes

the problem where all of the constraints and the main

objectives are stated. Section 4 outlines the mathe-

matical formulation, i.e. the variables, constraints and

objective function. Section 5 introduces the heuris-

tics to modify the scheduling algorithm and overcome

the problem of conﬂicting constraints. Section 6 dis-

cusses the performance of the algorithm in generat-

ing schedules using both quantitative and qualitative

metrics. Finally, section 7 presents a summary of the

paper and highlights future experiments.

2 PREVIOUS WORK

Employee scheduling is of utmost importance in

many industries. The research community has mainly

focused on the Nurse Scheduling Problem (NSP),

which tries to schedule hospital employees to vari-

ous shifts for different days depending on the demand.

Some examples of scheduling in the context of emer-

gency services can be found in (Beaulieu et al., 2000)

and (Camiat et al., 2019). Though each setting is

unique, they share a common objective of ﬁnding a

trade off between satisfactory coverage of the service

demand, labor regulations and personnel satisfaction.

The NSP has been studied extensively, as shown in

(Burke et al., 2004) and (den Bergh et al., 2013), so

that a consistent, automated generation of schedules

is possible, while ensuring adequate demand cover-

age and employee well-being.

Even though the problem models are easily trans-

ferable amongst different industries, many speciﬁc

examples of employee scheduling are described since

the constraints, the objective function and the heuris-

tics are variable. The most well studied domains are

transportation, supply chain, call centers, airlines and

health care. More examples are described in (Ernst

et al., 2004). It can also be applied in niche ﬁelds, as

shown in (Albornoz et al., 2015) (meat packing indus-

try), (Leiva and Albornoz, 2016) (soft drink industry),

or in (Lampoudi et al., 2015) (telescope industry). All

these examples show that specialized knowledge is re-

quired to come up with an automated solution that can

be adopted by an organization. Consequently, having

a domain expert is essential to the success of an auto-

mated scheduler.

Two papers, (A

gralı et al., 2017) and (Hojati and

Patil, 2011) hold our attention since they both have

a similar setup as us. For example, they all have

part-time workers with heterogeneous skills, ﬂexible

availability and variable demand to satisfy, and use

heuristics to overcome constraint conﬂicts. (Hojati

and Patil, 2011) showcases a 2-step method: the ﬁrst

one is to ﬁnd the optimal shifts (shift duration, place-

ment, and corresponding employees), and the second

one is to generate a schedule considering those good

shifts. Furthermore, heuristics are used to come up

with a feasible solution. Though both problem setups

are similar to ours, we have to deal with many more

constraints related to employee satisfaction.

The large number of constraints and variables cre-

ate a lot of constraint conﬂicts. Over-constrained

problems are difﬁcult to satisfy or optimize. One way

to resolve this issue is to apply constraint relaxation.

In (Junker, 2004), a divide-and-conquer method is de-

scribed to explain which constraints are responsible

for the conﬂicts. This form of constraint relaxation is

a powerful way to make a problem feasible, although

the method is aggressive since it removes some con-

straints. In our case, we want to avoid the complete

removal of a constraint to ensure employee satisfac-

tion and sufﬁcient demand coverage, both of which

are necessary for a successful adoption of the system.

(Burke et al., 2004) concludes that there has been

a lot of work on ﬁnding and tuning scheduling algo-

rithms. However, the applications that are highlighted

are often toy problems or problems with low dimen-

sions. In (De Causmaecker et al., 2004), several real

world scheduling problems are discussed. Yet, not

many studies demonstrate how to ﬁnd solutions in real

world scheduling issues with an over-constrained en-

vironment, where optimization methods coupled with

heuristics are used to ﬁnd a viable solution.

The main contribution of this paper is to provide

an exhaustive view of automated scheduling in online

tutoring, including a mathematical formulation of the

problem, the creation of heuristics with the help of a

domain expert, and the implementation of a graceful

degradation protocol.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

314

3 PROBLEM DEFINITION

In order to specify the schedule input parameters, a

week is broken up into seven days which are further

subdivided into one hour slots. A tutor shift refers to

a block of adjacent hour slots during which a tutor is

scheduled. Following that, information regarding the

number of required tutoring units needs to be speci-

ﬁed for every topic during each hourly slot.

Due to weekly changes in the tutors’ availability

and the student demand, i.e. the net volume of stu-

dents coming onto the platform for tutoring help, the

schedule input parameters need to be updated on a

weekly basis and the algorithm needs to be re-run.

Tutors specify their weekly availability at least four

days before the schedule is generated. For exam-

ple, tutors would set their availability for the week of

September 23rd to 30th by September 13th. The gen-

eral tutor availability can change due to tutors having

variable personal time commitments, but also due to

the growth of the tutor team which adds new sets of

availability. The student demand can change due to

seasonal inﬂuences such as midterms or assignment

deadlines, as well as the addition of new students to

the platform.

The tutor team changes in response to the platform

trafﬁc. Over the past year, the number of tutors have

almost tripled. Each tutor can cover a certain set of

topics. There are 47 topics, including algebra, En-

glish literature, chemistry, computer science, Span-

ish etc. For each topic, a certain number of tutors

have to be scheduled during each hourly slot based on

the past frequency of students needing help with the

topic. Usually, math and English literature tutors are

in high demand, meaning that the number of tutors

needed to cover these topics is generally higher than

less popular topics such as music theory. The number

of tutors scheduled per topic during each shift is de-

termined by following requirements from the service

department:

1. The minimum number of tutors that must be

scheduled (hard constraint). For example, Mon-

day 12 PM to 8 PM at least three calculus tutors

need to be scheduled.

2. The expected number of tutors that should cover

that topic at that hour (soft constraint). For exam-

ple, Monday 12 PM to 4 PM, scheduling around

six calculus tutors is optimal.

Based on the previous example, on Monday 12 PM -

4 PM, at least three and possibly ﬁve to seven calcu-

lus tutors will be scheduled. The objective function

is dedicated to scheduling as close to the prescribed

optimal amount of tutors as possible. All other inputs

expressed by the expert are implemented as hard con-

straints to ensure service quality and employee satis-

faction:

• A tutor should only be scheduled when they spec-

ify they are available to work.

• A tutor should not be scheduled more than the

maximum number of working hours they are al-

lowed, and more than 5 shifts per week. This is to

ensure work-life balance.

• A tutor should get an expected minimum of work-

ing hours. This is to ensure the fairness of the

schedule and hence employee satisfaction.

• A shift must last at least 3 hours and cannot ex-

ceed 6 hours. There should be at least 20 hours

between the beginning of two shifts.

• For every hour slot of the week, a certain mini-

mum number of tutors must be scheduled. This

constraint is to ensure that tutors will not be over-

whelmed by the ﬂow of students coming on the

platform.

• For each hour, the number of scheduled tutors has

an upper bound which can change from week to

week. This constraint is to prevent overschedul-

ing.

• There are a list of important topics, for which dur-

ing each hour, the number of scheduled tutors cov-

ering that topic must exceed some speciﬁed lower

bound.

• The cost of the weekly schedule must be less than

a pre-speciﬁed amount.

Knowing exactly what constraints have been sat-

isﬁed will allow us to easily evaluate the quality of the

schedule. Indeed, having a schedule that is transpar-

ent and interpretable is of utmost importance to en-

sure the quick adoption of the system and the fair-

ness of the schedules. While the large number of hard

constraints makes it more difﬁcult to ﬁnd a solution,

relaxing the constraints and the usage of heuristics re-

solve the problem. The ability to compromise is an

essential feature for the success of the scheduling al-

gorithm. This is achieved by either strategically omit-

ting some constraints or by changing the constraint

parameters so that they are less restrictive.

To sum up, the objective is to schedule tutors such

that each topic is covered adequately at all times.

In addition to that, the schedule must satisfy several

rules to ensure a high service quality and staff sat-

isfaction without exceeding the upper bound for the

schedule cost.

A Highly Constrained Integer Linear Program with Fuzzy Boundary Conditions for Scheduling in Online Tutoring

315

4 MATHEMATICAL

FORMULATION

The problem is expressed as a constrained optimiza-

tion problem with input parameters, linear constraints

and integer variables.

4.1 Input Parameters

• Tutors are enumerated by the index n, where n ∈

[1, N] and N = 100 in our experiments.

• A week is partitioned into one hour slots. These

hour slots are enumerated by the index s where

s ∈ [1, S] and S = 24 · 7 = 168. In this paper, the

ﬁrst hour of the week is Monday at midnight.

• The set of academic topics available for tutoring

are enumerated by the index k, where k ∈ [1, K]

and K = 47.

• Important topics are a subset of the topics enu-

merated by k ∈ [1, K] and designated by the set T

where T

⊆ [1, K]. Currently, there are less than

ten important topics but these topics absolutely

need to be covered during certain hours.

• Hourly salary of each tutor n is denoted by p

where n ∈ [1, N].

• Number of tutors required for each important

topic k during hour s is designated M

where

k ∈ T

and s ∈ [1, S]. These inputs are implemented

via hard constraints.

• The status of tutor n in their ability to teach topic

k is denoted by the binary input y

∈ {0, 1} where

n ∈ [1, N] and k ∈ [1, K]. This information is static

and gathered when the tutors are ﬁrst hired.

• Number of tutors available during hour s for topic

k is denoted O

∑

n=1

· y

where s ∈ [1, S]

and k ∈ [1, K].

• Number of required tutors per topic k during hour

s, i.e. demand, is denoted M

where k ∈ [1, K]

and s ∈ [1, S]. The demand is an input for the al-

gorithm speciﬁed by the expert. This information

is interpreted as a soft constraint.

• The availability of tutor n during hour s is given

by the binary input a

∈ {0, 1} where n ∈ [1, N]

and s ∈ [1, S].

4.2 Decision Variables

• Tutor shift assignment variable x

∈ {0, 1},

where n ∈ [1,N], s ∈ [1, S] represents whether tu-

tor n is scheduled during hour s. Assignment

of these binary variables is equivalent to the cre-

ation of a schedule. The variable x has dimension

N · S = 16800.

• Coverage of topic k during hour s based on the

generated schedule (via the x

variables) is de-

noted by c

∑

n=1

· y

, where s ∈ [1, S] and

k ∈ [1, K].

• Status if hour s is the beginning of a shift for tutor

n is denoted by the binary variable b

∈ {0, 1}

where n ∈ [1, N] and s ∈ [1, S] (Note that the di-

mension of b is also 16800).

• Status whether the demand of topic k during hour

s is satisﬁed is denoted by the binary variable

∈ {0, 1} where s ∈ [1, S] and k ∈ [1, K]. The

dimension of z is 7896.

All the variables discussed in this section are integers.

The binary variables take the values 0 or 1. There are

41496 variables in this optimization problem. All the

hard constraints outlined by the expert are deﬁned in

the next section. Furthermore, all the hard constraints

created to keep the problem setup linear are also dis-

cussed in the next section. A summary of the preced-

ing variables can be found in table 1.

4.3 Constraints

The hard constraints in section 3 are expressed as lin-

ear constraints since they are often easier to solve as

discussed in (Chinneck, 2001).

1. A tutor cannot work when not available.

∀n ∈ [1, N], s ∈ [1, S], x

≤ a

(1)

2. A tutor cannot work more than their maximum

number of working hours.

∀n ∈ [1, N],

∑

s=1

≤ H

(2)

3. A tutor cannot work more than 5 shifts per week.

∀n ∈ [1, N],

∑

s=1

≤ 5 (3)

4. A tutor should get an expected minimum number

of working hours as long as they put enough avail-

ability.

∀n ∈ [1, N],

∑

s=1

≥ min

−

∑

s=1

(4)

−

is deﬁned by the expert and can change from

week to week, to ensure a fair distribution of hours

among tutors.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

316

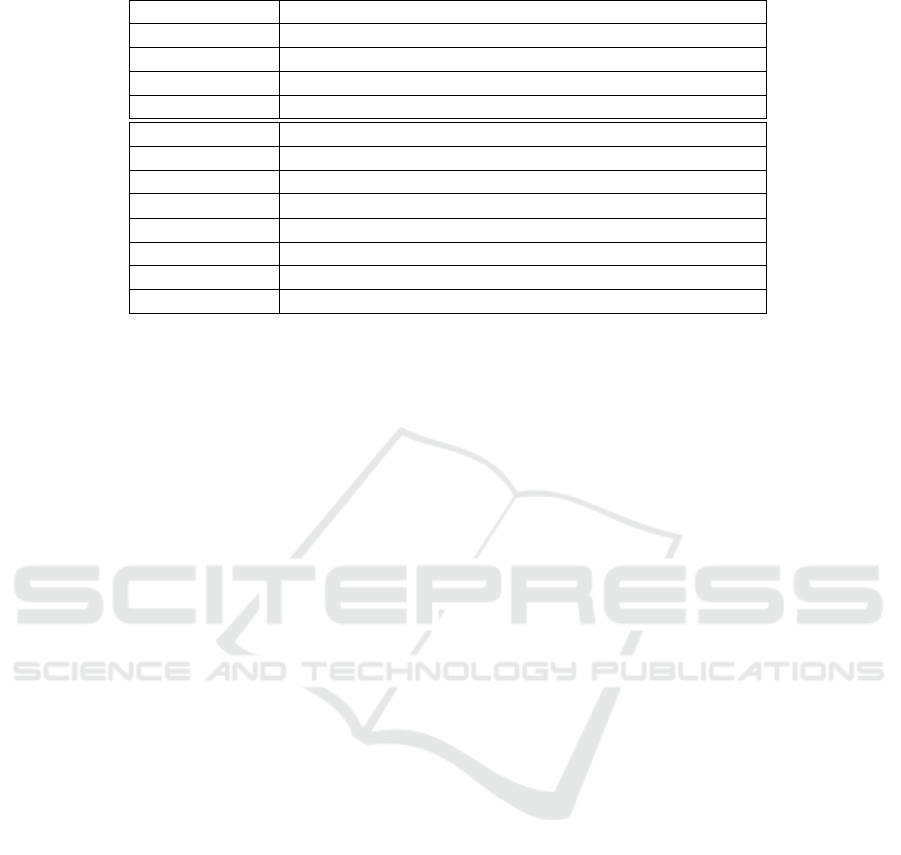
Table 1: Input parameters and variables.

Variable name Description

Tutor shift assignment

Status if it’s the beginning of a shift

Coverage of topic k during hour s

Status if expected demand of topic k is satisﬁed

Input parameter Description

/ C

×max

Hourly salary / Cost limit

Set of important topics

/ M

Number of required tutors, k ∈ [1, K] / k ∈ T

Tutors’ availability

Status if tutor n ∈ [1, N] teaches topic k ∈ [1, K]

−

/ H

Expected minimum / Maximum number of working hours

−

/ L

Minimum / Maximum number of scheduled tutors

5. A tutoring shift, i.e. adjacent hour slots a tutor is

scheduled, must add up to at least 3 hours.

∀n ∈ [1, N], s ∈ [1, S − 2], 3· b

≤

∑

i=0

n(s+i)

(5)

We also want to ensure that there is no shift start-

ing the last 2 hours of the week.

∀n ∈ [1, N], b

n(S−1)

= 0 = b

(6)

A shift must not exceed 6 hours.

∀n ∈ [1, N], s ∈ [1, S − 6],

∑

i=0

n(s+i)

≤ 6 (7)

6. There should be at least 20 hours between the be-

ginning of 2 shifts for a given tutor.

∀n ∈ [1, N], s ∈ [1, S − 19],

∑

i=0

n(s+i)

≤ 1 (8)

7. For each hour, there must be a minimum number

of scheduled tutors (L

−

, deﬁned by the expert) as

long as there are enough tutors available.

∀s ∈ [1, S],

∑

n=1

≥ min

−

∑

n=1

(9)

8. For each hour, the number of scheduled tutors

cannot exceed a certain number (L

, deﬁned by

the expert).

∀s ∈ [1, S],

∑

n=1

≤ L

(10)

9. For every hour and important topic, there must

be a minimum number of tutors scheduled who

can teach the respective topic provided there are

enough tutors available.

∀k ∈ T

, s ∈ [1, S], c

∑

n=1

· y

≥ min



, O



(11)

10. There is a price limit on the weekly schedule.

∑

n=1

∑

s=1

) ≤ C

max

(12)

11. A linear formulation of the beginning of shift vari-

ables (b

) is based on imposing hard constraints

and using the variables x

as shown below.

≥ x

− x

n(s−1)

(13)

≤ x

(14)

≤ 1 − x

n(s−1)

(15)

n,−1

is the information speciﬁed in the last hour

slot of the schedule corresponding to the previous

week’s schedule (In our case that corresponds to

11 PM - 12 AM on Sunday).

12. The demand satisfaction variable z

is linearly

formulated by imposing hard constraints on M

and c

and is shown below.

≥ M

− Z · (1 − z

) (16)

≤ M

− 1 + Z · z

(17)

Z is an upper bound on the variables c

and M

Since the demand and the number of available tu-

tors is bounded in this problem setup for a given

week, M

is bounded. We arbitrarily choose Z

to equal 50. This number may vary from week to

week.

4.4 Objective Function

The objective function was deﬁned to maximize the

instances where the required number of tutors (for

each topic and hour slot) were scheduled. Mathemat-

ically, this is equivalent to maximizing the instances

where the variables z

equals 1. Hence, the objective

function (to be maximized) can be written as

A Highly Constrained Integer Linear Program with Fuzzy Boundary Conditions for Scheduling in Online Tutoring

317

K ({z

}) =

∑

k=1

∑

s=1

. (18)

Each unit increment in the objective function is

due to the required number of tutors being scheduled

for a topic and an hour slot. This deﬁnition is both

intuitive and easy to implement.

5 HEURISTICS

The optimization problem discussed in this paper is

comprised of approximately 60, 000 hard constraints

and 40, 000 variables. Due to the large number of

constraints and variables, the solution space is often

empty since it is unfeasible to satisfy all of the con-

ditions. The gap between tutor availability and topic

demand is one of the major contributors to the infea-

sibility of ﬁnding a solution. Not being able to ﬁnd

a schedule for a given week would be unacceptable.

That is why the principle of graceful degradation is

adopted to gradually relax the set of constraints and

ﬁnd the best possible schedule. In subsection 5.1,

we discuss the approaches to relaxing the constraints,

while in subsection 5.2 the protocol that would lead to

the best compromise in ﬁnding a solution is discussed.

5.1 Constraint Parametrization

When a solution is infeasible corresponding to the

problem setup, the following strategies can be used

to relax the overly restrictive conditions:

1. Removing some of the more restrictive hard con-

straints. This option is not desirable since the hard

constraints are crucial for ensuring a high quality

schedule.

2. Reformulating some of the hard constraints to soft

constraints in the problem setup. The downside is

that such an objective function with multiple com-

peting goals makes the algorithm less predictable

and often leads to optimal solutions that are in re-

ality low quality schedules (according to the ex-

pert).

3. Re-parametrize the hard constraints to include a

relaxation parameter so that they are less restric-

tive and allow us to ﬁnd a schedule that is the best

possible quality for the given inputs. For example,

if the tutor availability for Calculus is low during

2 - 5 PM on Friday, we can reduce the minimum

required topic coverage accordingly (up to a point

beyond which external intervention such as hiring

more Calculus tutors might be necessary) in the

constraints.

Consider the re-parametrized hard constraint given by

equation (11).

∑

n=1

· y

≥ min



, O



− R

, (19)

where, the relaxation parameter R

is introduced to

allow us to strategically compromise on the important

topic coverage,

∈

{

1, 2, 3

}

when M

≤ O

. (20)

The constraint relaxation need not be subtractive but

can also be multiplicative as shown below in the re-

parametrized hard constraint given by equation (4) as

given below,

∑

s=1

≥ min

· H

−

∑

s=1

, (21)

where R

∈ {1, 0.8}.

In the following subsection, we discuss the pro-

tocol used to identify and relax the appropriate con-

straint and gradually sacriﬁce the quality of the re-

quired schedule to ﬁnd a solution.

5.2 Graceful Degradation Protocol

The idea behind graceful degradation is to ﬁnd the

weakest relaxation of constraints that will lead to a

feasible solution. An iterative process is adopted to

ﬁnd the best compromise. For each iteration, slight

changes are brought to the constraint boundaries, and

a feasibility check is performed. The next iteration

takes place when there is no feasible solution, other-

wise the process stops. This process is summarized

succinctly in algorithm 1.

Algorithm 1: Graceful Degradation Protocol.

input: ordered list of constraint parameter sce-

narios prioritized by schedule quality

output: constraint parameter scenario that lead

to the highest quality schedule (if it exists)

1: for scenario in constraint parameter scenarios

2: if scenario allows feasible solution then

3: return scenario

The degree to which the constraint parameters can

be relaxed is determined by the scheduling expert.

Following that, constraint scenarios are ordered in

terms of priority starting with the unrelaxed parameter

case and ending with the parameters that lead to the

least desirable schedule. The algorithm used in this

paper iterates through up to ﬁfteen stages to search for

a constraint scenario where a schedule can be gener-

ated.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

318

6 RESULTS

In this section we compare the performance metrics

of the automatically generated schedules to that of the

domain expert. It is worth noting that the comparison

was only possible when the volume of tutors required

to be scheduled was lower. Currently, the larger num-

ber of tutors required to be scheduled makes it impos-

sible to manually generate one in a reasonable amount

of time.

When all the inputs for the scheduling algorithm

have been gathered, the algorithm iterates through

each of the scenarios in the graceful degradation pro-

tocol described in subsection 5.2. For each itera-

tion, the OR tools library with the Python wrapper

(see (Perron and Furnon, 2019)) is used to determine

whether a feasible solution exists or not. It is not re-

quired to ﬁnd an optimal solution since the constraints

are setup to ensure that any solution will be sufﬁ-

ciently high quality. Determining whether the prob-

lem has a feasible solution takes under a few seconds

using a Mac mini with a processor Intel Core i5 (3

GHz), 6 cores, 8 GB of memory.

Once a scenario for which a feasible solution ex-

ists has been found, the algorithm proceeds to gener-

ate a sequence of solutions that are increasingly opti-

mal with respect to the objective function. This pro-

cess of optimizing the objective function converges

relatively fast and terminating it after two to ﬁve min-

utes leads to a good schedule (with negligible differ-

ences depending on how long the optimization was

carried out for). Alternatively, the algorithm can also

be terminated after the objective function reaches a

predeﬁned threshold. The total time taken for the al-

gorithm to ﬁnd a solution is dependent on the number

of scenarios the algorithm had to test before ﬁnding

a feasible scenario if one exists at all. Cumulatively,

testing each scenario until it ﬁnds a solution takes the

algorithm less than ﬁfteen minutes. This is a very

signiﬁcant improvement, considering that the manual

generation of a schedule would take up to three hours

(when the tutor team was small enough to schedule

manually). Furthermore, the algorithm has been able

to ﬁnd a feasible scenario to generate a solution in ev-

ery case utilizing the graceful degradation protocol.

A quantitative comparison of the schedules gen-

erated by the expert and the integer linear program-

ming (ILP) algorithm is based on the time required

to generate a schedule, the schedule cost, topic cover-

age, number of shifts of that were too short (less than

three hours) and the number of instances where the

tutor was scheduled more shifts than allotted. Over a

period of 12 weeks, the automated algorithm had 5%

higher topic coverage and at the same time, the cost

was 10% lower. Furthermore, the algorithm never

generated schedules with undesirable number and du-

ration of shifts while the expert had on average 2 to

5 tutors who were assigned more than six shifts and

between 5 to 10 shifts that were too short. The results

are summarized in table 2.

On a qualitative level, the expert’s evaluation of

the automated schedule is that it performs as well as

her schedules in terms of topic coverage and satisfy-

ing the expectations that the tutors have in terms of the

hours they are scheduled for. Week over week, the

expert has gained more and more conﬁdence in the

algorithm generating an appropriate schedule based

on her inputs. To develop the automated algorithm,

it was crucial that we relied heavily on the domain

expert’s experience to select the right constraints for

the problem setup. This was one of the key contri-

butions to the success and subsequent adoption of the

scheduling algorithms.

Lastly, since the metrics have been generated, the

platform has scaled a lot (+200% users), and the man-

ual creation of the schedule has become impossible

whereas the integer linear program can generate one

in less than 20 minutes.

7 CONCLUSION

Personnel scheduling is an essential recurring task

for a chat-based online tutoring platform. The em-

ployee availability and the number of required tutors

per topic vary weekly making it necessary to generate

a new schedule every week. Moreover, as the work-

force continues to grow, manually generating a sched-

ule will ultimately become impossible.

The solution discussed in this paper involves col-

laborating with a domain expert to translate the sched-

ule requirements as mathematical constraints and us-

ing integer linear programming to ﬁnd a solution. The

resulting algorithm is very reliable due to the mini-

mum standard set by all the hard constraints. One

of the most important requirements of the algorithm

is that a solution be found every week. Due to the

complex set of hard constraints in our setup, ﬁnding a

solution by a straightforward application of OR tools

is often infeasible. In this paper, a protocol based on

reparametrizing the hard constraints and relaxing the

new parameters is shown as an effective strategy to

ﬁnd a good compromise for the schedule. In most

NSP applications, a similar graceful degradation pro-

tocol would be immensely beneﬁcial. The constraint

relaxation is carried out in iterations according to the

priority set by the expert and when it fails, an external

intervention such as hiring more tutors is required.

A Highly Constrained Integer Linear Program with Fuzzy Boundary Conditions for Scheduling in Online Tutoring

319

Table 2: Quantitative evaluation of schedules over 12 weeks.

Metric Expert (N = 50) ILP (N = 50) Expert (N = 100) ILP (N = 100)

Time taken to generate 3 hours 15 min N/A 15 min

a schedule (< 5 iterations) (< 5 iterations)

Topic Coverage 65%-70% 70%-75% N/A 70%-75%

Number of shifts that 5-10 0 N/A 0

are too short

Number of tutors who are 2-5 0 N/A 0

scheduled more than six times

A quantitative comparison of the topic coverage,

cost and time taken to generate schedules show that

the scheduling algorithm outperforms the manually

generated schedules. The results show that the topic

coverage is higher by 5% and the cost is lowered by

10% for an equivalent coverage. The greatest advan-

tage is that it takes the algorithm less than 20 minutes

to generate a schedule compared to hours of work

(it ranged from 3 to 5 hours before the automated

scheduler was adopted) for the expert. Moreover, em-

ployee dissatisfaction with the hours they were sched-

uled compared to what they expected was negligible.

The algorithm’s performance has been very reli-

able and satisfactory leading to a rapid adoption of

a stable version in the platform. Areas of improve-

ment consist in forecasting the topic demand, so that

the expert does not have to input it manually; build-

ing a simulator to generate ﬂows of students coming

on the platform, so that we can evaluate the average

performance of a schedule in multiple scenarios; and

ﬁnding the best combination of tutors at each hour slot

taking into account how much work a tutor can han-

dle factoring in the number of simultaneous students

and their requested topic.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the contribution

of Chloe Sholl in articulating the subtle and implicit

rules behind tutor scheduling into comprehensible

conditions that can be expressed mathematically.

REFERENCES

Albornoz, V., Gonz

alez-Araya, M., Gripe, M., and Ro-

driguez, S. (2015). A mixed integer linear program

for operational planning in a meat packing plant.

gralı, S., Tas¸kın, Z. C., and

Unal, A. T. (2017). Em-

ployee scheduling in service industries with ﬂexible

employee availability and demand. Omega, 66:159 –

169.

Beaulieu, H., Ferland, J. A., Gendron, B., and Michelon,

P. (2000). A mathematical programming approach for

scheduling physicians in the emergency room. Health

Care Management Science, 3(3):193–200.

Burke, E. K., De Causmaecker, P., Berghe, G. V., and

Van Landeghem, H. (2004). The state of the art of

nurse rostering. Journal of Scheduling, 7(6):441–499.

Camiat, F., Restrepo, M., Chauny, J.-M., Lahrichi, N., and

Rousseau, L.-M. (2019). Productivity-driven physi-

cian scheduling in emergency departments. Health

Systems, pages 1–14.

Chinneck, J. W. (2001). Practical Optimization: A Gentle

Introduction.

De Causmaecker, P., Demeester, P., Vanden Berghe, G.,

Berghe, E., and Verbeke, B. (2004). Analysis of real-

world personnel scheduling problems.

den Bergh, J. V., Beli

en, J., Bruecker, P. D., Demeule-

meester, E., and Boeck, L. D. (2013). Personnel

scheduling: A literature review. European Journal of

Operational Research, 226(3):367 – 385.

Ernst, A., Jiang, H., Krishnamoorthy, M., and Sier, D.

(2004). Staff scheduling and rostering: A review of

applications, methods and models. European Journal

of Operational Research, 153(1):3 – 27. Timetabling

and Rostering.

Hojati, M. and Patil, A. S. (2011). An integer linear

programming-based heuristic for scheduling hetero-

geneous, part-time service employees. European

Journal of Operational Research, 209(1):37 – 50.

Junker, U. (2004). Quickxplain: Preferred explanations and

relaxations for over-constrained problems. pages 167–

172.

Lampoudi, S., Saunders, E., and Eastman, J. (2015). An

integer linear programming solution to the telescope

network scheduling problem.

Leiva, J. and Albornoz, V. (2016). Short-term production

scheduling in the soft drink industry. pages 416–423.

Perron, L. and Furnon, V. (2019). Or-tools.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

320