
Decision Support for Shipping Spare Parts in Bundles
Yizi Zhou
1a
, Jiyin Liu
2b
, Rupal Mandania
2c
, Kai Chen
1
and Rongjun Xu
1
1
Huawei Technologies Co Ltd, Bantian Huawei Base, Shenzhen, China
2
School of Business and Economics, Loughborough University, Loughborough, U.K.
Keywords: Parcel Delivery Pricing, Service Level Agreement, Optimisation, Mixed-Integer Programming.
Abstract: A telecommunication equipment company sends spare parts from local hubs to construction sites or other
local hubs in mainland China several times a day through parcel delivery services. Depending on the delivery
distance, there are various delivery options such as transportation via air, via road, via sea, via rail and via
inland waterways. Many choices named service levels are available within each transportation category. There
are three parcel delivery pricing policy: price per shipment, weight ranged price, and continuous pricing. Each
spare parts delivery usually has a priority level or delivery time requirement. Spare parts to be shipped from
the same hub or nearby hubs to the same or nearby destinations are considered being able to ship in bundles.
By observing the delivery pricing structure, it is usually beneficial to bundle spare parts together for shipment.
The problem is formulated as a mixed integer liner programming model. Numerical experiments are carried
out to observe the benefits and also reflect the features of parcel delivery pricing structure.
1 INTRODUCTION
We study a problem where a telecommunication
equipment company sends spare parts from local hubs
to construction sites or other local hubs in mainland
China twice a day. Typically, depending on the depot
hub and destinations of the shipment, there are
various means of freight transportation, such as
transportation via air, via road, via sea, via rail and
via inland waterways. Many choices named service
levels are available within each transportation
category. The service level agreement (SLA) is the
guaranteed delivery time of the parcel, e.g. the next
day by 18:00. The pricing of each delivery service is
different but typically increasing as SLA decreasing.
There are three types of parcel delivery pricing
policy. The first one is fixed price per shipment,
although there may be a limit on the maximum weight
or maximum number of items per shipment. This type
of delivery service is usually associated with truck
delivery or ship container delivery. The second
policy is range pricing with a minimum charge and a
unit price rate associated with each calculated
weight/volume range. Furthermore, the price can be
a
https://orcid.org/0000-0003-2140-801
b
https://orcid.org/0000-0002-2752-5398
c
https://orcid.org/0000-0002-9025-0569
of continuous charge with a fixed unit price and a base
charge. Express delivery services normally adopt this
kind of pricing policy. Calculated weight is the
maximum of the goods’ physical weight and the
volumetric weight. Volumetric or dimensional weight
is calculated based on the volume of the package
times the throw weight coefficient, and normally
international air transportation has a larger throw
weight coefficient than domestic road transportation.
One specific thing to take into consideration is the
price of shipping dangerous goods, such as liquid,
bio-hazardous substances. It requires additional
surcharges or charges at a higher unit price. Each
spare parts delivery usually has a priority level or
delivery time requirement. This requirement should
be met on or before SLA, the guaranteed delivery
time of the chosen delivery service. Spare parts
shipping from the same hub or nearby hubs to the
same or nearby destinations are considered to be able
to ship in bundles.
The traditional way is to send each spare part
separately once it is needed, or to bundle spare parts
with the same delivery time requirement. However,
this will incur more delivery cost and less profit
Zhou, Y., Liu, J., Mandania, R., Chen, K. and Xu, R.
Decision Support for Shipping Spare Parts in Bundles.
DOI: 10.5220/0008924803210328
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 321-328
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
321

margin. Moreover, this needs man hours on dealing
with each delivery order (e.g. tedious form filling
work). It will be beneficial to bundling spare parts
with different delivery time requirements together as
long as SLA satisfied all requirements for shipment.
For example, good A has a weight of 2kg and good B
has a weight of 1kg, both taking a range price delivery
option with 0-5kg, ¥1 per kg and minimum charge
of ¥5. Shipping these two goods separately will cost
¥10 and bundle them together only cost ¥5. This
simple example demonstrates the cost benefit of
shipment bundle. Given a set of spare parts to be
shipped, each with a delivery time requirement, from
one hub (or nearby hubs) to a destination hub (or
nearby hubs) and the available delivery options with
known pricing policies, the problem is to determine
how to bundle the spare parts to shipments so that the
total cost is minimised.
There has been research in the literature on
consolidation of shipments to save cost. For example,
Wong, et al (2009) and Li et al.(2012) studied the
shipment consolidation problems from the logistics
providers perspective. They formulate mixed integer
programming models to decide the consolidation of
shipments in different segments in the shipping
network to take advantage of economies of scale
while considering delivery target dates and handling
capacities. Nguyen et al. (2014) considered a problem
in which multiple suppliers consolidate their product
in long haul transportation to meet stochastic
demands of the perishable products. We have not
found previous research with the same settings as the
work in this paper which determines bundling of
shipments and selection of delivery services with
different pricing structures.
Section 2 of this paper demonstrates the features
of different delivery pricing policies. The above real-
life business problem can be abstracted and translated
using mathematical language. We formulate the
optimisation problem as a mixed integer linear
programming model with the objective of minimising
the total delivery cost. The decision variables are the
assignment of spare parts to delivery options which
reflects the bundles. The constraints are described
previously, including delivery time requirement and
the logistics of calculated delivery costs. The solution
approach and mathematical model is shown in section
3 and section 4. Numerical experiments are carried
out and explained in section 5. Section 6 gives some
real-life examples. Conclusions are drawn in section
7.
2 DELIVERY SERVICE PRICING
There are many different ways of post service charges
and different regulations and strategies applied (Crew
and Kleindorfer, 2013; Marcus and Petropoulos,
2017; Wilson, 1993). Three main categories of postal
service pricing policy are explained in details, which
summaries the signed delivery service contracts in the
company. The first is price per shipment contract. It
computes cost by unit price per container times the
number of containers needed, and normally the
maximum capacity of a container is big enough for
half a day demand from the same locations.
The second type is range pricing for either weight
unit or volume unit. With the pricing unit in weight,
an example of this type of pricing policy is shown in
Table 1. This price policy applies to a certain route
and the transportation mode is by air. The guaranteed
delivery is within four days. For example, we have a
parcel to send with a weight of 21KG and a volume
of 0.003 ݉
ଷ
. Firstly, we need to compute the
calculated weight, which is the maximum of the
Table 1: Pricing policy of a supplier with weight range charges 4 days SLA.
Supplier SLA SHIP TYPE MIN CHARGE RANGE_FROM RANGE_TO UNIT RATE
A 4 BY AIR 400 0 5 KG 55
4 BY AIR 400 5 45 KG 42
4 BY AIR 400 45 300 KG 38
4 BY AIR 400 300 99999 KG 37
Table 2: Pricing policy of a supplier with continuous charges.
Supplier SLA SHIP
TYPE
MIN CHARGE
WEIGHT
MINI CHARGE ADJ RATE UNIT RATE
B 4 BY
EXPRESS
1 182 0.5 KG 45
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
322

goods’ physical weight and the volumetric weight.
Volumetric or dimensional weight is calculated based
on the volume of the package times the throw weight
coefficient, which is 167. The volumetric weight is
167 0.003 0.5, which is less than the weight so the
calculated weight is 21KG for this parcel. 21KG is in
the second range, so the unit price is 42. The
calculated price is 42 21 882 . This price is higher
than the minimum charge, so the final charge is 882
for this example. Similar calculation process applies
when the pricing unit is volume. The only difference
is when calculating the weight converted volume, we
use weight divided by the throw rate, which is a
different throw rate from previous 167. Furthermore,
the throw rate varies from country to country.
The third type of price policy is continuous charge
policy such as the one shown in Table 2. The formula
is quite different from that in the second one. The
calculated weight is equal to the maximum of the
goods’ physical weight and the volumetric weight. If
the calculated weight is not more than the minimum
charge weight, the price is the minimum charge.
Otherwise, the amount above the minimum charge
weight is rounded up to the nearest half and charged
based on the unit rate. For example, if a parcel has a
weight of 2.7KG and a volume of 0.05
݉
ଷ
, using the
parameters in Table 2, the calculated weight is
max{2.7,0.05 167} 8.35
. The amount above the
minimum charge weight will be 8.35 1 7.35 KG
and rounded to 7.5KG. The charge for this part is
7.5 45 337.5 . Adding the basis charge, the final
charge for this parcel is then 519.5.
2.1 Features of the Pricing Policy
Structures
The weight range pricing policy has been plotted
partially for a parcel weight changing from 0KG to
50KG as shown in Figure 1. The bonus zone
[0, ]A
is where you can bundle as many as items into the
parcel and the total price would not change, where the
weight limit
/A MINI CHARGE RATE
.
Interestingly, the first price range does not take effect
as the calculated price will always be less or equal to
the minimum charges. In Figure 1, the arbitrage zone
[, ]BC
is where you can bundle more items or even
put package materials such as foam into the parcel to
reduce the total cost. The existence of an arbitrage
zone and a bonus zone verify the potential to reduce
total delivery cost by bundling items.
Figure 1: Partial plot of weight range pricing policy as in
Table 1.
The continuous pricing policy has been plotted
partially for a parcel weight changing from 0KG to
Table 3: Pricing policy of a supplier with weight range charges 3 days SLA.
Supplier SLA SHIP TYPE MIN CHARGE RANGE_FROM RANGE_TO UNIT RATE
A 3 BY AIR 400 0 5 KG 67
3 BY AIR 400 5 45 KG 52
3 BY AIR 400 45 300 KG 49
3 BY AIR 400 300 99999 KG 46
Table 4: Pricing policy of a supplier with weight range charges 2 days SLA.
Supplier SLA SHIP TYPE MIN CHARGE RANGE_FROM RANGE_TO UNIT RATE
A 2 BY AIR 600 0 5 KG 74
2 BY AIR 600 5 45 KG 68
2 BY AIR 600 45 300 KG 57
2 BY AIR 600 300 99999 KG 55
Decision Support for Shipping Spare Parts in Bundles
323
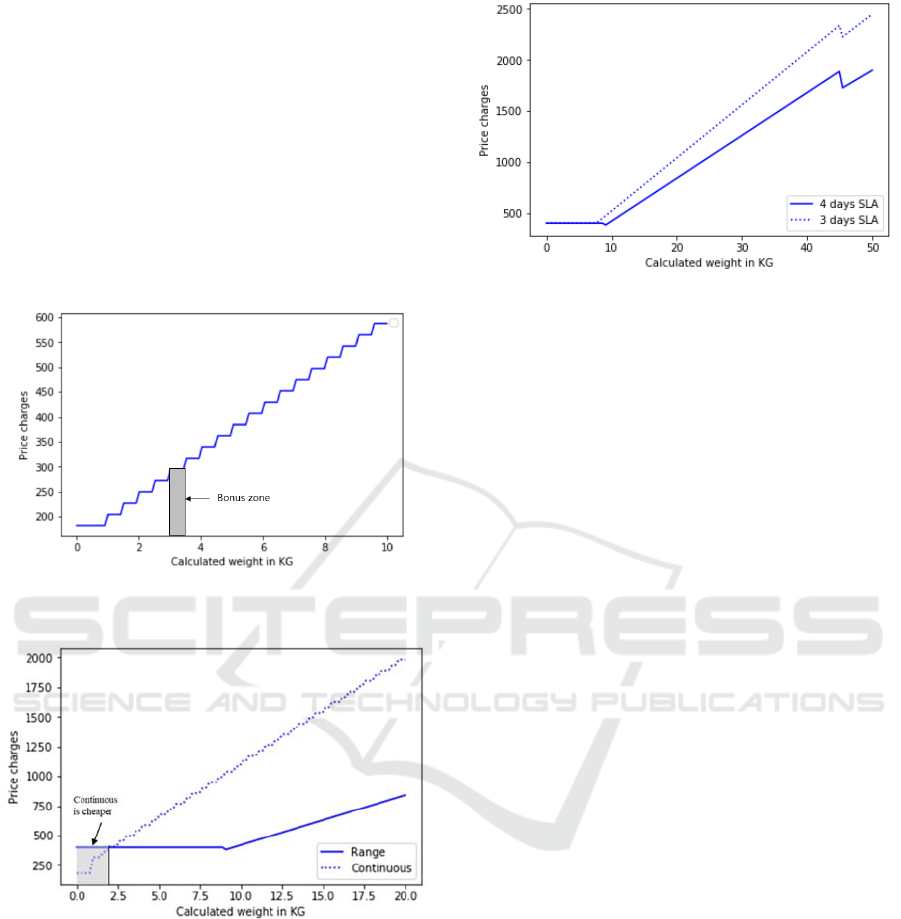
50KG as shown in Figure 2. It starts from a platform
according to the minimum charges and then moves
upwards as a staircase line. There are infinity many
small bonus zones like the one in Figure 1, but each
with a tiny width of 0.5KG. Those bonus zones are
created due to the round-to-half structure of the
pricing policy. The potential of reducing delivery cost
is much less than the range pricing policy. Figure 3
compares the pricing policy in Table 1 and Table 2.
When the weight of the parcel is less than or equal to
2KG, it is cheaper to choose continuous pricing
policy service; otherwise, it is better to send the parcel
with weight range pricing.
Figure 2: Partial plot of continuous pricing policy as in
Table 2.
Figure 3: Comparison of weight range pricing and
continuous pricing.
Figure 4 compares the same pricing policy structure
with different SLAs (weight range pricing). As the
data in Tables 3 and 4 show, the minimum charges of
3 days and 4 days are the same, but for every weight
range, 3 days service has a higher unit price rate. So
the service with 3 days SLA is in general more
expensive than that with 4 days SLA. In the situation
where the parcel is small and the price is the minimum
charge, a shorter SLA is more preferable. This should
be considered into the mathematical model as well.
With many different scenarios and combinations of
Figure 4: Comparison of weight range pricing with 4 days
SLA and 3 days SLA.
different SLA choices, it is extremely difficult to
solve the problem by hand or by searches guided by
rules found in this section, even given a long time. As
a consequence, we propose to formulate this problem
using mixed integer linear programming model. The
mathematical model can be solved by exact method
within seconds in most of the cases.
3 SOLUTION APPROACH
In the previous section, the features of different
delivery options with different SLA are
demonstrated.
The previous solution approach applied by the
company is to bundle orders by simple rules, which is
sending all orders with the same SLA in one parcel.
This is the rule based strategy for shipping spare parts
in bundles, but this may not lead to optimal solutions.
An alternative way to solve this is to formulate the
problem as a mathematically rigorous optimisation
problem, specifically a mixed integer programming
problem. The formulation is presented in section 4.
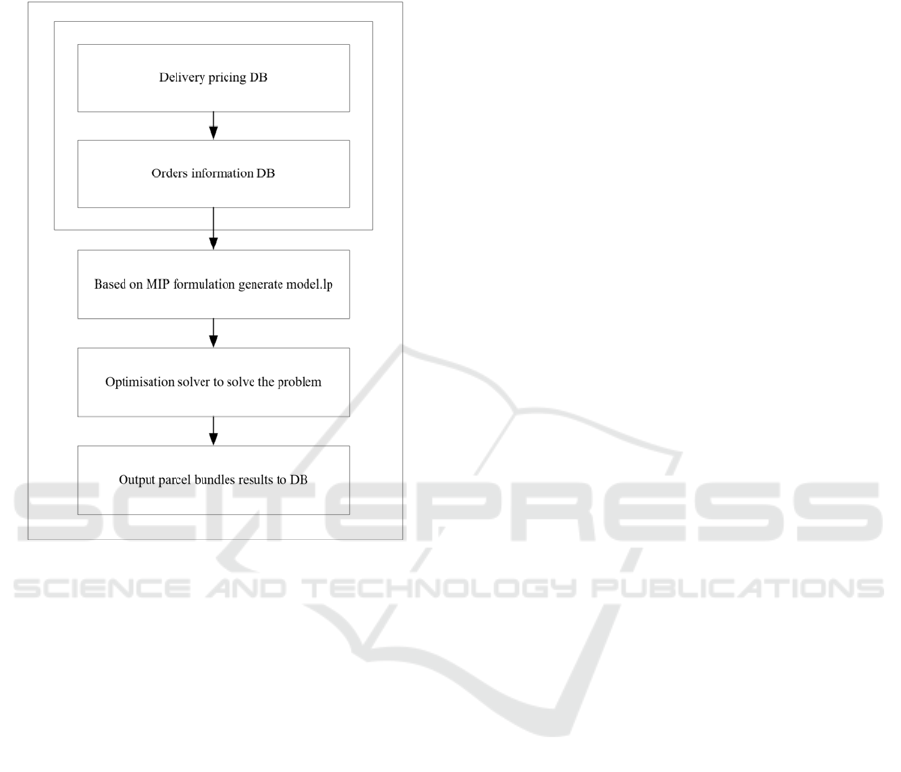
The solution framework is demonstrated in Figure 5.
4 MATHEMATICAL MODEL
A mixed integer programming model can be
formulated to demonstrate the problem of interest.
The objective is to minimise the total cost of all the
shipments after bundling spare parts. The constraints
are:
Orders from nearby depot hubs to nearby
destination hubs can be considered to be
bundled;
Delivery time requirement of each spare part
shipment must be satisfied;
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
324
The pricing policy of each delivery option is
strictly followed;
Dangerous goods are normally bundled with
dangerous goods and cannot be bundled with
ordinary goods.
Figure 5: Solution Framework.
4.1 Notations
Parameters:
i : index of spare parts that can be bundled together
k
: index of delivery options
l
: index of ranges in the range price policy
N : total number of spare parts
k
L : total number of ranges,
1, 3kKK
K
: set of indexes of all delivery options
k
1
K
: set of indexes of weight range price policy
delivery options
2
K
: set of indexes of continuous price policy
delivery options
3
K
: set of indexes of volume range price policy
delivery options
i
tr : delivery time requirement of spare part i
k
ts : service level agreement of delivery option
k
i
w : the weight of spare part i
i
v : the volume of spare part i
lk
b : beginning weight/volume of price range
l
of
delivery option
k
, for 1, 3kKK
lk
e : ending weight/volume of price range
l
of
delivery option
k
, for 1, 3kKK
lk
u : unit price rate of range
l
of delivery option
k
, for
1, 3kKK
k
r : the throw weight coefficient of delivery option
k
,
for
kK
k
d : the minimum charge of delivery option
k
, for
kK
k
g
: the conversion rate of delivery option
k
, for
kK
k
m : the minimum charge weight of delivery option
k
,
for
2kK
k
uc : unit price of delivery option
k
, for
2kK
M
: a big positive number.
Variables:
1,if spare part is allocated to delivery option
0, otherwise
ik
ik
X
1, if the cost of delivery option is in range
0, otherwise
lk
kl
1, if at least one item is allocated to delivery option
0, otherwise
k
k
k
WL : bundle pricing calculated weight of delivery
option
1, 3kKK
, 0 if no spare part is
allocated to it
k
RWL : bundle pricing calculated weight of delivery
option
2kK
, 0 if no spare part is allocated
to it
k
C : total delivery cost of bundled spare parts of
delivery option k
4.2 Mixed Integer Programming Model
The mathematical model is formulated as follows
Minimise
k
kK
C
(1)
Subject to:
1, [1,..., ]
ik
kK
X
iN
(2)
, [1,..., ],
iik kik
tr X ts X i N k K (3)
1
,1,2
N
kiik
i
WL w X k K K
(4)
1
,1,2
N
kkiik
i
WL r v X k K K
(5)
Decision Support for Shipping Spare Parts in Bundles
325

1
,3
N
i
kik
i
k
w
WL X k K
r
(6)
1
,3
N
kiik
i
WL v X k K
(7)
1
,
N
ik k
i
X
MkK
(8)
1
,
N
kik
i
X
kK
(9)
1
,1,3
k
L
lk k
l
kKK
(10)
(1 ) (1 ) ,
1, 3, 1,...,
lk lk k lk lk
k
bMWLeM
kKKl L
(11)
(1 ) , 1, 3, 1,...,L
klkk lk k
CuWL MkKKl
(12)
(1 ) ,
kk k
Cd M kK
(13)
(1 ) , 2
kk
kk k k
k
RWL m
Cd uc M kK
g
(14)
2 2 0.99999, 2
kkk
WL RWL WL k K
(15)
, {0,1}, , 1,...,
ik k
X
kKi N
(16)
{0,1}, 1, 3, 1,...,
lk k
kKKl L
(17)
,0,
kk
WL C k K (18)
is integer
k
RWL (19)
The objective (1) of the model is to minimise the
sum of delivery cost of all delivery options, and if
there is no spare parts allocated to a certain option,
0
k
C . Once there is a tie on price we will choose
the fastest delivery option in the post processing
check. Constraints (2) indicate that a spare part must
be allocated to exactly one delivery option.
Constraints (3) ensure that if spare part
i is allocated
to delivery option
k
, then the required time of spare
part
i (e.g. 3-day arrival) must not be shorter than the
guaranteed delivery time of option
k
(e.g. 2-day
SLA). In the program, we modelled constraints (3)
such that if
, [1,..., ],
ik
tr ts i N k K , then
0
ik
X
. Constraints (4) and (5) compute the sum of
calculated weight of delivery option
1, 2kKK ,
which is sum of the maximum weight (max of
physical weight or volumetric weight) of all spare
parts allocated to it. Constraints (6) and (7) compute
the sum of calculated volume of delivery option
3kK
, which is sum of the maximum volume (max
of physical volume or weight converted volume) of
all spare parts allocated to it. Constraints (8) and (9)
define that
1
k
means at least one spare part is
allocated to delivery option
k
. Then constraints (10)
require that if delivery option
k
is used, the
calculated weight/volume of spare parts to be
delivered using option
k
must fall into one and only
one range. Constraints (11) identify the right range
[,]
lk lk
be of delivery option 1, 3kKK which the
calculated weight falls in. Constraints (12) and (13)
calculate the total cost of delivery option
1, 3kKK
which is the maximum of the minimum charge and
the unit price times the calculated weight/volume.
Constraints (13), (14) and (15) calculate the total cost
of delivery option
2kK
which is the maximum of
the minimum charge and the continuous price charge
as stated in section 2. Constraints (15) ceil the
calculated weight
k
WL to the nearest half. One may
notice that
k
WL is defined for 1, 3kKK as well,
but calculated differently in constraints (15) for
2,kK
as for continuous price the calculated
weight is rounded every 0.5kg. In a word,
12
,WL WL
can be viewed as a different variable as
3
WL . The rest
constraints state that all decision variables are greater
or equal to zero, among them
,,
ik k lk
X
are binary
variables and
k
RWL only take integer values. For
dangerous goods, a separate problem will be
considered and solved using the same model, as they
cannot be shipped together with other spare parts.
5 NUMERICAL EXAMPLES
Three numerical examples are generated and selected
from real life data. The mathematical models are
solved using open source optimiser COIN-OR’s
COIN Branch and Cut Solver (CBC) under the
Eclipse Public License (Forrest and Lougee-Heimer,
2005). All test cases are run on a 2.11GHz Intel Core
i7-8650U (8 cores, 16GB) laptop.
5.1 Example One
The first example from real life data is shown in Table
5. The suppliers and price list are shown in Tables 1-
4. Among the five different options (suppliers and
price policies), the first three are selected. It is
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
326

interesting that item 2, 3, 4 required 4 days to arrive
are allocated to delivery option three with 3 days SLA,
and by doing this is the minimum-cost delivery plan.
The minimum total cost of sending these six items are
2292.21 with a computational time of 0.23 seconds.
If the items are sent out separately each in one parcel,
the total cost are 2593 (11.6%). If the items are
bundled by the same SLA, for example, items 2, 3, 4
can be bundled together and sent with 4 days service,
the total cost are 2367.45 (3.18%). The percentage of
the reduction in delivery cost of our plan is shown in
bracket.
Table 5: Example one item details.
INDEX SLA WEIGHT VOLUME Bundle
1 3 3.8 0.05 2
2 4 2 0.05 3
3 4 2.2 0.05 1
4 4 14.2 0.14 3
5 2 9.5 0.07 1
6 3 10.25 0.06 2
5.2 Example Two
This example demonstrates the importance of the
second objective functions, once there is a tie on the
delivery cost of different options. As all the items
require the same SLA, it is obvious to bundle all items
and send them with the four days SLA delivery
options. The delivery cost of the bundle with four
days delivery option is 400. However, the delivery
cost of the bundle to be shipped with three days SLA
is also 400, as demonstrated in Figure 4, the bundle
weight is in the bonus zone. With the second
objective function, when optimizing for this objective,
we only consider solutions that would not degrade the
objective values of delivery cost objectives.
Table 6: Example two item details.
INDEX SLA WEIGHT VOLUME Bundle
1 4 1 0.001 1
2 4 1 0.001 1
3 4 1 0.001 1
4 4 1 0.001 1
5.3 Example Three
This example shows an interesting case, where we
can add packing material into the parcel to increase
its weight and get a cheaper deal. The calculated
weight of the bundle is 44kg, corresponding to the
delivery option in Table 1. The delivery cost of the
bundle with 44kg is 1848, while we could add a little
bit weight to the current bundle and push it to the
arbitrage zone as shown in Figure 1. The optimal cost
of the bundle shipment is just above 1710, while we
augmented the parcel weight to just above 45kg. This
optimal cost is also found by solving the MIP problem.
Table 7: Example three item details.
INDEX SLA WEIGHT VOLUME Bundle
1 4 20 0.001 1
2 4 10 0.001 1
3 4 10 0.001 1
4 4 4 0.001 1
6 NUMERICAL EXPERIMENTS
The program is applied into one department’s daily
business since earlier this year and achieved around
17% savings on delivery cost every month comparing
to the same time period of last year. The program is
run several times daily and we selected 20 examples
from real life business to demonstrate the benefits of
applying this program. One example is one batch of a
particular day. The ORDERS column is the total
number of orders to be dispatched at that time period
of that day, and OPT_GROUPS column is the optimal
parcel numbers after we bundled shipment. The ratio
column is the bundle ratio, which is calculated as the
number of groups divided by the number of original
orders. The TIME column is the computational time
of the optimization problem.
In Table 8, we selected 20 batches of orders to be
dispatched. The average bundle ratio for this example
by the proposed optimisation program is 0.387. The
average computational time is 1.58 minutes. The
comparison between the new solution approach and
the traditional solution approach is shown in Table 9.
We increased the bundle ratio by 53.6%, which
means we largely reduced the packing time and
efforts for parcels. More importantly, the unit price
for sending those parcels before optimisation is 8.5
and after optimisation is 7, which indicates a 17.49%
reduction in delivery cost.
7 CONCLUSIONS
A telecommunication equipment company sends
spare parts from local hubs to construction sites or
other local hubs in mainland China several times a
day through parcel delivery services. Depending on
the delivery distance, there are various delivery
options such as transportation via air, via road, via
Decision Support for Shipping Spare Parts in Bundles
327

sea, via rail and via inland waterways. Many choices
named service levels are available within each
transportation category. There are three parcel
delivery pricing policies: price per shipment, weight
ranged price, and continuous pricing. Each spare parts
delivery usually has a priority level or delivery time
requirement. Spare parts to be shipped from the same
hub or nearby hubs to the same or nearby destinations
are considered to be able to ship in bundles. By
observing the delivery pricing structures, it is
beneficial to bundle spare parts together for shipment.
The company used to bundle shipment by hand,
following the rules of sending orders with the same
delivery time requirement in one parcel. We proposed
a new solution approach to tackle this problem. A
mixed integer programming problem is proposed
based on the delivery requirements as well as the
various ways to compute delivery cost based on
different delivery modes. Numerical experiments
have been carried out to observe the benefits and also
reflect the features of parcel delivery pricing
structures. Then 20 real life business examples are
selected. The average computational time is 1.58
minutes. Comparing to the traditional solution
approach, we are able to increase the bundle ratio or
in other words reduce the total number of parcels sent
by 53.6% while keeping the same number of orders.
This means that the time and efforts spent packing
parcels are greatly reduced. Furthermore, the total
delivery cost is reduced by 17% by using the new
solution approach.
Table 8: Real life examples.
I
D
ORDE
RS
OPT
_
GROU
PS
Ratio TIME
1 210 100 0.476 0.933
2 790 235 0.297 2.383
3 145 36 0.248 0.367
4 161 69 0.429 0.667
5 158 75 0.475 0.717
6 307 121 0.394 1.267
7 640 219 0.342 2.250
8 94 39 0.415 0.400
9 145 51 0.352 0.500
10 136 69 0.507 0.650
11 147 56 0.381 3.550
12 267 132 0.494 1.250
13 104 50 0.481 0.500
14 941 247 0.262 6.050
15 353 146 0.414 1.250
16 963 257 0.267 3.017
17 206 80 0.388 0.767
18 737 257 0.349 2.600
19 208 83 0.399 0.817
20 459 171 0.373 1.700
0.387 1.582
Table 9: Comparison with previous solutions by hand.
O
r
ders Groups Ratio Unit
Cos
t
By han
d
7171 5378 0.75 8.5
By
p
rogra
m
7171 2493 0.387 7
REFERENCES
Crew, M.A., Kleindorfer, P.R. eds., 2013. Postal and
delivery services: pricing, productivity, regulation and
strategy. Springer Science & Business Media.
Forrest, J., Lougee-Heimer, R., 2005. CBC user guide. In
Emerging theory, methods and applications. pp. 257-
277. INFORMS.
Li, Z., James H.Bookbinder, J.H. and Elhedhli, S., 2012,
Optimal shipment decisions for an airfreight forwarder:
Formulation and solution methods, Transportation
Research Part C: Emerging Technologies, 21(1),
pp.17-30.
Marcus, J.S., Petropoulos, G., 2017. E-commerce in
Europe: Parcel delivery prices in a digital single market.
In M. Crew, P. L. Parcu and T. Brennan (edd) The
Changing Postal and Delivery Sector, pp. 139-159.
Springer, Cham.
Nguyen, C., Dessouky, M. and Toriello, A., 2014,
Consolidation strategies for the delivery of perishable
products, Transportation Research Part E: Logistics
and Transportation Review, 69, pp.108-121.
Wilson, R.B., 1993. Nonlinear pricing, Oxford University
Press.
Wong, W.H., Leung, L.,C. and Hui, Y.V., 2009, Airfreight
forwarder shipment planning: A mixed 0–1 model and
managerial issues in the integration and consolidation
of shipments, European Journal of Operational
Research, 193(1), pp.86-97.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
328
