
MAGNET: Multi-Label Text Classification using Attention-based Graph
Neural Network
Ankit Pal, Muru Selvakumar and Malaikannan Sankarasubbu
Saama AI Research, Chennai, India
Keywords:
Multi-label Text Classification, Graph Neural Networks, Attention Networks, Deep Learning, Natural
Language Processing, Supervised Learning.
Abstract:
In Multi-Label Text Classification (MLTC), one sample can belong to more than one class. It is observed
that most MLTC tasks, there are dependencies or correlations among labels. Existing methods tend to ignore
the relationship among labels. In this paper, a graph attention network-based model is proposed to capture
the attentive dependency structure among the labels. The graph attention network uses a feature matrix and a
correlation matrix to capture and explore the crucial dependencies between the labels and generate classifiers
for the task. The generated classifiers are applied to sentence feature vectors obtained from the text feature
extraction network(BiLSTM) to enable end-to-end training. Attention allows the system to assign different
weights to neighbor nodes per label, thus allowing it to learn the dependencies among labels implicitly. The
results of the proposed model are validated on five real-world MLTC datasets. The proposed model achieves
similar or better performance compared to the previous state-of-the-art models.
1 INTRODUCTION
Multi-Label Text Classification (MLTC) is the task
of assigning one or more labels to each input sample
in the corpus. This makes it both a challenging and
essential task in Natural Language Processing(NLP).
We have a set of labelled training data {(x
i
,y
i
)}
n
i=1
,
where x
i
∈ R
D
are the input features with D dimen-
sion for each data instances and y
i
∈ {0, 1} are the
targets. The vector y
i
has one in the jth coordinate
if the ith data point belongs to jth class. We need to
learn a mapping (prediction rule) between the features
and the labels, such that we can predict the class label
vector y of a new data point x correctly.
MLTC has many real-world applications, such as
text categorization (Schapire and Singer, 2000), tag
recommendation (Katakis et al., 2008), information
retrieval (Gopal and Yang, 2010), and so on. Before
deep learning, the solution to the MLTC task used
to focus on traditional machine learning algorithms.
Different techniques have been proposed in the liter-
ature for treating multi-label classification problems.
In some of them, multiple single-label classifiers are
combined to emulate MLTC problems. Other tech-
niques involve modifying single-label classifiers by
changing their algorithms to allow their use in multi-
label problems.
The most popular traditional method for solv-
ing MLTC is Binary Relevance (BR) (Zhang et al.,
2018). BR emulates the MLTC task into multiple
independent binary classification problems. How-
ever, it ignores the correlation or the dependencies
among labels (Luaces et al., 2012). Binary Rele-
vance has stimulated research for finding approaches
to capture and explore the label correlations in various
ways. Some methods, including Deep Neural Net-
work (DNN) based and probabilistic based models,
have been introduced to model dependencies among
labels, such as Hierarchical Text Classification. (Sun
and Lim, 2001), (Xue et al., 2008), (Gopal et al.,
2012) and (Peng et al., 2019). Recently Graph-based
Neural Networks (Wu et al., 2019) e.g. Graph Convo-
lution Network (Kipf and Welling, 2016), Graph At-
tention Networks (Velickovic et al., 2018) and Graph
Embeddings (Cai et al., 2017) have received consid-
erable research attention. This is due to the fact that
many real-world problems in complex systems, such
as recommendation systems (Ying et al., 2018), so-
cial networks and biological networks (Fout et al.,
2017) etc, can be modelled as machine learning tasks
over large networks. Graph Convolutional Network
(GCN) was proposed to deal with graph structures.
The GCN benefits from the advantage of the Convo-
lutional Neural Network(CNN) architecture: it per-
494
Pal, A., Selvakumar, M. and Sankarasubbu, M.
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network.
DOI: 10.5220/0008940304940505
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 494-505
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

forms predictions with high accuracy, but a relatively
low computational cost by utilizing fewer parame-
ters compared to a fully connected multi-layer per-
ceptron (MLP) model. It can also capture essential
sentence features that determine node properties by
analyzing relations between neighboring nodes. De-
spite the advantages as mentioned above, we suspect
that the GCN is still missing an essential structural
feature to capture better correlation or dependencies
between nodes.
One possible approach to improve the GCN per-
formance is to add adaptive attention weights depend-
ing on the feature matrix to graph convolutions.
To capture the correlation between the labels bet-
ter, we propose a novel deep learning architecture
based on graph attention networks. The proposed
model with graph attention allows us to capture the
dependency structure among labels for MLTC tasks.
As a result, the correlation between labels can be au-
tomatically learned based on the feature matrix. We
propose to learn inter-dependent sentence classifiers
from prior label representations (e.g. word embed-
dings) via an attention-based function. We name the
proposed method Multi-label Text classification us-
ing Attention based Graph Neural NETwork (MAG-
NET). It uses a multi-head attention mechanism to
extract the correlation between labels for the MLTC
task. Specifically, these are the following contribu-
tions:
• The drawbacks of current models for the MLTC
task are analyzed.
• A novel end-to-end trainable deep network is pro-
posed for MLTC. The model employs Graph At-
tention Network (GAT) to find the correlation be-
tween labels.
• It shows that the proposed method achieves sim-
ilar or better performance compared to previous
State-of-the-art(SoTA) models across two MLTC
metrics and five MLTC datasets.
2 RELATED WORK
The MLTC task can be modeled as finding an opti-
mal label sequence y
∗
that maximizes the conditional
probability p(y |x), which is calculated as follows:
p(y | x) =
n
∏
i=1
p(y
i
| y
1
,y
2
,..,y
i−1
,x) (1)
There are mainly three types of methods to solve
the MLTC task:
• Problem transformation methods
• Algorithm adaptation methods
• Neural network models
2.1 Problem Transformation Methods
Problem transformation methods transform the multi-
label classification problem either into one or more
single-label classification or regression problems.
Most popular problem transformation method is Bi-
nary relevance (BR) (Boutell et al., 2004), BR learns
a separate classifier for each label and combines the
result of all classifiers into a multi-label prediction
by ignoring the correlations between labels. Label
Powers(LP) treats a multi-label problem as a multi-
class problem by training a multi-class classifier on
all unique combinations of labels in the dataset. Clas-
sifier Chains (CC) transform the multi-label text clas-
sification problem into a Bayesian conditioned chain
of the binary text classification problem. However,
the problem transformation method takes a lot of time
and space if the dataset and labels are too large.
2.2 Algorithm Adaptation Methods
Algorithm adaptation, on the other hand, adapts the
algorithms to handle multi-label data directly, instead
of transforming the data. Clare and King (2001) con-
struct a decision tree by modifying the c4.5 algo-
rithm (Quinlan, 1993) and develop resampling strate-
gies. (Elisseeff and Weston 2002) propose the Rank-
SVM by amending a Support Vector Machine (SVM).
(Zhang and Zhou 2007) propose a multi-label lazy
learning approach (ML-KNN), ML-KNN uses corre-
lations of different labels by adopting the traditional
K-nearest neighbor (KNN) algorithm. However, the
algorithm adaptation method is limited to utilizing
only the first or second order of label correlation.
2.3 Neural Network Models
In recent years, various Neural network-based mod-
els are used for MLTC task. For example, (Yang
et al., 2016) propose hierarchical attention networks
(HAN), uses the GRU gating mechanism with hier-
archical attention for document classification. Zhang
and Zhou (2006) propose a framework called Back-
propagation for multilabel learning (BP-MLL) that
learns ranking errors in neural networks via back-
propagation. However, these types of neural networks
don’t perform well on high dimensional and large-
scale data.
Many CNN based model, RCNN (Lai et al.,
2015), Ensemble method of CNN and RNN by Chen
et al. (2017), XML-CNN (Liu et al., 2017), CNN
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
495

(Kim, 2014a) and TEXTCNN (Kim, 2014a) have
been proposed to solve the MLTC task. However,
they neglect the correlations between labels.
To utilise the relation between the labels some Hi-
erarchical text classification models have been pro-
posed, Transfer learning idea proposed by (Xiao
et al., 2011) uses hierarchical Support Vector Ma-
chine (SVM), (Gopal et al., 2012) and (Gopal and
Yang, 2015) uses hierarchical and graphical depen-
dencies between class-labels, (Peng et al., 2018) uti-
lize the graph operation on the graph of words. How-
ever, these methods are limited as they consider only
pair-wise relation due to computational constraints.
Recently, the BERT language model achieves
state-of-the-art performance in many NLP tasks. (De-
vlin et al., 2019b)
3 MAGNET ARCHITECTURE
3.1 Graph Representation of Labels
A graph G consists of a feature description M ∈R
n×d
and the corresponding adjacency matrix A ∈ R
n×n
where n denotes the number of labels and d denotes
the number of dimensions.
GAT network takes the node features and adja-
cency matrix that represents the graph data as in-
puts. The adjacency matrix is constructed based on
the samples. In our case, we do not have a graph
dataset. Instead, we learn the adjacency matrix, hop-
ing that the model will determine the graph, thereby
learning the correlation of the labels.
Our intuition is that by modeling the correlation
among labels as a weighted graph, we force the GAT
network to learn such that the adjacency matrix and
the attention weights together represent the correla-
tion. We use three methods to initialize the weights of
the adjacency matrix. Section 3.5 explains the initial-
ization methods in detail.
In the context of our model, the embedding vec-
tors of the labels act as the node features, and the ad-
jacency matrix is a learn-able parameter.
3.2 Node Updating Mechanism in
Graph Convolution
In Graph Convolution Network Nodes can be updated
by different types of node updating mechanisms. The
basic version of GCN updates each node i of the `-th
layer, H
(`+1)
i
, as follows.
H
(`+1)
= σ
AH
`
W
`
(2)
Where σ(·) denote an activation function, A is an
adjacency matrix and W
(`)
is the convolution weights
of the `-th layer. We represent each node of the graph
structure as a label; at each layer, the label’s features
are aggregated by neighbors to form the label features
of the next layer. In this way, features become increas-
ingly more abstract at each consecutive layer. e.g., la-
bel 2 has three adjacent labels 1, 3 and 4. In this case,
another way to write equation (2) is
H
(`+1)
2
= σ
H
(`)
2
W
(`)
+ H
(`)
1
W
(`)
+H
(`)
3
W
(`)
+ H
(`)
4
W
(`)
(3)
So, in this case, the graph convolution network
sums up all labels features with the same convolution
weights, and then the result is passed through one ac-
tivation function to produce the updated node feature
output.
3.3 Graph Attention Networks for
Multi-Label Classification
In GCNs, the neighborhoods of nodes combine with
equal or pre-defined weights. However, the influ-
ence of neighbors can vary greatly, and the attention
mechanism can identify label importance in corre-
lation graph by considering the importance of their
neighbor labels.
The node updating mechanism, equation (3), can
be written as a linear combination of neighboring la-
bels with attention coefficients.
H
(`+1)
2
= ReLU
α
(`)
22
H
(`)
2
W
(`)
+ α
(`)
21
H
(`)
1
W
(`)
+α
(`)
23
H
(`)
3
W
(`)
+ α
(`)
24
H
(`)
4
W
(`)
(4)
where α
`
i j
is an attention coefficient which mea-
sures the importance of the jth node in updating the
ith node of the `-th hidden layer. The basic expression
of the attention coefficient can be written as
α
(`)
ij
= f
H
(`)
i
W
(`)
,H
(`)
j
W
(`)
(5)
The attention coefficient can be obtained typically
by i) a similarity base, ii) concatenating features, and
iii) coupling all features. We evaluate the attention
coefficient by concatenating features.
α
ij
= ReLU
(H
i
W) k
H
j
W
T
(6)
In our experiment, we are using multi-head attention
(Vaswani et al., 2017) that utilizes K different heads
to describe labels relationships. The operations of
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
496

Figure 1: Illustration of overall structure of MAGNET model with a single Graph Attention layer for multi label text clas-
sification.
x
(n)
,y
(n)
,n = 1,2,.. . ,N is input for BiLSTM to generate the feature vectors. x
(n)
are encoded using BERT
embeddings. Input for Graph attention network is the Adjacency matrix A ∈ R
n×n
and label vectors M ∈ R
n×d
. GAT output
is attended label features which is applied on the feature vectors obtained from the BiLSTM.
the layer are independently replicated K times (each
replication is done with different parameters), and the
outputs are aggregated feature wise (typically by con-
catenating or adding).
H
(`+1)
i
= Tanh
1
K
K
∑
k=1
∑
j∈N(i)
α
`
i j,k
H
`
j
W
`
!
(7)
Where α
i j
is the attention coefficient of label j to
i. N(i) represents the neighborhood of label i in the
graph. We use a cascade of GAT layers. For first
layer the input is label embedding matrix M ∈ R
n×d
.
H
1
i
= Tanh
1
K
K
∑
k=1
∑
j∈N(i)
α
(0)
i j,k
MW
(0)
!
(8)
The output from the previous GAT layer is fed into
the successive GAT layer similar to RNN but the GAT
layer weights are not shared
H
(`+1)
i
= Tanh
1
K
K
∑
k=1
∑
j∈N(i)
α
`
i j,k
H
`
i
W
`
!
| {z }
attended label features
(9)
The output from the last layer is the attended label
features H
gat
∈ R
c×d
where c denotes the number of
labels and d denotes the dimension of the attended
label features. which is applied to the textual features
from the BiLSTM.
3.4 Feature Vector Generation
We are using bidirectional LSTM (Hochreiter and
Schmidhuber, 1997) to obtain the feature vectors. We
use BERT for embedding the words and then feed it to
BiLSTM for fine-tuning for the domain-specific task,
BiLSTM reads the text sequence x from both direc-
tions and computes the hidden states for each word,
−→
h
i
=
−−−−→
LSTM
−→
h
i−1
,x
i
←−
h
i
=
←−−−−
LSTM
←−
h
i+1
,x
i
(10)
We obtain the final hidden representation of the i-
th word by concatenating the hidden states from both
directions,
h
i
=
h
−→
h
i
;
←−
h
i
i
(11)
F = f
rnn
(f
BERT
(s;θ
BERT
);θ
rnn
) ∈ R
D
(12)
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
497

Where s is the sentence, θ
rnn
is Rnn parameters,
θ
BERT
is BERTs parameter, D is hidden size of BiL-
STM. Later we multiply feature vectors with attended
label features to get the final prediction score as,
ˆy = FH
gat
(13)
Where H
gat
∈ R
c×d
and F is feature vectors obtained
from BiLSTM model. Figure 1 shows the overall
structure of the proposed model.
3.5 Adjacency Matrix Generation
In this section, we explain how to initialize the ad-
jacency matrix for the GAT network. We use three
different methods to initialize the weights..
• Identity Matrix
We use the Identity matrix as the adjacency ma-
trix. Ones on the main diagonal and zeros else-
where, i.e., starting with zero correlation as a
starting point.
• Xavier Initialization
We use Xavier initialization (Glorot and Bengio,
2010) to initialize the weight of adjacency matrix.
±
√
6
√
n
i
+ n
i+1
(14)
where n
i
is the number of incoming network con-
nections.
• Correlation Matrix
The correlation matrix is constructed by count-
ing the pairwise co-occurrence of labels. The fre-
quency vector is vector F ∈ R
n
where n is the
number of labels and F
i
is the frequency of label i
in the overall training set. The co-occurrence ma-
trix is then normalized by the frequency vector.
A = M / F (15)
where M ∈ R
n×n
is the co-occurrence matrix and
F ∈ R
n
is the frequency vector of individual la-
bels. This is similar to how the correlation matrix
built-in (Chen et al., 2019), except we do not em-
ploy binarization.
3.6 Loss Function
We use Cross-entropy as the loss function. If the
ground truth label of a data point is y ∈ R
c
, where
y
i
= {0, 1}
L =
C
∑
c=1
y
c
log(σ (
ˆ
y
c
)) + (1 −y
c
)log (1 −σ(
ˆ
y
c
)) (16)
Where σ is sigmoid activation function
4 EXPERIMENT
In this section, we introduce the datasets, experiment
details, and baseline results. Subsequently, the au-
thors make a comparison of the proposed methods
with baselines
4.1 Datasets
In this section, we provide detail and use the source
of the datasets in the experiment. Table 2 shows the
Statistics of all datasets.
Reuters-21578 is a collection of documents collected
from Reuters News Wire in 1987. The Reuters-21578
test collection, together with its earlier variants, has
been such a standard benchmark for the text catego-
rization (TC) (Debole and Sebastiani, 2005). It con-
tains 10,788 documents, which has 8,630 documents
for training and 2,158 for testing with a total of 90
categories.
RCV1-V2 provided by Lewis et al. (2004) (Lewis
et al., 2004), consists of categorized newswire stories
made available by Reuters Ltd. Each newswire story
can have multiple topics assigned to it, with 103 top-
ics in total. RCV1-V2 contains 8,04,414 documents
which are divided into 6,43,531 documents for train-
ing and 1,60,883 for testing.
Arxiv Academic Paper Dataset (AAPD) is provided
by Yang et al. (2018). The dataset consists of the ab-
stract and its corresponding subjects of 55,840 aca-
demic papers, and each paper can have multiple sub-
jects. The target is to predict subjects of an academic
paper according to the content of the abstract. The
AAPD dataset then divides into 44,672 documents
for training and 11,168 for testing with a total of 54
classes.
Slashdot dataset was collected from the Slashdot
website and consists of article blurbs labeled with the
subject categories. Slashdot contains 19,258 samples
for training and 4,814 samples for testing with a total
of 291 classes.
Toxic Comment Dataset, We are using toxic com-
ment dataset from Kaggle. This dataset has large
number of comments from Wikipedia talk page edits.
Human raters have labeled them for toxic behavior.
4.2 Experiment Details
We implement our experiments in Tensorflow on an
NVIDIA 1080Ti GPU. Our model consists of two
GAT layers with multi-head attention. Table 1 shows
the hyper-parameters of the model on five datasets.
For label representations, we adopt 768 dim BERT
trained on Wikipedia and BookCorpus. For the cate-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
498

gories whose names contain multiple words, we ob-
tain the label representation as to the average of em-
beddings for all words. For all datasets, the batch
size is set to 250, and out of vocabulary(OOV) words
are replaced with unk. We use BERT embedding to
encode the sentences. We use Adam optimizer to
minimize the final objective function. The learning
rate is initialized to 0.001 and we make use of the
dropout 0.5 (Srivastava et al. 2014) to avoid over-
fitting and clip the gradients (Pascanu, Mikolov, and
Bengio 2013) to the maximum norm of 10.
4.3 Performance Evaluation
miF1 In the micro-average method, the individual
true positives, false positives, and false negatives of
the system are summed up for different sets and ap-
plied to get Micro-average F-Score.
F1 −Score
micro
=
∑
L
j=1
2t p
j
∑
L
j=1
(2t p
j
+ f p
j
+ f n
j
)
Precision
micro
=
∑
L
j=1
t p
j
∑
L
j=1
t p
j
+ f p
j
Recall
micro
=
∑
L
j=1
t p
j
∑
L
j=1
t p
j
+ f n
j
(17)
Hamming Loss (HL): Hamming-Loss is the frac-
tion of labels that are incorrectly predicted. (Dester-
cke, 2014). Therefore, hamming loss takes into ac-
count the prediction of both an incorrect label and
a missing label normalized over the total number of
classes and the total number of examples.
HL =
1
|N|·|L|
|N|
∑
i=1
|L|
∑
j=1
xor(y
i, j
,z
i, j
) (18)
where y
i, j
is the target and z
i, j
is the prediction. Ide-
ally, we would expect Hamming loss, HL = 0, which
would imply no error; practically the smaller the value
of hamming loss, the better the performance of the
learning algorithm.
4.4 Comparison of Methods
We compare the performance of 27 algorithms, in-
cluding state-of-the-art models. Furthermore, we
compare the latest state-of-the-art models on the rcv1-
v2 dataset. Compared algorithms can be categorized
into three groups, as described below:
• Flat Baselines
Flat Baseline models transform the documents
and extract the features using TF-IDF (Ramos,
), later use those features as input to Logistic
regression (LR) (Allison, 1999) , Support Vec-
tor Machine (SVM)(Hearst, 1998) , Hierarchi-
cal Support Vector Machine (HSVM) (Vural and
Dy, 2004) , Binary Relevance (BR)(Boutell et al.,
2004), Classifier Chains(CC)(Read et al., 2011).
Flat Baseline methods ignore the relation between
words and dependency between labels.
• Sequence, Graph and N-gram based Models
These types of models first transform the text
dataset into sequences of words, the graph of
words or N-grams features, later apply differ-
ent types of deep learning models on those fea-
tures including CNN (Kim, 2014b), CNN-RNN
(Chen et al., 2017), RCNN (Lai et al., 2015),
DCNN (Schwenk et al., 2017), XML-CNN (Liu
et al., 2017), HR-DGCNN (Peng et al., 2018),
Hierarchical LSTM (HLSTM) (Chen et al.,
2016), multi-label classification approach based
on a conditional cyclic directed graphical model
(CDN-SVM) (Guo and Gu, 2011), Hierarchical
Attention Network (HAN) (Yang et al., 2016) and
Bi-directional Block Self-Attention Network (Bi-
BloSAN) (Shen et al., 2018) etc. for the multi-
label classification task For example, Hierarchi-
cal Attention Networks for Document Classifica-
tion (HAN) uses a GRU grating mechanism to
encode the sequences and apply word and sen-
tence level attention on those sequences for doc-
ument classification. Bi-directional Block Self-
Attention Network (BI-BloSAN) uses intra-block
and inter-block self-attentions to capture both lo-
cal and long-range context dependencies by split-
ting the sequences into several blocks.
• Recent State-of-the-Art Models
We compare our model with different state-of-the-
art models for multi-label classification task in-
cluding BP-MLL
RAD
(Nam et al., 2014), Input
Encoding with Feature Message Passing (FMP)
(Lanchantin et al., 2019), TEXT-CNN(Kim,
2014a), Hierarchical taxonomy-aware and atten-
tional graph capsule recurrent CNNs framework
(HE-AGCRCNN)(Peng et al., 2019), BOW-
CNN(Johnson and Zhang, 2014), Capsule-B
networks(Zhao et al., 2018), Hierarchical Text
Classification with Reinforced Label Assignment
(HiLAP)(Mao et al., 2019), Hierarchical Text
Classification with Recursively Regularized Deep
Graph-CNN (HR-DGCNN)(Peng et al., 2018),
Hierarchical Transfer Learning-based Strategy
(HTrans)(Banerjee et al., 2019), BERT (Bidirec-
tional Encoder Representations from Transform-
ers)(Devlin et al., 2019b), BERT-SGM(Yarullin
and Serdyukov, 2019), For example FMP +
LaMP is a variant of LaMP model which
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
499

Table 1: Main experimental hyper-parameters.
Dataset Vocab Size Embed size Hidden size Attention
heads
Reuters-21578 20,000 768 250 4
RCV1-V2 50,000 768 250 8
AAPD 30,000 768 250 8
Slashdot 30,000 768 300 4
Toxic Comment 50,000 768 200 8
Table 2: Statistics of the datasets.
Dataset Domain #Train #Test Labels
Reuters-21578 Text 8,630 2,158 90
RCV1-V2 Text 6,43,531 1,60,883 103
AAPD Text 44,672 11,168 54
Slashdot Text 19,258 4,814 291
Toxic Comment Text 126,856 31,714 7
uses Input Encoding with Feature Message Pass-
ing (FMP). It achieves state-of-the-art accuracy
across five metrics and seven datasets. HE-
AGCRCNN uses a hierarchical taxonomy em-
bedding method to learn the hierarchical relations
among the labels.is another recent state-of-the-art
model, which has shown outstanding performance
in large-scale multi-label text classification. It
uses a hierarchical taxonomy embedding method
to learn the hierarchical relations among the la-
bels. BERT (Bidirectional Encoder Representa-
tions from Transformers) is a recent pre-trained
language model that has shown groundbreaking
results in many NLP tasks. BERT uses atten-
tion mechanism (Transformer) to learns contex-
tual relations between words in a text.
5 PERFORMANCE ANALYSIS
In this section, we will compare our proposed method
with baselines on the test sets. Table 4 shows the
detailed Comparisons of Micro F1-score for various
state-of-the-art models.
5.1 Comparisons with State-of-the-Art
First, we compare the result of Traditional Ma-
chine learning algorithms. Among LR, SVM, and
HSVM, HSVM performs better than the other two.
HSVM uses SVM at each node of the Decision tree.
Later we compare the result of Hierarchical, CNN
based models and graph-based deep learning mod-
els. Among Hierarchical Models HLSTM, HAN,
HE-AGCRCNN, HR-DGCNN, HiLAP, and HTrans,
HE-AGCRCNN performs better compared to other
Hierarchical models. HAN and HLSTM methods
are based on recurrent neural networks. While ana-
lyzing the performance of the recurrent model with
baseline Flat models, recurrent neural networks per-
form worse than HSVM even though there was
an ignorance of label dependency in baseline mod-
els. RNN faces the problem of vanishing gradi-
ents and exploding gradients when the sequences are
too long. Graph model, HR-DGCNN, performs bet-
ter than recurrent and baseline models. Comparing
the CNN-based model RCNN, XML-CNN, DCNN,
TEXTCNN, CNN, and CNN-RNN, TEXTCNN per-
forms better among all of them while RCNN performs
worse among them.
The sequence generator model treats the multi-
label classification task as a sequence generation.
When comparing the sequence generator models
SGM-GE and seq2seq, SGM performs better than the
seq2seq network. SGM utilizes the correlation be-
tween labels by using sequence generator model with
a novel decoder structure.
Comparing the proposed MAGNET against the
state-of-the-art models, MAGNET significantly im-
proved previous state-of-the-art results, we see ~20%
improvement in miF1 comparison to HSVM model.
While comparing with the best Hierarchical text clas-
sification models, we observe ~11%, ~19%, ~5%
and ~8% accuracy improvement compared to HE-
AGCRCNN, HAN, HiLAP, HTrans respectively. The
proposed model produced a ~16% improvement in
miF1 over the popular bi-directional block self-
attention network (Bi-BloSAN).
Comparing with CNN group models, proposed
model improves the performance by ~12% and ~6%
accuracy compared with TEXTCNN and BOW-CNN
method respectively. MAGNET achieves ~2% im-
provement over state-of-the-art BERT model.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
500
5.2 Evaluation on Other Datasets
We also evaluate our proposed model on four differ-
ent datasets rather than RCV1 to observe the perfor-
mance of the model on those datasets, which vary in
the number of samples and the number of labels. Ta-
ble 3 shows the miF1 scores for different datasets, and
we also report the Hamming loss in Table 5. Evalu-
ation results show that proposed methods achieve the
best performance in the primary evaluation metrics.
We observe 3% and 4% miF1 improvement in AAPD
and Slashdot dataset, respectively, as compared to the
CNN-RNN method.
5.3 Analysis and Discussion
Here we discuss a further analysis of the model and
experimental results. We report the evaluation results
in terms of hamming loss and macro-F1 score. We
are using a moving average with a window size of 3
to draw the plots to make the scenarios more comfort-
able to read.
5.3.1 Impact of Initialization of the Adjacency
Matrix
We initialized the adjacency matrix in three differ-
ent ways random, identity, and co-occurrence ma-
trix. We hypothesized that the co-occurrence ma-
trix would perform the best since the model is fed
with richer prior information than the identity matrix,
where the correlation is zero and random matrix. To
our surprise, random initialization performed the best
at 0.887, and identity matrix performed the worst at
0.865, whereas the co-occurrence matrix achieved the
micro-F1 score of 0.878. Even though Xavier initial-
izer performed the best, all the other random initial-
izers performed better than co-occurrence and iden-
tity matrices. This shows that the textual information
from samples contain richer information than that in
the label co-occurrence matrix that we initialize the
adjacency with, and both co-occurrence and identity
matrix, traps the model in a local minima.
5.3.2 Results on Different Types of Word
Embeddings
In this section, we investigate the impact of the four
different word embeddings on our proposed archi-
tecture, namely the Word2Vec embeddings(Mikolov
et al., 2013), Glove embeddings (Pennington et al.,
2014), Random embeddings, BERT embeddings (De-
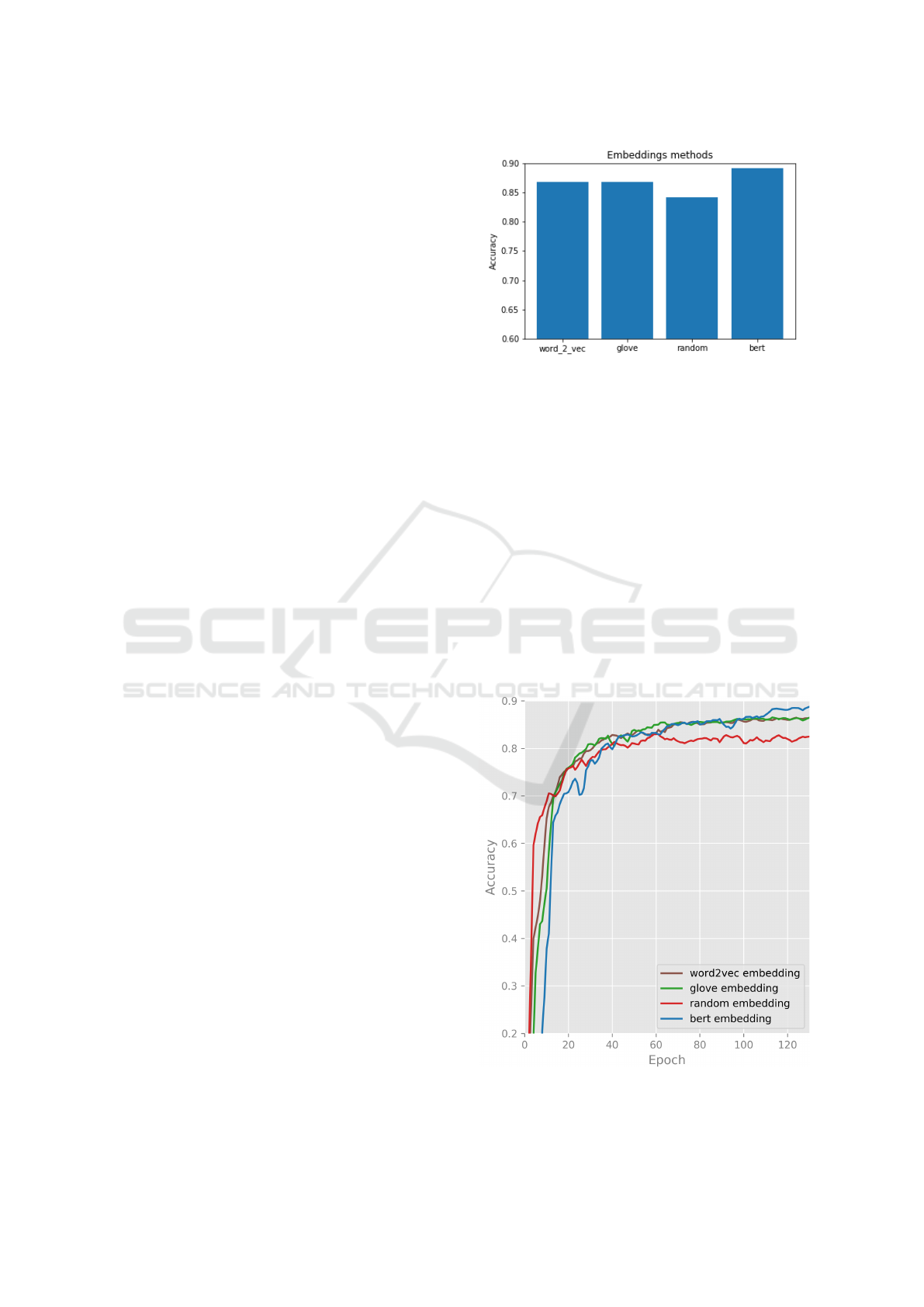
vlin et al., 2019a). Figure (2) and Figure (3) shows
the f1 score of all four different word embeddings on
the (unseen) test dataset of Reuters-21578.
Figure 2: Different types of word embeddings performance
on MAGNET x axis refer to the different types of word em-
beddings and y axis refer to the Accuracy ( F1-score).
Accordingly, we make the following observations:
• Glove and word2vec embeddings produce simi-
laer results.
• Random embeddings perform worse than other
embeddings. Pre-trained word embeddings have
proven to be highly useful in our proposed archi-
tecture compared to the random embeddings.
• BERT embeddings outperform other embeddings
in this experiment. Therefore, using BERT fea-
ture embeddings increase the accuracy and per-
formance of our architecture.
Our proposed model uses BERT embeddings for en-
coding the sentences.
Figure 3: Performance of proposed model on different types
of word embeddings. x-axis is the number of epoch and the
y-axis refers to the micro-F1 score.
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
501
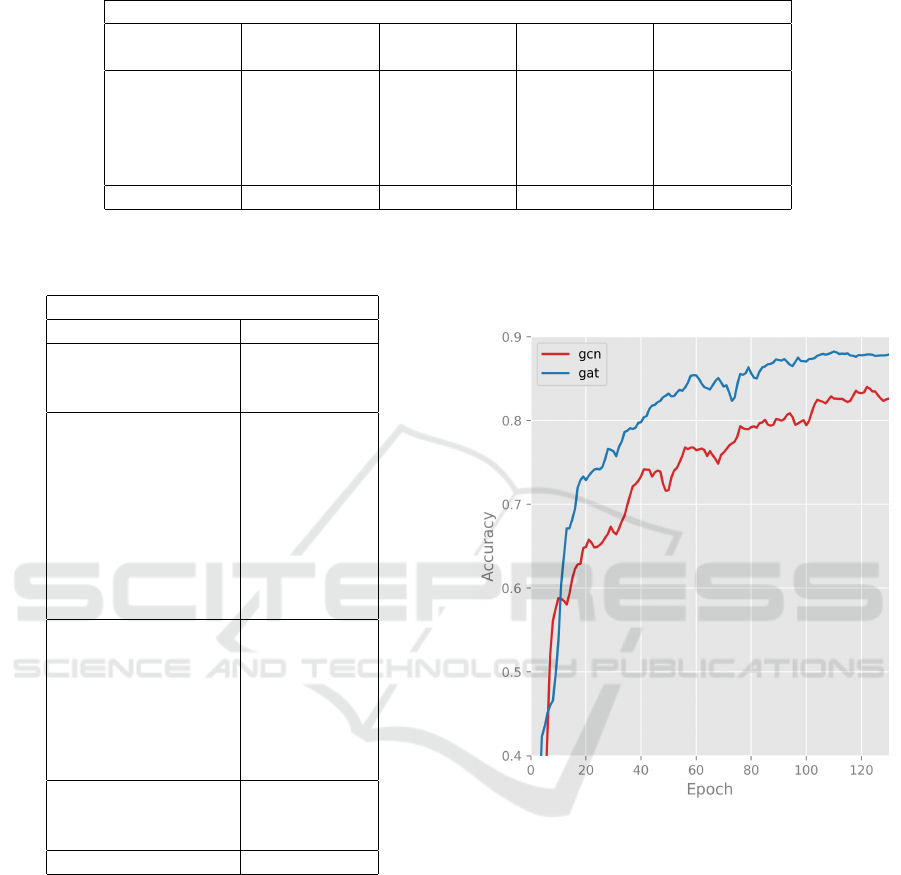
Table 3: Comparisons of Micro F1-score for various models on four benchmark datasets.
F1-accuracy
Methods Reuters-
21578
AAPD Slashdot Toxic
BR 0.878 0.648 0.486 0.853
BR-support 0.872 0.682 0.516 0.874
CC 0.879 0.654 0.480 0.893
CNN 0.863 0.664 0.512 0.775
CNN-RNN 0.855 0.669 0.530 0.904
MAGNET 0.899 0.696 0.568 0.930
Table 4: Comparisons of Micro F1-score for various state-
of-the-art models on Rcv1-v2 dataset.
Rcv1-v2
Method Accuracy
LR 0.692
SVM 0.691
HSVM 0.693
HLSTM 0.673
RCNN 0.686
XML-CNN 0.695
HAN 0.696
Bi-BloSAN 0.72
DCNN 0.732
SGM+GE 0.719
CAPSULE-B 0.739
CDN-SVM 0.738
HR-DGCNN 0.761
TEXTCNN 0.766
HE-AGCRCNN 0.778
BP-MLL
RAD
0.780
HTrans 0.805
BOW-CNN 0.827
HilAP 0.833
BERT 0.864
BERT + SGM 0.846
FMP + LaMP
pr
0.877
MAGNET 0.885
5.3.3 Comparison between Two Different Graph
Neural Networks
In this section, we compare the performance of GAT
and GCN networks. The critical difference between
GAT and GCN is how the information aggregates
from the neighborhood. GAT computes the hidden
states of each node by attending over its neighbors,
following a self-attention strategy where GCN pro-
duces the normalized sum of the node features of
neighbors.
GAT improved the average miF1 score by 4% over
the GCN model. It shows that the GAT model cap-
tures better label correlation compare to GCN. The
attention mechanism can identify label importance in
correlation graph by considering the significance of
their neighbor labels.
Figure 4: Performance of GAT vs GCN. x-axis is number
of epochs and y-axis is micro-F1 score.
Figure (4) shows the accuracy of both neural net-
work on Reuters-21578 dataset.
6 CONCLUSION
The proposed approach can improve the accuracy and
efficiency of models and can work across a wide range
of data types and applications. To model and capture
the correlation between labels, we proposed a GAT
based model for multi-label text classification.
We evaluated the proposed model on various
datasets and presented the results. The combination
of GAT with bi-directional LSTM shows that it has
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
502

Table 5: Comparisons of hamming loss for various models on four benchmark datasets. The smaller the value, the better.
Hamming-loss
Methods Rcv1-v2 AAPD Reuters-
21578
Slashdot Toxic
BR 0.0093 0.0316 0.0032 0.052 0.034
CC 0.0089 0.0306 0.0031 0.057 0.030
CNN 0.0084 0.0287 0.0033 0.049 0.039
CNN-RNN 0.0086 0.0282 0.0037 0.046 0.025
MAGNET 0.0079 0.0252 0.0029 0.039 0.022
achieved consistently higher accuracy than those ob-
tained by conventional approaches.
Even though our proposed model performs very
well, there are still some limitations. When the
dataset contains a large number of labels correlation
matrix will be very large, and training the model can
be difficult. Our work alleviates this problem to some
extent, but we still think the exploration of more ef-
fective solutions is vital in the future.
REFERENCES
Allison, P. (1999). Logistic Regression Using Sas®: Theory
and Application. SAS Publishing, first edition.
Banerjee, S., Akkaya, C., Perez-Sorrosal, F., and Tsiout-
siouliklis, K. (2019). Hierarchical transfer learning
for multi-label text classification. In Proceedings of
the 57th Conference of the Association for Computa-
tional Linguistics, ACL 2019, Florence, Italy, July 28-
August 2, 2019, Volume 1: Long Papers, pages 6295–
6300.
Boutell, M. R., Luo, J., Shen, X., and Brown, C. M.
(2004). Learning multi-label scene classification. Pat-
tern Recognition, 37(9):1757 – 1771.
Cai, H., Zheng, V. W., and Chang, K. C. (2017). A compre-
hensive survey of graph embedding: Problems, tech-
niques and applications. CoRR, abs/1709.07604.
Chen, G., Ye, D., Xing, Z., Chen, J., and Cambria, E.
(2017). Ensemble application of convolutional and
recurrent neural networks for multi-label text catego-
rization. In 2017 International Joint Conference on
Neural Networks (IJCNN), pages 2377–2383.
Chen, H., Sun, M., Tu, C., Lin, Y., and Liu, Z. (2016).
Neural sentiment classification with user and prod-
uct attention. In Proceedings of the 2016 Conference
on Empirical Methods in Natural Language Process-
ing, EMNLP 2016, Austin, Texas, USA, November 1-4,
2016, pages 1650–1659.
Chen, Z.-M., Wei, X.-S., Wang, P., and Guo, Y. (2019).
Multi-Label Image Recognition with Graph Convolu-
tional Networks. In The IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR).
Debole, F. and Sebastiani, F. (2005). An analysis of the
relative hardness of reuters-21578 subsets: Research
articles. J. Am. Soc. Inf. Sci. Technol., 56(6):584–596.
Destercke, S. (2014). Multilabel prediction with probability
sets: The hamming loss case. In Information Process-
ing and Management of Uncertainty in Knowledge-
Based Systems - 15th International Conference, IPMU
2014, Montpellier, France, July 15-19, 2014, Proceed-
ings, Part II, pages 496–505.
Devlin, J., Chang, M., Lee, K., and Toutanova, K. (2019a).
BERT: pre-training of deep bidirectional transform-
ers for language understanding. In Proceedings of
the 2019 Conference of the North American Chap-
ter of the Association for Computational Linguistics:
Human Language Technologies, NAACL-HLT 2019,
Minneapolis, MN, USA, June 2-7, 2019, Volume 1
(Long and Short Papers), pages 4171–4186.
Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K.
(2019b). Bert: Pre-training of deep bidirectional
transformers for language understanding. In NAACL-
HLT.
Fout, A., Byrd, J., Shariat, B., and Ben-Hur, A. (2017).
Protein interface prediction using graph convolutional
networks. In Proceedings of the 31st International
Conference on Neural Information Processing Sys-
tems, NIPS’17, pages 6533–6542, USA. Curran As-
sociates Inc.
Glorot, X. and Bengio, Y. (2010). Understanding the dif-
ficulty of training deep feedforward neural networks.
In Proceedings of the Thirteenth International Confer-
ence on Artificial Intelligence and Statistics, AISTATS
2010, Chia Laguna Resort, Sardinia, Italy, May 13-
15, 2010, pages 249–256.
Gopal, S. and Yang, Y. (2010). Multilabel classification
with meta-level features. pages 315–322.
Gopal, S. and Yang, Y. (2015). Hierarchical bayesian infer-
ence and recursive regularization for large-scale clas-
sification. TKDD, 9(3):18:1–18:23.
Gopal, S., Yang, Y., Bai, B., and Niculescu-Mizil, A.
(2012). Bayesian models for large-scale hierarchi-
cal classification. In Advances in Neural Informa-
tion Processing Systems 25: 26th Annual Conference
on Neural Information Processing Systems 2012. Pro-
ceedings of a meeting held December 3-6, 2012, Lake
Tahoe, Nevada, United States, pages 2420–2428.
Guo, Y. and Gu, S. (2011). Multi-label classification us-
ing conditional dependency networks. In IJCAI 2011,
Proceedings of the 22nd International Joint Confer-
ence on Artificial Intelligence, Barcelona, Catalonia,
Spain, July 16-22, 2011, pages 1300–1305.
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
503

Hearst, M. A. (1998). Support vector machines. IEEE In-
telligent Systems, 13(4):18–28.
Johnson, R. and Zhang, T. (2014). Effective use of word
order for text categorization with convolutional neural
networks. CoRR, abs/1412.1058.
Katakis, I., Tsoumakas, G., and Vlahavas, I. (2008). Multi-
label text classification for automated tag suggestion.
In Proceedings of the ECML/PKDD 2008 Discovery
Challenge.
Kim, Y. (2014a). Convolutional neural networks for sen-
tence classification. In Proceedings of the 2014 Con-
ference on Empirical Methods in Natural Language
Processing, EMNLP 2014, October 25-29, 2014,
Doha, Qatar, A meeting of SIGDAT, a Special Inter-
est Group of the ACL, pages 1746–1751.
Kim, Y. (2014b). Convolutional neural networks for sen-
tence classification. CoRR, abs/1408.5882.
Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-
sification with graph convolutional networks. CoRR,
abs/1609.02907.
Lai, S., Xu, L., Liu, K., and Zhao, J. (2015). Recurrent con-
volutional neural networks for text classification. In
Proceedings of the Twenty-Ninth AAAI Conference on
Artificial Intelligence, January 25-30, 2015, Austin,
Texas, USA, pages 2267–2273.
Lanchantin, J., Sekhon, A., and Qi, Y. (2019). Neural
message passing for multi-label classification. CoRR,
abs/1904.08049.
Lewis, D. D., Yang, Y., Rose, T. G., and Li, F. (2004). Rcv1:
A new benchmark collection for text categorization
research. J. Mach. Learn. Res., 5:361–397.
Liu, J., Chang, W., Wu, Y., and Yang, Y. (2017). Deep learn-
ing for extreme multi-label text classification. In Pro-
ceedings of the 40th International ACM SIGIR Con-
ference on Research and Development in Information
Retrieval, Shinjuku, Tokyo, Japan, August 7-11, 2017,
pages 115–124.
Luaces, O., D
´
ıez, J., Barranquero, J., del Coz, J. J., and
Bahamonde, A. (2012). Binary relevance efficacy for
multilabel classification. Progress in Artificial Intelli-
gence, 1(4):303–313.
Mao, Y., Tian, J., Han, J., and Ren, X. (2019). Hierar-
chical text classification with reinforced label assign-
ment. CoRR, abs/1908.10419.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and
Dean, J. (2013). Distributed representations of words
and phrases and their compositionality. In Advances
in Neural Information Processing Systems 26: 27th
Annual Conference on Neural Information Processing
Systems 2013. Proceedings of a meeting held Decem-
ber 5-8, 2013, Lake Tahoe, Nevada, United States.,
pages 3111–3119.
Nam, J., Kim, J., Loza Menc’ia, E., Gurevych, I., and
F
¨
urnkranz, J. (2014). Large-scale multi-label text
classification - revisiting neural networks. In Machine
Learning and Knowledge Discovery in Databases -
European Conference, ECML PKDD 2014, Nancy,
France, September 15-19, 2014. Proceedings, Part II,
pages 437–452.
Peng, H., Li, J., Gong, Q., Wang, S., He, L., Li, B., Wang,
L., and Yu, P. S. (2019). Hierarchical taxonomy-aware
and attentional graph capsule rcnns for large-scale
multi-label text classification. CoRR, abs/1906.04898.
Peng, H., Li, J., He, Y., Liu, Y., Bao, M., Wang, L., Song,
Y., and Yang, Q. (2018). Large-scale hierarchical text
classification with recursively regularized deep graph-
cnn. In Proceedings of the 2018 World Wide Web
Conference on World Wide Web, WWW 2018, Lyon,
France, April 23-27, 2018, pages 1063–1072.
Pennington, J., Socher, R., and Manning, C. D. (2014).
Glove: Global vectors for word representation. In
Proceedings of the 2014 Conference on Empirical
Methods in Natural Language Processing, EMNLP
2014, October 25-29, 2014, Doha, Qatar, A meeting
of SIGDAT, a Special Interest Group of the ACL, pages
1532–1543.
Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-
ing. Morgan Kaufmann Publishers Inc., San Fran-
cisco, CA, USA.
Ramos, J. Using tf-idf to determine word relevance in doc-
ument queries.
Read, J., Pfahringer, B., Holmes, G., and Frank, E. (2011).
Classifier chains for multi-label classification. Ma-
chine Learning, 85(3):333–359.
Schapire, R. E. and Singer, Y. (2000). Boostexter: A
boosting-based system for text categorization. Ma-
chine Learning, 39(2/3):135–168.
Schwenk, H., Barrault, L., Conneau, A., and LeCun, Y.
(2017). Very deep convolutional networks for text
classification. In Proceedings of the 15th Conference
of the European Chapter of the Association for Com-
putational Linguistics, EACL 2017, Valencia, Spain,
April 3-7, 2017, Volume 1: Long Papers, pages 1107–
1116.
Shen, T., Zhou, T., Long, G., Jiang, J., and Zhang, C.
(2018). Bi-directional block self-attention for fast
and memory-efficient sequence modeling. CoRR,
abs/1804.00857.
Sun, A. and Lim, E. (2001). Hierarchical text classification
and evaluation. In Proceedings of the 2001 IEEE In-
ternational Conference on Data Mining, 29 November
- 2 December 2001, San Jose, California, USA, pages
521–528.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J.,
Jones, L., Gomez, A. N., Kaiser, L., and Polo-
sukhin, I. (2017). Attention is all you need. CoRR,
abs/1706.03762.
Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Li
`
o,
P., and Bengio, Y. (2018). Graph attention networks.
In 6th International Conference on Learning Repre-
sentations, ICLR 2018, Vancouver, BC, Canada, April
30 - May 3, 2018, Conference Track Proceedings.
Vural, V. and Dy, J. G. (2004). A hierarchical method for
multi-class support vector machines. In Proceedings
of the Twenty-first International Conference on Ma-
chine Learning, ICML ’04, pages 105–, New York,
NY, USA. ACM.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Yu,
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
504

P. S. (2019). A comprehensive survey on graph neural
networks. CoRR, abs/1901.00596.
Xiao, L., Zhou, D., and Wu, M. (2011). Hierarchical clas-
sification via orthogonal transfer. In Proceedings of
the 28th International Conference on Machine Learn-
ing, ICML 2011, Bellevue, Washington, USA, June 28
- July 2, 2011, pages 801–808.
Xue, G., Xing, D., Yang, Q., and Yu, Y. (2008). Deep
classification in large-scale text hierarchies. In Pro-
ceedings of the 31st Annual International ACM SIGIR
Conference on Research and Development in Infor-
mation Retrieval, SIGIR 2008, Singapore, July 20-24,
2008, pages 619–626.
Yang, Z., Yang, D., Dyer, C., He, X., Smola, A. J., and
Hovy, E. H. (2016). Hierarchical attention networks
for document classification. In NAACL HLT 2016,
The 2016 Conference of the North American Chap-
ter of the Association for Computational Linguistics:
Human Language Technologies, San Diego Califor-
nia, USA, June 12-17, 2016, pages 1480–1489.
Yarullin, R. and Serdyukov, P. (2019). Bert for sequence-
to-sequence multi-label text classification.
Ying, R., He, R., Chen, K., Eksombatchai, P., Hamilton,
W. L., and Leskovec, J. (2018). Graph convolutional
neural networks for web-scale recommender systems.
CoRR, abs/1806.01973.
Zhang, M.-L., Li, Y.-K., Liu, X.-Y., and Geng, X.
(2018). Binary relevance for multi-label learning: an
overview. Frontiers of Computer Science, 12(2):191–
202.
Zhao, W., Ye, J., Yang, M., Lei, Z., Zhang, S., and Zhao, Z.
(2018). Investigating capsule networks with dynamic
routing for text classification. CoRR, abs/1804.00538.
MAGNET: Multi-Label Text Classification using Attention-based Graph Neural Network
505
