The Maximum Feasible Scenario Approach
for the Capacitated Vehicle Routing Problem with Uncertain Demands
Zuzana Bor
ˇ
cinov
´
a and
ˇ
Stefan Pe
ˇ
sko
Department of Mathematical Methods and Operations Research, Faculty of Management Science and Informatics,
University of
ˇ
Zilina, Univerzitn
´
a 8215/1,
ˇ
Zilina, Slovakia
Keywords:
Capacitated Vehicle Routing Problem, Uncertain Demands, Robust Optimization, Worst-case Scenario.
Abstract:
This study deals with the Capacitated Vehicle Routing Problem where customer demands are uncertain with
unknown probability distribution. We follow the robust optimization methodology to formulate and solve
the Robust Vehicle Routing Problem with Demand Uncertainty. Since the robust solution is a route plan,
which optimizes the worst case that could arise, our focus is concentrated on determining the worst-case
demands to solve the robust optimization model. The computational experiments examined two proposed
strategies to indicate their performance in terms of the extra cost and unmet demands.
1 INTRODUCTION
The Capacitated Vehicle Routing Problem (CVRP)
is one of the combinatorial optimization problems
which aims to find a set of minimum total cost routes
for a fleet of capacitated vehicles based at one depot,
to serve a set of customers under the following con-
straints:
(1) each route begins and ends at the depot,
(2) each customer is visited exactly once,
(3) the total demand of each route does not exceed
the capacity of the vehicle (Laporte, 2007).
The first mathematical formulation and algorithm for
the solution of the CVRP was proposed by Dantzig
and Ramser (1959) and five years later, Clarke
and Wright (1964) proposed the first heuristic for
this problem. Till to date many solution methods
for the CVRP have been published. General sur-
veys can be found in (Toth and Vigo, 2014) and (La-
porte, 2009). The CVRP belongs into the category
of NP hard problems that can be exactly solved only
for small instances of the problem. Therefore, re-
searchers have concentrated on developing heuristic
algorithms to solve this problem, for example (La-
porte et al., 2014), (Gendreau et al., 2010).
Contrary to the deterministic CVRP, which as-
sumes that the problem parameters (e.g. the customer
demands, travelling costs, service times, etc.) are de-
terministic and known, the robust CVRP (RVRP) con-
siders the parameters affected by uncertainty with un-
known probability distribution. In robust optimiza-
tion methodology introduced by Ben-Tal and Ne-
mirovski (1998), uncertainty is modeled as a bounded
set U which contains all possible continuous or dis-
crete values referred as scenarios. The objective of
the RVRP is to obtain a robust solution, that is feasi-
ble for all scenarios in U .
There are some works in the literature dealing
with the RVRP with different (combined or sepa-
rated) uncertain parameters. For example, Sungur
et al. (2008), Moghaddam et al. (2012), Gounaris
et al. (2013), Gounaris et al. (2016) and Pessoa
et al. (2018) study the RVRP with uncertain de-
mands. Toklu et al. (2013), Han et al. (2013) and
Solano-Charris et al. (2014) apply robust optimiza-
tion for the RVRP with uncertain travel costs. Lee
et al. (2012) and Sun et al. (2015) consider RVRP in
which travel times and also demands are uncertain.
This paper deals with the RVRP in which the cus-
tomer demands are uncertain and the distribution of
them is unknown. Our research is inspired by a work
of Sungur et al. (2008), who proposed the first so-
lution procedure for the RVRP with demand uncer-
tainty. The authors used a robust version of the CVRP
formulation with Miller-Tucker-Zemlin constraints
based on specific uncertainty to determine vehicle
routes that minimize transportation costs while satis-
fying all possible demand realizations. Their model
may be perceived as a worst-case instance of the de-
terministic CVRP in which the nominal demand pa-
rameter is replaced by a modified one from the uncer-
tainty set, thus solving the RVRP is no more difficult
than solving a single deterministic CVRP. But, de-
pending on the nature of the scenarios, some RVRPs
may become infeasible problems. Therefore, we are
Bor
ˇ
cinová, Z. and Peško, Š.
The Maximum Feasible Scenario Approach for the Capacitated Vehicle Routing Problem with Uncertain Demands.
DOI: 10.5220/0008943801590164
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 159-164
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159

interested in extending of this method to infeasible in-
stances.
The structure of this paper is organized as follows.
Section 2 is devoted to introduce the RVRP formula-
tion whith uncertain demands which is derived from
our two-index CVRP formulation (Bor
ˇ
cinov
´
a, 2017).
Next, our robust solution approach is presented in
Section 3. In Section 4 the computational results are
reported and compared with adopted method of Sun-
gur et al. Finally in Section 5, conclusions are drawn.
2 THE RVRP WITH UNCERTAIN
DEMANDS FORMULATION
The RVRP with demand uncertainty can be defined
by a complete directed graph G = (V, H, c) with V =
{0, 1, 2, . . . , n} as the set of nodes and H = {(i, j) :
i, j ∈ V, i 6= j} as the set of arcs, where node 0 repre-
sents the depot for a fleet of p vehicles with the same
capacity Q and remaining n nodes represent geo-
graphically dispersed customers.
The positive travel cost c
i j
is associated with each
arc (i, j) ∈ H. The cost matrix is symmetric, i.e.
c
i j
= c
ji
for all i, j ∈ V, i 6= j and satisfies the trian-
gular inequality, c
i j
+ c
jl
≥ c
il
for all i, j, l ∈ V .
The uncertain demands associated with each cus-
tomer j ∈ V −{0} are modeled as discrete scenarios.
The scenarios are constructed as deviations around an
expected demand d
0
j
, i.e. demand d
k
j
of customer j in
scenario k is positive value, d
0
j
−εd
0
j
≤ d
k
j
≤ d
0
j
+εd
0
j
,
where ε is a non negative constant, which determines
the maximum perturbation percentage.
Two-index decision variables x
i j
are used as bi-
nary variables equal to 1 if arc (i, j) belongs to the
optimal solution and 0 otherwise. For all pairs of
nodes i, j ∈ V − {0}, i 6= j we calculate the savings s
i j
for joining the cycles 0 → i → 0 and 0 → j → 0
using arc (i, j) as in Clarke and Wright’s saving
method (1964), i.e. s
i j
= c
i0
+c
0 j
−c
i j
. Then, instead
of minimizing the total cost, we will maximize the to-
tal saving (Bor
ˇ
cinov
´
a, 2017). To ensure the continu-
ity of the route and to eliminate sub-tours, we define
an auxiliary continuous variable y
j
, which shows (in
the case of collecting of the goods) the vehicle load
after visiting customer j. To simplify mathematical
modelling, we replace each feasible route 0 → v
1
→
v
2
→ · · · → v
t
→ 0 by a path from node 0 to node v
t
,
i.e. 0 → v
1
→ v
2
→ ··· → v
t
.
The RVRP with uncertain demands seeks the op-
timal solution that satisfies all demand realizations.
Let U
d
denotes a set which contains all scenario vec-
tors, U
d
= {d
k
, k = 1, . . . , m}, where m is a given
number of scenarios. Then, according to Bertsimas
and Sim (2003), the robust optimization model of
the problem can be stated as
RVRP 1:
max
n
∑
i=1
n
∑
j=1
i6= j
s
i j
x
i j
, (1)
subject to
n
∑
j=1
x
0 j
= p, (2)
n
∑
i=1
x
i0
= 0, (3)
n
∑
i=0
i6= j
x
i j
= 1, ∀ j ∈ V − {0}, (4)
n
∑
j=1
i6= j
x
i j
≤ 1, ∀i ∈ V − {0}, (5)
y
i
+ d
k
j
x
i j
− Q (1 − x
i j
)≤ y
j
,
∀d
k
∈ U
d
, i, j ∈ V − {0}, i 6= j, (6)
d
k
j
≤ y
j
≤ Q, ∀d
k
∈ U
d
, j ∈ V − {0}, (7)
x
i j
∈ {0, 1}, ∀i, j ∈ V, i 6= j. (8)
In this formulation, the objective function (1)
maximizes the total travel saving. The constraints (2),
(3), (4) and (5) are the indegree and outdegree con-
straints for depot and customers. Constraints (6) are
the route continuity and sub-tour elimination con-
straints and the constraints given in (7) are capac-
ity bounding constraints which restrict the upper and
lower bounds of y
j
. Finally, (8) are the obligatory
constraints.
The general approach of robust optimization is
to optimize the worst-case value over all data uncer-
tainty (Sungur et al., 2008). Let d
w
j
denotes the de-
mand of customer j in the worst scenario. Then, we
replace the constraints (6) and (7) with the constraints
y
i
+ d
w
j
x
i j
− Q (1 − x
i j
)≤ y
j
,
∀i, j ∈ V − {0}, i 6= j, (9)
d
w
j
≤ y
j
≤ Q, ∀ j ∈ V − {0}. (10)
Thus, similar to Sungur et al.(2008), we can solve
the RVRP as an instance of the CVRP. We refer to the
resulting model as RVRP 2.
3 DETERMINING
THE WORST-CASE SCENARIO
The key step in this approach is to identify the worst-
case scenario and subsequently substitute its values
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
160

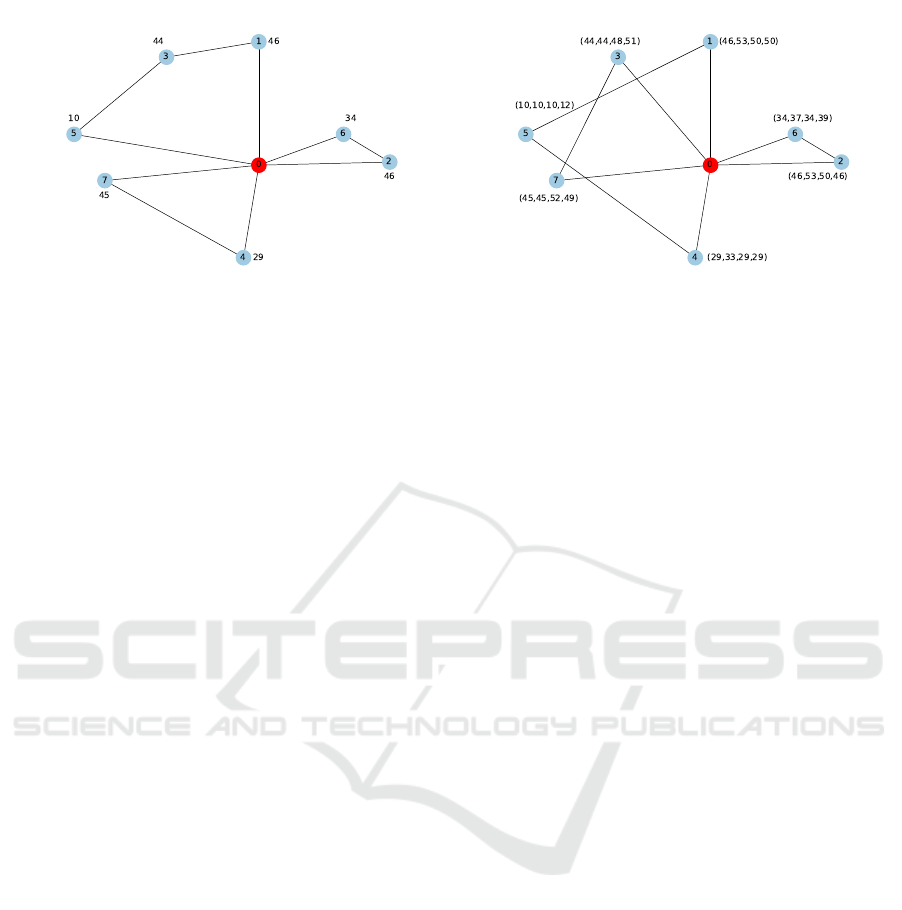
Figure 1: CVRP: Optimal deterministic solution. Figure 2: RVRP: Robust solution.
d
w
j
into the constraints (9) and (10). We suggest
following two strategies for determining the worst-
case scenario: the maximum demand scenario and
the maximum feasible demand scenario.
3.1 The Maximum Demand Scenario
In the first strategy (Strategy 1) we consider that all
customer demands take their maximum values in each
scenario (Ord
´
o
˜
nez, 2010), i.e. the worst-case sce-
nario values are d
w
j
= d
max
j
= max{max
k
d
k
j
, d
0
j
} for
j ∈ V − {0}, k ∈ {1, . . . , m}, where m is a number
of scenarios. This strategy gives a solution, which
is immune to demand variation under each scenario.
However, the CVRP with the maximum demand sce-
nario may be infeasible if vehicles have not sufficient
capacity. Then a robust solution can not be found.
3.2 The Maximum Feasible Demand
Scenario
The main idea of this strategy (Strategy 2) is to serve
as many demands as possible, i.e. we find such a sce-
nario with values d
w
j
∈ {d
k
j
, k = 0, . . . , m} to maximize
the sum of satisfied demands with respect the fleet
size and vehicle capacities.
We assume the decission variables t
i jk
, which in-
dicate whether vehicle i serves demand d
k
j
or not.
The mathematical model that determines feasible sce-
nario with maximum sum of satisfied demands can be
described as follows:
max
p
∑
i=1
n
∑
j=1
m
∑
k=0
t
i jk
d
k
j
, (11)
subject to
n
∑
j=1
m
∑
k=0
t
i jk
≥ 1, ∀i ∈ {1, . . . , p}, (12)
p
∑
i=1
m
∑
k=0
t
i jk
= 1, ∀ j ∈ {1, . . . , n}, (13)
n
∑
j=1
m
∑
k=0
t
i jk
d
k
j
≤ Q, ∀i ∈ {1, . . . , p}, (14)
t
i jk
∈ {0, 1},
∀i ∈ {1, . . . , p}, j ∈ {1, . . . , n}, k ∈ {0, . . . , m}. (15)
The objective function (11) maximizes the sum of
the demand values selected from a set of scenarios
to be served. The constraints (12) express that each
vehicle must serve at least one customer. The con-
straints (13) impose that every customer is visited
once by one vehicle and exactly one its demand value
is selected to be served. The constraints (14) ensure
that the total load does not exceed the capacity of
any vehicle. Finally, the constraints (15) define the bi-
nary decission variables. Obviously, it is not guaran-
tee that all the demand of each customer will be met
under this strategy.
4 COMPUTATIONAL
EXPERIMENTS
In order to assess the efficiency and quality of the pro-
posed robust solution approach, we design compu-
tational experiments and analyze the robust solu-
tions obtained with alternative strategies in terms of
their demand and cost performances. The mathe-
matical models were coded in Python 3.7 (2019) and
solved by the solver Gurobi 8.1 (2019). A computer
with an Intel Xeon 32 cores, 2.4 GHz processor and
256 GB of RAM was used to perform the computa-
tional experiments.
The Maximum Feasible Scenario Approach for the Capacitated Vehicle Routing Problem with Uncertain Demands
161

4.1 Test Instances
We use standard instances publicly available at
www.coin-or.org/SYMPHONY/branchandcut/VRP/
data/ for our computational experiments. Because
the instances are originally designed for deterministic
CVRP, it was necessary to modify them to include
demand uncertainty. The customer demands specified
in the benchmark were taken to be their nominal
values d
0
j
. For each deterministic CVRP benchmark,
we construct four classes of uncertainty sets of 5
scenarios within the allowed perturbation percentage
ε ∈ {0.05, 0.1, 0.15, 0.2}. All instances were solved
with a runtime limit of one hour.
4.2 Performance Measures
To evaluate the performance of the proposed strate-
gies, we use the performance measures presented
in (Sungur, 2008) including the relative extra cost and
unmet demands.
Let z
r
and z
d
be the cost of robust and determinis-
tic solutions respectively. The ratio ζ =
z
r
− z
d
z
d
quan-
tifies the relative extra cost of the robust solution ver-
sus the deterministic optimal one. It is clear, that
smaller ζ means the better cost performance.
Let g
d
and g
r
represent the maximum unmet de-
mand that can occur when using the deterministic and
robust solution respectively and D is the total nomi-
nal demand, i.e. D =
n
∑
i=1
d
0
i
. The unmet demand is
the sum of demands in each route that exceeds the ve-
hicle capacity. The ratio γ =
g
d
− g
r
D
, reflects the rel-
ative decrease of unmet demand in the robust solution
compare to deterministic optimal one when it faces
the maximum demand scenario. Obviously, the larger
γ indicate the better demand performance. We notice
that every solution found by Strategy 1 has g
r
= 0.
Example:
Figure 1 shows a CVRP optimal solution
with n = 7 customers and p = 3 vehicles of
the capacity Q = 100. Customer demands
d = (46, 46, 44, 29, 10, 34, 45) are displayed next
to the nodes. The cost of this solution z
d
= 227.
Figure 2 illustrates a robust solution of the same
problem with m = 4 discrete scenarios of uncertain
demands, which were generated randomly by pertu-
bation ε = 0.20:
d
1
= (46, 46, 44, 29, 10, 34, 45),
d
2
= (53, 53, 44, 33, 10, 37, 45),
d
3
= (50, 50, 48, 29, 10, 34, 52),
d
4
= (50, 46, 51, 29, 12, 39, 49).
The route demands in particular scenarios are:
• Route 1, 5, 4 : 85, 96, 89, 91
• Route 3, 7 : 89, 89, 100, 100
• Route 2, 6 : 80, 90, 84, 85
It is evident, that the total demand of any route in each
scenario does not exceed vehicle capacity. The cost
of robust solution z
r
= 291, i.e. the relative extra cost
ζ = 0.282.
Since Strategy 1 failed in solving this problem, de-
picted robust solution was found by Strategy 2,
whereby the maximum feasible scenario is d
w
=
(53, 53, 51, 33, 12, 39, 49). To evaluate the demand
performance, we calculate the total demands in each
route for a case if all customer demands take their
maximum value d
max
= (53, 53, 51, 33, 12, 39, 52).
The summations of demands in the optimal solution
routes are 116, 85 and 92, i.e. there is g
d
= 16 un-
satisfied demands. In the robust solution, the sum-
mations of demands in the routes are 98, 103 and 92,
therefore g
r
= 3 and the relative decrease of unmet
demand γ = 0.051.
4.3 Numerical Results
The results of both proposed strategies are summa-
rized in the Table 1.
In this table, the first column represents the name
of instances. The name of each instance allows deter-
mine its characteristics, since it has a format X-nA-
kB-eC, where A is the number of nodes, B represents
the number of vehicles and C indicates perturbation
percentage. For example an instance P-n16-k8-e5 has
16 nodes, 8 vehicles and was derived from the in-
stance P-n16-k8 by demand generation with ε = 0.05.
The columns Cost performance and Demand per-
formance show the two performance measures ζ and
γ respectively, as explained before. An indicator ”in”
denotes an infeasible instance.
As we can observe from Table 1 the strategy,
which optimizes the maximum demand scenario
(Strategy 1) results to infeasible solutions in some
cases, while strategy based on the maximum feasible
demand scenario approach (Strategy 2) has an appro-
priate solution in all cases. For all other cases both
of strategies have achieved the same results, because
the maximum feasible demand scenario is equal to
the maximum demand scenario. It means, that Strat-
egy 2 is an extension of Strategy 1 for problems with
infeasible maximum demand scenario.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
162

Table 1: The comparison of two strategies.
Strategy 1 Strategy 2
Instance Cost Demand Cost Demand
perform. perform. perform. perform.
P-n16-k8-e5 0.000 0.000 0.000 0.000
P-n16-k8-e10 0.000 0.004 0.000 0.000
P-n16-k8-e15 0.027 0.008 0.027 0.008
P-n16-k8-e20 in in 0.027 0.004
P-n20-k2-e5 0.005 0.006 0.005 0.006
P-n20-k2-e10 0.005 0.010 0.005 0.010
P-n20-k2-e15 in in 0.023 0.003
P-n20-k2-e20 in in 0.009 0.000
P-n23-k8-e5 0.091 0.006 0.091 0.006
P-n23-k8-e10 0.091 0.006 0.091 0.006
P-n23-k8-e15 in in 0.174 0.000
P-n23-k8-e20 in in 0.102 0.000
E-n13-k4-e5 0.121 0.021 0.121 0.021
E-n13-k4-e10 0.121 0.053 0.121 0.053
E-n13-k4-e15 0.121 0.082 0.121 0.082
E-n13-k4-e20 0.166 0.117 0.166 0.117
E-n22-k4-e5 0.043 0.008 0.043 0.008
E-n22-k4-e10 0.043 0.008 0.043 0.008
E-n22-k4-e15 0.043 0.007 0.043 0.007
E-n22-k4-e20 0.043 0.006 0.043 0.006
E-n23-k3-e5 0.002 0.005 0.002 0.005
E-n23-k3-e10 0.002 0.026 0.002 0.026
E-n23-k3-e15 in in 0.000 0.000
E-n23-k3-e20 in in 0.000 0.000
A-n34-k5-e5 0.000 0.000 0.000 0.000
A-n34-k5-e10 0.000 0.000 0.000 0.000
A-n34-k5-e15 0.042 0.004 0.042 0.004
A-n34-k5-e20 in in 0.042 0.004
A-n44-k6-e5 0.000 0.000 0.000 0.000
A-n44-k6-e10 0.002 0.004 0.002 0.004
A-n44-k6-e15 0.049 0.019 0.049 0.019
A-n44-k6-e20 in in 0.044 0.009
A-n53-k7-e5 0.032 0.000 0.032 0.000
A-n53-k7-e10 0.028 0.008 0.028 0.008
A-n53-k7-e15 in in 0.049 0.035
A-n53-k7-e20 in in 0.046 0.026
5 CONCLUSIONS
In this paper the robust optimization was used to
solve the Capacitated Vehicle Routing Problem with
demand uncertainty. The main contribution of our
work is to design a new strategy to cope with uncer-
tain demands. At first, we present the mathematical
model RVRP 2, derived from our two-index CVRP
formulation, which optimizes the worst-case scenario.
Then we are concerned with determining the worst-
case scenario. In Strategy 1, the worst-case scenario
takes the maximum demand values, which sometimes
leads to an infeasible problem. Therefore we propose
strategy (Strategy 2) based on an idea to satisfy as
many demands as possible with respect the fleet size
and vehicle capacities. Hence, in contrast to Strat-
egy 1, it always designes an appropriate solution, even
though it is not strictly robust.
A possible future research is to extend this study
to solving large-scale problem instances.
ACKNOWLEDGEMENTS
The paper was conducted within the project KEGA
041
ˇ
ZU-4/2017 Experimental Mathematics Accessi-
ble for All (granted by Ministry of Education), sup-
ported by the research grants APVV-14-0658 Opti-
mization of urban and regional public personal trans-
port and VEGA 1/0342/18 Optimal dimensioning of
service systems.
REFERENCES
Ben-Tal, A., Nemirovski, A. (1998). Robust convex
optimization. Mathematics of Operations Research,
23(4):769–805.
Bertsimas, D., Sim, M. (2003). Robust discrete optimiza-
tion and network flows. Mathematical Programming
Series B, 98(1-3):49–71.
Bor
ˇ
cinov
´
a, Z. (2017). Two models of the capacitated vehi-
cle routing problem. In: Croatian operational research
review.,8(2):463–469.
Clarke, G., Wright, J. W. (1964). Scheduling of vehicles
from a central depot to a number of delivery points. Op-
erations Research, 12(4):568–581.
Dantzig, G. B., Ramser, J. H. (1959). The truck dispatching
problem. Management Science, 6(1):80–91.
Gendreau, M., Potvin, J. Y. (2010). Handbook of Meta-
heuristics, Second Edition, Springer, New York.
Gounaris, C. E.,Wiesemann, W., Floudas, C. A. (2013).
The robust capacitated vehicle routing problem under
demand uncertainty. Operations Research, 61(3):677–
693.
Gounaris, C. E., Repoussis, P. P., Tarantilis, C. D., Wiese-
mann, W., Floudas, C. A. (2016). An Adaptive Mem-
ory Programming Framework for the Robust Capac-
itated Vehicle Routing Problem. Transportation Sci-
ence, 50(4): 1239–1260.
The Maximum Feasible Scenario Approach for the Capacitated Vehicle Routing Problem with Uncertain Demands
163

Gurobi (2019). Gurobi Optimizer Reference Man-
ual, version 8.1. Gurobi Optimization, Inc.
https://www.gurobi.com/documentation/8.1/refman/
index.html. Accessed 03/04/19
Han, J., Lee, C., Park, S. (2013). A robust scenario ap-
proach for the vehicle routing problem with uncertain
travel times. Transportation Science, 48(3):373–390.
Laporte, G.,Ropke, S., Vidal, T. (2014). Heuristics for the
vehicle routing problem. Vehicle routing: Problems,
Methods and Applications, Second Edition. Philadel-
phia: SIAM, 18–87.
Laporte, G. (2009). Fifty Years of Vehicle Routing. Trans-
portation Science, 43(4):408–416.
Laporte, G. (2007). What you should know about the vehi-
cle routing problem. Naval Research Logistics, 54:811–
819.
Lee, C., Lee, K., Park, S. (2012). Robust vehicle routing
problem with deadlines and travel time/demand uncer-
tainty. Journal of the Operational Research Society,
63(9):1294–1306.
Moghaddam, B. F., Ruiz, R., Sadjadi, S. J. (2012). Vehicle
routing problem with uncertain demands: An advanced
particle swarm algorithm. Computers & Industrial En-
gineering, 62:306–317.
Ord
´
o
˜
nez, F. (2010). Robust Vehicle Routing. INFORMS
Tutorials in Operations Research, 153–178.
Pessoa, A., Poss, M., Sadykov, R., Vanderbeck, F. (2018).
Solving the robust CVRP under demand uncertainty.
ODYSSEUS, Jun 2018, Calgliari, Italy. 7th Interna-
tional Workshop on Freight Transportation and Logis-
tics.
Python (2019). The Python Language Reference. Python
Software Foundation. https://docs.python.org/3/. Ac-
cessed 03/04/19
Solano-Charris, E. L., Prins, C., Santos, A. C. (2014). A ro-
bust optimization approach for the vehicle routing prob-
lem with uncertain travel cost. In Control, Decision and
Information Technologies (CoDIT) International Con-
ference, pp. 098–103.
Sun, L., Wang, B. (2015). Robust optimization approach
for vehicle routing problems with uncertainty. Interna-
tional Journal of Computer Applications in Technology.
Sungur, I, Ord
´
o
˜
nez, F., Dessouky, M. (2008). A robust opti-
mization approach for the capacitated vehicle routing
problem with demand uncertainty. IIE Transactions,
40(5):509–523.
Toklu, N. E., Montemanni, R., Gambardella, L. M. (2013).
An ant colony system for the capacitated vehicle routing
problem with uncertain travel costs. IEEE Symposium
on Swarm Intelligence (SIS), pp. 32–39.
Toth, P., Vigo, D. (2014). Vehicle routing: Problems, Meth-
ods and Applications. Society for Industrial and Ap-
plied Mathematics (SIAM).
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
164