Variational Inference of Dirichlet Process Mixture using Stochastic

Gradient Ascent

Kart-Leong Lim

Nanyang Technological University, 50 Nanyang Ave 639788, Singapore

Keywords:

Bayesian Nonparametrics, Dirichlet Process Mixture, Stochastic Gradient Ascent, Fisher Information.

Abstract:

The variational inference of Bayesian mixture models such as the Dirichlet process mixture is not scalable to

very large datasets, since the learning is based on computing the entire dataset each iteration. Recently, scalable

version notably the stochastic variational inference, addresses this issue by performing local learning from

randomly sampled batches of the full dataset or minibatch each iteration. The main problem with stochastic

variational inference is that it still relies on the closed form update in variational inference to work. Stochastic

gradient ascent is a modern approach to machine learning and it is widely deployed in the training of deep

neural networks. It has two interesting properties. Firstly it runs on minibatch and secondly, it does not rely

on closed form update to work. In this work, we explore using stochastic gradient ascent as a baseline for

learning Bayesian mixture models such as Dirichlet process mixture. However, stochastic gradient ascent

alone is not optimal for learning in terms of convergence. Instead, we turn our focus to stochastic gradient

ascent techniques that use decaying step-size to optimize the convergence. We consider two methods here.

The commonly known momentum approach and the natural gradient approach which uses an adaptive step-

size through computing Fisher information. We also show that our new stochastic gradient ascent approach

for training Dirichlet process mixture is compatible with deep ConvNet features and applicable to large scale

datasets such as the Caltech256 and SUN397. Lastly, we justify our claims when comparing our method to an

existing closed form learner for Dirichlet process mixture on these datasets.

1 INTRODUCTION

A common task in Dirichlet process mixture (DPM)

is to automatically estimate the number of classes to

represent a dataset (a.k.a model selection) and clus-

ter samples accordingly in area such as image pro-

cessing, video processing and natural language pro-

cessing. The variational inference (VI) of DPM (Blei

et al., 2006; Bishop, 2006) is mainly based on closed

form coordinate ascent learning where it iteratively

repeats its computational task (or algorithm) on the

entire sequence of dataset samples each iteration, also

known as batch learning. (Blei et al., 2003; Kuri-

hara and Welling, 2009; Bishop, 2006), Scalable

algorithms of VI also allows DPM to scale up to

larger dataset at fractional cost. Due to the recent

paradigm shift towards deep ConvNet (Krizhevsky

et al., 2012; He et al., 2016) and deep generative net-

works (Kingma and Welling, 2014; Goodfellow et al.,

2014), it is very rare to ﬁnd newer works focusing

on scalable DPM. Unlike DPM, deep ConvNet and

deep autoencoder do not speciﬁcally deal with model

selection. The more recent work addressing scalable

DPM or scalable Bayesian nonparametrics in general

is the stochastic variational inference (SVI) (Hoffman

et al., 2013; Paisley et al., 2015; Fan et al., 2018).

It is based on stochastic optimization (Robbins and

Monro, 1985) where it repeats its computational task

on a smaller set of randomly drawn samples each

iteration (or minibatch learning). This allows the

algorithm to see the entire dataset especially large

datasets when sufﬁcient iterations has passed. SVI

was demonstrated on models with complex Bayesian

posteriors such as the hierarchical Dirichlet process

mixture (Hoffman et al., 2013) and on large datasets

as large as 3.8M documents and 300 topics. However,

SVI do not involve actual computation of gradient as-

cent. Instead, SVI fundamentally rely on closed form

coordinate ascent for learning. Also, the rate of step-

size decay in SVI is ﬁxed and the optimal value is

usually unknown. This means that SVI cannot adapt

its step-size value according to the statistics of the

minibatch randomly drawn each iteration. Tradition-

ally, variational inference and stochastic gradient as-

Lim, K.

Var iational Inference of Dirichlet Process Mixture using Stochastic Gradient Ascent.

DOI: 10.5220/0008944300330042

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 33-42

ISBN: 978-989-758-397-1; ISSN: 2184-4313

cent are mutually exclusive. Recently, stochastic gra-

dient ascent (SGA) with constant step-size has been

discussed for VI in (Mandt et al., 2017). In a stochas-

tic or noisy setting (i.e. randomly drawn minibatch

samples), SGA with constant step-size alone may not

be efﬁcient. There is a requirement for a decaying

step-size to ensure convergence in SGA. This is to

avoid SGA bouncing around the optimum of the ob-

jective function (Robbins and Monro, 1985).

When considering what are the current issues with

variational inference:

The main problems with VI (Blei et al., 2006) are:

a) Batch learning is slow.

b) Require analytical solution.

The main problems with SVI (Hoffman et al., 2013)

are:

b) Require analytical solution.

c) Fixed step-size decay for closed form learn-

ing.

The main problem with constant step-size SGA

(Mandt et al., 2017) is:

d) Constant step-size for SGA learning.

In this work, our goal is to learn a DPM to automat-

ically compute the number of clusters to represent

a dataset. We also seek to address the above prob-

lems in (a,b,c,d) by using SGA as a scalable algo-

rithm for DPM (in terms of CPU time) while seeking

to achieve at least on-par performance (i.e. cluster-

ing and model selection) with traditional VI. In order

to to achieve that, we turn our focus to stochastic op-

timization techniques that use decaying step-size to

optimize the learning in SGA. Instead of ﬁxing the

rate of decay in SGA such as in the momentum ap-

proach, natural gradient (Amari, 1998) can provides

an adaptive step-size for SGA using Fisher informa-

tion. This is possible as directional search employ-

ing Fisher information in gradient ascent is akin to

directional search along the curvature of the objective

(variational posterior).

We test the performance of our proposed learner

on large class dataset such as Caltech256 and

SUN397 and obtained signiﬁcant improvement over

VI. To the best of our knowledge, it is very rare to

ﬁnd DPM task carried out on large scale image clas-

siﬁcation dataset i.e. large class sizes (397) and large

dataset (108K) such as Caltech256 and SUN397. The

experiments also conﬁrmed that our proposed meth-

ods can handle large dimensional features (4096) such

as deep ConvNet features.

The novel contributions in this work are:

i) Avoid analytical solution.

ii) Adaptive step-size decay.

iii) Lower cost without sacriﬁcing perfor-

mance.

This paper is organized as follows: Firstly, we present

a new technique based on constant step-size SGA to

take over VI for training a DPM. In order to have a

decreasing step-size effect, we smoothen the estima-

tion of SGA using the momentum approach. Thirdly,

instead of ﬁxing the rate of step-size decay in the

momentum approach, we propose another alternative

by applying Fisher information to SGA, which adap-

tively learns a step-size decay from the variational

posterior, each iteration. We reported experimental

results on six datasets including the more challenging

Caltech256 and SUN397 for our DPM task. We ﬁrst

compare the computational cost and the performance

of the proposed SGA to VI. Lastly, we compare our

method with state-of-the-arts methods for DPM.

1.1 Related Works

The use of SGA to perform VI is certainly not new.

We call these works as SGA-VI (Ranganath et al.,

2014; Paisley et al., 2012; Kingma and Welling, 2014;

Welling and Teh, 2011; Rezende and Mohamed,

2015). The key idea of SGA-VI is to take the gradient

of the evidence lower bound (ELBO) with a step size

for updating corresponding VI parameters. Some no-

table works in this area include the black box VI (Ran-

ganath et al., 2014), VI with stochastic search (Pais-

ley et al., 2012) and the stochastic gradient variational

Bayes (Kingma and Welling, 2014). An emphasis in

these works (e.g. black box VI) is the use of Monte

Carlo integration to approximate the expectation of

the ELBO. There are two advantages. Firstly, there is

no need to constrain the learning of variational pos-

teriors expectation to analytical solution. Secondly,

MCMC approximated solutions lead to true poste-

riors at the expense of greater computational cost.

However, most works usually demonstrated SGA-VI

on non-DPM related task such as the logistic regres-

sion(Welling and Teh, 2011; Mandt et al., 2017; Pais-

ley et al., 2012). Non-DPMs do not deal with in-

complete data or cluster label issue. Thus, the learn-

ing of the SGA-VI (Ranganath et al., 2014; Paisley

et al., 2012; Kingma and Welling, 2014; Welling and

Teh, 2011) described above are more suitable to rel-

atively simpler parameter inference problems. Also,

these works on SGA-VI were mainly demonstrated

on datasets with smaller datasets of 10 classes with

60K image sizes such as MNIST. In this paper we tar-

get BNP task of up to 108K images with 397 object

classes and high dimensions features of 4096 using

VGG16 pretrained on ImageNet and Place205. Our

work also falls under the SGA-VI category. Instead

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

of Monte Carlo integration, we use the Maximum a

posterior (MAP) estimate for approximating the ex-

pectation of the ELBO for simplicity. Although, a

similar technique known as constant SGA for varia-

tional EM was concurrently proposed in (Mandt et al.,

2017), it was demonstrated on the logistic regression

model (classiﬁcation) rather than for DPM.

In stochastic optimization (Robbins and Monro,

1985), there is a requirement for a decaying step-

size to ensure convergence in SGA. This is to avoid

SGA bouncing around the optimum of the objective

function. In the constant SGA for variational EM

(Mandt et al., 2017), the authors suggest using con-

stant step-size SGA for SGA-VI. Our empirical ﬁnd-

ing suggest that constant step-size for SGA-VI is not

ideal for learning since convergence is slow. Instead,

we use Fisher information to assume the role of iter-

atively adapting the step-size in SGA. While the use

of Fisher information for VI has been proposed in the

past (Hoffman et al., 2013; Honkela et al., 2010), this

is the ﬁrst time it has been applied to a SGA-VI ap-

proach. Most works (Welling and Teh, 2011; Mandt

et al., 2017; Paisley et al., 2012) only consider the

use of ﬁxed decaying step-size SGA-VI. In (Honkela

et al., 2010), the authors applied it to the batch opti-

mization of VB-GMM rather than the stochastic op-

timization here. In (Hoffman et al., 2013), the au-

thors showed that the weights updating rule in SVI

can be viewed as a Fisher information enhanced VI

algorithm. However in SVI, it is unclear how we

should select the weight decay parameters and since

it is ﬁxed, the Fisher information in SVI cannot adapt

locally to each minibatch per iteration.

2 BACKGROUND

2.1 Dirichlet Process Mixture

We assume the mixture model in DPM is Gausian dis-

tributed, x | z, µ ∼ N (µ, σ)

. DPM models a set of N

observed variable denoted as x =

{

}

n=1

∈ R

with

a set of hidden variables, θ =

{

µ, z, v

}

. The total di-

mension of each observed instance is denoted D. The

mean is denoted µ =

{

}

k=1

∈ R

. We assume diag-

onal covariance i.e. Σ

= σ

I and deﬁne variance as

a constant, σ

= σ ∈ R

. The cluster assignment is

denoted z =

{

}

n=1

where z

is a 1 − o f − K binary

vector, subjected to

∑

k=1

= 1 and z

∈

{

0, 1

}

We follow the truncated stick-breaking (Sethura-

man, 1994) process to DPM with truncation level de-

noted K. Starting with a unit length stick, the propor-

tional length of each broken off piece (w.r.t remainder

of stick) is a random variable v drawn from a Beta

distribution and is denoted v =

{

}

k=1

∈ R. All bro-

ken off pieces add up to a unit length of the full stick.

This value can be seen as the the cluster weight and is

given as π

= v

∏

k−1

l=1

(1 − v

In the maximum likelihood approach to DPM i.e.

θ = argmax

p(x | µ, z), z

cannot be optimized by π

and v

. Instead, we turn to the Bayesian approach,

where each hidden variable is now modeled by a prior

distribution as follows

z | v ∼ Mult(π)

µ ∼ N (m

, λ

)

v ∼ Beta(1, a

)

(1)

We refer to N , Beta, Mult as the Gaussian, Beta

and Multinomial distribution respectively. The terms

and m

refer to the Gaussian prior hyperparameters

for cluster mean. a

is the Beta prior hyperparameter.

The hyperparameters are treated as constants. With-

out the We refer the readers to (Lim and Wang, 2018;

Blei et al., 2006) for further details on DPM.

2.2 Variational Inference and Learning

Variational inference (Bishop, 2006) approxi-

mates the intractable integral of the marginal

distribution

p(x) =

p(x | θ)p(θ)dθ

. This

approximation can be decomposed as a sum

ln p(x) = L + KL

divergence

where L is a lower

bound on the joint distribution between observed

and hidden variable. A tractable distribution

q(θ) is used to compute L =

q(θ)ln



p(x,θ)

q(θ)



dθ

and KL

divergence

= −

q(θ)ln



p(θ|x)

q(θ)



dθ. When

q(θ) = p(θ|x), the Kullback-Leibler divergence is

removed and L = ln p(X). The tractable distri-

bution q(θ) is also called the variational posterior

distribution and assumes the following factorization

q(θ) =

∏

q(θ

). Variational log posterior distribution

is expressed as lnq(θ

) = E

i6= j

[ln p(x, θ

)] + const.

The DPM joint probability can be derived as fol-

lows

p(x, µ, z, v) = p(x | µ, z)p(µ)p(z | v)p(v)

(2)

Next, we treat the hidden variables as variational log

posteriors, ln q(θ) and we use mean-ﬁeld assumption

and logarithm to simplify their expressions (Bishop,

2006)

lnq(µ, z, v) = ln q(µ) + lnq(z) + ln q(v) (3)

The variational log-posteriors are deﬁned using ex-

pectation functions (Bishop, 2006) as follows

lnq(µ) = E

[ln p(x | µ, z) + ln p(µ)] + const.

lnq(v) = E

[ln p(z | v) + ln p(v)] + const.

lnq(z) = E

µ,v

[ln p(x | µ, z) + ln p(z | v)] + const.

(4)

Variational Inference of Dirichlet Process Mixture using Stochastic Gradient Ascent

Variational log-posteriors (VLP) such as the ones

in eqn (4) are analytically intractable to learn. Welling

and Kurihara (Kurihara and Welling, 2009) discussed

a family of alternating learners and they are classi-

ﬁed into Expectation Expectation (EE), Expectation

Maximization (EM), Maximization Expectation (ME)

and Maximization Maximization (MM). Our main in-

terest is the MM algorithm due to its simplicity as

demonstrated in (Lim and Wang, 2018). In the learn-

ing of VI or closed form coordinate ascent algorithm,

the goal is to alternatively compute the expectations

of ln q [θ] and lnq [z] (deﬁned as E [θ] and E [z] respec-

tively) each iteration. In DPM, θ refers to µ and v. In

MM, these expectations are actually MAP estimated

and the objective function of MM is given as

E [z] ↔ E [θ]

≈ arg max

lnq(z) ↔ arg max

lnq(θ)

(5)

The argument for the convergence of MM is

brieﬂy discussed as follows (Lim and Wang, 2018):

“By restricting the mixture component to ex-

ponential family, the RHS is a convex func-

tion, hence a unique maximum exist. In the

LHS, for independent data points x

, ...x

with

corresponding cluster assignment z

, ..., z

given sufﬁcient statistics each data point

should only fall under one cluster, meaning

that for LHS there is indeed a unique maxi-

mum. It is further discussed in (Neal and Hin-

ton, 1998; Titterington, 2011; Bishop, 2006)

that the above function monotonic increases

for each iteration and will lead to conver-

gence.”

3 PROPOSED SGA LEARNER

FOR VARIATIONAL

POSTERIORS

Previously in VI, VLP are updated by computing their

expectation via closed form solution. In this section,

we wish to estimate these expectations of VLP using

SGA. We start with the constant step-size SGA, then

we present two more variants which introduce decay-

ing step-size to SGA.

3.1 Stochastic Gradient Ascent with

Constant Step-size (SGA)

We propose how to perform learning on a variational

log posterior, ln q (θ) using SGA. Recall that previ-

ously, the goal of VI is to ﬁnd an expression for es-

timating the expectation of ln q(θ) i.e. E [θ]. Instead

of estimating a closed form expression for E [θ] in VI,

using the MAP approach which is a global maximum,

we now seek the local maximum of lnq (θ) as below

E [θ] = arg max

lnq (θ)

= E [θ]

+ η∇

lnq(θ)

(6)

E [θ]

refers to the initial or previous iteration

value of E [θ] and η is the learning rate.

3.2 Stochastic Gradient Ascent with

Momentum (SGA+M)

A standard SGA technique in backpropagation is to

apply the momentum method to smoothen the gradi-

ent search as it reaches the local optimum. The update

is computed as

E [θ] = E [θ]

+ γ

new

= αγ

old

+ η∇

lnq(θ)

(7)

The purpose of α in eqn (7) is to slow the step size

learning but it is a constant value and typically ﬁxed

at 0.9. When α = 0, we recover SGA.

3.3 Stochastic Gradient Ascent with

Fisher Information (SGA+F)

Since we are dealing with an approximate poste-

rior or VLP which is assumed convex, a more

superior gradient learning is the natural gradient

learning. It uses Fisher information matrix, G =



∇

lnq(θ)(∇

lnq(θ))



, as the steepest ascent di-

rectional search is in Riemannian space. Natural gra-

dient learning is superior to gradient learning because

the shortest path between two point is not a straight-

line but instead falls along the curvature of the VLP

objective (Honkela et al., 2007).

In order to adapt the step-size to a stochastic set-

ting (i.e. randomly drawn minibatch samples) rather

than ﬁxing a value (e.g. α = 0.9 in SGA+M), we

can utilize Fisher information F as the direction of

steepest gradient ascent (Honkela et al., 2007; Amari,

1998) as follows

E [θ] = E [θ]

+ F

−1

η∇

lnq(θ) (8)

Where we deﬁne Fisher information as follows

= E [∇

lnq(θ) ◦ ∇

lnq(θ)]

(9)

In the above expression, F

is a scalar when we

assume diagonal covariance (i.e. each dimension is

independent), and ◦ refers to element wise product.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

4 PROPOSED ALGORITHM FOR

TRAINING DPM

We propose in Algo. 1, an algorithm for training

DPM using SGA. In DPM, our main goal is to up-

date two continuously distributed variational poste-

riors, ln q (µ) and ln q (v) each iteration. ln q (z) is a

discrete distribution and is solved traditionally using

MAP estimation. For brevity we use the following

expression

g(θ) =

∑

n=1

∇

lnq(θ) (10)

to represent the gradient averaged from each mini-

batch for ln q (µ) and lnq (v). As seen in Section 3,

all SGA discussed here fundamentally require solv-

ing for ∇

lnq(θ).

Algorithm 1: Proposed Training of DPM.

1) Input: x ←

{

minibatch

}

2) Output: E [µ

], E [v

], E [z

]

3) Initialization:

i) DPM hyperparameters a

, m

, λ

ii) learning rate 0.1 ≤ η ≤ 0.001

iii) K is the user deﬁned trunction level.

iv) use kmeans to initialize E [µ

] then compute

E [z

] followed by E [v

]

4) Repeat until max iteration or convergence

i) Compute E [µ

] using SGA

ii) Compute E [z

] using MAP

iii) Compute E [v

] using SGA

4.1 Gradient of ln q (µ)

In its simplest SGA form, solving the expectation of

lnq (µ) is expressed as follows

E [µ] = E [µ]

+ ηg (µ)

(11)

The gradient update is expressed as follows

∇

lnq(µ

) = ∇

[ln p(x

| µ

, z

) + ln p(µ

)]

= ∇



−

−µ

)

2σ

E [z

] −

(µ

−m

)

2σ





−µ

)

E [z

] −

(µ

−m

)



(12)

4.2 Gradient of ln q (v)

Next, when deﬁning the expectation of ln q (v) using

SGA as follows,

E [v] = E [v]

+ ηg (v)

(13)

we need to deﬁne the gradient below as follows

∇

lnq(v

) = ∇

[ln p(z | v

) + ln p(v

)]

= ∇

{

E [z

]ln v

∑

j=k+1

ln(1 − v

)E [z

n j

] +

∑

k=1

− 1)ln(1 − v

)

E[z

]

−

∑

j=k+1

[

n j

]

1−v

−

−1)

1−v

(14)

4.3 MAP learning of lnq(z)

Since we have a ﬁxed number of states and z

is rep-

resented by a 1 − o f − K vector, the expectation of

lnq (z) is obtained by the MAP estimate of lnq(z) as

follows

E [z

] ≈ argmax

lnq(z

)

≈ argmax

µ,v

[ln p(x

| z

, µ

) + ln p(z

| v

)]

≈ argmax

lnE [v

] +

∑

k−1

l=1

ln(1 − E [v

])

+ln





−

−E[µ

])

2σ

(15)

4.4 SGA with Fisher Information,

Momentum

It is straightforward to extend eqn (11) and (13) to

other SGA techniques discussed earlier. If we are in-

terested in ﬁnding F

over a set of M random samples,

the equation is as follows

∑

n=1

(∇

lnq(θ))

(16)

For momentum, the computation only involves an

additional memory caching of γ

old

in eqn (7).

5 EXPERIMENT: PROPOSED

SGA LEARNER VS

TRADITIONAL VI LEARNER

Our objective in this experiment is to ﬁrst ensure the

proposed SGAs should return on-par performance to

MM (Lim and Wang, 2018). The minibatch sizes are

empirically adjusted to reﬂect this. Then we mea-

sure the computational time. The experimental results

should justify our claim that as scalable algorithm for

computing DPM: SGAs is faster to compute, but must

retain on-par performance to traditional VI learner.

Variational Inference of Dirichlet Process Mixture using Stochastic Gradient Ascent

5.1 Evaluation Metric

In the followings, we evaluate ﬁve criterias:

i) Sample size per iteration (Fig. 2)

ii) Computational time (Fig. 1)

iii) Normalized mutual information (Fig. 3)

iv) Accuracy (Fig. 4)

v) Estimated model (Table 2)

5.1.1 Sample Size per Iteration

Batch learners such as MM typically takes the en-

tire dataset for computation per iteration. This is also

due to the theoretical deﬁnition behind VI. Whereas

in stochastic learning, both SGA and SVI runs on a

random subset of samples or minibatch per iteration.

When the number of samples per dataset is too large

for the batch learner, we limit this batch size to a ran-

dom subset of the entire dataset (e.g. N = 5000) as

seen in Fig. 1. The main difference between batch

and minibatch learners is that, for batch this subset

of samples have ﬁxed sequence for each iteration.

Whereas for minibatch, the subset of samples are not

ﬁxed and minbatch has a random chance to “see” the

entire dataset each iteration. Empirically, we found

that having at least 20 images per class for deﬁning

the minibatch size is necessary for sufﬁcient statistics.

5.1.2 Evaluation Metrics

We use Normalized Mutual Information (NMI) and

Accuracy (ACC) to evaluate the performance of our

learning. For NMI and ACC (based on Hungarian

mapping) we use the code in (Cai et al., 2005). The

deﬁnition for ACC (clustering) and NMI is as follows

ACC =

∑

n=1

δ(gt

, map (mo

))

NMI =

in f o

(gt, mo)

max(H (gt), H (mo))

where gt, mo, map, δ (·) , MU

in f o

, H refers to

ground truth label, model’s predicted label, permuta-

tion mapping function, delta function (δ(gt, mo) = 1

if gt = mo and equal 0 otherwise), mutual information

and entropy respectively. We can see that for ACC, it

is measuring how many times the model can produce

the same label as the ground truth on average. For

NMI, it is measuring how much is the overlap or

mutual information between ground truth entropy and

model entropy. Model refers to the model selection

estimated by each approach.

5.1.3 Computational Time

For a given budget, it is often unnecessary to run DPM

until full convergence especially when the dataset or

class is huge. Instead, we observed that typically

in the early stages, DPM aggressively prune away

computed empty clusters (v

= 0) from its given ini-

tial large cluster trucation size and the pruning will

slowly become relunctant after around sufﬁcient it-

erations has passed. This is where it signiﬁes it has

converged to a certain number of dominant clusters

close to ground truth. Empirically, we found that typ-

ically 30 to 60 iterations in our experiments is sufﬁ-

cient for good compromise between performance and

CPU cost.

5.1.4 Dataset Size

The object and scene categorization datasets used in

our experiments are detailed in Table 1. There are 3

objects and 3 scene datasets in total. The total num-

ber of images can range from 3K to 108K. We split

the datasets into train or test partition. Ground truth

refers to the number of classes per dataset. It ranges

from 10 to about 400 classes or clusters in our case.

Also, for unsupervised learning we do not require

class labels for learning our models. However, we re-

quire setting a truncation level for each dataset as our

model cannot start with an inﬁnite number of clus-

ters in practice. We typically use a large truncation

value (e.g. K = 1000 for SUN397) from the ground

truth to demonstrate that our model is not dependent

on ground truth as shown in Table 2.

For all datasets, we do not use any bounding box

information for feature extraction. Instead, we repre-

sent the entire image using a feature vector. For our

DPM input, we mainly extract FC7 of VGG16 as our

image feature extractor. The FC7 feature dimension

is 4096. We use VGG16 pretrained on Imagenet.

5.2 Experimental Results

In this section, we visually compare (Fig. 1-

4 and Table 2) the 5 evaluation criterias between

the MM learner (Lim and Wang, 2018) with our

newly proposed SGA learners (with learning rate η =

0.1) for the DPM model on six datasets (Table 1).

Speciﬁcally, we compare MM with “SGA+F” and

“SGA+M”. We rerun the experiments for at least 5

times and take their average results for each dataset.

We ﬁrst look at dataset #1 (Caltech10) and #4

(Scene15). Both are considered small datasets with

less than 5K images and 10-15 classes. We set the

initial truncation level to 50. We ran both MM (full

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

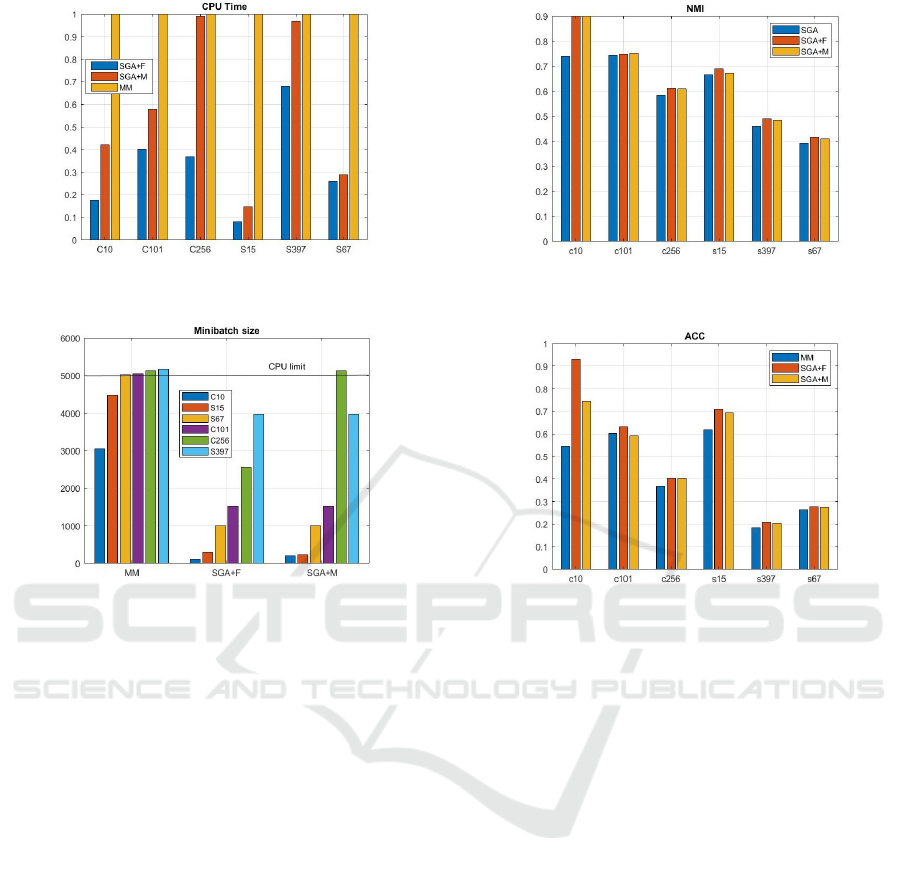
Figure 1: CPU time of SGA learners as a factor of batch

learner (MM). Lesser time is better.

Figure 2: Batch size capped at 5000 random samples for

MM. Least minibatch size for SGAs to achieve similar ACC

to MM. Smaller size reduces computational time.

dataset) and SGA (minibatch of 100 and 300 respec-

tively) for 30 iterations each. We observed that all

SGAs outperforms MM on all 5 evaluation criteria for

both datasets in terms of NMI and Accuracy, closer

to ground truth model selection, faster to compute as

a direct consequence of smaller sample size per it-

eration. The clustering performance (ACC & NMI)

of the proposed methods are indeed on-par or better

than MM. Also, it is evident that using SGAs allows it

to signiﬁcantly reduce the computation time as com-

pared to its batch counterpart MM. This ﬁnding is ac-

tually consistent throughout all the datasets.

Next, we look at dataset #2 (Caltech101), #5

(MIT67) and #3 (Caltech256). These datasets are

slightly more challenging as they have 67-256 classes

and about 2-10 times the image size than earlier at

about 8K, 15K and 30K. We set the initial truncation

level to about twice the ground truth at 200, 100 and

500 respectively. For batch learners such as MM or

VI, they cannot handle these kind of dataset as the en-

tire datset size is too large. Instead, we ﬁx the batch

size at around 5K and take a random subset of the

entire dataset that do not change for each iteration.

Meaning there is a large portion of dataset that MM

will never see. This is where SGAs are handy as it

Figure 3: NMI for closed form (MM) vs SGA learners.

Larger NMI is better.

Figure 4: Accuracy for closed form (MM) vs SGA learners.

Larger ACC is better.

can skip and access the entire dataset when the num-

ber of iterations increases as compared to MM. We set

the minibatch size to 1515 (10 random samples per

class), 1005 (15 random samples per class) and 2560

(10 random samples per class) respectively. We can

see that after 30 iterations, SGAs outperforms MM

once again on all 5 criteria.

Lastly, we look at dataset #6 (SUN397). This

dataset is considered quite large at >0.1M images and

almost 400 class. Using 1000 classes for truncation

level, we see that MM is unable to learn as quickly

as SGAs after 30 iterations as the estimated model is

quite large at 838 compared to 570.5 for the SGA+F.

Also for SGAs, there are some minor improvements

for NMI and ACC as compared to MM. The compu-

tational time is also 30% faster for SGA+F.

6 COMPARISON WITH

LITERATURE

In this section, we are mainly comparing the cluster-

ing performance of our proposed method with results

reported by the state–of-the-arts methods.

Variational Inference of Dirichlet Process Mixture using Stochastic Gradient Ascent

Table 1: Datasets partitioned (Caltech, Scenes) for our ex-

periments.

Dataset Train Test

Caltech10 500 2544

Caltech101 3030 5647

Caltech256 7680 22,102

Scene15 750 3735

MIT67 3350 12,270

SUN397 39,700 69,054

Table 2: Model Selection.

Truth Trunc. MM SGA+F SGA+M

10 50 13.3 11.7 24

101 200 126.3 118.7 139.7

256 500 464.7 314.2 392.7

15 50 17.7 18 19

67 100 81.8 74.6 84.3

397 1000 838 570.5 577

6.1 Baselines

We conducted a literature search of recent Bayesian

nonparametrics citing the datasets we use. We ﬁrst

discuss the baselines in Table 3 as follows: MMGM

(Chen et al., 2014), DDPM-L (Nguyen et al., 2017),

LDPO (Wang et al., 2017), DPmeans (Kulis and Jor-

dan, 2012), VB-DPM (Blei et al., 2006), MM-DPM

(Lim and Wang, 2018) and OnHGD(Fan et al., 2016).

We also implemented SVI (Hoffman et al., 2013) for

DPM.

6.2 Features

MMGM and DDPM-L are using the 128 dimensional

SIFT features. DPmeans, VB-DPM and MM-DPM

are using the 2048 dimensional sparse coding based

Fisher vector in (Liu et al., 2014). For LDPO, the au-

thors use the FC7 of Alexnet pretrained on Imagenet.

We did not cite the patch mining variant of LDPO as

it is mainly related to feature extraction rather than

BNP, hence it is not a direct comparison. For our im-

plementation of SVI, we use VGG16 pretrained on

ImageNet. For our proposed method, we use VGG16

pretrained on Place205 as the image feature extractor.

6.3 Truncation Level

The truncation level of MMGM and DDPM-L are not

given in (Nguyen et al., 2017). For LDPO, it is ﬁxed

to the ground truth (Wang et al., 2017). For VB-DPM,

MM-DPM and SVI, the truncation setting are identi-

cal to this work. For DPmeans, we use ground truth

to initialize its parameter for convenience as reported

in (Lim and Wang, 2018).

6.4 Comparisons on Caltech10

We ﬁnd that none of the baselines can outperform

the proposed method partly due to the discriminative

power that deep feature offers and the use of the pro-

posed stochastic optimization approach.

6.5 Comparisons on Scene15 & MIT67

In Table 6, LDPO-A-FC performs better than

SGA+Fisher on Accuracy for Scene15 but underper-

formed for NMI on MIT67. In fact, LDPO is only on

par with Kmeans for NMI on MIT67.

For DDPM-L and MMGM, there is a huge disad-

vantage on their results due to using handcrafted fea-

ture. However, from their extended results in (Nguyen

et al., 2017) we infer that the performance of DDPM-

L should be slightly better than DPM using MM when

the same deep feature is used.

In (Lim and Wang, 2018), MM-DPM is shown

to outperforms its VB-DPM counterpart on scene15.

Given that MM (of DPM) when assuming d = 0 is

almost similar to MM-DPM except without modeling

precision, the result of MM-DPM should be slightly

better than MM (of DPM) when using deep features.

6.6 Comparisons on Caltech101,

Caltech256 and SUN397

To the best of our knowledge, it is very rare to ﬁnd

any recent BNP works addressing datasets beyond 67

classes for image datasets. The main reason is that it

is difﬁcult to scale up BNP, which is one of the main

reason why we proposed the SGA learner over MM.

Although, the authors in (Fan et al., 2016) ap-

plied a BNP model to SUN397, they mainly use it for

learning a Bag-of-Words representation (Csurka et al.,

2004). It appears they then use a supervised learner

such as Bayes’s decision rule for classiﬁcation. For

SUN397, the Accuracy reported in (Fan et al., 2016)

for their online hierarchical Dirichlet process mix-

ture of generalized Dirichlet (onHGD) is 26.52% on

SUN397. It is somewhat comparable to our Accuracy

of 20.9% using SGA since we do not use hierarchi-

cal representation nor generalized Dirichlet mixture.

The authors of (Fan et al., 2016) also reported an Ac-

curacy of 67.34% for SUN16. Although this is not a

direct comparison to Scene15 as the classes in SUN16

are different, it provides some insight on our method.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

Table 3: Recent Bayesian nonparametrics vs best proposed result on the object and scene categorization dataset. Evaluation

using NMI and Accuracy (in diamond bracket).

Caltech10 Scene15 MIT67 SUN397

MMGM (Chen et al., 2014) - 0.186 - -

DDPM-L (Nguyen et al., 2017) - 0.218 - -

DPmeans (Kulis and Jordan, 2012) 0.418 0.316

- -

VB-DPM (Blei et al., 2006) 0.446 0.317 - -

- -

MM-DPM (Lim and Wang, 2018) 0.387 0.321 - -

<39.14> <33.59>

Kmeans (Wang et al., 2017) - 0.659 0.386 -

<65.0> <35.6>

LDPO-A-FC (Wang et al., 2017) - 0.705 0.389 -

<73.1> <37.9>

OnHGD (Fan et al., 2016) - - - -

<67.34> <26.52>

SVI 0.810 0.670 0.413 0.489

<78.98> <63.56> <30.76> <23.93>

SGA+Fisher 0.898 0.70 0.53 0.60

<93.1> <70.3> <37.8> <31.9>

Our only concern is whether their result is attainable

using SIFT. Once again, we should point out that in

(Fan et al., 2016), the authors use OnHGD for learn-

ing a bag-of-words representation while our method

mainly learns the cluster mean of each class in Table

7 CONCLUSION

Scalable algorithm of variational inference allows

Bayesian nonparametrics such as Dirichlet process

mixture to scale up to larger dataset at fractional

cost. In this paper, we target up to about 100K im-

ages and 400 object classes and high dimensional fea-

tures using VGG16 pretrained on ImageNet. How-

ever, the main problem is that most scalable Dirich-

let process mixture algorithms today still rely on the

closed form learning found in variational inference

from the past two decades. Stochastic gradient as-

cent is a modern approach to machine learning and

it is widely deployed in the training of deep neu-

ral networks. However, variational inference and

stochastic gradient ascent are mutually exclusive. In

this work, we propose using stochastic gradient as-

cent as a learner in variational inference. Unlike the

closed form learner in variational inference, stochas-

tic gradient ascent do not require closed form expres-

sion for learning the variational posterior expectata-

tions. However, stochastic gradient ascent alone is

not optimal for learning. It suffers from being a lo-

cal optimum approach and when applied to stochastic

dataset, it takes a long time to converge. Stochastic

optimization methods rely on decreasing step-size for

guaranteed convergence and better local search. Thus,

we explored using well known stochastic optimiza-

tion methods to improve the stochastic gradient ascent

learning of variational inference. Speciﬁcally, we ex-

plored Fisher information and the momentum method

to achieve a faster convergence. We compare our new

stochastic learner on the Dirichlet process Gaussian

mixture. We showed the performance gained in terms

of NMI, accuracy, model selection and computational

time on large scale datasets such as the MIT67, Cal-

tech101, Caltech256 and SUN397.

REFERENCES

Amari, S.-I. (1998). Natural gradient works efﬁciently in

learning. Neural computation, 10(2):251–276.

Bishop, C. M. (2006). Pattern recognition and machine

learning. springer.

Blei, D. M., Jordan, M. I., et al. (2006). Variational infer-

ence for dirichlet process mixtures. Bayesian analysis,

1(1):121–144.

Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent

Variational Inference of Dirichlet Process Mixture using Stochastic Gradient Ascent

dirichlet allocation. the Journal of machine Learning

research, 3:993–1022.

Cai, D., He, X., and Han, J. (2005). Document clustering

using locality preserving indexing. IEEE Transactions

on Knowledge and Data Engineering, 17(12):1624–

1637.

Chen, C., Zhu, J., and Zhang, X. (2014). Robust bayesian

max-margin clustering. In Advances in Neural Infor-

mation Processing Systems, pages 532–540.

Csurka, G., Dance, C., Fan, L., Willamowski, J., and Bray,

C. (2004). Visual categorization with bags of key-

points. In Workshop on statistical learning in com-

puter vision, ECCV, volume 1, pages 1–2. Prague.

Fan, W., Bouguila, N., Du, J.-X., and Liu, X. (2018). Ax-

ially symmetric data clustering through dirichlet pro-

cess mixture models of watson distributions. IEEE

transactions on neural networks and learning systems,

30(6):1683–1694.

Fan, W., Sallay, H., and Bouguila, N. (2016). Online

learning of hierarchical pitman–yor process mixture

of generalized dirichlet distributions with feature se-

lection. IEEE transactions on neural networks and

learning systems, 28(9):2048–2061.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In

Advances in neural information processing systems,

pages 2672–2680.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition, pages 770–778.

Hoffman, M. D., Blei, D. M., Wang, C., and Paisley, J. W.

(2013). Stochastic variational inference. Journal of

Machine Learning Research, 14(1):1303–1347.

Honkela, A., Raiko, T., Kuusela, M., Tornio, M., and

Karhunen, J. (2010). Approximate riemannian con-

jugate gradient learning for ﬁxed-form variational

bayes. Journal of Machine Learning Research,

11(Nov):3235–3268.

Honkela, A., Tornio, M., Raiko, T., and Karhunen, J.

(2007). Natural conjugate gradient in variational in-

ference. In International Conference on Neural Infor-

mation Processing, pages 305–314. Springer.

Kingma, D. P. and Welling, M. (2014). Stochastic gradi-

ent vb and the variational auto-encoder. In Second In-

ternational Conference on Learning Representations,

ICLR.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Advances in neural information process-

ing systems, pages 1097–1105.

Kulis, B. and Jordan, M. I. (2012). Revisiting k-means:

New algorithms via bayesian nonparametrics. In Pro-

ceedings of the 29th International Conference on Ma-

chine Learning (ICML-12), pages 513–520.

Kurihara, K. and Welling, M. (2009). Bayesian k-means as

a maximization-expectation algorithm. Neural com-

putation, 21(4):1145–1172.

Lim, K.-L. and Wang, H. (2018). Fast approximation of

variational bayes dirichlet process mixture using the

maximization–maximization algorithm. International

Journal of Approximate Reasoning, 93:153–177.

Liu, L., Shen, C., Wang, L., van den Hengel, A., and Wang,

C. (2014). Encoding high dimensional local features

by sparse coding based ﬁsher vectors. In Advances in

Neural Information Processing Systems, pages 1143–

1151.

Mandt, S., Hoffman, M. D., and Blei, D. M. (2017).

Stochastic gradient descent as approximate bayesian

inference. The Journal of Machine Learning Re-

search, 18(1):4873–4907.

Neal, R. M. and Hinton, G. E. (1998). A view of the em

algorithm that justiﬁes incremental, sparse, and other

variants. In Learning in graphical models, pages 355–

368. Springer.

Nguyen, V., Phung, D., Le, T., and Bui, H. (2017). Dis-

criminative bayesian nonparametric clustering. In IJ-

CAI 2017: Proceedings of the 26th International Joint

Conference on Artiﬁcial Intelligence, pages 2550–

2556. AAAI Press.

Paisley, J., Blei, D. M., and Jordan, M. I. (2012). Variational

bayesian inference with stochastic search. In Proceed-

ings of the 29th International Coference on Interna-

tional Conference on Machine Learning, pages 1363–

1370. Omnipress.

Paisley, J., Wang, C., Blei, D. M., and Jordan, M. I. (2015).

Nested hierarchical dirichlet processes. IEEE trans-

actions on pattern analysis and machine intelligence,

37(2):256–270.

Ranganath, R., Gerrish, S., and Blei, D. (2014). Black box

variational inference. In Artiﬁcial Intelligence and

Statistics, pages 814–822.

Rezende, D. J. and Mohamed, S. (2015). Variational in-

ference with normalizing ﬂows. In Proceedings of

the 32nd International Conference on International

Conference on Machine Learning-Volume 37, pages

1530–1538. JMLR. org.

Robbins, H. and Monro, S. (1985). A stochastic approxi-

mation method. In Herbert Robbins Selected Papers,

pages 102–109. Springer.

Sethuraman, J. (1994). A constructive deﬁnition of dirichlet

priors. Statistica sinica, pages 639–650.

Titterington, D. M. (2011). The em algorithm, variational

approximations and expectation propagation for mix-

tures. Mixtures: Estimation and Applications, 896.

Wang, X., Lu, L., Shin, H.-C., Kim, L., Bagheri, M.,

Nogues, I., Yao, J., and Summers, R. M. (2017). Un-

supervised joint mining of deep features and image

labels for large-scale radiology image categorization

and scene recognition. In Applications of Computer

Vision (WACV), 2017 IEEE Winter Conference on,

pages 998–1007. IEEE.

Welling, M. and Teh, Y. W. (2011). Bayesian learning via

stochastic gradient langevin dynamics. In Proceed-

ings of the 28th International Conference on Machine

Learning (ICML-11), pages 681–688.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods