Efficiency of Meme Usage in Evolutionary Algorithm

Jaroslav Janacek and Marek Kvet

Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia

Keywords: Location, Emergency Medical Service System, Approximate Approach, Evolutionary Algorithm, Meme.

Abstract: Emergency medical service system design attracts attention of a broad researcher and practitioner community

due to increasing public demand for more safe life. A basic model of the design problem is known as the

weighted p-median problem. Large instances of the problem as are hard to solve in general and very often it

is necessary to obtain a series of solutions to be able to offer a spectrum of various solutions. For this purpose,

an evolutionary metaheuristic seems to be a suitable tool, as it processes simultaneously a family of solutions.

A standard evolutionary algorithm is based on developing a population using some nature inspired operations

with solutions-members of the population, which produce candidates for population updating. This

evolutionary process is characterized by fast improvement of the best-found-solution at the beginning and

very slow improvement at the end, when the best-found-solution is near to the optimal one. To improve the

first phase of the evolutionary process, numerous authors recommend to plug increasing procedures called

memes in the process. Within this paper, we will study an impact of the meme plugin on acceleration of the

evolutionary process, when big instances of the weighted p-media problem are solved. The study will be

performed on instances of an emergency service system design problem solved by genetic algorithm with

elite set and the studied meme will be based on exchange neighborhood searching.

1 INTRODUCTION

The emergency service system design problem

represents a hard solvable combinatorial problem,

where p service center locations should be selected

from a finite set of possible center locations so that

disutility perceived by system users be minimal

(Brotcorne et al., 2003, Doerner et al., 2005,

Jánošíková and Žarnay, 2014, Jánošíková et al., 2019,

Marianov and Serra, 2002, Reuter-Oppermann et al.,

2017). Disutility is often computed as a sum of

weighted time-distances from individual users’

locations to the nearest service center, where the

weights correspond to frequency of emergency events

at the individual users’ locations. The emergency

service system design problem can be presented and

solved as a weighted p-median problem by an exact

optimization algorithm (Avella el al, 2007, Current et

al., 2002, Elloumi et al., 2004, García et al., 2011,

Guerriero et al. 2016, Janáček, 2008, Sayah and

Irnich, 2016). The exact approaches were mostly

based on so called radial formulation of the p-median

problem and this formulation also enables

construction of a fast approximate approach (Janáček

and Kvet, 2016).

In spite of existence of the exact and approximate

fast approaches, there are many situations, which are

not covered by enough efficient solving tools. It

concerns very large instances of the p-median

problem or necessity of producing a series of good

different solutions. Such a demand can be satisfied

my metaheuristic approaches (Gendreau, and Potvin,

2010).

As the problem can be studied as searching across

a set of unit hypercube vertices, genetic algorithm

represents a suitable tool for obtaining good solution

in predetermined computational time (Daskin,. 2015,

Reeves, 2010, Sastry and Goldberg, 2005, Rybičková

et al., 2016 ). Nevertheless, the progress of the best-

found-solution objective function value along

computational time resembles convex decreasing

function, which converges slowly to the optimal

value. To accelerate convergence of an evolutionary

algorithm in general, many authors recommend

plugging an improving heuristic called meme in the

evolutionary process (Resende, 2004, Moscato and

Cotta, 2010, Gupta and Ong, 2019,). We concentrate

our effort on memes based on neighborhood

searching, where the neighborhood of a current

solution is represented by all p-median solutions,

Janacek, J. and Kvet, M.

Efﬁciency of Meme Usage in Evolutionary Algorithm.

DOI: 10.5220/0008946301650171

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 165-171

ISBN: 978-989-758-396-4; ISSN: 2184-4372

165

which can be obtained from the current solution by

replacing a current center location with an

unoccupied one. The increasing neighborhood

searching process can be restricted by several means,

e.g. by limited number of objective function

evaluations. Within the paper, we deal with meme

efficiency in the above mentioned evolutionary

process. We want to answer the question, under

which conditions can meme usage improve the

process convergence and when the meme complexity

represents such a computational burden that the

process becomes inefficient.

The paper is organized in the following way. The

next section concisely describes a genetic algorithm

including a special implementation of its basic

operations of crossover and mutation. The third

section gives an insight in an efficient increasing

meme construction used for hybridization of the

genetic algorithm. The fourth section introduces a

way of measuring of convergence speed and

comments on possible meme application in the

genetic algorithm. The fifth section contains results

of the numerical experiments aimed at solving the

meme efficiency problem. The last section

summarizes the obtained findings.

2 GENETIC ALGORITHM FOR

P-MEDIAN PROBLEM

A genetic algorithm (GA) imitates a naturel process

of species development in general. The algorithm

processes a current population of individuals, where

each individual corresponds to a solution of the

solved problem. So called fitness of an individual

usually reflects objective function value of the

associated solution. The algorithm starts with creation

of an initial population of different individuals-

solutions and computing their fitness values. Then,

the evolutionary process is simulated by creating

candidates for a new population, by forming the new

population and by a way of population exchange. This

process is repeated until a termination rule is met, e.g.

until used computational time reaches a given limit.

Pool of the candidates is created using two operations

performed on individuals selected from the current

population, where the selection is performed

randomly and probability of an individual choice

depends on its fitness. The first of the operations is

called crossover and it combines a pair of individuals

and creates two new individuals. The new individuals

are subjected to the second operation – mutation and

then, they are inserted into the pool of candidates.

After the pool has been completed, the new

population is formed by selection of some individuals

from the pool and by including some elite individuals

of the current population. Creating of the new

population is completed by fitness evaluation of each

individual and by updating the best-found-solution.

As can be seen, no special improving algorithm is

included into the basic evolutionary process. Quality

of the resulting solution is achieved only by the two

selections (parent’s selection for crossover and the

selection of individuals for new population from the

pool) and by keeping the best-found-solution or so

called elite sub-set of the current population.

Efficiency of GA algorithm implementation is

determined by a design of the two mentioned

operations, which usually exploit characteristics of

the solved problem to speed up the algorithm

performance. In the studied case, the emergency

system design problem is solved.

The emergency system design consists of choice

of p service center locations from the set I consisting

of m possible service center locations so that the min-

sum objective function reflecting system users’

disutility is minimal. It is assumed that the system

users are concentrated at a finite set J of users’

locations, where b

denotes a volume of weight of user



J, e.g. b

may correspond to an average number of

emergency calls from the user’s location j. If symbol

denotes the integer time-distance between

locations i



I and j



J, and if the service center

deployment is described by zero-one m-dimensional

vector y of variables y

denoting the center location by

unit value, we can describe the problem by the

formula (1).

min{ min{ : , 1}

:{0,1}, }

jij i

bdiIy







(1)

As concerns the emergency system design, it is

assumed that a user demand is satisfied from the

nearest service center. From the mathematical point

of view, the set of some vertices of m-dimensional

hypercube is searched through, to obtain optimal

solution.

The studied genetic algorithm is not able to find

the optimal solution in general, but it tries to produce

as good as possible solution using the specific

crossover and mutation operations. Both the

operations are designed so that the resulting offspring

are feasible solutions, i.e. they contains exactly p

located centers.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

166

The suggested operation of crossover is

performed with two individuals-parents x and y,

where each parent is represented by a vector

consisting of m zero-one components. Each

component corresponds to one possible service center

location and unit value of component i indicates that

the associated solution-individual locates a service

center at the possible service location. Thus, each

vector contains exactly p units and m-p zeros at the m

positions. Comparing the associated components of

vectors x and y, it can be found that the components

can be categorized into three classes. The first class

consists of components, at which positions the both

vectors have the zero values. The second class

consists of u components with units in the both

vectors and the third class contains b components, at

which one vector has unit value and the other has zero

value. As totally 2p units are contained in the both

vectors and 2u units are placed at components from

the second class, then b=2p-2u units occupy positions

of the third class, i.e. b is even number.

The suggested crossover operation lets offspring’s

components of the first and second class unchanged

and distributes the b units randomly among the

offspring’s components of the third class so that each

offspring gets exactly b/2 units.

This way, each offspring represents a feasible

solution of the p-median problem.

The mutation used in this genetic algorithm is

based on the exchange operation, which randomly

chooses a position occupied by a center and moves it

at some unoccupied position, which is also chosen

randomly.

As concerns the parent selection for crossover, a

tournament approach is used in the studied case of

GA. Elite set for the new generation completion is

defined as the set of BSize different individuals with

the best fitness values withdrawn from the current

population.

Diversity of the new population is assured by

exclusion of individuals, fitness of which is equal to

a fitness value of already accepted individual of the

new population.

3 MEME FOR P-MEDIAN

PROBLEM

Generally, noun “meme” denotes an arbitrary

heuristic, which can improve some input solution of

the solved problem (Gupta and Ong, 2019). Within

this paper, we will concentrate on a special case of

memes designed as an intensification tool for

metaheuristics, which solve p-median problem. The

studied meme is increasing heuristic based on

neighborhood searching applied to a current p-

median solution, where the neighborhood of the

current solution consists of all p-median solutions,

which differ from the current one in exactly one

located service center. If the meme is run, the

neighborhood of the current solution is searched

through by inspecting results of the individual

exchanges occupied center locations for unoccupied

ones. The searching process proceeds until either a

limited number t of inspections is reached or an

admissible exchange is found. In the second case, a

current solution is updated by the better one and

neighborhood searching is repeated until either t

inspections have been performed or the current

neighborhood has been inspected unless an

admissible solution has been found.

The meme can be described by following five

steps, where I denotes the set of all possible center

locations, P denotes the set of p chosen center

locations, which determine the current solution. F(P)

represents value of the objective function value

connected with the solution P. Definition of the

function value F(P) is described in the formula (1).

Meme(P,t)

0. Initialize F

=F(P), P

=P, C=I-P,

done=false, s=0, mark all elements of P and

C as uninspected, and go to step 1.

1. If there is any uninspected element of P and

done=false and s<t hold, choose an

uninspected element i from P and perform

step 2, otherwise go to step 4.

2. If there is any uninspected element of C and

done=false and s<t hold, choose an

uninspected element j from C and perform

step 3, otherwise mark element i as

inspected and all elements of C as

uninspected and go to step 1.

3. Set s=s+1, P = (P-{i}){j} and compute

F(P), mark j as inspected. If F(P)<F

, then

set F

=F(P) and P

=P and done=true. Go to

step 2.

4. If s≥t or done=false, then terminate, the

resulting solution is P

and its objective

function is F

, else if done=false, then set

P=P

, C=I-P, done=false, mark all elements

of P and C as uninspected and go to step 1.

Efficiency of the above presented standard

exchange algorithm obviously depends on a way of

objective function value computing. If the objective

function value of a solution P is computed in a

Efﬁciency of Meme Usage in Evolutionary Algorithm

167

standard way according to formula presented in

model (1), then complexity of the computational

process is O(J.P ), where J .denotes cardinality of

the set J of users and the cardinality P  equals to the

number p of located centers.

In our implementation of the process, we make

use of the fact that most of the inspected solutions P

differ from the current solution P only in one service

center. It enabled us to compute the objective function

value F(P) with complexity O(2J  ). This effect was

achieved by determining and saving the first and

second minimal values of the set {d

: i



P} for each

jJ. These data are used for fast computation of

objective function value of any solution P, which

differs from P in only one element.

This meme can be used in the genetic algorithm

for p-median problem solving, to improve some

portion of individuals from the pool of candidates or

elite set before creating new population.

4 MEME APPLICATION AND

CONVERGENCE OF

EVOLUTIONARY PROCESS

To be able to study impact of meme usage on an

evolutionary process, some way of convergence

evaluation must be defined. We want to study

characteristics of the evolutionary process limited by

given computational time. As the tested heuristic

need not reach the exact optimum, but it generally

produces near-to-optimal solutions in the given time,

there is no use to define quality of process

convergence only by the objective function value of

the resulting solution. That is why, we suggest the

following measure based on progress of the best-

found-solution objective function value in the

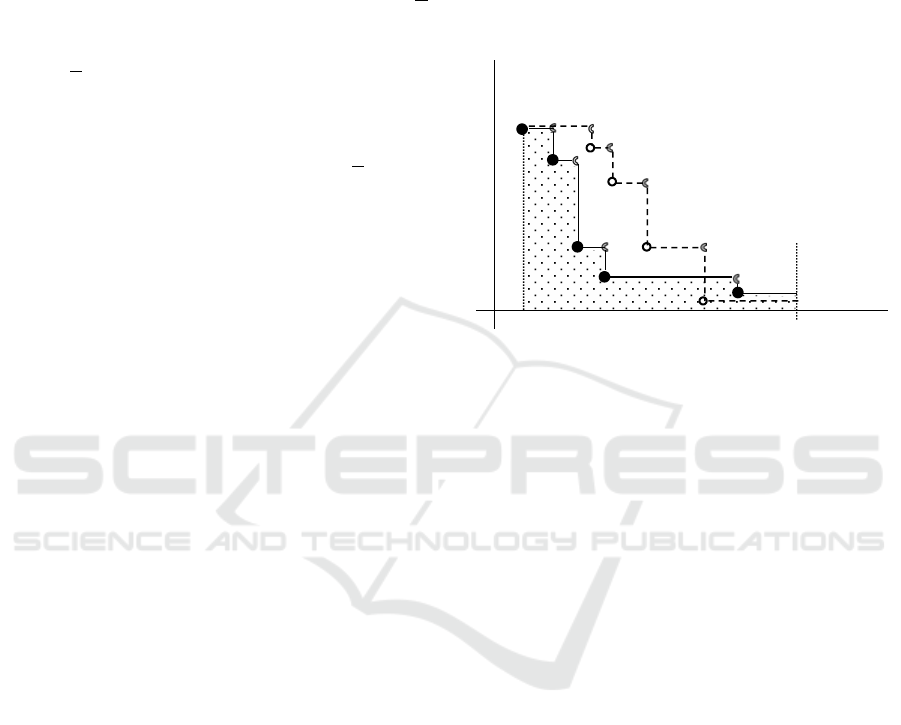
running time. Intuitively, we consider that the process

depicted in Figure 1 by bold lines is better than the

process depicted by the dash lines.

Applied measure of the convergence quality is

defined here as the area below the graph determined

by the progress.

In the remainder of the paper, we will study

influence of meme usage on convergence of the

evolutionary process. Due to big computational time

demand of the suggested meme, we restricted our

study only on the case, when a meme is applied at

most once in population exchange and, in addition, it

will be applied to the best solution of the current

population. Under these assumptions, we will study

following schemes of meme applications.

a) A meme is applied to the best solution of the

current population before the new population

is created.

b) A meme is applied with given constant

probability to the best solution of the current

population.

c) A meme is applied with probability, which

decreases with the number of performed

population exchanges.

Figure 1: Possible progresses of the objective function

values of the best found solutions depending on the running

time of the GA. Dotted area below the full line curve

represents possible evaluation of the associated process

convergence.

5 NUMERICAL EXPERIMENTS

To perform the planned study, the genetic algorithm

including the above described meme was

programmed in programming language JAVA in

NetBeansIDE 7.3 and the associated experiments

were run on a PC equipped with the Intel® Core™ i7

5500U processor with the parameters: 2.4 GHz and

16 GB RAM. The used benchmarks were obtained

from the road network of Slovak self-governing

regions. The mentioned instances are further denoted

by the names of capitals of the individual regions

followed by triples (XX, m, p), where XX is

commonly used abbreviation of the region

denotation, m stands for the number of possible centre

locations (cardinality of the set I) and p is the number

of service centres, which are to be located in the

mentioned region. The list of instances follows:

Bratislava (BA, 87, 14), Banská Bystrica (BB, 515,

36), Košice (KE, 460, 32), Nitra (NR, 350, 27),

Prešov (PO, 664, 32), Trenčín (TN, 276, 21), Trnava

(TT, 249, 18) and Žilina (ZA, 315, 29).

All cities and villages with corresponding number

of inhabitants were taken into account. The

coefficients b

were rounded to hundreds. The set of

Running time

Objective of the best found solution

Time limit

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

168

communities represents both the set J of users’

locations and the set I of possible center locations as

well.

To verify the results obtained for the regular self-

governing regions, we constructed bigger

benchmarks by union of the original regions. Thus,

we obtained the additional instances (ESR, 1124,

112), (WSR, 1792, 180) and (HSR, 2916, 273).

Parameters of the studied genetic algorithm were

set up at the following most fitting values according

to preliminary experiments. The size of the

population (PopSize) was determined to correspond

with cardinality of so called near-to-maximal

uniformly deployed set of p-median problem for

given m and p (Janáček and Kvet, 2019, Kvet and

Janáček, 2019). The size of elite set (BSize) was equal

to (1/3)PopSize and the size of pool of candidates was

(3/2)PopSize. The probability of mutation was set up

at the value of 0.3. The computational time of one

original benchmark solution was 5 seconds. The

maximal solving time of the additional benchmarks

was set up to 20 seconds.

Each run of the genetic algorithm was repeated 50

times with the same benchmark and average results

are reported in the following tables.

Table 1 gives an overview of the benchmarks,

their exact optimal solutions (optSol) and results of

the standard version of the above described genetic

algorithm without any meme application.

The table refers about size of population

(PopSize), average resulting objective function value

(bestFit), number of population exchanges during run

of the algorithm (noPop). The column labeled by

“RedArea” contains evaluation of the algorithm

convergence described in the previous section. In the

tables is given so called reduced area, which differs

from the full area by subtracting the product of bestFit

and associated time of the run.

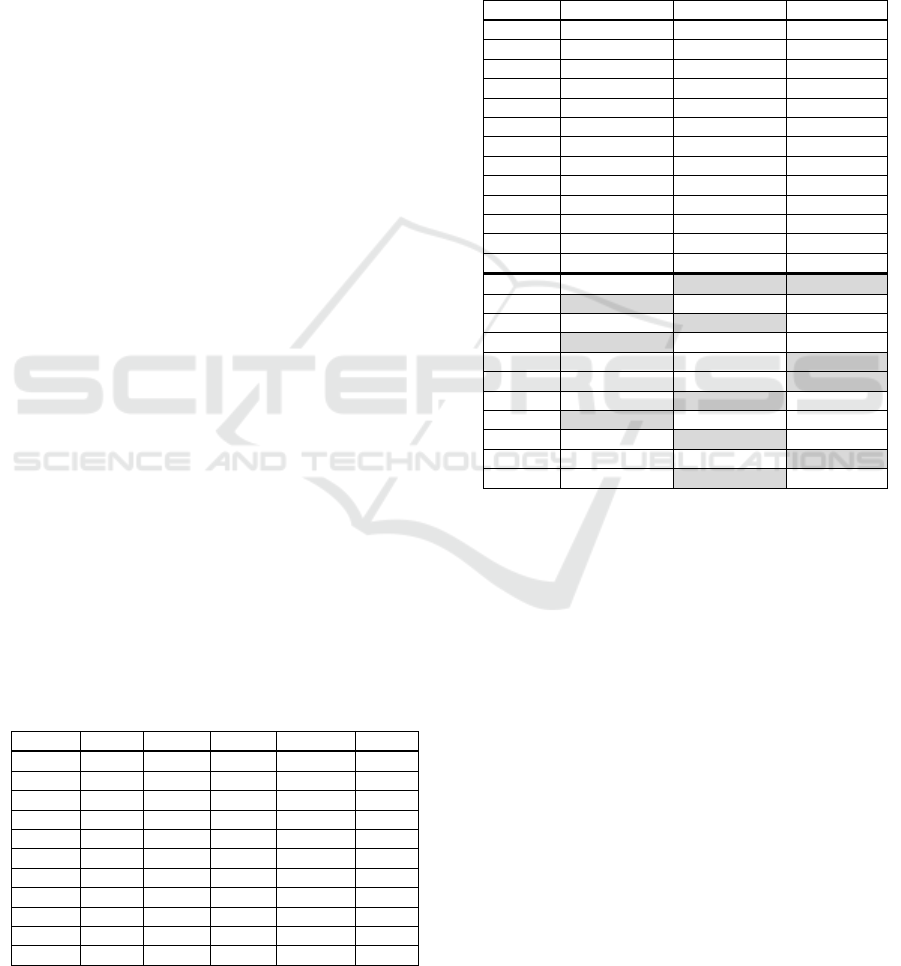
Table 1: Characteristics of benchmarks and results of

standard version of the genetic algorithm without meme

application.

Region optSol PopSize bestFit RedArea noPop

BA 19325 23 19325 9 98368

BB 29873 172 30083 5233 625

KE 31200 60 31290 3172 2428

NR 34041 83 34051 1393 2891

PO 39073 232 39352 6809 464

TN 25099 137 25099 403 2939

TT 28206 212 28206 470 2384

ZA 28967 112 28971 1329 1951

ESR 40713 200 42696 82574 355

WSR 108993 200 124605 906515 111

HSR 161448 200 296142 296142 19

An individual experiment using the scheme a) and

b) were organized so that the meme described in

Section 3 for t= p*64 was applied to the best solution

of the current population with the probability 1/(2

)

for parameter values T= 0, 1, …,5. It must be noted

that experiments for T= 0 correspond to the case a),

where the meme is applied once to the best solution

in each population.

Table 2: Reduced area of the experiments a) and b).

Reg\T 0 1 2

BA 14 9 8

BB 5487 5092 4610

KE 3288 2911 2672

NR 1735 1466 1334

PO 7733 7116 6781

TN 509 455 415

TT 511 482 479

ZA 1562 1432 1328

ESR 104056 95287 89018

WSR 1022991 959206 908363

HSR 1496960 1475589 1457807

Reg\T 3 4 5

BA 7 6 6

BB 4604 4838 4790

KE 2657 2519 2668

NR 1113 1165 1238

PO 6647 6384 6365

TN 405 406 401

TT 454 436 449

ZA 1214 1240 1295

ESR 86416 83311 86312

WSR 905763 895335 877440

HSR 1452485 1444251 1455430

Comparing the column for T=0 of the Table 2 to

the column RedArea of the Table 1, it can be found

that meme application has worsen convergence of the

algorithm. This effect can be explained by big

computational demand of the used meme, which has

lowered the number of population exchanges

(compare the column for T=0 of the Table 3 to the

column noPop of the Table 1) and thus it decreases

efficiency of the evolutionary operations. Our

experiments showed that lower probability of the

meme application (for T=3, 4, 5) can considerably

improve the convergence of hybridized GA

algorithm.

Efﬁciency of Meme Usage in Evolutionary Algorithm

169

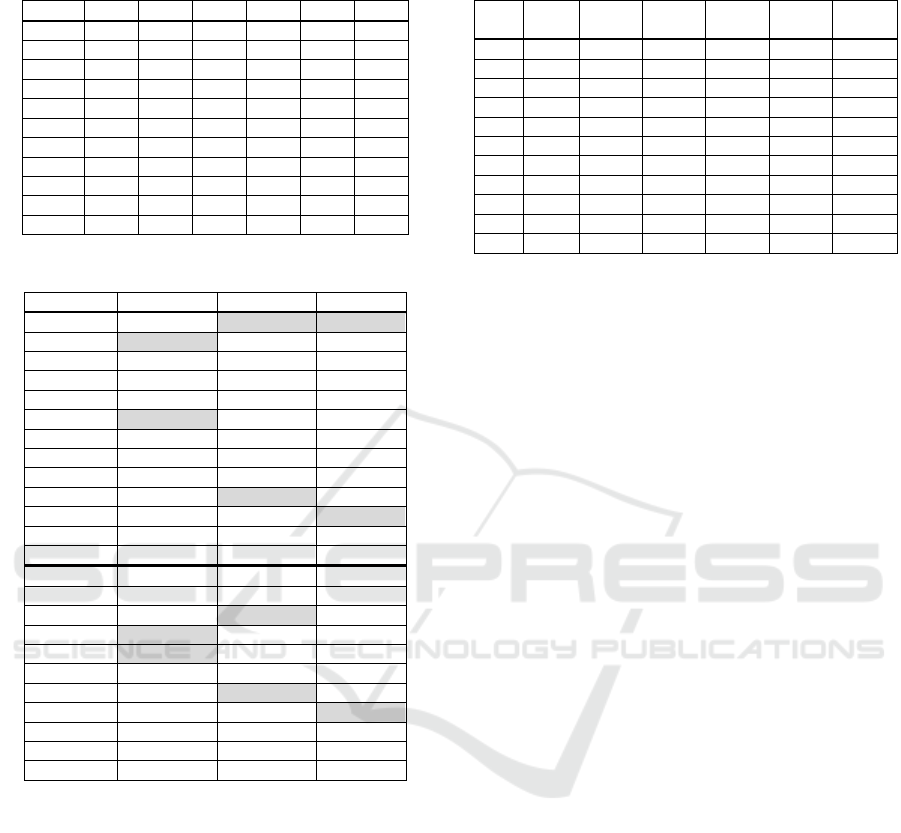
Table 3: Number of population exchanges of the

experiments a) and b).

Reg\T 0 1 2 3 4 5

BA 18636 31502 47893 64861 78899 88472

BB 402 487 538 566 586 597

KE 945 1376 1750 2051 2223 2319

NR 1341 1868 2331 2636 2832 2957

PO 321 380 418 442 451 452

TN 1667 2137 2488 2699 2832 2900

TT 1593 1932 2140 2265 2322 2377

ZA 1052 1350 1558 1694 1779 1829

ESR 245 290 318 335 345 348

WSR 79 93 102 107 109 111

HSR 17 18 19 20 20 20

Table 4: Reduced area of the experiments c).

Reg\T 0 1 2

BA 10 9 9

BB 4854 4986 4867

KE 3185 3144 3351

NR 1185 1261 1444

PO 6995 6801 6991

TN 418 438 421

TT 491 512 499

ZA 1427 1346 1389

ESR 78515 79120 79679

WSR 849673 843178 845608

HSR 1441520 1488013 1433971

Reg\T 3 4 5

BA 10 10 10

BB 4873 5162 5219

KE 3004 2713 2746

NR 1152 1241 1241

PO 6651 6798 7098

TN 448 448 461

TT 485 477 479

ZA 1370 1331 1328

ESR 82681 84750 89350

WSR 863891 884460 903266

HSR 1503572 1464120 1511966

The experiments for scheme c) were performed

for the situation, when the probability Pr of meme

application was dynamically lowered with the

increasing number noP of performed population

exchanges according to (2), where T is so called

shaping parameter of the probability progress.

(1 ) / 2

noP





(2)

In this case, the convergence of GA has been also

improved in comparison to the standard GA

algorithm, but the improvement was not as big as in

case of the scheme b). Contrary to scheme b), it must

be noted that bigger value of the parameter T in

scheme c) according to (2) means slower decrease of

probability depending on noP.

Table 5: Number of population exchanges of the

experiments c).

Reg\

0 1 2 3 4 5

BA 99985 100213 100248 100342 100380 100255

BB 603 615 617 609 604 599

KE 2399 2436 2420 2450 2429 2388

NR 3081 3119 3128 3113 3083 3080

PO 452 458 461 460 458 446

TN 2932 2952 2968 2958 2938 2938

TT 2303 2318 2335 2323 2319 2300

ZA 1823 1826 1815 1810 1802 1802

ESR 363 363 363 362 356 350

WSR 118 119 118 117 113 106

HSR 20 20 19 19 18 18

6 CONCLUSIONS

The paper reports on research conducted to increase

the efficiency of the genetic algorithm in cases where

real-time emergency service system instances need to

be resolved and, in addition, a whole set of good

alternative solutions is required. To estimate

contribution of genetic algorithm hybridization, we

studied an impact of the meme plugin on acceleration

of the evolutionary process applied to the emergency

system design.

The performed experiments showed that usage of

meme in the evolutionary process need not inevitably

contribute to acceleration of the process. Two

schemes of random meme application were suggested

and their influence on evolutionary process

convergence was studied. It was found that suitable

setting of application probability may lead to

considerable improvement of the evolutionary

process.

Future research may be aimed at a deeper research

of the meme application and parameter tuning

including learning process and other tools of artificial

intelligence.

ACKNOWLEDGEMENTS

This work was supported by the research grants

VEGA 1/0342/18 “Optimal dimensioning of service

systems”, VEGA1/0089/19 “Data analysis methods

and decisions support tools for service systems

supporting electric vehicles”, and VEGA 1/0689/19

“Optimal design and economically efficient charging

infrastructure deployment for electric buses in public

transportation of smart cities” and APVV-15-0179

“Reliability of emergency systems on infrastructure

with uncertain functionality of critical elements”.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

170

REFERENCES

Avella, P., Sassano, A. and Vasil'ev, I. 2007. Computational

study of large scale p-median problems. Mathematical

Programming, 109: pp. 89-114.

Brotcorne, L., Laporte, G., Semet, F. 2003. Ambulance

location and relocation models. European Journal of

Operational Research 147, pp. 451–463

Current, J., Daskin, M., Schilling, D. 2002. Discrete

network location models. In Drezner Z. (ed) et al.

Facility location. Applications and theory, Berlin,

Springer, pp 81-118

Daskin, M., S. 2015. The p-Median Problem. Location

Science, edited by G. Laporte, S. Nickel and F.

Saldanha da Gama, Springer, pp. 21-45

Doerner, K. F., et al. 2005. Heuristic Solution of an

Extended Double-Coverage Ambulance Location

Problem for Austria. Central European Journal of

operations research, Vol. 13, No 4, pp. 325-340

Elloumi, S., Labbé, M., Pochet, Y. 2004. A new formulation

and resolution method for the p-center problem.

INFORMS Journal on Computing 16, pp. 84-94

García, S., Labbé, M., Marín, A. 2011. Solving large p-

median problems with a radius formulation. INFORMS

Journal on Computing, Vol. 23, No 4, pp. 546-556

Gendreau, M., Potvin, J. 2010. Handbook of Metaheuristics,

Springer Science & Business Media, 648 p.

Guerriero, F., Miglionico, G., Olivito, F. 2016. Location

and reorganization problems: The Calabrian health care

system case. European Journal of Operational

Research 250, pp. 939-954

Gupta, A., Ong, Y. 2019. Memetic Computation: The

Mainspring of Knowledge Transfer in a Data-Driven

Optimization Era, Springer, 2019, 104 p.

Janáček, J. 2008. Approximate Covering Models of

Location Problems. In Lecture Notes in Management

Science: Proceedings of the 1st International

Conference ICAOR, Yerevan, Armenia, pp. 53-61

Janáček, J., Kvet, M. 2016. Sequential approximate

approach to the p-median problem. Computers &

industrial engineering, Vol. 94, pp. 83-92.

Janáček, J., Kvet, M. 2019. Usage of uniformly deployed

set for p-location min-sum problem with generalized

disutility. In SOR 2019: International symposium on

Operational Research, Bled, Slovenia, pp. 494-499

Jánošíková, Ľ., Žarnay, M. 2014. Location of emergency

stations as the capacitated p-median problem. In

International scientific conference: Quantitative

Methods in Economics-Multiple Criteria Decision

Making XVII, Virt, Slovakia

Jánošíková, Ľ. et al. 2019. An optimization and simulation

approach to emergency stations relocation. Central

European Journal of Operations Research, Vol. 27.

No. 3, pp. 737-758

Kvet, M., Janáček, J. 2019. Population diversity

maintenance using uniformly deployed set of p

-location

problem solutions. In SOR 2019: International

symposium on Operational Research, Bled, Slovenia,

pp. 354-359

Marianov, V., Serra, D. 2002. Location problems in the

public sector. In Drezner, Z. (Ed.). Facility location -

Applications and theory, Berlin: Springer, pp. 119-150

Reeves, C., R. 2010. Genetic Algorithms. Handbook of

Metaheuristics, edited by M. Gendreau and Jean-Yves

Potvin, Second Edition, Springer, pp. 109-139

Resende, M., G., C. 2004. A Hybrid Heuristic for the p-

Median Problem. Journal of Heuristics, 10, Kluwer

Academic Publishers, pp. 59-88

Moscato, P., Cotta, C. A 2010. Modern Introduction to

Memetic Algorithms. Handbook of Metaheuristics,

edited by M. Gendreau and Jean-Yves Potvin, Second

Edition, Springer, pp. 141-183

Reuter-Oppermann, M., van den Berg, P. L., Vile, J. L.

2017. Logistics for Emergency Medical Service

systems. Health Systems, Vol. 6, No 3, pp 187-208

Rybičková, A., Burketová, A., Mocková, D. 2016. Solution

to the lacating – routing problem using a genetic

algorithm. In SmaRTT Cities Symposiuum Prague,

Prague, pp. 1 - 6

Sastry, K., Goldberg, D. 2005. Genetic Algorithms. Search

Methodologies: Introductory Tutorials in Optimization

and Decision Support Techniques, edited by E. K.

Burke, G. Kendall, Springer, pp. 97-125

Sayah, D., Irnich, S. 2016. A new compact formulation for

the discrete p-dispersion problem. European Journal of

Operational Research, Vol. 256, No 1, pp. 62-67

Efﬁciency of Meme Usage in Evolutionary Algorithm

171