
Mitigate Catastrophic Forgetting by Varying Goals
Lu Chen
1
and Murata Masayuki
2
1
Kyoto Institute of Technology, Kyoto, Japan
2
Osaka University, Osaka, Japan
Keywords:
Modular Network, Catastrophic Forgetting, Neural Network.
Abstract:
Catastrophic forgetting occurs because neural network learning algorithms change connections to learn a new
skill which encodes previously acquired skills. Recent research suggests that encouraging modularity in neural
networks may overcome catastrophic forgetting because it should reduce learning interference. However,
manually constructing modular topology is hard in practice since it involves expert design and trial and error.
Therefore, an automatic approach is needed. Kashtan et al. find that evolution under an environment that
changes in a modular fashion can lead to the spontaneous evolution of modular network structure. However,
goals in their research are made of a different combination of subgoals, while real-world data is rarely perfectly
separable. Therefore, in this paper, we explore the application of such approach to mitigate catastrophic
forgetting in a slightly practical situation, that is applying it to classification of small sized real images and
applying it to the increment of goals. We find that varying goals can improve catastrophic forgetting in a
CIFAR-10 based classification problem. We find that when learning a large set of goals, a relatively small
switching interval is required to have the advantage of mitigating catastrophic forgetting. On the other hand,
when learning a small set of goals, an appropriate large switching interval is preferred since this less worsens
the advantage and also can improve accuracy.
1 INTRODUCTION
Learning a variety of different skills for different
problems is a long-standing goal in artificial intel-
ligence (Ellefsen et al., 2015). However, in neural
networks, when it learns a new skill, it typically los-
ing previously acquired skills (Ellefsen et al., 2015).
This problem called catastrophic forgetting, and it oc-
curs because learning algorithms change connections
to learn a new skill which encode previously acquired
skills (Ellefsen et al., 2015).
Catastrophic forgetting has been studied for a few
decades (French, 1999). Recently, in computational
biology field, a modular approach for neural net-
works is considered to be needed as learning problems
grow in scale and complexity (Amer and Maul, 2019).
(Ellefsen et al., 2015) studied whether catastrophic
forgetting can be reduced by evolving topological
modular neural networks. They said that modularity
intuitivelyshould reduce learning interference by sep-
arating functionality into physically distinct modules.
Their results suggest that encouraging modularity in
neural networks may overcome catastrophic forget-
ting. However, in their approach, the input data is
needed to be partitioned in advance so that different
modules can be assigned. Since manual data modu-
larization is usually based on some heuristic, expert
knowledge or analytical solution, a good partitioning
requires a good prior understanding of the problem
and its constraints, which is rarely the case for neural
network learning tasks (Amer and Maul, 2019).
Although there are several manual techniques for
constructing modular topology, manual formation is
hard in practice since manual techniques involve ex-
pert design and trial and error(Amer and Maul, 2019).
Therefore, an automatic approach is needed. In the
field of computational biology, (Kashtan and Alon,
2005) find that evolution under an environment that
changes in a modular fashion leads to the sponta-
neous evolution of modular network structure. That
is, they repeatedly switch between several goals, each
made of a different combination of subgoals, which
they call MVG (modularly varying goals). Although
modular structures are usually less optimal than non-
modular ones (Kashtan and Alon, 2005; Alon, 2003),
they find that modular networks that evolve under
such varying goals can remember their history (Parter
et al., 2008).
530
Chen, L. and Masayuki, M.
Mitigate Catastrophic Forgetting by Varying Goals.
DOI: 10.5220/0008950005300537
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 530-537
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Moreover, (Kashtan and Alon, 2005) showed that
MVG also leads to spontaneous evolution of network
motifs, bifan and diamond motif, which are kinds of
four-node subgraphs which occur significantly often
than that in random networks. Bifan and diamond
motifs are relatively highly connected among the
four-node motifs existing in a feedforward neural net-
work. These motifs are interesting because they could
be considered that contribute to the modularity since a
network with high modularity is considered that net-
works having densely connected groups of vertices
with only sparse connections between them (New-
man, 2006). Also, bifan and diamond motifs are in-
teresting because they could be thought as structural
motifs able to provide large and diverse functional
interactions. (Sporns and K¨otter, 2004) suggest that
biological neuronal networks have evolved such that
their repertoire of potential functional interactions is
both large and highly diverse, while their physical ar-
chitecture is constructed from structural motifs that
are less numerous and less diverse. A large functional
repertoire facilitates flexible and dynamic processing,
while a small structural repertoire promotes efficient
encoding and assembly. Since bifan and diamond mo-
tifs have symmetric structures, those could be thought
as structural motifs able to provide large and diverse
functional interactions.
Our study explores the application of MVG to mit-
igate catastrophic forgetting in a slightly practical sit-
uation. In (Kashtan and Alon, 2005), they not only
showed switching goals made of a different combina-
tion of subgoals can lead to spontaneous evolution of
modular network structure, but also pointed out that
randomly changing environments do not seem to be
sufficient to produce modularity. However, real-world
data is neither perfectly separable nor random. For
example, it is popular that images have similar fea-
tures, e.g. edge, intersecting lines, curves (Li et al.,
2015). This is not the situation considered in (Kash-
tan and Alon, 2005). Although MVG uncovers the
fundamental mechanism of the spontaneous evolution
of modular network structure, there is still a long way
to practical use. Therefore, to show the availability of
MVG in a practical situation, in this paper we explore
the application of MVG in a slightly practical situ-
ation, in detail, applying it to classification of small
sized real images, such as CIFAR-10. Also, although
2 goals are evaluated in (Kashtan and Alon, 2005), we
explore the increment of goals since a large amount
of data would be expected to learn in practical use.
To distinguish from MVG which is targeted to goals
made of a different combination of subgoals, the ap-
proach in this paper is renamed as CFVG (mitigate
Catastrophic Forgetting by Varying Goals).
In the evaluation, we compare CFVG with neu-
ral networks learned a single goal, which is the most
common method in practical use. The reason why
there is no comparison with existing catastrophic for-
getting methods is that there is no CIFAR-10 sized
image learn-able method with generating modules,
which is considered able to learn problems grow in
scale and complexity (Amer and Maul, 2019). In
recent research, (Kirkpatrick et al., 2017) has pro-
posed a practical solution to overcome catastrophic
forgetting to train a neural network by protecting the
weights important for previous goals. However, exact
recognition (French, 1999) is required which could be
inferred having a limitation in learning goals. In fact,
there is a parameter that exists, which sets how im-
portant the old goal is compared with the new one. In-
stead of it, in this paper, the amount of time it required
to relearn the original goal is measured, which does
not require exact recognition, therefore could be ex-
pected to deal with goals grow in scale and complex-
ity. Also, the existing scenario for evaluating CIFAR-
10 is not used. This is because it does not capture the
property of real world data. For example, in (Kirk-
patrick et al., 2017), they generated goals by shuffling
the order of pixels. Although this leads to the equal
difficulty for each goal, it is easy to infer that the pro-
cedure disorder features presented in the original im-
ages.
From the result, we find that varying goals can im-
prove catastrophic forgetting compared to neural net-
works learned a single goal in a CIFAR-10 based clas-
sification problem. And, we find that when learning a
large set of goals, a relatively small switching interval
is required to have the advantage of mitigating catas-
trophic forgetting. On the other hand, when learning
a small set of goals, an appropriate large switching
interval is preferred since this less worsens the ad-
vantage and also can improve accuracy. Moreover,
from exploring the obtained neural network structure,
we find that, after pruning some unimportant connec-
tions, it shows strong motif of bifan and diamond mo-
tifs, which suggest that the obtained neural networks
are modular, and this could be the reason of mitigat-
ing catastrophic forgetting.
This paper is organized as follows. Section 2
briefly explains goals for evaluation. Section 3 shows
the effect of CFVG toward classification based on
CIFAR-10. Section 4 shows the effect of CFVG to-
ward increment of goals. Section 5 shows network
motifs of neural networks obtained by CFVG.
Mitigate Catastrophic Forgetting by Varying Goals
531

2 GOALS FOR EVALUATION
MVG (Modularly varying goals) is to repeatedly
switch between several goals, each made of a different
combination of subgoals (Kashtan and Alon, 2005).
Although there is no detail information about how to
generate the goals, two examples are given in (Kash-
tan and Alon, 2005). For electronic combinatorial
logic circuits problem, the switching goals are given
as G1 and G2:
G1 =(X XOR Y) AND (Z XOR W), (1)
G2 =(X XOR Y) OR (Z XOR W). (2)
where, X, Y, Z, W are inputs, and G1, G2 are outputs.
G1 and G2 have share subproblems (X XOR Y) and
(Z XOR W). Circuits implementing each goal with
NAND gates are explored by GA. Another example
is for 8 bit-sized pattern recognition problem. The
goal is to recognize objects in the left and right sides
of the retina. The switching goals are given as G3 and
G4:
G3 = L and R, (3)
G4 = L or R. (4)
A left object exists if the four left pixels match one of
the patterns of a predefined set L. A right object exists
if the four right pixels match one of the patterns of a
predefined set R. G3 and G4 have shard subproblems
L and R. Neural networks implementing each goal are
explored by GA.
In this paper we explore the application of MVG
in a slightly practical situation, that is applying it
to classification of small sized real images, such as
CIFAR-10. Since real-world data is neither perfectly
separable nor random, it is not the situation consid-
ered in (Kashtan and Alon, 2005). Goals are set to
learn whether images belong to a given class. Since
CIFAR-10 is used for evaluation, for example, the
goals can be expressed as:
G5 = Airplane, (5)
G6 = Ship. (6)
Different goals have different labels for each input,
which represents whether the input image is the tar-
get goal or not. The input data is the same for every
goal. Therefore, changing goals means to change the
label. Although the goals are set in a rough fashion,
and it is true that the goals do not share clear subprob-
lems, it is popular that images have similar features,
e.g. edge, intersecting lines, curves (Li et al., 2015).
Since real-world data is rarely perfectly separable, it
is valuable to explore using such goals. To distin-
guish from MVG which is targeted to goals made of
a different combination of subgoals, the approach in
this paper is renamed as CFVG (mitigate Catastrophic
Forgetting by Varying Goals).
In more detail, since the aim of this research is
to apply MVG to a practical situation, CIFAR-10
CNN introduced in Keras documentation
1
is used.
The dataset used for evaluation is 50,000 32x32 color
training images, which is originally labeled over 10
categories. The input data is the same for every goal,
which is 50,000 32x32 color training images. The
output data is relabeled based on the original labels
from 10 categories to 2 categories, which represents
whether the input image is the target goal or not. The
labels are different for the same input for different
goals.
3 EVALUATION FOR
CATASTROPHIC FORGETTING
In this section, we show that CFVG can mitigate
catastrophic forgetting. Forgetting is discussed by a
traditional measurement that measures the amount of
time it required to relearn the original goal (French,
1999).
Since the aim of this research is to apply MVG
to a practical situation, CIFAR-10 CNN introduced
in Keras documentation is used. The dataset used
for evaluation is 50,000 32x32 color training im-
ages, which is originally labeled over 10 cate-
gories(airplane, automobile, bird, cat, deer, dog, frog,
horse, ship, truck), and relabeled to 2 categories,
which represents whether the input image is the target
goal or not. The input data is the same for every goal,
which is 50,000 32x32 color training images, and the
labels are different for each goal. To balance the re-
tagged training data, class weight is set. The layer
structure of the neural network is unchanged from
CIFAR-10 CNN except for the output layer since the
number of categories changed from 10 to 2, which is
afterword:
input − 32C3− 32C3− MP2− 64C3− 64C3
−MP2− 512FC− 2softmax
Again, since the aim of this research is to apply MVG
to a practical situation, those parameters that have
been shown to be useful for practical use is remain
unchanged from Keras documentation. The optimiza-
tion algorithm is changed from RMSprop to SGD
without momentum and decay. Since RMSprop de-
creases the learning rate, it is not compatible with
CFVG. The learning rate of SGD is set to 0.1 after
several times tuning. Note that, preprocessing and
1
https://github.com/fchollet/keras
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
532

0 200 400 600
Epoch
0.9
0.95
1
Acc.
Goal: Airplane
Ship
(a) FG.
0 200 400 600
Epoch
0.9
0.95
1
Acc.
(b) CFVG (Interval:1).
0 200 400 600
Epoch
0.9
0.95
1
Acc.
(c) CFVG (Interval:10).
0 200 400 600
Epoch
0.9
0.95
1
Acc.
(d) CFVG (Interval:50).
(e) Evaluation (Goal: Airplane).
Figure 1: Evaluation of learning 2 goals. (a) Accuracy of neural networks learning airplane and ship respectively(FG). (b, c, d)
Accuracy of neural networks learning airplane and ship by CFVG in switching interval 1, 10, 50 respectively. (e) Evaluation
against neural network obtained in (a, b, c, d). Accuracy of learning airplane against those neural networks are shown.
Figure 2: Accuracy of neural networks learning each goal
respectively(FG).
data augmentation originated in Keras documentation
is left unchanged since those are done for practical
use. The accuracy showed in the evaluation below is
training accuracy, and it is categorical accuracy. Since
this research focusing on catastrophic forgetting, eval-
uating training accuracy is more clear than showing
test accuracy which could be affected by other rea-
sons.
For comparison, we do not compare using exist-
ing scenario, since it does not capture the property
of real-world data that they are intermediate modu-
lar, which is neither perfectly separable nor random,
for example, images have similar features, e.g. edge,
intersecting lines, curves (Li et al., 2015). In recent
research for overcome catastrophic forgetting (Kirk-
patrick et al., 2017), for evaluation goals, they gener-
ated goals by shuffling the order of pixels. Although
this leads to the equal difficulty to each goal, it is
easy to infer that the procedure disorder the features
presented in the original images. Therefore, instead
of comparing with it, we compare with neural net-
works learned a single goal, which is the most com-
mon method in practical use. Note that, to avoid ex-
ploding gradients, the learning rate is set to 0.01 for
FG, which is less aggressive than that used in CFVG.
However, the results below show significant differ-
ence that could not be improved only by setting the
learning rate.
Figure 1a shows the accuracy of neural networks
learning airplane and ship respectively. This is called
FG(Fixed Goal). We regard FG as a neural network
catastrophically forgotten previous goals. From the
result, we can see that both achieved more than 0.98.
Figure 1b to Fig. 1d shows the accuracy of neural net-
works learning airplane and ship by CFVG in switch-
ing interval 1, 10, 50 respectively. We can see, al-
though the accuracy trained using CFVG is lower than
that of FG, the trained neural network can learn each
task faster as the epoch increase.
To show the amount of time it required to relearn
the original goal, the accuracy of learning airplane is
shown for some trained FG and CFVG neural net-
works. The neural networks used for evaluation are
the neural networks trained by airplane and ship using
CFVG in switching interval 1, 5, 10, 20, 50, 100 for
600 epoch. From Fig. 1e, we can see that CFVG can
reach 0.965 in a few epochs, which is much smaller
compare to that with Fig. 1a. Moreover, we can see
from Fig. 1 that CFVG neural networks learn the orig-
inal goal faster than FG learned ship. Therefore, the
results suggest that catastrophic forgetting can be mit-
igated by CFVG.
Mitigate Catastrophic Forgetting by Varying Goals
533

0 200 400 600
0.9
0.95
1
Acc.
3 Goals
0 200 400 600
0.9
0.95
1
5 Goals
0 200 400 600
Epoch
0.9
0.95
1
Acc.
8 Goals
0 200 400 600
Epoch
0.9
0.95
1
10 Goals
(a) CFVG (Interval: 1).
0 200 400 600
0.9
0.95
1
Acc.
3 Goals
0 200 400 600
0.9
0.95
1
5 Goals
0 200 400 600
Epoch
0.9
0.95
1
Acc.
8 Goals
0 200 400 600
Epoch
0.9
0.95
1
10 Goals
(b) CFVG (Interval: 10).
0 200 400 600
0.9
0.95
1
Acc.
3 Goals
0 200 400 600
0.9
0.95
1
5 Goals
0 200 400 600
Epoch
0.9
0.95
1
Acc.
8 Goals
0 200 400 600
Epoch
0.9
0.95
1
10 Goals
(c) CFVG (Interval: 20).
0 200 400 600
0.9
0.95
1
Acc.
3 Goals
0 500 1000
0.9
0.95
1
5 Goals
0 200 400 600 800
Epoch
0.9
0.95
1
Acc.
8 Goals
0 500 1000
Epoch
0.9
0.95
1
10 Goals
(d) CFVG (Interval: 100).
Figure 3: Accuracy of neural networks learning 3, 5, 8, 10 goals in different switching intervals. (a) Learning with switching
interval 1. (b) Learning with switching interval 10. (c) Learning with switching interval 20. (d) Learning with switching
interval 100.
4 EVALUATION FOR
INCREMENT OF GOALS
In this section, we evaluate CFVG against increment
of goals.
Before showing the results of CFVG, the accu-
racy of training different classes using FG is shown in
Fig. 2. We can see that after 600 epochs the accuracy
are all above 0.96. Also, we can see that the accuracy
of learning automobile, ship, and truck are higher,
and that of bird, dog, and cat is lower. This could
be because non-rigid objects like animals are difficult
to classify since their intra-class pose and appearance
variations are expected to be very high(Ramesh et al.,
2019).
Figure 3 shows the accuracy of training by CFVG
for a different number of goals with different switch-
ing intervals. Goals are given by a certain order as
Table 1: Goals For Evaluation.
3 Goals Airplane, Ship, Automobile
4 Goals Airplane, Ship, Automobile, Bird
5 Goals Airplane, Ship, Automobile, Bird, Cat
6 Goals Airplane, Ship, Automobile, Bird, Cat,
Deer
7 Goals Airplane, Ship, Automobile, Bird, Cat,
Deer, Dog
8 Goals Airplane, Ship, Automobile, Bird, Cat,
Deer, Dog, Frog
9 Goals Airplane, Ship, Automobile, Bird, Cat,
Deer, Dog, Frog, Horse
10 Goals Airplane, Ship, Automobile, Bird, Cat,
Deer, Dog, Frog, Horse, Truck
Tab. 1. Figure 3a shows the result of switching inter-
val 1. We can see that, as goals increase, the upper
end of accuracy decreases. Figure 3b, Fig. 3c, Fig. 3d
shows the results of switching interval 10, 20, 100 re-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
534
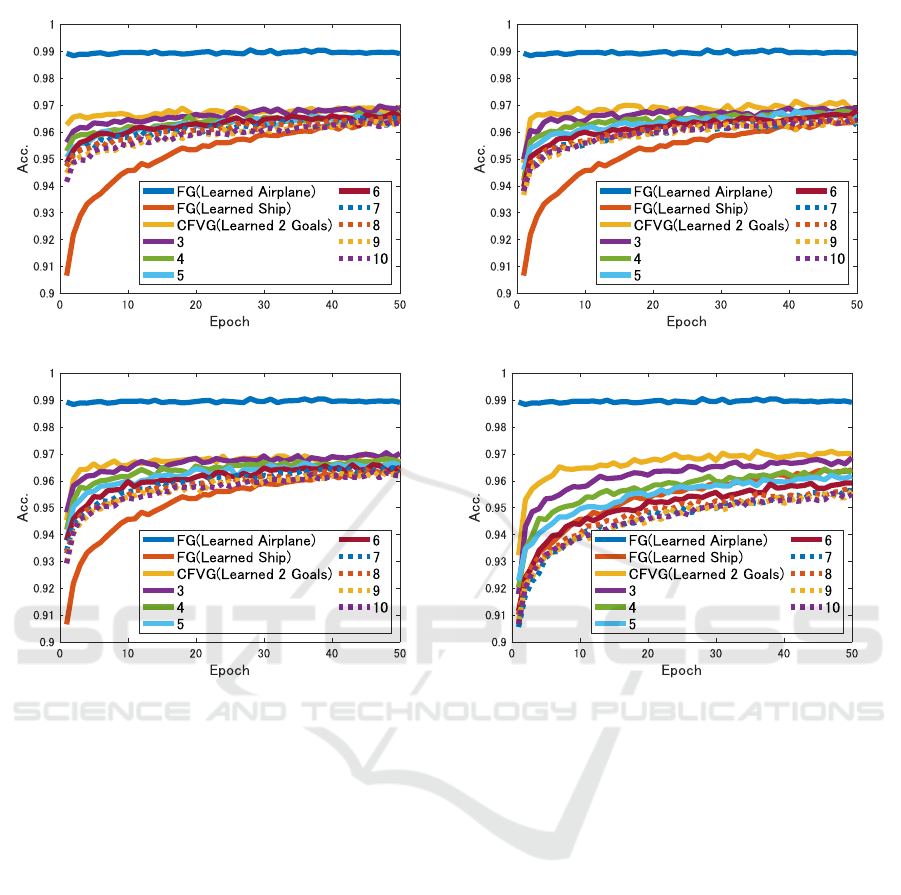
(a) CFVG (Interval: 1). (b) CFVG (Interval: 10).
(c) CFVG (Interval: 20). (d) CFVG (Interval: 100).
Figure 4: Evaluation against neural network obtained by CFVG(Fig.3). Accuracy of learning airplane against those neural
networks are shown. Although Fig.3 only showed several results of learning goals for page limitation, the number of learning
goals from 2 to 10 are all evaluated. (a) Learning with switching interval 1. (b) Learning with switching interval 10. (c)
Learning with switching interval 20. (d) Learning with switching interval 100.
spectively. We can see that the accuracy of 3 goals
increases as the switching interval increase. Also, we
can see that the decrease in the upper end become less
as switching interval increase.
Figure 4a to Fig. 4d shows the amount of time re-
quired to relearn the original goal for neural networks
trained by CFVG with different number of goals. Ac-
curacy of learning airplane is shown for some trained
CFVG neural networks. The neural networks used
for evaluation are the neural networks obtained in the
last epoch in Fig. 3. Those are trained until the epoch
where the goals go around for the first time beyond
600 epoch. For comparison, The accuracy for neural
networks trained using FG against airplane and ship
are shown. Figure 4a shows the result of switching in-
terval 1. We can see that CFVG learns faster than FG
learned ship. In detail, the smaller number of goals it
learns, the faster it learns the original goal. Figure 4b,
Fig. 4c, Fig. 4d shows the results of switching interval
10, 20, 100 respectively. We can see that CFVG learns
less fast as the interval increase, and for switching in-
terval 100, training with more than 6 goals will re-
duce the speed of relearning. Therefore, when learn-
ing a large set of goals, a small switching interval rela-
tive to the total learning epoch is required to have the
advantage of mitigating catastrophic forgetting. On
the other hand, when learning a small set of goals, an
appropriate large switching interval is preferred since
this less worsens the advantage and also can improve
accuracy.
5 EVALUATION FOR NETWORK
MOTIFS
In this section, we show whether CFVG leads to
module structure. (Kashtan and Alon, 2005) showed
MVG lead to spontaneous evolution of modular net-
Mitigate Catastrophic Forgetting by Varying Goals
535

0 20 40 60 80
-4
-2
0
2
REL # of M204
10
5
FG
0 20 40 60 80
-4
-2
0
2
REL # of M204
10
5
CFVG 2 Goals
0 20 40 60 80
-4
-2
0
2
REL # of M204
10
5
CFVG 5 Goals
0 20 40 60 80
q
-4
-2
0
2
REL # of M204
10
5
CFVG 10 Goals
INTVL: 1
10
20
100
M204
(a) Bifan Motif(M204).
0 20 40 60 80
-4
-2
0
2
REL # of M904
10
5
FG
0 20 40 60 80
-4
-2
0
2
REL # of M904
10
5
CFVG 2 Goals
0 20 40 60 80
-4
-2
0
2
REL # of M904
10
5
CFVG 5 Goals
0 20 40 60 80
q
-4
-2
0
2
REL # of M904
10
5
CFVG 10 Goals
INTVL: 1
10
20
100
M904
(b) Diamond Motif(M904).
0 20 40 60 80
-4
-2
0
2
REL # of M74
10
5
FG
0 20 40 60 80
-4
-2
0
2
10
5
CFVG 10 Goals
M74
(c) M74
0 20 40 60 80
-4
-2
0
2
REL # of M76
10
5
FG
0 20 40 60 80
-4
-2
0
2
10
5
CFVG 10 Goals
M76
(d) M76.
0 20 40 60 80
-4
-2
0
2
REL # of M392
10
5
FG
0 20 40 60 80
-4
-2
0
2
10
5
CFVG 10 Goals
M392
(e) M392.
0 20 40 60 80
-4
-2
0
2
REL # of M328
10
5
FG
0 20 40 60 80
-4
-2
0
2
10
5
CFVG 10 Goals
M328
(f) M328.
Figure 5: The relative number of motifs to weight randomized networks. (a) Bifan motif of FG and CFVG obtained neural
networks with switching between 2 goals, 5 goals, and 10 goals. For CFVG, results of switching interval with 1, 10, 20, 100
is shown. For FG, results against 10 different goals are shown, and so on. (b) Same as (a) but for diamond motif. (c, d, e)
Motifs with one link removed from bifan and diamond motif of FG and CFVG with switching between 10 goals. (f) Same as
(c, d, e) but for a motif supposed to have almost the same number with weight randomized networks.
work and network motifs. Unlike MVG, since CFVG
is varying goals that are neither perfectly separable
nor random, it is interesting to know whether the ob-
tained neural networks also gain such modular struc-
ture. To unclear this, we evaluate network motifs
against obtained neural network structure.
We evaluate the number of motifs of obtained
CNN to weight randomized neural networks, refer to
Z-score which is not calculable because of the net-
work size. Since the entire network of CNN is too
large to compute, a network is extracted from convo-
lutional layers of the CNN. We assume channels as
nodes. A link exists from a node represent a input
channel X to a node represent an output channel Y if
the kernel used against X for calculatingY has a larger
variance than p in its elements. p is calculated for
each layer, and it is the qth percentile of the variance
of all the kernels in a layer. In other words, unim-
portant connections are pruned following q (Hou and
Kwok, 2018). Note that, no links are pruned when q
is 0. Since the two dense layers have a large num-
ber of nodes, they are not included in the network for
calculating network motif. However, to delete redun-
dant links in the network, the dense layers are once
connected, and links that are unable to reach output
layers are deleted. To connect the dense layer, we
consider neuron in dense layer as a node. For links
between a convolutions layer and a dense layer, it ex-
ists if the variance of weights of links headed to the
same neuron is above the qth percentile of all the vari-
ance. For links between two dense layers, it exists if
the link weight is above the qth percentile of all the
weights. For weight randomized neural network, the
number of layers and the number of nodes in each
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
536

layer is set to the same value as the real trained neural
network. Then, pruning unimportant connections fol-
lowing q. Although a network with 5 layers is calcu-
lated, to set the conditions the same as the real trained
neural network, nodes in the dense layers are attached
for deleting links that are not reachable to the out-
put layer. The number of motifs is calculated against
10 weight randomized neural networks. The average
value of the result is used as a reference value. The
value shown in Fig. 5 are values that are subtracted
by the reference value. Note that, since the struc-
ture of neural networks obtained by FG and CFVG is
the same, the same weight randomized networks are
used. MFINDER1.21 is used for detecting network
motifs (Milo et al., 2004).
From the result of Fig. 5, we can see a tendency
that neural network obtained with CFVG have a rela-
tively large number of bifan and diamond motif, while
they have less number of those motifs with one link
removed from bifan and diamond motif especially
when q is 20. Moreover, although FG has the same
tendency, the tendency is even stronger in CFVG ob-
tained neural networks. This suggest that neural net-
works obtained by CFVG are more modular than that
by FG. And, the reason for CFVG having the advan-
tage in mitigating catastrophic forgetting could be be-
cause of the such structure the networks gained.
6 CONCLUSION AND FUTURE
WORK
In this paper, we explore the application of MVG to
mitigate catastrophic forgetting in a slightly practical
situation, that is applying it to classification of small
sized real images and applying it to the increment of
goals. From the result, we find that varying goals
can improve catastrophic forgetting using SGD in a
CIFAR-10 based classification problem. We find that,
when learning a large set of goals, a relatively small
switching interval is required to have the advantage
of mitigating catastrophic forgetting. On the other
hand, when learning a small set of goals, an appro-
priate large switching interval is preferred since this
less worsens the advantage and also can improve ac-
curacy. Also, from exploring the obtained neural net-
work structure, we find that, after pruning some unim-
portant connections, it shows strong motif of bifan
and diamond motifs, which suggest that the obtained
neural networks are modular, and this could be the
reason of mitigating catastrophic forgetting.
For future work, the proposed approach should be
examined in other tasks and other layer structures, and
theoretical analysis is needed.
ACKNOWLEDGMENT
Thanks to Nadav Kashtan for providing his source
code. This work was supported by JSPS KAKENHI
Grant Number JP19K20415. The computational re-
source was partially provided by large-scale computer
systems at the Cybermedia Center, Osaka University.
REFERENCES
Alon, U. (2003). Biological networks: The tinkerer as an
engineer. Science, 301(5641):1866–1867.
Amer, M. and Maul, T. (2019). A review of modulariza-
tion techniques in artificial neural networks. Artificial
Intelligence Review, 52(1):527–561.
Ellefsen, K. O., Mouret, J.-B., and Clune, J. (2015). Neural
modularity helps organisms evolve to learn new skills
without forgetting old skills. PLoS Computational Bi-
ology, 11(4):e1004128.
French, R. M. (1999). Catastrophic forgetting in con-
nectionist networks. Trends in Cognitive Sciences,
3(4):128–135.
Hou, L. and Kwok, J. T. (2018). Power law in spar-
sified deep neural networks. arXiv e-prints, page
arXiv:1805.01891.
Kashtan, N. and Alon, U. (2005). Spontaneous evolution
of modularity and network motifs. Proceedings of
the National Academy of Sciences, 102(39):13773–
13778.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J.,
Desjardins, G., Rusu, A. A., Milan, K., Quan, J.,
Ramalho, T., Grabska-Barwinska, A., Hassabis, D.,
Clopath, C., Kumaran, D., and Hadsell, R. (2017).
Overcoming catastrophic forgetting in neural net-
works. Proceedings of the National Academy of Sci-
ences, 114(13):3521–3526.
Li, Y., Wang, S., Tian, Q., and Ding, X. (2015). A survey
of recent advances in visual feature detection. Neuro-
computing, 149:736–751.
Milo, R., Itzkovitz, S., Kashtan, N., Levitt, R., Shen-Orr,
S., Ayzenshtat, I., Sheffer, M., and Alon, U. (2004).
Superfamilies of evolved and designed networks. Sci-
ence, 303(5663):1538–1542.
Newman, M. E. (2006). Modularity and community
structure in networks. Proceedings of The National
Academy of Sciences, 103(23):8577–8582.
Parter, M., Kashtan, N., and Alon, U. (2008). Facilitated
variation: How evolution learns from past environ-
ments to generalize to new environments. PLoS Com-
putational Biology, 4(11):e1000206.
Ramesh, B., Yang, H., Orchard, G. M., Le Thi, N. A.,
Zhang, S., and Xiang, C. (2019). Dart: Distribu-
tion aware retinal transform for event-based cameras.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, pages 1–1.
Sporns, O. and K¨otter, R. (2004). Motifs in brain networks.
PLoS Biology, 2(11):e369.
Mitigate Catastrophic Forgetting by Varying Goals
537
