Deep Learning of Heuristics for Domain-independent Planning

Otakar Trunda

and Roman Bart

Charles University, Faculty of Mathematics and Physics, Czech Republic

Keywords:

Heuristic Learning, Automated Planning, Machine Learning, State Space Search, Knowledge Extraction,

Zero-learning, STRIPS, Neural Networks, Loss Functions, Feature Extraction.

Abstract:

Automated planning deals with the problem of ﬁnding a sequence of actions leading from a given state to a

desired state. The state-of-the-art automated planning techniques exploit informed forward search guided by a

heuristic, where the heuristic (under)estimates a distance from a state to a goal state. In this paper, we present

a technique to automatically construct an efﬁcient heuristic for a given domain. The proposed approach is

based on training a deep neural network using a set of solved planning problems from the domain. We use a

novel way of generating features for states which doesn’t depend on usage of existing heuristics. The trained

network can be used as a heuristic on any problem from the domain of interest without any limitation on

the problem size. Our experiments show that the technique is competitive with popular domain-independent

heuristic.

1 INTRODUCTION

Heuristic learning is a relatively new ﬁeld which stud-

ies how machine learning (ML) can be used to con-

struct a heuristic used in informed forward-search al-

gorithms such as A* and IDA*. The objective is to

train a regression-based ML model to be able to es-

timate goal-distances of states and then to use the

trained model as a heuristic function during search.

Automated planning, which deals with ﬁnding

a sequence of actions leading to a goal state, ex-

ploits heuristics heavily. Domain-speciﬁc heuristics

are hand-tailored for a speciﬁc domain and hence they

are very efﬁcient. However, developing them requires

tremendous human effort and access to expert knowl-

edge. Domain-independent heuristics are more pop-

ular in automated planners as they are designed once

and then they work across all domains. Nevertheless,

none of them works well on all domains. Again, a

signiﬁcant human effort would be required to select

the best performing heuristic for the problem at hand,

otherwise the search might be inefﬁcient. This issue

can partially be solved by using a portfolio-planner.

In this paper, we present a ML technique that au-

tomatizes the process of developing domain-speciﬁc

heuristics for planning. We work with the standard

STRIPS planing and we use supervised learning, with

https://orcid.org/0000-0002-7868-7039

https://orcid.org/0000-0002-6717-8175

a multi-layered feed-forward neural network as the

ML model. Expert knowledge about the domain is

extracted automatically from a set of training sam-

ples. Using ML techniques for this task can be advan-

tageous because in this particular case, the training

samples can be obtained without human assistance,

unlike in typical applications of ML where samples

need to be human-labeled.

Our technique falls into category of zero-learning

as the heuristic is constructed from scratch, without

any human-knowledge initially added. This approach

allows us to combine wide usability of domain-

independent heuristics with accuracy of domain-

speciﬁc ones without any assistance of a human ex-

pert.

Our main contribution is twofold. We propose a

novel way of assigning features to states based on

counting subgraphs of a graph-based representation

of the state. The method produces ﬁxed-size fea-

ture vectors without depending on existing heuristics.

Second, we study the effect of the choice of loss func-

tion used during the training, on performance of the

learned heuristic during the search. We show that

Mean Squared Error (MSE) alone might not be the

best loss function for heuristic learning task, and also

that low error on training and test sets doesn’t au-

tomatically imply good performance of the learned

heuristic.

Trunda, O. and Barták, R.

Deep Learning of Heuristics for Domain-independent Planning.

DOI: 10.5220/0008950400790088

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 79-88

ISBN: 978-989-758-395-7; ISSN: 2184-433X

2 BACKGROUND AND RELATED

WORKS

2.1 STRIPS Planning

We work with classical planning problems, that is,

with ﬁnding a sequence of actions transferring the

world from a given initial state to a state satisfying

certain goal condition (Nau et al., 2004). World states

are represented as sets of predicates that are true in

the state (all other predicates are false in the state).

For example the predicate at(r1, l1) represents infor-

mation that some object r1 is at location l1. Actions

describe how the world state can be changed. Each

action a is deﬁned by a set of predicates prec(a) as

its precondition and two disjoint sets of predicates

eff

(a) and eff

−

(a) as its positive and negative ef-

fects. Action a is applicable to state s if prec(a) ⊆ s

holds. If action a is applicable to state s then a new

state γ(a, s) deﬁnes the state after application of a as

γ(a, s) = (s ∪ eff

(a)) − eff

−

(a) Otherwise, the state

γ(a, s) is undeﬁned. The goal g is deﬁned as a set of

predicates that must be true in the goal state. Hence

the state s is a goal state if and only if g ⊆ s.

The satisﬁcing planning task is formulated as fol-

lows: given a description of the initial state s

, a set

A of available actions, and a goal condition g, is there

a sequence of actions (a

, . . . , a

), called a solution

plan, such that a

∈ A, a

is applicable to state s

, each

s.t. i > 1 is applicable to state γ(a

i−1

, . . . γ(a

, s

)),

and g ⊆ γ(a

, γ(a

n−1

, . . . γ(a

, s

)))? Assume that each

action a has some cost c(a). An optimal planning task

is about ﬁnding a solution plan such that the sum of

costs of actions in the plan is minimized.

In practice, the planning problem is speciﬁed in

two components: a planning domain ﬁle and a plan-

ning problem ﬁle. The domain ﬁle speciﬁes the names

of predicates describing properties of world states and

actions that can be used to change world states. The

problem ﬁle then speciﬁes a particular goal condition

and an initial state and hence it also gives the names

of used objects (constants) and their types.

In the rest of the text we use the following nota-

tion. P denotes a planning problem, s

denotes the

initial state of P, S

the set of all states of P, Dom(P)

a set of all planning problems from the same domain

as P and S

Dom(P)

a set of states of all problems from

the same domain as P. For a state s

∈ S

, h

∗

) de-

notes the goal-distance of s

in P, i.e. the cost of the

optimal plan from s

, or ∞ if there is no path from s

to a goal state.

2.2 Heuristic Learning

A heuristic learning (HL) system works with a set

of training samples, where each training sample is a

pair (s

, h

∗

)), s

is a state of some planning problem

and h

∗

) is its goal-distance. The system involves a

ML model M that is trained to predict h

∗

) from s

Most of ML models work with ﬁxed-size real valued

vectors as their inputs, hence another component is

required that transforms states into this form. We call

this component a features generator and denote it by

F. We call F(s) the features of s, and h

∗

(s) the target

of s. There are several variants of HL based on their

usage scenarios:

Type I: several problems P

, P

, . . . P

and P from

the same domain are given as input and the task is

solving the problem P as quickly as possible. Time

required for generating the training data and training

the model is considered a part of the solving process.

The ML model is trained speciﬁcally for P, it is not

intended to work on different problems.

Type II: several problems P

, P

, . . . P

from the

same domain Dom are given and the task is solving

new problems from Dom. Time required for generat-

ing the training data and training the model is NOT

considered a part of the solving process. It is con-

sidered a pre-processing, or a domain analysis phase.

The ML model captures knowledge about the whole

domain, i.e., it can generalize to other, previously un-

seen problems from the same domain. The training

phase can in this case take several hours or even days.

After the model is trained, new problems from the

same domain can be solved quickly. The Type II HL

system requires a much more ﬂexible features genera-

tor, as features of states of different problems must be

comparable. Those different problems might contain

different numbers of objects and might have different

goal conditions.

Type III: Training samples from several differ-

ent domains are given and the ML model serves as

a multi-domain heuristic, or a domain-independent

heuristic. To our best knowledge, no serious attempt

has been made in this area.

In this paper, we work with the Type II HL and our

approach is domain-independent in a sense that the

domain from which the training problems come might

be arbitrary. We conducted experiments on domains

without action costs but the technique is applicable to

domains with costs as well.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

2.3 Related Works

Many attempts have been made to utilize ML in plan-

ning or in general search (Jim

enez et al., 2012). ML

has been used to learn reactive policies (Groshev

et al., 2017; Mart

ın and Geffner, 2004; Groshev et al.,

2018), control knowledge (Yoon et al., 2008), for

plan recognition (Bisson et al., 2015) and for other

planning-related tasks (Konidaris et al., 2018). ML

tools are also often used to combine several heuris-

tics (Samadi et al., 2008; Fink, 2007) and in par-

ticular to help portfolio-based planners to efﬁciently

combine multiple search algorithms (Cenamor et al.,

2013). A lot of papers exist that utilize ML in

neoclassical planning paradigm (partial observability,

non-deterministic actions, extended goals etc.), like

robotics (Takahashi et al., 2019). These techniques

are not directly related to our work.

Heuristic learning was investigated by (Arfaee

et al., 2010) where the authors use a bootstrapping

procedure with a NN to successively learn stronger

heuristics using a set of small planning problems

for training. The paper proposed an efﬁcient way

of generating training data based on switching be-

tween learning and search phases. The technique be-

come popular and was successfully used by other au-

thors (Chen and Wei, 2011; Thayer et al., 2011). We

use a modiﬁed version of this technique as well. A

domain-independent generalization of this approach

was published later (Geissmann, 2015).

Most papers deal with the Type I HL scenario and

almost all of them use a set of simple heuristics as

features (Arfaee et al., 2011; Brunetto and Trunda,

2017). A serious attempt to use other kind of features

was made in (Yoon et al., 2008).

Authors mostly use simple ML models like linear

regression or a shallow NN. ML models are often just

used as a tool and ML-related issues like generaliza-

tion capabilities, number and distribution of training

samples, choice of loss function, etc. are not analyzed

at all. Few exceptions exist: in (Thayer et al., 2011)

the authors proposed a modiﬁcation to the loss func-

tion used during the training to bias the model towards

under-estimation which increased quality of solutions

found during the subsequent search.

3 THE FRAMEWORK

We will use heuristic learning in automated planning

using the following framework. First, during the

training phase, the deep NN will learn the heuris-

tic from example plans. Then, during the deploy-

ment phase, the obtained NN will be used to calculate

heuristic values that will be exploited by A* search to

ﬁnd plans. The focus of this paper is on the training

phase, in particular, on novel approach to generating

features for training and on selecting appropriate loss

function.

3.1 Obtaining the Training Data

Ideally, the training data should be given as inputs.

That might be possible in some speciﬁc situations

when historical data are available, but in general the

training data need to be generated. This involves

two tasks: generating states s

and computing h

∗

)

for those states. As computing h

∗

) is very time-

consuming, majority of existing works use states for

which it is easy to compute h

∗

), such as the states

close to goal.

From the ML perspective, it is important that

training data come from the same probability distri-

bution as the data encountered during the deployment.

This would require to predict what kind of states will

A* expand during the search. Making such predic-

tions is tricky as the set of expanded nodes depends

on the heuristic used which depends on how well the

model is trained and that depends back on the choice

of training data.

We adopt a popular technique (Arfaee et al.,

2010), which solves this issue by an iterative proce-

dure that combines training and search steps. The ﬁrst

set of training samples is generated by random walks

from the goal state. Then, in each iteration, the model

is trained on current set of samples and a time-limited

search is performed on the training problems using

the trained model as the heuristic. States that the al-

gorithm expanded are collected and used as training

samples in the next iteration. This process continues

until sufﬁcient amount of samples is generated or all

training problems can be solved within the time limit.

To speed up the training phase, we use ad-hoc

solvers to calculate goal-distances of samples. This

allows us to work with larger training problems in

reasonable time and not having to rely on backward

search to calculate h

∗

. Pseudocode for the training

phase is presented as Algorithm 1.

4 GENERATING FEATURES

The important step in ML is selecting features that

will be used in learning. Given a set of planning prob-

lems {P

, P

, . . . P

} ⊂ Dom, the feature generator F

realizes a mapping F : S

Dom

7→ R

, i.e., assigns a real

valued vector to any state of any problem from the

domain of interest.

Deep Learning of Heuristics for Domain-independent Planning

Algorithm 1: Training phase.

Input: Set of planning problems

} ⊂ Dom used for training

features generator F

Output: Trained model M that realizes

mapping from F[S

Dom

] 7→ R

1 L := 1;

2 trainingStates := initial states of all P ∈ {P

};

3 repeat

4 compute h

∗

) for each state s

∈

trainingStates;

5 assign features f

= F(s

) to all states s

∈

trainingStates;

6 M := train neural net on data

{( f

, h

∗

))};

7 foreach problem P ∈ {P

} do

8 run IDA* on P with time limit L

using M as heuristic;

9 T := states of P that were expanded

during the search;

10 trainingStates := trainingStates ∪ T ;

11 end

12 L := L + 1;

13 until termination criterion is met;

14 return M;

Length of the feature vector needs to be ﬁxed and

independent of the speciﬁc planning problem. Fea-

tures should also be informative in a sense that states

with different goal-distances should have different

features, and comparable among problems from the

whole domain so that knowledge is transferable to

previously unseen problems.

When assigning features to state s ∈ S

, properties

of P that affect h

∗

(s) have to be taken into account,

namely the set of available actions and the goal condi-

tion. The model is trained on problems from a single

domain and for such problems the set of actions is al-

ways the same so it is not necessary to encode it into

features of states. Goal conditions, however, must be

encoded so that the learned knowledge is transferable

to problems with different goal states.

4.1 Heuristics as Features

Vast majority of papers on HL use a ﬁxed set of

simple heuristics as features. Given a sequence of

heuristics H = (h

, h

, . . . h

), we can deﬁne F

(s) =

(s), h

(s), . . . , h

(s)). Most papers use a set of pat-

tern database heuristics (PDBs). This approach is

popular as the feature vector has ﬁxed length, is quite

informative and its computation is fast.

This approach is advantageous in the Type I HL

scenario but not so in Type II that we deal with. PDB

is based on a pattern: a set of objects from the plan-

ning problem. It is possible to us it if all the problems

are given in advance. In the Type II scenario, how-

ever, the model needs to be applicable to new, unseen

problems from the domain. If we use a ﬁxed set of

PDBs, new problems might not contain the same ob-

jects, and even if they do, meaning of those objects

might be different so the features would not be com-

parable.

Also we want to avoid dependency on existing

human-designed heuristics as such dependence might

prevent the model from achieving super-human per-

formance. Development in the ﬁelds of sound, im-

age, and language processing during the last ten years

showed that ML systems with little to none expert

knowledge encoded might achieve better results than

sophisticated human-designed tools.

4.2 Graph-based Features

We use a direct encoding of the state to an integer-

valued vector. We transform the PDDL representa-

tion of both the current state and the goal condition

to a labeled graph and use this graph to generate fea-

tures. We select a set of small connected graphs and

then use the number of occurrences of these graphs in

the original graph as features. The idea is inspired by

Bag-Of-Words model (Goldberg, 2017) that is used to

assign ﬁxed-length feature vectors to variable-length

texts by counting number of occurrences of selected

words or phrases.

4.2.1 Object Graph

An object graph for a state s of a planning problem

A (denoted G(s

)) is a vertex-labeled graph G(s) =

(V, E) deﬁned as follows. The set of vertices is com-

posed by four disjoint sets. There is a vertex v

for

every constant c in the problem, a vertex v

for every

predicate symbol used in the deﬁnition of the prob-

lem, a vertex v

for every instantiated predicate q that

is true in s, and a vertex v

for every predicate q in

goal conditions of A (we don’t support negative goal

conditions as they can be compiled-away). The set E

contains an edge e

from v

or v

to v

if instanti-

ated predicate q uses the predicate symbol P, and an

edge e

from v

to v

or v

if instantiated predicate q

contains constant c.

The labelling function w : V 7→ N

looks as fol-

lows. Every v

is assigned the same number 0. Ev-

ery v

is assigned a unique number from [1,2, . . . , #P]

where #P is the number of predicate symbols. Every

is assigned the same number #P + 1 and every v

assigned the same number #P + 2. Types are treated

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

as unary predicate symbols. Labels were intention-

ally chosen such that the number of labels does not

depend on the size of the problem.

In ﬁgure 1 there is an example of object graph for

the initial state of the problem pﬁle2 of the zenotravel

domain. Constants are colored red, types blue, pred-

icate symbols pink, initial predicates green and goal

predicates gold.

The object graph is an equivalent representation

of the current state and goal condition. The original

PDDL representation of the state and the goal can be

reconstructed back from the graph.

4.2.2 Generating Features

The size of the object graph depends on the number

of constants and the number of valid predicates in the

state and in the goal. Hence we need a method to en-

code information from G(s) in a feature vector whose

length is independent of state and goal. This is where

we will use the node labels and the subgraph-counting

method.

Let B

be a sequence of all connected non-

isomorphic vertex-labeled graphs containing at most

q vertices where the labels are from {1, 2 . . . k}. See

ﬁgure 2 for an example of graphs B

- colors represent

labels.

Occurrence of a graph G

in graph G

is a set of

vertices T of G

such that induced subgraph of G

T is isomorphic to G

Given a state s and q ∈ N, the feature vector of s

(denoted F

(s)) is an integer-valued vector of size |B

whose i-th component is the number of occurrences of

the i-th graph from B

in G(s).

4.2.3 Example

Consider the graph G in the left-hand side of ﬁg-

ure 2 with two different labels represented by col-

ors. We use q = 2, i.e. we count occurrences of

connected subgraph of size up to 2. On the right-

hand side of ﬁgure 2 there are graphs from B

that

we will use to assign features to G. The resulting

vector is F

(G) = (5, 3, 5, 2, 1) which corresponds to

number of occurrences of the individual graphs in G.

For example: occurrences of the second graph are

{2}, {7}, {8}, occurrences of the fourth one are {3, 6}

and {5, 6}, etc.

The length of F

(.) can be controlled by adjusting

the parameter q. With low q, the vector will be short

and will contain less information about the state but

its computation will be faster, and vice versa. Given a

graph with n vertices, it is not known whether or not

(G) uniquely determines the graph for some q < n.

It is an open problem in graph theory known as the

Reconstruction conjecture.

Length of the vector is at most

∑

i=1

i(i−1)

(k),

where k is the number of labels, q is the maximum

size of subgraphs considered, 2

i(i−1)

is the number of

graphs on i vertices and C

(k) =

(k+i−1)!

i!(k−1)!

is the num-

ber of combinations with repetition of size i from k

elements. In practice, |F

(.)| is much lower since we

only use subgraphs that occurred at least once in the

training data and most graphs do not occur due to the

way how the object graph is deﬁned. E.g. every predi-

cate symbol has its own label l

and every object graph

contains exactly one vertex with such label so sub-

graphs that contain more than one vertex labeled l

can never occur.

From the planning perspective, features capture

relations between objects in the given state. E.g. in

blocksworld, occurrence of a certain subgraph of size

4 can capture the fact, that there are 2 blocks A on top

of B and B is not correctly placed (so both of them

have to be moved), etc.

4.2.4 Computing features from Scratch

Given the object graph G(s), feature vector F

(s) can

be computed by a recursive procedure that iterates

through all connected subgraphs with size up to q in

the graph and its time complexity is proportional to

the number of such subgraphs. It is difﬁcult to esti-

mate the number in general as it strongly depends on

the structure of the graph. E.g. a cycle with n ver-

tices contains just n connected induced subgraphs of

size q < n, while a clique on n vertices contains





such subgraphs. The number depends on the edge-

connectivity of the graph as well as on degrees of

vertices. Experiments show that the time complex-

ity grows exponentially in both n (size of the graph)

and q.

4.2.5 Computing Features Incrementally

∗

expands nodes in a forward manner and two suc-

cessive states differ only locally. It is therefore possi-

ble and useful to calculate the features incrementally.

Given a state s, its feature vector F(s) and an action

a, we can calculate F(γ(a, s)) of the successor state

without having to enumerate all its subgraphs again.

Unfortunately, F(s) and a alone are not sufﬁcient

to determine features of the successor. For any ﬁxed

q there exist states s

6= s

and action a

such that

) = F

) but F

(γ(a

, s

)) 6= F

(γ(a

, s

)) so

a more sophisticated approach is needed. Apply-

ing action to a state s can be viewed as performing

some local changes in G(s). These changes can be

Deep Learning of Heuristics for Domain-independent Planning

Figure 1: Example of an object graph for the initial state of problem pﬁle2 of the zenotravel domain.

Figure 2: Left-hand side: a simple graph used to demon-

strate computation of features. Right-hand side: a set of

graphs B

decomposed into a sequence of several atomic op-

erations of 3 types: AddVertex, RemoveVertex and

AddEdge. For example, in Zenotravel, there is an ac-

tion a = load(person1, city1, plane1). Given G(s),

we can construct G(γ(a, s)) by ﬁrst removing ver-

tex that represents predicate at(person1, city1), then

adding vertex for predicate in(person1, plane1) and

then successively adding edges between the new ver-

tex and vertices for in, person1 and plane1.

Given graph G, its vertex v and a set of graphs B

we deﬁne contribution of a vertex v to F(G) denoted

by C(v) as a set of all occurrences of graphs from

in G which intersect with v. We will now show

how each of the three atomic operations can be per-

formed incrementally given G(s), F(s) and C(v) for

every vertex of G(s).

Remove Vertex: For each c ∈ C(v), remove c

from every C(v

) that contains it, decrease values in

F(s) accordingly. Remove v from G(s).

Add Vertex: Add v to G(s), add one new occur-

rence of a subgraph containing a single vertex with

the given label to C(v), increment the the correspond-

ing element of F(s).

Add Edge:

1. replace every occurrence c ∈ C(v

)∩C(v

) by oc-

currence of a graph with the same vertex set and

one more edge added at the corresponding loca-

tion.

2. for every occurrence c ∈ C(v

) \ C(v

) such that

|c| ≤ q − 1 create a new occurrence on vertices

c∪{v

}. If c contained some vertex adjacent to v

edges between these vertices and v

will be taken

into account when determining which graph from

occurred on c ∪ {v

3. repeat the previous step symmetrically for v

, then

add the edge to G(s).

Using a carefully designed data structure, we can

perform AddVertex, RemoveVertex as well as the step

1 of AddEdge in time O (1), steps 2 and 3 can be

performed in time O (|C(v

)|) and O(|C(v

)|) respec-

tively.

5 ERROR FUNCTION FOR THE

TRAINING

We train the network by a standard gradient-descent

optimizer which iteratively updates parameters of the

network in order to minimize the given loss func-

tion. We are solving a regression task - predict-

ing a real number for each state. We experimented

with two loss functions: standard MSE deﬁned as

MSE =

∑

−

)

and a MSE transformed by a log-

arithm (denoted LogMSE), deﬁned as LogMSE =

∑

[log(Y

+1)−log(

+1)]

, where Y

is target of the i-th

sample (i.e., the real goal distance of the i-th state),

is output of the model on the i-th sample (i.e. the

value that would be used as a heuristic estimate for

the i-th state) and n is the number of samples. The

sum goes over all samples.

Figure 3 presents a histogram of ﬁt of the trained

model when MSE is used. On the x-axis there is dif-

ference between target value and output, the height

of the column represents the number of samples that

fall into each category. Yellow columns show training

data, purple ones show test data. In Figure 4 we can

see accuracy of the model on samples with different

targets (blue columns). On the x-axis there is target

and the height of the column represents average of ab-

solute values of absolute error among all samples with

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

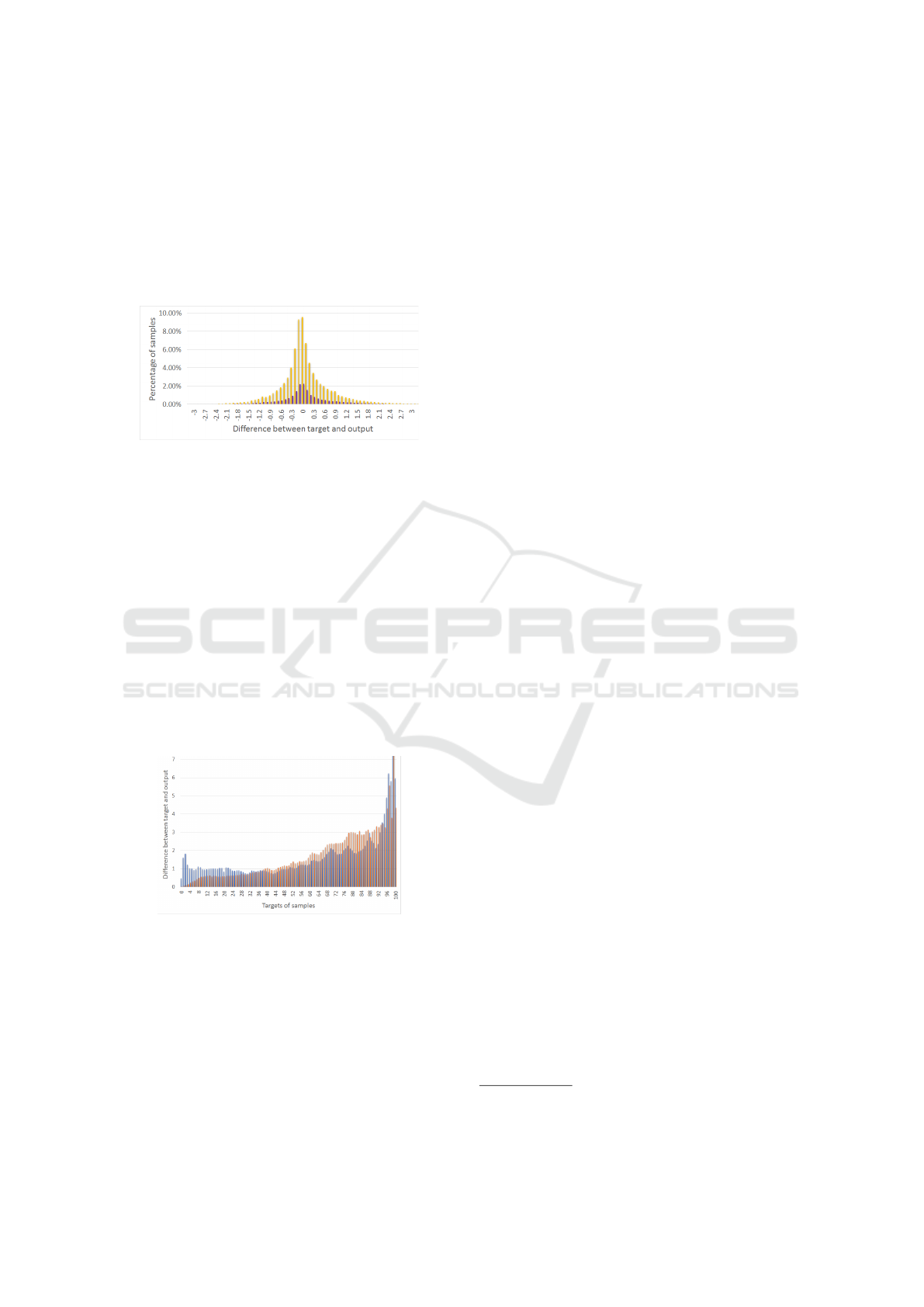
corresponding target value. The model is well trained

having small error on both training and test data. The

use of MSE loss function leads to an even distribution

of the error among all samples regardless of their tar-

get (up to goal distance about 50). For example, the

model makes error of ±1.5 on states 50 steps from

goal, but makes about the same error (±1.5) also on

states that are 2 steps from goal.

Figure 3: Accuracy of the model. Yellow columns represent

training data, purple one represent test data.

During the deployment phase, however, the model

perform poorly. The heuristic is very accurate on

states far from goal, but our analysis showed that

making relatively large mistakes on states close to

goal hurts the performance a lot.

In order to improve the search efﬁciency, the ac-

curacy of the heuristic on states close to goal (i.e.

with target 0-10) needs to be much higher. This can

be achieved by using LogMSE as the loss function.

LogMSE minimizes the average of relative error, i.e.,

the ratio between target and output which enforces

low absolute error on samples close to goal and tol-

erates larger absolute error on samples further from

goal.

Figure 4: Absolute error on samples with different targets.

On the X-axis there is target - i.e. real goal distance, height

of the column shows average of absolute error (| Y

−

over all samples that fall into that category. Blue color cor-

responds to network trained by MSE, orange to LogMSE.

Figure 4 illustrates this behavior as it compares

absolute and relative error on training and test sam-

ples for both loss functions. MSE (in blue) makes

large relative error on states close to goal while

LogMSE (orange) performs much better on these

states but has slightly larger error on states further

from goal. The total sum of error is similar for both

functions but its distribution with respect to the tar-

get is quite different. Experiments show that us-

ing LogMSE leads to better performance during the

search.

6 EXPERIMENTS

We conducted experiments on two standard bench-

mark domains: zenotravel and blocks because it is

easy to obtain training data for these domains. For the

purpose of the experiments, we implemented ad-hoc

solvers for the two domains and used them to gener-

ate training data. Our solvers are based on a genetic

algorithm combined with a greedy search, they are ca-

pable of solving most problems within a few seconds

and provide optimal or close-to-optimal solutions. We

test the method on 20 problems available for zeno-

travel

and the ﬁrst 27 problems from blocks

For each problem P, we train the model using

the other problems from the domain (except P) as

the training data, and then use the trained model as

a heuristic with an A* algorithm to solve P. We com-

pare the quality of the resulting heuristic with the

Fast-Forward heuristic h

(Hoffmann and Nebel,

2001). The heuristic has been around for quite some

time now but it is still often used as a baseline in ex-

periments, like in (H

oller et al., 2019) for example.

The NN we used have 5 hidden layers with sizes of

(256, 512, 128, 64, 32) neurons respectively, and two

DropOut layers. We used ReLU activation function,

Xavier weight initialization and Adam as the training

algorithm (Goodfellow et al., 2016). The last layer

contained a single neuron with a linear activation to

compute the output. Architecture of the network was

chosen according to best practices for this kind of sce-

nario. The network is large enough to create efﬁcient

representation of the data and drop-out layers prevent

overﬁtting. Similarly to other zero-learning scenar-

ios, the amount of time required for training is quite

high. For every problem, training the net took about 8

hours using over 1 million training samples for zeno-

travel and over 1.8 million for blocks.

We experimented with values of parameter q (size

of subgraphs) from 2 to 4. For values larger that

4, computing features of states is too costly and the

heuristic is not competitive. We experimented with

the two loss functions - MSE and LogMSE, and we

also tried to include value of the h

among the fea-

tures of states. I.e., we ﬁrst trained the network having

api.planning.domains/json/classical/problems/17

api.planning.domains/json/classical/problems/112

Deep Learning of Heuristics for Domain-independent Planning

Figure 5: Results of experiments.

only the graph-based features as its inputs and then

another network that used both graph-based features

and h

value of the state as its inputs. We conducted

experiments for all combinations of these parame-

ters: q ∈ {2, 3, 4}, lossFunction ∈ {MSE, LogMSE},

FFasFeature ∈ {true, f alse}. This gives us 12 differ-

ent neural net-based heuristics.

We used all 13 heuristics (12 NN-based + h

) to

solve each of the problems. Search time was capped

at 30 minutes per problem instance. None of the

heuristic is admissible so they don’t guarantee ﬁnding

optimal plans. We compared performance of heuris-

tics using the IPC-Score. Given a search problem P,

a minimization criterion R (e.g. length of the plan)

and algorithms A

, A

, . . . , A

, the IPC-Score of A

problem P is computed as follows: IPC

, P) = 0 if

didn’t solve P, or

∗

otherwise, where R

is value of

the criterion for the i-th algorithm and R

∗

= min

For every problem P, IPC

, P) ∈ [0, 1] and higher

means better. We can then sum up the IPC-Score over

several problem instances to get accumulated results.

The IPC-Score takes into account both number of

problems solved as well as quality of solutions found.

We monitor four criteria: total number of problems

solved, IPC-Score of time, IPC-Score of plan length

and IPC-Score of number of expansions.

Figure 5 shows results for the two domains.

We can see that network trained by LogMSE is

superior to the one trained by MSE in all criteria on

both domains. As expected, higher values of q lead

to a more accurate heuristic: the number of expanded

nodes as well as plan length are better. The difference

is apparent especially for values 2 and 3. Using value

q = 4 still helps but computing features in this case is

slower and so A* expands less nodes per second and

overall results are not that much better than for q = 3.

Adding h

as feature has a mixed effect. It is

very helpful on blocks domain when q ∈ {2, 3}, but

not much helpful when q = 4. See ﬁgure 6. This

indicates that subgraphs of size 2 and 3 cannot cap-

ture useful knowledge about a blocks problem hence

the network rely on h

as the source of informa-

tion. Subgraphs of size 4 seem to be able to pro-

vide the required knowledge already and adding h

doesn’t help anymore. This phenomenon is domain-

dependent and should be analyzed further in the fu-

ture. In general, adding h

improves accuracy of the

NN so the resulting heuristic is more informed which

improves both number of expansions and plan length.

Due to the slow-down, though, adding h

doesn’t

often improve number of problems solved.

Figure 6: Number of problems solved in blocks domain

(sum of both MSE and LogMSE). On the X-axis there is

q value, blue columns correspond to networks trained with-

out using h

as feature, orange columns show networks

trained with h

included.

Among the neural-based heuristics, the setting

with q = 4, h

added and LogMSE performs best. If

we compare it with the h

, we see that our method

vastly outperforms the baseline on blocks where it

solved 26 out of 27 problems while h

can only

solve 8 problems. Even on problems solved by both

methods, the NN heuristic ﬁnds shorter plans and ex-

pands less nodes. On the zenotravel domain, our

method outperforms h

in all criteria except Time.

As h

can ﬁnd suboptimal plans very quickly in

zenotravel, it is difﬁcult to achieve better score even

though our method solved more problems within the

time limit.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

6.1 Performance Guarantees

The resulting heuristic is neither admissible nor ε-

admissible for any ε but we can still provide some the-

oretical guarantees of solution quality. We will only

provide here a simple bound and sketch of a proof.

Tighter bounds together with formal statements of

theorems and full proofs will be published in a sep-

arate paper.

Due to the stochastic nature of the NN-training al-

gorithm, output of the trained network on state s (de-

noted H(s)) must be considered a random variable.

Cost of the solution that A* ﬁnds with NN as heuris-

tic from state s (denoted A

(s)) is a random variable

as well. Assuming that ∀s

6= s

, H(s

) and H(s

) are

independent, we can state the following theorem.

Theorem 1. If for all states s: E[H(s)] = h

∗

(s), then

∀c > 1 : Prob[A

) ≥ c ∗ (h

∗

))

] <

Proof (sketch). Lets denote by Opt(s

) the optimal

path from s

to goal (a sequence of states). The

weighted A* efﬁciency theorem (Pearl, 1984) states

that

∀ε ≥ 1 : ∀s : h(s) ≤ ε ∗ h

∗

(s) ⇒ A

) ≤ ε ∗ h

∗

)

By a contraposition of the previous, we have

∀ε ≥ 1 : A

) > ε ∗ h

∗

) ⇒ (1)

∃s

∈ Opt(s

) : H(s

) > ε ∗ h

∗

) (2)

hence

P[A

) > ε ∗ h

∗

)] ≤ (3)

P[∃s

∈ Opt(s

) : H(s

) > ε ∗ h

∗

)] ≤ (4)

∑

∈Opt(s

)

P[H(s

) > ε ∗ h

∗

)] (5)

(3) ≤ (4) comes from (1) ⇒ (2), while (4) ≤ (5)

can be achieved by applying Boole’s inequality which

states:

Lemma 2 (Boole’s inequality). Let A

be events, then

Prob[

] ≤

∑

Prob[A

]

Now, Markov’s inequality states that

∀s

: P[H(s

) ≥ ε ∗ h

∗

)] ≤

E[H(s

)]

ε ∗ h

∗

)

(6)

By substituting (6) to (5) we get:

∑

∈Opt(s

)

P[H(s

) > ε ∗ h

∗

)] ≤

∑

∈Opt(s

)

=| Opt(s

) | ∗

≤ h

∗

) ∗

Now for given c > 1, we set ε = c ∗ h

∗

) which

gives us the required bound.

The proof works for planning without action costs,

i.e. where cost of every action is 1 but the theorem

still holds for planning with action costs.

We don’t require that all H(s

) are identically dis-

tributed. Assumptions of independence and unbiased-

ness of H(s

) can be justiﬁed by analyzing the bias-

variance tradeoff for NNs (Hastie et al., 2001). NNs

in general have high variance and low bias hence for

a large enough network, H(s) should be unbiased and

∀s

, s

: H(s

) and H(s

) should be close to indepen-

dent. Tighter bounds can be acquired if we take vari-

ance of H(s

) into account.

7 CONCLUSIONS & FUTURE

WORK

We presented a technique to automatically construct

a strong heuristic for a given planning domain. Our

technique is domain-independent and can extract

knowledge about any domain from a given set of

solved training problems without any assistance from

a human expert. The knowledge in represented by a

trained neural network.

We analyzed how the choice of loss function used

during the training affects performance of the learned

heuristic. We showed that the Mean Squared Error

– the most popular loss function – is not appropriate

for heuristic learning task and we presented a better

alternative.

We developed a novel technique for generating

features for states where we encode the state de-

scription directly without using existing heuristics.

The method allows to compute features incrementally

which is very useful in planning application. Our ap-

proach falls into category of zero-learning as it works

without any human-knowledge initially added. The

presented technique signiﬁcantly outperforms a popu-

lar domain-independent heuristic h

in both number

of problems solved and solution quality. We have also

provided a simple theoretical bound on solution qual-

ity when using learned heuristic, similar to bounds for

weighted A*.

As a future work, we will provide better bounds

on solution quality and conduct larger experiments on

Deep Learning of Heuristics for Domain-independent Planning

more domains to properly back the claims made in

this paper.

ACKNOWLEDGMENT

Research is supported by the Czech Science Founda-

tion under the project P103-18-07252S.

REFERENCES

Arfaee, S. J., Zilles, S., and Holte, R. C. (2010). Boot-

strap learning of heuristic functions. In Felner, A. and

Sturtevant, N. R., editors, Proceedings of the Third

Annual Symposium on Combinatorial Search, SOCS

2010. AAAI Press.

Arfaee, S. J., Zilles, S., and Holte, R. C. (2011). Learn-

ing heuristic functions for large state spaces. Artiﬁcial

Intelligence, 175(16).

Bisson, F., Larochelle, H., and Kabanza, F. (2015). Using a

recursive neural network to learn an agent’s decision

model for plan recognition. In Twenty-Fourth Interna-

tional Joint Conference on Artiﬁcial Intelligence.

Brunetto, R. and Trunda, O. (2017). Deep heuristic-learning

in the rubik’s cube domain: an experimental evalua-

tion. In Hlav

cov

a, J., editor, Proceedings of the 17th

conference ITAT 2017, pages 57–64. CreateSpace In-

dependent Publishing Platform.

Cenamor, I., De La Rosa, T., and Fern

andez, F. (2013).

Learning predictive models to conﬁgure planning

portfolios. In Proceedings of the 4th workshop on

Planning and Learning (ICAPS-PAL 2013).

Chen, H.-C. and Wei, J.-D. (2011). Using neural networks

for evaluation in heuristic search algorithm. In AAAI.

Fink, M. (2007). Online learning of search heuristics. In

Artiﬁcial Intelligence and Statistics, pages 115–122.

Geissmann, C. (2015). Learning heuristic functions in clas-

sical planning. Master’s thesis, University of Basel,

Switzerland.

Goldberg, Y. (2017). Neural network methods for natural

language processing. Synthesis Lectures on Human

Language Technologies, 10(1):1–309.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Groshev, E., Goldstein, M., et al. (2017). Learning gen-

eralized reactive policies using deep neural networks.

Symposium on Integrating Representation, Reason-

ing, Learning, and Execution for Goal Directed Au-

tonomy.

Groshev, E., Tamar, A., Goldstein, M., Srivastava, S., and

Abbeel, P. (2018). Learning generalized reactive poli-

cies using deep neural networks. In 2018 AAAI Spring

Symposium Series.

Hastie, T., Tibshirani, R., and Friedman, J. (2001). The

Elements of Statistical Learning. Springer Series in

Statistics. Springer New York Inc., New York, NY,

USA.

Hoffmann, J. and Nebel, B. (2001). The ff planning system:

Fast plan generation through heuristic search. Journal

of Artiﬁcial Intelligence Research, 14:253–302.

oller, D., Bercher, P., Behnke, G., and Biundo, S. (2019).

On guiding search in htn planning with classical plan-

ning heuristics. IJCAI.

Jim

enez, S., De la Rosa, T., Fern

andez, S., Fern

andez, F.,

and Borrajo, D. (2012). A review of machine learning

for automated planning. The Knowledge Engineering

Review, 27(4):433–467.

Konidaris, G., Kaelbling, L. P., and Lozano-Perez, T.

(2018). From skills to symbols: Learning symbolic

representations for abstract high-level planning. Jour-

nal of Artiﬁcial Intelligence Research, 61.

Mart

ın, M. and Geffner, H. (2004). Learning generalized

policies from planning examples using concept lan-

guages. Applied Intelligence, 20(1):9–19.

Nau, D., Ghallab, M., and Traverso, P. (2004). Automated

Planning: Theory & Practice. Morgan Kaufmann

Publishers Inc., San Francisco, CA, USA.

Pearl, J. (1984). Heuristics: Intelligent Search Strategies

for Computer Problem Solving. The Addison-Wesley

Series in Artiﬁcial Intelligence. Addison-Wesley.

Samadi, M., Felner, A., and Schaeffer, J. (2008). Learning

from multiple heuristics. In Fox, D. and Gomes, C. P.,

editors, AAAI, pages 357–362. AAAI Press.

Takahashi, T., Sun, H., Tian, D., and Wang, Y. (2019).

Learning heuristic functions for mobile robot path

planning using deep neural networks. In Proceedings

of the International Conference on Automated Plan-

ning and Scheduling, volume 29, pages 764–772.

Thayer, J., Dionne, A., and Ruml, W. (2011). Learning

inadmissible heuristics during search. In Proceedings

of International Conference on Automated Planning

and Scheduling.

Yoon, S., Fern, A., and Givan, R. (2008). Learning control

knowledge for forward search planning. Journal of

Machine Learning Research, 9(Apr):683–718.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence