
Progressive Training in Recurrent Neural Networks for Chord
Progression Modeling
Trung-Kien Vu, Teeradaj Racharak, Satoshi Tojo, Nguyen Ha Thanh and Nguyen Le Minh
School of Information Science, Japan Advanced Institute of Science and Technology, Ishikawa, Japan
Keywords:
Recurrent Neural Network, Chord Progression Modeling, Sequence Prediction, Knowledge Compilation.
Abstract:
Recurrent neural networks (RNNs) can be trained to process sequences of tokens as they show impressive
results in several sequence prediction. In general, when RNNs are trained, their goals are to maximize the
likelihood of each token in the sequence where each token could be represented as a one-hot representation.
That is, the model learns for its sequence prediction from true class labels. However, this creates a potential
drawback, i.e., the model cannot learn from the mistakes. In this work, we propose a progressive learning
strategy that can mitigate the mistakes by using domain knowledge. Our strategy gently changes the training
process from using the class labels guiding scheme to the similarity distribution of class labels instead. Our
experiments on chord progression modeling show that this training paradigm yields significant improvements.
1 INTRODUCTION
Recurrent neural networks (RNNs) can be used to
produce sequences of tokens, given input/output
pairs. Generally, they are trained to maximize the
likelihood of each target token given the current
state of the model and the previous target token, in
which target tokens could be in one-hot representa-
tions (Bengio et al., 2015). This training process helps
the model to learn a language model over sequences
of tokens. In fact, RNNs and their variants, such as
the Long Short-Term Memory (LSTM) and Gated Re-
current Unit (GRU), have shown impressive results in
machine translation such as (Sutskever et al., 2014;
Bahdanau et al., 2015; Meng and Zhang, 2019), im-
age captioning such as (Vinyals et al., 2015), and
chord progression such as (Choi et al., 2016).
When the model is trained from input/output pairs,
it may cause the model per se to mistake the predic-
tion during training steps. Indeed, the model is fully
guided by the true labels at its correct prediction; but,
is less guided otherwise. Different kinds of method-
ologies were proposed to mitigate this kind of learn-
ing efficiency by enriching the input’s information via
transfer learning like word embedding (cf. (Mikolov
et al., 2013; Pennington et al., 2014)) or knowledge
graph embedding (cf. (Ristoski et al., 2019)). This
technique exploits a learnt vector representation at
training time and the learning paradigm can be done
as usual. Despite its promising result, representa-
tion learning requires a large amount of training data,
which may be not easily available. On the other hand,
a learning efficiency can be improved by injecting do-
main knowledge for guiding the learning process. For
instance, (Song et al., 2019) injected medical ontolo-
gies to regularize learnable parameters. In this work,
we concentrate on the latter approach, i.e., how do-
main knowledge can be incorporated at training time?
Intuitively, to address this difficulty, we observe
that the model could be guided by domain knowledge
when it is learnt to produce a wrong prediction. Like
the work done by (Bengio et al., 2015), the model
can be guided by more than one target vectors dur-
ing training. RNNs usually optimize the loss func-
tion between a predicted sequence and the true se-
quence. This kind of optimization causes a potential
drawback, i.e., the model may be mistaken when its
predicted sequence is incorrect. To alleviate this prob-
lem, we compile domain knowledge in terms of sim-
ilarity distribution of class labels. Then, we propose
to change the training process by forcing the model
to learn from two different vectors (i.e. the true tar-
get distribution and the similarity target distribution).
For this, we introduce a progressive learning strategy
which gradually switches from similarity target dis-
tribution to the true target distribution. Doing so, the
model can be learnt to predict a reasonable outcome
when the model generates a token deviating from the
true label. This enables the model to be learnt for pre-
dicting correctly later when it mistakes its prediction
Vu, T., Racharak, T., Tojo, S., Thanh, N. and Minh, N.
Progressive Training in Recurrent Neural Networks for Chord Progression Modeling.
DOI: 10.5220/0008951500890098
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 89-98
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
89
earlier. For instance, in chord progression modeling, a
mistake for predicting G[maj instead of F]maj should
not gain feedback for training equally as a mistake
prediction of Cmaj for the same chord F]maj. This
observation is reasonable because G[maj and F]maj
are fundamentally the same chord (which are named
differently); and, Cmaj and F]maj have no relation-
ship to each other. A neural network should be able to
utilize feedback from similarity information between
class labels at training time.
The contributions of this paper are twofold. First,
we introduce an approach to compile domain knowl-
edge as similarity distributions for injecting at train-
ing time. Second, we propose a progressive learning
strategy to gradually switch the training target from
the similarity distribution to the true distribution. We
elaborate our proposed approach with more techni-
cal details in Section 3. Furthermore, Section 2 and
Section 4 present preliminaries and experimental re-
sults, respectively. Section 5 makes comparisons of
our work with others. Finally, Section 6 discusses the
conclusion and future directions.
2 RNN-BASED SEQUENCE
PREDICTION MODEL
The Hopfield Networks (John, 1982) is the precur-
sor to recurrent neural networks. The architecture of
these neural networks allows the reception of signals
from consecutive inputs. RNNs were invented with
the main idea of using information from the previous
steps to give the most accurate prediction for the cur-
rent prediction step.
In a feed-forward neural network, inputs are pro-
cessed separately; as a result, it cannot capture the re-
lation information between entities in a sequence. In
contrast, a recurrent neural network maintains a loop
of information in its architecture. After being pro-
cessed, an output is fed back into the network to be
processed with the next inputs. RNN has many vari-
ations, but the most famous one is LSTM (Hochreiter
and Schmidhuber, 1997) and GRU (Cho et al., 2014).
Despite the ability to combine information from
inputs of sequences, the recurrent neural network
models have a weakness namely “vanishing gra-
dients”. Processing a long sequence, the model
feeds information across multiple layers and multi-
ple timesteps; as a result, the parameter sequence be-
comes longer. During the training process, loss value
is back-propagated from the output layer to previous
layers for updating all the weights. However, in a long
sequence of parameters, the loss becomes zero at the
beginning of the sequence.
To solve such problems of the recurrent neu-
ral network architecture, Long short-term memory
(LSTM) network was proposed with the idea that
not all inputs in the sequence contribute with impor-
tant information. The LSTM architecture allows the
model to choose which inputs in the sequence are im-
portant and forget the others. A standard LSTM con-
tains an input gate, an output gate and a forget gate as
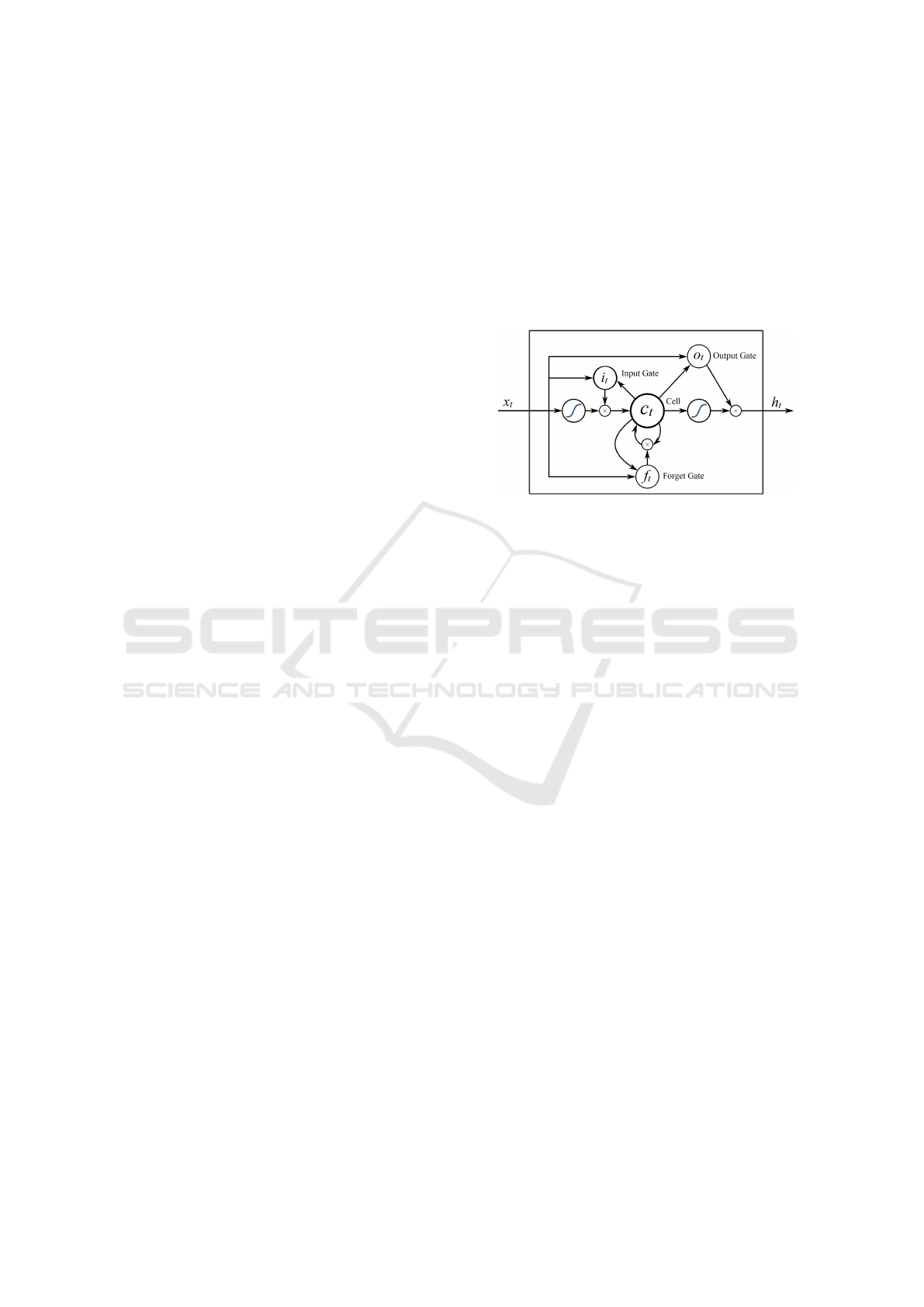
shown in Figure 1.
Figure 1: LSTM architecture can capture longer input se-
quence.
Let i, f and o denote the input, forget and out-
put gates, respectively. Then, the hidden state h
t
in a
LSTM network is calculated as follows:
i
t
= σ(x
t
U
i
+ h
t−1
W
i
+ b
i
) (1)
f
t
= σ(x
t
U
f
+ h
t−1
W
f
+ b
f
) (2)
o
t
= σ(x
t
U
o
+ h
t−1
W
o
+ b
o
) (3)
˜
C
t
= tanh(x
t
U
g
+ h
t−1
W
g
+ b
g
) (4)
C
t
= σ( f
t
∗C
t−1
+ i
t
∗
˜
C
t
) (5)
h
t
= tanh(C
t
) ∗ o
t
(6)
In the equations, U is the weight matrix from the input
and W is the weight matrix from the hidden layer in
the previous time step. C
t
is the memory of the unit
and
˜
C
t
is the candidate for cell state at timestamp t. σ
denotes the sigmoid function and ∗ is the elementwise
multiplication.
LSTM models are effective in sequential tasks. In
sequence tagging, (Huang et al., 2015) proposed a
model that processes the feature in both directions.
In speech recognition, (Graves et al., 2013) used the
bidirectional LSTM and achieved state-of-the-art re-
sults in phoneme recognition. In language modeling,
(Sundermeyer et al., 2012) proved that using LSTM
can bring significant improvement in this task.
3 PROPOSED APPROACH
Multi-class classification is the task of classifying in-
stances into one of K classes and can be trained for
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
90

sequence prediction (cf. Section 2). For that, a neu-
ral network classifier is given a vectorized represen-
tation of an input and produces a K-dimensional pre-
dicted vector
ˆ
y
:
= [ ˆy
1
,..., ˆy
K
], which is a probability
distribution representing the confidence of the clas-
sifier over K classes. In the standard training pro-
cess, the network is trained to generate a high confi-
dence towards the correct class by updating its weight
θ to minimize Kullback-Leibler divergence between
its prediction vector
ˆ
y and the one-hot representation
y of the correct class (cf. Equation 7).
D
KL
(y,
ˆ
y)
:
=
K
∑
i=1
y
i
log
y
i
ˆy
i
(7)
In general, a target distribution y
:
= [y
1
,. ..,y
K
]
can be defined in term of one-hot representation, i.e.,
the true distribution. However, using the true distribu-
tion as a target distribution can cause a neural network
to gain feedback merely through the predicted confi-
dence of the correct class. The feedback through other
classes, which may be helpful for training, is entirely
disregarded. As exemplified in Section 1, the pre-
dicted confidence for each class indeed provides feed-
back for training unequally. A neural network should
be informed that the mistake of prediction on classes
similar to the target class indeed provides more signif-
icant feedback than the unrelated classes. To incorpo-
rate knowledge about similarity perception between
classes, we propose to involve the following steps at
training time:
1. Initialize a distribution capturing the similarity be-
tween classes (cf. Subsection 3.1),
2. Train progressively from the similarity distribu-
tion to the true distribution (cf. Subsection 3.2).
3.1 Similarity Distribution Initialization
To address how the similarity distribution should be
initialized, we first take a look into the literature of
similarity measure. The most basic (but useful) one
was developed by (Tversky, 1977). In Tversky’s
model, an object constitutes a number of properties
(or features). Then, the similarity of two objects is
measured by the relationship between a number of
common properties and a number of different prop-
erties. Nevertheless, not every properties need to be
taken into account for similarity perception. The stud-
ies in (Hesse, 1965; Waller, 2001) reported that prop-
erties involved in similarity perception should be rel-
evant to the context of an application domain. Taking
into account these characteristics, we define the no-
tion of similarity as follows.
Let P
:
= {p
1
, p
2
,. .., p
n
} be a set of properties
constituting all classes in the dataset. We denote the
property set of class a by P
a
, in which P
a
⊆ P . To
capture the notion of relevancy, we define a function
w : P → R
≥0
capturing the importance of properties,
in which w(p
k
) > 0 indicates that p
k
has more impor-
tance and w(p
k
)
:
= 0 indicates that p
k
is of no impor-
tance in an application context. Then, the similarity
between class a and b (denoted by s(a,b)) can be de-
fined in the following equation.
s(a,b)
:
=
∑
p∈P
a
∩P
b
w(p) (8)
Intuitively, Equation 8 calculates the summation of
weighted common properties between two classes.
Let s
a
:
= [s
a1
,. ..,s
aK
] be a vector representing the
similarity of class a against other classes. Equation
9 expresses an approach to construct arbitrary vector
s
a
. Observe that we employ the summation in the de-
nominator part as a normalizing factor.
s
ak
:
=
s(i,k)
∑
K
j=1
s(i, j)
(9)
To turn a similarity vector into a probability mass
distribution t
a
:
= [t
a1
,. ..,t
aK
], we employ the softmax
function as defined in Equation 10. Intuitively, a sim-
ilarity distribution t
a
captures the similarity of class a
against other classes.
t
ak
:
= softmax(s
ak
)
:
=
exp(s
ak
/T )
∑
K
j=1
exp(s
a j
/T )
(10)
where T is a temperature used to control the probabil-
ity mass assigned to a property. Observe that when T
approaches the infinity, the distribution becomes uni-
form. Hence, the common properties shared mostly
among classes contribute a large probability mass. On
the other hand, as T approaches 0, the distribution is
similar to the argmax operation, i.e., it is similar to
one-hot representation. Hence, the unique properties
of constituting classes contribute a large probability
mass.
3.2 Progressive Training with Decay
This subsection proposes a training strategy called
progressive training that enables to train the model
with a similarity distribution and a true distribution.
To handle this style of training properly, we force the
training process to gradually change the target distri-
bution from the similarity distribution to the true dis-
tribution. For that, T must be high at the beginning of
training and periodically be decreased during training.
This training scheme enables the neural network to
learn from common properties at the early stages; and
also, learn from unique properties at the later stages.
Progressive Training in Recurrent Neural Networks for Chord Progression Modeling
91
Specifically, we use a scheduler to decrease tem-
perature T
t
at training epoch t in a similar manner
used by modern stochastic gradient approaches for
decreasing the learning rate. Equation 11 expresses
the scheduler employed in this work.
T
t
:
=
T
t−1
1 + λt
(11)
where T
0
indicates the initial temperature and λ rep-
resents a decay rate. At training epoch t, we generate
a distribution t
a
of the relevant class a with tempera-
ture T
t
and update the parameter θ which minimizes
the loss function D
KL
(t
a
,
ˆ
y). We summarize the train-
ing process in Algorithm 1. Furthermore, Figure 2
illustrates a transition of the similarity target distribu-
tion according to each temperature. We also note that
other schedulers also exist (e.g. linear and exponential
decays) which are not engaged in our experiments;
thus, are remained to investigate as future tasks.
Algorithm 1: Progressive learning with class
similarity distribution.
Input : Property set P , weight function w,
initial temperature T
0
, decay rate λ
Output: Optimal parameter θ
t
1 Compute similarity vector t
a
for any class a
using Equation 9
2 Initialize the parameters θ
0
3 t ← 0
4 while θ
t
not converged do
5 t ← t + 1
6 Compute temperature T
t
using Equation 11
7 Compute similarity target t
a
for class a at
temperature T
t
using Equation 10
8 Update the parameter θ
t
to minimize the
loss function D
KL
(t
a
,
ˆ
y)
9 end
4 EXPERIMENTS
In this section, we specify chord properties used
to generate a similarity distribution and demonstrate
the effectiveness of the proposed method on model-
ing chord progression in Beethoven string quartets.
Source code for all experiments is available online
1
.
4.1 Dataset
The Annotated Beethoven Corpus (ABC) (Neuwirth
et al., 2018) used in this paper contains harmonic
1
https://github.com/kienvu58/chord-progression-
modeling
analyses of all sixteen Beethoven string quartets. Six-
teen string quartets (70 movements) were composed
between 1800–1826, comprising Beethoven’s middle
and late creative phrases; and hence, both the high
Classical and early Romantic eras. We split each
piece into phrases and removed continuous chord rep-
etitions in each phrase since we would not model
the duration of each chord. In total, there were 968
phrases with an average length of 21.
We used 5-fold cross-validation and reported the
performance of models in terms of perplexity and ac-
curacy. For each fold, there were about 200 phrases
to evaluate models and remaining phrases were split
into training and validation set. For the training set,
we augmented the data by transposing each phrase
into 12 keys, resulting in the training dataset of about
8000 samples.
For chord vocabulary, we used 273 chord tokens.
Each chord token has two parts: the key and the chord
type. There are 21 keys which are A, B, C, D, E, F, G,
A[, B[, C[, D[, E[, F[, G[, A], B], C], D], E], F], and
G]. Furthermore, there are 13 chord types which are:
major triad, minor triad, augmented triad, diminished
triad, dominant seventh chord, minor seventh chord,
major seventh chord, diminished seventh chord, half-
diminished seventh chord, augmented seventh chord,
Italian augmented sixth chord, German augmented
sixth chord, and French augmented sixth chord.
4.2 Experimental Settings
4.2.1 Chord Properties
In our experiments, we defined according to the music
structure that a chord consists of 6 properties and they
were used to compute the similarity between chords.
These properties are formally given as follows:
P = {token name,key name,key number,
triad form, figured bass, note pair }
Property token name is the name of the token us-
ing to represent a chord. If property token name is
the only property in the set P , then this is equivalent
to using a one-hot representation as a target distribu-
tion.
Property key name is the name of a chord key,
which takes one of 21 values mentioning in the previ-
ous section.
Property key number is the value of the chord key,
which is a number from 0 to 11. If two chords have
the same key number but the different key name, then
their keys are enharmonic. For example, F] and G[
are enharmonic keys.
Property triad form is the chord form of the first
three notes in a chord. There are four kinds of
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
92
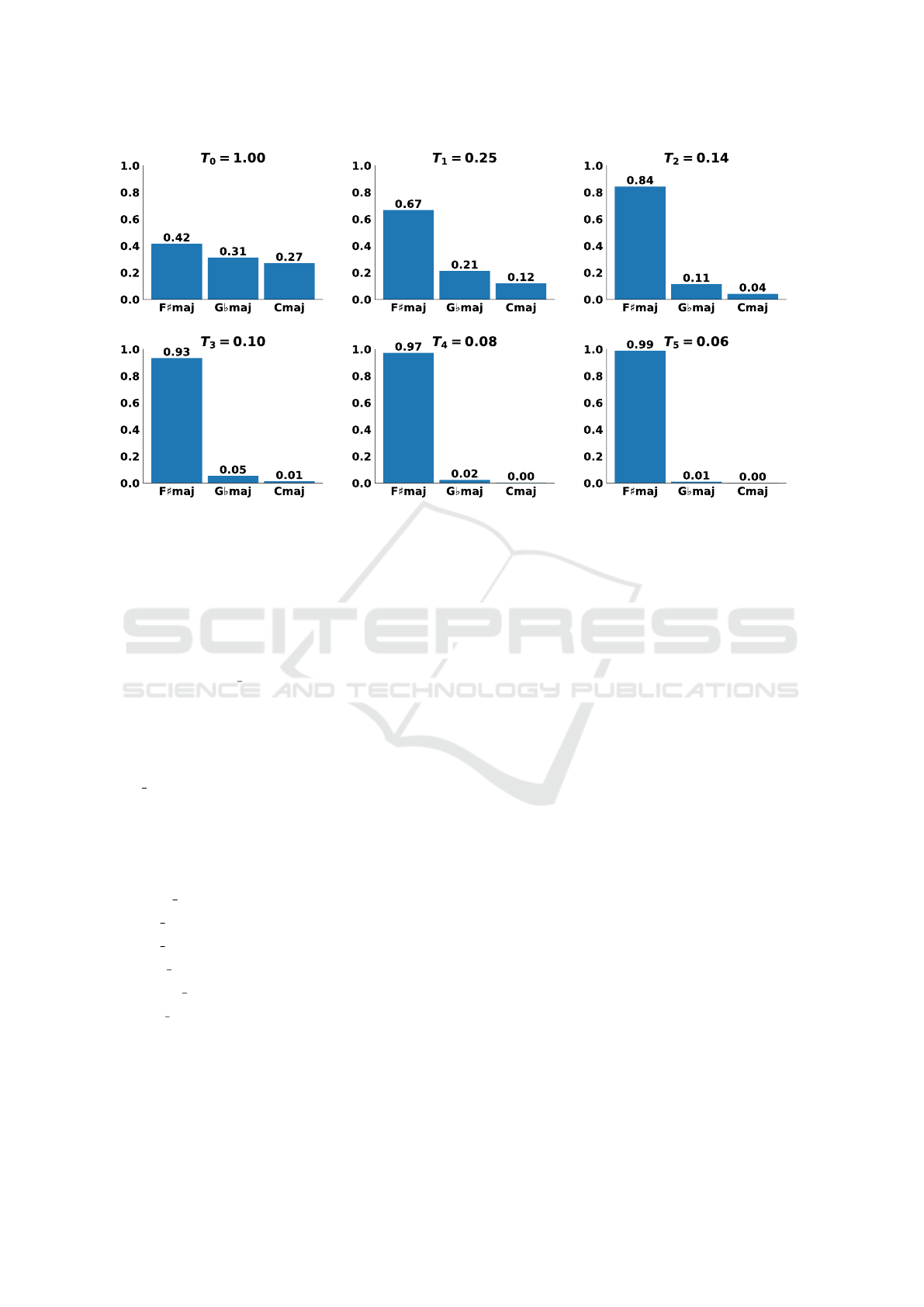
Figure 2: Transition of a similarity target distribution according to each temperature. The initial temperature is T
0
:
= 1.00 and
the decay rate is λ
:
= 3.00. The similarity target gradually becomes a one-hot representation.
chord form, namely minor, major, diminished, or aug-
mented form. Each chord form produces a different
musical effect. For instance, the major form is gen-
erally perceived as positive-sounding and the minor
is generally perceived as negative-sounding (Bakker
and Martin, 2015; Gagnon and Peretz, 2003).
Property figured bass is used to categorize a chord
into a triad, a seventh, or an augmented sixth. Each of
these chord types has a different role in a chord pro-
gression. For example, augmented sixth chords are
usually used as a predominant function.
Furthermore, each chord can have multiple
note pair properties, which are note pairs created
from the chord note set.
Finally, we exemplify the identification of a chord
according to these properties, For example, C domi-
nant seventh chord contains 4 notes C(0), E(4), G(7),
B[(10). It has the following properties:
• token name: C7
• key number: 0
• key name: C
• triad
form: major
• figured bass: 7
• note pair: (0, 4), (0, 7), (0, 10) (4, 7), (4, 10), (7,
10)
4.2.2 Temperature Decay Configurations
As proposed in Section 3.2, we periodically update
similarity distributions during the training stage us-
ing Equation 11. To find optimal values of the initial
temperature and decay rate, we grid-search the initial
temperature in {0.01,0.025,0.05,0.0075,0.1} and
the decay rate in {0.0005,0.001, 0.0025,0.005, 0.01}.
Also, we compared the performance of models
when training with similarity distributions generated
from fixed temperatures and scheduled temperatures.
We sampled 10 fixed temperatures from the schedul-
ing equation (Equation 11).
4.2.3 Model Configurations
We investigated the effectiveness of the proposed
method on an LSTM-based neural network, consist-
ing of 3 layers: embedding, recurrent, and fully-
connected layers. We used Adam optimizer (Kingma
and Ba, 2014) with the learning rate of 0.001 and de-
fault hyper-parameters suggested by the authors. For
all experiments, the maximum number of epochs was
set to 200, and early stopping with the patience value
of 10 was used to prevent over-fitting. All hyper-
parameter settings are summarized in Table 1.
4.3 Experimental Results
4.3.1 One-hot vs. Similarity Distributions
Table 2 shows the performance of models training
with similarity distributions and one-hot distributions.
In this experiment, we used the same weight for all
chord properties and different initial temperatures and
decay rates to generate similarity distributions.
Progressive Training in Recurrent Neural Networks for Chord Progression Modeling
93

Table 1: Hyper-parameter settings for all experiments.
Hyper-parameter Setting
Embedding
Embedding size 128
Recurrent cells
LSTM hidden size 128
Fully-connected
Number of layers 1
Fully-connected hidden size 128
Training
Optimizer Adam
Learning rate α 0.001
β
1
0.9
β
2
0.999
ε 10
−8
Batch size 32
Maximum number of epochs 200
Early stopping patience 10
In general, the performance of all models training
with similarity distributions is better than one train-
ing with one-hot distributions. The highest accuracy
is 0.71, which is about 29% higher than the model
training with one-hot distributions. The lowest per-
plexity is 2.44, which is about 30% lower.
Moreover, there is a relation between the magni-
tude of initial temperatures and decay rates in the re-
sults. When the initial temperature is high, using large
decay rates produce a better model and vice versa.
This suggests that we can fix a reasonable initial tem-
perature and grid-search for an optimal decay rate.
This reduces the search space of hyper-parameters.
4.3.2 Fixed vs. Scheduled Temperature
Table 3 and Table 4 show the performance of mod-
els training with fixed and scheduled temperatures in
terms of accuracy and perplexity. The first column
in these tables shows the property weight set used
to generate similarity distribution and the headers’ ti-
tle indicates the temperature values. We used Equa-
tion 11 with T
0
= 0.05 and λ = 0.001 to schedule the
temperature. We sampled temperatures at 10 time-
steps with the interval value of 20 to generate fixed
similarity distributions.
In general, models training with scheduled tem-
peratures have better performance than ones train-
ing with fixed temperatures. At fixed temperature
settings, models training with high temperatures had
worse performance than ones training with low tem-
peratures. The reason is similarity distributions gen-
erated with high temperatures have higher entropy,
thus models fitting these distributions tend to produce
Table 2: Performance of models training with uniform
weight set (1, 1, 1, 1, 1, 1).
T
0
λ accuracy perplexity
0.1 0.01 0.68 2.60
0.1 0.005 0.71 2.47
0.1 0.0025 0.71 2.50
0.1 0.001 0.69 2.57
0.1 0.0005 0.66 2.77
0.075 0.01 0.70 2.44
0.075 0.005 0.69 2.55
0.075 0.0025 0.71 2.48
0.075 0.001 0.68 2.62
0.075 0.0005 0.67 2.71
0.05 0.01 0.67 2.55
0.05 0.005 0.70 2.46
0.05 0.0025 0.70 2.50
0.05 0.001 0.71 2.49
0.05 0.0005 0.64 2.93
0.025 0.01 0.63 2.73
0.025 0.005 0.64 2.73
0.025 0.0025 0.70 2.46
0.025 0.001 0.70 2.53
0.025 0.0005 0.69 2.59
0.01 0.01 0.56 3.19
0.01 0.005 0.55 3.31
0.01 0.0025 0.58 3.04
0.01 0.001 0.64 2.67
0.01 0.0005 0.66 2.64
Train with one-hot 0.55 3.48
more random predictions.
Also, we investigated the effect of individual
properties in contribution to the performance of mod-
els. We specify the weight of each property in a
6-dimension tuple, each dimension is correspond-
ing to one of six properties: token
name, key name,
triad form, figured bass, and note pair respectively.
We used only two properties once at a time, with
one of them is property token name since this is the
unique property to distinguish chords from each other.
We fixed the weight of the property token name with
a value of 16 and grid-searched the weight of the other
property in {2, 4,8, 16,32}. Weights of unused prop-
erties were set to zeros.
The results show that the models training with
similarity distributions generated using two properties
token name and note pair have better performance
than others on average. This could be expected since
intuitively the property note pair encodes more infor-
mation than other properties. Also, similarity distri-
butions generated from all properties probably still
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
94

Table 3: Accuracy of models training with fixed and scheduled temperature.
Properties’ Weight Scheduled 5.00E-02 4.06E-02 2.23E-02 8.31E-03 2.13E-03 3.77E-04 4.63E-05 3.98E-06 2.41E-07 1.04E-08
(16, 0, 0, 0, 0, 1) 0.57 0.38 0.41 0.52 0.55 0.55 0.54 0.54 0.54 0.55 0.53
(16, 0, 0, 0, 0, 2) 0.68 0.33 0.34 0.45 0.54 0.54 0.55 0.54 0.54 0.54 0.54
(16, 0, 0, 0, 0, 4) 0.69 0.26 0.31 0.37 0.54 0.55 0.54 0.53 0.55 0.55 0.54
(16, 0, 0, 0, 0, 8) 0.70 0.26 0.26 0.37 0.51 0.54 0.54 0.54 0.55 0.54 0.55
(16, 0, 0, 0, 0, 16) 0.70 0.19 0.26 0.35 0.47 0.54 0.54 0.55 0.52 0.54 0.55
(16, 0, 0, 0, 0, 32) 0.70 0.16 0.20 0.31 0.43 0.54 0.55 0.55 0.54 0.54 0.55
(16, 0, 0, 0, 1, 0) 0.61 0.39 0.39 0.52 0.55 0.53 0.54 0.55 0.54 0.54 0.54
(16, 0, 0, 0, 2, 0) 0.68 0.26 0.30 0.40 0.54 0.54 0.55 0.55 0.54 0.54 0.54
(16, 0, 0, 0, 4, 0) 0.69 0.10 0.11 0.31 0.47 0.53 0.54 0.55 0.55 0.53 0.54
(16, 0, 0, 0, 8, 0) 0.67 0.08 0.08 0.14 0.43 0.54 0.54 0.54 0.54 0.54 0.54
(16, 0, 0, 0, 16, 0) 0.64 0.07 0.07 0.09 0.22 0.48 0.54 0.55 0.55 0.54 0.54
(16, 0, 0, 0, 32, 0) 0.65 0.06 0.07 0.08 0.12 0.46 0.55 0.55 0.53 0.54 0.53
(16, 0, 0, 1, 0, 0) 0.56 0.43 0.49 0.55 0.54 0.54 0.55 0.55 0.54 0.55 0.54
(16, 0, 0, 2, 0, 0) 0.67 0.37 0.45 0.49 0.54 0.54 0.55 0.54 0.54 0.54 0.54
(16, 0, 0, 4, 0, 0) 0.68 0.18 0.26 0.42 0.53 0.53 0.55 0.54 0.54 0.55 0.54
(16, 0, 0, 8, 0, 0) 0.67 0.15 0.10 0.24 0.49 0.55 0.54 0.54 0.53 0.55 0.54
(16, 0, 0, 16, 0, 0) 0.66 0.08 0.09 0.13 0.40 0.53 0.54 0.54 0.53 0.55 0.55
(16, 0, 0, 32, 0, 0) 0.65 0.07 0.08 0.10 0.18 0.46 0.55 0.54 0.54 0.54 0.55
(16, 0, 1, 0, 0, 0) 0.54 0.55 0.55 0.54 0.55 0.54 0.55 0.54 0.54 0.54 0.54
(16, 0, 2, 0, 0, 0) 0.53 0.50 0.53 0.53 0.54 0.53 0.54 0.55 0.54 0.55 0.53
(16, 0, 4, 0, 0, 0) 0.55 0.37 0.43 0.54 0.54 0.55 0.55 0.54 0.55 0.54 0.54
(16, 0, 8, 0, 0, 0) 0.59 0.31 0.32 0.46 0.54 0.54 0.53 0.55 0.55 0.54 0.54
(16, 0, 16, 0, 0, 0) 0.65 0.25 0.27 0.38 0.51 0.54 0.54 0.54 0.54 0.55 0.54
(16, 0, 32, 0, 0, 0) 0.65 0.24 0.26 0.34 0.48 0.55 0.53 0.55 0.54 0.55 0.55
(16, 1, 0, 0, 0, 0) 0.53 0.55 0.54 0.55 0.55 0.54 0.55 0.54 0.53 0.54 0.54
(16, 2, 0, 0, 0, 0) 0.54 0.55 0.54 0.54 0.55 0.54 0.55 0.54 0.55 0.55 0.53
(16, 4, 0, 0, 0, 0) 0.54 0.52 0.54 0.54 0.55 0.54 0.54 0.54 0.54 0.54 0.54
(16, 8, 0, 0, 0, 0) 0.56 0.40 0.44 0.54 0.54 0.55 0.51 0.54 0.54 0.54 0.54
(16, 16, 0, 0, 0, 0) 0.59 0.36 0.40 0.51 0.54 0.54 0.54 0.54 0.55 0.55 0.55
(16, 32, 0, 0, 0, 0) 0.60 0.31 0.35 0.45 0.53 0.55 0.54 0.54 0.55 0.54 0.53
(1, 1, 1, 1, 1, 1) 0.71 0.10 0.10 0.26 0.40 0.54 0.55 0.54 0.55 0.54 0.55
Table 4: Perplexity of models training with fixed and scheduled temperature.
Properties’ Weight Scheduled 5.00E-02 4.06E-02 2.23E-02 8.31E-03 2.13E-03 3.77E-04 4.63E-05 3.98E-06 2.41E-07 1.04E-08
(16, 0, 0, 0, 0, 1) 3.19 32.86 19.17 5.06 3.47 3.49 3.51 3.56 3.53 3.51 3.74
(16, 0, 0, 0, 0, 2) 2.54 73.81 55.23 12.79 3.65 3.52 3.50 3.61 3.78 3.63 3.56
(16, 0, 0, 0, 0, 4) 2.50 109.18 89.79 37.77 4.27 3.51 3.56 3.80 3.47 3.51 3.65
(16, 0, 0, 0, 0, 8) 2.46 121.70 114.00 61.17 7.40 3.58 3.65 3.62 3.52 3.53 3.48
(16, 0, 0, 0, 0, 16) 2.45 133.34 117.52 76.82 14.45 3.81 3.60 3.50 3.98 3.66 3.46
(16, 0, 0, 0, 0, 32) 2.44 135.78 124.38 84.53 20.14 5.13 3.51 3.52 3.57 3.55 3.46
(16, 0, 0, 0, 1, 0) 2.87 42.33 28.85 5.43 3.48 3.70 3.59 3.49 3.65 3.52 3.57
(16, 0, 0, 0, 2, 0) 2.59 100.39 80.88 26.54 3.79 3.60 3.46 3.46 3.65 3.59 3.56
(16, 0, 0, 0, 4, 0) 2.59 138.53 132.11 75.39 9.41 3.73 3.53 3.53 3.48 3.73 3.61
(16, 0, 0, 0, 8, 0) 2.71 144.80 142.20 119.56 33.43 3.65 3.62 3.60 3.53 3.54 3.62
(16, 0, 0, 0, 16, 0) 3.03 147.71 143.68 129.42 78.43 7.56 3.55 3.52 3.47 3.55 3.70
(16, 0, 0, 0, 32, 0) 2.91 147.03 143.16 131.12 94.99 24.03 3.46 3.46 3.87 3.61 3.74
(16, 0, 0, 1, 0, 0) 3.34 15.90 8.25 3.50 3.61 3.57 3.40 3.48 3.54 3.46 3.60
(16, 0, 0, 2, 0, 0) 2.55 52.35 23.36 7.21 3.65 3.57 3.54 3.61 3.55 3.65 3.58
(16, 0, 0, 4, 0, 0) 2.67 113.22 89.94 29.01 3.90 3.66 3.53 3.57 3.62 3.44 3.55
(16, 0, 0, 8, 0, 0) 2.73 117.66 127.01 78.11 9.31 3.48 3.62 3.55 3.90 3.43 3.60
(16, 0, 0, 16, 0, 0) 2.85 137.28 129.85 102.09 28.62 3.77 3.64 3.60 3.82 3.50 3.49
(16, 0, 0, 32, 0, 0) 2.91 138.28 132.57 106.69 56.22 8.10 3.49 3.59 3.63 3.56 3.48
(16, 0, 1, 0, 0, 0) 3.68 3.82 3.59 3.54 3.43 3.61 3.52 3.57 3.50 3.56 3.52
(16, 0, 2, 0, 0, 0) 3.93 7.98 4.98 3.75 3.60 3.98 3.53 3.46 3.66 3.48 3.74
(16, 0, 4, 0, 0, 0) 3.46 28.21 16.40 4.10 3.55 3.48 3.49 3.54 3.52 3.65 3.53
(16, 0, 8, 0, 0, 0) 3.00 63.37 46.70 11.80 3.68 3.61 3.87 3.48 3.53 3.52 3.61
(16, 0, 16, 0, 0, 0) 2.66 97.26 80.50 28.65 5.02 3.55 3.55 3.60 3.57 3.49 3.64
(16, 0, 32, 0, 0, 0) 2.64 108.11 93.90 48.26 9.78 3.54 3.69 3.52 3.59 3.42 3.44
(16, 1, 0, 0, 0, 0) 3.66 3.44 3.64 3.48 3.50 3.65 3.47 3.67 4.10 3.61 3.53
(16, 2, 0, 0, 0, 0) 3.51 3.71 3.62 3.57 3.47 3.56 3.43 3.58 3.47 3.52 3.80
(16, 4, 0, 0, 0, 0) 3.55 6.83 4.38 3.55 3.44 3.59 3.70 3.55 3.63 3.65 3.61
(16, 8, 0, 0, 0, 0) 3.27 26.90 14.02 3.82 3.56 3.49 4.25 3.53 3.63 3.54 3.60
(16, 16, 0, 0, 0, 0) 3.01 53.50 35.36 7.15 3.58 3.64 3.61 3.56 3.50 3.50 3.48
(16, 32, 0, 0, 0, 0) 2.96 72.86 54.11 16.19 4.17 3.53 3.56 3.56 3.54 3.62 3.78
(1, 1, 1, 1, 1, 1) 2.49 159.26 145.45 112.62 38.33 3.88 3.51 3.56 3.51 3.63 3.43
Progressive Training in Recurrent Neural Networks for Chord Progression Modeling
95

produce better models than similarity distributions
generated from two individual properties.
To further investigate, we chose the best weight
(in terms of accuracy then perplexity) for each prop-
erty in these experiments and combined them into the
weight set (16,32,16,4,4,32). Table 5 shows the per-
formance of models training with this weight set. The
best perplexity and accuracy are 2.39 and 0.71 respec-
tively. This is slightly better than training with a uni-
form weight set. This means we probably do not need
to search for an optimal weight set but can still get a
significant improvement when comparing to training
with one-hot distributions.
Table 5: Performance of models training with weight set
(16, 32, 16, 4, 4, 32).
T
0
λ accuracy perplexity
0.1 0.01 0.58 3.21
0.1 0.005 0.59 3.13
0.1 0.0025 0.58 3.32
0.1 0.001 0.59 3.17
0.1 0.0005 0.57 3.23
0.075 0.01 0.71 2.41
0.075 0.005 0.71 2.42
0.075 0.0025 0.63 2.79
0.075 0.001 0.60 2.99
0.075 0.0005 0.59 3.11
0.05 0.01 0.66 2.70
0.05 0.005 0.70 2.45
0.05 0.0025 0.69 2.52
0.05 0.001 0.69 2.47
0.05 0.0005 0.61 2.91
0.025 0.01 0.64 2.87
0.025 0.005 0.66 2.65
0.025 0.0025 0.68 2.55
0.025 0.001 0.71 2.39
0.025 0.0005 0.66 2.58
0.01 0.01 0.62 2.95
0.01 0.005 0.66 2.68
0.01 0.0025 0.64 3.31
0.01 0.001 0.68 2.59
0.01 0.0005 0.63 2.81
5 RELATED WORK
Most of the literature on enhancing learning’s effi-
ciency relies on the idea of exploiting much knowl-
edge at training; for instance, transfer learning, multi-
task learning, knowledge compilation, and curriculum
learning. We review each of them as follows.
In transfer learning, two different application do-
mains (called the source and the target) are consid-
ered, in which its main purpose is to utilize the learnt
parameters from the source domain into the target
problem. Efforts on this issue have been made in sev-
eral areas such as computer vision (cf. (Krizhevsky
et al., 2012) for an example of pre-trained model
on ImageNet) and natural language processing (cf.
Word2Vec (Mikolov et al., 2013; Pennington et al.,
2014) for the word embedding using neural net-
works). Approaches similar to Word2Vec can be also
applied to learn vector-based representations from
structured knowledge like ontologies and knowledge
graph. For instance, (Ristoski et al., 2019) exploited
medical ontologies to improve the quality of the learnt
representations and prediction performance. Despite
their promising results, this approach requires a large
volume of the source dataset.
Multi-task learning aims at leveraging the inter-
class relationship at training time. For instance, (Vu-
ral et al., 2009) developed a multi-class large margin
classifier that extracts and takes advantage of class re-
lationships. For the subject of video classification,
(Wu et al., 2014) learned feature relationships and ex-
ploited the class relationship in a neural network to
improve the prediction.
Knowledge can be compiled and distilled to a tar-
get problem. For instance, (Hinton et al., 2015) as-
sumed that two different models (called a teacher
model and a student model) do exist and proposed a
technique for distilling the knowledge of the teacher
model to the student model. Indeed, the authors
aimed at developing a compression technique in a
sense that the teacher model is an ensemble of many
models or a large highly regularized model and the
student model can be a smaller one. This technique
can be also used as a regularization method such that a
target model can imitate a source model to avoid over-
fitting (cf. (Asami et al., 2017)). Furthermore, when
categorical information is available for compilation,
feature vectors can also be built from similarity across
categories. For instance, (Cerda et al., 2018) proposed
a similarity encoding approach to obtain a better rep-
resentation of categorical variables, especially in the
presence of dirty categorical data.
In curriculum learning, two different kinds of
training examples, viz. the easy ones and the diffi-
cult ones, are considered at training time. Then, this
approach starts the training from easy examples and
gradually increase the difficulty of learning by train-
ing with difficult examples. For instance, (Bengio
et al., 2015) employed this style of learning for se-
quence prediction, in which the easy examples were
the known tokens and the difficult examples were the
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
96

realistic ones provided by the model itself. The au-
thors also showed that several sequence prediction
tasks could yield performance improvements and did
not incur longer training times.
Considering the interclass relationship and sched-
uled learning, our approach is similar to multi-task
learning and curriculum learning. However, our
method differs from those in the sense that the domain
knowledge about classes’ structure is used to con-
struct the similarity target distribution and the train-
ing objective is forced to go from the similarity dis-
tribution to the true distribution. Indeed, the domain
knowledge about similarity is used to penalize the
model when a wrong-but-not-totally-incorrect predic-
tion has been made. Experiments in chord progress
modeling were conduced to warrant our investigation.
6 CONCLUSION
This paper introduces an approach to incorporate the
domain knowledge about class similarity at training
time. For that, we define similarity as weighted com-
mon properties and propose a learning strategy called
progressive training for enabling the model to learn
from both a similarity distribution and the true distri-
bution during training. Specifically, instead of consid-
ering merely one-hot encoding, our method leverages
interclass similarity encoding by utilizing the temper-
ature during the training phase. Our experiments on
chord progression reveal that our proposed approach
can yield predictive performance improvement with-
out incurring longer training time.
It is worth observing that the idea proposed in this
work is general enough in such a way that it should
be applicable to a variety of common tasks; for in-
stance, classes in CIFAR-10
2
are somewhat hierar-
chical; also, certain words in the embedding space
are distinguishable whether they are similar or not.
Hence, it is a natural step for us to extend the exper-
iments to these tasks. Another interesting direction
involves further investigation on the automatic con-
struction of similarity encoding, as well as exploring
alternative methods for scheduling strategies and sim-
ilarity distance functions.
REFERENCES
Asami, T., Masumura, R., Yamaguchi, Y., Masataki, H., and
Aono, Y. (2017). Domain adaptation of dnn acoustic
2
https://www.cs.toronto.edu/∼kriz/cifar.html
models using knowledge distillation. In 2017 IEEE In-
ternational Conference on Acoustics, Speech and Sig-
nal Processing (ICASSP), pages 5185–5189.
Bahdanau, D., Cho, K., and Bengio, Y. (2015). Neural
machine translation by jointly learning to align and
translate. In 3rd International Conference on Learn-
ing Representations, ICLR 2015, San Diego, CA, USA,
May 7-9, 2015, Conference Track Proceedings.
Bakker, D. R. and Martin, F. H. (2015). Musical chords
and emotion: Major and minor triads are processed
for emotion. Cognitive, Affective, & Behavioral Neu-
roscience, 15(1):15–31.
Bengio, S., Vinyals, O., Jaitly, N., and Shazeer, N. (2015).
Scheduled sampling for sequence prediction with re-
current neural networks. In Proceedings of the 28th
International Conference on Neural Information Pro-
cessing Systems - Volume 1, NIPS’15, pages 1171–
1179, Cambridge, MA, USA. MIT Press.
Cerda, P., Varoquaux, G., and K
´
egl, B. (2018). Similarity
encoding for learning with dirty categorical variables.
Machine Learning, 107(8):1477–1494.
Cho, K., Van Merri
¨
enboer, B., Gulcehre, C., Bahdanau, D.,
Bougares, F., Schwenk, H., and Bengio, Y. (2014).
Learning phrase representations using rnn encoder-
decoder for statistical machine translation. arXiv
preprint arXiv:1406.1078.
Choi, K., Fazekas, G., and Sandler, M. B. (2016). Text-
based LSTM networks for automatic music composi-
tion. CoRR, abs/1604.05358.
Gagnon, L. and Peretz, I. (2003). Mode and tempo relative
contributions to “happy-sad” judgements in equitone
melodies. Cognition and emotion, 17(1):25–40.
Graves, A., Mohamed, A.-r., and Hinton, G. (2013).
Speech recognition with deep recurrent neural net-
works. In 2013 IEEE international conference on
acoustics, speech and signal processing, pages 6645–
6649. IEEE.
Hesse, M. B. (1965). Models and analogies in science.
Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling
the knowledge in a neural network. arXiv preprint
arXiv:1503.02531.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9(8):1735–1780.
Huang, Z., Xu, W., and Yu, K. (2015). Bidirectional
lstm-crf models for sequence tagging. arXiv preprint
arXiv:1508.01991.
John, J. H. (1982). Neural network and physical systems
with emergent collective computational abilities. Pro-
ceedings of the National Academy of Sciences of the
United States of America, 79:2554–2558.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in Neural Information Pro-
cessing Systems 25: 26th Annual Conference on Neu-
ral Information Processing Systems 2012. Proceed-
ings of a meeting held December 3-6, 2012, Lake
Tahoe, Nevada, United States., pages 1106–1114.
Progressive Training in Recurrent Neural Networks for Chord Progression Modeling
97

Meng, F. and Zhang, J. (2019). DTMT: A novel deep tran-
sition architecture for neural machine translation. In
The Thirty-Third AAAI Conference on Artificial Intel-
ligence, AAAI 2019, The Thirty-First Innovative Ap-
plications of Artificial Intelligence Conference, IAAI
2019, The Ninth AAAI Symposium on Educational
Advances in Artificial Intelligence, EAAI 2019, Hon-
olulu, Hawaii, USA, January 27 - February 1, 2019.,
pages 224–231.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).
Efficient estimation of word representations in vector
space. arXiv preprint arXiv:1301.3781.
Neuwirth, M., Harasim, D., Moss, F. C., and Rohrmeier,
M. (2018). The Annotated Beethoven Corpus (ABC):
A Dataset of Harmonic Analyses of All Beethoven
String Quartets. Frontiers in Digital Humanities, 5:16.
Pennington, J., Socher, R., and Manning, C. (2014). Glove:
Global vectors for word representation. In Proceed-
ings of the 2014 Conference on Empirical Methods in
Natural Language Processing (EMNLP), pages 1532–
1543, Doha, Qatar. Association for Computational
Linguistics.
Ristoski, P., Rosati, J., Noia, T. D., Leone, R. D., and Paul-
heim, H. (2019). Rdf2vec: RDF graph embeddings
and their applications. Semantic Web, 10(4):721–752.
Song, L., Cheong, C. W., Yin, K., Cheung, W. K., Fung,
B. C. M., and Poon, J. (2019). Medical concept em-
bedding with multiple ontological representations. In
Proceedings of the Twenty-Eighth International Joint
Conference on Artificial Intelligence, IJCAI-19, pages
4613–4619. International Joint Conferences on Artifi-
cial Intelligence Organization.
Sundermeyer, M., Schl
¨
uter, R., and Ney, H. (2012). Lstm
neural networks for language modeling. In Thirteenth
annual conference of the international speech commu-
nication association.
Sutskever, I., Vinyals, O., and Le, Q. V. (2014). Sequence to
sequence learning with neural networks. In Proceed-
ings of the 27th International Conference on Neural
Information Processing Systems - Volume 2, NIPS’14,
pages 3104–3112, Cambridge, MA, USA. MIT Press.
Tversky, A. (1977). Features of similarity. Psychological
review, 84(4):327.
Vinyals, O., Toshev, A., Bengio, S., and Erhan, D. (2015).
Show and tell: A neural image caption generator. In
IEEE Conference on Computer Vision and Pattern
Recognition, CVPR 2015, Boston, MA, USA, June 7-
12, 2015, pages 3156–3164.
Vural, V., Fung, G., Rosales, R., and Dy, J. G. (2009).
Multi-class classifiers and their underlying shared
structure. In IJCAI.
Waller, B. N. (2001). Classifying and analyzing analogies.
Informal Logic, 21(3).
Wu, Z., Jiang, Y.-G., Wang, J., Pu, J., and Xue, X. (2014).
Exploring inter-feature and inter-class relationships
with deep neural networks for video classification. In
Proceedings of the 22Nd ACM International Confer-
ence on Multimedia, MM ’14, pages 167–176, New
York, NY, USA. ACM.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
98
