
Improving Semantic Similarity of Words by Retrofitting Word Vectors in
Sense Level
Rui Zhang
a
, Peter Schneider-Kamp
b
and Arthur Zimek
c
Mathematics & Computer Science, University of Southern Denmark, Campusvej 55, Odense, Denmark
Keywords:
Natural Language Processing, Post-processing Model, Retrofitting, Word Representations, Knowledge-based
Sense Representations, Negative Sampling, Semantic Similarity.
Abstract:
This paper presents an approach for retrofitting pre-trained word representations into sense level representa-
tions to improve semantic distinction of words. We use semantic relations as positive and negative examples
to refine the results of a pre-trained model instead of integrating them into the objective functions used during
training. We experimentally evaluate our approach on two word similarity tasks by retrofitting six datasets gen-
erated from three widely used techniques for word representation using two different strategies. Our approach
significantly and consistently outperforms three state-of-the-art retrofitting approaches.
1 INTRODUCTION
Distributed word representations based on word vec-
tors learned from distributional information about
words in large corpora have become a central tech-
nique in Natural Language Processing (NLP). On ba-
sis of the distributional hypothesis (Harris, 1954),
methods convert words into vectors by linguistic con-
texts as “predictive” models (Mikolov et al., 2013a,b;
Bojanowski et al., 2017; Grave et al., 2017) or by
co-occurring words as “count-based” models (Pen-
nington et al., 2014). Both of them depend on “co-
occurrence” information on words in a large unla-
beled corpus. In general, we can observe that the
larger data they use, the better such methods tend to
perform on NLP tasks.
These approaches for constructing vector spaces
predominantly focus on contextual relationships or
word morphology. They disregard the constraints ob-
tainable from lexicons which provide semantic in-
formation by identifying synonym, antonym, hyper-
nymy, hyponymy, and paraphrase relations. This im-
pedes their performance on word similarity tasks and
applications where word similarity plays a significant
role such as, e.g., text simplification.
Existing approaches for exploiting external se-
mantic knowledge to improve word vectors can
a
https://orcid.org/0000-0001-9126-9790
b
https://orcid.org/0000-0003-4000-5570
c
https://orcid.org/0000-0001-7713-4208
be grouped into two categories (Vulic and Glavas,
2018): (1) joint specialization models integrate se-
mantic constraints on word similarity by modify-
ing the objective of the original word vector train-
ing in joint neural language models (Yu and Dredze,
2014; Mikolov et al., 2018) or by incorporating
relation-specific constraints like the co-occurrence
matrix (Chang et al., 2013) or word ordinal ranking
(Liu et al., 2015a) into models; (2) post-processing
models retrofit or refine the pre-trained distributional
word vectors in order to fit the semantic constraints
(Faruqui et al., 2015; Shiue and Ma, 2017; Lee et al.,
2018; Vulic and Glavas, 2018).
Compared with joint specialization models, post-
processing models are more flexible because they can
be applied to all kinds of distributional spaces. Fur-
thermore, post-processing approaches do not need to
re-train models on the large corpora typically used,
which is more convenient both for research purposes
and in applications.
Recent work on post-processing approaches,
mainly based on the graph-based learning technique
(Faruqui et al., 2015; Yu et al., 2017; Lee et al., 2018),
has had a great influence on the field of retrofitting
word vectors. Yet, these studies specifically show
the significant improvements on benchmarks of eval-
uation datasets such as MEN (Bruni et al., 2014) or
WordSim-353 (Finkelstein et al., 2002) which con-
flate relatedness or association with similarity rather
than on datasets that exclusively focus on word simi-
larity.
108
Zhang, R., Schneider-Kamp, P. and Zimek, A.
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level.
DOI: 10.5220/0008953001080119
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 108-119
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In this paper, we propose a new approach that ob-
tains the new word vectors by retrofitting pre-trained
vectors by exploiting synonyms and antonyms ob-
tained from thesaurus.com
1
for the 100,000 most
frequently-used English words from Wiktionary.
2
For
evaluation purposes, we use the same standard bench-
marks as used by Vulic and Glavas (2018), i.e.,
SimLex-999 (Hill et al., 2015) and SimVerb-3500
(Gerz et al., 2016), and also Stanford’s Contextual
Word Similarities (Huang et al., 2012) used by Lee
et al. (2018).
We find that our model consistently provides sig-
nificant improvements in word similarity compared to
state-of-the-art retrofitting models. Specifically, we
obtain a Spearman correlation of 0.765 on SimLex-
999, improving on the score of 0.76 achieved by the
best published model (Recski et al., 2016). Our ap-
proach uses negative sampling (Mikolov et al., 2013b)
for simplifying the process of neural networks with
complicated hidden layers (Vulic and Glavas, 2018).
The contributions of this paper are twofold: (i) we
generate the vectors of a word with different def-
initions using the original pre-trained word vector,
based on the synonym and antonym sets in the dif-
ferent word senses, and (ii) we enhance the perfor-
mance of word vectors on the task of semantic sim-
ilarity of words by only using superficial synonyms
and antonyms knowledge.
Figure 1 depicts the structure of our approach. We
input the synonyms of a target word with the j-th
sense into our model which are the positive samples
giving a positive influence on this target word. The
antonyms of this target word are added to adjust the
probability of this target word. Such adjustments can
also affect these synonyms such that we could update
the vectors of these synonyms first. Finally under the
influence of the updated synonyms and the antonyms,
the vector of the target word is retrofitted with the j-th
sense.
This paper is structured as follows. An overview
on recent related work is provided in Section 2. In
Section 3, we introduce the principle of our model,
define the objective, and describe the steps of opti-
mization as well as how to update word embeddings
into sense embeddings. In Section 4 we describe our
experimental setup with datasets, evaluation proce-
dures, and the evaluated tasks. In Section 5 we discuss
the results of different configurations on the bench-
marks. Finally, we present conclusions and future
challenges in Section 6.
1
https://www.thesaurus.com/
2
https://gist.github.com/h3xx/1976236
s
i
j1
s
i
j2
s
i
j(n−1)
s
i
jn
Hidden
Layer
Input w ∪ant
j
w
s
i−1
j1
s
i−1
j2
s
i−1
j(n−1)
s
i−1
jn
w
i
j
.
.
.
.
.
.
Figure 1: Graphical sketch of the proposed model. s
i
jn
refers
to the n-th synonym of the target word w with the j-th sense
in the i-th step and ant(w
j
) indicates the antonym set of the
target word w with the j-th sense.
2 RELATED WORK
The representation of words which provide continu-
ous low-dimensional vector representations of words
plays a pivotal role and has been widely studied in
NLP domain. Vector Space Models (VSM) is the ba-
sis of many prominent methodologies for word rep-
resentation learning. The earliest VSMs considered
a vector space in document level which uses the vo-
cabulary directly as the features (Salton et al., 1975).
Subsequently many kinds of weight computation met-
rics of individual dimensions such as word frequen-
cies or normalized frequencies (Salton and McGill,
1986) have been proposed. This research has suc-
ceeded in various NLP tasks.
However, one crucial problem with the huge cor-
pus is the high dimensionality of the produced vec-
tors. A common solution is dimensionality reduc-
tion making use of the Singular Value Decomposition
(SVD). Learning low-dimensional word representa-
tions directly from text corpora is another strategy
that has been achieved by leveraging neural networks.
These models are commonly known as word embed-
dings. Some prominent word embedding architec-
tures have been constructed depending on contextual
relationships or word morphology. Beyond that, more
complex approaches have been proposed attempting
to cure some deficiencies (e.g., conflation of meaning)
by exploiting sub-word units (Wieting et al., 2016),
probability distributions (Athiwaratkun and Wilson,
2017), specialized similarity measures (Soares et al.,
2019), knowledge resources (Camacho-Collados and
Pilehvar, 2018), etc.
The process of producing word embeddings is
not able to capture different meanings of the same
word. And for downstream tasks, the meaning con-
flation can have a negative influence on accurate se-
mantic modeling, e.g., “mouse-screen” and “mouse-
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
109

cow”. There is no relation between “screen” and
“cow”, but they can be connected by two different
senses of “mouse”, i.e., computer device and animal.
Partitioning the meanings of words into multiple
senses is not an easy task. Computational approaches
relying on text corpora or semantic knowledge (such
as a dictionary or thesaurus), generally can be cate-
gorized into unsupervised techniques and knowledge-
based techniques.
2.1 Unsupervised Techniques
Unlabeled monolingual corpora can be exploited for
word sense disambiguation by clustering-based ap-
proaches or joint models. Clustering the context
in which an ambiguous word occurs can discern
senses automatically. Context-group discrimination
(Sch
¨
utze, 1998) is an approach to compute the cen-
troid vector of the context of an ambiguous word, and
then cluster these context centroid vectors into a pre-
determined number of clusters. Context clusters for
an ambiguous word are interpreted as representations
for different senses of this word. Models applying
this strategy are also called two-stage models (Erk and
Pad
´
o, 2008; Van de Cruys et al., 2011).
Joint models (Li and Jurafsky, 2015; Qiu et al.,
2016) are proposed as various extensions of tradi-
tional word embedding models. The primary differ-
ence in contrast to clustering-based approaches is that
joint models merge the clustering and the sense rep-
resentation step. In this way, the joint model can dy-
namically select the potential sense for an ambigu-
ous word during training. Topical Word Embeddings
(TWE) (Liu et al., 2015b) are proposed for inducing
the sense representations of a word based only on its
local context, which reduces computational complex-
ity. Joint models have serious limitations, though,
which require the disambiguation of the context of
a word as well as predetermining a fixed number of
senses per word.
Another recent branch of unsupervised techniques
is to generate contextualized word embeddings. Here,
context-sensitive latent variables for each word are
inferred from a fuzzy word clustering and then inte-
grated to the sequence tagger as additional features
(Li and McCallum, 2005).
2.2 Knowledge-based Techniques
Knowledge-based techniques about semantic repre-
sentations fall into three categories: (1) improv-
ing word representations, (2) using sense represen-
tations, and (3) using concept and entity repre-
sentations. Studies related to all three categories
make use of similar knowledge resources. In par-
ticular, WordNet (Baker et al., 1998) as an ex-
ample of expert-made resources and Wikipedia as
an example of collaboratively-constructed resources
are widely applied (Camacho-Collados and Pile-
hvar, 2018). Some similar collaborative works pow-
ered by Wikipedia like Freebase (Bollacker et al.,
2008) and DBpedia (Bizer et al., 2009) also pro-
vide large structured data in the form of the knowl-
edge base. Further examples are BabelNet (Nav-
igli and Ponzetto, 2012), a combination of expert-
made resources and collaboratively-constructed re-
sources, and ParaPhrase DataBase (PPDB) (Ganitke-
vitch et al., 2013) gathering over 150 million para-
phrases and providing a graph structure. In the fol-
lowing, we shortly recap some of the relevant related
work for each of the three categories.
2.2.1 Improving Word Representations
The earlier attempts to improve word embedding us-
ing lexical resources modified the objective func-
tions of a neural network model for learning a word
representation (Yu and Dredze, 2014; Kiela et al.,
2015). Typically, they integrate the external seman-
tic constraints into the learning process directly, re-
sulting in joint specialization models. Some recent
approaches try to improve the pre-trained word vec-
tors through post-processing (Faruqui et al., 2015;
Lengerich et al., 2018), which is a more versatile
approach than the joint models. The popular term
“retrofitting” is used when implanting external lexi-
con knowledge into random pre-trained word vectors.
Given any pre-trained word vectors, generated by any
tools or techniques, the main idea of graph-based
retrofitting is to minimize the distance between syn-
onyms and maximize the distance between antonyms.
Building upon the retrofitting idea, explicit retrofitting
constructs a neural network by modeling pairwise re-
lations (Goikoetxea et al., 2015; Vulic and Glavas,
2018), which also specialize vectors of words unseen
in external lexical resources.
2.2.2 Using Sense Representations
The second category consists of sense vector repre-
sentation techniques. These generate vectors by “de-
conflating” a word (with conflated meanings) into
several individuals with different senses. Methods
based on linear models draw support by the synonym
and antonym sets of the target word with different
senses to retrofit the original word vectors (Pilehvar
and Collier, 2016; Lee et al., 2018). Chen et al. (2015)
exploit a convolutional neural network architecture
for initializing sense embedding. Neelakantan et al.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
110

(2015) rely on the Skip-gram model for learning sense
embeddings. The Lesk algorithm (Vasilescu et al.,
2004) has been adapted for learning word sense em-
beddings (Yang and Mao, 2016).
2.2.3 Using Concept and Entity Representations
The main idea in this branch is to construct a strong
relation between related entities. Given a knowledge
base as a set of triples {(e
1
,e
2
,r)}, where e
1
and
e
2
are entities and r is the relation between them,
the goal is to approach the entities by the relation r
(~e
1
+~r ≈ ~e
2
) for all triples in the space. Typical ap-
proaches integrating concepts and entities from ex-
ternal knowledge bases rely exclusively on knowl-
edge graphs to build an embedding space for enti-
ties and relations (Bordes et al., 2013). In addition,
some hybrid models have been proposed to exploit
text corpora and knowledge bases as well (Camacho-
Collados et al., 2016).
2.3 Summary
The approach we propose is inspired by Word2Vec
(Mikolov et al., 2013b,a) which reduces the complex-
ity of the hidden layer so that the approach is both
simple and practical. Considering the importance of
semantic relation and sense representation, we retrofit
the unitary pre-trained word vectors from the corpus
into sense level representations by external semantic
knowledge.
3 NEGATIVE-SAMPLING
RETROFITTING
An important aspect in Natural Language Processing
is the Statistical Language Model which can be used
to calculate the probability of a sentence
Pr(w
1
w
2
...w
N
).
We assume w
N
1
= (w
1
w
2
...w
N
). According to Bayes’
theorem, this probability could be decomposed into
conditional probabilities
Pr(w
1
),Pr(w
2
|w
1
),... , Pr(w
N
|w
N−1
1
)
which are the parameters of a Language Model. In or-
der to find the optimal model parameters, we will do
optimization on an objective function Pr(w| POS(w))
generated by a maximum likelihood estimate method,
where POS(w) is the positive sample set of the tar-
get word w. That is, under the positive condition, the
probability of w should be greater than under the neg-
ative condition. Thus, we explore a method that uses
a set of linguistic constraints from an external lexical
resource,
LC = {(w
j
,syn(w
j
),ant(w
j
))|w ∈ V },
each consisting of a word w from the associated
vocabulary V with the j-th sense and its syn-
onyms (syn(w
j
)) as positive samples and its antonyms
(ant(w
j
)) as negative samples to retrofit the vector of
each target word. More specifically, the synonyms
and antonyms of the corresponding senses helps us to
refine the vectors into a sense level. We employ Neg-
ative Sampling (Mikolov et al., 2013b), a simplified
version of Noise Contrastive Estimation (NCE) (Gut-
mann and Hyv
¨
arinen, 2010) which aims at improving
the quality of results and decreasing training time.
Our approach consists of two major components:
(1) updating the synonym set of the target word in the
j-th sense, and (2) generating the corresponding new
sense embedding of this word.
3.1 Objective Functions
Let X
X
X = {x
x
x
w
|w ∈ V }, x
x
x
w
∈ R
d
be the pre-trained
d-dimensional distributed vector space and let Y
Y
Y =
{y
y
y
w
|w ∈ V }, y
y
y
w
= {y
y
y
w
j
}
|sense
w
|
j=1
, y
y
y
w
j
∈ R
d
be the cor-
responding retrofitted sense vector space. Recall that
syn(w) is the positive sample set and ant(w) is the
negative sample set of target word w, respectively.
Therefore, for any word u in the pre-trained word vec-
tor space, we first define Equation (1) to denote the
label of word u. That means if the word u is the target
word, the corresponding optimization process for the
objective function will be activated.
L
w
(u) =
(
1, u = w
0, otherwise
(1)
According to the given positive sample set syn(w),
the objective is to maximize the conditional probabil-
ity of a word under a condition of its synonyms. Cer-
tainly, each synonym can affect this condition, either
on its own or with other related synonyms. On the
basis of the above, we propose two strategies for this
goal. One would be to maximize a series of probabil-
ity functions if we set each synonym as an individual
(NS-sv):
L =
∏
w∈V
∏
e
w∈syn(w)
g(x
x
x
w
,θ
θ
θ)
=
∏
w∈V
∏
e
w∈syn(w)
∏
u∈{w}∪ant(w)
Pr(x
x
x
u
|x
x
x
e
w
)
(2)
where θ is the parameter matrix of the hidden layer,
and g is the objective conditional probability function.
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
111

An alternative strategy is to maximize the con-
ditional probability under the integration of the syn-
onyms (NS-sv-sum):
L =
∏
w∈V
g(x
x
x
w
,θ
θ
θ)
=
∏
w∈V
∏
u∈{w}∪ant(w)
Pr(x
x
x
u
|x
x
x
e
w
)
(3)
where
e
w is composed of all synonyms instead of each
single word. In our approach, we integrate them by:
x
x
x
e
w
=
∑
s∈syn(w)
x
x
x
s
(4)
3.2 Optimization
No matter which strategy we use to produce the ob-
jective, the goal is to maximize the probability of the
positive sample and, simultaneously, to minimize the
probability of the negative sample. We use a sigmoid
function as the activation function:
σ(x) =
1
1 + exp(x)
(5)
such that the derivative of sigmoid function is:
σ
0
(x) = σ(x)[1 − σ(x)] (6)
Thence, Pr(x
x
x
u
|x
x
x
e
w
) could be denoted as:
Pr(x
x
x
u
|x
x
x
e
w
) =
(
σ
x
x
x
T
e
w
θ
θ
θ
u
, L
w
(u) = 1
1 − σ
x
x
x
T
e
w
θ
θ
θ
u
, L
w
(u) = 0
(7)
Putting the pieces together, g(w, θ
θ
θ) would become:
g(x
x
x
w
,θ
θ
θ) =
∏
u∈{w}∪ant(w)
σ
x
x
x
T
e
w
θ
θ
θ
u
L
w
(u)
·
1 − σ
x
x
x
T
e
w
θ
θ
θ
u
1−L
w
(u)
(8)
The purpose of training by negative sampling is to
maximize the objective with respect to the model pa-
rameters by the commonly used log-likelihood func-
tion:
logg(x
x
x
w
,θ
θ
θ) =
∑
u∈{w}∪ant(w)
n
L
w
(u) · log
σ
x
x
x
T
e
w
θ
θ
θ
u
+
[1 − L
w
(u)] · log
1 − σ
x
x
x
T
e
w
θ
θ
θ
u
o
(9)
To explain the procedure in detail, we let F
i j
w
represent
the log-likelihood function of the target word w in the
i-th step with the j-th sense:
F
i j
w
= L
w
i j
(u) · log
σ
x
x
x
T
e
w
θ
θ
θ
u
i j
+
1 − L
w
i j
(u)
· log
1 − σ
x
x
x
T
e
w
θ
θ
θ
u
i j
(10)
We choose gradient ascent for optimization. The pa-
rameters θ
θ
θ
u
i j
and x
x
x
e
w
are updated by the learning rate α
as follows:
θ
θ
θ
u
i j
= θ
θ
θ
u
i j
+ α
∂F
i j
w
∂θ
θ
θ
u
i j
x
x
x
e
w
= x
x
x
e
w
+ α
∑
u∈{w}∪ant
j
(w)
∂F
i j
w
∂x
x
x
e
w
(11)
The gradients above are calculated as follows:
∂F
i j
w
∂θ
θ
θ
u
i j
=
F
i j
w
− σ
x
x
x
T
e
w
θ
θ
θ
u
i j
x
x
x
e
w
∂F
i j
w
∂x
x
x
e
w
=
F
i j
w
− σ
x
x
x
T
e
w
θ
θ
θ
u
i j
θ
θ
θ
u
i j
(12)
Consequently, we obtain the updating function for the
parameter matrix and the synonym embeddings.
3.3 Generating Sense Vectors
In this part, we collect the updated synonym vectors
of the target word in the j-th sense to generate the tar-
get word vector with the j-th sense:
y
y
y
w
j
:= x
x
x
w
+
∑
s∈syn(w
j
)
x
x
x
s
(13)
Moreover, to ensure that each synonym could con-
tribute to the new word vector even if it has no pre-
trained vector, we give such a synonym an initial vec-
tor randomly, and revise it by the target word vector:
x
x
x
s
k
:= λx
x
x
s
k
+ (1 − λ)x
x
x
w
(14)
where λ is a weight for unknown neighbor vectors to
keep balance of the whole vector space.
3.4 Result
As a result of the procedure, we have sense embed-
dings
y
y
y
i
i
i
= {y
y
y
w
j
}
|sense
w
i
|
j=1
of each word w in the vocabulary V . For each word w,
we update the embeddings of the synonyms of w with
the j-th sense by the pre-trained word vector of w.
Likewise, the antonyms of w are utilized for negative
sampling. After traversing of all synonyms, we ag-
gregate these updated synonym embeddings with the
pre-trained word embedding x
x
x
w
to produce the new
j-th sense embedding of word w.
Experimental experience tells that initializing the
parameter matrix to be the same as the pre-trained
vector matrix can generate effective sense retrofitted
vectors with only a few iterations.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
112

4 EXPERIMENTAL SETUP
We evaluate our approach on two aspects: semantic
relatedness and contextual word similarity. We use
the average of all sense vectors to represent the miss-
ing word. For all models reported in this paper, the
same processing method and the same computation
method are applied to compare their performance.
4.1 Datasets
We first experiment with three widely used and pub-
licly available pre-trained word vectors for English
corpora.
1. Word2Vec (Mikolov et al., 2013b,a): Word2Vec
is fast and widely used. In practice, we use the
python module
3
(Sujono, 2015) (which imple-
ments the core of Word2Vec as the gensim im-
plementation (
ˇ
Reh
˚
u
ˇ
rek and Sojka, 2010)) to train
enwik9
4
by CBOW model and Skip-gram model
with Negative Sampling separately in 300 dimen-
sions, where we use context windows of size 5 and
5 negative examples.
2. GloVe Vectors
5
(Pennington et al., 2014): The
GloVe word vector approach integrates the global
co-occurrence matrix of word pairs. We use
the pre-trained word vectors directly. 6B.50d,
6B.100d, 6B.200d and 6B.300d are trained on
Wikipedia 2014 with English Gigaword in vec-
tor length of the range 50 to 300 respectively, and
42B.300d is trained on Common Crawl in 300 di-
mensions.
3. FastText Vectors
6
(Bojanowski et al., 2017):
FastText is an extension of the continuous skip-
gram model by summing the n-gram vectors. We
use their pre-trained word vector files directly.
crawl-300d-2M is trained on Common Crawl in-
cluding 2 million word vectors, and wiki-300d-
1M is trained on Wikipedia 2017, UMBC web-
base corpus and statmt.org dataset including 1
million word vectors.
As we mentioned above, we generated the syn-
onym sets and antonym sets of the 100,000 most-
frequently used words from Wiktionary via the API
of thesaurus.com
7
. Each word is a leader of its syn-
onym and antonym sets corresponding to its defini-
tions. After inputting them into our program, we are
going to mark the leading word as w# j, denoting the
3
https://github.com/deborausujono/word2vecpy
4
http://mattmahoney.net/dc/textdata.html
5
https://nlp.stanford.edu/projects/glove/
6
https://fasttext.cc/docs/en/english-vectors.html
7
https://github.com/Manwholikespie/thesaurus
word w with the j-th sense. It is worth mentioning
that we choose thesaurus.com as our knowledge base
rather than WordNet which considers both semantic
relations and lexicon relations. That is because the
primary but superficial semantic knowledge is a cost
effective way during training in practice.
4.2 Evaluation Measure
For semantic relatedness task, we evaluate the quality
of the retrofitted embedding spaces on two word sim-
ilarity benchmarks: SimLex-999 (Hill et al., 2015),
which comprises 666 noun pairs, 222 verb pairs and
111 adjective pairs; and SimVerb-3500 (Gerz et al.,
2016), which consists of 3500 verb pairs covering all
normed verb types of 827 distinct verbs.
For contextual word similarity task, we conduct
experiments with the Stanford’s Contextual Word
Similarities (SCWS) (Huang et al., 2012) which in-
cludes 2003 word pairs together with human-rated
scores. Higher scores indicate higher semantic sim-
ilarity.
Our experiments are all based on intrinsic evalu-
ation for the quality and coherence of vector space.
We use Spearman’s ρ rank correlation coefficient
(Well and Myers, 2003) between the cosine similar-
ity scores calculated by the retrofitted vectors and the
human-provided ratings for assessment.
On the other hand, according to Faruqui et al.
(2016) and Rastogi et al. (2015), it is necessary to per-
form statistical significance tests to the difference be-
tween the Spearman’s Correlations even for compar-
isons on small evaluation sets. Rastogi et al. (2015)
introduce σ
ρ
p
0
as the Minimum Required Difference
for Significance (MRDS) which satisfies the the fol-
lowing:
(ρ
AB
<ρ)∧
|
ˆ
ρ
BT
−
ˆ
ρ
AT
|< σ
ρ
p
0
⇒ p-value> p
0
(15)
where A and B are the lists of ratings over the same
items, produced by the competitive models and T
denotes the gold ratings T . ρ
AT
, ρ
BT
, and ρ
AB
de-
note the Spearman’s correlations between A : T , B :
T , and A : B, respectively. Then let
ˆ
ρ
AT
,
ˆ
ρ
BT
, and
ˆ
ρ
AB
be their empirical estimates. This proposition
indicates that differences in correlations, if below
the MRDS threshold, are not statistically significant.
Rastogi et al. (2015) also provide the MRDS values
for SimLex-999 word similarity dataset and here we
provide the threshold
8
for SimVerb-3500 and Stan-
ford’s Contextual Word Similarities in Table 1.
8
https://github.com/se4u/mvlsa provides the way to as-
sign a minimum threshold to a testset.
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
113

Table 1: The Minimum Required Difference for Significance (MRDS) values for SimLex-999 (SL), SimVerb-3500 (SV) and
Stanford’s Contextual Word Similarities (SCWS).
Dataset Size σ
0.5
0.01
σ
0.7
0.01
σ
0.9
0.01
σ
0.5
0.05
σ
0.7
0.05
σ
0.9
0.05
SL 999 0.073 0.057 0.032 0.052 0.040 0.023
SV 3500 0.039 0.030 0.017 0.027 0.021 0.012
SCWS 2003 0.051 0.04 0.023 0.036 0.028 0.016
Table 2: Spearman’s correlation for three word distributed representations (300 dimensions), Word2Vec (w2v), GloVe (glove)
and FastText (FT) on SimLex-999, and the performance comparison with two strategies of retrofitting models, NS-sv and
NS-sv-sum (MaxSim / AveSim) using σ
0.9
0.05
as the threshold.
w2v.cb w2v.sg glove.42B glove.6B FT.wiki FT.crawl
baseline 0.230 0.293 0.374 0.371 0.450 0.503
NS-sv 0.642/0.650 0.640/0.637 0.688/0.698 0.706/0.725 0.678/0.688 0.723/0.765
NS-sv-Sum 0.609/0.571 0.596/0.487 0.674/0.62 0.693/0.675 0.667/0.633 0.733/0.698
4.3 Task 1: Semantic Relatedness
This task is to model the semantic similarity. A higher
score indicates the higher semantic similarity. The
sense evaluation metrics learned from Reisinger and
Mooney (2010) compute two kinds of scores, maxi-
mum score for the evaluation of sense representations
and average score for the evaluation of word repre-
sentations:
MaxSim = max
w
m
j
∈D
w
m
,w
n
k
∈D
w
n
cos
x
x
x
w
m
j
,x
x
x
w
n
k
(16)
AveSim =
∑
w
m
j
∈D
w
m
∑
w
n
j
∈D
w
n
cos
x
x
x
w
m
j
,x
x
x
w
n
k
|D
w
m
| · |D
w
n
|
(17)
where D
w
m
is the definition set of the word w
m
, and
D
w
n
is the definition set of the word w
n
. Compared
with the original metrics based on unsupervised tech-
niques, we do not need to predetermine the number of
sense clusters which should differ from word to word.
Thus, instead of the uniform number of clusters, we
use the number of senses of each word to average the
word similarity.
4.4 Task 2: Contextual Word Similarity
The goal of this task is to measure the semantic relat-
edness with contextual information which covers the
shortage in semantic relatedness task. We also adopt
MaxSimC / AvgSimC metrics to compute scores for
each word pair (Reisinger and Mooney, 2010). A
higher score indicates the higher semantic similarity.
MaxSimC = d(
ˆ
π(x
x
x
w
m
),
ˆ
π(x
x
x
w
n
)) (18)
AveSimC =
∑
w
m
j
∈D
w
m
∑
w
n
j
∈D
w
n
d
c,w
m
j
d
c
0
,w
n
k
d
x
x
x
w
m
j
,x
x
x
w
n
k
|D
w
m
| · |D
w
n
|
(19)
where d
c,w
m
j
= cos(v
v
v(c),x
x
x
w
m
) is the likelihood of
context c belonging to the j-th sense group of the
word w
m
, and
ˆ
π(w
m
) = argmax
w
m
j
∈D
w
m
d
c,w
m
j
. We
select 5 words before and after the target word in the
word pairs respectively. Stopwords are removed from
the context. There are total 10 word involved in as
the context of the target word under the perfect con-
dition. And the context vector of the target word as
v
v
v(c) are integrated with all context word embeddings.
Note that based on our word vector space, the context
is not disambiguation, so the solution is the sum of all
sense vectors of each context word.
4.5 Model Configuration
For our model, we set a learning rate varying with the
number of the synonyms of the target word and the
initialized iteration as 1.0. Moreover, the parameter
λ to revise the undefined word vector is set 0.5. In
all experiments except the iteration part, we choose
iter = 100 for NS-sv and iter = 10 for NS-sv-sum.
And for statistical significance, we choose σ
0.9
0.05
, the
small threshold value in Table 1.
5 RESULTS AND DISCUSSION
In this part, we show experiment results from our
retrofitting method.
5.1 Baseline Methods
Tables 2 and 3 show the results of retrofitting the three
standard vectors on each benchmark dataset. The
second row in each table shows the performance of
the baseline vectors. If there is only one sense of
a word, its maximum score (MaxSim) and average
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
114

Table 3: Spearman’s correlation for three word distributed representations (300 dimensions), Word2Vec (w2v), GloVe (glove)
and FastText (FT) on SimVerb-3500, and the performance comparison with two strategies of retrofitting models, NS-sv and
NS-sv-sum (MaxSim / AveSim), using σ
0.9
0.05
as the threshold.
w2v.cb w2v.sg glove.42B glove.6B FT.wiki FT.crawl
baseline 0.160 0.184 0.226 0.227 0.357 0.426
NS-sv 0.592/0.569 0.594/0.568 0.604/0.591 0.614/0.609 0.623/0.615 0.639/0.659
NS-sv-Sum 0.524/0.477 0.502/0.412 0.584/0.558 0.597/0.578 0.562/0.532 0.632/0.611
Table 4: Spearman’s correlation for two word distributed representations (100 dimensions) on SimLex-999 (SL) and SimVerb-
3500 (SV) , prior works and our approach, using σ
0.9
0.05
as the threshold.
Corpus Dataset GloVe re-Faruqui GenSense ER-Specialized NS-sv NS-sv-sum
Wikipedia SL 0.265 0.421 0.446/0.417 0.445 0.683/0.684 0.648/0.600
SV 0.154 0.240 0.289/0.259 0.281 0.609/0.594 0.557/0.526
Twitter SL 0.122 0.295 0.290/0.244 0.365 0.651/0.631 0.589/0.495
SV 0.052 0.145 0.160/0.127 0.225 0.583/0.558 0.529/0.473
Table 5: Spearman’s correlation using GloVe vectors (100 dimensions) on the Stanford’s Contextual Word Similarities
(SCWS) task, prior work and our approach (MaxSimC / AvgSimC), computing with the sum of context word embeddings
(SCWS-sum) and with the average of context word embeddings (SCWS-avg), using σ
0.9
0.05
as the threshold.
SCWS-sum SCWS-avg
glove.twitter 0.428 0.428
GenSense 0.428/0.322 0.428/0.272
NS-sv 0.467 /0.313 0.467/0.313
NS-sv-sum 0.444/0.264 0.444/0.264
score (AveSim) will be the same. From Tables 2 and
3, the MaxSim and AveSim both prove the proposed
model is robust and useful. The largest improvement
is an increase of more than 0.3 on two word similarity
tasks and FastText Crawl retrofitted vectors produce
the top correlation score of 0.765. The average cor-
relation between a human rater and the average of all
other raters is 0.78 and the latest top record by Recski
et al. (2016) is 0.76, which implies that our method
does promote the measuring of semantic similarity of
words. In contrast with NS-sv-sum, in general, NS-
sv yields the better results because the connections
among the synonyms are weak. That means the syn-
onyms are the condition of the word sense during our
study rather than the constraints of hierarchical se-
mantic relations. But the experiment of vector length
later also indicates that the gap of performance of NS-
sv and NS-sv-sum reduces with increasing word vec-
tor length. We conjecture that this is the case as the
vectors with higher dimensions have higher expres-
sivity regarding the difference and, consequently, are
less easily offset during integration.
5.2 Comparison with Prior Works
A comparison to prior works is shown in Table 4.
The three previous models are: re-Faruqui
9
(Faruqui
9
https://github.com/mfaruqui/retrofitting
et al., 2015), GenSense
10
(Lee et al., 2018), and ER-
Specialized
11
(Vulic and Glavas, 2018), trained on
Wikipedia and Twitter using the GloVe tool. We run
their published code to obtain word vectors. Except
for GenSense which needs the weights for their se-
mantic lexicons to discriminate senses of the target
word, we applied these models with our new lexicons
to decrease the difference. In addition, we kept their
default parameter values without any change. Surpris-
ingly, although the prior models still keep their supe-
riority compared with baseline vectors, they become
somewhat weak when the models only rely on the pri-
mary semantic relations. From Table 4, the outcome
of this experiment suggests that the quality of our
vectors significantly improves compared to each of
the three models. The Spearman’s correlation scores
of both NS-sv and NS-sv-sum exceed GenSense by
more than 0.2, which also shows a great performance
under word vectors from Wikipedia corpus. And un-
der the word vector from Twitter, NS-sv and NS-sv-
sum surpass ER-Specialized by more than 0.2.
5.3 Contextual Word Similarity
Table 5 shows the Spearman’s correlation of SCWS
dataset. With the contextual information, sense
10
https://github.com/y95847frank/GenSense
11
https://github.com/codogogo/explirefit
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
115
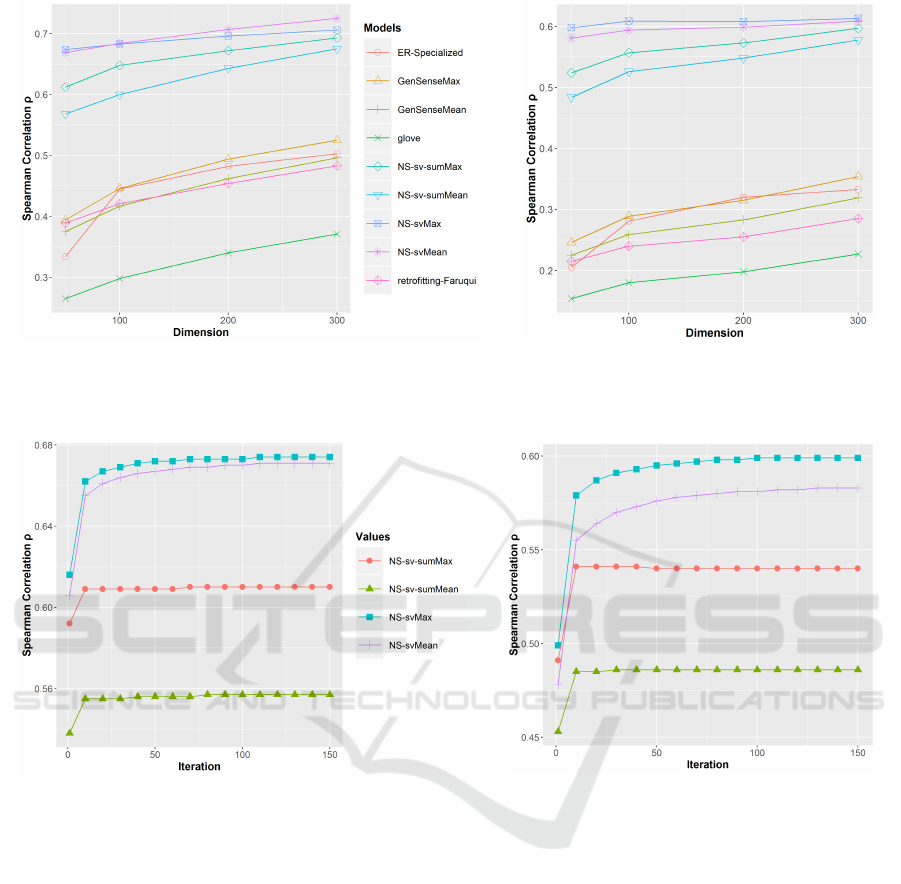
(a) Simlex-999
(b) SimVerb-3500
Figure 2: Spearman’s correlation on word similarity tasks in different vector dimensions using GloVe vectors (from 50 to 300
dimensions).
(a) SimLex-999
(b) SimVerb-3500
Figure 3: The influence of iteration on word similarity tasks using GloVe vectors (50 dimensions).
embedding models outperform the word embedding
model GloVe and retrofittig model GenSense. GloVe
as the baseline method is based on word level so its
score is only the similarity between two words in the
dataset. The metrics MaxSimC and AveSimC take the
context of the target word into account which are gen-
erally used. However, for the trained sense vectors, it
is hard to manage the polysemous context word em-
beddings of a target word. We inexactly use the av-
erage sense vectors of each context word. This limits
the accuracy of our models. Furthermore, from Ta-
ble 5, we find that MaxSimC is superior to AveSimC.
And for context word vectors, the sum and the average
of the vectors have little difference on discriminating
the distinct senses.
5.4 Comparison of Word Vector Length
We tested our model and prior works with different di-
mensions, using GloVe word vectors involving 400K
vocabularies. Figure 2 illustrates the different upward
trend. The correlation ρ of each model rises con-
tinuously and stably from 50 to 300 on Simlex-999
task. On SimVerb-3500 task, the correlation ρ also in-
creases with increasing word vector length, but nearly
keeps steady after 100 dimensions. NS-sv performs
well in all experimental word vector lengths and the
gap with NS-sv-sum decreases constantly. We have
reason to believe that with the word vectors of which
the length is long enough, the performance of SV-
sv and SV-sv-sum should tend to be constant. How-
ever, 300-dimensional vectors are the most common
used because of their high accuracy and acceptable
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
116

data size, so we did not try the vectors with more
than 300 dimensions which is barely used in prac-
tice. It is worth mentioning that even with 50 dimen-
sions the sense vector generated by our model can still
be highly accurate, suggesting to use the low dimen-
sional vectors for applications instead of training the
large word vectors with much resource consumption.
5.5 The Influence of Iteration
Figure 3 shows the Spearman’s correlation score gen-
erated by our model for different number of iteration.
Convergence is the only standard in our experiments
to stop iteration. And according to the experiment of
iteration, we finally decided to select iter = 100 as the
default iteration for NS-sv model and iter = 10 for the
default setup of NS-sv-sum model. From Figure 3, we
can see both NS-sv and NS-sv-sum have obvious im-
provements from 1 to 10 iterations. And compared
with NS-sv, NS-sv-sum approaches convergence al-
ready after only few iterations. However, its perfor-
mance is not as good as the one of NS-sv in this case,
mainly due to the use of only 50-dimensional vectors.
The experiment of vector length revealed that NS-sv
and NS-sv-sum will perform probably both great on
the vectors with higher dimension, while with low
dimension the integration among the synonyms may
lose features, negatively affecting the final outcome.
When all synonyms contribute together, it approaches
convergence faster, which is the reason why NS-sv-
sum converges faster while NS-sv needs more time.
6 CONCLUSION
In this paper, we presented a technique to retrofit word
vectors from the word level to the more fine-grained
level of word sense by two strategies named NS-sv
and NS-sv-sum in this paper. This technique only
employs primary semantic knowledge to improve the
performance of the pre-trained word vectors and par-
titions the meaning of words into multiple senses.
This is a post-processing approach, which avoids re-
training on a large corpus, and can be applied on any
pre-trained word vectors. The retrofitting procedure
does not have many hyperparameters, yielding steady
and efficient results in a multitude of application sce-
narios without costly hyperparameter optimization.
Our model is proposed for semantic similarity of
words. It consists of four parts: (1) We provide the
synonym and antonym sets of the most commonly
used words in Wiktionary and use them as training
examples for our negative-sampling-based neural net-
work model; (2) we take advantage of the semantic
knowledge from external resources (the synonym and
antonym sets) to refine the word representations and
construct sense representations; (3) our model signif-
icantly reduces the number of hyperparameters and,
based on experiments, the default parameters do typ-
ically not have to be modified even if the input and
the environment change; (4) the retrofitted word vec-
tors can achieve the highest score 0.765 on SimLex-
999. Our experiments have provided evidence for the
effectiveness of our model on word similarity tasks.
It outperforms the baseline methods and the previous
work on three popular types of pre-trained word vec-
tors of commonly used dimensions.
ACKNOWLEDGEMENTS
Rui Zhang was supported by the China Scholarship
Council for 4 years of study at the University of
Southern Denmark.
REFERENCES
Athiwaratkun, B. and Wilson, A. G. (2017). Multimodal
word distributions. arXiv preprint arXiv:1704.08424.
Baker, C. F., Fillmore, C. J., and Lowe, J. B. (1998). The
berkeley framenet project. In 36th Annual Meeting
of the Association for Computational Linguistics and
17th International Conference on Computational Lin-
guistics, COLING-ACL ’98, August 10-14, 1998, Uni-
versit
´
e de Montr
´
eal, Montr
´
eal, Quebec, Canada. Pro-
ceedings of the Conference., pages 86–90.
Bizer, C., Lehmann, J., Kobilarov, G., Auer, S., Becker, C.,
Cyganiak, R., and Hellmann, S. (2009). Dbpedia-a
crystallization point for the web of data. Web Seman-
tics: science, services and agents on the world wide
web, 7(3):154–165.
Bojanowski, P., Grave, E., Joulin, A., and Mikolov, T.
(2017). Enriching word vectors with subword infor-
mation. TACL, 5:135–146.
Bollacker, K., Evans, C., Paritosh, P., Sturge, T., and Tay-
lor, J. (2008). Freebase: a collaboratively created
graph database for structuring human knowledge. In
Proceedings of the 2008 ACM SIGMOD international
conference on Management of data, pages 1247–
1250. AcM.
Bordes, A., Usunier, N., Garcia-Duran, A., Weston, J., and
Yakhnenko, O. (2013). Translating embeddings for
modeling multi-relational data. In Advances in neural
information processing systems, pages 2787–2795.
Bruni, E., Tran, N., and Baroni, M. (2014). Multimodal
distributional semantics. J. Artif. Intell. Res., 49:1–47.
Camacho-Collados, J. and Pilehvar, M. T. (2018). From
word to sense embeddings: A survey on vector repre-
sentations of meaning. CoRR, abs/1805.04032.
Camacho-Collados, J., Pilehvar, M. T., and Navigli, R.
(2016). Nasari: Integrating explicit knowledge and
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
117

corpus statistics for a multilingual representation of
concepts and entities. Artificial Intelligence, 240:36–
64.
Chang, K., Yih, W., and Meek, C. (2013). Multi-relational
latent semantic analysis. In Proceedings of the
2013 Conference on Empirical Methods in Natural
Language Processing, EMNLP 2013, 18-21 October
2013, Grand Hyatt Seattle, Seattle, Washington, USA,
A meeting of SIGDAT, a Special Interest Group of the
ACL, pages 1602–1612.
Chen, T., Xu, R., He, Y., and Wang, X. (2015). Improving
distributed representation of word sense via wordnet
gloss composition and context clustering. In Proceed-
ings of the 53rd Annual Meeting of the Association for
Computational Linguistics and the 7th International
Joint Conference on Natural Language Processing of
the Asian Federation of Natural Language Processing,
ACL 2015, July 26-31, 2015, Beijing, China, Volume
2: Short Papers, pages 15–20.
Erk, K. and Pad
´
o, S. (2008). A structured vector space
model for word meaning in context. In Proceedings
of the 2008 Conference on Empirical Methods in Nat-
ural Language Processing, pages 897–906.
Faruqui, M., Dodge, J., Jauhar, S. K., Dyer, C., Hovy, E. H.,
and Smith, N. A. (2015). Retrofitting word vectors to
semantic lexicons. In NAACL HLT 2015, The 2015
Conference of the North American Chapter of the As-
sociation for Computational Linguistics: Human Lan-
guage Technologies, Denver, Colorado, USA, May 31
- June 5, 2015, pages 1606–1615.
Faruqui, M., Tsvetkov, Y., Rastogi, P., and Dyer, C. (2016).
Problems with evaluation of word embeddings using
word similarity tasks. In Proceedings of the 1st Work-
shop on Evaluating Vector-Space Representations for
NLP, pages 30–35, Berlin, Germany. Association for
Computational Linguistics.
Finkelstein, L., Gabrilovich, E., Matias, Y., Rivlin, E.,
Solan, Z., Wolfman, G., and Ruppin, E. (2002). Plac-
ing search in context: the concept revisited. ACM
Trans. Inf. Syst., 20(1):116–131.
Ganitkevitch, J., Van Durme, B., and Callison-Burch, C.
(2013). Ppdb: The paraphrase database. In Proceed-
ings of the 2013 Conference of the North American
Chapter of the Association for Computational Lin-
guistics: Human Language Technologies, pages 758–
764.
Gerz, D., Vulic, I., Hill, F., Reichart, R., and Korhonen, A.
(2016). Simverb-3500: A large-scale evaluation set of
verb similarity. In Proceedings of the 2016 Confer-
ence on Empirical Methods in Natural Language Pro-
cessing, EMNLP 2016, Austin, Texas, USA, November
1-4, 2016, pages 2173–2182.
Goikoetxea, J., Soroa, A., and Agirre, E. (2015). Random
walks and neural network language models on knowl-
edge bases. In NAACL HLT 2015, The 2015 Confer-
ence of the North American Chapter of the Associa-
tion for Computational Linguistics: Human Language
Technologies, Denver, Colorado, USA, May 31 - June
5, 2015, pages 1434–1439.
Grave, E., Mikolov, T., Joulin, A., and Bojanowski, P.
(2017). Bag of tricks for efficient text classification.
In Proceedings of the 15th Conference of the Euro-
pean Chapter of the Association for Computational
Linguistics, EACL 2017, Valencia, Spain, April 3-7,
2017, Volume 2: Short Papers, pages 427–431.
Gutmann, M. and Hyv
¨
arinen, A. (2010). Noise-contrastive
estimation: A new estimation principle for unnormal-
ized statistical models. In Proceedings of the Thir-
teenth International Conference on Artificial Intelli-
gence and Statistics, pages 297–304.
Harris, Z. S. (1954). Distributional structure. Word, 10(2-
3):146–162.
Hill, F., Reichart, R., and Korhonen, A. (2015). Simlex-999:
Evaluating semantic models with (genuine) similar-
ity estimation. Computational Linguistics, 41(4):665–
695.
Huang, E. H., Socher, R., Manning, C. D., and Ng, A. Y.
(2012). Improving word representations via global
context and multiple word prototypes. In Proceed-
ings of the 50th Annual Meeting of the Association
for Computational Linguistics: Long Papers-Volume
1, pages 873–882. Association for Computational Lin-
guistics.
Kiela, D., Hill, F., and Clark, S. (2015). Specializing word
embeddings for similarity or relatedness. In Proceed-
ings of the 2015 Conference on Empirical Methods in
Natural Language Processing, EMNLP 2015, Lisbon,
Portugal, September 17-21, 2015, pages 2044–2048.
Lee, Y., Yen, T., Huang, H., Shiue, Y., and Chen, H. (2018).
Gensense: A generalized sense retrofitting model. In
Proceedings of the 27th International Conference on
Computational Linguistics, COLING 2018, Santa Fe,
New Mexico, USA, August 20-26, 2018, pages 1662–
1671.
Lengerich, B. J., Maas, A. L., and Potts, C. (2018).
Retrofitting distributional embeddings to knowledge
graphs with functional relations. In Proceedings of the
27th International Conference on Computational Lin-
guistics, COLING 2018, Santa Fe, New Mexico, USA,
August 20-26, 2018, pages 2423–2436.
Li, J. and Jurafsky, D. (2015). Do multi-sense embed-
dings improve natural language understanding? arXiv
preprint arXiv:1506.01070.
Li, W. and McCallum, A. (2005). Semi-supervised se-
quence modeling with syntactic topic models. In
AAAI, volume 5, pages 813–818.
Liu, Q., Jiang, H., Wei, S., Ling, Z., and Hu, Y. (2015a).
Learning semantic word embeddings based on ordi-
nal knowledge constraints. In Proceedings of the 53rd
Annual Meeting of the Association for Computational
Linguistics and the 7th International Joint Conference
on Natural Language Processing of the Asian Federa-
tion of Natural Language Processing, ACL 2015, July
26-31, 2015, Beijing, China, Volume 1: Long Papers,
pages 1501–1511.
Liu, Y., Liu, Z., Chua, T.-S., and Sun, M. (2015b). Topical
word embeddings. In Twenty-Ninth AAAI Conference
on Artificial Intelligence.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a).
Efficient estimation of word representations in vector
space. CoRR, abs/1301.3781.
Mikolov, T., Grave, E., Bojanowski, P., Puhrsch, C., and
Joulin, A. (2018). Advances in pre-training distributed
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
118

word representations. In Proceedings of the Eleventh
International Conference on Language Resources and
Evaluation, LREC 2018, Miyazaki, Japan, May 7-12,
2018.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and
Dean, J. (2013b). Distributed representations of words
and phrases and their compositionality. In Advances
in Neural Information Processing Systems 26: 27th
Annual Conference on Neural Information Processing
Systems 2013. Proceedings of a meeting held Decem-
ber 5-8, 2013, Lake Tahoe, Nevada, United States.,
pages 3111–3119.
Navigli, R. and Ponzetto, S. P. (2012). Babelnet: The au-
tomatic construction, evaluation and application of a
wide-coverage multilingual semantic network. Artifi-
cial Intelligence, 193:217–250.
Neelakantan, A., Shankar, J., Passos, A., and McCallum, A.
(2015). Efficient non-parametric estimation of mul-
tiple embeddings per word in vector space. CoRR,
abs/1504.06654.
Pennington, J., Socher, R., and Manning, C. D. (2014).
Glove: Global vectors for word representation. In
Proceedings of the 2014 Conference on Empirical
Methods in Natural Language Processing, EMNLP
2014, October 25-29, 2014, Doha, Qatar, A meeting
of SIGDAT, a Special Interest Group of the ACL, pages
1532–1543.
Pilehvar, M. T. and Collier, N. (2016). De-conflated se-
mantic representations. In Proceedings of the 2016
Conference on Empirical Methods in Natural Lan-
guage Processing, EMNLP 2016, Austin, Texas, USA,
November 1-4, 2016, pages 1680–1690.
Qiu, L., Tu, K., and Yu, Y. (2016). Context-dependent sense
embedding. In Proceedings of the 2016 Conference on
Empirical Methods in Natural Language Processing,
pages 183–191.
Rastogi, P., Van Durme, B., and Arora, R. (2015). Mul-
tiview lsa: Representation learning via generalized
cca. In Proceedings of the 2015 Conference of the
North American Chapter of the Association for Com-
putational Linguistics: Human Language Technolo-
gies, pages 556–566, Denver, Colorado. Association
for Computational Linguistics.
Recski, G., Ikl
´
odi, E., Pajkossy, K., and Kornai, A. (2016).
Measuring semantic similarity of words using concept
networks. In Proceedings of the 1st Workshop on Rep-
resentation Learning for NLP, pages 193–200.
ˇ
Reh
˚
u
ˇ
rek, R. and Sojka, P. (2010). Software framework
for topic modelling with large corpora. In Proceed-
ings of the LREC 2010 Workshop on New Challenges
for NLP Frameworks, pages 45–50, Valletta, Malta.
ELRA. http://is.muni.cz/publication/884893/en.
Reisinger, J. and Mooney, R. J. (2010). Multi-prototype
vector-space models of word meaning. In Human
Language Technologies: The 2010 Annual Confer-
ence of the North American Chapter of the Associ-
ation for Computational Linguistics, pages 109–117.
Association for Computational Linguistics.
Salton, G. and McGill, M. J. (1986). Introduction to Mod-
ern Information Retrieval. McGraw-Hill, Inc., New
York, NY, USA.
Salton, G., Wong, A., and Yang, C.-S. (1975). A vector
space model for automatic indexing. Communications
of the ACM, 18(11):613–620.
Sch
¨
utze, H. (1998). Automatic word sense discrimination.
Computational linguistics, 24(1):97–123.
Shiue, Y. and Ma, W. (2017). Improving word and sense
embedding with hierarchical semantic relations. In
2017 International Conference on Asian Language
Processing, IALP 2017, Singapore, December 5-7,
2017, pages 350–353.
Soares, V. H. A., Campello, R. J. G. B., Nourashrafeddin,
S., Milios, E., and Naldi, M. C. (2019). Combining
semantic and term frequency similarities for text clus-
tering. Knowledge and Information Systems.
Sujono, D. (2015). word2vecpy.
https://github.com/deborausujono/word2vecpy.
Van de Cruys, T., Poibeau, T., and Korhonen, A. (2011). La-
tent vector weighting for word meaning in context. In
Proceedings of the Conference on Empirical Methods
in Natural Language Processing, pages 1012–1022.
Association for Computational Linguistics.
Vasilescu, F., Langlais, P., and Lapalme, G. (2004). Eval-
uating variants of the lesk approach for disambiguat-
ing words. In Proceedings of the Fourth International
Conference on Language Resources and Evaluation,
LREC 2004, May 26-28, 2004, Lisbon, Portugal.
Vulic, I. and Glavas, G. (2018). Explicit retrofitting of dis-
tributional word vectors. In Proceedings of the 56th
Annual Meeting of the Association for Computational
Linguistics, ACL 2018, Melbourne, Australia, July 15-
20, 2018, Volume 1: Long Papers, pages 34–45.
Well, A. D. and Myers, J. L. (2003). Research design &
statistical analysis. Psychology Press.
Wieting, J., Bansal, M., Gimpel, K., and Livescu, K. (2016).
Charagram: Embedding words and sentences via
character n-grams. arXiv preprint arXiv:1607.02789.
Yang, X. and Mao, K. (2016). Learning multi-prototype
word embedding from single-prototype word embed-
ding with integrated knowledge. Expert Syst. Appl.,
56:291–299.
Yu, L., Wang, J., Lai, K. R., and Zhang, X. (2017). Refining
word embeddings for sentiment analysis. In Proceed-
ings of the 2017 Conference on Empirical Methods in
Natural Language Processing, EMNLP 2017, Copen-
hagen, Denmark, September 9-11, 2017, pages 534–
539.
Yu, M. and Dredze, M. (2014). Improving lexical embed-
dings with semantic knowledge. In Proceedings of
the 52nd Annual Meeting of the Association for Com-
putational Linguistics, ACL 2014, June 22-27, 2014,
Baltimore, MD, USA, Volume 2: Short Papers, pages
545–550.
Improving Semantic Similarity of Words by Retrofitting Word Vectors in Sense Level
119
