Design of Scenario-based Application-Optimized Data Replication

Strategies through Genetic Programming

Syed Mohtashim Abbas Bokhari and Oliver Theel

Department of Computer Science, University of Oldenburg, Germany

Keywords: Distributed Systems, Fault Tolerance, Data Replication, Quorum Protocols, Operation Availability, Operation

Cost, Voting Structures, Optimization, Machine Leaning, Evolutionary Strategies, Genetic Programming.

Abstract: A distributed system is a paradigm which is indispensable to the current world due to countless requests with

every passing second. Therefore, in distributed computing, high availability is very important. In a dynamic

environment due to the scalability and complexity of the resources and components, systems are fault-prone

because millions of computing devices are connected to each other via communication links. Distributed

systems allow many users to access shared computing resources which makes faults inevitable. Replication

plays its role in masking failures in order to achieve a fault-tolerant distributed environment. Data replication

is an appropriate means to provide highly available data access operations at relatively low operation costs.

Although there are several contemporary data replication strategies being used, the question still stands which

strategy is the best for a given scenario or application class assuming a certain workload, its distribution across

a network, availability of the individual replicas, and cost of the access operations. In this regard, research

focuses on analysis, simulation, and machine learning approaches to automatically identify and design such

replication strategies that are optimized for a given application scenario based on predefined constraints and

properties exploiting a so-called voting structure.

1 INTRODUCTION

To provide highly available data access operations is

a widely discussed prevalent problem in computer

science. Relying on a single replica significantly

confines the availability of the data. Therefore, the

increase in the number of replicas to store the data

objects is inevitable, which, when smartly applied,

increases the availability of the data object and makes

it more fault-tolerant. Because now, it can be

accessed by approaching other replicas, too. But then

the challenge comes up of managing those replicas

and maintain consistency so that replicas always yield

correct values. The goal of the operations is also to

behave in a replicated system the same as they would

do in a non-replicated system. This is known as one-

copy serializability (1SR) (Bernstein, P. et al., 1987).

As for this, these replicas are managed by protocols

known as data replication strategies (DRSs). These

strategies impose a threshold of a minimal number of

replicas known as read quorum (rq) and write quorum

(wq) to be accessed to perform the preferred access

operations. These access operations are either a read

or a write operation. The decisions to choose suitable

DRSs are trade-offs between choosing various quality

metrics such as load, capacity, availability (Naor, M.,

and Wool, A., 1998), scalability, and cost (Jimenez-

Peris, R. et al., 2001). The availabilities of read and

write operations are optimally point symmetrical to

each other (Theel, O., Pagnia, H., 1998). For instance,

an increased availability for a write operation would

compromise the availability of a read operation to a

certain extent and vice versa. It is more like the same

case with the cost of the read and write operations,

too. The questions arise as what are those

compromises, to what extent particular values can be

compromised and at the expense of what? These

compromises could be highly application-specific

and comprised of many scenarios which will be

discussed further in Section 2. This research intends

to provide application-optimized DRSs to fulfil such

specified scenarios.

The paper is written as follows. Section 2 specifies

and discusses the problem statement. Section 3

discusses the current state-of-the-art DRSs and other

contemporary approaches to address the problem and

their limitations. Section 4 defines the fault model,

describes the adopted methodology to approach the

120

Bokhari, S. and Theel, O.

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming.

DOI: 10.5220/0008955301200129

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 120-129

ISBN: 978-989-758-395-7; ISSN: 2184-433X

problem, and argues about the reason for opting this

approach over others. Section 5 states the

implementation aspects of the research. Section 6

presents the outcome, results, and their comparisons,

followed by a conclusion.

2 PROBLEM STATEMENT

The problem is illustrated by a triangle given in

Figure 1 where the consistency part is static because

1SR is maintained all the time. This leaves us room

to fully play around the availability and cost of the

access operations (provided a threshold of the total

number of replicas and the probability of individual

replicas). It can be seen that there are many scenarios

between availability and cost of the access operations

in a distributed paradigm. There exist many

contemporary strategies to manage those distributed

replicas, but the question still stands, which strategy

is best for a given scenario or application class.

Considering the fact that not every strategy fulfils

each scenario, leaves many scenarios unaddressed,

for which no optimal strategy exists. Hence, there is

no best solution (in terms of a global optima) but

solutions that serve a particular purpose (i.e., local

optima). Our research focuses on the automatic

identification and design of such an optimized data

replication strategy.

Figure 1: Data replication scenarios.

3 RELATED WORK

DRSs in general are categorized into two major

classes: unstructured and structured DRSs.

Unstructured DRSs, for instance, the Majority

Consensus Strategy (Thomas, R, H., 1979) use

combinatorics and minimum quorum cardinalities to

specify a quorum system. The Majority Consensus

Strategy requires n/2 replicas for the read and

(n+1)/2 for the write quorum to execute any

operation in a system comprising n replicas. This

threshold-based quorum system allows all the

replicas an equal opportunity to be in a read or write

quorum. However, it succumbs to high operational

cost and scalability issues because of linearly

increasing quorum cardinalities. This is not the case

in structured replication strategies where structural

properties and patters are used to specify the quorum

system. For instance, the Grid Protocol (Cheung, S. et

al., 1992) imposes a logical rectangular i * j grid

structure where i indicates column and j rows for a

system comprised of i * j = n replicas. A read quorum

consists of replicas from each column while a write

quorum constitutes all the replicas from a column

along with one replica from each column to satisfy

the quorum system intersection property. As shown

in Figure 2, there exist many other contemporary

strategies such as Read-One-Write-All (Bernstein, P.,

and Goodman, N., 1984), the Tree Quorum Protocol

(Agrawal, D., and Abbadi, A., 1990), the Weighted

Voting Strategy (Gifford, D., 1979), the Hierarchical

Quorum Consensus (Kumar, A., 1991), the

Triangular Lattice Protocol (Wu, C., and Belford, G.,

1992), etc. But the current state-of-the-art has not

much focused on a hybrid approach to explore new

strategies.

Figure 2: Contemporary data replication strategies (Lee, Y.-

J. et al., 2009).

There have been only a few limited efforts made

towards hybrid strategies because of its cumbersome

nature. So, there are some attempts, i.e., (Theel, O.,

1993), (Theel, O., 1994), (Pagnia, H., and Theel, O.,

1998), and (Bokhari, S, M, A., and Theel, O., 2020)

on hybrid approaches which manually design DRSs

but lack automation. Moreover, there exist only a few

papers, i.e., (Arai, M. et al., 2004), (Choi, S., and

Youn, H., 2012), etc. on hybrid approaches which

primarily attempt to combine Tree Quorum Protocols

with Grid Protocols but they do not impose any

unified structure on the nodes which greatly limits the

operability of the approach. Because of the diverse

nature of topologies (as shown in Figure 2), there is

less room for a hybrid approach to work effectively

as it cannot incorporate the varied strategies freely.

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming

121

As a consequence, many scenarios could be left

unaddressed. Whereas, to address this issue, if a

hybrid approach is applied to such a diverse nature of

topologies, the problem easily goes out of hand.

Section 4 addresses this limitation and provides a

solution to that problem.

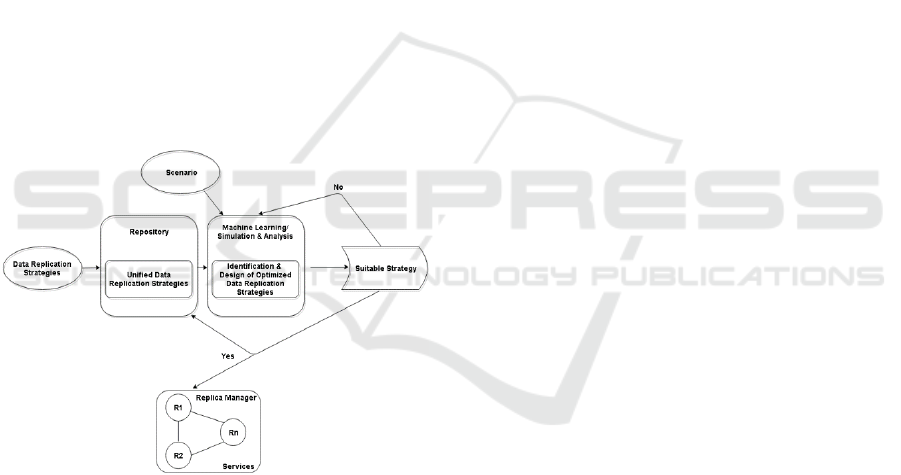
4 METHODOLOGY

Figure 3 shows the proposed methodology in a

simplified manner. It starts from replication strategies

being injected into a database repository and a

scenario. Both, the nature of the repository and the

scenario will be explained in detail in this section.

The analysis and simulations (shown later in this

paper) are performed on the repository until the

desired solution is met which then is inserted back to

the repository for future use. Here, the question also

arises of selecting the appropriate machine learning

and simulation techniques for the identification and

for the design of optimized data replication strategies.

Let us dissect all these components one by one in the

following.

Figure 3: Methodology.

4.1 Fault Model

Prior to discussing the components, we state the fault

model and other assumptions first. The access

operations are either read or write and are performed

only when the proper quorum is acquired. The

replicas are supposed to manifest a fail-silent

behaviour. All failures are assumed to be independent

of each other. The network is supposed to be fully

connected without communication failures. Only

nodes (machines) with replicas can fail and the

probability that a node has failed at any particular

point in time is (1-p). p gives the probability that a

node is available at an arbitrary point in time. The

strategies are supposed to be version-based to avoid

additional time synchronization issues, i.e., a replica

does not only consist of some “payload” data but also

a version number. A replica with a highest version

number has the up-to-date payload.

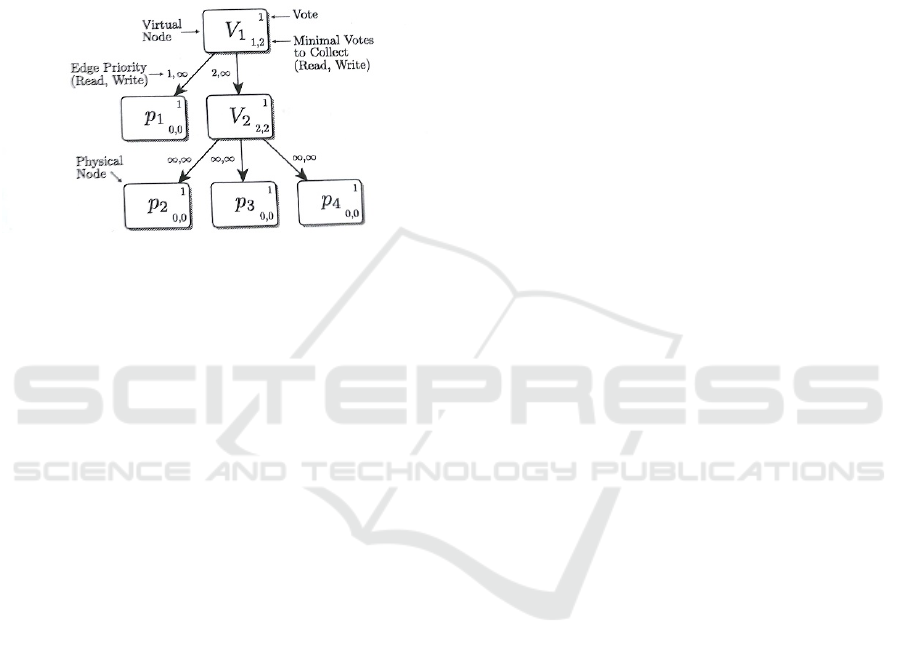
4.2 Voting Structures

To address the mentioned topological and diversity

issues between DRSs, a unified representation of

these strategies by a concept like General Structured

Voting (Theel, O., 1993) is required for the

simulation and machine learning approaches to be

applied over it. Expert-based manual designs of

optimized DRSs using the concept of voting

structures have been presented in (Theel, O., 1994),

and (Pagnia, H., and Theel, O., 1998). Figure 4

represents a quorum system by a directed acyclic

graph (DAG) named a voting structure. A voting

structure is traversed recursively by an algorithm to

derive the quorums for respective access operations

at run time independent of the varied topologies of the

strategies. The nodes of a voting structure are either

physical nodes representing actual replicas or virtual

nodes that constitute the groupings of physical and

virtual nodes. The virtual nodes are labelled Vi,

where i = 1, 2, … while the physical nodes are

labelled p

where 1 ≤ j ≤ n and n represent the total

number of replicas of a system. Irrespective of being

a physical or virtual node, every node is endowed

with votes comprised of a natural number (top right

corner) which could also be comprehended as the

weightage of that node. Furthermore, each node is

equipped with a pair of minimal quorums (called

“minimal votes” in the figure) to collect from its child

nodes to build the read and write quorums. The

minimal quorums for each node to gather per

operation has to be less than or equal to the sum of the

votes of its children. Some replication strategies, i.e.

the Tree Quorum Protocol imposes a partial order on

the quorums by which to use quorums for operation

execution. The specification of such an ordering

allows certain quorums to be used prior to others. In

such cases, the directed edges of voting structures can

be marked with operation-specific priorities imposing

such orderings. An edge priority of 1 annotates the

highest while the symbol ∞ represents the lowest

priority. This voting structure is traversed by the

recursive algorithm to derive respective quorums. It

starts from the root node and queries as many of its

child nodes as specified in the minimal quorums to

orchestrate the quorums of physical replicas for the

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

122

respective access operations. On each level, if the

voting structure has a total number of votes V, then

the quorums for intersection abide by the following

rules in general:

1. rq + wq > V (to avoid read-write conflicts) (1)

2. wq > V/2 (to avoid write-write conflicts) (2)

Where rq (wq) is a number representing the minimal

read (write) quorum.

Figure 4: Example of a voting structure (Storm, C., 2012).

For instance, the voting structure shown in Figure 4

produces the following read (RQ) and write quorum

sets (WQ):

RQ = {{p1}, {p2, p3}, {p2, p4}, {p3, p4}}

WQ = {{p1, p2, p3}, {p1, p2, p4}, {p1, p3, p4}}

4.3 Scenario Parameters

A scenario for DRSs consists of constraints which

determine the fitness of a strategy holistically to judge

the goodness of a solution. These constraints may

vary among different applications depending upon

their nature, requirements, and resources.

4.3.1

Consistency of Operations

There exists a variety of data consistency models for

DRSs ranging from strict data consistency to

relatively weaker notions. As already stated,

consistency model opted for our approach is static

and strictly meets the 1SR property. The 1SR

property is maintained in a DRS when 1) every read

quorum intersects every write quorum, 2) all write

quorums intersect with each other, 3) replicas can be

locked exclusively for write operations and locked

shared for read operations.

4.3.2

Number of Replicas

There is a threshold imposed on the total number of

replicas n that for any strategy, n cannot exceed the

specified threshold value ε. This is, because it

certainly costs to create new nodes to host replicas.

N, ε ∈ ⁺

∧ n ≤ ε (3)

4.3.3 Availability of Access Operations

The probability that the data access operations are

available for a DRS depends on the characteristics of

the strategy, the probability of individual replicas p

and number of replicas n. It is defined by Ar(p, n) and

Aw(p, n) respectively, where Ar(p, n), Aw(p, n) ∈

[0,1]. For some DRSs, there exist closed formulas to

calculate the availability as well as the costs.

However, generally, the equations given below are

used to analyse the data access operations’

availability of a DRS. All the RQs and WQs are

derived from a DRS to calculate Ar(p, n) and Aw(p,

n) for given p and n values. Equations 4 and 5

calculate the read and write operation availabilities

respectively. For this, they rely on a so-called set of

all possible read (write) quorums RQS (WQS). In the

scope of the example of Figure 4, RQS equals RQ ∪

{{p1,p2,p3,p4}} (WQS equals WQ ∪

{{p1,p2,p3,p4}}). The equations take the sum of the

probability of all elements of RQS or WQS being

available for a given probability p of individual

replicas.

Ar(p, n) = Σ

∀q∈ RQS

|q|

(1− p)

n−|q|

(4)

Aw(p, n) = Σ

∀q∈ WQS

|q|

(1− p)

n−|q|

(5)

These availabilities are probabilities and constraints

restrict them to be within the specified thresholds α,

β.

Ar, Aw, α, β ∈ [0, 1]

∧ Ar ≥ α

∧ Aw ≥ β (6)

4.3.4 Cost of Access Operations

The minimal average costs for the data access

operations are represented by Cr(p, n) and Cw(p, n)

respectively. The read Cr(p, n) and write Cw(p, n)

costs reckon the average minimal number of replicas

out of the total number of replicas n, which are

mandatory to perform an operation for a given

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming

123

probability of individual replicas p. This cost is

calculated by taking the sum of the minimum number

of replicas minRQ (minWQ) obligatory to form a

read (write) quorum for each replica set in RQS

(WQS) with the probability of the replica set

appearing. Furthermore, the resulted sum has to be

divided by Ar(p, n) or Aw(p, n) depending upon the

particular access operation.

Cr(p, n) = Σ

∀q∈ RQS

|q|

(1− p)

n−|q|

minRQ(q)

(7)

Ar(p, n)

Cw(p,n) = Σ

∀q∈ WQS

|q|

(1− p)

n−|q|

minWQ(q)

(8)

Aw(p, n)

These costs are real positive numbers and constraints

restrict them to be within the specified thresholds γ, δ.

Cr, Cw, γ, δ ∈ ⁺

∧ Cr ≤ γ

∧ Cw ≤ δ

(9)

4.3.5 Fitness Weightage

We use a so-called fitness weightage (fw) that

suggests a scenario to be biased towards either cost or

availability (or even being neutral), to be able to

convert a multi-objective into a single objective

problem. This makes the optimization problem

somewhat easier to solve.

fw ∈ [0,1] (10)

4.3.6

Probability of Individual Replicas

There is a subtle difference between the availability

of access operations and the availability of individual

replicas p. p refers to the probability by which the

replicas are available which means the probability

that a replica has failed at any particular point in time

is (1-p) while the user performs the operations with

access operations’ probability. In a scenario, we

restrict p to be in the interval between pmin ≤ p ≤

pmax.

pmin, p, pmax ∈ [0,1]

∧ pmin ≤ p ≤ pmax (11)

4.4 Database Repository

Figure 5 shows the data replication strategies Grid

Protocol (left) and Triangular Lattice Protocol (right)

converted into a unified representation of a voting

structure each. These voting strategies are stored in a

scalable database repository in the form of JSON

documents and can be queried upon any desirable

criteria.

Figure 5: Voting structures as DAGs representing DRSs.

4.5 Genetic Programming

The research proposes genetic programming (GP)

(Koza, J, R., 1992) and (Banzhaf, W. et al., 1998) as

a subset of machine learning to automatically identify

or design application-optimized DRSs. The major

difference of GP with other genetic variants of

machine learning is the representation. GP is used to

evolve computer programs. It consists of an encoding

scheme, random crossover, mutation, a fitness

function, and multiple generations of evolution to

solve the specified task on its termination condition.

The encoding scheme consists of a genotype (coding

space) carrying an underlying set of traits and a

phenotype (solution space) which is the behavioural

expression of this genotype in a specific environment.

Hence, the question arises which encoding scheme

should be used since poor representations may lead to

poor results. The crossover (

Syswerda, G., 1992)

operator mixes up the genetic material of parents in

anticipation of forming a better off-spring. It splits up

the genome of two existing solutions at an arbitrary

point and swaps them to create the off-spring

solutions inheriting properties from both of the parent

solutions. The mutation operator changes the solution

randomly but slightly, i.e., by flipping one or more

bits from the previous offspring to generate a new

altered child solution. In the pursuit of a solution, the

questions of crossover and mutation types as well as

points are also thought-provoking to address.

Moreover, the population size also matters because a

very small size implies few possibilities of executing

the crossovers. Therefore, only a fraction of the

search space can be explored. Alternatively, a very

large size may slow down the genetic approach.

Although, it is highly problem-specific but very large

populations do not solve the problem faster than

moderate-sized populations. Figure 6 illustrates the

problem in the context of genetic programming where

we start from a scenario and an accordingly initial

population. The initial population is analyzed based

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

124

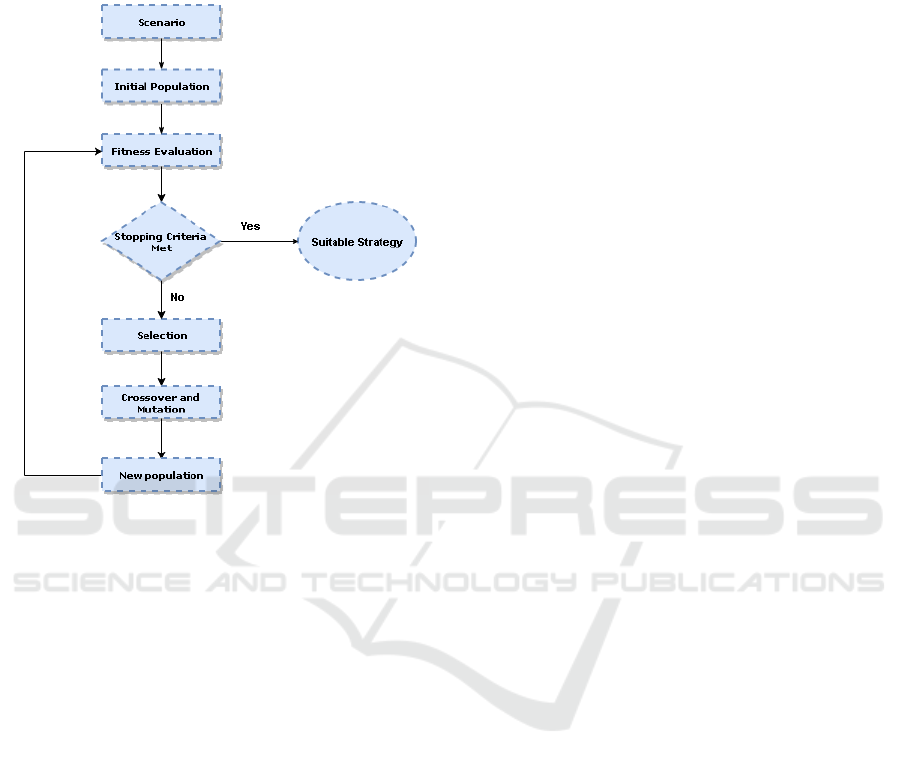
on its fitness to the scenario in order to choose better

strategies to perform crossover and sometimes also

mutation in anticipation of a constant evolutionary

trajectory until a solution is found.

Figure 6: Genetic programming.

5 IMPLEMENTATION

Having discussed the methodology, terminologies,

and semantics, let us examine the implementation

aspect comprising the parameters, functions, and the

algorithm itself in detail. Once the scenario is

specified to find a suitable DRS to fulfil it, the system

parameters are set for the algorithm to run.

5.1 Mu, μ, and Lambda, λ

Having provided the repository to select the

respective DRSs, the μ and λ values are also set as

system parameters for the algorithm to start. μ is the

restriction on the number of parents that are used to

form next generation and λ is the restraint on the

number of off-spring strategies generated using μ

number of parent DRSs.

5.2 Crossover

There are various ways by which the DRSs can be

combined and the resulting hybrid strategy will

certainly exhibit different properties than the parents.

The virtual nodes of two parent strategies are

swapped to form new offspring strategies.

Additionally, there are crossover points in every DRS

represented by a Boolean variable which allows the

crossover to be performed only on those points and in

such a way that it maintains the DRSs’ 1SR property

throughout the process. While performing crossovers,

the algorithm also restricts the number of replicas not

to grow beyond a certain threshold ε specified in the

scenario.

5.3 Mutation

The algorithm also performs mutation on the DRSs

with the probability specified in the system

parameters. This mutation modifies the votes of the

strategies allowing some replicas to be more

important in the weightage than other replicas. Once

the votes are changed, the quorum also needs to be

updated accordingly under the conditions (1) and (2)

to uphold the 1SR property. In addition, the algorithm

identifies the mutation points by a Boolean variable

to avoid the DRS to be inconsistent and thereby,

again, maintaining 1SR all the time.

5.4 Algorithm

Having specified a scenario and given it to the

program, scenarioFitness is calculated. μ and λ are

defined along with mutation probability. The list

μList contains parent DRSs, the list λList comprises

offspring DRSs, whereas the list initPopList consists

of an initial population of DRSs. The Boolean

variable isFit determines whether a strategy has

achieved the expected level of fitness. The genetic

program loops through all the passed on DRSs,

calculates the fitness of every individual strategy, and

selects the μ best strategies to the μList, in case, there

is no satisfactory solution found in the initial

population. This μList is then sent to the while loop

to select the DRSs randomly from it and perform the

crossovers and mutations to create λ offspring

strategies. The λList constitutes newly created

strategies which are evaluated again to check if they

satisfy the standard criteria. If the criteria are met,

then the relevant newly generated optimized strategy

is stored in the repository, the while loop terminates

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming

125

and so does the program. If not, it selects the μ best

DRSs to the μList from (μList + λList) for the next

generation. This process continues until a suitable

strategy is found.

lgorithm

1 Specify a scenario;

2 Calculate scenarioFitness;

3 Define μ and λ;

4 Initialize μList;

5 Initialize λList;

6 Boolean isFit = false;

7 Generate initial population of DRSs to the repository;

8 Retrieve, parse & store the generated DRSs to initPopList

9 geneticProgramming(initPopList) {

10 Loop through initPopList

11 Calculate fitness;

12 if (fitness ≥ scenarioFitness) {

13 isFit = true;

14 return;

}

15 END

16 Choose μ best DRSs to the μList;

17 Do

18 Empty λList;

19 Loop to λ

20 Select randomly DRS1 from μList;

21 Select randomly DRS2 from μList;

22 Perform crossover of DRS1, DRS2;

23 Generate off-spring DRSs;

24 Perform mutation on the off-spring;

25 Calculate fitness;

26 if (fitness ≥ scenarioFitness) {

27 isFit = true;

28 Store

off-spring DRS into

the repository;

}

29 Add off-spring DRSs to the λList;

30 END

31 Select

μ best DRSs to the μList from (μList

+ λList) for next generation;

32 While (!isFit);

}

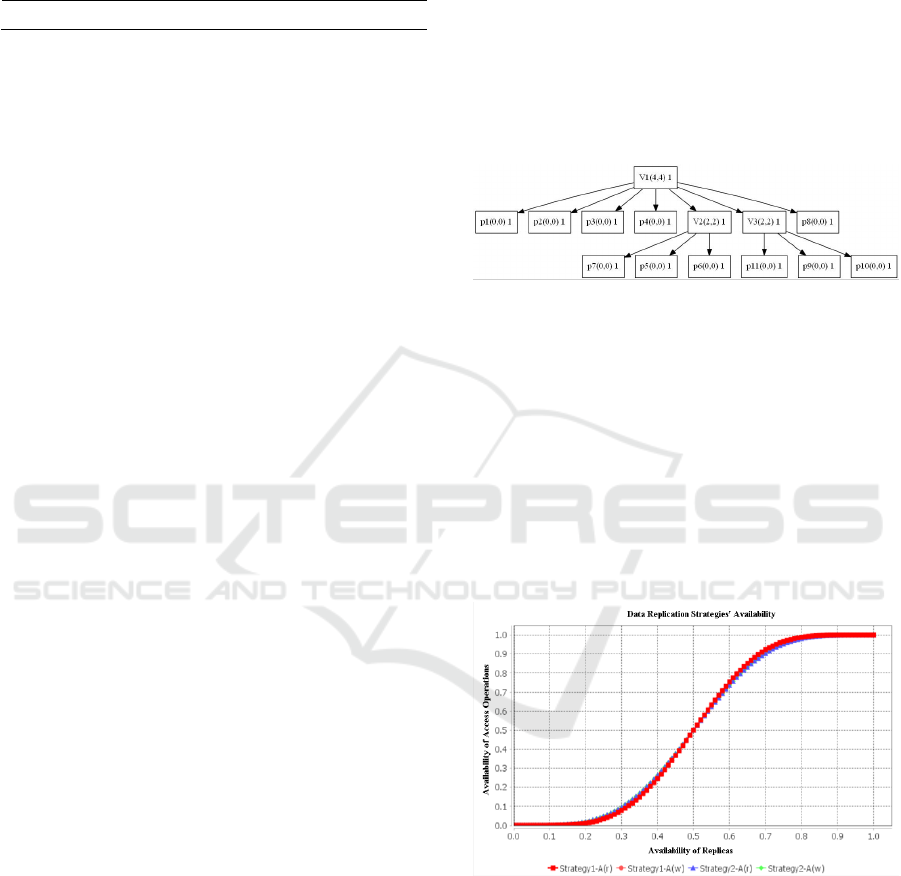
6 EXPERIMENTS & RESULTS

Figure 7 gives a relatively simple example of a hybrid

DRS generated by the algorithm which consists of 11

replicas. It can be seen that although the DRS is not

very complex and maintains a tree-like structure

rather than an acyclic one, yet it is so powerful and

optimized in terms of its availability and cost that it is

competing the Majority Consensus Strategy (MCS)

which is believed to be the best strategy in terms of

its availability of write access operations. When

compared, the hybrid DRS in terms of its availability

is so close to MCS. It is almost the same for higher

values of p, however, it is far better when it comes to

the cost comparison.

Figure 7: Hybrid strategy.

The availability and cost graphs on the discretized

values of p are shown in Figure 8 and Figure 9,

respectively, where Strategy 1 indicates the MCS

while the Strategy 2 represents a hybrid DRSs. Both

strategies consist of 11 replicas each. It can be seen

that in terms of operational availability the hybrid

strategy is converging on to the same values as MCS

for higher values of p. This is a quite good availability

but more importantly, it outclasses the MCS in terms

of its cost in all the cases. Hence, it covers a scenario

which could have been left unaddressed otherwise.

Figure 8: Availability graph of access operations.

In the best case, out of 11, it only takes four replicas

each to perform a read and a write operation while the

total cost for MCS is 12 for all the cases. This is a

good example of a relatively less complicated DRS

where we have not compromised the availability and

yet reduced the cost significantly by using the hybrid

approach via genetic programming.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

126

Figure 9: Cost graph of access operations.

6.1

Scenario

Let us specify a sample scenario and apply our

approach to find out whether a suitable replication

strategy can be found. The scenario consists of

desired read and write availabilities and their

respective costs, which must be achieved within the

threshold of maximum 16 replicas and some

availability p of individual replicas. However, cost is

not important in this case, therefore, full weightage is

given to availability.

6.2 Scenario

Parameters

The desired read availability and write availability

thresholds are 0.80 and 0.72, respectively, using a

node availability of 0.6 inside a 16 replicas limit. Cost

is specified being less than seven for each operation,

but the fitness weightage determines the availability

to be fully important.

p = 0.6

ε = 16

α = 0.80

β = 0.72

γ = 7.0

δ = 7.0

fw = 1.0

6.3 System

Parameters

Having defined the scenario, now the system

parameters are set to run the algorithm accordingly.

Here, the number of parent and offspring strategies

are set to six and 15, respectively. The initial

population is only used once, namely in the crossover

process in the very first generation. The crossovers

are performed all the time while the mutation is

performed with a probability of 0.2.

μ = 6

λ= 15

mutationProb = 0.2

6.4

Results

This section shows the graphical visualization of the

results generated by the algorithm on the provided

parameters. It analyzes the fitness of every individual,

every generation, and designs new strategies in the

course of fulfilling the specified criteria when it is not

found in the repository.

6.4.1

Fitness Analysis

Figure 10 depicts the fitness of every individual DRS

and the way it evolves. The x-axis represents the

number of DRSs and y- axis denotes the fitness value

of every individual strategy. The red line indicates

fitness of the DRSs while the pink and blue lines

represent the availabilities of read and write

operations, respectively. It can be noticed that it starts

with only a few strategies of low fitness which

implies that the repository does not have a

satisfactory solution to the problem. Then, the fitness

improves and begins to evolve gradually through

crossover and mutation operators of genetic

programming until the loop stops over the desired

termination condition.

Figure 10: Fitness graph.

6.4.2 Population Analysis

Figure 11 illustrates how the fitness of DRSs grows

by every generation. The graph shows the fitness of

the best DRSs among every generation. The x-axis

represents the number of generations while the y-axis

indicates the fitness value of the best replication

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming

127

strategy of a respective generation. It took 10

generations for the system to find a suitable DRS that

satisfies the given scenario. It starts from a fitness of

1.365 and gradually but consistently continues to

climb up until the desired fitness of 1.525 is achieved.

Figure 11: Populations’ evolution.

6.4.3 Hybrid Data Replication Strategy

Figure 12 shows the identified suitable strategy

optimized for the mentioned scenario of Section 6.2.

This strategy is comprised of 16 replicas which meets

our threshold criterion ε. Moreover, the variable

votes, quorums, and the structure itself reflect its

hybrid nature that works together to serve the purpose

and provide an up-to-now unknown replication

strategy.

Figure 12: Optimized hybrid DRS for the given scenario.

6.4.4 Availability Analysis

Figure 13 shows the availability graph for the access

operations of the identified DRS on discretized values

of p. The newly designed DRS fulfils the specified

scenario of thresholds. The x-axis represents the node

availability while y-axis indicates the availability of

the access operations. The point symmetry of the

graph overtly displays an extremely high availability

for the access operations.

This availability is, again, very close to MCS

(particularly for higher p values) which is considered

the best in terms of the critical write operations’

availability, and at the same time, our hybrid

approach is reasonably economical in terms of cost.

In best cases, it takes only five replicas each for the

access operations out of 16 unlike MCS with a cost of

17 replicas in total for read and write, which is very

expensive.

Figure 13: Availability graph of read and write operations.

In this manner, the proposed machine learning

framework provides a strong opportunity to explore

and design new unknown DRSs for any specified

scenario and optimize them over several generations

of evolution to meet the specified scenario-specific

criteria.

7 CONCLUSIONS

This paper proposes an innovative, automated

mechanism for designing new hybrid optimized

DRSs for specified application-specific scenarios for

which no optimal strategy may exist. It designs the

DRSs without trying brute force all the possible

combinations since the search space is huge. The

novel approach does not only consider the availability

aspect, but also the cost aspect and successfully

models a scenario into a replication strategy. The

research is quite innovative in proposing a strong

machine learning mechanism towards data

replication and fault tolerance. Our proposed

approach has the potency to open whole new doors of

exploring unknown replication strategies which

otherwise potentially would not have been found.

Furthermore, it unprecedentedly uses voting

structures in the context of genetic programming to

generate new unknown optimized hybrid DRSs. More

complex crossover and mutation operators will be

taken into consideration as a part of future work to

further strengthen our approach.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

128

REFERENCES

Bernstein, P., Hadzilacos, V., and Goodman, N., 1987.

Concurrency Control and Recovery in Database

Systems, ISBN-13 978-0201107159, Addison Wesley,

p. 370.

Naor, M., and Wool, A., 1998. The Load, Capacity, and

Availability of Quorum Systems, SIAM Journal on

Computing, vol 27, no. 2, pp. 423-447.

Jimenez-Peris, R., Patino-Martınez, M., Alonso, G., and

Kemme, B., 2001. How to Select a Replication Protocol

According to Scalability, Availability, and

Communication Overhead, in Proceedings 20th IEEE

Symposium on Reliable Distributed Systems (SRDS).

Theel, O., Pagnia, H., 1998. Optimal Replica Control

Protocols Exhibit Symmetric Operation Availabilities,

in Proceedings of the 28th International Symposium on

Fault-Tolerant Computing (FTCS-28), pp. 252-261.

Thomas, R, H., 1979. A Majority Consensus Approach to

Concurrency Control for Multiple Copy Databases,

ACM Transactions on Database Systems 4.2, pp. 180–

207.

Cheung, S., Ammar, M., Ahamad, M., 1992. The Grid

Protocol: A High Performance Scheme for Maintaining

Replicated Data, IEEE Transactions on Knowledge and

Data Engineering, vol 4, issue 6.

Bernstein, P., and Goodman, N., 1984. An Algorithm for

Concurrency Control and Recovery in Replicated

Distributed Databases, ACM Transactions on Database

Systems (TODS), vol. 9, pp. 596–615.

Agrawal, D., and Abbadi, A., 1990. The Tree Quorum

Protocol: An Efficient Approach for Managing

Replicated Data, in Proceedings of the 16th

International Conference on Very Large Data Bases

(VLDB), pp. 243–254.

Gifford, D., 1979. Weighted Voting for Replicated Data,

Proceedings of the Seventh ACM Symposium on

Operating Systems Principles (SOSP), pp. 150-162.

Kumar, A., 1991. Hierarchical Quorum Consensus: A New

Algorithm for Managing Replicated Data, IEEE

Transactions on Computers, vol 40, issue 9, pp. 996–

1004.

Wu, C., and Belford, G., 1992. The Triangular Lattice

Protocol: A Highly Fault Tolerant and Highly Efficient

Protocol for Replicated Data, in Proceedings of the

11th Symposium on Reliable Distributed Systems

(SRDS), IEEE Computer Society Press.

Theel, O., 1993. Meeting the Application's Needs: A Design

Study of a Highly Customized Replication Scheme, in

Proceedings of the Pacific Rim International

Symposium on Fault Tolerant Computing, Melbourne,

Australia, pp. 111-117.

Theel, O., 1994. Rapid Replication Scheme Design using

General Structured Voting, in Proceedings of the 17th

Annual Computer Science Conference, Christchurch,

New Zealand , pp. 669-677.

Pagnia, H., and Theel, O., 1998. Priority-based Quorum

Protocols for Replicated Objects, in Proceedings of the

2nd International Conference on Parallel and

Distributed Computing and Networks (PDCN),

Brisbane, Australia, pp. 530-535.

Bokhari, S, M, A., and Theel, O., 2020. A Flexible Hybrid

Approach to Data Replication in Distributed Systems,

Computing Conference (SAI), London, UK (to be

published).

Arai, M., Suzuki,T., Ohara, M., Fukumoto, S., Iwasak, K.,

and Youn, H., 2004. Analysis of Read and Write

Availability for Generalized Hybrid Data Replication

Protocol, in Proceedings of the 10th IEEE Pacific Rim

International Symposium on Dependable Computing

(PRDC).

Choi, S., and Youn, H., 2012. Dynamic Hybrid Replication

Effectively Combining Tree and Grid Topology, The

Journal of Supercomputing, vol. 59, issue 3, pp. 1289-

1311.

Lee, Y.-J., Kim, H.-Y., Lee, C.-H., 2009. Cell

Approximation Method in Quorum Systems for

Minimizing Access Time, Cluster Computing, vol. 12,

pp. 387-398.

Theel, O., 1993. General Structured Voting: A Flexible

Framework for Modelling Cooperations, in

Proceedings of the 13th International Conference on

Distributed Computing Systems, pp. 227-236.

Storm, C., 2012. Specification and analytical evaluation of

heterogeneous dynamic quorum-based data replication

schemes, Springer Vieweg, ISBN 978-3-8348-2380-9,

pp. 1-350.

Koza, J, R., 1992. Genetic Programming: On the

Programming of Computers by Means of Natural

Selection, MIT Press, Cambridge.

Banzhaf, W., Francone, F, D., Keller, R, E., and Nordin, P.,

1998. Genetic Programming: An Introduction: on the

Automatic Evolution of Computer Programs and Its

Applications, Morgan Kaufmann Publishers Inc., San

Francisco, CA, USA.

Syswerda, G., 1992. Simulated Crossover in Genetic

Algorithms, In Foundations of Genetic Algorithms

(FOGA), pp. 239-255.

Design of Scenario-based Application-optimized Data Replication Strategies through Genetic Programming

129