High-performance Algorithms using Deep Learning in Turn-based

Strategy Games

Tomihiro Kimura and Ikeda Kokolo

Japan Advanced Institute of Science and Technology, JAIST, Ishikawa, Japan

Keywords:

Turn-based Strategy Games, Deep Neural Network, Deep Reinforcement Learning, Policy Network, Value

Network, AlphaZero, Residual Network.

Abstract:

The development of AlphaGo has increased the interest of researchers in applying deep learning and reinforce-

ment learning to games. However, using the AlphaZero algorithm on games with complex data structures and

vast search space, such as turn-based strategy games, has some technical challenges. The problem involves

performing complex data representations with neural networks, which results in a very long learning time.

This study discusses methods that can accelerate the learning of neural networks by solving the problem of

the data representation of neural networks using a search tree. The proposed algorithm performs better than

existing methods such as the Monte Carlo Tree Search (MCTS). The automatic generation of learning data by

self-play does not require a big learning database beforehand. Moreover, the algorithm also shows excellent

match results with a win rate of more than 85% against the conventional algorithms in the new map which is

not used for learning.

1 INTRODUCTION

Games such as Chess, Shogi (Japanese Chess), and

Go have long been used as test cases in artiﬁcial intel-

ligence (AI) research. Currently, AI agents for Chess

and Shogi have been developed that can perform be-

yond the professional level of humans. In contrast,

it was initially thought that making an AI with pro-

fessional Go player-level agents is difﬁcult; however,

in 2016, AlphaGo (Silver et al., 2016) was released,

which is the ﬁrst program to beat professional Go

players at full board size without a handicap. Fol-

lowing the success of AlphaGo, DeepMind released

AlphaGoZero in 2017 (Silver et al., 2017), which is

and improvement of AlphaGo by not requiring data

to be learned from previous games. Instead, AlphaGo

Zero learns by only playing against itself making it

stronger than all previous versions. That same year,

AlphaZero, a general-purpose version of AlphaGo

Zero (Silver et al., 2018), was released, that masters

the games of Chess, Shogi, and Go. Since then, the

development and research of game AI that incorpo-

rates deep learning and reinforcement learning have

been popular.

Turn-based strategy and war simulation games

have been popular in the board and video game mar-

ket. However, AI programs for turn-based strategy

games have not been able to satisfy the level of human

players, because of the following two reasons.

Firstly, turn-based strategy games have a vast

search space, which is larger than Go or Shogi.

Hence, even the ﬁrst turn could lead to a compu-

tational explosion. Secondly, the complexity of the

game system makes programming difﬁcult. These

problems are caused by a variety of factors that make

gaming systems complex and engaging.

One of the factors that complicate games is the

variety of pieces and the various characteristics of to-

pographicelements; these pieces and topographic fea-

tures do not exist in Go or Shogi. Moreover, the initial

layout of the map is not ﬁxed as in Go and Shogi, and

a wide variety of maps can be designed in many cases.

Furthermore, in turn-based strategy games, all

units can sequentially operate during a turn, providing

more options and making this condition more suscep-

tible to computational explosions.

In addition, board game researchers who study

Go, Chess, and Shogi have accumulated game data

through many years of research, which is not the

case for most turn-based strategy games; hence, re-

searchers have to gather the data themselves if neces-

sary.

Deep learning, which is used in AlphaGo, is be-

coming very popular and is expected to be used as a

Kimura, T. and Kokolo, I.

High-performance Algorithms using Deep Learning in Turn-based Strategy Games.

DOI: 10.5220/0008956105550562

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 555-562

ISBN: 978-989-758-395-7; ISSN: 2184-433X

555

search technique for games with huge search spaces

far more complex than Go and Shogi. AlphaZero’s

algorithm, although called MCTS, is quite different

from the traditional MCTS algorithm. AlphaZero

uses the probabilistic output of the policy network as

a guide for proceeding with the search. It is consid-

ered to be general and can be applied in cases where

the original MCTS algorithm is applicable. Hence, it

would be interesting to evaluate the performance of

AlphaZero’s algorithm on other games.

In this paper, we evaluate the performance of Al-

phaZero’s algorithm in terms of the difﬁculty and in-

genuity in applying it to complex games and of its

ability to accelerate learning.

The original name of the algorithm is APV-MCTS

(Asynchronous Policy and Value MCTS). We modify

it here by removing the element A; hence, our algo-

rithm is called PV-MCTS.

2 TUBSTAP

To address the difﬁculties stated above, we use the

Turn-Based Strategy Games as an Academic Platform

(TUBSTAP) (Fujiki et al., 2015), which allows the

development and comparisons of the performance of

turn-based strategy game AI agents. The game rules

are examined, extracted, simpliﬁed, and abstracted

from the rules of various turn-based strategies such

as “Famicon Wars”. Hence, the basic operation of the

turn-based strategy game can be investigated on this

platform.

2.1 TUBSTAP Game Rules

The following units are available in TUBSTAP: In-

fantry, Panzer, Cannon, Anti-air Tank, Fighter planes,

and Attack Aircraft. In addtion, six types of terrain

cells are available: mountain, forest, plain, road, sea,

and fortress. All units have an initial hit point (HP),

which is an integer between one and ten such that the

unit is, removed from the board when it reaches an

HP of 0. The HP decreases when units attack; simul-

taneously, the HP of the attacking side unit decreases

during a counterattack. TUBSTAP is similar to “Fam-

icom Wars”. The game progresses by having ﬁghting

RED and BLUE forces ﬁght each other with multi-

unit movements in one turn. The match ends when

either units are completely destroyed, or the speciﬁed

number of turns is reached. The winning side is the

one that destroys the other unit or has a higher total

HP above a threshold value speciﬁed at the end of the

game.

2.2 TUBSTAP Game Maps

TUBSTAP users can create and test a wide variety of

maps. Figure 1 (a) shows an example of a battle map

in TUBSTAP, which is used in game competitions and

AI combat capability. Although the map size is rela-

tively small, i.e., 6 × 6, current AI programs used on

this map still have difﬁculties in selecting the optimal

operation. In fact, there are no algorithms that can

perform better than the level of humans except for the

MCTS-type algorithms, which has been found to per-

form satisfactorily. On this map, it is difﬁcult for an

AI program to always select the optimum operation,

and sometimes it selects the operation which is very

disadvantageous. There is no algorithm beyond hu-

man action. Among the game algorithms, the MCTS

type algorithm is the only one that seems to be able to

operate competitively.

We prepared a collection of benchmark problems

(Kimura and Ikeda, 2016) in AI research, including

pathﬁnding problems, tracking problems, and multi-

unit cooperation problems, with varying levels of dif-

ﬁculty. Figure 1 (b) shows an example of bench-

mark maps, representing the pinch problem (sand-

wich problem). In the pinch problem map, the search

algorithm has to search deep and wide ranges to ob-

tain the right answer, which is difﬁcult to read accu-

rately.

Considering reasonable learning time and execu-

tion time, the map size is set to 6 × 6, and all evalua-

tions are made on maps of this size.

2.3 Previous Works

The algorithms applicable to TUBSTAP are limited

by the computational complexity of turn-based strat-

egy games. Although MCTS and its variations (Kato

et al., 2013) and the minimax method, which divides

the aspects (Sato et al., 2015; Sato and Ikeda, 2016),

have been found to be applicable, the obtained perfor-

mance is still poor. A recent study has applied, deep

learning to TUBSTAP (Kimura and Ikeda, 2019),

(a) Battle map example.

(b) Pinch problem map.

Figure 1: TUBSTAP Map Examples.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

556

which learns a large number of match records to cre-

ate a policy network; however, it does not have a

search method. In relation to this, a recent study de-

veloped a search method that combines a policy net-

work and the value network introduced in AlphaZero

(Kimura, 2019); however, detailed technical data and

analyses are insufﬁcient. This paper will provide a

more detailed technical analysis of the scheme.

3 PROPOSED SYSTEM

The basic principles of the proposed system follow

the AlphaZero’s system but with changes incorpo-

rated for TUBSTAP. The changes include a function

for multi-unit operations, an additional operation for

searching attack nodes with priority, and a neural net-

work with improved performance. The proposed sys-

tem consists of a tree search part, a reinforcement

learning part, and a neural network part.

In the learning part, data are generated by the

search of PV-MCTS. In the normal game play phase,

the ﬁnal next move is decided by the search based on

the prediction of the learned neural network.

3.1 New Design Part

Many parts of this research are added to the Alp-

haZero design. To solve the complex data structure

problem of the turn-based strategy game, change the

output structure of the neural network and move the

unit designation from output to input. We try to sim-

plify complex games by incorporating a structure for

selecting multiple units into the search tree. To speed

up node selection in the MCTS, we introduce a bias

term to make the search efﬁcient. Introducing new

knowledge to change the design of neural networks,

aiming for a design that converges faster.

3.2 Tree Search Design

The PV-MCTS search is an MCTS-type search that

uses deep neural networks with both policies and val-

ues. The search proceeds based on the probability

distribution vector p output of the policy network and

node selection by simulation. The node with the high-

est visit count is selected. Note that search does not

use the rollouts commonly used in MCTS. During

self-play, the node is reused for the next search.

In simple TUBSTAP output representation, unit

selection and action should be in the output, but in this

study, the unit selection is placed on the input side and

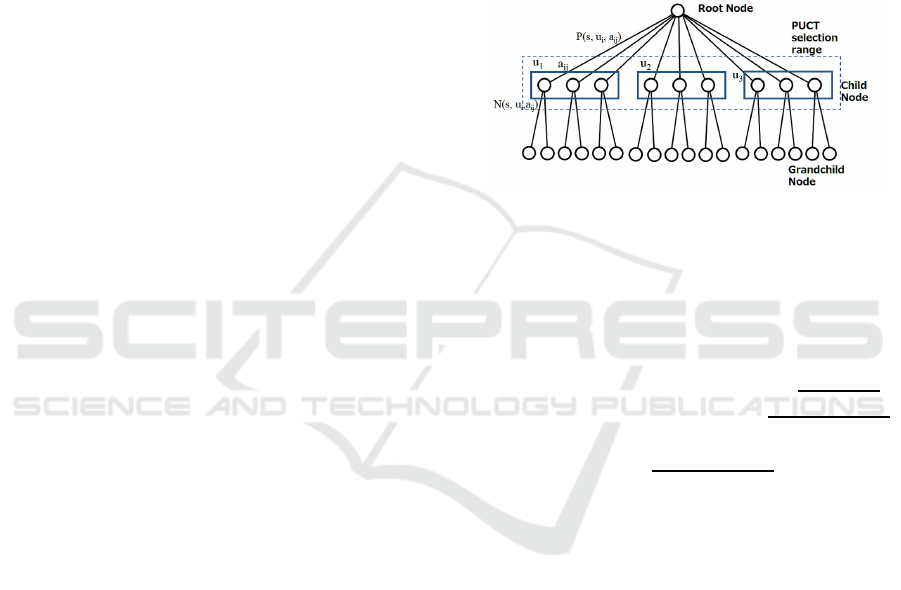
included in the tree search. Figure 2 shows that the se-

lection of units is performed simultaneously by node

selection using predictor upper conﬁdence bound ap-

plied to trees (PUCT) (Silver et al., 2017; Rosin,

2011) values. When the number of units is one, the

algorithm is the same as the usual PUCT search. We

assume that the action a

i, j

is a pointer for each unit

of TUBSTAP, and the aspect represented by each

node transits to the aspect of the next node through

the edge a

i, j

. Child nodes are expanded individually

for each u

as shown in the boxed area in Figure 2, and

unit selection information is included in the selected

node. If there are n units on the map, the search is

performed n times and all units are selected.

Figure 2: Node selection range.

To select a node to search: For all possible action

nodes of the unit, calculate the PUCT value according

to the following formula and select the node with the

largest PUCT value.

PUCT(s,u

) =Q(s,u

CpuctP(s,u

)

∑

N(s,b)

1+ N(s,u

)

attack

1+ N(s,u

)

(1)

i, j

, u

= argmax

a,u

(PUCT(s,u

)) (2)

Here, Q(s,u

) is the mean action value, Cpuct

is an exploration constant set to 0.8, P(s,u

) is

the prior probability, N(s,u

) is the visit count of

node, and B

attack

is a newly introduced term for ac-

celerating learning, experimentally determined to be

3.7, which is used so that attack nodes are searched

preferentially. The B

attack

term operates during both

learning and normal operation. The effect of this term

will be compared later in the experiment.

Dirichlet noise for a wide range search is added

but only to the root node of the search tree. A Boltz-

mann probability selection with temperature decay is

carried out in deciding the move for self-play.

The information stored in each node includes the

number of visits N, the selection probability P, the to-

tal value W, the average value Q, value network out-

put v, and the links to the child nodes of the node.

High-performance Algorithms using Deep Learning in Turn-based Strategy Games

557

After the search reaches the game end, the number

of visits and the value are updated by N(s

) =

N(s

) + 1, W(s

) = W(s

) + v, Q(s

) =

W(s

)

N(s

)

. The node with the most visits in the last stage

of the search becomes the next move.

3.3 Reinforcement Learning Design

Self-plays start from various initial maps and continue

through PV-MCTS until the game state reaches a ter-

minal node. The game state s and the probability dis-

tribution π obtained by the tree search and the value v

by the game result z are stored in the replay memory

(Mnih et al., 2015), and the neural network is peri-

odically learned. Note that z = 1 if the game is won,

z = −1 if the game is lost, and z = 0 if the game is

a draw. Based on randomly sampled data from the

accumulated reply memory, learning is performed to

minimize the loss function by a gradient method as

described later. To enrich data and prevent bias in the

neural network, rotation, and mirror data augmenta-

tion are performed.

3.4 Neural Network Design

The design of the AlphaZero neural network is modi-

ﬁed in several ways to meet the game’s speciﬁcations.

For the input, the map terrain data, the unit position

and HP data, and the data of the moved unit are en-

coded and normalized from 0 to 1. In this study, the

map size is ﬁxed to 6 x 6 and the data consists of 5

layers, so the input data form is 6× 6 × 5.

The data output from the Residual part is divided

into a policy head part and a value head part. The

policy output unit expresses a probability obtained by

combining a movement destination position for ex-

pressing an operation of the unit and a position for

expressing an attack. The output of the value head is

a scalar value of [-1,1] and uses tanh as the activation

function, which predicts the outcome of the game.

3.4.1 Output Data Representation

In this research, 36× 36 × 5 = 6480 output neurons

are required when the data of (acting unit position)

× (moving destination position) × (attack direction)

representing the unit behavior is considered. How-

ever, as proposed in this study, the number of output

neurons is reduced to 36×5= 180 by moving the unit

selection from output to input. A recurrent network

can be used to reduce the number of output neurons

(Kimura and Ikeda, 2019); however,the integration of

the value network is difﬁcult.

3.4.2 Neural Network Block

In the neural network block, the Conv2D layer on the

input layer is connected to the Residual part. The

Residual part has 8 identical Residual blocks with

shortcut connections as shown in Figure 3.

The ﬁlter size is 128 on the input layer and Resid-

ual layers, and batch normalization(BN) and ReLU

units are provided. In the policy head section, after

180 afﬁne layers, BN layers, and ReLU, the Soft-

max is used as the activation function. In the value

head section, after BN and ReLU layers, there are 128

and 1 afﬁne layers, and tanh function as an activation

function.

The representation of the unit’s action requires 6

x 6 = 36 cells in the destination representation, and

four direction encoding in the attack representation,

so that 36+ 36×4 = 180 cells are required in one-hot

expression for a single unit.

Figure 3: Neural Network Block.

3.4.3 Residual Network Block

A block diagram of the Residual Network (He et al.,

2015) used in this study is shown in Figure 4. Al-

though eight blocks of Residual layers are stacked

after the input layer, backpropagation in learning is

easily propagated by the shortcut connection of the

Residual Network, which greatly improvesthe perfor-

mance. To improve the convergence of learning, the

using Wide Residual Network (Zagoruyko and Ko-

modakis, 2016) is used as a reference and, dropout

is included in the central part. SeparableConv2D is

used instead of the commonly used Conv2D to save

memory and to increase speed. It is a combina-

tion of DepthwiseConv2D (Howard et al., 2017) and

Conv2D and is written as SepConv2D in the graph.

3.4.4 Learning Setting

For the learning setting, the loss function is expressed

by the following equation.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

558

Figure 4: Residual Network Block.

loss = (z− v)

+ D

(πkp) + L2Reg (3)

Here, D

(πkp) is the Kullback–Leibler diver-

gence, which is used to stabilize convergence. L2Reg

is the L2 regularization term, where the coefﬁcient is

set to 1×10

−4

. SGD + momentum with Nesterov op-

tion is used as the optimizer, and the moment term

constant is 0.9. The batch size is 128.

4 EXPERIMENTAL RESULTS

This section describes the map group used for learn-

ing, the transition of learning loss, the effect of the

Residual layer and the effect of parameters, the effect

of long-term learning.

4.1 Learning Setting and Results

Comparisons of learning losses were performed to

evaluate the adequacy of the design of the neural net-

work part.

4.1.1 Learning Map Setting

In TUBSTAP, various terrains and units can be used,

but in this paper, we limit it to 6 × 6 size maps where

infantries ﬁghts in the plains. The maps used for the

learning process in self-play were mixed with the fol-

lowing structure to simulate all situations and accel-

erate learning.

• Random maps. Random placement and conﬁgu-

ration to cover diverse situations. Set HP and po-

sition randomly. The number of units is arranged

in all cases to one vs one, one vs two, and two vs

two (Figure 5 (a)) .

• Technical aspect maps. Maps that manually cuts

out a situation where a speciﬁc procedure is re-

quired in an important aspect of the game as

shown in Figure 5 (b).

4.1.2 Learning Curves

To compare the effect of the number of blocks of the

Residual layer, learning of 4, 6, and 8 blocks were

carried out on 500 learning maps, which is approxi-

mately 5000 iterations (because the maximum num-

ber of turns is set to 16, and approximately 8 to 16

turns are executed per game), are shown in Figure 6.

Here, n represents the number of blocks of the Resid-

ual layer. The results show that n = 4 is slightly in-

ferior, while n = 6 and n = 8 almost have equivalent

losses.

Figure 7 compares the policy loss in the same

learning for n = 8, 6, and 4. The results show that

there is no apparent difference in policy loss for dif-

ferent n.

Figure 8 compares the value loss for n = 8, 6, and

4. The results show that n = 4 is slow to converge,

degrades performance, and has an overall bottleneck

performance.

To compare the performance of the Conv2D and

SepConv2D parts in the Residual block, the learn-

ing curves are measured as shown in Figure 9 with

Conv2D having n = 6 and SepConv2D having n = 8.

The results show that both have similar performances.

However, SepConv2D requires less working memory

than Conv2D.

4.2 Experiments

Battle experiments were conducted to evaluate the

performance of the learned neural network and PV-

MCTS. The following two algorithms were employed

as opponents.

• Primitive Monte Carlo (PMC). Simple Monte

Carlo method without tree search. There are 100

rollouts until the end of the game.

(a) Random map.

(b) Technical aspect map.

Figure 5: Learning Map Examples.

High-performance Algorithms using Deep Learning in Turn-based Strategy Games

559

Figure 6: Total loss as of n = 8/6/4.

Figure 7: Policy loss as of n = 8/6/4.

Figure 8: Value loss as of n = 8/6/4.

Figure 9: Loss of n = 8 Seq Conv2D and n =6 Conv2D .

• MCTS. One of conventional Monte Carlo

tree search algorithm using the equation

UCB1 = number of wins/visit count +

(log(total visit count/visit count). A total

of 2000 simulations are performed by the rollout.

The rollout continues until the end of the game,

and if the number of visits to each node exceeds

the threshold, the node is expanded.

An experimental battle map, Map01 is shown in Fig-

ure 10 (a). This map is unobstructed, has a size of 6 ×

6, and has two infantry units on each side. This map

is simple at ﬁrst glance, but because it is a setting with

many movement destinations, it is difﬁcult to search

and is suitable for the evaluation of our algorithm.

4.2.1 Match Settings

The proposed PV-MCTS plays several games against

one of PMC/MCTS. When using a map and playing

2n games on it, PV-MCTS plays Red side n games,

and Blue side n games respectively.

The game ends when either soldier is annihilated

or when the number of turns reaches 16. If it is an-

nihilated, the surviving side wins, and if the number

of turns reaches 16, it is a draw. For PV-MCTS, 500

simulations are always reserved for searching.

To conform to the effect of long-term learning, the

training time was set for approximately 3 weeks with

the parameter setting considered to be adequate, oth-

erwise, it was set to 500 games iterations as the short

mode.

4.2.2 Match Results in Map01

Table 1 shows the parameters in Map01 and the re-

sults of the game experiments. Here, n is the number

of blocks in the Residual layer, time is the training

time, Long denotes a game for approximately 3 weeks

, and Short denotes 500 game iterations.

To investigate the effect of the number of blocks in

the Residual layer, a battle experiment was performed

with n = 8, 6, and 4. We ﬁnd the performance of

(a) Map01.

(b) Map02.

Figure 10: Experiment Maps.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

560

Table 1: PV-MCTS match results in Map01.

Opponent Time n Sep/Conv2D B

attack

Dropout Win Draw Lose Win Rate(%)

PMC Short 4 SepConv2D 3.7 Yes 7 3 40 14.0

MCTS Short 4 SepConv2D 3.7 Yes

3 5 42 6.0

PMC Short 6 SepConv2D 3.7 Yes 18 5 27 36.0

MCTS Short 6 SepConv2D 3.7 Yes

13 9 28 26.0

PMC Short 8 SepConv2D 3.7 Yes 16 1 33 32.0

MCTS Short 8 SepConv2D 3.7 Yes 11 4 35 22.0

PMC Short 6 Conv2D 3.7 Yes 17 6 27 34.0

MCTS Short 6 Conv2D 3.7 Yes 20 4 26 40.0

PMC Long 8 SepConv2D 0.0 Yes 20 3 27 40.0

MCTS Long 8 SepConv2D 0.0 Yes

24 2 26 48.0

PMC Short 8 SepConv2D 3.7 No 7 3 40 14.0

MCTS Short 8 SepConv2D 3.7 No

6 1 43 12.0

PMC Long 8 SepConv2D 3.7 Yes 130 5 15 86.7

MCTS Long 8 SepConv2D 3.7 Yes 128 6 16 85.3

the n = 8 type is relatively good. Moreover, the per-

formance of Conv2D and SepConv2D in the Resid-

ual blocks, are approximately similar, but Conv2D

requires more memory. The results show that the

win rate in the long training time when B

attack

= 3.7

is approximately half that when B

attack

= 0.0, which

conﬁrms that the B

attack

term has an impact on the

method’s performance. In addition, the win rate is

lower in the setting without dropout, which conﬁrms

that dropout must be added to improve the method’s

performance.

To verify the improvement of the performance af-

ter sufﬁcient learning time, the result of continuing

the training under the same condition for a long time

is presented in the last row of Table 1, which shows a

very high win rate.

4.3 Generalization Ability

As a ﬁnal test, to evaluate the generalization perfor-

mance of the neural network and determine its ability

to cope with new situations, a battle was performed

on a map that was not used for learning.

Table 2: PV-MCTS match results in map02.

Opponent Win Draw Lose Win Rate(%)

PMC 28 5 17 56.0

MCTS

24 5 21 48.0

Figure 10 (b) shows Map02 with a size of 6 ×

6, which is not included in the learning map of four

infantries at a time. The version of the neural network

used has long term learning, has 8 Residual blocks

with dropout, has SepConv2D, and has B

attack

= 3.7.

The match results are shown in Table 2.

Although Map02 is an new map for PV-MCTS,

the method’s competitive performance remains su-

perior due to the generalization performance of the

neural networks and the searching capability of

PV-MCTS.

4.4 Discussion

Considering the result of experiments about the num-

ber of Residual blocks, it can be said that the num-

ber should be carefully set according to the exper-

imental results. It was also shown that the perfor-

mance of SepConv2D could be equivalent to the typ-

ical Conv2D convolution layer if set appropriately.

The experimental data showed that the bias term in-

troduced in the PUCT equation and the inﬂuence of

dropout in Residual layer were effective in the search.

Although the performance of the long-term learn-

ing version was excellent, more effective methods of

accelerating learning are desired because it is disad-

vantageous to have long learning times.

PV-MCTS performed well for battles in an new

map not part of the learning process, which indicated

the superiority of the algorithm. Considering that the

number of simulations was only 500 for PV-MCTS,

3000 to 5000 for PMC, and 2000 for MCTS, PV-

MCTS allowed effective search using the experience

accumulated in neural networks.

5 CONCLUSIONS

The PV-MCTS algorithm, which combines a pol-

icy network and a value network introduced by Al-

phaZero, was applied to a turn-based strategy game

to evaluate its performance. Besides, some modiﬁca-

tions of algorithms were proposed and added to adapt

to the difﬁculties of such games. The advantage of

High-performance Algorithms using Deep Learning in Turn-based Strategy Games

561

PV-MCTS eliminates the need for a huge database of

game records, reduces the burden of designing neural

networks, and improves learning efﬁciency.

The design of the search tree had to be modiﬁed

to allow the neural network to output complex data

structures representing the actions of the units of turn-

based strategy games. By moving the data of the op-

erating unit from the output of the neural network to

the input, we succeeded in signiﬁcantly reducing the

design load of the neural network. The unit selection

problem necessary for the multi-unit operation pecu-

liar to turn-based strategy games was also solved by

integrating unit selection into the search tree. Effec-

tive changes such as SepConv2D, B

attack

, and dropout

were also introduced and evaluated. The number of

blocks in the Residual layer was also evaluated.

The new method showed excellent performance as

compared to two simple and classical algorithms. It

also performed well on unlearned maps and showed

generalization by learning. However, when the num-

ber of units was increased, the operation time in-

creased, which is a problem that needs to be ﬁxed in

the future.

In future research, we aim to test the method on a

wide variety of map situations and on maps with more

units.

REFERENCES

Fujiki, T., Ikeda, K., and Viennot, S. (2015). A platform

for turn-based strategy games, with a comparison of

monte-carlo algorithms. In 2015 IEEE Conference on

Computational Intelligence and Games (CIG), pages

407–414.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep resid-

ual learning for image recognition. 2016 IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 770–778.

Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D.,

Wang, W., Weyand, T., Andreetto, M., and Adam,

H. (2017). Mobilenets: Efﬁcient convolutional neu-

ral networks for mobile vision applications. CoRR,

abs/1704.04861.

Kato, C., Miwa, M., Tsuruoka, Y., and Chikayama, T.

(2013). Uct and its enhancement for tactical decisions

in turn-based strategy games. In Game Programming

Workshop 2013, pages 138–145.

Kimura, T. (2019). Application of reinforcement learning

algorithm using policy network and value network to

the turn-based strategy game. In Game Programming

Workshop 2019.

Kimura, T. and Ikeda, K. (2016). Offering new benchmark

maps for turn based strategy game. In Game Program-

ming Workshop 2016, pages 36–43.

Kimura, T. and Ikeda, K. (2019). Designing policy network

with deep learning in turn-based strategy games. In

16th Advances in Computer Games Conference.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A., Veness, J.,

Bellemare, M., Graves, A., Riedmiller, M., Fidjeland,

A., Ostrovski, G., Petersen, S., Beattie, C., Sadik,

A., Antonoglou, I., King, H., Kumaran, D., Wierstra,

D., Legg, S., and Hassabis, D. (2015). Human-level

control through deep reinforcement learning. Nature,

518:529–33.

Rosin, C. D. (2011). Multi-armed bandits with episode

context. Annals of Mathematics and Artiﬁcial Intel-

ligence, 61(3):203–230.

Sato, N., Fujiki, T., and Ikeda, K. (2015). An approach to

evaluate turn-based strategy game positions with of-

ﬂine tree searches in simpliﬁed games. In Game Pro-

gramming Workshop 2015, pages 61–68.

Sato, N. and Ikeda, K. (2016). Three types of forward

pruning techniques to apply the alpha beta algorithm

to turn-based strategy games. In 2016 IEEE Con-

ference on Computational Intelligence and Games

(CIG), pages 1–8.

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,

van den Driessche, G., Schrittwieser, J., Antonoglou,

I., Panneershelvam, V., Lanctot, M., Dieleman, S.,

Grewe, D., Nham, J., Kalchbrenner, N., Sutskever, I.,

Lillicrap, T., Leach, M., Kavukcuoglu, K., Graepel,

T., and Hassabis, D. (2016). Mastering the game of

go with deep neural networks and tree search. Nature,

529:484–503.

Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai,

M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D.,

Graepel, T., Lillicrap, T., Simonyan, K., and Hass-

abis, D. (2018). A general reinforcement learning

algorithm that masters chess, shogi, and go through

self-play. Science, 362:1140–1144.

Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I.,

Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M.,

Bolton, A., Chen, Y., Lillicrap, T., Hui, F., Sifre, L.,

Driessche, G., Graepel, T., and Hassabis, D. (2017).

Mastering the game of go without human knowledge.

Nature, 550:354–359.

Zagoruyko, S. and Komodakis, N. (2016). Wide residual

networks. Computing Research Repository (CoRR),

abs/1605.07146.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

562