
Integer Overflow Detection in Hardware Designs at the
Specification Level
Fritjof Bornebusch
1
, Christoph L
¨
uth
1,3
, Robert Wille
1,2
and Rolf Drechsler
1,3
1
Cyber-Physical Systems, DFKI GmbH, Bremen, Germany
2
Integrated Circuit and System Design, Johannes Kepler University Linz, Austria
3
Mathematics and Computer Science, University of Bremen, Germany
Keywords:
Hardware Designs, Integer Overflows, Proof Assistants, Functional HDLs, Hardware Synthesis.
Abstract:
In this work, we present a hardware design approach that allows the detection of integer overflows by describ-
ing finite integer types at the specification level. In contrast to the established design flow that uses infinite
integer types at the specification level. This causes a semantic gap between these infinite types and the finite
integer types used at the model level. The proposed design approach uses dependent types in combination
with proof assistants. The combination allows the arguing about the behavior of finite integer types that is
used to detect integer overflows at the specification level. To achieve this, we utilized the CompCert integer
library that describes finite data types as dependent types.
1 INTRODUCTION
Nowadays, circuits are in almost every part of our live
and their complexity continues to increase. With the
increasing complexity the number of potential errors
increase as well. For this reason, the development
process of hardware designs should consider the com-
plexity from the beginning.
Hardware designs are described at different lev-
els to address the complexity of such designs.
First, the design is formally specified, e.g. in
SysML/OCL (Drechsler et al. 2012; OMG 2014;
OMG 2019; Weilkiens 2007), which enables the
specification of properties that argue about the de-
sired design (Brucker and Wolff 2006; Hilken et
al. 2014). Afterwards the specification is translated
into a SystemC model which is the de facto stan-
dard for high-level synthesis (HLS) (Arnout 2000;
Takach 2016). This translation is manual as OCL con-
straints cannot be translated into executable SystemC
code automatically. For the final synthesizing step,
the model is manually translated into in a low-level
implementation, e.g. VHDL, as SystemC does not
support the synthesis of arbitrary hardware models,
because of its restricted synthesizeable subset (Ac-
cellera 2016; Stoppe et al. 2013).
We consider this approach as the established hard-
ware design approach in the rest of the paper. Looking
at the established design approach in terms of its in-
teger type implementation a semantic gap is revealed
between the infinite types of the SysML/OCL specifi-
cation and the finite types of the SystemC model. As
a result, properties of the SysML/OCL specification
might not hold in the SystemC model. One result of
this semantic gap is an integer overflow that occurs
when an integer operation is executed in the SystemC
model (Cousot et al. 2005; Cuoq et al. 2012; Dietz et
al. 2015). An overflow leads to unintended behavior.
The missing tool support for detecting integer over-
flows automatically results in the detection of integer
overflows in the SystemC model explicitly by the en-
gineer.
To address the basic problem of the semantic gap
of the established design approach, we propose an al-
ternative hardware design approach that enables the
description of finite integer types at the specification
level. This enables the description of types that are
semantic equivalent to those of the model level. As
a result, properties that argue about such types also
hold on the model level. To achieve this, we uti-
lized the CompCert integer library (Leroy et al. 2016)
to describe hardware designs by the proof assistant
Coq (Bertot and Cast
´
eran 2004; Chlipala 2013). This
specification can subsequently be extracted into an
executable functional model automatically (Borneb-
usch et al. 2020).
We present our work as follows: First, we explain
the established hardware design approach in detail by
Bornebusch, F., Lüth, C., Wille, R. and Drechsler, R.
Integer Overflow Detection in Hardware Designs at the Specification Level.
DOI: 10.5220/0008960200410048
In Proceedings of the 8th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2020), pages 41-48
ISBN: 978-989-758-400-8; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
41
referring to a running example and discuss the prob-
lem between infinite and finite integer types of this
approach while Section 3 discusses the related work.
Section 4 proposes our approach and explains how
integer overflows are detected in this flow and how
the extraction from a specification to a model is im-
plemented. Section 5 summarizes and concludes this
work.
2 MOTIVATION
In this section, we briefly review the specification
and the modeling of hardware designs in the es-
tablished approach which uses SysML/OCL (OMG
2014; OMG 2019) at the specification level and
SystemC (Arnout 2000; Takach 2016) at the model
level. Based on that, the main problem of this ap-
proach is shown that describes why integer overflows
occur during the translation from the specification to
the model which motivates this work. A running ex-
ample is introduced in this section to illustrate the
established hardware design approach as well as the
proposed approach.
2.1 The Established Approach
Considering the established hardware design ap-
proach, the design is first described as a SysML/OCL
specification. This specification describes the struc-
ture of a hardware design in SysML while the be-
havior is described by OCL constraints. In this
work, we consider a traffic light controller (inspired
by (Przigoda et al. 2016)) as a running example:
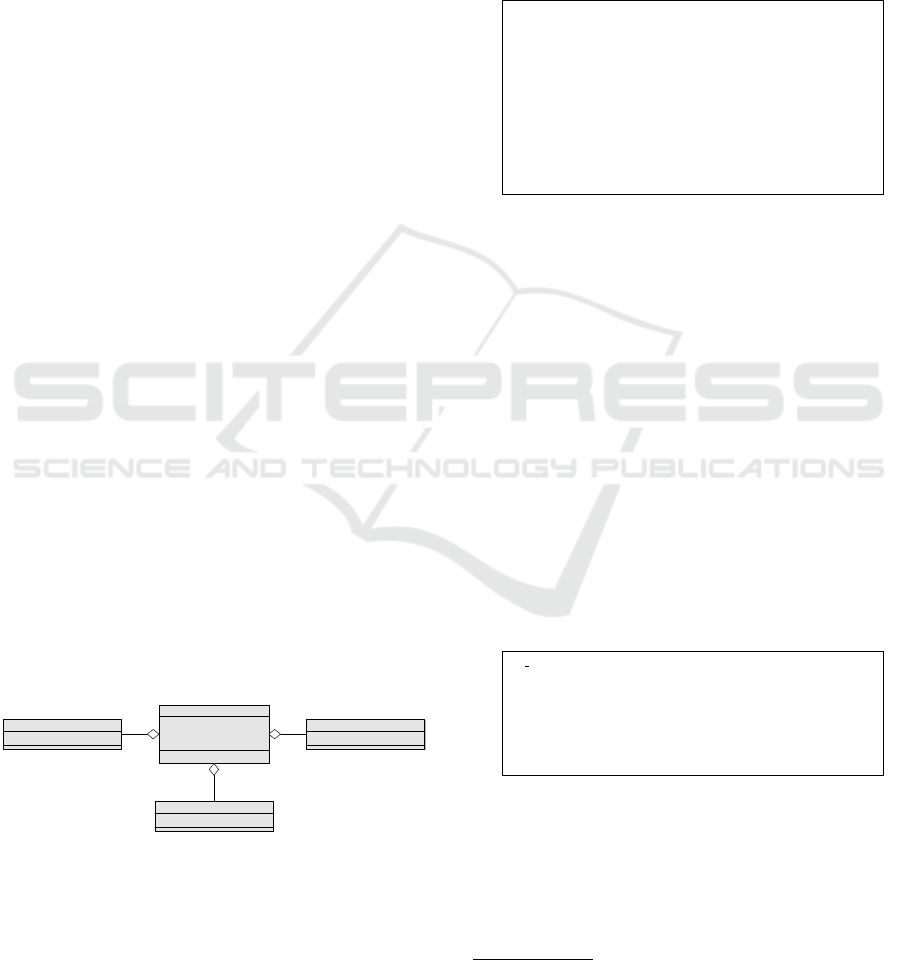
Example 1. Figure 1 shows the SysML class diagram
of the traffic light controller. The controller consists
of three different traffic lights: for the trams, cars and
pedestrians, as seen in Figure 1.
trafficLightController
+
+
+
-
delay: Integer
counter: Integer
clockFrequency: Integer
tick(): void
carsTrafficLight
+
value: enum<trafficLight>
pedestriansTrafficLight
+
value: enum<trafficLight>
tramsTrafficLight
+
value: enum<trafficLight>
1 1
1
1
11
Figure 1: SysML class diagram.
This traffic light controller iterates over pre-defined
states which determines whether the individual traf-
fic lights are switched on or off. The transition from
one state to the next depends on a given delay. If the
delay is expired, the transition to the next state is trig-
gered, e.g. from green to yellow for the cars. To allow
the consideration of traffic situations, such as rush-
hour, the delay can be changed at run-time. After de-
scribing the structure of the controller in SysML, the
desired behavior is described by OCL constraints, as
the ones seen in Listing 1. The tick function represents
the clock and evaluates whether the traffic light state
is triggered or not, depending on the delay
1
. The vari-
able clockFrequency is constant and describes the
frequency of the hardware the controller runs on.
1 c o n te x t t r a f f i c L i g h t C o n t r o l l e r : : t i c k ( )
2 pre : s e l f . c o u n t e r ∗ s e l f . d e l a y <
3 s e l f . c o u n t e r ∗ s e l f . c l o c k F r e q u e n c y
4 p o s t : s e l f . c o u n t e r = s e l f . c o u n t e r @p r e +1
5
6 c o n t e x t t r a f f i c L i g h t C o n t r o l l e r : : t i c k ( )
7 pre : s e l f . c o u n t e r ∗ s e l f . d e l a y >=
8 s e l f . c o u n t e r ∗ s e l f . c l o c k F r e q u e n c y
9 p o s t : s e l f . c o u n t e r = 1
10
11 i n v : s e l f . c o u n t e r > 0
12 i n v : s e l f . d e l a y > 0
13 i n v : s e l f . d e l a y < s e l f . c l o c k F r e q u e n c y
Listing 1: OCL constraints of the tick function.
The conditions in Line 1 of Listing 1 ensures that
the counter variable of the controller is increased by
one until the precondition no longer holds, i.e. the
upper bound is reached. In this case the counter is
reset to 1 as seen in Line 9 of Listing 1.
After the behavior is specified in SysML/OCL, a
SystemC model is implemented as shown in the next
example. The transformation from a SysML/OCL
specification to a SystemC model is manual. The
SysML structure can indeed be translated to SystemC
classes automatically, but there is no automatic pro-
cess that translates OCL constraints into executable
SystemC code.
Example 2. Listing 2 shows the implementation of
the tick function, described above, which implements
the OCL constraints, seen in Listing 1.
1s c u i n t <32> co u n t e r , d e l a y , c l o c k F r e q u e n c y ;
2
3v o i d t i c k ( ) {
4i f ( c o u n t e r ∗ d e l a y < c o u n t e r ∗ c l o c k F r e q u e n c y )
5c o u n t e r + + ;
6e l s e
7c o u n t e r = 1 ;
8}
Listing 2: SystemC model of the tick function.
Like in the specification of the tick function, the
counter is increased until it reaches its upper bound,
according to the specification, and is reset to 1 again.
If this upper bound is not yet reached the counter is
increased by one.
1
Note that this work considers integer overflows in hard-
ware designs. Therefore, the individual state transitions are
not considered, as they do not cause an integer overflow.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
42

2.2 Considered Problem
From the constraints in Listing 1, we can derive prop-
erties which hold for the specified system, as shown
in the next example.
Example 3. The safety property (stated as an invari-
ant) in Listing 3 can be derived from the specified be-
havior of the tick function. This means that if we im-
plement this function such that the constraints from
Listing 1 hold, then the implementation will satisfy
the safety property.
1c o n t e x t t r a f f i c L i g h t C o n t r o l l e r
2i n v : s e l f . c o u n t e r ∗ s e l f . d e l a y <=
3s e l f . c o u n t e r ∗ s e l f . c l o c k F r e q u e n c y
Listing 3: Safety property derived from the SysML/OCL
specification.
However, in the SystemC implementation the
safety property does not hold! To examine why, we
consider the proof in more detail. To show the safety
property, we need to show that, for each constraint of
the operation tick in Listing 1, if the precondition,
invariants and safety property hold in the pre-state
and the postconditions holds in the post-state, then the
safety property holds in the post state.
In the following, we use the notation x
0
to denote
the value of the variable x in the post-state, and we
elide the self prefix. We then have the following as-
sumption:
counter ∗ delay < counter ∗ clockFrequency
∧ counter ∗ delay ≤ counter ∗ clockFrequency
∧ counter
0
= counter + 1
(1)
We now need to show the safety property in the
post state
2
:
counter
0
∗ delay
0
≤ counter
0
∗ clockFrequency
0
⇐⇒ (counter + 1) ∗ delay ≤
(counter + 1) ∗ clockFrequency
⇐⇒ counter ∗ delay + delay ≤
counter ∗ clockFrequency + clockFrequency
(2)
For N and Z (the SysML Integer type represents
Z) this follows from the assumption and invariants
(line 13 in Listing 1) because of monotonicity of ad-
dition, a ≤ c ∧ b ≤ d =⇒ a + b ≤ c + d, but it does
not hold for integers of limited size precisely because
monotonicity does not hold there (e.g. in the quotient
ring N/32). In other words, multiplication in Z is not
semantic equivalent to the one in N/32.
2
Note that there is a tacit assumption that the values of
variables do not change unless mentioned otherwise; here,
we assume that clockFrequency
0
= clockFrequency and that
delay
0
= delay.
Example 4. Consider again the OCL constraints
from the SysML/OCL specification seen in Listing 1
and the resulting implementation of the SystemC
model, seen in Listing 2. The implementation assumes
that the multiplication operation applied in the model
is defined the same as the multiplication applied in
the specification. This assumption is reasonable, as
they define apparently the same behavior. However,
as described above this is not the case, as the speci-
fication defines infinite integer types while the model
defines finite ones. This means the SystemC model
violates the safety property in Listing 3, which holds
for the specification. This bears a direct impact on the
change of the transition time between the traffic lights
implemented by the controller in the SystemC model.
For instance, if the value is changed at run-time in a
rush-hour situation, the resulting behavior of the tick
function and by that of the entire state machine might
be unintended which is a serious problem.
The C++ standard describes two different behav-
iors of integer arithmetic (ISO/IEC 2017). Unsigned
integer arithmetic might cause unintended behavior
as seen in Listing 2, but does technically not over-
flow. The result is always performed modulo 2
n
so it
is never too big to be interpreted, i.e this type imple-
ments a wraparound behavior. Signed integer arith-
metic, on the other hand, does not perform modulo 2
n
so the result can be too big to be interpreted. Such an
overflow causes undefined behavior as it is not speci-
fied by the standard how to proceed in this case, e.g. it
may also wrap around, because of the 2’s complement
or trap on some platforms. Therefore, the signed in-
teger arithmetic operations in C++ are partial and not
total as in SysML. The term integer overflow often
refers to both behaviors as they share the same basic
problem (Cousot et al. 2005; Dietz et al. 2015). For
this reason, we use this term in the rest of the paper to
address the problem discussed above.
The problem of the semantic gap between
SysML’s infinite types and SystemC’s finite types
motivates our work. In order to address this problem
a semantic equivalent (finite) integer type is needed
at the specification level as hardware designs rely on
these types. Such a type allows the specification of
a function that clearly distinguishes an integer over-
flow from the actual result of the integer operation
by considering the lower and upper bounds of the
finite integer type. In the next section, we evaluate
the related work which, indeed, does not address the
problem of the established hardware design approach
properly. This leads to the design approach proposed
in this work.
Integer Overflow Detection in Hardware Designs at the Specification Level
43

3 RELATED WORK
In this section, we discuss the related work which
shows that SysML/OCL at the specification level and
SystemC at the model level are not suitable to detect
integer overflows. To detect integer overflows in a
SysML/OCL specification the implementation of se-
mantic equivalent (finite) integer types to those of the
SystemC model are required. However, this is not
supported by the SysML standard (OMG 2019). Of
course, constants could be introduced to artificially
restrict the range of an infinite integer type by describ-
ing the lower and upper bounds. These bounds, how-
ever, are independent of the actual type, i.e. the one
used in the SystemC model. The introduction of these
bounds do not address the problem, discussed above,
as if in the development phase of the model the actual
type changes, e.g. from unsigned32 to unsigned31,
such bounds invalidate the model which again trigger
an integer overflow.
To detect integer overflows directly in the
SystemC model, the overflow detection of programs
in C++ has to be considered. The detection of such
overflows in this language is quite challenging. The
basic problem is that the low-level nature of C++ does
not allow the detection of overflows reliably as bit
manipulations are common in this language (Dietz et
al. 2015). Furthermore, C++ has undefined behavior
semantics for signed integer types which allow opti-
mizations by the compiler (Dietz et al. 2015). C++
compiler are able to detect integer overflows if it is
constant-expression evaluation, but there is no sup-
port for the automatic detection in general.
As a result, the automatic and reliable detection
of arbitrary integer overflows is not supported, as it
is not possible to distinguish a behavior intended by
the engineer from unintended. As there is no support
from the compiler, some static source-code analysis
tools, such as
Astr
´
ee (Cousot et al. 2005), aims to prove the ab-
sence of run-time errors in C programs, like integer
overflows, through abstract interpretation (Cousot
2012; F
¨
ahndrich and Logozzo 2010). Abstract inter-
pretation is used to derive a computable abstract se-
mantic interpretation from a behavior described in a
programming language. This interpretation does not
contain the actual values, but focuses on certain parts
of the program execution. These parts determine the
scope of the static analysis and what kind of errors
are detected. Abstract interpretation reaches its limits
when it comes to the analysis of loops, as they have an
infinite number of paths in the abstract interpretation
tree. As SystemC designs allow loops, the static anal-
ysis of integer overflows by abstract interpretation is
not suitable to detect them in a hardware design, in
general.
Frama-C is another source-code analyzing tool
which relies on C Intermediate Language (CIL) (Nec-
ula et al. 2002) and supports annotations written in
ANSI/ISO C Specification Language (ACSL) (Cuoq
et al. 2012). It allows the application of different
static analysis techniques which includes the deduc-
tive verification of annotated C programs by external
automatic provers, e.g. Z3 (Cuoq et al. 2012). Con-
sidering the detection of integer overflows, Frama-C
provides the Runtime Error Annotation Generation
(RTE) plugin which includes the generation of an-
notations by syntactic constant folding in the form
of assertions for integer overflows. The main pur-
pose of RTE is seed these annotations into other plug-
ins, e.g. for the generation of weakest-preconditions,
with proof obligations. However, Astr
´
ee and Frama-C
cover integer overflows in C programs while SystemC
models are not supported. For this reason, they are
not suitable to address the problem of the established
hardware design flow properly.
As described above, the detection of integer over-
flows using SysML/OCL at the specification and
SystemC at the model level is not suitable. At the
specification level the integer type is infinite and at
the model level the engineer needs to detect overflows
pro-active and explicitly since there is little to no tool
support. For this reason, the safety property described
in Listing 1 cannot be implemented properly with-
out the explicit and pro-active consideration of integer
overflows occurred in the model, by the engineer.
The considered problem, described in Section 2.2,
in connection with the related work discussed in this
section lead to the following question: Can an alter-
native hardware design approach be developed that
allows the verifiable detection of integer overflows at
the specification level?
4 PROPOSED SOLUTION
This section reviews alternative methods which de-
scribe finite integer types at the specification level
since this is the main problem of the established hard-
ware design approach as described in Section 2.2. Af-
ter reviewing these methods, we propose a hardware
design approach that enables the formal specification
as well as the verifiable detection of integer overflows
in hardware designs.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
44

4.1 Proof Assistants
An alternative approach to specify and subsequently
verify an arbitrary behavior at the specification level
are proof assistants, so-called interactive theorem
provers (Bertot and Cast
´
eran 2004). Proof assistants
formally specify the functional behavior of programs
in a higher-order logic (specification language). This
behavior is defined by total functions which allows
the verification of properties. A property φ is proven
if and only if φ is derivable in the logic of the proof
assistant. As higher-order logic is too expressive
for automated theorem proving, the proof assistant
is guided interactively through the proof process by
the engineer. Apart from the specification and verifi-
cation of functional behavior, some proof assistants,
like Coq, allows the extraction of this behavior into
executable code. This way of program development
is called certified programming (Chlipala 2013). It
is achieved by embedding a functional language into
the specification language of the proof assistant. This
functional language enables the extraction of a speci-
fication into a functional programming language, e.g.
Haskell or Ocaml, by syntactical substitution.
4.2 Dependent Types
To describe the limited size bit vectors of hardware
designs for the in- and outputs of a circuit function-
ally, dependent types are used. Describing hardware
designs using dependent types is not new and started
back in the 90s (Brady et al. 2007; Hanna and Daeche
1992). A dependent type allows a type definition that
relies on an additional value. For instance, the type
A
n
defines a vector of length n with components of
type A. We say that A depends on n what makes A
n
a
dependent type and enables the definition of finite in-
teger types, e.g. Unsigned
32
. As proof assistants, like
Coq, allow the description of dependent types by the
user, this gives us the opportunity to describe finite
integer types at the specification level. We utilized
CompCert’s integer library to describe finite signed
and unsigned integer types in Coq (Leroy et al. 2016).
This library describes these types as dependent types
which allows the definition of arbitrary limited size
types.
4.3 The Proposed Approach
To address the problem of the semantic gap between
the specification and the model level, as described in
Section 2.2, we propose a hardware design approach
that utilizes the proof assistant Coq in connection with
1t y p e a o p t i o n = None | Some o f a
2s a f e m u l t : n ∈ N
3⇒ U nsigned
n
4→ U nsigned
n
5→ option(Unsigned
n
)
6s a f e m u l t x y =
7i f y 6= 0 ∧ x > max u n s i g n e d ( x ) / y )
8then None
9e l s e Some ( x ∗ y )
Listing 4: Function definition for unsigned multiplication
overflow detection.
the usage of dependent types to detect integer over-
flows at the specification level.
In contrast to a specification described in
SysML/OCL, the approach proposed in this work de-
scribes a hardware design specification in Coq’s func-
tional specification language.
4.3.1 Detecting Integer Overflows
The unsigned integer multiplication overflow in the
SystemC model, seen in Listing 2 occurs when im-
plementing the multiplication, because of the seman-
tic gap between the infinite types of SysML and finite
types of SystemC.
The basic problem behind the semantic gap is that
the arithmetic operations (like multiplication) behave
differently when we move to a finite type. That is, if
the result of a ∗ b is larger than the maximum size, the
value of a∗b in N and N/32, or Z and Z/32, no longer
agree. We propose to make this distinction explicit by
making the multiplication operation partial at the type
level. This is modeled by a datatype option with two
constructors, None and Some(a), where None stands
for undefined.
Listing 4 shows the definition of the explicitly
partial multiplication function. It will return None
whenever an overflow occurs, and Some(a*b) if not.
Based on the bounds of the finite integer type, a con-
dition checks whether an overflow occurs. This is
the case if (x ∗ y) > unsigned max(x), but we cannot
check this directly (because of the overflow); hence,
we check whether x is greater than the result of the
maximum value of the data type (unsigned max(x))
divided by y. The maximum value depends on the
dedicated unsigned integer type, i.e. 2
n
− 1, where
n ∈ N, is the number of bits used to represent the val-
ues of the type. To avoid a division-by-zero error, it is
ensured that y is not equal to 0 (in that case, no over-
flow can occur). The safe mult function essentially
wraps the multiplication function for Unsigned32 and
provides an overflow-save replacement.
Example 5. As described in Section 4.3, we utilized
the CompCert integer library as it provides the de-
scription of unsigned and signed integer types of ar-
bitrary sizes. In order to detect an integer overflow, a
Integer Overflow Detection in Hardware Designs at the Specification Level
45

1D e f i n i t i o n s a f e m u l t ( a b : Unsigned32 . i n t )
2: o p t i o n Unsigned32 . i n t :=
3i f b =? 0%u n s i g n e d 3 2
4then Some ( a ∗b )
5e l s e i f a <=? ( Un s i gned32 . m a x u ns i g ne d / b )
6then Some ( a ∗b )
7e l s e None .
8
9D e f i n i t i o n t i c k
10( c o u n t e r c l o c k F r e q u e n c y d e l a y : U n s i g n e d 3 2 . i n t )
11: o p t i o n Unsigned32 . i n t :=
12m atch ( s a f e m u l t c o u n t e r d e l a y ,
13s a f e m u l t c o u n t e r c l o c k F r e q u e n c y ) w i t h
14| ( Some a , Some b ) =>
15i f a <? b e l s e Some ( c o u n t e r +1%u n s i g n e d 3 2 )
16then Some (1% u n s i g n e d 3 2 )
17| => None
18end .
Listing 5: Function definitions in Coq.
clear distinction is needed between the occurrence of
the overflow and the result of the applied operation.
Coq describes a specification by total functions which
we used to define such a distinction. The safe mult
function, seen in Listing 5, implements the behavior
of the function described in Listing 4.
In order to clearly distinguish an overflow from
the result of the multiplication, the safe mult func-
tion returns a value of Coq’s built-in container type
option. This container type has the same semantic
behavior as the option type, defined in Listing 4. In
contrast to the SysML/OCL specification, introduced
in Section 2, our approach allows the definition of
an overflow save integer multiplication function at
the specification level. As a result, the multiplica-
tion operation in the tick function is replaced by the
safe mult function.
4.3.2 Proving Overflow Detection
To ensure that the above specification detects the
unsigned multiplication overflow reliable, properties
that describe how this overflow is detected are re-
quired. Considering the semantic gap between Z and
N/32, discussed in Section 2.2, two properties have
to be satisfied to either detect an overflow or to return
the result of the multiplication. These properties are
defined as theorem in Coq, as shown in Listing 6.
1 Theorem d e t e c t o v e r f l o w :
2 f o r a l l a b : Z ,
3 a <= Unsigned3 2 . m a x un s i g n e d / \
4 b <= Unsigned 3 2 . m a x uns i g n e d / \
5 a ∗ b > U n s i g n e d32 . m a x u n s i g n e d <−>
6 s a f e m u l t ( Un s i g n e d 3 2 . r e p r a )
7 ( Unsigned32 . r e p r b ) = None .
8
9 Theorem n o ov e r f l o w :
10 f o r a l l a b : Z ,
11 a <= Unsigned3 2 . m a x un s i g n e d / \
12 b <= Unsigned 3 2 . m a x uns i g n e d / \
13 a ∗ b <= Un signed32 . m a x u n s i g n e d <−>
14 s a f e m u l t ( Un s i g n e d 3 2 . r e p r a )
15 ( Unsigned32 . r e p r b ) =
16 Some ( ( Unsigned32 . r e p r a ) ∗
17 ( Unsigned32 . r e p r b ) ) .
Listing 6: Theorems in Coq to verify the behavior of the
safe mult function.
1Theorem s a f e t y p r o p e r t y n o o v e r f l o w :
2f o r a l l c o u n t e r d e l a y c l o c k F r e q u e n c y a b
3: Unsigned32 . i n t ,
4d e l a y < c l o c k F r e q u e n c y / \
5Some ( a ) = s a f e m u l t c o u n t e r d e l a y / \
6Some ( b ) = s a f e m u l t c o u n t e r c l o c k F r e q u e n c y
7<−> a <= b / \
8t i c k c o u n t e r d e l a y c l o c k F r e q u e n c y <> None .
9
10Theorem s a f e t y p r o p e r t y o v e r f l o w :
11f o r a l l c o u n t e r d e l a y c l o c k F r e q u e n c y
12: Unsigned32 . i n t ,
13d e l a y < c l o c k F r e q u e n c y / \
14None = s a f e m u l t c o u n t e r d e l a y / \
15None = s a f e m u l t c o u n t e r c l o c k F r e q u e n c y <−>
16t i c k c o u n t e r d e l a y c l o c k F r e q u e n c y = None .
Listing 7: Theorem in Coq that represents the OCL safety
property adapted to finite integer types.
The detect overflow theorem says: for all a and b
of the type Z which are less than or equal to the max-
imal unsigned32 value and the multiplication of both
values is greater than this maximal value if and only
if (<->) our defined safe mult function returns None
for the same values that are converted to equivalent
elements of the quotient ring Unsigned32. This prop-
erty ensures that only in the case of an overflow None
is returned. The second property that has to be sat-
isfied is that the result of the multiplication operation
has to be returned if no overflow occurs. The theorem
no overflow specifies this property and says: for all
a and b of the type Z which are less than or equal to
the maximal unsigned32 value and the multiplication
of both values is less than or equal to this maximal
value if and only if (<->) our defined safe mult func-
tion returns Some(). This property ensures that only
in the case where no overflow occurs the result of the
multiplication is returned.
To verify the derived safety property (stated as an
OCL invariant), described in Section 2, this invariant
has to be transformed first, as the proposed specifica-
tion uses finite types and the integer overflow has to
be considered. The resulting theorems are shown in
Listing 7.
For illustration purposes, we only explain
the theorem safety property no overflow in detail,
as the safety property overflow theorem works ana-
log. The theorem says: for all counter, delay
and clockFrequency, where the delay is smaller than
the clockFrequency and the multiplication does not
overflow (Some(a) and Some(b) are returned) if and
only if a is less than or equal to b and the spec-
ified tick function returns a constructor that is not
None, i.e. either Some(counter +1%unsigned32) or
Some(1%unsigned32), since the option type has two
constructors, as described above. As we have seen
above, the problem discussed in Section 2.2 was ad-
dressed my providing a total function that wraps the
multiplication operation. This function clearly distin-
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
46

1 s a f e m u l t : : ( U n s i gned 3 2 ) −> ( Unsign e d 3 2 )
2 −> CLaSH . P r e l ude . Maybe ( Unsign e d 3 2 )
3 s a f e m u l t a b =
4 c a s e ( CLaSH . P r e l u d e . = = ) b 0 o f {
5 CLaSH . P r e l ude . True −>
6 CLaSH . P r e l u d e . J u s t ( ( CLaSH . P relu d e . ∗ ) a b ) ;
7 CLaSH . P r e l ude . F a l s e −>
8 c a s e ( CLaSH . P rel u d e . <=) a
9 ( ( CLaSH . P r e l u d e . d i v ) ( ( 2 ˆ 3 2 ) −1) b ) o f {
10 CLaSH . P r e l u d e . True −> CLaSH . P r elu d e . J u s t
11 ( ( CLaSH . P r e l u d e . ∗ ) a b ) ;
12 CLaSH . P r e l u d e . F a l s e −>
13 CLaSH . P r e l u d e . Nothi n g }}
Listing 8: Extracted CλaSH model.
guishes between the result of the multiplication and
the overflow by a condition, because of Coq’s built-in
option type.
4.3.3 CλaSH Model Extraction
Having the hardware design specified and verified
in Coq, we applied the design flow proposed in this
work (Bornebusch et al. 2020), in order to extract an
executable model. This flow extracts a CλaSH (Baaij
et al. 2010) model from a specification automatically,
by syntactical substitution. The extracted model for
the safe mult function is seen in Listing 8.
Analog to the way hardware designs are described
in Coq, CλaSH describes circuits as recursive func-
tions and data types. The unique representation of
CλaSH models and the structured communication be-
tween their components, ensured by the static and
strong type system, enables an automatic analysis and
the final synthesis into low-level implementations,
e.g. VHDL.
4.3.4 Integer Overflow Detection Pattern
In order to generalize the mechanism applied above to
detect the integer multiplication overflow, we propose
a pattern that allows the detection of any integer oper-
ation overflows. Listing 9 shows the proposed pattern.
The angle brackets notate placeholders for the actual
implementation of the condition that detects the inte-
ger overflow (<overflowDetected>) and the desired
operation that is applied (<operation>).
1 f : a → a → o p t i o n ( a )
2 f x y = i f <o v e r f l o w D e t e c t e d>
3 th e n None
4 e l s e Some ( x <o p e r a t i o n > y )
Listing 9: Proposed overflow detection pattern.
This pattern uses the algebraic data type option, as
described in Section 4.3.1. Any function that calls f
has to make a case distinction: if the result is Some(a),
it can proceed with a as before, but if the result is
None, it has to propagate the indefiniteness (or handle
the overflow appropriately). This in turn makes the
function calling f partial, and forces the propagation
of the occurred overflow through the specification at
the type level which enables the verification of prop-
erties, as described in Section 4.3.2.
5 CONCLUSION
In this work we propose a hardware design approach
that allows the detection of integer overflows at the
specification level. The established design approach
uses SysML/OCL at the specification level which im-
plements infinite integer types. These types do not
share the semantic behavior of the types that are im-
plemented in a SystemC model as those are finite
which results in a semantic gap between these two
levels. This semantic gap motivates our approach, and
we address this problem by specifying hardware de-
signs using the proof assistant Coq and utilizing the
CompCert integer library that describes finite integer
types through dependent types. Such a specification
enables the verifiable detection of integer overflows
which is presented in this work. Furthermore, we
proposed a generalizable pattern to detect overflows
which extends our approach to detect overflows in any
integer operation.
ACKNOWLEDGMENTS
This work was supported by the German Federal Min-
istry of Education and Research (BMBF) within the
project SELFIE under grant no. 01IW16001 as well
as the LIT Secure and Correct System Lab funded by
the State of Upper Austria.
REFERENCES
Accellera. (2016). Accellera Systems Initiative Inc Sys-
temC Synthesizable Subset. (Version 1.5.7).
Arnout, G. (2000). Systemc standard. In Asia and
south pacific design automation conference (asp-dac)
(pp. 573–578).
Baaij, C., Kooijman, M., Kuper, J., Boeijink, A., & Ger-
ards, M. (2010). Cλash: Structural descriptions of syn-
chronous hardware using haskell. Euromicro confer-
ence on digital system design (dsd), 714–721.
Bertot, Y., & Cast
´
eran, P. (2004). Interactive theorem prov-
ing and program development - coq’art: The calculus
of inductive constructions. Texts in Theoretical Com-
puter Science. An EATCS Series. Springer.
Integer Overflow Detection in Hardware Designs at the Specification Level
47

Bornebusch, F., L
¨
uth, C., Wille, R., & Drechsler, R. (2020).
Towards automatic hardware synthesis from formal
specification to implementation. In Asia and south pa-
cific design automation conference (asp-dac).
Brady, E., McKinna, J., & Hammond, K. (2007). Con-
structing correct circuits: Verification of functional as-
pects of hardware specifications with dependent types.
In Trends in functional programming (tfp) (pp. 159–
176).
Brucker, A. D., & Wolff, B. (2006). The HOL-OCL book
(tech. rep. No. 525). ETH Zurich.
Chlipala, A. (2013). Certified programming with dependent
types - A pragmatic introduction to the coq proof as-
sistant. MIT Press.
Cousot, P. (2012). Formal verification by abstract interpre-
tation. In NASA formal methods - international sym-
posium, NFM (pp. 3–7).
Cousot, P., Cousot, R., Feret, J., Mauborgne, L., Min
´
e,
A., Monniaux, D., & Rival, X. (2005). The astre
´
e
analyzer. In European symposium on programming
(pp. 21–30).
Cuoq, P., Kirchner, F., Kosmatov, N., Prevosto, V., Signoles,
J., & Yakobowski, B. (2012). Frama-C - A software
analysis perspective. In International conference on
software engineering and formal methods (pp. 233–
247).
Dietz, W., Li, P., Regehr, J., & Adve, V. S. (2015). Un-
derstanding integer overflow in C/C++. ACM Trans.
Softw. Eng. Methodol. 25(1).
Drechsler, R., Soeken, M., & Wille, R. (2012). Formal
specification level: Towards verification-driven design
based on natural language processing. In Forum on
specification and design languages (fdl) (pp. 53–58).
F
¨
ahndrich, M., & Logozzo, F. (2010). Static contract check-
ing with abstract interpretation. In International con-
ference on formal verification of object-oriented soft-
ware (pp. 10–30).
Hanna, F. K., & Daeche, N. (1992). Dependent types and
formal synthesis.
Hilken, F., Niemann, P., Gogolla, M., & Wille, R. (2014).
Filmstripping and unrolling: A comparison of verifi-
cation approaches for UML and OCL behavioral mod-
els. In International conference on tests & proofs (tap)
(pp. 99–116).
ISO/IEC. (2017). ISO International Standard ISO/IEC
14882:2017(E) Programming Language C++. (Edi-
tion 5).
Leroy, X., Blazy, S., K
¨
astner, D., Schommer, B., Pister, M.,
& Ferdinand, C. (2016). Compcert – a formally veri-
fied optimizing compiler. In Embedded real time soft-
ware and systems (erts).
Necula, G. C., McPeak, S., Rahul, S. P., & Weimer, W.
(2002). CIL: intermediate language and tools for anal-
ysis and transformation of C programs. In European
joint conferences on theorey and & practice of soft-
ware (pp. 213–228).
OMG. (2014). Object Management Group Object Con-
straint Language (OCL). (Version 2.4).
OMG. (2019). Open Management Group System Modeling
Language (SysML). (Version 1.6).
Przigoda, N., Wille, R., & Drechsler, R. (2016). Analyzing
inconsistencies in UML/OCL models. Journal of Cir-
cuits, Systems, and Computers, 25(3).
Stoppe, J., Wille, R., & Drechsler, R. (2013). Data extrac-
tion from SystemC designs using debug symbols and
the SystemC API. In Ieee computer society annual
symposium on vlsi (isvlsi) (pp. 26–31).
Takach, A. (2016). High-level synthesis: Status, trends, and
future directions. IEEE Design & Test, 33(3), 116–
124.
Weilkiens, T. (2007). Systems engineering with sysml /
UML - modeling, analysis, design. Morgan Kauf-
mann.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
48
