
On the Similarity between Hidden Layers of Pruned and Unpruned
Convolutional Neural Networks
Alessio Ansuini
2
a
, Eric Medvet
1 b
, Felice Andrea Pellegrino
1 c
and Marco Zullich
1 d
1
Dipartimento di Ingegneria e Architettura, Università degli Studi di Trieste, Trieste, Italy
2
International School for Advanced Studies, Trieste, Italy
Keywords:
Machine Learning, Pruning, Convolutional Neural Networks, Lottery Ticket Hypothesis, Canonical
Correlation Analysis, Explainable Knowledge.
Abstract:
During the last few decades, artificial neural networks (ANN) have achieved an enormous success in regres-
sion and classification tasks. The empirical success has not been matched with an equally strong theoretical
understanding of such models, as some of their working principles (training dynamics, generalization proper-
ties, and the structure of inner representations) still remain largely unknown. It is, for example, particularly
difficult to reconcile the well known fact that ANNs achieve remarkable levels of generalization also in con-
ditions of severe over-parametrization. In our work, we explore a recent network compression technique,
called Iterative Magnitude Pruning (IMP), and apply it to convolutional neural networks (CNN). The pruned
and unpruned models are compared layer-wise with Canonical Correlation Analysis (CCA). Our results show
a high similarity between layers of pruned and unpruned CNNs in the first convolutional layers and in the
fully-connected layer, while for the intermediate convolutional layers the similarity is significantly lower. This
suggests that, although in intermediate layers representation in pruned and unpruned networks is markedly
different, in the last part the fully-connected layers act as pivots, producing not only similar performances but
also similar representations of the data, despite the large difference in the number of parameters involved.
1 INTRODUCTION
The present paper aims at exploring and connecting
two recent works on the topic of theoretical under-
standing on artificial neural networks (ANNs) work-
ing principles.
The first of these works (Frankle and Carbin,
2019) presents an iterative pruning technique, named
Iterative Magnitude Pruning (IMP), of the parameters
of a neural network allowing to obtain sparsity lev-
els on the parameters space up to 1% of the origi-
nal, while still matching the unpruned(complete) neu-
ral network test performance. The technique consists
in iteratively pruning a fixed proportion of parame-
ters having small magnitude, rewinding the network
to initialization, and re-training only the smaller sub-
network identified by the non-pruned parameters.
The second work (Raghu et al., 2017) intro-
duces Singular Vector Canonical Correlation Analy-
a
https://orcid.org/0000-0002-3117-3532
b
https://orcid.org/0000-0001-5652-2113
c
https://orcid.org/0000-0002-4423-1666
d
https://orcid.org/0000-0002-9920-9095
sis (SVCCA), a technique based on Canonical Corre-
lation Analysis (CCA) to compare two generic real-
valued matrices sharing row dimension. SVCCA is
applied to compare ANN layers by enabling a layer
to be represented as the matrix of activations of its
neurons in response to a dataset of fixed, finite size.
The application of CCA yields a vector of correla-
tions, which can be averaged to obtain a similarity
measure between layers, called Mean CCA Similar-
ity.
After training convolutional neural networks with
minimal architecture on an ensemble of problems of
incremental difficulty based on CIFAR10
1
, we con-
tinue by pruning those models using IMP for a de-
sired number of iterations, obtaining a set of pruned
networks, one for each problem and iteration num-
ber. For each of those networks, we compare each
layer with its unprunedcounterpart using SVCCA (af-
ter evaluating the layer activations on a subset of the
original dataset). The obtained similarities are then
analyzed relative to the pruning ratio, the location of
the layer within the network, and the difficulty of the
1
https://www.cs.toronto.edu/ kriz/cifar.html
52
Ansuini, A., Medvet, E., Pellegrino, F. and Zullich, M.
On the Similarity between Hidden Layers of Pruned and Unpruned Convolutional Neural Networks.
DOI: 10.5220/0008960300520059
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 52-59
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

classification task.
The remainder of this paper is organized as fol-
lows. Section 2 describes the relevant related works.
Section 3 briefly presents the two aforementioned
works giving an outline of the methodologies and the
underlying theory. Section 4 introduces the experi-
mental work, describing the problems on which our
networks have been trained, and explaining how the
tools have been applied on these models. Section 5
presents the numerical results of both the test perfor-
mance of the pruned networks, and the similarity be-
tween layers of pruned and unpruned networks, elab-
orating an interpretation of these ones; moreover, it
formulates some prompts for future work.
2 RELATED WORK
The contribution of the present paper is the follow-
ing: by combining two recent advances addressing
over-parametrization (Frankle and Carbin, 2019) and
hidden layers representation and comparison (Raghu
et al., 2017) in ANNs, we aim at providing a layer-
wise analysis of similarity in the representation of
CNNs for vision tasks. We here review previous
works that are somehow related to our aim.
2.1 Pruning Techniques for ANNs
Pruning techniques for ANNs have been proposed for
decades. Early attempts include L1 regularization on
the loss function (Goodfellow et al., 2016) in order to
induce sparsity in the parameters, or operating pool-
ing on the fully-connected layer(s) (Lin et al., 2013).
(Han et al., 2015) introduced a new technique
based pruning parameter with small magnitude, on
which IMP (Frankle and Carbin, 2019) is based upon.
More recently, a plethora of other techniques has
been proposed, like ADMM (Zhang et al., 2018),
or techniques for structured (block) pruning, sum-
marised in (Crowley et al., 2018).
Our paper focuses solely on IMP, while considera-
tions on other pruning techniques is left for the future.
2.2 Comparison of ANNs
Despite being a recent work, (Raghu et al., 2017) has
already prompted a number of researches utilizing
CCA in order to gain some knowledge on the simi-
larities between neural networks: for instance, (Wang
et al., 2018) use it to compare, layer-wise, the same
network when initialized differently, finding that “sur-
prisingly, representations learned by the same convo-
lutional layer of networks trained from different ini-
tializations are not similar [...] at least in terms of
subspace match”.
(Morcos et al., 2018) argued about weaknesses of
Mean CCA Similarity, instead proposing a new sim-
ilarity metric for layers, called Projection Weighted
Canonical Correlation Analysis.
On the other hand, other researches have intro-
duced different methodologies to achieve the compar-
ison: (Yu et al., 2018), for example, proposed a tech-
nique based upon the Riemann curvature information
of the “manifolds composed of activation vectors in
each fully-connected layer” of two deep neural net-
works. This technique is still at an early stage since
it enables comparison on fully-connected layers only,
and cannot be used for an analysis like ours.
(Kornblith et al., 2019), instead, offered some
considerations on CCA as a tool for layers compar-
ison in neural networks, arguing that it cannot “mea-
sure meaningful similarities between representations
of higher dimensions than the number of data points”,
hence proposingyet another methodology called Cen-
tered Kernel Alignment.
2.3 Pruned vs. Unpruned ANNs
To our knowledge, ours is the first work concerning
an in-depth, layer-by-layer analysis of the similarities
for pruned ANNs.
(Frankle and Bau, 2019) delved into the mechan-
ics of IMP (and other related magnitude pruning tech-
niques) by analyzing the interpretability (computed
through the identification of “convolutional units that
recognize particular human-interpretable concepts”)
of those networks, finding that pruning does not re-
duce it and prompting the conclusion that “parame-
ters that pruning considers to be superfluous for ac-
curacy are also superfluous for interpretability”. This
work does discuss the topic of pruned networks com-
parison, but it is rather a global analysis, not going
into the detail of the single layers. This work may be
thought of as an attempt, akin ours, to combine prun-
ing techniques with other recent advances in order to
gain additional insights on what may be called “prun-
ing dynamics".
(Morcos et al., 2018), instead, use CCA to com-
pare output layers of fully-trained, dense CNNs hav-
ing different number of filters in their convolutional
layers. The authors of the cited work attempt to
corroborate the Lottery Ticket Hypothesis (see Sec-
tion 3.1), but, in doing this, they do not actually oper-
ate any pruning, neither they compare hidden layers,
focusing solely on the output representation.
On the Similarity between Hidden Layers of Pruned and Unpruned Convolutional Neural Networks
53

3 TOOLS
3.1 Iterative Magnitude Pruning
Iterative Magnitude Pruning (IMP) is an algorithm
first introduced in (Frankle and Carbin, 2019) to oper-
ate pruning on the parameters of a generic ANN. The
authors start by formulating a hypothesis, called Lot-
tery Ticket Hypothesis, which claims the following:
dense, randomly-initialized, feed-forwardnet-
works contain subnetworks (“winning tick-
ets”) that—when trained in isolation—reach
test accuracy comparable to the original net-
work in a similar number of iterations
This substructure may be found via an iterative
method in which the parameters with the lowest mag-
nitude get progressively skimmed from the model un-
til a target sparsity is reached.
Denoting by ⊙ the element-by-element matrix
multiplication, and defined the pruning rate as the
proportion p ∈ [0, 1] of parameters we want to prune
from the network, the algorithm is the following:
Algorithm 1: IMP.
1: Randomly initialize parameters in neural net-
work, store them in structure Θ
0
;
2: Create trivial pruning mask M with same struc-
ture as Θ
0
, initialize it at 1;
3: Train the network for T iterations, store the pa-
rameters in Θ
T
;
4: Obtain the parameters of Θ
T
whose magnitude
falls below the p-th percentile; set the corre-
sponding mask entries to 0;
5: Apply the mask to the initial parameters Θ
0
, ob-
taining a new initialization: Θ
(1)
0
= Θ
0
⊙ M;
6: Re-train the network for other T iterations, ob-
taining a new final configuration Θ
(1)
T
;
7: Repeat 3–6, each time pruning only parameters
having a corresponding entry of 1 in the previous
mask, until a target sparsity rate is reached, or
performance falls below a desired threshold.
The authors showed that this algorithm effectively
finds winning tickets for shallow fully-connected and
CNNs, but fails to do so on deeper architectures, such
as VGG-19 (Simonyan and Zisserman, 2014) and
ResNet 18 (He et al., 2016), unless a warm-up phase
is employed. (Frankle et al., 2019) showed that, by
rewinding to an early-training stage of the unpruned
network (instead of rewinding at initialization), the al-
gorithm enjoys a stabler parameters configuration and
is able to converge to a solution whose performance
is similar to (or better than) the complete neural net-
work.
The method for determining the mask in IMP is
referred to in (Zhou et al., 2019) as LF-Mask (Large-
Final Mask). They produced a plethora of experi-
ments using a different number of masks and rewind-
ing policies (i.e., the scalar at which each parameter
having a value of 0 within the mask gets rewound to)
showing that, generally, the LF-Mask performs better
than all of their other proposals.
3.2 SVCCA
SVCCA is a technique introduced in (Raghu et al.,
2017), and later refined in (Morcos et al., 2018),
which enables the comparison between two matrices
sharing row size.
It can be applied to two generic layers of a fully-
connected neural network when they are represented
as the response of their neurons to the same fixed-
size dataset. Taking a layer L
1
of m
1
neurons, L
2
of m
2
neurons, by feeding n distinct datapoints to
their respective neural networks, we may store the
neurons’ response for each of those datapoints in
matrices: L
1
will be represented by an n × m
1
ma-
trix, L
2
by an n × m
2
matrix. The authors propose
to compare those two representations using Canon-
ical Correlation Analysis (CCA), which finds two
linear transforms W
1
∈ R
m
1
× ˜m
, W
2
∈ R
m
2
× ˜m
, where
˜m = min(m
1
, m
2
), which, applied to L
1
, L
2
, yield two
sets of ˜m unit vectors Z
1
, Z
2
:
Z
1
= L
1
W
1
(1)
Z
2
= L
2
W
2
(2)
The two transformations W
1
, W
2
are determined such
that the components of Z
1
, Z
2
are pairwise orthogonal
and maximize the residual mutual Pearson correla-
tion. This correlation is called canonical correlation:
CCA hence yields ˜m values of canonical correlation:
by averaging them, a measure of similarity between
two layers is obtained, which the authors call Mean
CCA Similarity.
Moreover, it is suggested that, by operating on the
two layers a Singular Value Decomposition (SVD)
for dimensionality reduction, with the aim of keep-
ing only the singular values accounting for 99% of
the variance, one may avoid some degenerate layers
configurations which would have produced overesti-
mations in the Mean CCA Similarity. This technique
(SVD + CCA on the layers represented as matrices)
has been named Singular Vector Canonical Correla-
tion Analysis (SVCCA).
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
54

Table 1: Categories composing each dataset described in
Section 4.1.
Dataset Categories
Cifar2 Automobile, Truck
Cifar4 Cifar2 + Airplane, Ship
Cifar6 Cifar4 + Cat, Dog
Cifar8 Cifar6 + Deer, Horse
Cifar10 Cifar8 + Bird, Dog
4 METHODS
As stated before, we aim at investigating, using
SVCCA, the similarities between pruned and un-
pruned layers in convolutional neural networks, the
pruned models being obtained via IMP.
For achieving this goal, we:
1. train an ensemble of convolutional neural net-
works for image classification on subsets of the
Cifar10 dataset;
2. prune those networks using IMP;
3. compare the pruned layers with their unpruned
counterparts using CCA Mean Similarity.
All of the implementations supporting the results
described in this paper were produced on Python
3.6.4, using libraries PyTorch 1.3.0, and NumPy
1.17.2; moreover, Google’s own implementation for
SVCCA
2
was used.
4.1 The Problems
Cifar10 is a publicly available collection of 60000 la-
belled color images of size 32 × 32, divided into 10
classes of 6000 images each. The dataset is already
split into train (50000 images) and test (10000 im-
ages) set.
In order to increase the number of observations,
meanwhile generating correlated measurements, we
built multiple subsets over the dataset so as to obtain
a set of incrementally more difficult problems. Ci-
far10 was subset over 2, 4, 6, 8 select image classes,
and the related dataset was called Cifar2, Cifar4, etc.;
the selection of classes was not operated randomly in
order not to create trivial problems, but the chosen
categories had to show, to some extent, some similar-
ities. The composition of all the categories is listed in
Table 1.
2
https://github.com/google/svcca
Table 2: Summary of the architectures for the CNNs for
each of the aforementioned problems. MP stands for Max-
Pooling;
*
indicates a layer with batch normalization;
§
in-
dicates a layer with dropout. Concerning training epochs T,
#
indicates deployment of early stopping with patience of
20 epochs and a validation dataset obtained on a stratified
random sampling of 10% of the training set observations.
Problem Conv. layers Full layers T
Cifar2 16
*
, 16, MP 256
§
, 10 50
Cifar4 16
*
, 16, MP, 32
*
,
32, MP
256
§
, 10 50
Cifar6 64
*
, 64, MP,
128
*
, 128, MP,
256
*
, 256, MP
256
§
, 10 100
Cifar8/10 64
*
, 64
*
, MP,
128
*
, 128
*
, MP,
256
*
, 256
*
, MP,
512
*
, 512
*
, MP
1024
§*
, 10 200
#
4.2 Convolutional Neural Networks
Architectures
The convolutional neural networks we designed were
based off of VGGNet core (Simonyan and Zisserman,
2014) Namely, the architecture consists in stacking
one or more convolutional blocks composed of 2, 3,
or 4 convolutional layers followed by a max-pooling
layer, to a fully-connected layer, eventually followed
by the output layer, having softmax activation func-
tion, and number of neurons equal to the number of
classes.
For our networks, we decided to employ batch
normalization (Ioffeand Szegedy, 2015) on some hid-
den layers (both convolutional and fully-connected)
and dropout (Srivastava et al., 2014) on fully-
connected layers only. The architectures and dataset-
specific hyperparameters are listed in Table 2.
All the networks were trained using Adam opti-
mizer (Kingma and Ba, 2014) with mini-batch size of
128, learning rate equal to 0.001, and weight decay
(L2 regularization) with parameter 0.0005. All of the
layers use the Rectified Linear Unit activation func-
tion (except for the output layer, which uses the soft-
max activation function). Moreover, for each training
mini-batch, a random data augmentation strategy was
applied consisting in a composition of cropping, hor-
izontal flipping, and roto-translation.
4.3 Application of IMP
IMP was applied with a strategy similar to (Zhou
et al., 2019): we established two separate pruning
rates, p
conv
for the convolutional layers parameters,
and p
fc
for the fully-connected layer parameters, and
On the Similarity between Hidden Layers of Pruned and Unpruned Convolutional Neural Networks
55

Table 3: Choices for pruning rates for the convolutional lay-
ers and fully-connected layer used during the application of
IMP.
Problem p
conv
p
fc
Cifar2 0.1 0.2
Cifar4 0.1 0.2
Cifar6 0.1 0.2
Cifar8 0.2 0.2
Cifar10 0.2 0.2
operated the pruning separately for convolutional lay-
ers (pooling together all the weights and biases per-
taining to those layers and pruning the p
conv
-th pa-
rameters with the smallest magnitude) and the fully-
connected layer. The choices for pruning rates are
shown in Table 3.
After training, IMP was applied for 20 iterations.
At each iteration, the network was rewound at the
third epoch, in order to stabilize the algorithm, as in-
dicated in Section 3.1.
4.4 Layers Comparison
Since CCA, as described in Section 3.2, works on
matrices, and the convolutional layers, if represented,
as in Section 3.2, as the response of their neurons to
a given dataset, are quadridimensional tensors (data-
points × channels × vertical image size × horizontal
image size), (Raghu et al., 2017) proposed to collapse
the dimensions corresponding to the image size into
the datapoints dimension, thus reshaping the tensor in
a matrix of shape (datapoints · vertical image size ·
horizontal image size) × channels.
Once the pruned networks were obtained, we pro-
ceeded as follows. For each problem:
1. We randomly subset the (non augmented) training
dataset (problem specific) on 5000 datapoints.
2. We evaluated each network (pruned and un-
pruned) on this subset, storing the representation
of each of layer for each network. We name
n
i
= {L
(0)
i
, . . . , L
(K)
i
} the network pruned at i-th it-
eration of IMP, represented as the set of its layers,
L
(0)
i
being the input layer, L
(K)
i
being the output
layer; henceforth, n
0
represent the unpruned net-
work. Note that K is problem specific.
3. For each nework, we compared, using SVCCA,
each convolutional, pooling, or fully-connected
layer of each pruned network with its un-
pruned counterpart, i.e., L
( j)
0
with L
( j)
i
, ∀i ∈
{1, . . . , 20}, ∀ j ∈ {1, . . . , K − 1}. The similarity
was then summarized using Mean CCA Similarity
(see Section 3.2).
5 RESULTS
5.1 Test Performance
Recalling from Section 4.3, we trained 5 unpruned
convolutional neural networks on problems directly
obtained from Cifar10; each of those networks were
pruned using IMP for 20 iterations, with pruning rates
as of Table 3.
We repeated the runs of IMP 20 times, each time
starting from the same unpruned network, but using a
different seed for the optimizer.
Median test accuracy of the aforementioned mod-
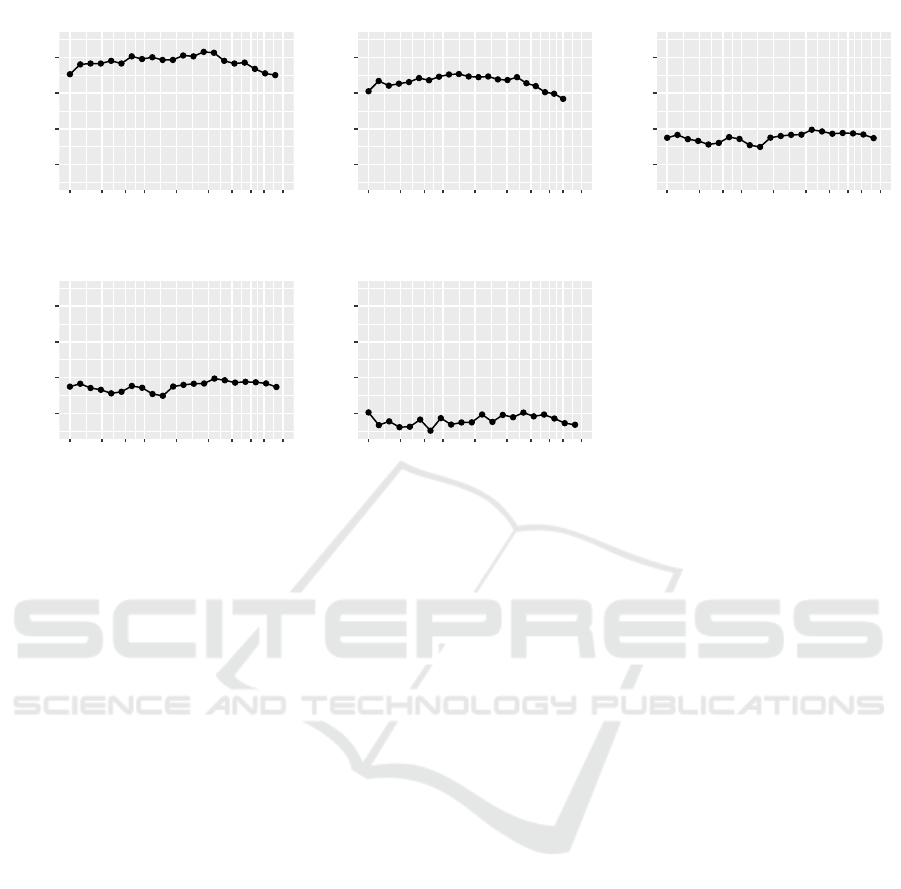
els, for each of iteration of IMP, are reported in Fig-
ure 1.
5.2 Layers Similarity
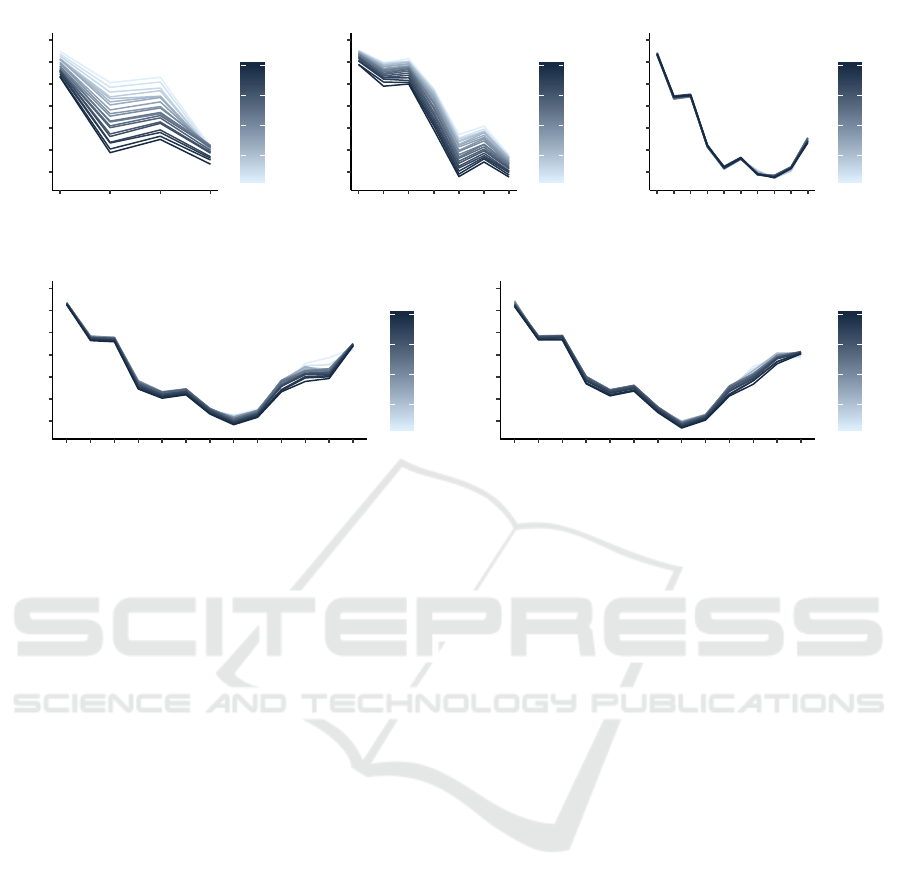
The results in terms of Mean CCA Similarity are
shown in Figure 2; again, since the pruning was re-
peated 20 times to increase robustness, the results,
for each layer and number of IMP iteration, are sum-
marised in the figure as median values.
We notice the presence of two different trends.
First, the neural networks for the datasets Cifar2 and
Cifar4 exhibit a decreasing similarity: (a) as the iter-
ation number increases and (b) as we progress along
the network, from input to output. If we do not con-
sider what would seem a slight incremental effect on
similarity which we can notice in almost all pooling
layers (also present in the other problems), the net-
works for Cifar2 and Cifar4 show a progressive de-
tachment from the input dataset;
Second, on the other hand, the networks for the
larger problems, Cifar6, Cifar8, and Cifar10, exhibit
a different behavior. The similarity starts high for the
first convolutional layer, it decreases until it bottoms
around the 3rd convolutional block, finally it grows
again with a spike on fully-connected layer. More-
over, while before we noted an increasing dissimilar-
ity w.r.t. the unpruned network layers as the IMP iter-
ation increased, now the range of similarity, layer per
layer, is much smaller.
These observations, especially on the second
group of problems indicated in the list above, may
hint at some insights on the roles of the hidden layers
in convolutional neural networks as the network gets
pruned.
First of all, from all of the graphs in Figure 2, we
can notice how pruning, even at small rates, produces
layers representation which are different from the un-
pruned network ones. All the graphs seem to exhibit
trends, which, especially considering that they’re the
result of multiple trials, allow us to rule out the pos-
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
56
0.86
0.88
0.90
0.92
1.000
0.500
0.300
0.200
0.100
0.050
0.030
0.020
0.015
0.010
Parameters sparsity
Test Accuracy
Cifar2
0.86
0.88
0.90
0.92
1.000
0.500
0.300
0.200
0.100
0.050
0.030
0.020
0.015
0.010
Parameters sparsity
Test Accuracy
Cifar4
0.86
0.88
0.90
0.92
1.000
0.500
0.300
0.200
0.100
0.050
0.030
0.020
0.015
0.010
Parameters sparsity
Test Accuracy
Cifar6
0.86
0.88
0.90
0.92
1.000
0.500
0.300
0.200
0.100
0.050
0.030
0.020
0.015
0.010
Parameters sparsity
Test Accuracy
Cifar8
0.86
0.88
0.90
0.92
1.000
0.500
0.300
0.200
0.100
0.050
0.030
0.020
0.015
0.010
Parameters sparsity
Test Accuracy
Cifar10
Figure 1: Median test accuracy for the models from Section 4.3. The point corresponding to Parameters sparsity equal to
1.000 refers to the unpruned model.
sibility of the results being purely the product of ran-
domness in the path of the optimizers.
Moreover, we can notice that, in harder problems,
pruning (with IMP) seems to have a stronger effect
on the convolutional layers, forcing them to produce
different representations; as we get closer to the fully-
connected layer, the network seems to be forced to
lead the representations produced by the intermediate
convolutional blocks towards a common representa-
tion for the fully-connected layer, in order to produce
a similar output, and thus getting a comparable, if not
better, test accuracy. Summarising, it would seem that
the fully-connected layer acts as a pivot during the
pruning, allowing for the network to produce simi-
lar performance despite different representations be-
ing learnt in the previous layers.
5.3 Limitations and Future Works
We remark that, as highlighted in Section 2, we are
aware of the existence of other metrics and method-
ologies for networks comparison, and we are aware
of the potential limitations of CCA raised by (Korn-
blith et al., 2019) as well. Our next step will be hence
devoted towards the incorporation of these works into
our research.
Since our work was carried out purely on a set
of convolutional neural networks for category-level
recognition, based on VGG, and trained on Cifar10,
a future goal would be to extend the analysis to other,
deeper networks (like VGG19, or Resnet 18), or to
other, more difficult problems—like ImageNet (Deng
et al., 2009)—to inspect whether the same results are
observable in these networks.
Moreover, as noted by (Han et al., 2015), since
the effectiveness of pruning techniques is essentially
a consequence of the over-parameterization of ANNs,
the present work may be potentially linked to other
papers addressing the issue of over-parameterization.
For example, in (Ansuini et al., 2019), the intrinsic di-
mensionality (ID) of a layer in a deep neural network
(i.e., the “minimal number of coordinates which are
necessary to describe its points without significant in-
formation loss”) is analyzed. The authors computed
the ID of layers for an ensemble of convolutional neu-
ral networks for image classification observing that
the ID was exhibiting a bell-shaped trend, somewhat
complementary to what we observed in our research
in Figure 2 for the three largest models: the ID started
low, increased, spiked at around 30–40% of the net-
work depth, then decreased, bottoming at the output
layer. A direction of future work is studying whether
the shape for layer-wise similarity in our research may
somewhat be connected to these observations on ID,
i.e., that the decrease in similarity in the mid-ranked
convolutional layers is low because ID of these lay-
ers is high, and, on the other hand, a low ID in the
early and later layers is what causes the representa-
tions to be similar as far as Mean CCA Similarity is
concerned.
On the Similarity between Hidden Layers of Pruned and Unpruned Convolutional Neural Networks
57
0.4
0.5
0.6
0.7
0.8
0.9
1.0
conv
conv
pool
f−c
Layer
Mean CCA similarity
5
10
15
20
Ite
Cifar2
0.4
0.5
0.6
0.7
0.8
0.9
1.0
conv
conv
pool
conv
conv
pool
f−c
Layer
Mean CCA similarity
5
10
15
20
Ite
Cifar4
0.4
0.5
0.6
0.7
0.8
0.9
1.0
conv
conv
pool
conv
conv
pool
conv
conv
pool
f−c
Layer
Mean CCA similarity
5
10
15
20
Ite
Cifar6
0.4
0.5
0.6
0.7
0.8
0.9
1.0
conv
conv
pool
conv
conv
pool
conv
conv
pool
conv
conv
pool
f−c
Layer
Mean CCA similarity
5
10
15
20
Ite
Cifar8
0.4
0.5
0.6
0.7
0.8
0.9
1.0
conv
conv
pool
conv
conv
pool
conv
conv
pool
conv
conv
pool
f−c
Layer
Mean CCA similarity
5
10
15
20
Ite
Cifar10
Figure 2: Median values of Mean CCA Similarity between pruned layers and their unpruned counterparts for models, and
IMP iteration number, from Section 4.4. Layers are ordered, left to right, from closer to input to closer to output. Line color
shade is related to iteration number of IMP.
6 CONCLUSIONS
In this paper, we applied IMP to CNNs based on
VGG, trained on an set of increasingly difficult prob-
lems derived from Cifar10. We then inspected the
layer-wise similarities between unpruned and pruned
networks using SVCCA. For the more difficult prob-
lems, as we got farther from the input layer, we ob-
served a decreasing similarity, bottoming at around
half of the network depth, and then an increase, as
the fully-connected layer is approached. That behav-
ior may indicate that the fully connected layer plays a
role of pivot for leading the differences produced by
convolutional layers back to somewhat similar repre-
sentations.
Future work includes exploiting some very recent
advances in the similarity measures for network lay-
ers and exploring the connection to existing results
on the over-parameterization in artificial neural net-
works.
REFERENCES
Ansuini et al., 2019Ansuini, A., Laio, A., Macke, J. H., and
Zoccolan, D. (2019). Intrinsic dimension of data rep-
resentations in deep neural networks. In NIPS 2019.
Crowley et al., 2018Crowley, E. J., Turner, J., Storkey, A.,
and O’Boyle, M. (2018). Pruning neural networks:
is it time to nip it in the bud? arXiv preprint
arXiv:1810.04622.
Deng et al., 2009Deng, J., Dong, W., Socher, R., Li, L.-J., Li,
K., and Fei-Fei, L. (2009). ImageNet: A Large-Scale
Hierarchical Image Database. In CVPR09.
Frankle and Bau, 2019Frankle, J. and Bau, D. (2019). Dis-
secting pruned neural networks. arXiv preprint
arXiv:1907.00262.
Frankle and Carbin, 2019Frankle, J. and Carbin, M. (2019).
The lottery ticket hypothesis: Finding sparse, train-
able neural networks. In International Conference on
Learning Representations.
Frankle et al., 2019Frankle, J., Dziugaite, G. K., Roy, D. M.,
and Carbin, M. (2019). Stabilizing the lottery ticket
hypothesis. arXiv preprint arXiv:1903.01611.
Goodfellow et al., 2016Goodfellow, I., Bengio, Y., and
Courville, A. (2016). Deep learning, chapter 7.1.2 -
L1 Regularization. MIT press.
Han et al., 2015Han, S., Pool, J., Tran, J., and Dally, W.
(2015). Learning both weights and connections for ef-
ficient neural network. In Cortes, C., Lawrence, N. D.,
Lee, D. D., Sugiyama, M., and Garnett, R., editors,
Advances in Neural Information Processing Systems
28, pages 1135–1143. Curran Associates, Inc.
He et al., 2016He, K., Zhang, X., Ren, S., and Sun, J. (2016).
Deep residual learning for image recognition. In Pro-
ceedings of the IEEE conference on computer vision
and pattern recognition, pages 770–778.
Ioffe and Szegedy, 2015Ioffe, S. and Szegedy, C. (2015).
Batch normalization: Accelerating deep network
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
58

training by reducing internal covariate shift. In ICML,
pages 448–456.
Kingma and Ba, 2014Kingma, D. P. and Ba, J. (2014). Adam:
A method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Kornblith et al., 2019Kornblith, S., Norouzi, M., Lee, H., and
Hinton, G. E. (2019). Similarity of neural network
representations revisited. In ICML, pages 3519–3529.
Lin et al., 2013Lin, M., Chen, Q., and Yan, S. (2013). Network
in network. arXiv preprint arXiv:1312.4400.
Morcos et al., 2018Morcos, A., Raghu, M., and Bengio, S.
(2018). Insights on representational similarity in neu-
ral networks with canonical correlation. In Ben-
gio, S., Wallach, H., Larochelle, H., Grauman, K.,
Cesa-Bianchi, N., and Garnett, R., editors, Advances
in Neural Information Processing Systems 31, pages
5732–5741. Curran Associates, Inc.
Raghu et al., 2017Raghu, M., Gilmer, J., Yosinski, J., and
Sohl-Dickstein, J. (2017). Svcca: Singular vector
canonical correlation analysis for deep learning dy-
namics and interpretability. In Guyon, I., Luxburg,
U. V., Bengio, S., Wallach, H., Fergus, R., Vish-
wanathan, S., and Garnett, R., editors, Advances
in Neural Information Processing Systems 30, pages
6076–6085. Curran Associates, Inc.
Simonyan and Zisserman, 2014Simonyan, K. and Zisserman,
A. (2014). Very deep convolutional networks
for large-scale image recognition. arXiv preprint
arXiv:1409.1556.
Srivastava et al., 2014Srivastava, N., Hinton, G., Krizhevsky,
A., Sutskever, I., and Salakhutdinov, R. (2014).
Dropout: a simple way to prevent neural networks
from overfitting. The journal of machine learning re-
search, 15(1):1929–1958.
Wang et al., 2018Wang, L., Hu, L., Gu, J., Hu, Z., Wu, Y.,
He, K., and Hopcroft, J. (2018). Towards understand-
ing learning representations: To what extent do differ-
ent neural networks learn the same representation. In
Bengio, S., Wallach, H., Larochelle, H., Grauman, K.,
Cesa-Bianchi, N., and Garnett, R., editors, Advances
in Neural Information Processing Systems 31, pages
9584–9593. Curran Associates, Inc.
Yu et al., 2018Yu, T., Long, H., and Hopcroft, J. E. (2018).
Curvature-based comparison of two neural networks.
In 2018 24th International Conference on Pattern
Recognition (ICPR), pages 441–447. IEEE.
Zhang et al., 2018Zhang, T., Ye, S., Zhang, K., Tang, J., Wen,
W., Fardad, M., and Wang, Y. (2018). A systematic
dnn weight pruning framework using alternating di-
rection method of multipliers. In Proceedings of the
European Conference on Computer Vision (ECCV),
pages 184–199.
Zhou et al., 2019Zhou, H., Lan, J., Liu, R., and Yosinski, J.
(2019). Deconstructing lottery tickets: Zeros, signs,
and the supermask. arXiv preprint arXiv:1905.01067.
On the Similarity between Hidden Layers of Pruned and Unpruned Convolutional Neural Networks
59
