
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor
Networks
A
¨
ıda Diop
1
, Maryline Laurent
2
, Jean Leneutre
3
and Jacques Traor
´
e
4
1
T
´
el
´
ecom SudParis, T
´
el
´
ecom ParisTech, Orange Labs, Caen, France
2
SAMOVAR, CNRS, T
´
el
´
ecom SudParis, Institut Polytechnique de Paris, France
3
LTCI, T
´
el
´
ecom ParisTech, Universit
´
e Paris-Saclay, France
4
Orange Labs, Caen, France
jacques.traore@orange.com
Keywords:
Security, Remote Attestation, Collective Attestation.
Abstract:
Embedded Internet of Things (IoT) devices are deployed in the functioning of a number of applications such
as industrial control, building automation, and the smart grid. The lack of robustness of IoT devices has
however rendered such systems vulnerable to a number of remote cyber-attacks. Remote attestation is a
security mechanism which enables to remotely verify the integrity of the software running on IoT devices.
Similarly, collective remote attestation protocols are designed to efficiently verify the integrity of a group
of devices. Existing collective attestation protocols do not provide an efficient and secure mechanism to
detect compromised devices. In particular, it is not possible to efficiently trace the origin of an erroneous
attestation response back to the concerned node. In this paper, we introduce CoRA, a highly scalable collective
attestation protocol, which leverages the aggregating property of the underlying cryptographic scheme during
the attestation process. CoRA is the first collective attestation protocol to also provide sequential detection,
where the identity of the compromised node is revealed. We provide rigorous security proofs for our protocol
and its underlying cryptographic primitive, and demonstrate its efficiency in highly scalable networks.
1 INTRODUCTION
Typically, connected Internet of Things (IoT) devices
are deployed in data-sensitive and safety-critical ap-
plications, spanning a number of IoT systems. The
safety of these systems is hindered by the lack of se-
curity and robustness of low-cost devices, resulting in
a number of remote cyber-attacks (Mansfield-Devine,
2016; Falliere et al., 2010). Remote attestation is a
security process which allows a trusted party, called
verifier, to verify the integrity of the software running
on each device. Traditionally, the attestation process
runs between a single device (the prover), and the ver-
ifier. However, many IoT applications rely on self-
organizing device mesh networks, also called swarms,
to perform a given task. The concept of collective
(or swarm) attestation, has been developped to pro-
vide scalable attestation protocols tailored for such
networks (Ambrosin et al., 2016; Carpent et al., 2017;
Ibrahim et al., 2016; Ibrahim et al., 2017; Kohnh
¨
auser
et al., 2017; Kohnh
¨
auser et al., 2018). The general
model of a collective attestation protocol, as illus-
trated in Figure 1, is comprised of the network op-
erator, who deploys devices in the field, the group
of devices performing a specific task, and the veri-
fier. Nodes in the swarm generate their individual
attestation responses, which are in turn accumulated
into a single attestation response. The topology of
the mesh network plays a crucial role in the effective-
ness of the attestation protocol. Notably, during the
attestation process, a spanning tree is generated over
the network, allowing each node to propagate their re-
sponse in the tree via their parent node. The root of
the spanning tree is directly linked to the verifier, who
collects a single aggregated report at the end of each
execution (Chan et al., 2006). The successful verifi-
cation of the final attestation response guarantees the
integrity of the entire network. Initially, collective
attestation protocols only mitigated against software
attacks (Asokan et al., 2015). The majority of IoT
applications we consider however require deploying
devices in the field, thus rendering them vulnerable to
physical attacks. Recent collective attestation propo-
sitions leverage the security provided by trusted com-
84
Diop, A., Laurent, M., Leneutre, J. and Traoré, J.
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks.
DOI: 10.5220/0008962700840095
In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 84-95
ISBN: 978-989-758-399-5; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
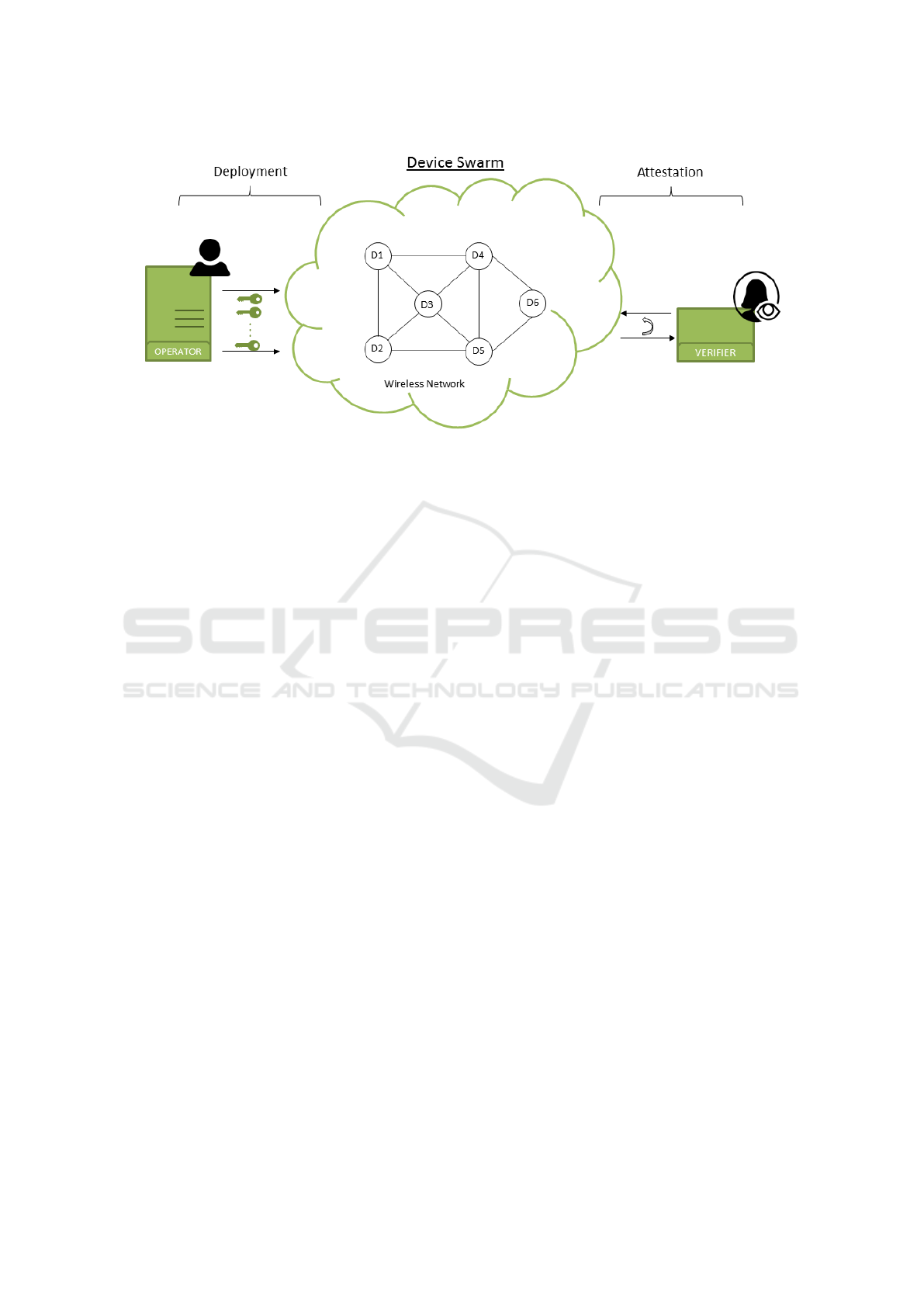
Figure 1: Overview of the collective attestation process.
puting by requiring each node to authenticate their at-
testation report with a cryptographic key (Ambrosin
et al., 2016; Ibrahim et al., 2016; Kohnh
¨
auser et al.,
2017). The key is stored in a hardware module, hence,
an adversary who attempts to forge an attestation is
compelled to physically tamper with the devices.
Existing collective attestation protocols produce a
binary response, stating whether or not the attestation
process was successful, thus proving the integrity, or
lack thereof, of the entire network. The nature of sen-
sor networks, which consists of multihop networks of
constrained and potentially remote devices, renders
the attestation process vulnerable to injection attacks.
In such attacks, the adversary is able to aggregate er-
roneous data in the final attestation response, without
physically compromising a given node. Notably, he is
able to remove the target node from the network, and
aggregate a random value in lieu of the expected at-
testation response from said node. Upon receiving the
aggregate response, the verifier has no way of tracing
the origin of the erroneous attestation back to the con-
cerned node. Indeed, existing aggregation schemes
based on signatures or MACs, do not allow the ex-
traction of an individual signature (or MAC) from the
aggregated result. Such attacks may therefore trigger
the verification process indefinitely, inducing a Denial
of Service (DoS) attack on the verifier. A detection
mechanism capable of tracing the origin and position
in the network of similar attacks is therefore crucial
to the overall security of the protocol. Indeed, the
network administrator will thus be able to take fur-
ther actions, which may consist in declaring the target
device as compromised, and induce further ramifica-
tions which are out of scope for this paper.
Contributions. We present CoRA, a collective at-
testation protocol for wireless networks, composed of
large numbers of low-cost and computationally con-
strained devices. CoRA is a secure and highly scal-
able attestation protocol, which efficiently verifies the
integrity of a large number of devices in sensor net-
works. Indeed, the protocol is based on aggregate al-
gebraic MACs, which guarantees the unforgeability
of individual attestation responses, even in the pres-
ence of adversaries in the network tampering with
the attestation process. The use of algebraic MACs,
as opposed to signatures, in the aggregation process
guarantees a more efficient verification step. In addi-
tion, we leverage the properties of algebraic MACs,
notably the secret key embedded in each device, to
provide a sequential detection mechanism. CoRA
thus enforces device accountability, and enables trac-
ing the origin of compromised nodes that attempt to
inject erroneous data during the attestation process.
We provide rigorous security proofs for CoRA and
its underlying cryptographic construction, namely ag-
gregate algebraic MACs. We then prove the efficiency
of the protocol, and its application in large wireless
networks of heterogeneous devices.
Outline. We present in Section 2 the related work
on collective attestation, and their limitations. Section
3 illustrates the system model, device requirements,
and threat model. In Section 4, we present the un-
derlying cryptographic scheme, used for secure and
scalable attestation generation and aggregation. The
CoRA protocol is introduced in Section 5, including
the attestation and detection processes. We evaluate
the efficiency of CoRA in Section 6, and prove the
security of the protocol in Section 7. Section 8 con-
cludes the paper.
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
85

2 RELATED WORK
In this section, we present the system and threat
model of a collective attestation protocol, and analyse
existing solutions and their shortcomings.
2.1 Collective Attestation
Remote attestation is a security mechanism which
enables a trusted third party, namely the verifier, to
remotely check the integrity of a device called the
prover. The process is initiated by the verifier, who
issues a challenge to the prover. The prover in turn
generates an attestation report on its current software
state, which the verifier is able to correctly verify.
Collective attestation protocols have been proposed
to efficiently attest large networks of interconnected
devices. In this scenario, the verifier issues the chal-
lenge to a network of devices via an entry node A
s
,
which is chosen based on its geographic proximity to
the verifier. The entry node propagates the challenge
to its children in a process that results in nodes be-
ing classified in a spanning tree rooted at A
s
. This
topology allows the efficient aggregation of attesta-
tion reports, and reduces communication overhead.
The concept of collective attestation was introduced
in SEDA (Asokan et al., 2015). Subsequently, a
number of solutions targeting the security and effi-
ciency shortcomings of SEDA were proposed. SANA
(Ambrosin et al., 2016) leverages the structure of ag-
gregate and multi-signature schemes, in order to ob-
tain a highly scalable attestation protocol. The so-
lution provides public verifiability, and limits phys-
ical attacks by authenticating reports within secure
hardware.Their solution however offers scalability at
the cost of efficiency, since the verification step re-
quires a number of costly pairing computations, that
are in addition linear in the number of devices in the
group. DoS attacks are mitigated in SeED (Ibrahim
et al., 2017) through the use of a secure clock, which
enables provers to periodically forward their attes-
tation reports in a non-interactive protocol. LISA
α
and LISA
s
(Carpent et al., 2017) provide more prac-
tial alternatives to SEDA by proposing a qualitative
classification of attestation protocols, each tailored
to specific security needs. DARPA (Ibrahim et al.,
2016) and SCAPI (Kohnh
¨
auser et al., 2017) provide
mitigation against physical attacks, while SALAD
(Kohnh
¨
auser et al., 2018) is a colletive attestation pro-
tocol suitable for dynamic and disruptive networks.
However, no solution provides the individual de-
tection of nodes responsible for a false attestation re-
sponse in the network. Indeed, the nature of wire-
less communication in mesh networks facilitates the
injection of a false attestation report (i.e. which has
not been authenticated by a valid key). In existing at-
testation protocols, the verification step of the result-
ing attestation report fails when such falsifications are
performed, however no further information on the ori-
gin of the injection is provided. Indeed, the underly-
ing model of secure in-network aggregation schemes
(Chan et al., 2006) does not allow report manipula-
tion detection. The result only stating retrospectively
that the aggregate message was manipulated. Existing
collective attestation protocols relying on aggregate
cryptographic authentication schemes, namely aggre-
gate MACs (Katz and Lindell, 2008; Eikemeier et al.,
2010) and aggregate signatures (Boneh et al., 2003;
Lu et al., 2006; Boldyreva et al., 2007), do not allow
a verifier to check the origin of an erroneous report
which has been aggregated into the final response.
Furthermore, the verification step in aggregate sig-
nature schemes requires a number of pairing compu-
tations linear in the number of nodes, which is pro-
hibitively expensive in sensor networks.
2.2 Efficient in-network aggregation
Large networks of embedded devices require highly
scalable data collection solutions in order to forward
individually collected data to a central base station.
In sensor networks, the base station in the attestation
process is the verifier. Aggregation methods allow a
collection of sensors to securely and collaboratively
compute an aggregation function on their respective
reports. The result of said function is thus forwarded
to the verifier, generating extremely low communica-
tion overhead in the process. This concept, known as
in-network aggregation (Chan et al., 2006), consider-
ably reduces communication overhead, and provides
a highly scalable data collection mechanism. Exist-
ing aggregation methods that are linear in the num-
ber of nodes, and that can be executed in a single
round (Ambrosin et al., 2016), are based on aggregate
digital signatures (Boneh et al., 2003). However as
discussed in Section 2.1, such constructions are ex-
tremely costly due to the use of pairing-based cryp-
tography.
In sensor networks, and more generally dis-
tributed networks of embedded devices, it is mostly
the case that the network administrator plays the role
of both the operator and the verifier (or both are op-
erated by the same entity, i.e. the owner). For ex-
ample, in the Smart grid, electrical companies issue
smart meters with a valid key, and periodically ver-
ify their proper operation. Thus the efficiency issues
in aggregate signatures, can be avoided by the use of
algebraic MAC schemes.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
86

3 SYSTEM MODEL AND
ASSUMPTIONS
3.1 Background
Collective Attestation Architecture. In the archi-
tecture presented in Figure 1, a collective attestation
protocol is divided into two main phases, namely the
deployment phase and the attestation phase. During
the former, the operator O deploys devices in the field
with a unique identifier ID
i
for device D
i
, and a secret
key sk
i
. The verifier V initiates the attestation phase
by generating a challenge Ch, as part of the attestation
request for a device A
s
in the network. The attestation
process will create a spanning tree rooted at A
s
, thus
enabling an efficient and scalable aggregation of the
individual attestation reports. A
s
then propagates the
request down the spanning tree. Upon each node gen-
erating, authenticating, and aggregating their attesta-
tion reports, the final aggregated response reaches A
s
,
who aggregates its own response, before forwarding
the result to V . The verifier, who is in possession of
the expected internal state of each device, is thus able
to verify the integrity of the entire network. For sim-
plicity, we assume in the remaining of the paper that
V and O are either the same entity, or are managed
by the same entity.
Definition and Security Model. We use the for-
mal remote attestation protocol definition and security
model of Francillon et al. (Francillon et al., 2012).
Let t
exp
be the upper-bound on the execution time of
the attestation procedure. The value t
exp
is defined
as a function of the total number of nodes in the net-
work, the time complexity of an individual attestation
computation, intermediary transmission time, and the
aggregation time. Francillon et al. (Francillon et al.,
2014) define the security of a remote attestation proto-
col, to be resistance against forgery. The security no-
tion of resistance against forgery considers the case
where an adversary has oracle access to the attesta-
tion generation function. Considering such adversary
A, that is thus able to request n − 1 attestations, A
should still be unable to produce a new valid attesta-
tion on a message he has not previously queried to the
attestation oracle.
3.2 Overview
We consider a network of low-end, heterogeneous,
embedded devices, communicating over a wireless
mesh network. Devices in the network have limited
computational power and storage capacity. In the in-
frastructure of the collective attestation protocol, we
assume the operator O to be the network administra-
tor, who initially deploys devices in the field. The
deployment phase is only executed once, and consists
in each device D
i
being initialized with a secret sym-
metric key sk
i
shared with O (and the verifier V ), as
well as a unique identifier ID
i
, which can be the IP ad-
dress of wireless devices for example. In order to ver-
ify the integrity of the internal software state of every
device in the network, the trusted verifier V periodi-
cally engages in the attestation protocol with the de-
vice swarm. At the beginning of the attestation phase,
a spanning tree of all nodes is formed, thus facilitating
the aggregation process. At the end of the attestation
phase, V collects a single attestation report, which
guarantees the integrity (or lack thereof) of the en-
tire swarm. The verifier possesses the list of expected
software state, hence allowing him to verify the valid-
ity of the final attestation response in correlation with
the expected values. Each device is equipped with the
minimal hardware requirements for a collective attes-
tation protocol, namely a Read-Only Memory (ROM)
to store the protocol code and cryptographic keys, as
well as a Memory Protection Unit (MPU). The MPU
controls access to the ROM, and ensure that only pro-
tocol code can access the secret keys. Each device
D
i
can compute a collision-resistant hash function,
as well as multiplications in elliptic curve groups.
Furthermore, we assume that initialized counters are
stored in the ROM and are only accessible by the
MPU, thus preventing any desynchronization attempt.
3.3 Threat Model
Adversary Model. We consider an adversary A ,
who has full access to the communication channel
(Dolev-Yao model). As such, A can eavesdrop, mod-
ify, insert, and drop messages exchanged between de-
vices. A can also capture nodes and access and mod-
ify their software state. Security against physical ad-
versaries (who are able to extract cryptographic keys),
cannot however be guaranteed (Ibrahim et al., 2016).
In contrast, we consider the following threat model:
an adversary A who has compromised the networks,
and potentially captured a number of devices (up to
n − 1 devices in a network comprising n devices),
should still be unable to forge a valid aggregate attes-
tation for the remaining nodes. With regards to Denial
of Service (DoS) attacks, existing attestation proto-
cols consider attacks where devices are rendered un-
available in the network, thus preventing the success-
ful completion of the process. Such attacks cannot
be prevented, as it is indeed impossible to guarantee
availability for an adversary A capable of dropping all
messages. In this paper, we also consider DoS attacks
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
87

against the verifier. Indeed, A is able to continuously
aggregate an erroneous message in the final response,
triggering a failed verification process each time. We
mitigate against such attacks by providing an efficient
detection mechanism in CoRA.
Security Objectives. As defined in Section 3.1, an
attestation protocol is secure if no adversary is able to
forge an attestation report, thus faking a healthy state
for a compromised device. In Section 7, we prove the
security of CoRA against such adversaries, based on
the security of the underlying cryptographic scheme.
4 MAC
BLS
AGGREGATION
SCHEME
We present in this section a hybrid cryptographic
scheme introduced by Dodis et.al. (Dodis et al.,
2012), namely algebraic MACs. Algebraic MACs
provide the best of both worlds, i.e. the algebraic
properties inherent to signature schemes, while avoid-
ing the costly public verification step. This is possi-
ble considering the fact that in sensor networks, the
same entity manages both the operator and the ver-
ifier. We later provide an aggregate algebraic MAC
scheme, which is subsequently used as the underly-
ing scheme for CoRA to authenticate individual at-
testation reports, and perform detection.
4.1 Notations
We introduce in this section the mathematical and
cryptographic notations used in the remaining of the
paper.
We define the sampling of a random element x from
a set X using the following notation: x
$
←− X. Pr[A]
denotes the probability of an event A. The notation G
denotes an algebraic group, while g ∈ G represents an
element g in group G. M = {m
1
,..., m
n
} denotes a set
M, comprised of n elements m
1
,..., m
n
.
4.2 Algebraic MACs
Algebraic MACs are MAC schemes based on group
operations, as opposed to block ciphers or hash func-
tions. Their primary goal is to take advantage of the
symmetry between the signer and the verifier in ap-
plications where the signer and verifier are the same
entity, in order to provide a more efficient verifica-
tion step. Algebraic MACs are used in CoRA to first
generate unforgeable attestations, while also allowing
the construction of an efficient and secure detection
mechanism based on each device’s knowledge of their
secret keys.
4.3 Aggregate Algebraic MACs
The underlying scheme for CoRA is an aggregate al-
gebraic MAC, named aggregate MAC
BLS
, and de-
rived from the Boneh, Lynn, Shacham (BLS) signa-
ture scheme (Boneh et al., 2001). Aggregate MAC
schemes, introduced by Katz and Lindell (Katz and
Lindell, 2008), allow a set of n users to generate n
tags on n potentially different messages, and aggre-
gate the result into a single tag of the same size as an
individual tag. The verification process, which is lin-
ear in the number of users, attests of the validity of
all tags in the final aggregate. We define an aggre-
gate algebraic MAC, where tags are group elements
as opposed to block ciphers or hash functions. Tags
are single group elements of size 256-bit (for exam-
ple elliptic curve group elements). The output size of
secure hash functions being comparable to such out-
put sizes, the use of algebraic MACs does not induce
additional space complexity.
The security of the aggregate MAC
BLS
scheme is
based on a standard discrete logarithm-based secu-
rity assumption, namely the Computational Diffie-
Hellman (CDH) assumption, defined as follows:
Computational Diffie-Hellman Problem (CDH).
Given g,g
a
,g
b
∈ G for a, b ∈ Z
q
, compute g
ab
∈ G.
The CDH assumption stipulates that any algo-
rithm A that runs in polynomial time has negligible
advantage in solving the CDH problem in G.
MAC
BLS
Construction. We first give the construc-
tion of an individual algebraic MAC scheme MAC
BLS
.
The MAC
BLS
scheme comprises the following algo-
rithms:
Setup(1
λ
). Create the public parameters
params = (G, q,g,H ) where G is a group of
prime order q of size λ, where CDH is hard. g
$
←− G is
a random generator of G. H
1
: {0,1}
∗
→ G is a hash
function, modeled as a random oracle in the security
analysis.
KeyGen(1
λ
). Select a random element x
i
$
←− Z
q
,
and sets the secret key sk
i
= x
i
. The algorithm also
outputs the public parameter iparams = X
i
, where
X
i
= g
x
i
.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
88

Mac(params,sk
i
,m
i
). Compute h
i
← H
1
(m
i
), and
compute the tag τ
i
= h
x
i
i
.
Verify(params,sk
i
, pk
i
,m
i
,τ
i
). Compute h
i
= H
1
(m
i
),
and accept if τ
i
= h
x
i
i
.
Theorem 1 A probabilistic polynomial-time adver-
sary against MAC
BLS
succeeds in returning a valid
forgery with only negligible probability under the
CDH assumption.
The proof for Theorem 1 is provided in appendix A.1.
Aggregate MAC
BLS
Construction. Based on the
MAC
BLS
scheme construction introduced above, we
define the aggregate MAC scheme in groups of prime
order. The aggregation function AggMac is public
and unkeyed, namely any node is able to aggregate its
own tag without a secret key (as opposed to the MAC
computation step). The aggregate MAC
BLS
scheme
is the MAC
BLS
scheme with the following additional
algorithms:
AggMac({τ
i
}
n
i=1
). Given a set of tags {τ
i
}
n
i=1
,
output the aggregate tag τ =
∏
n
i=1
τ
i
.
AggVerify(params, {(sk
i
, pk
i
)}
n
i=1
,{m
i
}
n
i=1
,τ).
For 1 ≤ i ≤ n, compute h
i
= H
1
(m
i
). Check if
τ =
∏
n
i=1
h
x
i
i
. Return accept if true, and reject
otherwise.
Theorem 2 Aggregate MAC
BLS
is unforgeable pro-
vided that the underlying MAC
BLS
scheme is unforge-
able.
The security definition of unforgeability for aggregate
algebraic MACs is that of existential unforgeability
under chosen message attack. This definition illus-
trates the fact that an adversary who has access to at
most n −1 secret keys, is still unable to output a valid
aggregate tag by n users (Boneh et al., 2003). We
prove Theorem 2 in appendix A.2.
5 CoRA
CoRA is a secure and scalable collective attestation
protocol, which consists of two phases, namely the
deployment phase presented in Section 5.2 and the
attestation phase in Section 5.3. The protocol also
comprises an optional detection phase, presented in
Section 5.4. The deployment phase is executed only
once by the operator O, who initializes the network.
Following deployment, the verifier V can periodi-
cally verify the software integrity of all devices in
the network by initiating the attestation phase. In the
case where verification fails, V initiates the detection
phase, in order to identify the origin of the failure. We
demonstrate the security of CoRA in Section 7, based
on the security of its underlying aggregation mecha-
nism.
5.1 Preliminaries
In the construction of CoRA, we use anonymous au-
thentication schemes, namely non-interactive zero-
knowledge proofs of knowledge (also known as sig-
natures of knowledge (Schnorr, 1991)). Signatures
of knowledge are highly efficient signature schemes,
that leverage the knowledge of a cryptographic secret,
in order to authenticate a given user. They are the
building block of numerous authentication schemes
such as group signatures or anonymous credentials.
In CoRA, signatures of knowledge are used in the at-
testation and detection phases to prove that a given
node has generated a given tag during the aggregation
process. To define our signatures of knowledge, we
use the Camenisch and Stadler notation (Camenisch
and Stadler, 1997), whereby π(m) = SoK{sk
i
: y =
g
sk
i
}(m) denotes a signature of knowledge on mes-
sage m. A device D
i
with secret key sk
i
signs message
m by proving that he knows the secret sk
i
, correspond-
ing to a discrete logarithm in base g.
Theorem 3 CoRA is secure against forgery attacks,
under the assumption that aggregate MAC
BLS
is un-
forgeable.
The proof for Theorem 3 is provided in Section 7.
5.2 Deployment Phase
In the deployment phase, the network operaror O
runs the Setup and KeyGen of the aggregate MAC
BLS
scheme, and obtains the public parameters params,
and the secret keys sk
i
for every device D
i
. Prior to
deployment, O initializes each device with a MAC
BLS
secret key sk
i
for i ∈ {1,...,n}, and its own MAC
BLS
public value pk
0
= X
0
. The secret keys are used by
devices to generate MAC
BLS
tags τ
i
on their internal
state S
i
. The tags will later be aggregated and for-
warded to V . The attestation and aggregation steps
are developped in Section 5.3. In addition, each D
i
is initialized with a counter value cnt
k
, which corre-
sponds to the attestation sequence k. cnt
k
is initial-
ized to 0, and incremented by the verifier V and each
node after each attestation process. The counters are
used to monitor the attestation sequence number, thus
preventing replay attacks. Indeed, upon receiving the
attestation request, node D
i
verifies that the value of
the associated counter is greater than or equal to the
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
89

Table 1: CoRA parameters notation.
Acronyms Description
O Network opera-
tor
V Network verifier
sk
O
, pk
O
O’s MAC
BLS
key
pair
D
i
Device i with
identifier ID
i
A
s
root device
sk
i
, pk
i
D
i
’s MAC
BLS
key
pair
S
i
attestation report
τ
i
MAC tag on
message s
i
attReq attestation re-
quest
GenAtt(key,s
i
) generates and au-
thenticates attes-
tation report
AggAtt(τ
1
,...,τ
m
) aggregates attes-
tation reports
VrfAggAtt({s
i
}
m
i=1
,τ) verifies aggre-
gated report
counter value stored locally. Each device in the net-
work possesses a unique identifier ID
i
, which can for
example, be derived from its IP address. O is able
to deploy new devices in the swarm at any time, by
executing the initialization process described above.
5.3 Attestation Phase
The attestation phase allows the network operator O
and the verifier V , to verify the integrity of every de-
vice in the swarm.
Overview. The goal of the attestation phase is to it-
eratively authenticate each device D
i
’s internal soft-
ware state S
i
, and propagate said attestation proofs
up the attestation tree until it reaches the verifier V .
The attestation phase of CoRA (Figure 2), is divided
in three sub-phases, namely request dissemination,
attestation, and verification. V initiates the request
dissemination phase by sending an attestation request
attReq to the closest device in his communication
range A
s
. Upon receiving attReq, A
s
verifies that it
is indeed a valid request from V , and forwards to its
children down the attestation tree. Each device in the
tree receiving the request, verifies its authenticity and
freshness. This initial step securely communicates to
each device that a new attestation process has been
initiated. Upon authenticating the request, leaf nodes
generate the attestation report on their internal soft-
ware state and send it to their parents. Intermediary
nodes authenticate said reports, generate their own
attestation, and in turn send the aggregated result to
their parents. V receives the final report from A
s
. He
then verifies the validity of the aggregate report, hence
confirming the integrity (or lack thereof) of every de-
vice in the network.
(1) Request Dissemination. V initiates the attesta-
tion phase by disseminating an attestation request
to the nearest device in its communication range
A
s
. The request attReq is generated as follows:
– Generate a random nonce N
k
$
←− {0, 1}
l
N
for the
current attestation process, where l
N
is the size
of the nonce.
– Update cnt
k
← cnt
k
+ 1
– Choose a random collision-resistant hash func-
tion H
– Generate a signature of knowledge on message
m = N
k
as π
0
= SoK{x
0
: X
0
= g
x
0
}(m).
– Define challenge c
0
← {n, X
0
,Cert
X
0
,π
0
},
where X
0
is the MAC
BLS
public key for O and
Cert
X
0
a valid certificate on X
0
. n is the size of
the swarm.
– attReq ← c
0
Upon receiving attReq, A
s
authenticates V by
verifying π
0
. It then propagates the request
down the attestation tree. Intermediary nodes
authenticate the request before forwarding it to
their children. This authentication step mitigates
against distributed DoS attacks, whereby an at-
tacker might render devices unavailable by send-
ing them false attestation requests.
(2) Attestation. Upon checking the authenticity and
freshness of attReq, each leaf node D
i
proceeds
to measuring its internal software software state
S
i
. It then runs the attestation generation function
GenAtt(sk
i
,S
i
) defined as follows:
GenAtt: (sk
i
,S
i
).
1: Generate τ
i
← MAC
BLS
(sk
i
,m
i
), where m
i
=
(N
k
||cnt
k
||S
i
). Including N
k
and cnt
k
in the mes-
sage ensures the freshness of the tag.
2: Generate a signature of knowledge π
i
, of the se-
cret key on the tag τ
i
, where π
i
= SoK{x
i
: τ
i
=
h
x
i
i
∧ X
i
= g
x
i
}(τ
i
).
3: Define an empty list C
i
=
/
0
4: Return report a
i
← (ID
i
,H (N
k
||cnt
k
),τ
i
,π
i
,C
i
)
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
90
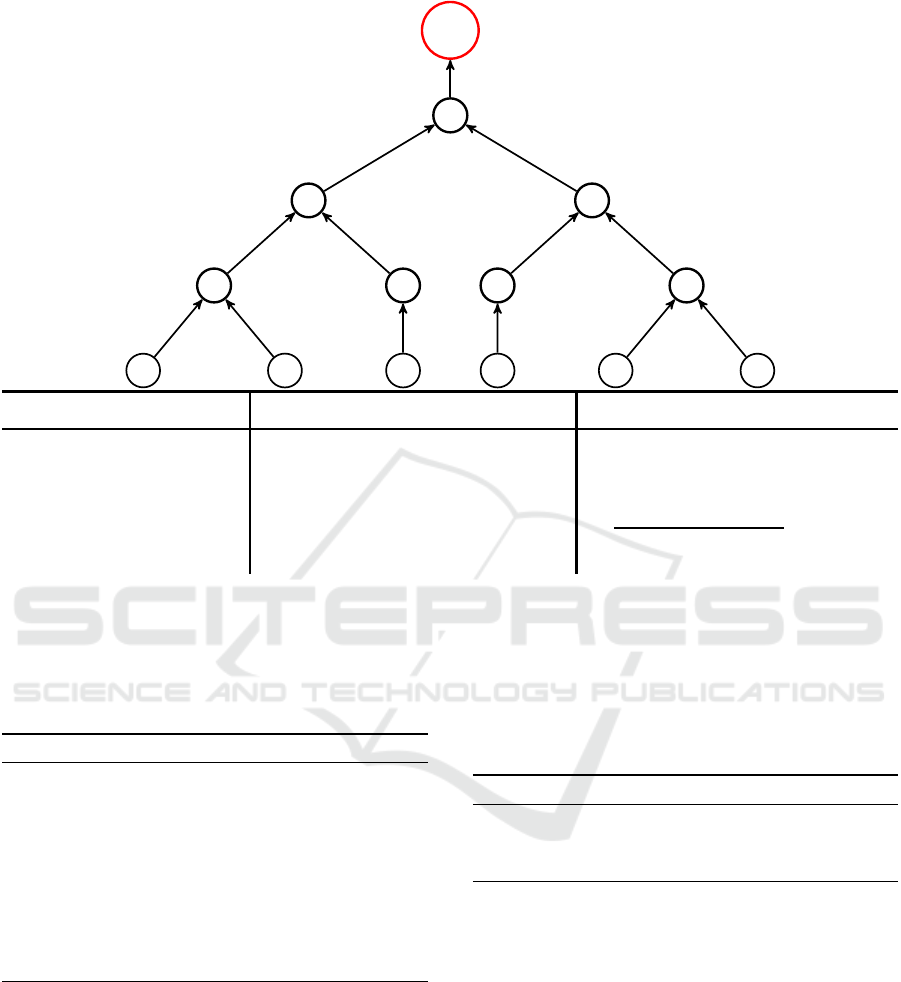
V
A
s
D
1
D
3
D
7
τ
7
D
8
τ
8
τ
3
D
4
D
9
τ
9
τ
4
τ
1
D
2
D
5
D
10
τ
10
τ
5
D
6
D
11
τ
11
D
12
τ
12
τ
6
τ
2
τ
s
Level 1 Level 2 Level 3 & 4
• [τ
7
] =Mac
sk
7
(s
7
) • [τ
3
] = AggMac({τ
7
,τ
8
,τ
3
}) • [τ
1
] = AggMac({τ
3
,τ
4
,τ
1
})
• [τ
8
] =Mac
sk
8
(s
8
) • [τ
4
] = AggMac({τ
9
,τ
4
,}) • [τ
2
] = AggMac({τ
5
,τ
6
,τ
2
})
.
.
.
.
.
.
• [τ
12
] =Mac
sk
12
(s
12
) • [τ
6
] = AggMac({τ
11
,τ
12
,τ
6
}) • [τ
s
] = AggMac({τ
1
,τ
2
,τ
s
})
Figure 2: Aggregation tree containing nodes {A
s
,D
1
,...,D
12
}.
Upon receiving the attestation reports a
i
and a
j
from its children, intermediary node D
l
runs the
attestation aggregation function AggAtt(τ
i
,τ
j
):
AggAtt: (τ
i
,τ
j
).
1: Verify π
i
and π
j
. If the verification succeeds, pro-
ceed to step 2. Else, set C
l
= {ID
k
}
k∈{i, j}
, where
the identifier(s) in C
l
corresponds to those whose
signature of knowledge verification failed.
2: Generate τ
l
← MAC
BLS
(sk
l
,m
l
), where message
m
l
= (N
k
||cnt
k
||S
l
)
3: Compute τ ← AggMAC
BLS
(τ
i
,τ
j
,τ
l
)
4: Generate π
l
= SoK{x
l
: τ
l
= h
x
l
l
∧ X
l
= g
x
l
}(τ)
5: Return a
l
← (ID
l
,H (N
k
||cnt
k
),τ, π
l
,C
l
)
At the end of the attestation generation, aggrega-
tion, and propagation phase, V receives the final
attestation report a
s
from A
s
, and proceeds to ver-
ifying its validity.
(3) Verification. Upon receiving the final re-
port in time t ≤ t
exp
, V runs the aggre-
gated attestation verification function VrfAg-
gAtt(sk
1
,..., sk
n
,τ
1
,..., τ
n
,{S
1
,..., S
n
}) on the list
of expected healthy states {S
1
,..., S
n
} it possesses.
The time t
exp
is defined through prior real-world
experiments, in order to estimate an upper-bound
of the overall attestation time. Such experiments
must include network delays, transmission times,
and individual attestation generation and aggrega-
tion times.
VrfAggAtt : ({sk
i
}
n
i=1
,{τ
i
}
n
i=1
,{S
i
}
n
i=1
).
1: b ← AggVerifyMAC
BLS
({sk
i
}
n
i=1
,τ,{S
i
}
n
i=1
)
2: If b = 1 and C
s
=
/
0, return 1
3: Otherwise return 0
If the function returns 1, V concludes that the net-
work is in a trustworthy state. Otherwise, he con-
cludes that at least one device is compromised and
proceeds to the detection phase.
5.4 Detection Phase
An attacker A who performed a mismatch attack, by
aggregating an erroneous attestation report, will be
identified in the detection phase. Let D
c
be the target
device in such attacks. Upon the function VrfAggAtt
returning 0, V proceeds as follows:
1. V requests the signatures of knowledge {π
i
}
n
i=1
for every node in the network.
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
91

2. V verifies the corresponding tags τ
i
n
i=1
.
3. V proceeds iteratively down the attestation tree
until it reaches the node D
i
which did not aggre-
gate the valid tag/SoK pair.
The signature of knowledge ensures that each node
remains accountable for the value it has previously
aggregated during the attestation phase. Consider-
ing the assumption that no adversary can easily per-
form physical attacks, and generate a valid MAC
BLS
tag without a valid secret key sk
i
, this ensures that V
is able to identify each node that aggregates an erro-
neous report.
6 PERFORMANCE EVALUATION
We implemented CoRA on a Teensy 3.2 micro-
controller. The Teensy 3.2 board is an Arduino-
compatible microcontroller, featuring a 32 bit ARM
processor with a 72 MHz Cortex-M4 core. It also fea-
tures 256 kB Flash and 64 kB RAM memory. The
board provides the minimal hardware requirements
for remote attestation as stated in Section 3.2. Cryp-
tographic algorithms are implemented based on the
micro-ecc(MacKay, 2017) library. As presented in
Table 2, we use a SHA-256 hash function.
Table 2: Performance of cryptographic algorithms on
Teensy 3.2.
Algorithm Run-time (ms)
SHA-256 0.244
SHA-256
HMAC
0.809
Table 3: Performance of MAC
BLS
functions.
Mac
Run-
time
(s)
Number
of de-
vices
AggMac
Run-
time
(s)
0.047
100 5.55
500 27.8
1000 56.1
1500 84.3
Table 3 shows the runtime performance of
MAC
BLS
. The choice of algebraic MACs (in elliptic
curve groups) provides a more efficient verification
step, considering that computing AggVer is the same
as computing AggMac. The implementation makes
use of secp160r1 curves (Research, 2000).
7 SECURITY ANALYSIS
In this section, we provide a proof of security of
CoRA, as stated by Theorem 3. As specified in
Section 3.1, a swarm attestation scheme is secure
against forgery if no adversary is able to produce a
forgery for an uncompromised device (for which he
doesn’t know the secret key), even after accessing at
most n − 1 attestation results. We derive the security
of our swarm attestation protocol by drawing the
parallel between the security definition for swarm
attestation forgery (Francillon et al., 2014), and the
security of the aggregate MAC
BLS
scheme.
In formal swarm attestation definition, the verifier V
returns 1 if AggVerify(params,{sk
i
}
n
i=1
,{m
i
}
n
i=1
,τ) =
1, i.e. if τ is a valid aggregate tag on the set of
expected valid states {S
i
}
n
i=1
, and the incorporated
nonce N
k
is the session nonce provided by V . Let
A be an attacker on the network whose goal is to
produce a valid forgery of the attestation response. A
has compromised prover D
c
. We consider two types
of adversaries:
Type 1: A
1
does not alter the attestation of D
c
to be included in the aggregate response.
Type 2: A
2
modifies the internal state of D
c
, and
generates an attestation τ
c
on (ID
c
,S
c
||N
k
||cnt
k
).
In the first case, according to our assumptions,
A
1
cannot physically compromise D
c
and retrieve its
secret key x
c
. A
1
’s only strategy is to use an attes-
tation response of a previously generated attestation
τ
c
prev
, on the same software configuration S
c
and
an old nonce N
prev
. Let N
curr
be the random nonce
generated by V in the current round of attestation.
The probability that N
prev
= N
curr
is equal to 2
−l
N
,
which is negligible for a sufficiently large nonce. A
1
will therefore output a valid attestation response only
with negligible probability.
In the second case, we observe the following
analogy: the security definition of resistance against
forgery for a remote attestation protocol, is exactly
the security definition of unforgeability of the
aggregate MAC
BLS
scheme, namely forgery for an
adversary who had access to up to n − 1 tags. A
2
’s
advantage in successfully producing a forgery is
therefore the same as A
2
’s advantage in producing a
valid aggregate MAC
BLS
forgery, which is negligible
under the CDH assumption in the random oracle
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
92

model (see proof in Appendix A.1). Indeed, in
order for A
2
to generate a valid attestation on a
modified state without physically compromising D
c
,
he needs to forge an aggregate MAC
BLS
scheme on
all aggregated tags, assuming that at least one device
in the network is honest. According to Theorem 2,
aggregate MAC
BLS
is unforgeable provided that
MAC
BLS
is unforgeable (see proof in Appendix A.2).
The probability of A
2
generating said valid attestation
is therefore negligible.
8 CONCLUSION
In this work we introduced CoRA, the first collective
attestation protocol with verifier detection for sensor
networks. Collective (or swarm) attestation is a se-
curity mechanism which efficiently verifies the in-
tegrity of large numbers of devices in wireless multi-
hop networks. CoRA leverages the aggregating prop-
erty of its underlying in-network aggregation mecha-
nism, namely aggregate MAC
BLS
, to provide a highly
scalable swarm attestation protocol with efficient ver-
ification. In order to detect the malicious injection of
erroneous attestation, CoRA comprises a scalable de-
tection algorithm, which leverages the algebraic prop-
erty of algebraic MACs to generate proofs of knowl-
edge, on a device’s secret key. The detection method
allows the identification of a compromised node in the
network, thus preventing DoS attacks on the verifier.
We provide a rigorous proof for the underlying cryp-
tographic construction, as well as the CoRA protocol.
Finally, we prove the efficiency of our scheme, based
on a prototype implementation on a standard micro-
controller.
REFERENCES
Ambrosin, M., Conti, M., Ibrahim, A., Neven, G., Sadeghi,
A., and Schunter, M. (2016). SANA: secure and scal-
able aggregate network attestation. In Proceedings of
the 2016 ACM SIGSAC Conference on Computer and
Communications Security, Vienna, Austria, October
24-28, 2016, pages 731–742.
Asokan, N., Brasser, F. F., Ibrahim, A., Sadeghi, A.,
Schunter, M., Tsudik, G., and Wachsmann, C. (2015).
SEDA: scalable embedded device attestation. In Pro-
ceedings of the 22nd ACM SIGSAC Conference on
Computer and Communications Security, Denver, CO,
USA, October 12-16, 2015, pages 964–975.
Boldyreva, A., Gentry, C., O’Neill, A., and Yum, D. H.
(2007). Ordered multisignatures and identity-based
sequential aggregate signatures, with applications to
secure routing. In Proceedings of the 2007 ACM Con-
ference on Computer and Communications Security,
CCS 2007, Alexandria, Virginia, USA, October 28-31,
2007, pages 276–285.
Boneh, D., Gentry, C., Lynn, B., and Shacham, H. (2003).
Aggregate and verifiably encrypted signatures from
bilinear maps. In Advances in Cryptology - EURO-
CRYPT 2003, International Conference on the Theory
and Applications of Cryptographic Techniques, War-
saw, Poland, May 4-8, 2003, Proceedings, pages 416–
432.
Boneh, D., Lynn, B., and Shacham, H. (2001). Short signa-
tures from the weil pairing. In Advances in Cryptol-
ogy - ASIACRYPT 2001, 7th International Conference
on the Theory and Application of Cryptology and In-
formation Security, Gold Coast, Australia, December
9-13, 2001, Proceedings, pages 514–532.
Camenisch, J. and Stadler, M. (1997). Proof systems for
general statements about discrete logarithms. Techni-
cal report.
Carpent, X., Defrawy, K. E., Rattanavipanon, N., and
Tsudik, G. (2017). Lightweight swarm attestation:
A tale of two lisa-s. In Proceedings of the 2017
ACM on Asia Conference on Computer and Commu-
nications Security, AsiaCCS 2017, Abu Dhabi, United
Arab Emirates, April 2-6, 2017, pages 86–100.
Chan, H., Perrig, A., and Song, D. X. (2006). Secure
hierarchical in-network aggregation in sensor net-
works. In Proceedings of the 13th ACM Conference on
Computer and Communications Security, CCS 2006,
Alexandria, VA, USA, Ioctober 30 - November 3,
2006, pages 278–287.
Dodis, Y., Kiltz, E., Pietrzak, K., and Wichs, D. (2012).
Message authentication, revisited. In Advances in
Cryptology - EUROCRYPT 2012 - 31st Annual Inter-
national Conference on the Theory and Applications
of Cryptographic Techniques, Cambridge, UK, April
15-19, 2012. Proceedings.
Eikemeier, O., Fischlin, M., G
¨
otzmann, J., Lehmann, A.,
Schr
¨
oder, D., Schr
¨
oder, P., and Wagner, D. (2010).
History-free aggregate message authentication codes.
In Security and Cryptography for Networks, 7th In-
ternational Conference, SCN 2010, Amalfi, Italy,
September 13-15, 2010. Proceedings, pages 309–328.
Falliere, N., Murchu, L. O., and Chien, E. (2010).
W32.stuxnet dossier. Symantec.
Francillon, A., Nguyen, Q., Rasmussen, K. B., and Tsudik,
G. (2012). Systematic treatment of remote attestation.
IACR Cryptology ePrint Archive.
Francillon, A., Nguyen, Q., Rasmussen, K. B., and Tsudik,
G. (2014). A minimalist approach to remote attesta-
tion. In 2014 Design, Automation & Test in Europe
Conference & Exhibition (DATE), pages 1–6. IEEE.
Ibrahim, A., Sadeghi, A., Tsudik, G., and Zeitouni, S.
(2016). DARPA: device attestation resilient to phys-
ical attacks. In Proceedings of the 9th ACM Confer-
ence on Security & Privacy in Wireless and Mobile
Networks, WISEC 2016, Darmstadt, Germany, July
18-22, 2016, pages 171–182.
Ibrahim, A., Sadeghi, A., and Zeitouni, S. (2017). Seed:
secure non-interactive attestation for embedded de-
vices. In Proceedings of the 10th ACM Conference
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
93

on Security and Privacy in Wireless and Mobile Net-
works, WiSec 2017, Boston, MA, USA, July 18-20,
2017, pages 64–74.
Katz, J. and Lindell, A. Y. (2008). Aggregate message au-
thentication codes. In Topics in Cryptology - CT-RSA
2008, The Cryptographers’ Track at the RSA Confer-
ence 2008, San Francisco, CA, USA, April 8-11, 2008.
Proceedings, pages 155–169.
Kohnh
¨
auser, F., B
¨
uscher, N., Gabmeyer, S., and Katzen-
beisser, S. (2017). SCAPI: a scalable attestation pro-
tocol to detect software and physical attacks. In Pro-
ceedings of the 10th ACM Conference on Security
and Privacy in Wireless and Mobile Networks, WiSec
2017, Boston, MA, USA, July 18-20, 2017, pages 75–
86.
Kohnh
¨
auser, F., B
¨
uscher, N., and Katzenbeisser, S. (2018).
SALAD: secure and lightweight attestation of highly
dynamic and disruptive networks. In Proceedings of
the 2018 on Asia Conference on Computer and Com-
munications Security, AsiaCCS 2018, Incheon, Re-
public of Korea, June 04-08, 2018, pages 329–342.
Lu, S., Ostrovsky, R., Sahai, A., Shacham, H., and Waters,
B. (2006). Sequential aggregate signatures and mul-
tisignatures without random oracles. In Advances in
Cryptology - EUROCRYPT 2006, 25th Annual Inter-
national Conference on the Theory and Applications
of Cryptographic Techniques, St. Petersburg, Russia,
May 28 - June 1, 2006, Proceedings, pages 465–485.
MacKay, K. (2017). micro-ecc library.
Mansfield-Devine, S. (2016). Ddos goes mainstream: how
headline-grabbing attacks could make this threat an
organisation’s biggest nightmare. Network Security.
Research, C. (2000). Sec 2: Recommended elliptic curve
domain parameters.
Schnorr, C. (1991). Efficient signature generation by smart
cards. J. Cryptology, 4(3):161–174.
A Security Analysis of MAC
BLS
and
Aggregate MAC
BLS
A.1 MAC
BLS
Security
In this section, we prove Theorem 1, which states that
MAC
BLS
is UF-CMVA in the random oracle model.
Let q
H
be the maximum number of queries an algo-
rithm A can make to O
Hash
, q
M
the maximum num-
ber of queries to O
MAC
, and q
V
the maximum num-
ber of queries to O
Verify
. Assume an algorithm A
(t,q
H
,q
M
,q
V
,ε)−breaks the UF-CMVA security of
MAC
BLS
. We use A to construct an algorithm B
that (t
0
,ε)−breaks computational Diffie-Hellman on
the group G. Using a sequence of security experi-
ments, we use the forger A to build the algorithm B
that breaks CDH on G.
Setup. B is given the challenge (g,g
a
,g
b
). G be-
ing a GDH group, B also has access to a DDH ora-
cle O
DDH
that outputs 1 if an argument of the form
(g,g
a
,h,h
b
) is a valid Diffie-Hellman tuple. B main-
tains a list (h
i
,τ
i
) for all hash and MAC queries. A
can request a hash on any message of its choice, to
which B responds with the corresponding h
i
. Simi-
larly, A can request a tag on any message of its choice,
and receives the corresponding τ
i
where i ∈ {1,...,l}
and l ≤ q
M
is the number of requests to O
MAC
. B sets
the operator’s parameters X = g
a
, thus implicitely set-
ting sk = a.
For 1 ≤ i ≤ q
H
, A picks a random i
∗
$
←− {1, ...,q
H
}.
A then selects a random r
i
$
←− Z
∗
q
for 1 ≤ i ≤ q
H
, sets
h
i
← (g
b
)g
r
i
∗
for i = i
∗
, and h
i
← g
r
i
otherwise. If
i 6= i
∗
, it sets τ
i
← (g
a
)
r
i
. If i = i
∗
, it sets τ
i
∗
= ? which
is a placeholder value.
Queries. When A requests a hash on m
i
, B outputs
h
i
. When A requests a tag on m
i
, if i 6= i
∗
B outputs τ
i
.
Otherwise if i = i
∗
, B declares failure and aborts. A
may also make verification queries on input (m
i
,τ
i
).
B then uses its DDH oracle O
DDH
, and outputs the
result obtained from O
DDH
on the tuple (g,g
a
,h
i
,τ
i
).
Response. At some point, A outputs a forgery
(m
∗
,τ
∗
) such that m was never queried to O
MAC
, and
Verify(sk,m, τ) = 1.
• The probability that B aborts is equal to 1/q
M
,
which is inverse polynomial. We can reduce this
value by repeating the experiment a polynomial
number of times.
• The r
i
’s are selected at random, therefore h
i
’s are
uniformly distributed in G, making O
Hash
a ran-
dom oracle. Moreover, if i 6= i
∗
, the tags τ
i
are-
all valid.If B does not abort, the simulation for A
is indistinguishable from a real execution of the
MAC algorithms.
• If A successfully outputs a forgery (m
∗
,τ
∗
) and
B does not abort, h
∗
= h
i
∗
= (g
b
)g
r
i
∗
. Therefore
h
a
i
∗
= (g
ab
g
r
i
∗
). B retrieves g
ab
=
τ
∗
(g
a
)
r
i
∗
. B out-
puts the valid answer to the CDH challenge.
• Adv
UF-CMVA
A
(1
λ
) = ε/q
M
. If we repeat the experi-
ment k times, the probability that algorithm B out-
puts a valid answer to the CDH challenge is equal
to (
ε
q
M
)
k
which is non-negligible.
A.2 Aggregate MAC
BLS
Security
In this section, we give the prove by reduction of The-
orem 2 in the random oracle model. We consider the
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
94

setting where the reduction maintains a list KeyList of
all public keys attached to each secret key sk
i
.
Let A be an adversary against the EUF-CMVA prop-
erty of aggregate MAC
BLS
. Using A as a subroutine,
we construct a reduction B against the UF-CMVA
property of the MAC
BLS
scheme run by a challenger
C . B receives the system public parameters params =
(G,q, g), and the public key pk
∗
for an unknown iden-
tity X
i
∗
= g
x
i
∗
where i
∗
∈ {1,...,l} and l = poly(λ).
B has access to two oracles: an oracle O
MAC
BLS
,sk
∗
(that we will refer to as O
Mac
to simplify notations)
for the unknown key x
∗
= x
i
∗
, and the oracle O
Verify
that checks the validity of any message/tag pair. C
initializes an empty list M that will store the subse-
quent messages from O
Mac
queries.
1. B chooses i
∗
$
←− {1,...,t};
2. For i = 1 to t:
• If i 6= i
∗
, select r
i
$
←− Z
∗
q
, and set h
i
← g
r
i
.
Choose x
i
$
←− Z
q
. Set X
i
= g
x
i
and add
(i, pk
i
= X
i
,sk
i
= x
i
) to KeyList. iparams =
{pk
1
,..., pk
t
}.
• If i = i
∗
, do nothing but implicitely set sk
i
∗
=
(sk
∗
).
3. B runs A(params,iparams) answering the
queries as follows:
• Hash
∗
(m
i
):B uses its MAC
BLS
hash oracle
O
Hash
to output the corresponding hash h
i
.
• AggMac
∗
({m
1
,..., m
q
}): B computes the ag-
gregate tag τ
i
using the known secret key sk
∗
. If
there is i ∈ {1,..., q} such that i = i
∗
, B queries
its own oracle O
Mac
on m
i
. Finally, B returns
the τ
i
.
4. At some point, A outputs M = {m
1
,..., m
n
)} and
an aggregate tag τ. Let j be the first index such
that A has never queried m
j
to Mac
∗
, and pk
j
6=
pk
∗
. If j 6= i
∗
then B abort; Otherwise, proceed as
follows:
(a) We therefore consider the case where j = i
∗
.
B computes the tag τ
∗
from τ =
∏
t
i=1
h
x
i
i
the
following way: τ
∗
=
τ
∏
t
l=1,l6=i
∗
h
x
l
l
.
(b) B has the secret keys corresponding to all iden-
tifiers that are not i
∗
, he is therefore able to
compute a valid τ
∗
. When j = i
∗
, B simply
queries Mac
∗
m to get the corresponding tag. Fi-
nally, B outputs (m
j
,τ
∗
) as a valid forgery of a
MAC
BLS
tag.
The proof of correctness follows from the follow-
ing observations:
• The probability that B aborts is equal to 1/t,
which is inverse polynomial. If B does not abort,
the simulation for A is indistinguishable from a
real execution of the aggregate MAC algorithms.
• If A successfully outputs a forgery for the aggre-
gate MAC scheme, and B does not abort, the as-
sumption stipulates that A has never queried B
on m
j
. Therefore B has never queried Mac
∗
(m
j
).
The success of algorithm A means that τ =
∏
t
i=1
τ
i
containing τ
∗
. The tag B outputs is therefore a
valid forgery of a MAC
BLS
tag.
CoRA: A Scalable Collective Remote Attestation Protocol for Sensor Networks
95
