GETS: Grammatical Evolution based Optimization of Smoothing
Parameters in Univariate Time Series Forecasting
Conor Ryan
1a
, Meghana Kshirsagar
1b
, Purva Chaudhari
2c
and Rushikesh Jachak
2d
1
Biocomputing Developmental Systems, University of Limerick, Ireland
2
Department of Computer Science, Government College of Engineering, Aurangabad, India
Keywords: Time Series Forecasting, Grammatical Evolution, Genetic Programming.
Abstract: Time series forecasting is a technique that predicts future values using time as one of the dimensions. The
learning process is strongly controlled by fine-tuning of various hyperparameters which is often resource
extensive and requires domain knowledge. This research work focuses on automatically evolving suitable
hyperparameters of time series for level, trend and seasonality components using Grammatical Evolution.
The proposed Grammatical Evolution Time Series framework can accept datasets from various domains and
select the appropriate parameter values based on the nature of dataset. The forecasted results are compared
with a traditional grid search algorithm on the basis of error metric, efficiency and scalability.
a
https://orcid.org/0000-0002-7002-5815
b
https://orcid.org/0000-0002-8182-2465
c
https://orcid.org/0000-0002-4613-937X
d
https://orcid.org/0000-0001-6036-0030
1 INTRODUCTION
1.1 Time Series
Time Series is a series of data points recorded at
equal intervals of time. In the context of healthcare
(Penfold, 2013), waste management (Nagori, 2019),
econometrics (Lütkepohl, 2004) etc. (Shumway,
2017), the primary aim of data analysis is time series
forecasting. Time Series forecasting is used to
forecast future information by constructing a model
that fits well on previous observations (Brockwell,
2016).
Time series data is typically decomposed into
four components level (L), trend (T), seasonality (S)
and residue (R). Level is the average value of
observations defined over a period. Trend is defined
as change in behaviour over time in observations
which is generally a constant movement in data. A
series of patterns which is repeated many times over
a short-term is known as seasonality, while
undesirable noise present in data is the residue.
These components are merged together as shown in
equation 1 in order to obtain actual time series
forecast at time t.
A(t) = L(t) + T(t) + S(t) + R(t)
(1)
However, time series models are often
challenging and resource extensive to comprehend
and execute on real world datasets, often requiring
much hyper parameter tuning for even implementing
the naivest forecasting model (Gardner, 1985).
1.2 Related Work
In traditional approaches to time series modelling,
the lag needs to be explicitly defined and tuned to
minimise the forecast error. In any parameter
estimation problem the challenge of tuning
parameters to optimal values usually require large
number of experimental trials and even if
convergence is guaranteed, it still becomes difficult
to choose among the solutions generated (Schmidt,
2006).
Grid Search (GS) is a traditional technique in
machine learning which is used to calculate the
appropriate parameters to use for any given model.
Its approach is to build the model by making all
possible combinations of the parameters. And hence,
it suffers from two fold drawback of being
Ryan, C., Kshirsagar, M., Chaudhari, P. and Jachak, R.
GETS: Grammatical Evolution based Optimization of Smoothing Parameters in Univariate Time Series Forecasting.
DOI: 10.5220/0008963305950602
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 595-602
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
595

computationally expensive as well as taking large
amount of time before getting the optimal
configurations.
(De Silva, 2013) produced an evolutionary
algorithm for predicting the load of electricity by
defining the grammar which generates better
features to incorporate in forecasting. (Cortez, 2001)
also provided an evolutionary technique for time
series forecasting, but was required to explicitly
define the time lag window. Inspired by racing
algorithms (Birattari, 2010) designed F-Race
algorithm, which evolves parameters among a given
set of candidate instances through statistical
evidence. But the approach becomes
computationally expensive as soon as the initial
configurations increases which is generally the case
in time series, as forecast results vary by a
minuscule change in parameters.
1.3 Structure of Paper
Section two of this paper provides an introduction to
how programs are evolved using Grammatical
Evolution. Section three presents the Grammatical
Evolution Time Series (GETS) framework with
subsections 3.1 and 3.2 defining grammar for
Average Smoothing and Exponential Smoothing
Forecasting where as fitness function is described in
subsection 3.3. Section four analyses the achieved
results and provides a comparison between GS and
GETS models followed by an extensive discussion
on Hourly Number of Riders, Hourly Mean
Temperature, Daily Waste Generation and Monthly
Car Sales datasets. Section five validates and
justifies the reasoning behind selection of models
and parameters through statistical test. Lastly,
conclusions and future work are outlined in section
six.
2 GRAMMATICAL EVOLUTION
Grammatical Evolution (GE) is a biologically
inspired state-of-the-art algorithm that uses
evolutionary computing techniques to automatically
generate computer programs (Ryan, 1998). GE
generates programs using a desired fitness function,
which either needs to minimised or maximised,
depending on the application (O'Neill, 2001).
Programs are represented using a genome, a variable
length string of codons (eight bits) and a grammar is
used to perform genotype to phenotype mapping
from the genome. GE uses Backus Normal Form
(BNF) (McCracken, 2003) which can be described
using a tuple {N, T, P, S}, with P being a set of
production rules which are used to map terminals
(T), that is, items which can appear in the final
program, from non-terminals (N), intermediate
symbols to facilitate the derivation, from the starting
symbol (S). The framework for the production rules
can be given as:
<expression> ::= <definition> (2)
Where expression is a non-terminal mapped to
definition consisting of both terminal and
nonterminal. For example, consider the following
production rule for generating numbers 0 to 9:
<var> ::= 0 | 1 | 2| 3 | 4 …| 9
(3)
GE uses its eight bit codons (positive integers) to
select from available definitions by taking modulus
with number of definitions possible. For example, if
we are expanding <var>, we need to take modulo of
codon value with 10, since the number of possible
rule definitions is 10. Whenever a choice is to be
made during an expansion of rules, a different codon
is to be used from chromosome. This process is
repeated until the expression has been derived and
no non-terminals remain. Each individual is
evaluated on its ability to produce correct output,
known as the fitness of an individual and fitness of
the function is defined as fitness obtained from the
generated optimal solution (Diosan, 2006).
3 GETS
Although generally used for evolving programs, GE
can also be used to evolve parameters for a program.
This is extremely beneficial especially in time series
forecasting where selection of parameters can vary
by as little as 0.00001. With a range of parameters to
be tuned such as smoothing coefficient for level,
trend and seasonality, period of seasonality and step
to make forecast ahead of times, selection of these
parameters without strong conceptual and domain
knowledge, is often a difficult job. Fortunately, GE
provides a powerful yet easy to implement model to
generate optimal parameters for various time series
forecasting models which results in more precise
prediction.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
596

Figure 1: Methodology Diagram for GETS framework (MA: Moving Average, SES, HES, HWES: {Simple, Holts’, Holts'
Winter} Exponential Smoothing). The population size of 500 is randomly initialized and is evolved till 100 generations for
each model of forecasting.
The GETS framework as illustrated in Figure 1
is designed to address these challenges by
employing concepts of evolutionary computation
and evolving optimal values for the hyper
parameters through grammatical evolution. The
framework helps in choosing the best values for
these hyper parameters to minimize the mean
squared error. The efficiency of the framework is
compared with state-of-the-art algorithms in terms
of error metric, efficiency and scalability. Promising
results are shown for parameter estimation and lower
error values for the metric root mean squared error.
3.1 Average Smoothing Method
Moving Average (MA) takes the mean of several
historical observations to predict future values
(Hansun, 2013). The forecaster uses data from the
current period to previous N observation depending
on the window width. The varying pattern in the
time series data affects the width of the window and
the amount of smoothing required to make
predictions.
forecast
t+k
= (W
t-1
+ W
t-2
+…W
t-n
) /N (4)
When computing future time series values using
MA, the model has to assume that there is no
seasonality, trend and forecast will be identical to
previous data. The width of the window in Moving
Average is parameter that needs to be tuned
manually to minimise the forecast error and
therefore, selecting appropriate window width is
essential in moving average model.
The grammar for Moving Average is shown in
Figure 2 where <window_var> generates the width
of window and <lag_var> generates the lag in time
series which is implemented using the shift function
provided in Python’s Pandas library to forecast by
substituting parameters in equation 4. The
GE_RANGE: N is replaced by N production rules
consisting of integer constants starting from 0.
GETS: Grammatical Evolution based Optimization of Smoothing Parameters in Univariate Time Series Forecasting
597

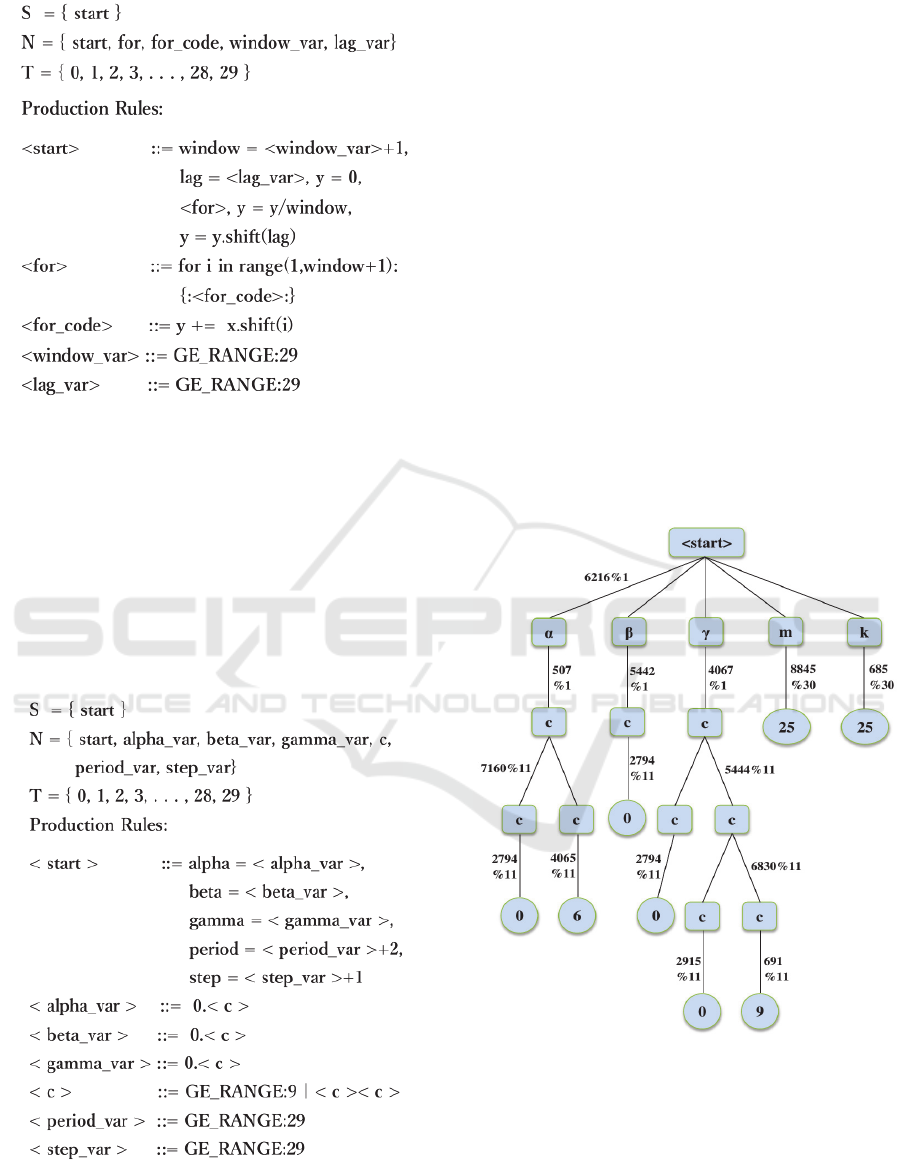
Figure 2: MA Grammar.
3.2 Exponential Smoothing Methods
Exponential Smoothing Methods produces forecast
using weighted averages of past observations, where
the importance of each observation reduces
exponentially as the observation gets older. There
are three types of Exponential Smoothing Methods
Simple Exponential Smoothing (SES), Holts’
Exponential Smoothing (HES) and Holts’ Winter
Exponential Smoothing (HWES).
Figure 3: SES, HES and HWES Grammar: {Simple,
Holts’ , Holts' Winter} Exponential Smoothing.
The grammar for the same is shown in Figure 3
where <alpha_var>, <beta_var> and
<gamma_var> generates the value of alpha, beta
and gamma ranging between 0 to 1 which are
smoothing coefficients of level, trend and
seasonality respectively. <step> generates a value
which is essential in making multi step ahead
forecast while <period_var> is used to generate
period of seasonality which can be 24 for hourly, 30
for daily and 12 for monthly forecast.
The expression tree generated from the random
genome sequence [6216, 507, 7160, 2794, 4065,
5442, 2794, 4067, 5444, 2794, 6830, 2915, 691,
8845, 685] for HWES on Daily Waste Generation
dataset is given in Figure 4. The internal nodes
represent the non-terminal symbol generated during
evolution of program while leaf nodes represent the
terminal symbols of the grammar. The edges depict
the procedure of mapping genome to production
rules (phenotype) using modulo function of
randomly generated codon value with number of
predicted rules.
Figure 4: Example tree generated through random
genome sequence for HWES where {α:alpha, β:beta,
γ:gamma, m:period of seasonality, k:step}.
3.2.1 Simple Exponential Smoothing
Simple Exponential Smoothing (SES) applies a
weighted average to historical observations to forecast
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
598

values in future while assuming there is no trend and
seasonality in time series (Hunter, 1986).
level
t
= level
t-1
+ (alpha) * (observed
t-1
- level
t-
1
) forecast
t + k
= level
t
(5)
SES is more adaptable compared to MA since
assigned weights in SES are decreasing in exponential
manner giving higher importance to recent
observations. The smoothing of level in a series is
controlled by parameter alpha, which needs to be
tuned to minimise the forecast error. The value of
alpha and lag are substituted in equation 5 to forecast
using SES. In SES, value of beta and gamma is
substituted as zero, since it assumes there is no trend
and seasonality.
3.2.2 Holts’ Exponential Smoothing
Holts’ Exponential Smoothing (HES) extends the
concept of SES to capture trend along with level in
the time series data to predict future values assuming
there is no seasonality component in series (Holt,
2004).
The level is the forecast of the value in the series,
which is controlled by the parameter alpha. While the
trend is expected growth in the series, is controlled by
another parameter beta, the smoothing constant for
trend. The trend can be additive or multiplicative and
hence the naive approach of time series forecasting
requires not only determining appropriate values of
alpha and beta but at the same time requires to know
underlying variation in patterns to know the trend
(Kalekar, 2004).
level
t
= level
t-1
+ trend
t-1
+ (alpha) * (observed
t-1
-
level
t-1
- trend
t-1
)
trend
t
= trend
t-1
+ beta *(level
t
- level
t-1
- trend
t-1
)
forecast
t + k
= level
t
+ trend
t
(6)
The generated optimal parameters for alpha, beta
and step are then substituted in equation 6 for
forecasting using HES. In HES, value of gamma is
substituted as zero, since it assumes there is no
seasonality.
3.2.3 Holts’ Winter Exponential Smoothing
Holts’ Winter Exponential Smoothing (HWES) is a
more robust equation allowing the model to capture
level and trend along with seasonality component.
Hence, the forecasting equation is a combination of
estimates determined using level, trend and seasonal
components.
As discussed in HES alpha and beta controls the
smoothing of level and trend respectively while
gamma is the smoothing factor for seasonality over a
period of time. This requires evolving five
parameters, mainly ‘alpha’, ‘beta’, ‘gamma’, ‘period
of seasonality’ and ‘step’ which are substituted in
equation 7 to make forecast using HWES.
level
t
= level
t-1
+ trend
t-1
+ (alpha) * (observed
t-1
-
level
t-1
- trend
t-1
- season
t-m
)
trend
t
= trend
t-1
+ beta *(level
t
- level
t-1
- trend
t-1
)
season
t
= season
t-m
+ gamma*(observed
t-1
-
level
t-1
- season
t-m
)
forecast
t + k
= level
t
+ trend
t
+ season
t + k - m
(7)
3.3 Fitness Function
Each time series forecasting models, is evolved using
root mean squared error (RMSE), described in
equation 8 as fitness function. This is commonly used
when forecasting numeric values and, as it is a
quadratic metric which also assess the mean extent of
errors.

1








(8)
As it is a negatively aligned metric, the
framework is built to minimise the fitness function.
Lower the RMSE, better the value of objective
function.
4 RESULTS
4.1 Analysis of Forecasting Methods
The essential parameters which were experimented
with are defined in Figure 1. The convergence value
i.e. RMSE of each model is shown in ‘GE Train Best
Fitness’ column of Table 1. We can see that RMSE
values of GE Best Fitness and GE Average Fitness
are competitive, indicating the performance of
framework is consistent and not an exceptional case.
The GETS has better performance on generalising the
forecasting models compared to GS which is
overfitting to training data in most of the cases.
From average fitness values given in Table 1, it
can be observed that the fitness values of SES, HES
and HWES on Hourly Mean Temperature are almost
GETS: Grammatical Evolution based Optimization of Smoothing Parameters in Univariate Time Series Forecasting
599

identical indicating there is no trend and seasonality.
The dataset of Hourly Number of Riders contains
level and seasonality, as average fitness of HWES is
low compared to both SES and HES. But it does not
contain trend, as SES and HES have similar fitness
values. The dataset of Daily Waste Generation does
not contain trend as well as seasonality which are
justified by nearly equal fitness values of SES, HES
and HWES. On the other hand, the Monthly Car Sales
dataset contains both the components trend and
seasonality and therefore the fitness values of SES,
HES, HWES are in the decreasing order.
The GE based time series modelling has
outperformed traditional GS algorithm in terms of
accuracy on both training as well as testing. A
comparison of the time required in seconds to make
forecasts using both GETS and GS is also shown in
Table 1. When dealing with small data sets the time
required by each is similar, but GETS is significantly
faster on the larger and more complex ones. When the
number of parameters to determine increases, for
example, with HES and HWES, GETS outperforms
GS by a large margin.
GE HWES forecast as shown in Figure 5 has
taken all the three components into consideration. The
period of seasonality obtained through GE HWES is
24, which is analogous to the number of hours in a
day, so it is not surprising that it has the smallest
forecast error at around 27 as shown in GE Train Best
Fitness in Table 1. The smoothing coefficients
obtained are 0.6, 0.01 and 0.01 for alpha, beta and
gamma respectively to make one step ahead forecast.
Figure 5: GE HWES test forecast on Hourly Number of
Riders dataset.
Table 1: Comparison of GETS and GS approach on various datasets using RMSE as a fitness function.
Dataset
(Instances / Unit)
Method
GE Train
Average Fitness
GE Train Best
Fitness
GE Test
Fitness
GS Train
Fitness
GS Test
Fitness
GETS
Time
GS
Time
Hourly Mean
Temperature
(29,734 / Degree
Celsius)
SES 0.174 0.17 4.92 0.15 4.9 161 1370
HES 0.072 0.072 0.052 0.06 47.90 463 8174
HWES 0.071 0.068 0.050 0.10 20.09 675 14512
MA 0.1572 0.15 5.68 2.61 4.1 103 146
Hourly Number of
Riders
(20,290 / Number
of Persons)
SES 54.71 31.31 186.39 31.27 186.37 137 27
HES 165.27 31.31 81.77 31.27 183.91 387 1011
HWES 58.67 26.72 62.26 21.56 152.65 540 9664
MA 56.12 31.37 189.87 67.25 235.85 109 113
Daily Waste
Generation
(1,186 / Kilograms)
SES 4798 4364 2633 4369.31 2633.47 19 10
HES 4620 4368 2633 4369.31 2633.47 41 68
HWES 4676 4314 2656 4665 3258 44 1300
MA 4503 4402 2581 4505.32 2568.89 59 10
Monthly Car Sales
(136 / Number of
Cars)
SES 4534.19 3290 3677 3239.65 3790.72 8 10
HES 4397 3289.8372 3856 3243.81 4461.61 13 54
HWES 1987 1451 2816 1425 2633 14 529
MA 3988.2549 3140.52 3815 3272.28 5681.35 35 10
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
600

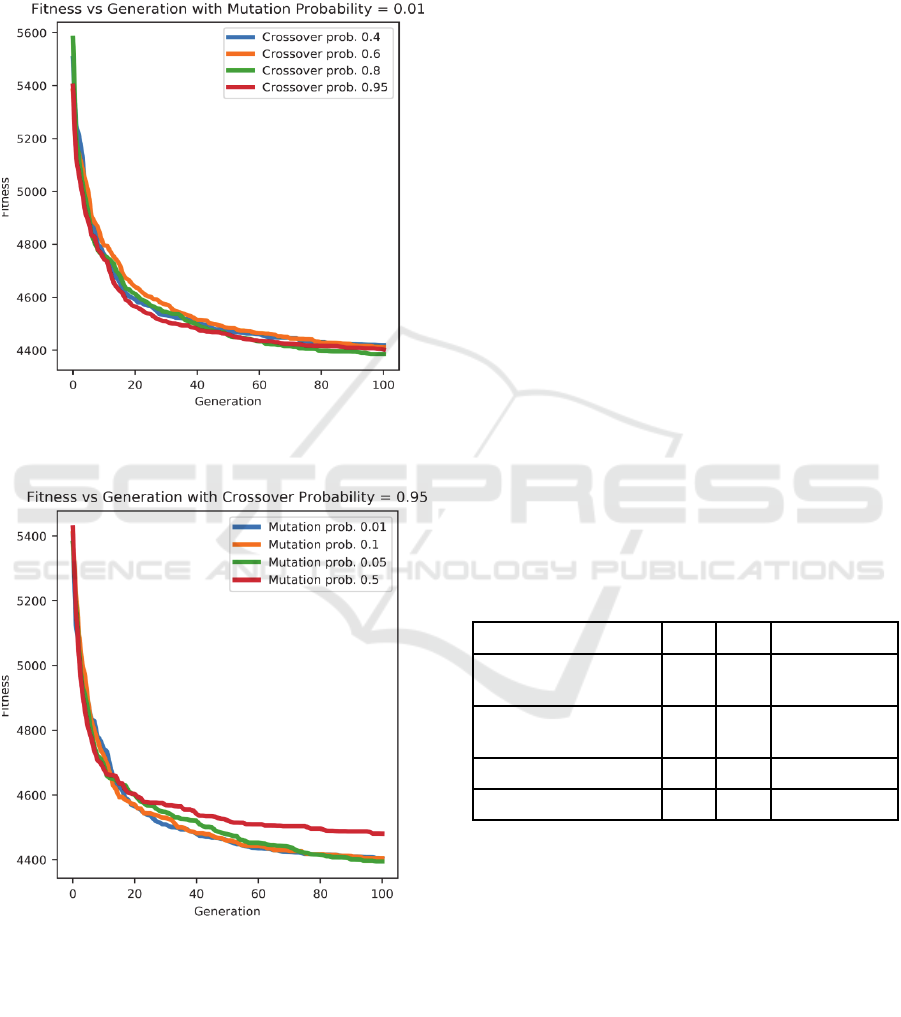
4.2 Exploration vs Exploitation
The effect of changes in Mutation (Exploration) and
Crossover (Exploitation) probabilities on evolution
is shown in Figure 6-7.
Figure 6: Fitness of Daily Waste Generation Dataset on
varying crossover probability.
Figure 7: Fitness of Daily Waste Generation Dataset on
varying mutation probability.
The mutation used is one int flap codon (O'neill,
2003) which works by replacing the integer value of
codon with new random integer with a probability of
0.01, 0.05, 0.1 and 0.5 were taken for
experimentation. Single point crossover with a
varying probability of 0.40, 0.60, 0.80 and 0.95 in
which, the production of two offspring takes place
by randomly selecting the crossover point and
swapping the tail of two parents. It can be seen that
with an increase in crossover probability, the
population evolves faster for all values of mutation
probability except for 0.5. The most promising
results were obtained at mutation probability equal
to 0.05 and cross over probability equal to 0.95, with
the population converging to more than 95% in less
than 40 generations. Most of the configurations
evolved to similar fitness after 100 generations,
except the individuals with mutation and crossover
probabilities as (0.50, 0.95) respectively which has
produced relatively high error.
5 DISCUSSION
Table 2 presents a summary of the statistical test
performed on configurations with and without trend
and then, with and without seasonality component at
a significance level of 5%. The null hypothesis for
the above test is formulated as:
Null Hypothesis H
0
: Difference Between mean of
two sample size is not statistically different.
Table 2: Statistical t-test for forecast with trend, and with
seasonality at a significance level of 5%, where L, T, S
denotes Level, Trend and Seasonality component
respectively and provides justification for selection of
forecasting model highlighted in Table 1.
Dataset L + T L + S Selected Model
Hourly Mean
Temperature
No No SES
Hourly Number of
Riders
No Yes HWES
Daily Waste Generation No No SES
Monthly Car Sales Yes Yes HWES
As seen from Table 2, there is no significant
difference with forecast including trend and
seasonality on dataset of Hourly Number of Riders
as well as Daily Waste Generation, which is justified
by selection of SES model in Table 2. On the
contrary, for Hourly Number of Riders dataset, there
is significant difference between forecast with and
without including seasonality component, justifying
the selection of HWES model. While for Monthly
Car Sales, we can observe significant difference by
including both trend as well as seasonality, validated
by decreasing error in HES as well as in HWES.
GETS: Grammatical Evolution based Optimization of Smoothing Parameters in Univariate Time Series Forecasting
601

6 CONCLUSIONS
In this work, we describe a grammatical evolution
based approach to time series modelling. The study
covers various Averaging and Smoothing time series
approaches for univariate forecasting. An important
feature of our framework concerns the optimisation
of the smoothing parameters for level, trend and
seasonality components which can increase the
accuracy of the forecast without explicitly defining
them. The individual solutions obtained through
large number of trials are validated using statistical
t-test.
The results indicate that the aggregated forecast
error calculated using root mean squared error and
time required for computation was marginally less or
similar to traditional machine learning approach for
smaller datasets, but significant difference was
observed for big datasets, making it scalable.
Moreover, grammar-based time series modelling
does not require the fine tuning of parameters as
required with Grid Search.
This approach can be extended to incorporate
other time series models like AutoRegression (AR)
and Autoregressive Integrated Moving Average
(ARIMA). This work was only tested for Univariate
time series analysis and research for multivariate
time series forecasting is being carried out by the
authors and is in its testing phase.
ACKNOWLEDGEMENT
This work is supported in part by the Science
Foundation of Ireland grant #16/IA/4605.
REFERENCES
Penfold, R. B., & Zhang, F. (2013). Use of interrupted
time series analysis in evaluating health care quality
improvements. Academic pediatrics, 13(6), S38-S44.
Nagori, M., Jachak, R. S., & Chaudhari, P. P. (2019,
February). A framework for segregating solid waste by
employing the technique of image annotation. In 2019
Second International Conference on Advanced
Computational and Communication Paradigms
(ICACCP) (pp. 1-6). IEEE.
Lütkepohl, H., Krätzig, M., & Phillips, P. C. (Eds.).
(2004). Applied time series econometrics. Cambridge
university press.
Shumway, R. H., & Stoffer, D. S. (2017). Time series
analysis and its applications: with R examples.
Springer.
Brockwell, P. J., & Davis, R. A. (2016). Introduction to
time series and forecasting. springer.
Gardner Jr, E. S. (1985). Exponential smoothing: The state
of the art. Journal of forecasting, 4(1), 1-28.
Schmidt, C., Branke, J., & Chick, S. E. (2006, April).
Integrating techniques from statistical ranking into
evolutionary algorithms. In Workshops on
Applications of Evolutionary Computation (pp. 752-
763). Springer, Berlin, Heidelberg.
De Silva, A. M., Noorian, F., Davis, R. I., & Leong, P. H.
(2013, December). A hybrid feature selection and
generation algorithm for electricity load prediction
using grammatical evolution. In 2013 12th
International Conference on Machine Learning and
Applications (Vol. 2, pp. 211-217). IEEE.
Cortez, P., Rocha, M., & Neves, J. (2001, June). Genetic
and evolutionary algorithms for time series
forecasting. In International Conference on Industrial,
Engineering and Other Applications of Applied
Intelligent Systems (pp. 393-402). Springer, Berlin,
Heidelberg.
Birattari, M., Yuan, Z., Balaprakash, P., & Stützle, T.
(2010). F-Race and iterated F-Race: An overview.
In Experimental methods for the analysis of
optimization algorithms (pp. 311-336). Springer,
Berlin, Heidelberg.
Ryan, C., Collins, J. J., & Neill, M. O. (1998, April).
Grammatical evolution: Evolving programs for an
arbitrary language. In European Conference on
Genetic Programming (pp. 83-96). Springer, Berlin,
Heidelberg.
O'Neill, M., & Ryan, C. (2001). Grammatical
evolution. IEEE Transactions on Evolutionary
Computation, 5(4), 349-358.
McCracken, D. D., & Reilly, E. D. (2003). Backus-naur
form (bnf).
Dioşan, L., & Oltean, M. (2006, April). Evolving
crossover operators for function optimization.
In European Conference on Genetic
Programming (pp. 97-108). Springer, Berlin,
Heidelberg.
Hansun, S. (2013, November). A new approach of moving
average method in time series analysis. In 2013
Conference on New Media Studies (CoNMedia) (pp.
1-4). IEEE.
Hunter, J. S. (1986). The exponentially weighted moving
average. Journal of quality technology, 18(4), 203-
210.
Holt, C. C. (2004). Forecasting seasonals and trends by
exponentially weighted moving
averages. International journal of forecasting, 20(1),
5-10.
Kalekar, P. S. (2004). Time series forecasting using holt-
winters exponential smoothing. Kanwal Rekhi School
of Information Technology, 4329008(13).
O'neill, M., Ryan, C., Keijzer, M., & Cattolico, M. (2003).
Crossover in grammatical evolution. Genetic
programming and evolvable machines, 4(1), 67-93.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
602