
Validation of a Low-cost Inertial Exercise Tracker
Sarvenaz Salehi
1
and Didier Stricker
2
1
Daimler Protics, Germany
2
German Research Center for Artificial Intelligence (DFKI), Germany
Keywords:
Inertial Sensors, Body-IMU Calibration, Body Motion Tracking, Exercise Monitoring.
Abstract:
This work validates the application of a low-cost inertial tracking suit, for strength exercise monitoring. The
procedure includes an offline processing for body-IMU calibration and an online tracking and identification of
lower body motion. We proposed an optimal movement pattern for the body-IMU calibration method from our
previous work. Here, in order to reproduce real extreme situations, the focus is on the movements with high
acceleration. For such movements, an optimal orientation tracking approach is introduced, which requires
no accelerometer measurements and it thus minimizes error due to outliers. The online tracking algorithm is
based on an extended Kalman filter(EKF), which estimates the position of upper and lower legs, along with
hip and knee joint angles. This method applies the estimated values in the calibration process i.e. joint axes
and positions, as well as biomechanical constraints of lower body. Therefore it requires no aiding sensors such
as magnetometer. The algorithm is evaluated using optical tracker for two types of exercises: squat and hip
abd/adduction which resulted average root mean square error(RMSE) of 9cm. Additionally, this work presents
a personalized exercise identification approach, where an online template matching algorithm is applied and
optimised using zero velocity crossing(ZVC) for feature extraction. This results reducing the execution time
to 93% and improving the accuracy up to 33%.
1 INTRODUCTION
Strength training is one of the critical components of
the most fitness and rehabilitation processes. Moni-
toring such exercises is beneficial, in terms of perfor-
mance improvement, injury prevention and rehabili-
tation(Bleser et al., 2015).
Wearable systems, including multiple sensors
such as inertial measurement units(IMUs), provide an
efficient solution for such applications. The kinemat-
ics analysis of body movements can be performed by
fusing and filtering the well calibrated IMU measure-
ments and extracting higher level information, such
as joint angles and the segment positions (Yan et al.,
2017; Chardonnens et al., 2013). In the previous work
(Salehi et al., 2014), we presented the design and
development of a low-cost tracking suit which com-
posed of a wired network of IMUs and can be used for
a long time exercise monitoring. In the current work
the system is validated by a sequence of processes in-
cluding body-IMU calibration, body pose estimation
and personalized exercise identification, in order to
provide a complete monitoring of user’s performance.
2 RELATED WORKS
2.1 Body-IMU Calibration
Body-IMU calibration is a key requirement for cap-
turing accurate body movements in applications based
on wearable systems (Zinnen et al., 2009). The
mounting positions of IMU with respect to joint is
critical information in joint angle estimation using ac-
celerometer measurements, especially during fast ro-
tations (Cheng and Oelmann, 2010) and when mod-
elling kinematic chains (Reiss et al., 2010). To obtain
such values from manual measurements or anthro-
pometric tables for different types of users is highly
error-prone and cumbersome. We previously pro-
posed a practical auto-calibration method for IMU
to body position estimation in (Salehi et al., 2015),
based upon a previously existing method by (Seel
et al., 2014). In contrast to (Seel et al., 2014), our
method considers three linked segments with IMUs
(pelvis, upper leg, lower leg) and, respectively, two
joints (hip, knee) in one estimation problem. This
makes it possible to benefit from an additional con-
straint, which has shown theoretically and experimen-
Salehi, S. and Stricker, D.
Validation of a Low-cost Inertial Exercise Tracker.
DOI: 10.5220/0008965800970104
In Proceedings of the 9th International Conference on Sensor Networks (SENSORNETS 2020), pages 97-104
ISBN: 978-989-758-403-9; ISSN: 2184-4380
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
97

tally to provide more robust and accurate results under
suboptimal movement conditions. However, in exper-
iments with real data the dependency to global IMU
orientation could degrade the results due to magnetic
disturbances and outliers in accelerometer measure-
ments. In the current work the algorithm is evaluated
using data from two different types of movements.
In order to minimize the error due to existing out-
liers, especially in high acceleration, an optimal ori-
entation tracking algorithm is proposed, which esti-
mates relative rotations of the segments using gyro-
scope measurements. Therefore, the system is vali-
dated by this process, considering its applicability for
different types of users, who perform the movements
with different intensities and mostly with high accel-
eration.
2.2 Body Pose Estimation
In order to provide higher-level information such as
body segments positions and joint angles, as well as
3D visualization of the movements in the targeted ex-
ercise monitoring application, a variety of techniques
are proposed in the literature. Commonly, they as-
sume the body segments to be rigid bodies, which are
connected at joints.
A real-time motion tracking system was presented
in (Zhu and Zhou, 2004), using a linear Kalman fil-
ter; the orientation of each body segment is calcu-
lated using accelerometer and magnetometer mea-
surements and fused with gyroscope measurements
in the Kalman filter, which results a smooth estima-
tion. This approach, however, doesn’t assume the
error caused by linear acceleration in accelerometer
measurement. Moreover, the magnetic disturbances
are not modelled. This could lead to faulty estimation
in the vicinity of ferromagnetic materials.
In order to consider the error of linear accelera-
tion, the idea of using physical and virtual sensor,
based on Newton-Euler equations, for estimating joint
angle is presented in (Dejnabadi et al., 2006). Ac-
cording to this method, acceleration of the joint can
be measured by placing a pair of virtual sensors on
the adjacent links at the joint center. In these ap-
proaches, joint angle is defined by the difference of
direction in measured acceleration of sensors in the
joint frame. (Cheng and Oelmann, 2010) provides
a survey, which compares four different methods for
measuring the joint angle in two dimensions. They
proved that when the sensors are mounted far from
the joint center, especially in fast rotations a method
called CMRGD: common-mode-rejection with gyro
differentiation has less error and is easier to imple-
ment than the other methods. In this method, the
gyroscope measurements are numerically differenti-
ated in order to derive the angular acceleration, which
is required to calculate the acceleration vector of the
joint center.
Instead of using the magnetometer measurements,
as they can easily distort the orientation estima-
tion, different studies applied the biomechanical con-
straints in order to improve the estimation of body
motion in the horizontal plane. Such studies can be
divided into two categories:
In the first category, the joint angles are estimated
in an state estimation approach, assuming the known
IMUs mounting orientations. In (Lin and Kuli
´
c,
2012), with the assumption of constant joint accel-
eration and using Denavit-Hartenberg (DH) conven-
tion, the angle related to each possible degree of
freedom(DOF) at hip and knee joints is estimated in
an EKF. Here the accelerometer measurement model
follows a similar approach in (Cheng and Oelmann,
2010) and (Dejnabadi et al., 2006).
In the second category, the state vector contains the
relative orientation and the position of the segments.
In (Kok et al., 2014), an optimization approach incor-
porates the biomechanical constraints together with
the biases of inertial sensors and the error of limited
DOF on knee joint. Other than body pose, the body-
IMU calibration parameters are simultaneously esti-
mated. However, (Kok et al., 2014) didn’t present any
evaluation of accuracy of such parameters. Moreover,
this approach can not be used in a real-time applica-
tion, as it requires a batch of observations.
In the same category of methods, (Luinge et al., 2011)
proposed the Kinematic Coupling(KiC) algorithm, at
first for a hinge joint; Assuming A and B are IMUs,
which are mounted on the adjacent segments of the
joint m, from the coupling concept the following con-
straint is defined:
G
∆
~
P =
G
~
lmB −
G
~
lmA (1)
,where
G
∆
~
P is the relative position of B wrt. A and
G
~
lmA,
G
~
lmB are the distance vector between joint m
and the respective IMUs, all defined in the global co-
ordinate system, G, which is typically aligned with
gravity and magnetic north. In this case the EKF state
vector contains relative positions and velocities of two
adjacent segments of the joint, the error in orientation
of the segments and gyroscope biases. In this work we
propose a similar approach to (Luinge et al., 2011),
in order to estimate the relative velocity and position
of a leg segments, in addition to hip and knee joint
angles. Using the biomechanical constraints and re-
sult of body-IMU calibration, the number of required
states is less in comparison to (Luinge et al., 2011),
plus there’s no need for extra measurements, such as
magnetic field.
SENSORNETS 2020 - 9th International Conference on Sensor Networks
98

2.3 Exercise Identification
It is common that trainers initially monitor trainees
and instruct them based on their health conditions,
while they are performing a strength exercise for the
first time, so that they can independently perform the
exercise later. Possibility of injuries are normally high
in this phase, as the correct way of the exercise can’t
be carefully controlled, considering body character-
istics and abilities of individuals. For example, in the
rehabilitation, where range of motion is limited in dif-
ferent stages of recovery. It is thus very important to
provide a personalized monitoring application.
Exercise identification is the process of identify-
ing the start and stop time of one repetition in an ex-
ercise, which could be composed of multiple smaller
components known as motion primitives. Usually a
repetition in an strength exercise comprises the se-
quence of increasing and decreasing velocity. There-
fore, zero velocity crossing(ZVC) approach is one of
the most optimal approaches to find the motion prim-
itives, where the velocity of signal changes the sign.
(Fod et al., 2002) applied ZVCs, in order to detect the
motion primitive of two DOFs.
Hidden Markov Model(HMM) is a stochastic ap-
proach, which considers a signal as unobservable se-
quences of Markov states. At each time point the sys-
tem undergoes a state transition, which is defined by a
probability in a transition matrix. In (Janus and Naka-
mura, 2005), a template free approach is proposed,
where the data is windowed and probability density
function of each window was used in a HMM to de-
tect different states of the movements. The segment is
identified, where the transition between states occurs.
HMM is more used in the template based ap-
proaches. In (Lin and Kuli
´
c, 2013) a two-stage ap-
proach is proposed to reduce the computational cost
by reducing the number of times that HMM should
run. This is achieved by first scanning the observa-
tion signal for the candidate segments using ZVC or
velocity peaks in joint angle.
There are other learning based classifiers, which
are used for motion identification such as Convolu-
tional Neural Network(CNN) (Um et al., 2017) or
Support Vector Machine(SVM) (Morris et al., 2014).
However, they require enough labelled training data
to increase the accuracy.
An alternative approach, which doesn’t require
any training data is template matching.
Dynamic Time Warping(DTW) is a popular tem-
plate matching algorithm, which creates a matrix of
the distances between each point of the observed sig-
nal and the template. Then this matrix is searched for
a warping path which leads to a minimum distance.
This can be used to identify an exercise using a tem-
plate of motion data, performed and captured with the
supervision of a trainer. However, it can be only ap-
plied in offline scenarios, due to its expensive compu-
tational cost, especially in higher dimensions. (Saku-
rai et al., 2007) proposed an online approach, which
addresses the problem of subsequent matching using
DTW. This algorithm is fast which means the process-
ing time of current observation point doesn’t depend
on the past data length. It only requires a single ma-
trix to find the matching subsequent. In (Sakurai et al.,
2007), an experiment on joint position data from op-
tical motion capture system is presented. Here, this
algorithm was evaluated for real time motion identifi-
cation based on IMU measurements.
3 PROCEDURE
3.1 Body-IMU Calibration
The calibration procedure is based on the method in
(Salehi et al., 2015), here using two different types of
movements: A) random movements in all directions,
B)separate movements on each DOF. Additionally, in
order to avoid problems such as outlier and distorted
measurements, caused when using accelerometer and
magnetometer, a new approach is proposed, specifi-
cally for movements of type B, in order to estimate
the relative orientations, which are required for cali-
bration procedure (see Figure 1). This is explained in
the following section:
3.1.1 Relative Orientation Estimation
Considering a hinge joint, n, the measurements of gy-
roscopes (
~
ω), mounted on its two adjacent segments
(B,C), provide useful information in order to iden-
tify the joint axis ~r
n
. As the rotation is limited to
only one direction i.e. joint axis, any difference be-
tween the angular velocities of the two segments, in
the plane perpendicular to the rotation, is in contrast
to that limited degree of freedom. It is also obvious
that the difference between the angular velocities of
the segments in the direction of the joint axis is the
joint angular velocity. These facts are defined in the
equations 2 and 3.
k
~
ω
B
×
B
~r
n
k − k
~
ω
C
×
C
~r
n
k = 0 (2)
˙
θ
n
= ω
B
·
B
~r
n
− ω
C
·
C
~r
n
(3)
,where · is scalar product. Thus the joint axis can
be estimated, using a set of measurements from two
gyroscopes on the joint segments, in an optimization
Validation of a Low-cost Inertial Exercise Tracker
99

Figure 1: The computation graph of body-IMU calibration procedure.
problem, with equation 2 as the cost function. The
relative segment orientation is obtained from integra-
tion of equation 3. Though this approach is explained
for knee joint, the same can be applied for hip, if the
movements are kept limited to only one DOF at a time
(see Figure 1). Therefore type B movements provides
optimal measurements for both joint axes and relative
orientation estimation, which are the prerequisites for
body-IMU calibration algorithm.
3.2 Body Pose Estimation
In this work an extended Kalman filter is designed to
estimate the knee and hip joint angles, as well as the
legs’ segments positions. The assumptions here are:
(1) a simple biomechanical model for leg with rigid
segments connected via frictionless joints: hip(m),
knee(n), (2) at least one IMU sitting on each rigid
segment that should be tracked: (A on pelvis, B on up-
per leg, C on lower leg), (3) forward kinematics equa-
tions, (4) constant acceleration for integration dura-
tion(sampling time).
The state vector, Equation 4, includes the
velocities(~v) and positions(
~
P) of the upper and
lower segments in addition to the hip rotation
quaternion(~q
AB
), and the knee joint angle(
~
θ
BC
), all of
which are wrt pelvis coordinate:
~x = [
A
~v
B
A
~v
C
A
~
P
B
A
~
P
C
~q
AB
~
θ
BC
] (4)
Kinematic Process Model is defined in Equation 5
(note: tilde superscripts indicate the measurements
and the vector signs is removed for simplicity).
A
v
B
k
=
A
v
B
k−1
+
A
˜a
B
k−1
∆T (5a)
A
v
C
k
=
A
v
C
k−1
+
A
˜a
C
k−1
∆T (5b)
A
P
B
k
=
A
P
B
k−1
+
A
v
B
k−1
∆T +
A
˜a
B
k−1
∆T
2
2
(5c)
A
P
C
k
=
A
P
C
k−1
+ ∆T
A
v
C
k−1
+
A
˜a
C
k−1
∆T
2
2
(5d)
q
AB
k
= exp(R
AB
k−1
˜
ω
B
k−1
−
˜
ω
A
k−1
)q
AB
k−1
(5e)
θ
BC
k
= θ
BC
k−1
+ ∆T (
˜
ω
C
k−1
·
C
r
n
−
˜
ω
B
k−1
·
B
r
n
) (5f)
,where
A
˜a
B
k−1
= R
AB
k−1
˜a
B
k−1
− ˜a
A
k−1
(6a)
A
˜a
C
k−1
= R
AB
k−1
R
BC
k−1
˜a
C
k−1
− ˜a
A
k−1
(6b)
Here, accelerometer( ˜a) and gyroscope(
˜
ω) measure-
ments are the control inputs. R
AB
is obtained from
q
AB
using the quaternion to rotation matrix conver-
sion and R
BC
is calculated from
~
θ
BC
and
B
r
n
using the
axis-angle to rotation matrix conversion. ∆T is the
sampling time.
Observation Model is defined based on assumption
1; the segments pelvis and upper leg connected in
hip joint (Equation 7a) and upper and lower legs con-
nected in knee joint (Equation 7b):
P
B
k
= −R
AB
B
lmB +
A
lmA (7a)
P
C
k
= −R
AB
(R
BC
C
lmC +
B
lmB) +
A
lmA, (7b)
3.3 Exercise Identification
In this work a template based exercise identification
algorithm is proposed, which deploys the recorded
supervised exercise motion as the template for later
identification of correct performance. Here, we ap-
plied a streaming subsequence matching method,
SPRING (Sakurai et al., 2007). For further optimiza-
tion of execution time, a preprocessing stage, includ-
ing motion primitive detection and a feature extrac-
tion step, are presented in this section.
3.4 Preprocessing
3.4.1 Motion Primitive Detection
As the strength exercises mostly contain the periodic
pattern, where the velocity of motion increases and
decreases sequentially, we chose ZVC method to de-
tect the motion primitives in the template as well as in
the streaming signal. Therefore the motion primitive
is detected, where the sign of derivative is changing
on the dominant DOF of motion signals e.g. positions
or joint angles. The derivative is calculated here using
a sliding window of 3 samples. The dominant DOF
SENSORNETS 2020 - 9th International Conference on Sensor Networks
100

is selected on each dataset by finding a dimension of
template signal which has the highest value.
3.4.2 Feature Extraction
The features consist of velocity, variance and mean of
each DOF in motion primitive. Therefore, for each
motion primitive tens of input samples are reduced to
3 features for each dimension. This, as it is shown
in the experimental results, has increased the speed of
identification.
4 EXPERIMENTAL RESULTS
4.1 Body-IMU Calibration
In order to evaluate the proposed method, we cap-
tured a dataset from 7 subjects, 2 women and 5 men,
each performing 3 trials using the IMU harness of the
tracking suit, presented in (Salehi et al., 2014), and an
optical reference system, the NaturalPoint OptiTrack,
with 12 Prime 13 cameras, operated with the Motive
software (Optitrack, 2019). The test setup is shown
in Figure 2. In this experiment, each IMU was rigidly
connected with a rigid body marker. The IMUs were
interconnected via textile cables. In order to reduce
artefacts due to movement of the garment, the IMU-
marker-sets were strapped firmly on the pelvis and
one leg. We also used straps in order to attach marker
clusters on anatomical landmarks around the hip and
knee joints, from which we determined the joint cen-
ter of rotations.
In each trial, the subjects performed movements
of type A and B. In order to assess the repeatability
of the process each subject has done three trials.
Data in both optical system and IMUs captured
with 50Hz rate. The IMU measurements then were
downsampled to 5Hz. A hand-eye calibration was
used to transform the optical system coordinate to
the IMU coordinates. Note that errors due to marker
positioning are present, however, similarly for all the
tested methods. The data from type B movements
was first used to estimate the joints’ axes, by applying
method described in 3.1.1. The calibration algorithms
were applied to both types of data. The following
describes the preprocessing and result analysis of
each one:
A. Calibration with Random Movements in All Di-
rections. For this type of movements, the global IMU
orientations were calculated based on a similar ap-
proach in (Harada et al., 2007), using IMU measure-
ments.
Figure 2: The red arrows show three IMUs which are
mounted on 1.pelvis (not visible), 2.upper leg and 3.lower
leg.
Figure 3 illustrates the overall RMSE in all the
four segments for all the trials, when applying the dif-
ferent calibration methods. This shows that the pro-
posed method provides more accurate results in 80%
of the trials, while a slightly worse performance can
be observed in the rest. The average error over all the
trials in the proposed method is 16.9±0.8cm, which is
lower than the ones of the Seel et al. method with
error of 18.13±0.7cm. The more detailed result of
proposed method is presented in Table 1. It can be
observed that the errors in segments lmA and lmB are
higher than the ones in lnB and lnC, as the movements
of these segments around the hip joint are more lim-
ited than the ones around the knee. This was also
proved theoretically, in the observability analysis in
(Salehi et al., 2015): conditions 2 and 3, which are
related to the angular velocity variations.
B. Calibration with Separate Movements on Each
DOF Both approaches are applied on the dataset,
which includes separate movements in each DOF.
Here, in order to estimate the relative orientations of
the segments, we applied the method in 3.1.1. Figure
4 illustrates the overall RMSE in all the four segments
for all the trials, which shows the proposed method
has more accurate results in all the trials with the av-
erage error of 15.1±0.6cm. The detailed result of pro-
posed method in Table 1.
It is shown that the proposed method with the
dataset of type B movements results better than the
type A, while the Seel et al. method results worse.
This proves the first condition of observability in
(Salehi et al., 2015). Moreover, during the experi-
ment with the random movements in order to excite
all the segments simultaneously the subjects have per-
formed fast and hardly controlled movements, which
led to high deviation of accelerometer measurements
Validation of a Low-cost Inertial Exercise Tracker
101
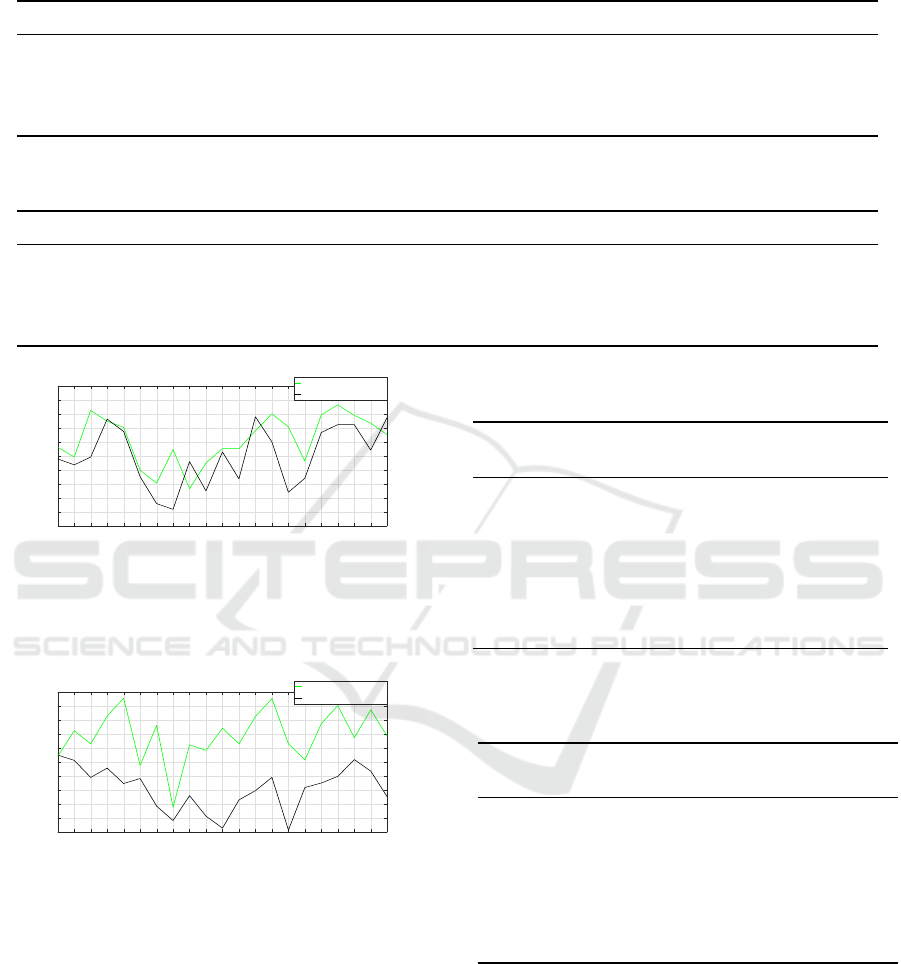
Table 1: The positions of each joint m,n with respect to each IMU A,B,C estimated by method in (Salehi et al., 2015) from 7
subjects performing type A movements.
cm s1 s2 s3 s4 s5 s6 s7
lmA 12.5±3.37 18.57±4.3 15.6±1.19 15.99±2.14 15.02±3.31 16.89±0.7 13.68±5.1
lmB 24.39±0.9 22.28±4.93 19.72±2.58 23.34±2.81 25.92±3.97 24.8±3.16 31.18±3.79
lnB 9.98 ±6.37 16.12±0.52 10.26±3.33 9.35±2.01 12.49±4.62 10.12±1.85 7.23±3.87
lnC 14.86±0.47 12.85±1.57 9.5±1.34 9.48±1.15 11.54±2.86 15.24±5.94 11.86±5.23
Table 2: The positions of each joint m, n with respect to each IMU A,B,C estimated by method in (Salehi et al., 2015) and
Section 3.1.1 from 7 subjects performing type B movements.
cm s1 s2 s3 s4 5 s6 s7
lmA 23.13±3.26 18.18±3.53 14.12±1.69 14±3.07 13.51±4.07 17.33±0.82 15.2±0.73
lmB 14.26±0.87 17.03±4.98 19.69±3.04 18.42±2.88 16.49±7.61 20.21±2.23 24.79±4.37
lnB 13.5±4.93 14.66±3.5 7.86±1.55 6.4±2.65 13.89±5.54 8.2±1.88 3.61±1.92
lnC 13.72±0.22 11.71±3.23 9.93±0.93 10.17±2.51 8.88±5.49 13.34±3.14 11.94±3.86
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Test number
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.2
0.21
0.22
Position error[m]
Seel method
Proposed method
Figure 3: Results on measurements from random move-
ments: RMSE of the body-IMU calibration using Seel et
al.(green) and the proposed method(black), with respect to
optical tracker. Test 1,2,3 is with subject 1, test 4,5,6 with
subject 2, etc.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Test number
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.2
0.21
0.22
Position error[m]
Seel method
Proposed method
Figure 4: Results on measurements from the movements on
each DOF separately: RMSE of the Body-IMU calibration
using Seel et al.(green) and the proposed method(black),
with respect to optical tracker.
from gravity. Commonly in most of the orientation
estimation filters, these measurements are considered
as outliers and the estimated orientation in the pres-
ence of such measurements is prone to error. This has
led to higher error in the proposed method than when
using type B measurements.
Table 3: Error of estimated upper and lower segments posi-
tions using the proposed method for squat exercise.
PB PC
cm [RMS, STD, Max] [RMS, STD, Max]
s1 [8.47, 10.02, 4.10] [8.98, 8.43, 36.16]
s2 [7.72, 5.13, 16.53] [7.69, 3.87, 14.20]
s3 [6.05, 4.44, 15.30] [9.12 5.49, 17.68]
s4 [6.57, 4.93, 19.92] [7.51, 6.14, 24.64]
s5 [8.91, 5.10, 18.02] [7.84, 4.14, 16.96]
s6 [7.20, 4.03, 13.73] [5.47, 3.55, 12.84]
s7 [6.40, 4.65, 15.27] [7.42, 5.15, 18.53]
Table 4: Error of estimated upper and lower segments posi-
tions using the proposed method for abduction and adduc-
tion exercise.
PB PC
cm [RMS, STD, Max] [RMS, STD, Max]
s1 [5.19, 3.38, 10.57] [10.53, 6.91, 21.40]
s2 [4.83, 2.97, 25.61] [9.96, 6.14, 24.84]
s3 [4.60, 1.99, 8.52] [10.63, 5.66, 21.18]
s4 [7.16, 3.87, 13.84] [12.31, 7.14, 24.65]
s5 [6.10, 3.64, 12.40] [12.43, 8.58, 27.58]
s6 [7.74, 4.58, 15.56] [16.28, 11.0, 34.62]
s7 [8.09, 5.95, 19.45] [16.33, 12.84, 42.45]
4.2 Lower Body Pose Estimation
The pose estimation approach in Section 3.2 was eval-
uated for lower body movements. The state vector is
initialized using the Equations 7a and 7b. The initial
global orientations and pelvis orientation were esti-
mated using a similar approach to in (Harada et al.,
2007). With the setup similar to Section 4.1, esti-
mation of a leg segments positions captured by both
SENSORNETS 2020 - 9th International Conference on Sensor Networks
102
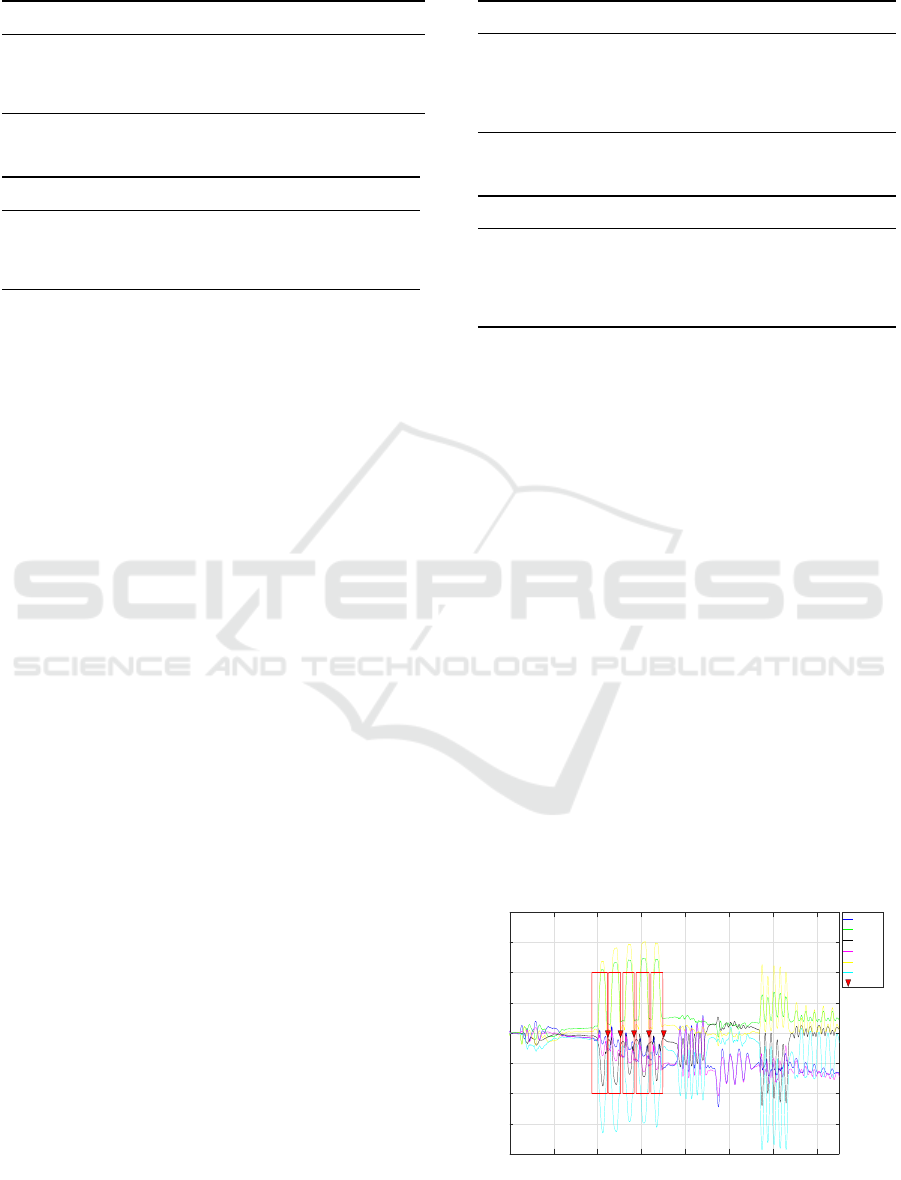
Table 5: Joint angle identification without ZVC.
s1 s2 s3 s4 s5 s6 s7
Accuracy[%] 99 99 99 99 99 99 99
Precision[%] 100 100 100 100 100 100 100
Time[s] 4.4 3.1 3.0 2.1 2.8 4.5 2.7
Table 6: Joint angle identification with ZVC.
s1 s2 s3 s4 s5 s6 s7
Accuracy[%] 99 77 99 99 98 99 98
Precision[%] 100 6 100 71 100 80 40
Time[s] 0.4 0.2 0.2 0.1 0.1 0.1 0.2
tracking suit and optical system. This experiment was
carried out with 7 subjects each performing squat and
hip abduction/adduction exercises.
The results for squat and abduction/adduction ex-
ercises are presented in Tables 3 and 4 respectively.
The average error for all subjects in estimation of
lower leg position, is higher than upper leg, as it con-
tains more error related to knee joint angle plus the
calibration error of IMU position in particular lnC.
4.3 Exercise Monitoring
The algorithm was evaluated using the result of body
motion tracking in section 4.2. The first squat which
was performed following the instruction of a supervi-
sor, was used as a template to identify the next repeti-
tions. After squats the subjects have performed other
movements, Figure 5.
As the joint angle is commonly used in the move-
ment identification, here this signal was used as a
baseline to evaluate the exercise identification for
when using ZVC for feature extraction. As it can be
seen from Tables 5 and 6, applying ZVC has a high
impact on the execution time.
For position signal, the average accuracy and pre-
cision are higher than these values for the joint angles.
This implies that the position signals in comparison to
the joint angles, contain more information related to
type of exercise. For more detailed comparison see
Tables 6,7.
The last experiment was done by using the pelvis
orientation as an additional input, as the correct per-
formance of the squat exercise is highly depends the
pelvis movements. The result is presented in Table 8.
It was noticed that in only one test, where the subject
didn’t follow the instructed exercise, the sensitivity is
lower in comparison to the previous experiment.
Table 7: Position identification with ZVC.
s1 s2 s3 s4 s5 s6 s7
Accuracy[%] 99 99 99 98 98 99 99
Precision[%] 100 83 100 100 100 100 100
Sensitivity[%] 25 100 60 20 28 20 20
Time[s] 0.6 0.2 0.1 0.1 0.1 0.2 0.1
Table 8: Position plus quaternion identification with ZVC.
s1 s2 s3 s4 s5 s6 s7
Accuracy[%] 99 99 99 98 98 99 99
Precision[%] 100 83 100 100 100 100 100
Sensitivity[%] 25 100 60 20 14 20 20
Time[s] 0.9 0.3 0.2 0.1 0.1 0.2 0.2
5 CONCLUSIONS
In this work the application of exercise monitoring is
presented in order to validate a low-cost inertial track-
ing suit. This has been achieved following three dif-
ferent processes: offline body-IMU calibration, on-
line body pose estimation and online exercise identi-
fication. It was shown that using the previous body-
IMU calibration method for random movements, de-
grade the results due to the presence of outliers espe-
cially from accelerometer measurements. Therefore
an optimal orientation tracking method was proposed,
which can be realized using only gyroscope measure-
ments, while the user performs separate movements
around each DOF. Using dataset from this type of
movements, the result showed overall improvement,
especially for the leg segments, which can not provide
enough useful movements for calibration. The body
pose estimation approach is based on EKF, where
only inertial measurements are contributing as control
inputs. In the proposed approach the lack of a reli-
able reference measurement for the horizontal plane,
0 10 20 30 40 50 60 70
Time[s]
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
Position[m]
PB
X
PB
Y
PB
Z
PC
X
PC
Y
PC
Z
Squat Identified
Figure 5: Online squat exercise identification. The red ar-
rows show the timestamps when the squats are identified.
Validation of a Low-cost Inertial Exercise Tracker
103

e.g. magnetic field, was compensated by modelling
the joints’ constraints in observation model and using
the body-IMU calibration results, i.e. joint axes and
positions. In order to monitor the strength exercises,
a personalized identification approach was proposed,
which doesn’t require a large labelled training dataset.
The idea is to use a template signal captured, where
users are instructed to perform the movements cor-
rectly according to their ability and health conditions.
Therefore, an online template matching algorithm is
optimized and applied to estimated position, which
led to improved accuracy and execution time. The ex-
perimental results of this validation showed relatively
good results, considering high intensity of the move-
ments. For further improvement in future , in order to
compensate for the intensive dynamic movements, an
outlier rejection approach can be implemented. Ad-
ditionally performance of EKF can be improved by
adaptive tuning of the noise covariances.
REFERENCES
Bleser, G., Steffen, D., Reiss, A., Weber, M., Hendeby, G.,
and Fradet, L. (2015). Personalized physical activity
monitoring using wearable sensors. In Smart health,
pages 99–124. Springer.
Chardonnens, J., Favre, J., Cuendet, F., Gremion, G., and
Aminian, K. (2013). A system to measure the kine-
matics during the entire ski jump sequence using iner-
tial sensors. Journal of biomechanics, 46(1):56–62.
Cheng, P. and Oelmann, B. (2010). Joint-angle measure-
ment using accelerometers and gyroscopes?a survey.
IEEE Transactions on instrumentation and measure-
ment, 59(2):404–414.
Dejnabadi, H., Jolles, B. M., Casanova, E., Fua, P., and
Aminian, K. (2006). Estimation and visualization of
sagittal kinematics of lower limbs orientation using
body-fixed sensors. IEEE Transactions on Biomedi-
cal Engineering, 53(7):1385–1393.
Fod, A., Matari
´
c, M. J., and Jenkins, O. C. (2002). Auto-
mated derivation of primitives for movement classifi-
cation. Autonomous robots, 12(1):39–54.
Harada, T., Mori, T., and Sato, T. (2007). Development of
a tiny orientation estimation device to operate under
motion and magnetic disturbance. The International
Journal of Robotics Research, 26(6):547–559.
Janus, B. and Nakamura, Y. (2005). Unsupervised proba-
bilistic segmentation of motion data for mimesis mod-
eling. In ICAR’05. Proceedings., 12th International
Conference on Advanced Robotics, 2005., pages 411–
417. IEEE.
Kok, M., Hol, J. D., and Sch
¨
on, T. B. (2014). An
optimization-based approach to human body motion
capture using inertial sensors. IFAC Proceedings Vol-
umes, 47(3):79–85.
Lin, J. F. and Kuli
´
c, D. (2012). Human pose recovery us-
ing wireless inertial measurement units. Physiological
measurement, 33(12):2099.
Lin, J. F.-S. and Kuli
´
c, D. (2013). Online segmentation of
human motion for automated rehabilitation exercise
analysis. IEEE Transactions on Neural Systems and
Rehabilitation Engineering, 22(1):168–180.
Luinge, H. J., Roetenberg, D., and Slycke, P. J. (2011).
Inertial sensor kinematic coupling. US Patent App.
12/534,526.
Morris, D., Saponas, T. S., Guillory, A., and Kelner, I.
(2014). Recofit: using a wearable sensor to find, rec-
ognize, and count repetitive exercises. In Proceedings
of the SIGCHI Conference on Human Factors in Com-
puting Systems, pages 3225–3234. ACM.
Optitrack (2019). Optitrack flex 13 (accessed 9/17/2014).
Reiss, A., Hendeby, G., Bleser, G., and Stricker, D.
(2010). Activity recognition using biomechanical
model based pose estimation. In 5th European Con-
ference on Smart Sensing and Context (EuroSSC),
pages 42–55.
Sakurai, Y., Faloutsos, C., and Yamamuro, M. (2007).
Stream monitoring under the time warping distance.
In 2007 IEEE 23rd International Conference on Data
Engineering, pages 1046–1055.
Salehi, S., Bleser, G., Reiss, A., and Stricker, D. (2015).
Body-imu autocalibration for inertial hip and knee
joint tracking. In Proceedings of the 10th EAI Interna-
tional Conference on Body Area Networks, BodyNets
’15, pages 51–57, ICST, Brussels, Belgium, Bel-
gium. ICST (Institute for Computer Sciences, Social-
Informatics and Telecommunications Engineering).
Salehi, S., Bleser, G., and Stricker, D. (2014). Design and
development of low-cost smart training pants (stants).
In 4th International Conference on Wireless Mobile
Communication and Healthcare, At Athen, Greece,
pages 39–44. IEEE.
Seel, T., Raisch, J., and Schauer, T. (2014). Imu-based
joint angle measurement for gait analysis. Sensors,
14(4):6891–6909.
Um, T. T., Babakeshizadeh, V., and Kuli
´
c, D. (2017). Ex-
ercise motion classification from large-scale wearable
sensor data using convolutional neural networks. In
2017 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS), pages 2385–2390.
IEEE.
Yan, X., Li, H., Li, A. R., and Zhang, H. (2017). Wear-
able imu-based real-time motion warning system for
construction workers’ musculoskeletal disorders pre-
vention. Automation in Construction, 74:2–11.
Zhu, R. and Zhou, Z. (2004). A real-time articulated human
motion tracking using tri-axis inertial/magnetic sen-
sors package. IEEE Transactions on Neural systems
and rehabilitation engineering, 12(2):295–302.
Zinnen, A., Blanke, U., and Schiele, B. (2009). An analysis
of sensor-oriented vs. model-based activity recogni-
tion. In 2009 International Symposium on Wearable
Computers, pages 93–100. IEEE.
SENSORNETS 2020 - 9th International Conference on Sensor Networks
104
