Information Preserving Discriminant Projections

Jing Peng

and Alex J. Aved

Department of Computer Science, Montclair State University, Montclair, NJ 07043, U.S.A.

Information Directorate, AFRL, Rome, NY 13441, U.S.A.

Keywords:

Classiﬁcation, Dimensionality Reduction, Feature Selection.

Abstract:

In classiﬁcation, a large number of features often make the design of a classiﬁer difﬁcult and degrade its

performance. This is particularly pronounced when the number of examples is small relative to the number

of features, which is due to the curse of dimensionality. There are many dimensionality reduction techniques

in the literature. However, most these techniques are either informative (or minimum information loss), as

in principal component analysis (PCA), or discriminant, as in linear discriminant analysis (LDA). Each type

of technique has its strengths and weaknesses. Motivated by Gaussian Processes Latent Variable Models, we

propose a simple linear projection technique that explores the characteristics of both PCA and LDA in latent

representations. The proposed technique optimizes a regularized information preserving objective, where

the regularizer is a LDA based criterion. And as such, it prefers a latent space that is both informative and

discriminant, thereby providing better generalization performance. Experimental results based on a variety of

data sets are provided to validate the proposed technique.

1 INTRODUCTION

In machine learning, a large number of features or

attributes often make the development of classiﬁers

difﬁcult and degrade their performance. This is par-

ticularly pronounced when the number of examples

is small relative to the number of features, which is

due to the curse of dimensionality (Bellman, 1961).

It simply states that the number of examples required

to properly compute a classiﬁer grows exponentially

with the number of features. For example, assuming

features are correlated, approximating a binary distri-

bution in a d dimensional feature space requires es-

timating O(2

) unknown variables (Breiman et al.,

1984).

Many machine learning problems are fundamen-

tally related to the problem of learning latent rep-

resentations or subspace learning, which potentially

beneﬁts many applications (Banerjee and Peng, 2005;

Peng, 1995; Heisterkamp et al., 2000; ?). The goal of

subspace learning is to discover the geometric prop-

erties of the input space, such as its Euclidean embed-

ding, intrinsic dimensionality, and connected compo-

nents from a set of high dimensional examples. Sub-

space learning is also related to embedding. Subspace

learning techniques can be categorized into linear and

non-linear techniques. In this paper, we are mainly

interested in linear techniques for simplicity and re-

duced computational complexity.

There are many dimensionality reduction tech-

niques in the literature (Belhumeur et al., 1997; Fuku-

naga, 1990; Huo and et al, 2003; Howland and Park,

2004; Peng et al., 2013; Aved et al., 2017; Zhang

et al., 2005). However, most these techniques are ei-

ther informative (or minimum information loss), as

in principal component analysis (PCA), or discrimi-

nant, as in linear discriminant analysis (LDA). Each

type of technique has its strengths and weaknesses.

For example, PCA is unsupervised, while LDA is su-

pervised. Thus, it seems that in classiﬁcation, LDA

should be able to outperform PCA. However, it has

been shown that PCA can outperform LDA in classi-

ﬁcation problems, given insufﬁcient training data per

subject (Martinez and Kak, 2001).

Motivated by Gaussian Processes (GP) latent

variable models (Lawrence, 2005; Rasmussen and

Williams, 2005; Urtasun and Darrell, 2007) and local-

ity preserving projections (He and Niyogi, 2003; Cai

et al., 2006), we investigate linear projection models

that exploit the characteristics of PCA and LDA in

latent representations. The latent representation com-

puted by PCA is most informative in terms of min-

imum information loss. On the other hand, it does

not take into account class label information. Thus,

162

Peng, J. and Aved, A.

Information Preserving Discriminant Projections.

DOI: 10.5220/0008967601620171

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 162-171

ISBN: 978-989-758-395-7; ISSN: 2184-433X

it is less discriminant in general. By combining the

characteristics of both PCA and LDA, it is expected

that the resulting latent can be both informative and

discriminant, thereby providing better generalization

performance. Experimental results using a variety of

data sets are provided to validate the proposed tech-

nique.

2 RELATED WORK

Many techniques have been proposed to take the ad-

vantage of the inherent low dimensional nature of the

data (Darnell et al., 2017; Harandi et al., 2017; Sarve-

niazi, 2014; Xie et al., 2017). Two major linear sub-

space learning techniques are PCA and LDA. Both

are capable of discovering the intrinsic geometry of

the latent subspace. However, they only compute the

global Euclidean structure.

Linear techniques based on graph Laplacians such

as locality preserving projections (LPP) can model

the local structure of the latent subspace (He and

Niyogi, 2003). These techniques construct an adja-

cency matrix that captures the local geometry of the

latent space from class label information. The pro-

jections are then computed by preserving such an ad-

jacency structure. However, the basis functions ob-

tained from LPP are not guaranteed to be orthogonal,

which makes the data reconstruction more difﬁcult.

Orthogonal LPP (OLPP) is a linear dimension re-

duction technique that has been proposed to address

the problems associated with LPP (Cai et al., 2006).

Similar to LPP, OLPP computes an adjacency ma-

trix that preserves locality information. On the other

hand, OLPP computes its basis functions that are

guaranteed to be orthogonal, Orthogonal basis func-

tions preserve the metric structure of the latent space.

It is shown OLPP outperforms LPP (Cai et al., 2006).

GP latent variable models are probabilistic tech-

niques for computing low dimensional subspaces

from high dimensional data (Gao et al., 2011;

Lawrence, 2005; Urtasun and Darrell, 2007; Jiang

et al., 2012). These techniques have been applied to

many problems such as image reconstruction and fa-

cial expression recognition (Abolhasanzadeh, 2015;

Cai et al., 2016; Eleftheriadis et al., 2015; Song et al.,

2015a).

GP latent variable models are generativeand com-

pute a latent subspace without taking into account

class label information, as in (Lawrence, 2005). They

are useful for visualization and regression analysis.

And as such, the resulting latent space may not be op-

timal for classiﬁcation. One way to address this prob-

lem is to introduce a prior distribution such as the uni-

form prior over the latent space to place constraints on

the resulting latent space (Urtasun and Darrell, 2007).

One of the main problems associated with GP latent

variable models is that for a given test example, a sep-

arate estimation process must take a place to compute

the corresponding latent position. This inference in-

troduces additional uncertainties in the entire GP la-

tent variable model computation and added computa-

tional complexity.

Integrating PCA and LDA for dimension reduc-

tion has been discussed in the literature (Yu et al.,

2007; Zhao et al., 2011). These techniques formulate

an objective as a linear combination of PCA and LDA

criteria. On the other hand, we optimize the PCA ob-

jective with LDA as regularizer. This regularization

view has a well established foundation in Gaussian

Process latent variable models.

3 GAUSSIAN PROCESS LATENT

VARIABLE MODELS

Gaussian Process (GP) latent variable models com-

pute a low dimensional latent representation of high

dimensional input data, using a GP mapping from the

latent space to the input data space. Here we brieﬂy

describe GP latent variable models to motivate the in-

troduction of the proposed technique.

Let

X = [x

,··· ,x

]

be a set of centered data, where x

∈ ℜ

, and t denotes

the transpose operator. Also, let

Z = [z

,· ·· ,z

]

represent the corresponding latent variables, where

∈ ℜ

, and q ≪ d. A typical relationship between

the two sets of variables can be described by

x = Wz+ ε, (1)

where W is a d × q matrix, and ε denotes the error

term. Assuming that p(ε) = N(0,β

−1

I) (i.e., isotropic

Gaussian), we have the following conditional proba-

bility distribution over the input space

p(x|z,W,β) = N(Wz,β

−1

I).

This implies that the likelihood of the data can be

written as (matrix normal distribution)

p(X|Z,W,β) =

∏

i=1

p(x

,W,β).

Here it is assumed that x

are independent and iden-

tically distributed (i.i.d.). Probabilistic PCA solution

Information Preserving Discriminant Projections

163

for W can be computed by integrating out the latent

variables (Tipping and Bishop, 1999).

A dual approach is to integrate out W and opti-

mize the latent variables (Lawrence, 2005; Urtasun

and Darrell, 2007). First, we specify a prior distri-

bution p(w

) = N(0,α

−1

I) for W, where w

is the ith

row of W. Then

p(W) =

∏

i=1

p(w

) =

exp(−

tr(αW

W))

(2π)

exp(−

tr(αW

W)). (2)

where C

is a normalization constant. Therefore, the

marginalized likelihood of X can be computed by in-

tegrating out W

p(X|Z,β) =

p(X|Z,W,β)p(W)dW

∝

|K|

d/2

exp(−

tr(K

−1

)), (3)

where

K = (α

−1

+ β

−1

I).

Thus, the distribution of the data given the latent vari-

ables is Gaussian. It can be shown that the solution

Z, obtained by maximizing the GP likelihood of the

latent variables (3), is equivalent to the PCA solution

(Lawrence, 2005; Tipping and Bishop, 1999).

One can place additional conditions on the latent

variables Z by introducing priors over Z. For exam-

ple, if we place a uniform prior on Z, the log prior

becomes

ln p(Z) = −

∑

i=1

Such a prior prefers the latent variables close to the

origin (Urtasun and Darrell, 2007). In classiﬁcation

context, one can incorporate class labels into the prior

(Eleftheriadis et al., 2015; Song et al., 2015b). This

can be accomplished based on discriminant analy-

sis (Fukunaga, 1990). For example, LDA J(Z) =

tr(S

−1

), where S

and S

denote the between and

within class matrices in the latent space, can be im-

posed. Here tr denotes the matrix trace. The prior

thus becomes (Urtasun and Darrell, 2007)

p(Z) = Cexp(−J

−1

One of drawbacks associated with GP latent mod-

els is that for a given test example, a separate esti-

mation process must take a place to compute the cor-

responding latent position. This inference introduces

additional uncertainties in the entire GP latent model

computation and added computational complexity.

4 INFORMATION PRESERVING

DISCRIMINANT

PROJECTIONS

In this section, we develop a novel algorithm that

combines some of the best features of Gaussian Pro-

cess latent models and locality preserving projections.

As discussed above, the optimization of the likeli-

hood (3) results in the PCA solution to the latent vari-

ables Z in the GP latent models. By introducing priors

over latent variables p(Z), one obtains the log poste-

rior (terms that the posterior depends on)

L = −

ln|K| −

tr(K

−1

) + lnp(Z). (4)

As noted in (Rasmussen and Williams, 2005; Urtasun

and Darrell, 2007), in a non-Bayesian setting, the log

prior ln p(Z) can be viewed as a penalty term. And

the maximum a posterior estimate of the latent vari-

ables can be interpreted as the penalized maximum

likelihood estimate. If one introduces a discriminant

prior, (4) represents a trade-off between informative

(as in PCA) and discriminant (as in LDA) representa-

tions. A major drawback is that a separate estimation

process must take place for each test example.

To overcome this problem, we introduce a simple

linear projection technique that preserves the repre-

sentation balance shown in (4), without a separate in-

ference process for test examples. Recall that PCA

ﬁnds the projection p by maximizing

J(p) = tr(p

p), (5)

where XX

denotes the covariance matrix, assuming

the data are centered. Projection p has the property

that the loss

∑

− pp

is minimum. Thus, PCA solutions are entirely infor-

mational in that the resultinglatent representation pre-

serves the maximum information.

To encourage the latent space to be discriminant,

we appeal to the idea behind GP latent variable mod-

els, where the prior over the latent variables place

constraints on variable positions in the latent space.

As noted above, the log prior can be simply inter-

preted as a regularizer. Along this line, we can in-

troduce a regularizer in (5)

J(p) = tr(p

p) + λr(p), (6)

where r(·) represents a regularizer and λ is the reg-

ularization constant. r(·) plays the role of the log

prior in GP latent models that places a constraint in

the resulting latent space. In this work, we introduce

the following regularizers: Laplacian and Linear Dis-

criminant Analysis (LDA).

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

164

4.1 Information Preserving Projections

with Laplacian Regularizer

A locality preserving projection (LPP) builds a graph

of the input data that preserves local neighborhoodin-

formation (He and Niyogi, 2003). LPP then computes

a linear projection from the Laplacian of the graph.

Let W be a n× n weight matrix, where



exp(−tkx

− x

) i 6= j and l(x

) = l(x

)

0 otherwise.

(7)

Here x

represents the ith training example, l(·) de-

notes the label of its input, and t is a kernel parameter.

Let p be a projection such that z

= p

. LLP com-

putes a linear projection by minimizing the following

ojective

∑

i, j

− z

)

A penalty is incurred when examples x

and x

that

are in the same class are projected far apart. It turns

out that the above objective can be rewritten as

∑

i, j

− z

)

∑

i, j

− p

)

= p

LXp, (8)

where L = D− W is the graph Laplacian, and D is

a diagonal matrix with diagonal entries D

∑

Since D

indicates the volume of z

, LLP places the

following constraint on the objective

min

LXp (9)

s.t. p

DXp = 1

The optimal solution can be obtained by solving the

generalized eigenvalue problem

LXp = λX

DXp. (10)

LPP has been shown to be effective in practice (He

and Niyogi, 2003; Cai et al., 2006).

In LPP (He and Niyogi, 2003), the optimal projec-

tion p is computed by minimizing p

LXp. There-

fore, the proposed Laplacian regularized PCA be-

comes

J(p) = tr(p

p) + λtr(p

LX)

−1

p). (11)

Thus, p can be computed by maximizing

IP−Lap

= tr(XX

+ λ(X

LX)

−1

). (12)

We call the resulting projection Information Preserv-

ing Laplacian Projection, or PLap. Note that (11) can

be interpreted as a regularized PCA, where LPP is the

regularizer. Or it can be viewed as a regularized LPP,

where the regularizer is PCA.

4.2 Information Preserving Projections

with LDA Regularizer

We can similarly introduce the LDA regularizer

J(p) = tr(p

p) + λtr(p

−1

p), (13)

where

∑

c=1

∑

i=1,x

∈c

− m

)(x

− m

)

and

∑

c=1

− m)(m

− m)

are the between-class and within-class matrices. Here

m represents the overall mean, m

denotes the mean

of class c, and t represents the transpose operator.

Projection p can be computed by maximizing

IP−LDA

= tr(XX

+ λS

−1

). (14)

We call the resulting projection Information Preserv-

ing LDA Projection, or PLda. Similar to PLap (11),

(13) can be interpreted as a regularized PCA, where

LDA is the regularizer. Or it can be viewed as a regu-

larized LDA, where the regularizer is PCA.

5 EXPERIMENTS

We now examine the performance of the proposed

techniques against competing techniques using sev-

eral examples.

5.1 Methods

The following methods are evaluated in the experi-

ments.

1. PLap–Information Preserving Projection with

Laplacian regularizer (Eq. 12).

2. PLda–Information Preserving Projection with

LDA regularizer (Eq. 14).

3. PCA–Projection that maximizes (Eq. 5)

J(p) = tr(p

p).

4. LDA–Projection that maximizes

J(p) = tr((p

−1

p),

where S

and S

are the within and between ma-

trices, respectively.

5. OLPP–Orthogonal Laplacian Projection (OLPP)

proposed in (Cai et al., 2006).

Information Preserving Discriminant Projections

165

-3 -2 -1 0 1 2 3

-1.5

-1

-0.5

0.5

1.5

-3 -2 -1 0 1 2 3

-1.5

-1

-0.5

0.5

1.5

-3 -2 -1 0 1 2 3

-0.6

-0.4

-0.2

0.2

0.4

0.6

-3 -2 -1 0 1 2 3

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-0.6

-0.4

-0.2

0.2

0.4

0.6

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-0.6

-0.4

-0.2

0.2

0.4

0.6

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-1.5 -1 -0.5 0 0.5 1 1.5 2

-2

-1.5

-1

-0.5

0.5

1.5

-1.5 -1 -0.5 0 0.5 1 1.5 2

-2

-1.5

-1

-0.5

0.5

1.5

Figure 1: Oil ﬂow data projected onto two dimensional

spaces. The left column (top to bottom) shows the two di-

mensional representation of the training examples by PCA,

LDA, PLap, PLda, and OLPP, respectively. The right col-

umn shows the two dimensional representation of the test

examples by PCA, PLap, PLda, LDA, and OLPP, respec-

tively.

Note that OLPP is along the line of LPP (9). It is

known that the solution to (10) may not be orthogonal.

To address this problem, OLPP ﬁrst projects the data

onto the PCA subspace, where it computes the solu-

tion to (10) that preserves orthogonality. It is shown

in (Cai et al., 2006) OLPP outperformsLPP. Thus, we

compare the proposed technique against OLPP in our

experiments.

5.2 Oil Flow Data

We have carried out an experiment to visually exam-

ine our proposed techniques. The data set is the multi-

phase oil ﬂow data (Bishop and James, 1993). This

data set contains examples in 12 dimensions. The data

set has three classes corresponding to the phase of

ﬂow in an oil pipeline: stratiﬁed, annular and homo-

geneous. In this experiment, for illustration purposes,

we randomly sampled 100 examples as the training

data, and additional 1000 examples as the test data.

Figure 1 shows the two dimensional projections

by the ﬁve competing techniques. The left column

(top to bottom) shows the two dimensional repre-

sentation of the training examples by PCA, LDA,

PLap, PLda, and OLPP, respectively. The right col-

umn shows the two dimensional representation of the

test examples by the corresponding techniques. For

PLap and PLda, regularization constant λ was to 100.

Kernel parameter t in Laplacian (9) was set to 0.01

for both PLap and OLPP. The plots show that the

proposed techniques provided better class separation

than the competing methods in the latent space.

Figure 2 shows two dimensional projections of the

test examples by PLap and PLda as a function of reg-

ularization constant λ: 20, 40, 60, and 80. The top

panel shows the representation by PLap, and the bot-

tom panel shows the representation by PLda. As λ in-

creases, the resulting latent space becomes more dis-

criminant. That is, as λ varies, the latent representa-

tions show the characteristics from PCA to LDA, as

expected.

5.3 AR Face Data

This experiment involves the AR-face database (Mar-

tinez and Kak, 2001). The precise nature of the data

set is described in (Martinez and Kak, 2001). For this

experiment, 50 different subjects (25 males and 25

females) were randomly selected from this database.

Images were normalized to the ﬁnal 85 × 60 pixel ar-

rays. Sample images are shown in Figure 3.

This experiment follows the exact setup of the

Small Training Data set experiment described in

(Martinez and Kak, 2001), whereit is shown that PCA

can outperform LDA, given insufﬁcient training data

per subject. Here we want to see how the proposed

techniques fare against PCA in such situations.

In this setup, the ﬁrst seven images from each sub-

ject are selected, resulting in a total of 350 images. To

highlight the effects of a small training data set, two

images from each subject are used as training and the

remaining ﬁve are used as testing. Following (Mar-

tinez and Kak, 2001), we use all 21 different ways of

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

166

-3 -2 -1 0 1 2 3

-2

-1.5

-1

-0.5

0.5

1.5

-3 -2 -1 0 1 2 3

-1.5

-1

-0.5

0.5

1.5

-3 -2 -1 0 1 2 3

-1.5

-1

-0.5

0.5

1.5

-3 -2 -1 0 1 2 3

-1.5

-1

-0.5

0.5

1.5

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5

-2

-1.5

-1

-0.5

0.5

1.5

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

Figure 2: Two dimensional representation of the test examples by PLap and PLda as a function of regularization parameter λ:

20, 40, 60 and 80. The top panel shows the representation by PLap, and the bottom panel shows the representation by PLda.

As λ increases, the resulting latent space becomes more discriminant.

Figure 3: AR sample images.

partitioning the data into training and testing for the

results reported here. The original images of 85× 60

pixels are ﬁrst transformed via PCA into a space of

350 dimensions spanned by the 350 face data. All the

methods see their input from this space.

Dimensions

0 5 10 15 20 25 30 35 40 45 50

Average Error Rate

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

PLap

PLda

LDA

OLPP

PCA

Figure 4: Average error rate registered by PLap, PLda,

LDA, OLPP, and PCA with increasing dimensionality on

the AR face data.

The average error rates in a subspace with 49 di-

mensions over the 21 runs are shown in the ﬁrst row

in Table 1. Figure 4 plots the average error rates reg-

istered by the competing methods over 21 runs on the

AR face data as a function of increasing dimensions.

On average both PLap and PLda clearly outperform

PCA across the 49 subspaces, and consistently per-

form better than the competing methods.

5.4 Additional Data Sets

Additional data sets are used to illustrate the general-

ization performance by each competing technique.

1. MNIST Data (MNIST). The MNIST dataset con-

sists of handwritten digits from the US National

Institute of Standards and Technology (NIST)

(yann.lecun.com/exdb/mnist/). Each digit is a 28

by 28 pixels of intensity values. Thus each digit is

a feature vector of 784 intensities. In this exper-

iment, we randomly selected 100 examples from

each digit, for a totla of 1000 examples.

2. Cat and Dog data (CatDog). This image data set

consists of two hundred images of cat and dog

faces. Each image is a black-and-white 64 × 64

pixel image, and the images have been registered

by aligning the eyes. Sample cat and dog images

are shown in Figure 5.

Figure 5: Sample images of the cat and dog data.

3. Multilingual Text (MText). This data set is a mul-

tilingual text data set (Amini et al., 2009). It is

from the Reuters RCV1 and RCV2 collections.

The data set consists of six categories of docu-

ments: 1) Economics, 2) Equity Markets, 3) Gov-

ernment Social, 4) Corporate/Industrial, 5) Per-

formance, and 6) Government Finance. Each doc-

ument in English has a corresponding document

Information Preserving Discriminant Projections

167

in French, German, Italian and Spanish, translated

using PORTAGE (Uefﬁng et al., 2007). The doc-

uments in English are used in this experiment,

where each document is represented by a bag of

words model in 21531 dimensions. In this exper-

iment, we randomly selected 100 examples from

each class. Thus, the data set has 600 examples in

21531 dimensions.

4. Iris Data (Iris). The iris data set is a publicly

available WVU multimodal data set (Crihalmeanu

et al., 2007). The data set consists of iris images

from subjects of different age, gender, and eth-

nicity, as described in (Crihalmeanu et al., 2007).

The data set is difﬁcult because many examples

are low quality due to blur, occlusion, and noise.

Sample iris images are shown in 6. The evaluation

was done on a randomly selected pair of subjects,

where one subject has 27 examples, and the other

subject has 36 examples for a total of 63 exam-

ples.

To compute features, iris images are segmented

into 25 × 240 templates (Pundlik et al., 2008).

Since Gabor features have been shown to pro-

duce better representation for iris data (Daugman,

2004), these templates are convolved with a log-

Gabor ﬁlter at a single scale to obtain a 6000 fea-

tures.

Figure 6: Sample Iris images.

5. Fingerprint Data (Finger). Similar to the iris

data set, the ﬁnger data set is obtained from pub-

licly available WVU multimodal data sets (Cri-

halmeanu et al., 2007). The data set consists of

ﬁngerprint images from a randomly chosen pair

of subjects. Again, the data set is difﬁcult because

many examples are low quality due to blur, oc-

clusion, and noise. Sample ﬁngerprint images are

shown in 7. This data set has 124 examples, where

one subject has 61 instances, while the other has

63. To represent ﬁngerprints, ridge and bifurca-

tion features are computed using publically avail-

able code (sites.google.com/site/athisnarayanan/).

Resulting feature vectors have 7241 components.

Figure 7: Sample ﬁngerprint images.

6. Feret Face Data (FeretFace). The FERET face

data set consists of 50 subjects, randomly cho-

sen from the Feret face database (Phillips, 2004).

Each subject has 8 instances. Therefore, we have

a set of 400 facial images. The images used here

involvevariations in facial expressionsand illumi-

nation. Each image has 150× 130 pixels. Sample

images are shown in Figure 8.

Figure 8: Normalized Feret sample images.

Table 1: Average error rates registered by the competing

methods on the 7 data sets.

PCA PLap PLda LDA OLPP

ARFace 0.307 0.245 0.245 0.394 0.314

MNIST 0.143 0.152 0.143 0.402 0.148

CatDog 0.492 0.216 0.210 0.457 0.286

MText 0.405 0.217 0.232 0.365 0.305

Iris 0.480 0.133 0.133 0.141 0.136

Finger 0.466 0.378 0.387 0.444 0.467

FeretFace 0.088 0.042 0.042 0.092 0.098

Ave 0.340 0.198 0.199 0.328 0.251

5.5 Experimental Results

In the additional six data set experiments, all training

data have been normalized to have zero mean and unit

variance along each dimension. The test data are sim-

ilarly normalized using training mean and variance.

In the resulting latent space, the one nearest neighbor

rule is used to perform classiﬁcation. The regulariza-

tion constant λ and the kernel parameter t in Lapla-

cian (9) were chosen through ﬁve fold cross valida-

tion. Table 1 shows the 10-fold crossed validated er-

ror rates of the ﬁve competing methods on the 6 data

sets described above.

The table shows that on average both PLap and

PLda outperformed all the competing techniques ex-

amined here. And PLap and PLda performed simi-

larly on these data sets. The results show that classi-

ﬁcation performed in a space that is both informative

and discriminant provides better generalization per-

formance than in either the PCA or LDA subspace

alone.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

168

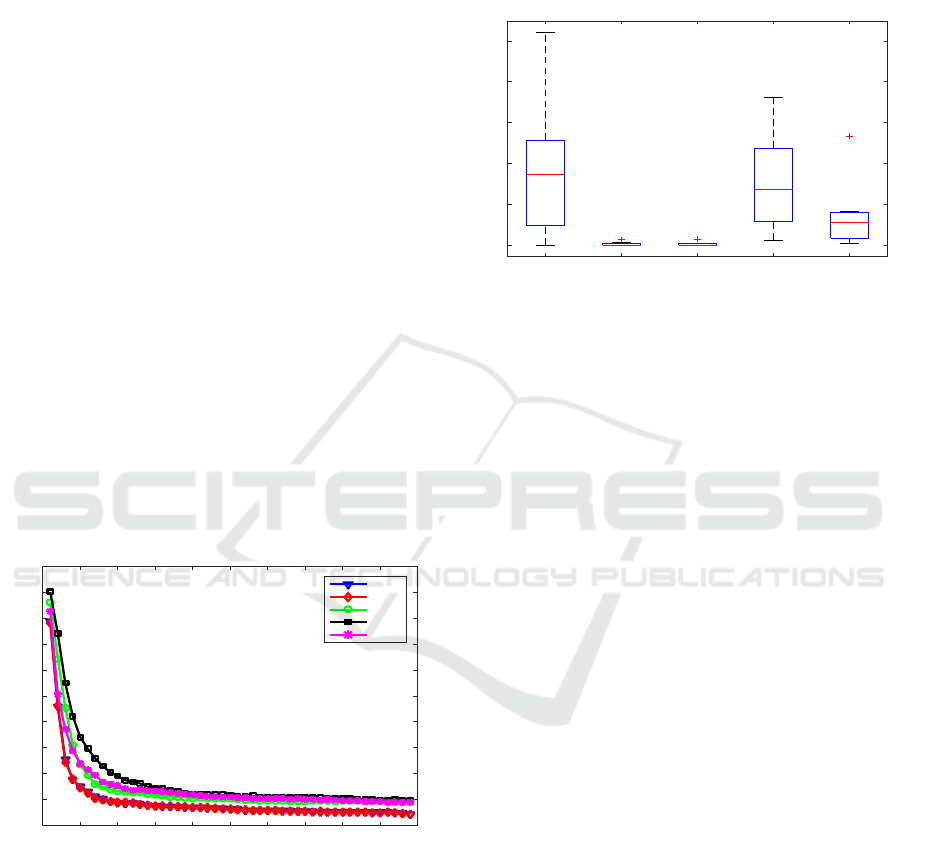
Figure 9 plots the 10-fold error rates computed by

each method on the Feret face data as a function of in-

creasing dimensions. As can be seen, both PLap and

PLda consistently outperform the competing meth-

ods across the 49 subspaces, again demonstrating that

classiﬁcation performed in a space that is both infor-

mative and discriminant provides better generaliza-

tion performance.

5.6 Robustness of Performance

PLap and PLda clearly achieved the best or near best

performance over the 7 data sets, followed by OLPP.

It seems natural to ask the question of robustness.

That is, how well a particular method m performs on

average in situations that are most favorable to other

methods. We compute robustness by computing the

ratio b

of its error rate e

and the smallest error rate

over all methods being compared in a particular ex-

ample:

= e

/ min

1≤k≤5

Thus, the best method m

∗

for that example has b

∗

1, and all other methods have larger values b

≥ 1,

for m 6= m

∗

. The larger the value of b

, the worse

the performance of the mth method is in relation to

the best one for that example. The distribution of the

values for each method m over all the examples,

therefore, seems to be a good indicator of robustness.

Dimensions

0 5 10 15 20 25 30 35 40 45 50

Average Error Rate

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

PLap

PLda

LDA

OLPP

PCA

Figure 9: Average error rate registered by PLap, PLda,

LDA, OLPP, and PCA with increasing dimensionality on

the Feret face data.

Figure 10 plots the distribution of b

for each

method over the 7 data sets. The dark area represents

the lower and upper quartiles of the distribution that

are separated by the median. The outer vertical lines

show the entire range of values for the distribution.

It is clear that the most robust method over the data

sets are PLap. In 5/7 of the data its error rate was the

best (median = 1.0). In the worst case it was no worse

than 62.9% higher than the best error rate. This is fol-

lowed by PLda. In the worst case PLda was no worse

than 69.1%. In contrast, PCA has the worst distribu-

tion, where the worst case was 360.9% higher than

the best error rate.

PCA PLap PLda LDA OLPP

1.5

2.5

3.5

Figure 10: Error distributions of PCA, PLap, PLda, LDA,

and OLPP over the 7 data sets.

6 SUMMARY

We have developed information preserving linear dis-

criminant projections for computing latent represen-

tations. The proposed technique exploits the charac-

teristics of PCA, LDA, and graph Laplacian to com-

pute latent representations that are both informative

and discriminant. As a result, the proposed technique

provides better generalization performance. Experi-

mental results are provided that validate the proposed

technique. We note that the proposed technique is lin-

ear. We plan on extending this technique to the non-

linear case by incorporating kernel tricks in our future

work.

REFERENCES

Abolhasanzadeh, B. (2015). Gaussian process latent vari-

able model for dimensionality reduction in intrusion

detection. In 2015 23rd Iranian Conference on Elec-

trical Engineering, pages 674–678.

Amini, M., Usunier, N., and Goutte, C. (2009). Learning

from multiple partially observed views-an application

to multilingual text categorization. In Advances in

Neural Information Processing Systems, pages 28–36.

Aved, A., Blasch, E., and Peng, J. (2017). Regular-

ized difference criterion for computing discriminants

for dimensionality reduction. IEEE Transactions on

Aerospace and Electronic Systems, 53(5):2372–2384.

Banerjee, B. and Peng, J. (2005). Efﬁcient learning of

multi-step best response. In Proceedings of the Fourth

International Joint Conference on Autonomous Agents

Information Preserving Discriminant Projections

169

and Multiagent Systems, AAMAS ’05, pages 60–66,

New York, NY, USA. ACM.

Belhumeur, V., Hespanha, J., and Kriegman, D. (1997).

Eigenfaces vs. ﬁsherfaces: Recognition using class

speciﬁc linear projection. IEEE Transaction on Pat-

tern Analysis and Machine Intelligence, 19(7):711–

720.

Bellman, R. E. (1961). Adaptive Control Precesses: A

Guided Tour. Princeton University Press.

Bishop, C. and James, G. (1993). Analysis of mul-

tiphase ﬂows using dual-energy gamma densitome-

try and neural networks. Nuclear Instruments and

Methods in Physics Research Section A: Accelerators,

Spectrometers, Detectors and Associated Equipment,

327(2):580–593.

Breiman, L., Friedman, J. H., Olshen, R. A., and Stone,

C. J. (1984). Classiﬁcation and Regression Trees.

Wadsworth and Brooks, Monterey, CA.

Cai, D., He, X., Han, J., and Zhang, H. (2006). Orthogonal

laplacianfaces for face recognition. Trans. Img. Proc.,

15(11):3608–3614.

Cai, L., Huang, L., and Liu, C. (2016). Age estima-

tion based on improved discriminative gaussian pro-

cess latent variable model. Multimedia Tools Appl.,

75(19):11977–11994.

Crihalmeanu, S., Ross, A., Schukers, S., and Hornak, L.

(2007). A protocol for multibiometric data acqui-

sition, storage and dissemination. In Technical Re-

port, WVU, Lane Department of Computer Science

and Electrical Engineering.

Darnell, G., Georgiev, S., Mukherjee, S., and Engelhardt, B.

(2017). Adaptive randomized dimension reduction on

massive data. Journal of Machine Learning Research,

18(140):1–30.

Daugman, J. (2004). How iris recognition works. IEEE

Trans. on Circuits and Systems for Video Technology,

14(21):21–30.

Eleftheriadis, S., Rudovic, O., and Pantic, M. (2015).

Discriminative shared gaussian processes for multi-

view and view-invariant facial expression recognition.

IEEE Transactions on Image Processing, 24(1):189–

204.

Fukunaga, K. (1990). Introduction to statistical pattern

recognition. Academic Press.

Gao, X., Wang, X., Tao, D., and Li, X. (2011). Super-

vised gaussian process latent variable model for di-

mensionality reduction. IEEE Transactions on Sys-

tems, Man, and Cybernetics, Part B (Cybernetics),

41(2):425–434.

Harandi, M., Salzmann, M., and Hartley, R. (2017). Joint

dimensionality reduction and metric learning: A ge-

ometric take. In Precup, D. and Teh, Y. W., edi-

tors, Proceedings of the 34th International Conference

on Machine Learning, volume 70, pages 1404–1413,

International Convention Centre, Sydney, Australia.

PMLR.

He, X. and Niyogi, P. (2003). Locality preserving projec-

tions. In Proceedings of the 16th International Con-

ference on Neural Information Processing Systems,

NIPS’03, pages 153–160. MIT Press.

Heisterkamp, D., Peng, J., and Dai, H. (2000). Feature rele-

vance learning with query shifting for content-based

image retrieval. In Proceedings 15th International

Conference on Pattern Recognition. ICPR-2000, vol-

ume 4, pages 250–253.

Howland, P. and Park, H. (2004). Generalizing discriminant

analysis using the generalized singular valuke decom-

position. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 26(8):995–1006.

Huo, X. and et al (2003). Optimal reduced-rank quadratic

classiers using the fukunaga-koontz transform, with

applications to automated target recognition. In Proc.

of SPIE Conference.

Jiang, X., Gao, J., Wang, T., and Zheng, L. (2012). Su-

pervised latent linear gaussian process latent variable

model for dimensionality reduction. IEEE Transac-

tions on Systems, Man, and Cybernetics, Part B (Cy-

bernetics), 42(6):1620–1632.

Lawrence, N. (2005). Probabilistic non-linear principal

component analysis with gaussian process latent vari-

able models. J. Mach. Learn. Res., 6:1783–1816.

Martinez, A. M. and Kak, A. (2001). Pca versus lda.

IEEE Trans. Pattern Analysis and Machine Intelli-

gence, 23(2):228–233.

Peng, J. (1995). Efﬁcient memory-based dynamic program-

ming. In Proceedings of the Twelfth International

Conference on Machine Learning, pages 438–446.

Peng, J., Seetharaman, G., Fan, W., and Varde, A. (2013).

Exploiting ﬁsher and fukunaga-koontz transforms in

chernoff dimensionality reduction. ACM Transactions

on Knowledge Discovery from Data, 7(2):8:1–8:25.

Phillips, P. (2004). The facial recognition technology (feret)

database. IEEE Trans. Pattern Analysis and Machine

Intelligence, 22.

Pundlik, S., Woodard, D., and Birchﬁeld, S. (2008). Non-

ideal iris segmentation using graph cuts. In IEEE Con-

ference on Computer Vision and Pattern Recognition

Workshops, pages 1–6.

Rasmussen, C. and Williams, C. (2005). Gaussian Pro-

cesses for Machine Learning (Adaptive Computation

and Machine Learning). The MIT Press.

Sarveniazi, A. (2014). An actual survey of dimensionality

reduction. American Journal of Computational Math-

ematics, 4(2):55–72.

Song, G., Wang, S., Huang, Q., and Tian, Q. (2015a).

Similarity gaussian process latent variable model for

multi-modal data analysis. In 2015 IEEE Interna-

tional Conference on Computer Vision (ICCV), pages

4050–4058.

Song, G., Wang, S., Huang, Q., and Tian, Q. (2015b).

Similarity gaussian process latent variable model for

multi-modal data analysis. In 2015 IEEE Interna-

tional Conference on Computer Vision (ICCV), pages

4050–4058.

Tipping, M. and Bishop, C. (1999). Probabilistic princi-

pal component analysis. JOURNAL OF THE ROYAL

STATISTICAL SOCIETY, SERIES B, 61(3):611–622.

Uefﬁng, N., Simard, M., Larkin, S., and Johnson, J. (2007).

NRC’s PORTAGE system for WMT 2007. In In ACL-

2007 Second Workshop on SMT, pages 185–188.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

170

Urtasun, R. and Darrell, T. (2007). Discriminative gaus-

sian process latent variable model for classiﬁcation. In

Proceedings of the 24th International Conference on

Machine Learning, ICML ’07, pages 927–934, New

York, NY, USA. ACM.

Xie, P., Deng, Y., Zhou, Y., Kumar, A., Yu, Y., Zou, J.,

and Xing, E. (2017). Learning latent space mod-

els with angular constraints. In Precup, D. and Teh,

Y. W., editors, Proceedings of the 34th International

Conference on Machine Learning, volume 70 of Pro-

ceedings of Machine Learning Research, pages 3799–

3810, International Convention Centre, Sydney, Aus-

tralia. PMLR.

Yu, J., Tian, Q., Rui, T., and Huang, T. S. (2007). Inte-

grating discriminant and descriptive information for

dimension reduction and classiﬁcation. IEEE Trans-

actions on Circuits and Systems for Video Technology,

17(3):372–377.

Zhang, P., Peng, J., and Domeniconi, C. (2005). Kernel

pooled local subspaces for classiﬁcation. IEEE Trans-

actions on Systems, Man, and Cybernetics, Part B

(Cybernetics), 35(3):489–502.

Zhao, N., Mio, W., and Liu, X. (2011). A hybrid pca-lda

model for dimension reduction. In The 2011 Inter-

national Joint Conference on Neural Networks, pages

2184–2190.

Information Preserving Discriminant Projections

171