
An Approximate Method for Integrated
Stochastic Replenishment Planning with Supplier Selection
Rabin Kumar Sahu
1,2 a
, Clarisse Dhaenens
2 b
, Nadarajen Veerapen
2 c
and Manuel Davy
1
1
Vekia, Euratechnologies-B
ˆ
atiment Urbawood, 58 All
´
ee Marie-Th
´
er
`
ese Vicot-Lhermitte, F-59000 Lille, France
2
Universit
´
e de Lille, CNRS, Centrale Lille, UMR 9189 - CRIStAL - Centre de Recherche en Informatique Signal et
Automatique de Lille, F-59000 Lille, France
Keywords:
Stochastic Demand, Supplier Selection, Replenishment Planning, Heuristic, Integrated Planning.
Abstract:
A practical methodology for integrated stochastic replenishment planning with supplier selection is proposed
for the single item inventory system. A rolling horizon strategy is adopted to implement the ordering decisions.
Our method works in two stages. The first stage is a general black box stage that gives the minimum expected
“coverage period” cost. The second stage uses a dynamic programming approach to compute the minimum
expected cost for the rolling horizon. The proposed method is applicable for both stationary and non-stationary
demand distributions and even for problems with minimum order quantity constraints. We also propose to
examine the benefits of a dynamic supplier selection approach in comparison to selecting a common supplier.
We conduct extensive numerical analyses on synthetic data sets for validation.
1 INTRODUCTION
Integrated replenishment planning with supplier se-
lection is one of the core problems faced by retailers.
With growing competitiveness in the current market,
inclusion of purchasing price and thereby supplier se-
lection in inventory optimization becomes very im-
portant. The inherent multi stage stochastic pro-
gramming (MSSP) (Homem-de Mello and Bayrak-
san, 2014) problem for the multi-period inventory op-
timization problem is very difficult to solve optimally
due to the well known curse of dimensionality (De-
fourny et al., 2012). Supplier selection adds addi-
tional decision or action states and further increases
the complexity. In this paper, we first analyze the eco-
nomic benefits of dynamic supplier selection and af-
terwards develop an approximate method to solve this
problem.
Supplier selection has received considerable atten-
tion in the inventory optimization literature post 2003.
Initially, supplier selection or multiple sourcing op-
tions have been seen as a measure of supply chain risk
mitigation. However, in addition to that, multiple sup-
pliers can have significant monetary benefits in terms
of costs. Most of the replenishment planning models
a
https://orcid.org/0000-0003-1597-6324
b
https://orcid.org/0000-0002-6590-7215
c
https://orcid.org/0000-0003-3699-1080
with multiple suppliers optimize the total cost. This
cost is the summation of the replenishment costs, in-
ventory holding costs and shortage costs. Replenish-
ment costs consist of purchasing cost of the item, and
fixed order/setup costs for placing an order. Typically,
the fixed order cost is independent of order quantity
and charged for every order placed. The purchasing
cost can be different for each supplier and influenced
by any discounting schemes. Shortage costs repre-
sent the costs paid by the buyer when it is unable to
fulfill its demand. It can be either for backordering,
lost sales or a mix of both. Additionally, costs such
as disposal costs for perishable items, miscellaneous
operational costs (i.e. investments, operations, main-
tenance costs) are also taken into account in some lit-
erature. A detailed review of supplier selection prob-
lems can be found in (Yao and Minner, 2017).
Retailers plan their inventory with a short review
period. Availability of multiple suppliers for the same
item poses greater challenge for cost effective opera-
tion. Since the total cost (and thereby the profitabil-
ity) is closely related to the purchase price of an item,
an integrated planning method becomes essential. A
single supplier for a planning horizon is more prac-
tical than dynamic supplier selection. However, any
decision must be taken with due consideration to its
cost implications. Contributions of this article in this
regard are as follows.
80
Sahu, R., Dhaenens, C., Veerapen, N. and Davy, M.
An Approximate Method for Integrated Stochastic Replenishment Planning with Supplier Selection.
DOI: 10.5220/0008970500800088
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 80-88
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

1. We analyze the impact of dynamic a supplier se-
lection approach on overall cost over selecting a
common supplier for the whole planning horizon.
2. We propose a practical framework for dynamic
supplier selection and replenishment planning
with stochastic demand.
The rest of this article is organized as follows.
Section 2 presents the context of the problem dis-
cussed and the motivations behind it. Then in Sec-
tion 3, we present the framework for comparison
between dynamic supplier selection and selecting a
common supplier for the whole planning horizon. We
also propose a near-optimal method for dynamic sup-
plier selection which can be used for real-world ap-
plications. In Section 4 we present the results of the
experiments and discuss their relevance. At last we
conclude the article and propose some future research
directions.
2 CONTEXT AND MOTIVATIONS
The problem considered in this paper was motivated
by a real-world retailer. It has multiple point of sales
at different places along with a central warehouse.
Because of economy of scale, all point-of-sales re-
ceive the items from the central warehouse. The cen-
tral warehouse in turn orders from the external suppli-
ers (Refer Figure 1). The demand information known
at the point of sales is stochastic. Therefore, the de-
mand at the central warehouse can also be interpreted
as a stochastic process. For each item there are multi-
W H
POS
1
POS
2
POS
3
POS
4
POS
N
s = 1
s = 2
s = 3
s = S
Suppliers
Warehouse
Point of Sale
Figure 1: The supply chain network under study.
ple suppliers. Those suppliers differ by the price they
charge per unit item, available batch sizes, lead time
and fixed cost charged per order. The fixed cost is
charged for the transportation and administrative ex-
penses. The retailer aims to minimize total cost in-
curred during a product life cycle. The usual costs
incurred are purchase cost, fixed ordering cost, inven-
tory cost and shortage cost. Any order placed by the
warehouse to any supplier is delivered immediately
without any lead time. Any product left over after the
end of the planning horizon can still be used. There-
fore, the salvage value is not taken into consideration.
Only inventory cost is charged at the end of the plan-
ning horizon.
From the ease of practical applications, two ap-
proaches arise. First, when the retailer chooses only
one supplier for a planning horizon (usually shorter
than the product life cycle), and orders from that sup-
pliers only. This approach is easier to implement in
practice and the computation process of order quan-
tities is comparatively less expensive than its multi-
supplier counterpart. The second approach is to se-
lect suppliers dynamically during each ordering deci-
sion. This approach is computationally more expen-
sive than the previous one due to increase in number
of possible decisions in a dynamic programming set-
ting. Beside, this approach is difficult to implement
in practice. However, dynamic supplier selection has
the potential to be more economical. In this article,
we aim to first analyze the economic benefits of dif-
ferent supplier selection approaches and propose the
retailer a cost benefit analysis. Practical difficulty can
be offset by higher economic gain.
The methods discussed in the previous paragraph
give rise to MSSPs. Those MSSPs can become in-
tractable with increase in number of time periods and
with increase in number of suppliers. Previous meth-
ods given in (Cheaitou and Van Delft, 2013), (Berling
and Mart
´
ınez-de Alb
´
eniz, 2015) and (Berling and
Mart
´
ınez-de Alb
´
eniz, 2016) consider demand distri-
butions to be independent across time. In practice we
often encounter dependent or correlated demand and
distributions not following parametric distributions.
Such application conditions requires new methods.
The aim of this article is to develop a general frame-
work replenishment planning problem with multiple
suppliers, that can be implemented in practice.
3 PROBLEM FORMULATION
In this section, we propose the optimization mod-
els for both, the common supplier selection and the
dynamic supplier selection. Afterwards, we present
An Approximate Method for Integrated Stochastic Replenishment Planning with Supplier Selection
81

an approximate optimization framework based on dy-
namic programming for minimizing the total cost
over the rolling horizon. We also present some pre-
liminary concepts used in our methodology. The no-
tations used throughout the paper are presented in Ta-
ble 1. We consider a planning horizon of length
ˆ
T and
S suppliers.
Table 1: Notations for the parameters and variables.
Sets
T Set of time periods t ∈ {1, ...,
ˆ
T }
S Set of suppliers s ∈ {1, ..., S}
Parameters
d
t
Random demand at time t, ∈ R
+
R
s
Unit purchase price from supplier s, ∈ R
+
K
s
Fixed cost of ordering per order from sup-
plier s, ∈ R
+
H Inventory holding cost per unit inventory
per unit time period, ∈ R
+
W Backorder cost per unit, ∈ R
+
Decision Variables
q
st
Order quantity from supplier s at time t, ∈
Z
+
α
st
Binary indicator for positive order from
supplier s at time t, ∈ {0, 1}
I
t
Inventory at the end of time t, ∈ Z
+
3.1 Preliminaries
Two preliminary concepts are presented which are
used throughout the article. First, we present vari-
ous control strategies for multi-period stochastic in-
ventory optimization problems, and then we present a
rolling horizon framework. The notations used in this
article are presented in Table 1.
The control strategy or the uncertainty strategy
for the multi-period stochastic inventory optimization
problem is defined based on two conditions: when the
decisions regarding the order timings (schedule) are
taken, and when the corresponding order quantities
are decided. Those control strategies are broadly di-
vided into three categories: static, static-dynamic, and
dynamic uncertainty (Rossi et al., 2015). When the
decision maker determines both the ordering sched-
ule and the order quantities at the very beginning of
the planning horizon, it falls under the static uncer-
tainty strategy. In case of the static-dynamic uncer-
tainty strategy, timing of inventory reviews are fixed
at the beginning of the planning horizon and the as-
sociated order quantities are decided upon only when
orders are issued. The dynamic uncertainty strategy
allows the decision maker to decide dynamically at
each time period whether or not to place an order and
how much to order. This strategy is known to be cost-
optimal (Scarf, 1959). Our proposed methodology
follows a static-dynamic uncertainty strategy. This is
due to difficulty in practical implementation of a dy-
namic uncertainty strategy.
Next, we discuss rolling horizon approach. A
rolling horizon is usually a planning period shorter
than the planning horizon. An approach utilizing a
rolling horizon scheme might compute optimal order-
ing decisions for the whole horizon but, implements
only the first one. There are two justifications for
adopting a rolling horizon approach. First is the curse
of dimensionality. For any MSSP with increase in the
number of stages the problem becomes computation-
ally intractable. At the same time the optimal solution
of a MSSP with few stages is usually a myopic solu-
tion of the global problem. Therefore, a compromise
can be made between the computation time and solu-
tion quality by implementing the decisions in a rolling
horizon manner (Rahdar et al., 2018). Second jus-
tification is that, with demand information farther in
the future the forecast quality is usually less accurate.
Therefore, inclusion of forecast information very far
in future only adds to computation time without any
substantial gain to the solution quality.
The mechanism of a rolling horizon approach is as
follows. Under this, the demand information up to
ˆ
T
(length of the planning horizon) periods is available.
The total length of the planning horizon can extend up
to infinity. A suitable length of rolling horizon T ≤
ˆ
T
is then chosen. During the beginning of each period t,
ordering decisions are determined considering the de-
mand during the rolling horizon and initial inventory
level at that time. Depending upon the adopted con-
trol strategy, multiple ordering decisions may be eval-
uated but, only the first one is implemented. The pro-
cess is then repeated for each of the next periods with
updated inventory level and demand information. A
rolling horizon approach enables tackling dependent
demand scenario with updated forecast in each order
cycle.
3.2 Common Supplier Selection
The multi-period stochastic inventory optimization
problem with a common supplier for every period is a
finite-stage MSSP. It can be solved optimally with dy-
namic programming (
¨
Ozen et al., 2012). This requires
the end state to be known and demands across time to
be independent. The optimal cost can be found for
each supplier independently. Then the supplier hav-
ing the minimum cost for the planning horizon can
be selected. The functional equation of the resulting
dynamic program is as follows. With C
s
t
(I
t−1
) being
the optimal cost for supplier s with state I
t−1
at time
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
82
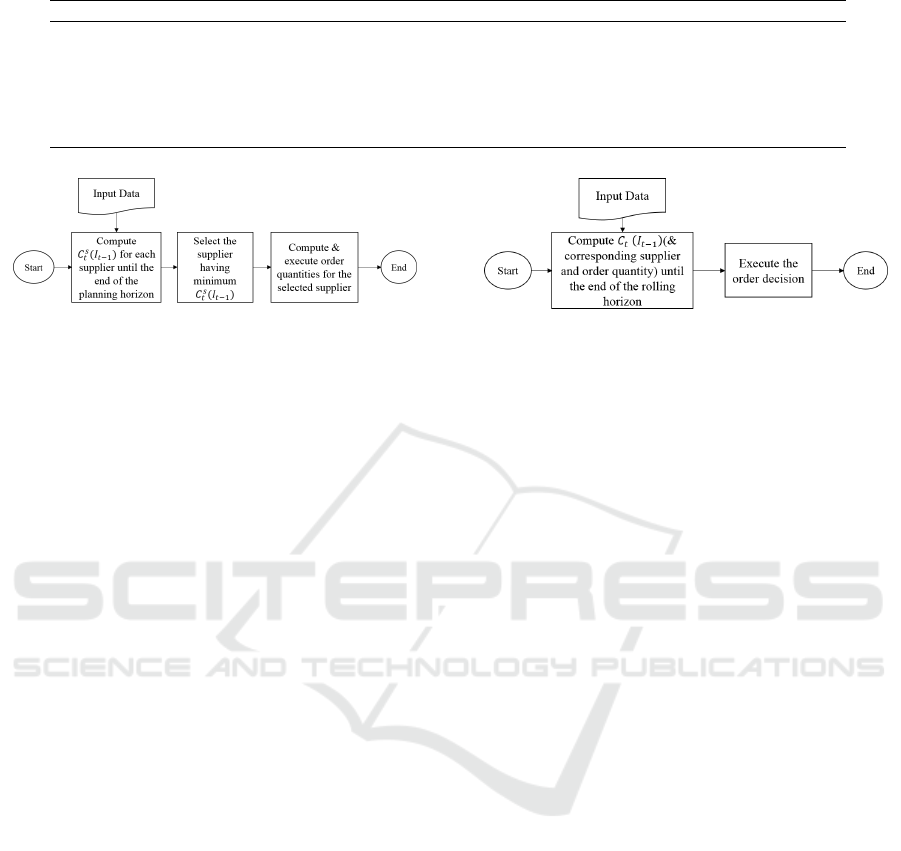
Table 2: MCPC Calculations.
t = 1 t = 2 ... ... t = T − 1 t = T
˜
C
∗
s
(I
0
, q, 1, 1)
˜
C
∗
s
(0, q, 2, 2) ... ...
˜
C
∗
s
(0, q, T − 1, T − 1)
˜
C
∗
s
(0, q, T, T )
˜
C
∗
s
(I
0
, q, 1, 2)
˜
C
∗
s
(0, q, 2, 3) ... ...
˜
C
∗
s
(0, q, T − 1, T )
... ... ... ...
... ... ... ...
˜
C
∗
s
(I
0
, q, 1, T − 1)
˜
C
∗
s
(0, q, 2, T )
˜
C
∗
s
(I
0
, q, 1, T )
Figure 2: Working of common supplier selection.
t, and q
st
being the actions
C
s
t
(I
t−1
) = min
q
st
E
H(I
t−1
+ q
st
− d
t
)
+
+W [−I
t−1
− q
st
+ d
t
]
+
+ K
s
α
st
+
S
∑
s=1
R
s
q
st
+ C
t+1
(I
t−1
+ q
st
− d
t
)
(1)
α
st
=
(
1 if q
st
> 0
0 otherwise
(2)
The first, second, third and fourth terms represent
the expected inventory holding costs, expected short-
age costs, fixed order cost and purchase costs respec-
tively for period t. The last term represents the min-
imum expected cost for the next period. The above
equation can be solved optimally by value iteration
(Puterman, 2014). The methodology is summarized
in Figure 2.
3.3 Dynamic Supplier Selection
The dynamic supplier selection problem is quite
similar to the common supplier problem except, it
has several sets of possible actions. In the case of
common supplier selection, we considered the set
of possible actions q
st
for each supplier s separately.
However, in case of a dynamic supplier selection, we
consider all possible actions from all possible sup-
pliers in a single dynamic program. The functional
equation is given below. With C
t
(I
t−1
) being the
optimal cost with state I
t−1
at time t, and q
st
being
the actions
Figure 3: Working of dynamic supplier selection.
C
t
(I
t−1
) = min
q
st
,s∈S
E
H(I
t−1
+
S
∑
s=1
q
st
− d
t
)
+
+W [−I
t−1
−
S
∑
s=1
q
st
+ d
t
]
+
+
S
∑
s=1
K
s
α
st
+
S
∑
s=1
R
s
q
st
+ C
t+1
(I
t−1
+
S
∑
s=1
q
st
− d
t
)
(3)
In the above program, we do not consider the ca-
pacity constraint for the suppliers. Inclusion of capac-
ity constraint can affect the ordering decisions and,
we plan to study this in future research. Dynamic sup-
plier selection can be achieved using the above formu-
lation. Choice of supplier at an ordering epoch is af-
fected by the inventory position, unit purchase price,
fixed order cost and minimum order quantities, etc.
The methodology is summarized in Figure 3.
3.3.1 Approximation Framework
The dynamic programs presented previously can be-
come intractable when the number of periods is high.
In this section we present an approximation frame-
work to alleviate the curse of dimensionality without
compromising the solution quality substantially.
We introduce a term called minimum coverage pe-
riod cost (MCPC) which is formally defined as fol-
lows. Under the assumption of discrete time periods
the MCPC is the minimum expected cost during a
coverage period of length not less than one. A cov-
erage period is such that any order received in the
beginning would suffice till the end. Our proposed
method has two major stages. The first stage is a gen-
eral black box which gives the optimal order quantity
and cost for any discrete coverage period. Such meth-
ods are given in (Sahu et al., 2019) for any general
An Approximate Method for Integrated Stochastic Replenishment Planning with Supplier Selection
83

distributions and (
¨
Ozen et al., 2012) for parametric
distributions. Once we get those costs, we can pro-
ceed to minimize the cost for the whole rolling hori-
zon in the second stage using a dynamic programming
approach XDP. The process is depicted in Figure 4.
Inputs
BLACK BOX XDP
Outputs
Figure 4: Illustration of the approximation framework. The
inputs required are current inventory level, demand infor-
mation and cost parameters. The BLACK BOX gives the
MCPC for any given coverage period. The XDP used those
costs to minimize the rolling horizon cost using a dynamic
program.
3.3.2 Rolling Horizon Cost Optimization
We propose a dynamic programming approach to
minimize the total cost over the rolling horizon. The
process is presented in Figure 5.
Let us consider a rolling horizon of length T . An
order can be placed at any time t ∈ {1, 2, ..., T }. When
the decision is taken at time t = 1, order can be placed
at any one of the suppliers s ∈ {1, 2, ..., S}. The order
quantity for any supplier can have coverage period
upto {1, 2, ..., T }. If we go further in time at t = 2,
we can have different ordering options based on the
state of inventory. However, our initial definition of
coverage period states that the delivered quantity suf-
fices till the end of that coverage period. Therefore,
for each time period t > 1, we compute the optimal
order quantity and cost assuming the inventory state
equal to zero. Hence, if an ordering decision is made
at time t = 2 of the same rolling horizon, the order
quantity for any supplier can have coverage period
up to {2, 3, ..., T }. Similarly, if a ordering decision
is made at time t of the same rolling horizon, the
order quantity for any supplier can have coverage
period {t, t + 1, ..., T }. From the above we have, at
t = 1, there are ST ordering options, at t = 2, there
are S(T − 1) ordering options and so on. At t = T ,
there are S ordering options. Additionally, no order
option can also be adopted. Let
˜
C
∗
s
(I
T
1
, q, T
1
, T
2
)
represent the MCPC for supplier s, for the coverage
period T
1
to T
2
(T
2
≥ T
1
). From the analysis given
in the paragraph above, all possible ordering options
during a rolling horizon of length T are given in
Table 2. Those values are provided by the BLACK
BOX along with corresponding order quantities.
Mathematically,
˜
C
∗
s
(I
T
1
, q, T
1
, T
2
) is defined as fol-
lows.
˜
C
∗
s
(I
T
1
, q, T
1
, T
2
) = min E
T
2
∑
t=T
1
H[I
T
1
+ q
sT
1
−
t
∑
τ=T
1
d
τ
]
+
+W [−I
T
1
− q
sT
1
+
t
∑
τ=T
1
d
τ
]
+
+ R
s
q
sT
1
+ α
sT
1
K
s
(4)
The possible different
˜
C
∗
s
(I
T
1
, q, T
1
, T
2
) are presented
in Table 2. We end up with
T (T+1)
2
different costs for
a rolling horizon of length T . After the computation
of all the minimum expected costs, we can solve the
multi-stage problem for the whole rolling horizon us-
ing a dynamic programming formulation as presented
below. All the MCPCs are computed at zero initial
inventory.
Z
T
= min
s
˜
C
∗
s
(0, q, T, T ) (5)
Z
T −1
= min
min
s
˜
C
∗
s
(0, q, T − 1, T − 1) + Z
T
,
min
s
˜
C
∗
s
(0, q, T − 1, T )
(6)
Z
T −2
= min
min
s
˜
C
∗
s
(0, q, T − 2, T − 2) + Z
T −1
,
min
s
˜
C
∗
s
(0, q, T − 2, T − 1) + Z
T
,
min
s
˜
C
∗
s
(0, q, T − 2, T )
(7)
Z
1
= min
min
s
˜
C
∗
s
(0, q, 1, 1) +Z
2
,
min
s
˜
C
∗
s
(0, q, 1, 2) +Z
3
, ...,
min
s
˜
C
∗
s
(0, q, 1, T − 1) + Z
T
min
s
˜
C
∗
s
(0, q, 1, T )
(8)
The above formulation is a backward recursion.
At t = T , we have the option of ordering only to cover
the period T . Therefore, its expected minimum cost
is the minimum of expected costs across the suppliers
with coverage period T . Similar computations for the
whole rolling horizon is of the order
ST (T+1)
2
.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
84

t = 1
I
0
q
s1
t =
ˆ
T
T
T
1
T
2
˜
C
s
(I
0
= 0, q, T
1
, T
2
)
T
1
= 1 T
2
= 1
˜
C
s
(I
0
, q, 1, 1)
T
1
= 1 T
2
= 2
˜
C
s
(I
0
, q, 1, 2)
Figure 5: Illustration of an ordering mechanism and cost computation with a rolling horizon length T and planning horizon
length
ˆ
T . During each time period t order quantities are determined considering the opening inventory level and demand over
a t to t + T window. The black box stage give the optimal cost for all possible coverage periods T
1
to T
2
.
4 NUMERICAL RESULTS
In this section, we present the experimental protocol
and the detailed numerical results. To test the per-
formance of our proposed method, we compare its
cost with the optimal cost obtained with dynamic pro-
gramming.
4.1 Experimental Protocol
In the previous section, we have explained our pro-
posed two-stage method. In the first stage, we ap-
proximate the minimum expected costs for all pos-
sible coverage periods. We use these costs to formu-
late a dynamic programming approach to compute the
minimum cost over the whole rolling horizon.
Our test-bed is as follows. At the beginning of
time period t = 1, the demand forecasts upto period
T are available. The decision maker uses this demand
information, current inventory and cost parameters to
compute the order quantity and places the ordered for
the first period. The problem instances are presented
in Table 3. In the beginning, we start with inventory
I
0
= 0 and zero backorder. Any order placed is deliv-
ered immediately. A random demand following the
same distribution as forecast is received and the corre-
sponding excess inventory or backorder levels are up-
dated. The period cost is computed as the sum of fixed
order cost, inventory cost and backorder cost. The
process is repeated until period T with demand infor-
mation of period {2, 3, ..., T }, {3, 4, ..., T } and so on
upto {T }. The total cost is then computed as the sum
of all period costs. We first obtain the optimal cost of
the above process using dynamic programming. We
conduct simulation to assess the expected cost with
our proposed method. Since our method uses sam-
ples, we conduct 10
3
such simulations to estimate the
expected cost of the planning horizon. We conduct
tests for stationary demand that follow poisson dis-
tribution, with means equal to 5 and a planning hori-
zon length of 20 periods. For the first set, inventory
costs are H = {1, 0.5, 0.1}, the backorder cost W = 20
and for second set, the inventory cost is kept fixed at
H = 1 and backorder costs are W = {30, 25, 15}. Our
An Approximate Method for Integrated Stochastic Replenishment Planning with Supplier Selection
85

Table 3: Problem instances.
H W K
s
R
s
MOQ
Set − 1
1 20 [20,20,20,20] [10,9,8,7] 0
1 20 [20,40,80,150] [10,10,10,10] 0
1 20 [20,40,80,150] [10,9,8,7] 0
1 20 [20,40,80,150] [10,8,7,5] 0
0.5 20 [20,20,20,20] [10,9,8,7] 0
0.5 20 [20,40,80,150] [10,10,10,10] 0
0.5 20 [20,40,80,150] [10,9,8,7] 0
0.5 20 [20,40,80,150] [10,8,7,5] 0
0.1 20 [20,20,20,20] [10,9,8,7] 0
0.1 20 [20,40,80,150] [10,10,10,10] 0
0.1 20 [20,40,80,150] [10,9,8,7] 0
0.1 20 [20,40,80,150] [10,8,7,5] 0
Set − 2
1 30 [20,20,20,20] [10,9,8,7] 0
1 30 [20,20,40,80] [10,10,10,10] 0
1 30 [20,20,40,80] [10,9,8,7] 0
1 30 [20,20,40,80] [10,8,7,5] 0
1 25 [20,20,20,20] [10,9,8,7] 0
1 25 [20,20,40,80] [10,10,10,10] 0
1 25 [20,20,40,80] [10,9,8,7] 0
1 25 [20,20,40,80] [10,8,7,5] 0
1 15 [20,20,20,20] [10,9,8,7] 0
1 15 [20,20,40,80] [10,10,10,10] 0
1 15 [20,20,40,80] [10,9,8,7] 0
1 15 [20,20,40,80] [10,8,7,5] 0
Set − 3
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [0,5,10,15]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [1,6,12,18]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [2,7,14,21]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [3,8,16,24]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [4,9,18,27]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [5,10,20,30]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [6,11,22,33]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [7,12,24,36]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [8,13,26,39]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [9,14,28,42]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [10,15,30,45]
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [11,16,32,48]
Table 4: Comparison of optimal expected costs of common
supplier selection (CS) and dynamic supplier selection (DS)
approaches for input data Set − 1. Backorder cost W = 20,
MOQ = None.
H K
s
R
s
CS DS(Gain %)
1 [20,20,20,20] [10,9,8,7] 1032.0 1032.0(0.0)
1 [20,40,80,150] [10,10,10,10] 1331.8 1331.8(0.0)
1 [20,40,80,150] [10,9,8,7] 1331.8 1330.6(0.1)
1 [20,40,80,150] [10,8,7,5] 1245.3 1242.9(0.2)
0.5 [20,20,20,20] [10,9,8,7] 943.5 943.5(0.0)
0.5 [20,40,80,150] [10,10,10,10] 1244.4 1244.4(0.0)
0.5 [20,40,80,150] [10,9,8,7] 1230.2 1223.2(0.6)
0.5 [20,40,80,150] [10,8,7,5] 1107.4 1090.4(1.5)
0.1 [20,20,20,20] [10,9,8,7] 827.5 827.5(0.0)
0.1 [20,40,80,150] [10,10,10,10] 1130.1 1130.1(0.0)
0.1 [20,40,80,150] [10,9,8,7] 1032.0 1003.5(2.8)
0.1 [20,40,80,150] [10,8,7,5] 825.7 806.0(2.4)
problem has 4 suppliers. Their unit price, fixed or-
der costs are presented in respective result tables. We
also test when minimum order quantity constraint is
also present. The rolling horizon length is set at 20
periods.
Table 5: Comparison of optimal expected costs of common
supplier selection (CS) and dynamic supplier selection (DS)
approaches for input data Set − 2. Inventory holding cost
H = 1, MOQ = None.
W K
s
R
s
CS DS(Gain %)
30 [20,20,20,20] [10,9,8,7] 1049.7 1049.7(0.00)
30 [20,40,80,150] [10,10,10,10] 1352.9 1352.9(0.00)
30 [20,40,80,150] [10,9,8,7] 1352.9 1350.7(0.17)
30 [20,40,80,150] [10,8,7,5] 1265.7 1262.7(0.24)
25 [20,20,20,20] [10,9,8,7] 1041.5 1041.5(0.00)
25 [20,40,80,150] [10,10,10,10] 1343.1 1343.1(0.00)
25 [20,40,80,150] [10,9,8,7] 1343.1 1341.3(0.13)
25 [20,40,80,150] [10,8,7,5] 1257.6 1254.5(0.24)
15 [20,20,20,20] [10,9,8,7] 1018.2 1018.2(0.00)
15 [20,40,80,150] [10,10,10,10] 1314.7 1314.7(0.00)
15 [20,40,80,150] [10,9,8,7] 1314.7 1313.4(0.10)
15 [20,40,80,150] [10,8,7,5] 1228.9 1227.2(0.14)
Table 6: Comparison of optimal expected costs of com-
mon supplier selection (CS) and dynamic supplier selection
(DS) approaches for input data Set − 3. Inventory hold-
ing cost H = 1, backorder cost W = 20, fixed order costs
K
s
= [40, 40, 40, 40], Purchase prices R
s
= [10, 9, 8, 7].
MOQ CS DS Gain (%)
[0, 5, 10, 15] 1152.09 1149.01 0.27
[1, 6, 12, 18] 1156.56 1150.89 0.49
[2, 7, 14, 21] 1163.27 1154.51 0.76
[3, 8, 16, 24] 1172.33 1159.80 1.08
[4, 9, 18, 27] 1194.99 1171.65 1.99
[5, 10, 20, 30] 1209.36 1183.54 2.18
[6, 11, 22, 33] 1222.40 1195.97 2.21
[7, 12, 24, 36] 1264.04 1215.25 4.01
[8, 13, 26, 39] 1288.67 1235.14 4.33
[9, 14, 28, 42] 1304.23 1253.52 4.05
[10, 15, 30, 45] 1310.69 1271.93 3.05
[11, 16, 32, 48] 1317.82 1289.63 2.19
4.2 Results and Discussion
The results are divided into two parts. Tables 4, 5 and
6 present the comparison between the common sup-
plier selection and dynamic supplier selection. When
the suppliers are equivalent in terms of fixed cost or
unit purchase price, both approaches yield equal cost.
Only when suppliers are different in both parameters,
there is a cost difference. The results from Tables 4,
5 show that the cost difference is higher when the
ratio of backorder cost to inventory holding cost is
higher. When the minimum order quantity constraint
is present, even with equal fixed cost for all suppli-
ers, results show a cost different between both ap-
proaches. In each instance, dynamic supplier selec-
tion outperforms common supplier selection. The av-
erage runtime for common supplier selection is 2821
seconds on average.
In the second part, we present the results using our
proposed approximate method in Tables 7, 8 and 9
for the same problem instances. We get major gain in
terms of runtime. The average runtime of our method
is 6 milliseconds. The average error for the problem
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
86

Table 7: Comparison of approximate expected costs using XDP for common supplier selection (CS) and dynamic supplier
selection (DS) approaches for input data Set − 1. Inventory holding cost W = 20, MOQ = None.
H W K
s
R
s
CS Error(%) DS Error (%)
1 20 [20,20,20,20] [10,9,8,7] 1033.40 0.14 1033.40 0.14
1 20 [20,40,80,150] [10,10,10,10] 1347.88 1.20 1347.88 1.20
1 20 [20,40,80,150] [10,9,8,7] 1335.87 0.30 1332.54 0.14
1 20 [20,40,80,150] [10,8,7,5] 1246.06 0.06 1245.53 0.21
0.5 20 [20,20,20,20] [10,9,8,7] 948.54 0.53 948.54 0.53
0.5 20 [20,40,80,150] [10,10,10,10] 1260.60 1.30 1260.60 1.30
0.5 20 [20,40,80,150] [10,9,8,7] 1232.75 0.20 1226.30 0.26
0.5 20 [20,40,80,150] [10,8,7,5] 1117.98 0.95 1108.49 1.66
0.1 20 [20,20,20,20] [10,9,8,7] 836.30 1.07 836.30 1.07
0.1 20 [20,40,80,150] [10,10,10,10] 1133.79 0.32 1133.79 0.32
0.1 20 [20,40,80,150] [10,9,8,7] 1041.51 0.92 1010.19 0.67
0.1 20 [20,40,80,150] [10,8,7,5] 830.07 0.53 811.55 0.69
Average 0.63 0.68
Table 8: Comparison of approximate expected costs using XDP for common supplier selection (CS) and dynamic supplier
selection (DS) approaches for input data Set − 2. Backorder cost H = 1, MOQ = None.
H W K
s
R
s
CS Error(%) DS Error (%)
1 30 [20,20,20,20] [10,9,8,7] 1 059.74 0.96 1059.74 0.96
1 30 [20,20,40,80] [10,10,10,10] 1 383.74 2.28 1383.74 2.28
1 30 [20,20,40,80] [10,9,8,7] 1 381.00 2.07 1378.49 2.06
1 30 [20,20,40,80] [10,8,7,5] 1 266.37 0.05 1263.33 0.05
1 25 [20,20,20,20] [10,9,8,7] 1 051.27 0.93 1051.27 0.93
1 25 [20,20,40,80] [10,10,10,10] 1 353.66 0.79 1353.66 0.79
1 25 [20,20,40,80] [10,9,8,7] 1 383.64 3.02 1365.56 1.81
1 25 [20,20,40,80] [10,8,7,5] 1 261.35 0.30 1259.22 0.37
1 15 [20,20,20,20] [10,9,8,7] 1 030.42 1.20 1030.42 1.20
1 15 [20,20,40,80] [10,10,10,10] 1 369.00 4.13 1369.00 4.13
1 15 [20,20,40,80] [10,9,8,7] 1 349.40 2.64 1319.11 0.44
1 15 [20,20,40,80] [10,8,7,5] 1 235.79 0.56 1229.82 0.21
Average 1.58 1.26
Table 9: Comparison of approximate expected costs using XDP for common supplier selection (CS) and dynamic supplier
selection (DS) approaches for input data Set − 3. Inventory holding cost H = 1, backorder cost W = 20, fixed order costs
K
s
= [40, 40, 40, 40], Purchase prices R
s
= [10, 9, 8, 7].
H W K
s
R
s
MOQ CS Error(%) DS Error (%)
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [0,5,10,15] 1192.09 3.47 1178.31 2.55
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [1,6,12,18] 1168.56 1.04 1154.84 0.34
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [2,7,14,21] 1174.27 0.95 1172.75 1.58
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [3,8,16,24] 1212.33 3.41 1162.70 0.25
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [4,9,18,27] 1203.99 0.75 1187.47 1.35
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [5,10,20,30] 1226.36 1.41 1217.51 2.87
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [6,11,22,33] 1238.40 1.31 1214.87 1.58
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [7,12,24,36] 1272.04 0.63 1224.24 0.74
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [8,13,26,39] 1306.67 1.40 1259.84 2.00
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [9,14,28,42] 1320.23 1.23 1270.82 1.38
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [10,15,30,45] 1327.69 1.30 1274.98 0.24
1 20 [40, 40, 40, 40] [10, 9, 8, 7] [11,16,32,48] 1341.82 1.82 1317.23 2.14
Average 1.56 1.42
problem instance is less than 2% for both common
supplier selection and dynamic supplier selection
5 CONCLUSIONS
In this article, we address the integrated replenish-
ment planning and supplier selection problem. This
problem can be formulated as a multi-stage stochas-
An Approximate Method for Integrated Stochastic Replenishment Planning with Supplier Selection
87

tic problem. Due to the curse of dimensionality,
it is intractable for medium to large size problems.
For its practical importance and complexity, it has
received considerable attention in the literature post
2003, however, mostly as a measure of risk mitiga-
tion. Nowadays, multi-brand retailers face the prob-
lem during their day to day operation. This gives rise
to the need of its study as a economic option and the
development of faster optimization method. We first
conduct the financial benefit analysis of dynamic sup-
plier selection versus selecting a common supplier for
the planning horizon. Then we propose an approxi-
mation framework for the dynamic supplier selection
problem.
A common supplier for the whole planning hori-
zon is a practically more appealing feature. However,
the dynamic supplier selection results in higher eco-
nomic benefits. Both of the aforementioned prob-
lems are multi-stage stochastic optimization prob-
lems. However, the latter one is relatively more com-
plex due to its increased number of possible actions.
Numerical analysis suggest that the dynamic supplier
supplier selection approach always outperforms the
approach with one common supplier, especially when
the inventory holding costs and the backorder costs
are very different, and when the suppliers impose a
minimum order quantity constraints. Finding the op-
timal solutions of any of the above approaches is time
consuming. Hence, we develop an approximation
framework based on dynamic programming.
The framework works in two stages. The first
stage is a general black box which gives the opti-
mal order quantity and cost for discrete coverage pe-
riod. We then end up with
T (T+1)
2
different costs for
a rolling horizon of length T . Afterwards, a dynamic
programming approach optimizes the total cost for the
rolling horizon. We conduct numerical analysis to at-
test the performance of our proposed method. For the
synthetic instances the approach provides near opti-
mal solution at a fraction of the computation time.
On average the optimality gap is 1.18%. The average
computation time is 6 milliseconds.
Future research aspects are to test the method in
lost sale environments and when the suppliers give
quantity discounts which are some of the common
practices nowadays in retail. Also, deeper analysis
can be done to suggest when the economic benefits of
a dynamic supplier selection problems outweighs the
practical benefits of selecting a common supplier.
REFERENCES
Berling, P. and Mart
´
ınez-de Alb
´
eniz, V. (2015). Dynamic
speed optimization in supply chains with stochastic
demand. Transportation Science, 50(3):1114–1127.
Berling, P. and Mart
´
ınez-de Alb
´
eniz, V. (2016). A charac-
terization of optimal base-stock levels for a multistage
serial supply chain. Naval Research Logistics (NRL),
63(1):32–46.
Cheaitou, A. and Van Delft, C. (2013). Finite horizon
stochastic inventory problem with dual sourcing: Near
myopic and heuristics bounds. International Journal
of Production Economics, 143(2):371–378.
Defourny, B., Ernst, D., and Wehenkel, L. (2012). Multi-
stage stochastic programming: A scenario tree based
approach to planning under uncertainty. In Deci-
sion theory models for applications in artificial intel-
ligence: concepts and solutions, pages 97–143. IGI
Global.
Homem-de Mello, T. and Bayraksan, G. (2014). Monte
carlo sampling-based methods for stochastic opti-
mization. Surveys in Operations Research and Man-
agement Science, 19(1):56–85.
¨
Ozen, U., Do
˘
gru, M. K., and Tarim, S. A. (2012).
Static-dynamic uncertainty strategy for a single-
item stochastic inventory control problem. Omega,
40(3):348–357.
Puterman, M. L. (2014). Markov Decision Processes.: Dis-
crete Stochastic Dynamic Programming. John Wiley
& Sons.
Rahdar, M., Wang, L., and Hu, G. (2018). A tri-level op-
timization model for inventory control with uncertain
demand and lead time. International Journal of Pro-
duction Economics, 195:96–105.
Rossi, R., Kilic, O. A., and Tarim, S. A. (2015). Piece-
wise linear approximations for the static–dynamic un-
certainty strategy in stochastic lot-sizing. Omega,
50:126–140.
Sahu, R. K., Dhaenens, C., Veerapen, N., and Davy, M.
(2019). A sample-based optimization approach for the
stochastic replenishment planning. Submitted.
Scarf, H. (1959). The optimality of (s, S) policies in the dy-
namic inventory problem. Technical report, Stanford
Univ Calif Applied Mathematics and Statistics Labs.
Yao, M. and Minner, S. (2017). Review of multi-supplier
inventory models in supply chain management: An
update. Available at SSRN 2995134.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
88
