
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State
Space and Action Space via Deep Reinforcement Learning
Gurpreet Singh
1
, Daniel M. Lofaro
2
and Donald Sofge
2
1
Robotics and Intelligent Systems Engineering (RISE) Laboratory, Naval Air Warfare Center Aircraft Division,
Lakehurst NJ 08733, U.S.A.
2
Distributed Autonomous Systems Group, U.S. Naval Research Laboratory, 4555 Overlook Ave SW,
Washington DC 20375, U.S.A.
Keywords:
Swarm Robotics, Deep Reinforcement Learning, Continuous Space, Actor Critic.
Abstract:
In this paper we address the pursuit-evasion problem using deep reinforcement learning techniques. The
goal of this project is to train each agent in a swarm of pursuers to learn a control strategy to capture the
evaders in optimal time while displaying collaborative behavior. Additional challenges addressed in this paper
include the use of continuous agent state and action spaces, and the requirement that agents in the swarm
must take actions in a decentralized fashion. Our technique builds on the actor-critic model-free Multi-Agent
Deep Deterministic Policy Gradient (MADDPG) algorithm that operates over continuous spaces. The evader
strategy is not learned and is based on Voronoi regions, which the pursuers try to minimize and the evader tries
to maximize. We assume global visibility of all agents at all times. We implement the algorithm and train the
models using Python Pytorch machine learning library. Our results show that the pursuers can learn a control
strategy to capture evaders.
1 INTRODUCTION
From flocks of birds to fish schools in the sea, many
social groups in nature work together to survive and
thrive. These natural behaviors inspire humans to
mimic them with robots because robots that can coop-
erate in large numbers could achieve things that would
be difficult or even impossible for a single entity. For
example, following an earthquake, a swarm of search
and rescue robots could quickly explore multiple col-
lapsed buildings looking for signs of life. Addition-
ally, areas that may be threatened by large wildfires
may benefit from the use of swarms of drones assist-
ing the emergency services in helping track and pre-
dict the fire’s spread. The characteristics from swarms
in nature that appeal to researchers are robustness,
flexibility, and scalability. Swarms in nature are ro-
bust because agents in the swarm can be lost without
affecting the performance of a task the swarm as a
whole is trying to achieve. Agents can also adapt and
respond to changing work needs which makes them
flexible. The scalability of swarm size is the most im-
portant characteristic because the decentralized orga-
nization of agents in swarms in nature is sustainable
with 100 or 100,000 agents.
In swarm robotics the goal is to achieve com-
plex emergent behavior from simple robots with de-
centralized control. Each robot acts based on local
perception and local coordination with neighboring
robots. There are many challenges for multi-agent
settings addressed in (Nguyen et al., 2018), such
as non-stationary environments, partial observability,
and continuous action spaces. When dealing with
non-stationary environments, where the underlying
model of the environment changes over time, agents
usually have to continually re-adapt themselves to the
changing dynamics of the environment. This causes
two problems: 1) the time for relearning how to
behave makes the performance drop during the re-
adjustment phase; and 2) the system, when learning
a new optimal policy, forgets the old one, and conse-
quently makes the relearning process necessary even
for dynamics which have already been experienced.
There are cases when agents only have partial observ-
ability of the environment. In other words, complete
information of states pertaining to the environment is
not known to the agents when they interact with the
environment. In such situations the agents observe
partial information about the environment and need
to make the best decision during each time step. An-
226
Singh, G., Lofaro, D. and Sofge, D.
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State Space and Action Space via Deep Reinforcement Learning.
DOI: 10.5220/0008971502260233
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 226-233
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
other challenge is that agents can operate in discrete
action space (e.g., up, down, left, right), or continu-
ous action space (e.g., velocity). The complexity of
the problem increases when agents have continuous
actions because large action spaces are difficult to ex-
plore efficiently and can make training intractable.
In this work we consider the pursuit-evasion or
predator-prey problem and use a deep reinforcement
learning technique to solve this problem. Pursuit-
evasion is a problem where a group of agents col-
lectively try to capture one or multiple evaders while
the evaders try to avoid getting caught. Our goal is
to train agents to make decentralized decisions and
display swarm-like behavior. For our approach we
use the Multi-Agent DDPG (MADDPG) algorithm
introduced by (Lowe et al., 2017). MADDPG ex-
tends DDPG (Lillicrap et al., 2015) to the multi-agent
setting during training, potentially resulting in much
richer behavior between agents. This is an actor-critic
approach. This paper describes a centralized multi-
agent training algorithm leading to decentralized in-
dividual policies. Each agent has access to all other
agents’ state observations and actions during critic
training, but tries to predict its own actions with only
its own state observations during execution.
2 METHODOLOGY
In this section we give an intuitive explanation of the
theory behind reinforcement learning and then intro-
duce the recent developments in deep reinforcement
learning implemented herein.
2.1 Reinforcement Learning
Reinforcement Learning (RL) is a goal-oriented
reward-based learning technique. In RL agents inter-
act with an environment in discrete time-steps and at
each time-step, the agent observes the environment,
then takes an action and receives a numeric reward
based on the action. The goal of RL is to learn a good
strategy (policy) for the agent from experimental tri-
als and relatively simple feedback received (reward
signal). With the learned strategy, the agent is able to
actively adapt to the environment to maximize future
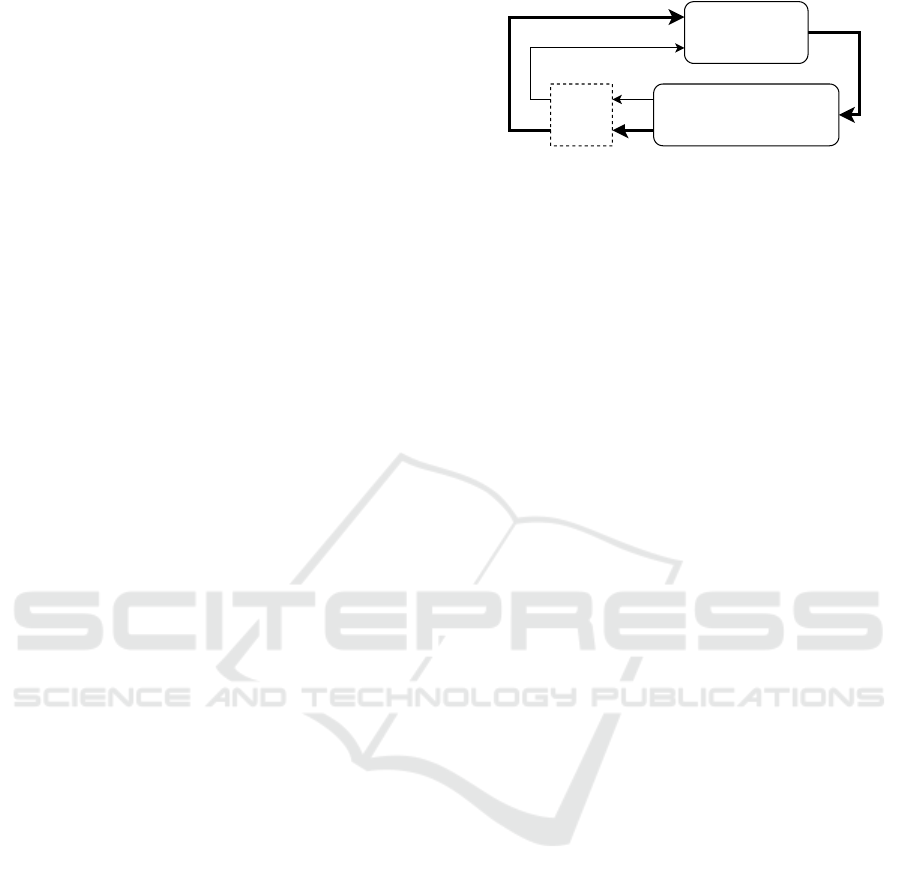
rewards. Figure 1 shows the RL framework.
The RL framework can be formalized using a
Markov Decision Process (MDP) defined by a set of
states S, a set of actions A, an initial state distribution
p(s
0
), a reward function r : S x A 7→ R, transition prob-
abilities P(s
t+1
|s
t
, a
t
), and a discount factor γ. The
agents take action based on their policy denoted by
Reward
r
t
Action
a
t
Agent
r
t+1
Environment
sampling
s
t+1
State
s
t
Figure 1: Reinforcement learning framework simplified
system diagram based on (Sutton and Barto, 2018).
π
θ
parameterized by θ, which can be either determin-
istic or stochastic. Deterministic policies are used in
environments where for every state you have a clear
defined action you will take. Stochastic policies are
used in environments where for every state, for you to
take an action, you draw a sample from possible ac-
tions that follow a distribution. A value function mea-
sures the goodness of a state or how rewarding a state
or action is by predicting the future reward. The goal
for the agent is to learn an optimal policy that tells it
which actions to take in order to maximize its own to-
tal expected reward R
i
=
∑
T
t=0
γ
t
r
i
t
, where 0 < γ < 1.
The discount factor penalizes the rewards in the future
because future rewards have higher uncertainty.
To learn an optimal policy, Richard Bellman, an
American applied mathematician, derived the Bell-
man equations which allowed us to start solving
MDPs. He made use of the state-value function de-
noted by:
V
π
(s, a) =
E
π
[R
t
|s
t
= s] (1)
and the action-value function denoted by
Q
π
(s, a) =
E
π
[R
t
|s
t
= s, a
t
= a] (2)
to derive the Bellman equations. The state-value func-
tion specifies the expected return of a state s
t
when
following an optimal policy, whereas the action-value
function specifies the expected return when choosing
action a
t
in state s
t
and following an optimal policy.
Once we have the optimal value functions, then we
can obtain the optimal policy that satisfies the Bell-
man optimality equations given by:
V
∗
(s) = max
a
0
∈A
∑
s
0
,r
P(s
0
, r|s, a)[r + γV
∗
(s
0
)] (3)
Q
∗
(s, a) =
∑
s
0
,r
P(s
0
, r|s, a)[r + max
a
0
∈A
Q
∗
(s
0
, a
0
)] (4)
The common approaches to RL are Dynamic
Programming (DP), Monte Carlo (MC) methods,
Temporal-Difference (TD) learning, and Policy Gra-
dient (PG) methods. If we have complete knowl-
edge of the environment or all the MDP variables,
following Bellman equations, we can use DP to iter-
atively evaluate value functions and improve the pol-
icy. DP methods are known as model-based methods
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State Space and Action Space via Deep Reinforcement Learning
227

Pass State
Experience to Memory
Agent
Sample Experience
Memory
Random Action
Actor
Actor (target)
Critic
Critic (target)
Train Actor and Critic
Actor
Critic
Replay Buffer
Agent 1
Actor
Critic
Replay Buffer
Agent 2
MADDPG Training Phase
State
Linear
ReLU
Linear
ReLU
Tanh
Action
Actor
States
(agent 1, agent 2, ... , agent n)
Critc
Linear
ReLU
Linear
ReLU
Linear
Q-Value
Actions
(agent 1, agent 2, ... , agent n)
MADDPG ExecutionDDPG Actor-Critic Architecture
Figure 2: (LEFT): Block diagram of the Actor-Critic architecture used in the DDPG algorithm. Here an agent is trained
for a fixed number of episodes and time steps. For each time step in an episode: choose an action for the given state; take
an action and receive the next state, reward, and completion status (whether the episode is finished); store the current state,
action, next state, reward, and completion status in a buffer; sample random batch of experiences; and train Actor and Critic
networks by sampling experiences from replay buffer and minimizing a loss function. Note: Both models (Actor and Critic)
get better in their own roles as time passes. (CENTER): Centralized training phase for multi-agent implementation of DDPG
(i.e. MADDPG). (RIGHT): decentralized execution of MADDPG. The MADDPG algorithm uses centralized training and
decentralized execution. Each action from the agent is used only during the training phase. During execution, the policy
network returns the actions for given states. A key improvement over the DDPG approach is that it shares the actions taken
by all agents to train each agent.
because we have complete knowledge of the environ-
ment. However, in most cases we do not know the
P(s
0
, r|s, a) or R(s, a), so we cannot solve MDPs by di-
rectly using the Bellman equations. This is where MC
methods become helpful. MC methods are model-
free and learn directly from episodes of experience
without any prior knowledge of MDP transition func-
tions P(s
0
, r|s, a) and reward functions R(s, a). How-
ever, this can only be applied to episodic MDPs be-
cause an episode has to terminate before we can
calculate any returns. Here, we do not do update
estimates after every action, but rather after every
episode. TD learning is a combination of DP and MC
methods. Like MC methods, TD methods are model-
free, meaning these methods can learn from episodes
with no prior knowledge of the environment. Like DP,
TD methods update estimates iteratively based in part
on other learned estimates, without waiting for the fi-
nal outcome.
2.2 Q-Learning
Q-Learning (Watkins and Dayan, 1992) is an off pol-
icy RL algorithm that seeks to find the best action to
take given the current state. It learns the action-value
function, Q
π
(s, a), by building a Q-table that stores
Q-values for all possible combinations of state and
action (s, a). The action-value function (Q-function)
takes two inputs: state and action. It returns the Q-
value (expected future reward) of that action at that
state. The Q-values are iteratively updated as we ex-
plore the environment by using the Bellman equation:
Q(s, a) ← Q(s, a) + α[r
t+1
+ γ max
a
Q(s
t+1
, a) − Q(s
t
, a
t
)]
(5)
2.3 Deep Q-Networks (DQN)
Theoretically, we can memorize the Q-table for all
state-action pairs in Q-learning. However, it quickly
becomes computationally infeasible when the state
and action are large discrete or continuous spaces.
Thus we have to use function approximators (e.g.
neural networks), to approximate Q-values. We can
estimate the Q-function by a supervised learning al-
gorithm with the input and output for the training
given by the reinforcement learning algorithm. The
loss function that drives the function approximator to
output the correct Q-values parameterized by learning
parameters θ is given by:
L(s
t
, a
t
, r
t+1
, s
t+1
, θ) =
(r
t+1
+ γmax
a
Q(s
t+1
, a;θ) − Q(s
t
, a
t
;θ))
2
(6)
DQN, introduced by DeepMind (Mnih et al.,
2013), was the first breakthrough in the fusion of RL
and Deep Learning. It used neural networks to ap-
proximate Q-values and showed that deep learning
with convolutional layers can enable reinforcement
learning algorithms to successfully learn to play Atari
2600 games. An improved version of DQN was in-
troduced in (Mnih et al., 2015) that was able to use
direct training from pixels to actions to play 49 differ-
ent Atari games without the need to change the hyper-
parameters of the network. The performance on Atari
games was impressive, as the learned policies were
often able to outperform human players. The only
input used for training the networks was the pixel im-
ages and the game score.
Neural networks are nonlinear function approxi-
mators and Q-learning suffers from instability and di-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
228

vergence when combined with a nonlinear Q-value
function approximation. The loss function above in-
cludes the θ parameter twice, which would make the
learning unstable. Q(s
t+1
, a;θ), which is the fore-
sight into the future, should now depend on the θ.
The DQN training method therefore introduces a tar-
get Q-network that copies the parameters from the
trained Q-network only after several hundred or sev-
eral thousand training steps and thus does not change
rapidly and enables the algorithm to learn stable long
term dependencies (Mnih et al., 2015). The loss func-
tion changes to:
L(s
t
, a
t
, r
t+1
, s
t+1
, θ, θ
−
) = (r
t+1
+
γmax
a
Q(s
t+1
, a;θ
−
) − Q(s
t
, a
t
;θ))
2
(7)
Using simple gradient descent on the loss function
with the target network can still lead to unstable train-
ing. DQN uses a variant of stochastic gradient descent
on the loss function and experience replay memory
to store the training examples. The experience replay
memory stores transitions between states sampled in
the past, and also memorizes the corresponding ac-
tions and rewards to correctly calculate the loss at ev-
ery time step in the future. Thus, the memory consists
of samples (s
i
, a
i
, r
i+1
, s
i+1
) for each recorded time
step. The idea behind stochastic gradient descent is
to use random samples of relatively few training ex-
amples from the experience replay buffer to estimate
the expectation of the true training error. When the
examples are sampled from very different time steps
and were generated under different conditions, they
can be sufficient to provide a good estimate of the true
training error with relatively low variance.
To summarize, there are two processes that are
happening in the DQN algorithm. We sample the en-
vironment where we perform actions and store the
observed experience-tuples in the experience replay
memory. Next, we select a small batch of experience-
tuples randomly and learn from them using a gradient
descent update step.
2.4 Policy Gradients (PG)
Using Q-Learning and DQN, it is possible to derive
reasonably performing policies from good estimates
of value functions. However, policies derived from
value functions search over a discrete number of Q-
values to find the best action, so it is not possible to
directly obtain policies that output continuous actions.
The policy gradient methods update the policy param-
eters at each step in the direction of an estimate of the
gradient of performance, ∇
θ
J(π
θ
), with respect to the
policy parameters. The fundamental result that under-
lies policy gradient methods is the Policy Gradient
Theorem given by:
∇
θ
J(π
θ
) =
E
s∼ρ
π
,a∼π
θ
[∇
θ
logπ
θ
(a|s)Q
π
(s, a)] (8)
2.5 Deterministic Policy Gradient
(DPG)
The deterministic policy gradient method was derived
in (Silver et al., 2014). Given a deterministic policy
parameterized by θ, and a discounted state distribu-
tion, ρ
µ
(s), induced by the policy, a performance ob-
jective function J(µ
θ
) can be defined as the expected
reward under the state distribution.
J(µ
θ
) =
E
s∼ρ
µ
[r(s, µ
θ
(s))] (9)
and (Silver et al., 2014) proved that the gradient of
this objective function is given by:
∇
θ
J(µ
θ
) =
E
s∼ρ
µ
[∇
θ
µ
θ
(s)∇
a
Q
µ
(s, a)|
a=µ
θ
(s)
] (10)
2.6 Deep Deterministic Policy Gradient
(DDPG)
DDPG (Lillicrap et al., 2015) combines DPG with a
DQN to obtain the deep deterministic policy gradient
(DDPG) algorithm. It uses an Actor-Critic architec-
ture to learn both the value function and the policy,
since knowing the value function can assist the policy
update. Actor and Critic are two neural network mod-
els. The Critic updates the value function parameters,
w, and depending on the algorithm it could represent
the action-value Q
w
(a|s) or state-value V
w
(s). The
Actor updates the policy parameters θ for π
θ
(a|s), in
the direction suggested by the Critic. A block dia-
gram of the DDPG actor-critic method can be seen in
Figure 2.
In DDPG the agent is trained for a fixed number
of episodes and a fixed number of time-steps in each
episode. In each time-step in each episode, the agent
chooses an action for the given state and takes the ac-
tion to receive a reward. The agent will store the expe-
rience, which consists of the current state, action, next
state, and reward, in the replay memory. Afterward,
the agent will sample a random batch of experiences
to train the Actor and the Critic. In training, the Actor
network takes states as input and returns the actions,
whereas the Critic network takes states and actions as
input and returns the values. Like DQN, the DDPG
algorithm uses target networks for both the Actor and
the Critic. The critic loss is given by:
L =
1
N
∑
i
(y
i
− Q(s
i
, a
i
|θ
Q
))
2
(11)
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State Space and Action Space via Deep Reinforcement Learning
229

Figure 3: (LEFT): Actor (agent) model that the neural network uses for the MADDPG algorithm. Note the numbers of inputs
and outputs on the input layer and the dense layer. (RIGHT): Critic model that the neural network uses for the MADDPG
algorithm. Note how the numbers of inputs and outputs on the input layer and the dense layer are different from that of the
Actor model.
This is the average of squared differences between
the target action-value and the expected action-value
where the expected action-value is given by the lo-
cal Critic network that takes state and action as input.
The target action-value is calculated as:
y
i
= r
i
+ γQ
0
(s
i+1
, µ
0
(s
i+1
|θ
µ
0
)|θ
Q
0
) (12)
This calculates the target estimate by adding the re-
ward and discounted action-value where the target
critic network takes states and actions as input and
returns the action-values. The Actor is updated using
sampled policy gradient.
∇
θ
µ
J ≈
1
N
∑
i
∇
a
Q(s, a|θ
Q
)|
a=µ(s
i
)
s=s
i
∇
θ
µ
µ(s|θ
µ
)|
s=s
i
(13)
This is the average of action-values given by the lo-
cal Critic network that takes states and actions as in-
put where the action is estimated by the local Ac-
tor network that takes states as input. In contrast to
DQN, the target networks are updated after each gra-
dient step to slowly replicate the changes made to the
trained networks.
2.7 Multi-Agent Deep Deterministic
Policy Gradient (MADDPG)
(Lowe et al., 2017) proposed the multi-agent deep
deterministic policy gradient (MADDPG) algorithm
which extended DDPG to an environment where mul-
tiple agents coordinate to complete tasks. When the
environment has multiple agents, training agents in-
dependently does not work well because the agents
are independently updating their policies as learning
progresses and this causes the environment to appear
non-stationary from the viewpoint of a single agent.
MADDPG was designed for handling the problem of
non-stationarity. It adopts the framework of a cen-
tralized Critic training and a decentralized execution
approach. In this approach all agents have access to
all other agents’ state observations and actions during
Critic training, but during execution each agent pre-
dicts the action based on its own state. This way the
environment becomes stationary from the viewpoint
of all the agents.
The Actor policy gradient with parameter θ is
given by:
∇
θ
i
J ≈
1
S
∑
j
∇
θ
i
µ
i
(o
j
i
)∇
a
i
· Q
µ
i
(x
j
, a
j
1
, . . . , a
j
N
)
a
i
=µ
i
(o
j
i
)
(14)
where D is the memory buffer for experience re-
play containing the tuples (x, x
0
, a
1
, ..., a
N
, r
1
, ..., r
N
)
of recording experiences from all the agents. The cen-
tralized Critic function is updated by minimizing the
loss function:
L(θ
i
) =
1
S
∑
j
y
j
− Q
µ
i
(x
j
, a
j
1
, . . . , a
j
N
)
2
(15)
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
230

Table 1: Hyperparameters.
Params Value Description
γ 0.99 Discount Factor
τ 0.1 Soft update of target pa-
rameters
Actor FC1 256 Input channels for actor
fully connected hidden
layer 1
Actor FC2 128 Input channels for actor
fully connected hidden
layer 2
Critic FC1 256 Input channels for critic
fully connected hidden
layer 1
Critic FC2 128 Input channels for critic
fully connected hidden
layer 2
Actor
Learning
Rate
0.0001 Learning rate for actor
Adam optimizer
Critic
Learning
Rate
0.0001 Learning rate for critic
Adam optimizer
Batch Size 256 Number of episodes to
optimize at the same
time
Experience
Replay
Memory
Size
10M Size of the replay buffer
that stores experiences
Episodes 2048 Number of episodes
Episode
Length
256 Length of each episode
where
y
j
= r
i
+ γQ
µ
0
i
(x
0
, a
0
1
, . . . , a
0
N
)
a
0
j
=µ
0
j
(o
j
)
(16)
3 TESTS AND RESULTS
We applied the MADDPG algorithm to the pursuit-
evasion task using a simulation environment provided
by Lincoln Centre for Autonomous Systems Research
(L-CAS) (H
¨
uttenrauch et al., 2018). In this simulation
environment the agents are point robots with a unicy-
cle model. Note: the simulation environment is open-
source and available online
1
. The state of an agent is
given by:
1
Lincoln Centre for Autonomous Systems Re-
search (L-CAS): Deep RL for Swarm Systems:
https://github.com/LCAS/deep rl for swarms
s
i
= [x
i
, y
i
, φ
i
] ∈ S = {[x, y, φ] ∈ R
3
:
0 ≤ x ≤ x
max
, 0 ≤ y ≤ y
max
, 0 ≤ φ ≤ 2π}
(17)
Listing 1: Implementation of the MADDPG Algorithm
from (Lowe et al., 2017).
f o r e p i s o d e = 1 t o M do
I n i t i a l i z e a random p r o c e s s N f o r
a c t i o n e x p l o r a t i o n
R e ce i v e i n i t i a l s t a t e x
f o r t = 1 t o max −episode − length do
f o r eac h a g e n t i , s e l e c t a c t i o n
a
i
= µ
θ
i
(o
i
) + N
t
w . r . t . t h e
c u r r e n t p o l i c y and
e x p l o r a t i o n
E x ec u t e a c t i o n s a = (a
1
, .. . , a
N
)
and o b s e r v e rew a rd r
and new s t a t e x
0
S t o r e (x, a, r, x
0
) i n r e p l a y
b u f f e r D
x ← x
0
f o r a g e n t i = 1 to N
Sampl e a random m i n i b a t c h o f
S s a m p les (x
j
, a
j
, r
j
, x
0
j
)
fro m D
S e t y
j
= r
j
i
+ γQ
µ
0
i
(x
0
j
, a
1
0
, .. . , a
0
N
)|
a
0
k
=µ
0
k
(o
j
k
)
Up da te c r i t i c by m i n i mizi n g
t h e l o s s
L(θ
i
) =
1
S
∑
j
y
j
− Q
µ
i
(x
j
, a
j
1
, .. . , a
j
N
)
2
Up da te a c t o r u s i n g t h e
sa m pl ed p o l i c y g r a d i e n t s :
∇
θ
i
J ≈
1
S
∑
j
∇
θ
i
µ
i
(o
j
i
)∇
a
i
·
Q
µ
i
(x
j
, a
j
1
, .. . , a
j
N
)
a
i
=µ
i
(o
j
i
)
end f o r
Up da te t a r g e t n et w ork
p a r a m e t e r s f o r eac h a g e n t i :
θ
0
i
← τθ
i
+ (1 − τ)θ
0
i
end f o r
end f o r
The linear and angular velocities can be controlled by
the agents. The kinematics model is given by:
˙x =vcosφ
˙y =vsinφ
˙
φ =ω
(18)
The environment is enclosed with x
max
= 100 and
y
max
= 100. The evader agents are 2x faster than the
pursuers. The max values for the linear and angular
velocities for the pursuer agents is in the range [−1, 1].
However, for the evader agents, the range is [−2, 2].
We keep the linear velocity constant for all the agents
so that our model only has to predict a single continu-
ous variable, angular velocity. The reward function is
expressed in terms of the distance to the closest pur-
suer,
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State Space and Action Space via Deep Reinforcement Learning
231

6
1
5
2
4
3
Evader
Pursuers
Capture
(Start)
(End)
Figure 4: Experiment running in the simulation environment. Four pursuer agents successfully learn how to capture an evader
agent. The simulator used is the Deep RL for Swarm Systems by the Lincoln Centre for Autonomous Systems Research
(L-CAS). In this simulation each of the pursuers and the evader use a unicycle motion model in a non-toroidal environment.
The evader agent’s maximum angular and translational velocity is twice as fast as the pursuers’. The x and y axis units are in
meters. The evader is captured when a pursuer is less than r
e
+r
p
distance from the evader where r
e
is the radius of the evader
and r
p
is the radius of the pursuer. This example shows the results after the knee of the capturing convergence rate graph as
shown in Figure 5 (i.e. after 350 episodes). Note: The frames above are denoted in chronological order, starting with one and
ending with six.
R(s, a) = −
1
d
o
min(d
min
, d
o
) (19)
where
d
min
= min(d
1,e
, ..., d
N,e
). (20)
We will be operating with global observability;
therefore, d
o
is the maximum possible distance of d
i,e
.
The simulation environment and a four pursuer/one
evader example is shown in Figure 4.
Figure 5: Capturing convergence percentage (y-axis) vs.
training episodes for the four pursuer one evader system.
After approximately 350 episodes the capturing percentage
converges on a steady state of just under 100% captures.
The state observation for any pursuer agent is
given by the current position, linear and angular ve-
locities of all of the pursuer agents, the position and
velocity of the evader agent, and the distances be-
tween the pursuer agent and all other pursuers in
the environment. For example, if we have p pur-
suer agents and e evader agents, the state observa-
tion for a single agent is size given by: 8 + (p +
e − 2) = 8 + (4 + 1 − 2) = 11. The state observa-
tion for pursuer agent 1 from the example will be:
(x
p
1
, y
p
1
, v
p
1
φ
, v
p
1
ω
, x
e
1
, y
e
1
, v
e
1
φ
, v
e
1
ω
, d
1,2
, d
1,3
, d
1,4
). We
trained the pursuers using the hyperparameters shown
in Table 1. This is the input supplied to the Actor
deep neural network training using the MADDPG al-
gorithm which outputs the actions or angular veloci-
ties the agent should apply. The neural network struc-
ture for both Actor and Critic is shown in Figure 3.
The convergence of the model can be seen in Figure 5.
After 350 episodes, the capturing rate for the pursuers
is close to 100%.
4 CONCLUSIONS
In this paper we applied the MADDPG algorithm
to the pursuit-evasion task. We trained a model for
a swarm of pursuers that has learned to capture the
evader. In the future, we would like to research how
to train the pursuers to capture agents in a torus world.
We will also compare our results using MADDPG
with those obtained using the Trust Region Policy
Optimization (TRPO) and Proximal Policy Optimiza-
tion (PPO) algorithms. Finally, we will implement all
of the latter items on a physical multi-agent/swarm
system such as the Lighter-Than-Air Autonomous
Agents, (Schuler et al., 2019).
ACKNOWLEDGEMENTS
This work was performed at the U.S. Naval Research
Laboratory and was funded by the Office of Naval
Research under contract N0001418WX01828 for the
project ”Coherence and Decoherence of Patterns in
Swarms with Potential Collisions”. The views, po-
sitions and conclusions expressed herein reflect only
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
232

the authors’ opinions and expressly do not reflect
those of the Office of Naval Research, nor those of
the U.S. Naval Research Laboratory.
REFERENCES
H
¨
uttenrauch, M., Sosic, A., and Neumann, G. (2018). Deep
reinforcement learning for swarm systems. CoRR,
abs/1807.06613.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-
uous control with deep reinforcement learning. arXiv
preprint arXiv:1509.02971.
Lowe, R., Wu, Y., Tamar, A., Harb, J., Abbeel, O. P.,
and Mordatch, I. (2017). Multi-agent actor-critic
for mixed cooperative-competitive environments. In
Advances in Neural Information Processing Systems,
pages 6379–6390.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Nguyen, T. T., Nguyen, N. D., and Nahavandi, S. (2018).
Deep reinforcement learning for multi-agent systems:
a review of challenges, solutions and applications.
arXiv preprint arXiv:1812.11794.
Schuler, T., Lofaro, D., McGuire, L., Schroer, A., Lin, T.,
and Sofge, D. (2019). A study of robotic swarms
and emergent behaviors using 25+ real-world lighter-
than-air autonomous agents (lta3). In 2019 3rd In-
ternational Symposium on Swarm Behavior and Bio-
Inspired Robotics (SWARM).
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and
Riedmiller, M. (2014). Deterministic policy gradient
algorithms.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Watkins, C. J. and Dayan, P. (1992). Q-learning. Machine
learning, 8(3-4):279–292.
Pursuit-evasion with Decentralized Robotic Swarm in Continuous State Space and Action Space via Deep Reinforcement Learning
233
