Fabrication of Micro Spiral Phase Plates in Fused Silica using

-Laser Microstructuring

Sebastian Buettner, Michael Pfeifer and Steffen Weissmantel

Laserinstitut Hochschule Mittweida, Technikumplatz 17, Mittweida, Germany

Keywords: Fluorine Laser, Fused Silica, Microstructuring, Orbital Angular Momentum, Spiral Phase Plates.

Abstract: The results of our investigations on direct laser fabrication of micro spiral phase plates (SPPs) in fused silica

using the fluorine laser microstructuring technique will be presented. The process, which based on the mask

projection technique, enables the generation of SPPs with different topological charges, handedness, modu-

lation depths and level numbers. For this, a special double mask rotation system was developed, which allows

the fabrication of micro SPPs with an individual configuration with regard to the mentioned parameters.

Moreover, the phase of a spherical lens can be added to the helical phase of the SPP using a special mask

geometry. Furthermore, we build up a measurement system for a first optical characterization of the fabricated

SPPs.

1 INTRODUCTION

Nowadays data communication become more im-

portant, than ever. But the capacity of optical chan-

nels is limited by nonlinear effects in fibers, using

classical wavelength or polarization multiplexing

(Richardson, 2010). Regarding to the expected in-

crease of the data traffic and the desired transmission

speed, new multiplexing methods are required. One

of these new method is to use the orbital angular mo-

mentum (OAM) of light, which could enhance the ca-

pacity of optical data communication channels (Xie

et al., 2018). Moreover, the integration of electro-op-

tical systems become more interesting and has been

realized also the field of data communication (Neitz

et al., 2017). For this purpose, we developed a new

method for the fabrication of Fresnel lenses using the

fluorine laser microstructuring technique (Pfeifer et

al., 2015). In the last few years, a variety of methods

and techniques were developed to manufacture opti-

cal elements in the micrometer scale and in particular

for polymer and other low melting materials

(Kasztelanic et al., 2013; Xing et al., 2016; Qui et al.

2018). Whereas the available fabrication techniques

for the processing of fused silica and other wide band

gap materials are limited. The fluorine laser micro-

structuring technique provides a very flexible alterna-

tive to lithographic processes. Based on our research

in microstructuring of blaze gratings (Pfeifer, Weiss-

mantel and Reisse, 2013), diffractive optical elements

(Pfeifer et al., 2014), cylindrical lenses and lens ar-

rays (Buettner, Pfeifer and Weissmantel, 2019), we

now developed a method for the fabrication of micro

spiral phase plates. This could be interesting for a new

kind of integrated optical multiplexing systems,

which based on the OAM of light.

2 FUNDAMENTALS AND

EXPERIMENTAL SETUP

2.1 Orbital Angular Momentum

The wavelength, amplitude, phase and polarization

are well known properties of electromagnetic waves

(EMW). The latter is also known as the spin angular

momentum of photons. But there is another kind of

momentum, the OAM, which was measured first by

Allen et al., in 1992 (Allen et al., 1992). This momen-

tum results from helical phase which is characterized

by an azimuthal phase term. The modulation of an

even wave front with a helical phase term gives the

linear momentum of the photons an azimuthal com-

ponent. The summation of this components enhance

the OAM. Due to this, this momentum is a result of

the interaction of several photons (Allen and Padgett,

2011). Nevertheless, this can be used to encode clas-

sical information. There are some methods to create

light and in particular laser beams with a defined

114

Buettner, S., Pfeifer, M. and Weissmantel, S.

Fabrication of Micro Spiral Phase Plates in Fused Silica using F2-Laser Microstructuring.

DOI: 10.5220/0008973301140121

In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 114-121

ISBN: 978-989-758-401-5; ISSN: 2184-4364

OAM. One of them is to use a vortex grating, the

other is to use an SPP. Both methods were already

used for data communication experiments (Xie et al.,

2018; Bozinivic et al. 2013).

2.2 Calculation of the Process

Parameters for SPP Fabrication

Using SPPs is an effective and flexible way to gener-

ate very different and individual OAMs. SPPs are a

special kind of diffractive phase elements and in gen-

eral assigned to the group of computer generated hol-

ograms. These elements can be used to convert a

Gaussian intensity distribution to a circular intensity

distribution. This can be reached by modulating the

phase of an even EMW with a helical phase shift. In

general the efficiency of diffractive phase elements

depends on the number of levels (O’Shea et al.,

2004). For our investigations we have chosen three

different numbers of levels (8, 16, 32). Regarding to

the design wavelength and the appropriate optical

thickness of the material for a 2π phase shift, the step

size has to be calculated. A phase shift of 2π is equal

to a modulation depth of m = ±1. The sign of the mod-

ulation depth defines handedness of the helical phase.

A right-handed SPP lead to left-handed OAM of a

transmitting EMW from the backside.

For our investigations, we have chosen the com-

mon laser wavelength of 532 nm. For this, the refrac-

tive index (n = 1.46) of the fused silica Corning 7980

were calculated using the Sellmeier equation. The

corresponding depth of the microstructure at a modu-

lation depth of 2π is 776.72 nm. The required ablation

depth per pulse and the appropriate laser pulse flu-

ence for different numbers of levels was calculated

using the Lambert-Beer’s law and the appropriate ab-

lation parameters of the material (see Table 1).

Table 1: Calculated step size and required laser pulse flu-

ence (ablation threshold and absorption coefficient for

Corning 7980: H

= 0.56 J/cm², α = 12.98 · 10

-1

level step size laser pulse fluence

8 97.09 n

1.97 J/cm²

16 48.42 n

1.05 J/cm²

32 24.27 n

0.77 J/cm²

2.3 Microstructuring Process

The microstructuring is done by the laser microm-

achining station EX-157, which was built by 3D-Mi-

cromac AG. A detailed description of the station is

given in our previous work. The setup is basically

comparable to the one for the fabrication of micro

Fresnel-lenses.

The microstructuring process is based on the

mask projection technique. By using a pulsed excimer

laser system, every laser pulse remove a certain

amount of material depending on the laser and mate-

rial parameters. Due to the homogenization of the la-

ser beam, the laser pulse fluence H is homogenously

distributed in the whole mask area and thereby in the

image plane of the imaging system too. Therefore, the

ablation depth is the same in the whole ablation area.

This area is formed by the mask geometry. In general,

the depth of the microstructures depends on the laser

pulse fluence and the number of pulses per area. The

generation of a helical phase shift can be done by in-

fluencing the optical thickness of a transparent mate-

rial. For this, the required structure is comparable to

a spiral staircase. The fabrication of these three di-

mensional microstructures requires the control of the

microstructuring depth within the ablation area and in

particular in rotation direction. This can be realized

by a combination of two semi-circular masks, which

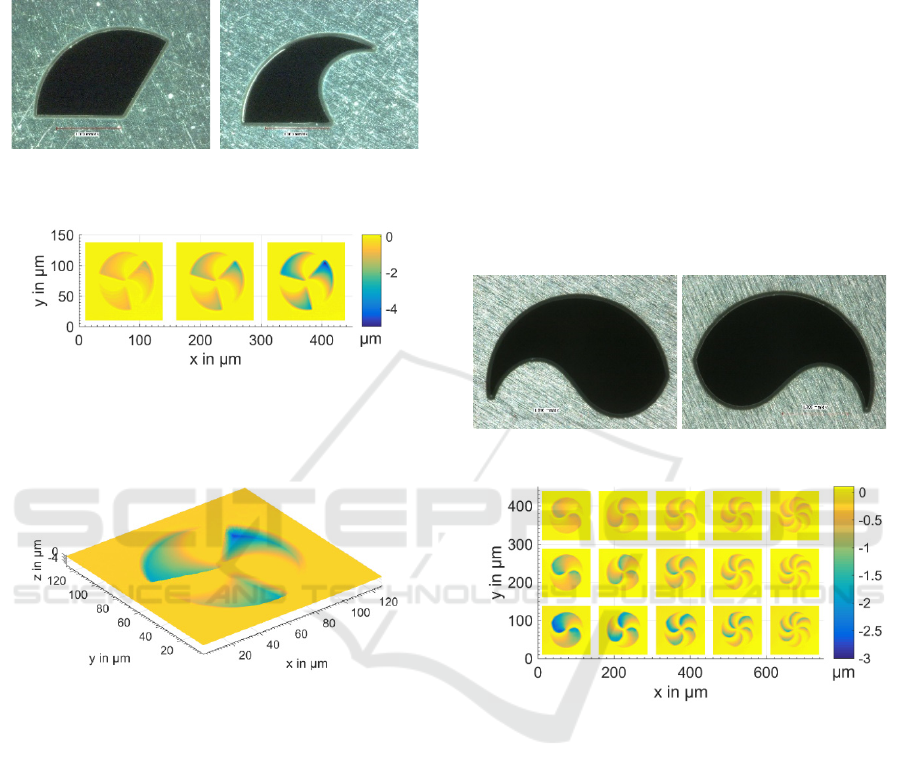
are placed in a row. A sample is shown in Figure

For this, a mask rotation system was developed. This

system consists of two rotary axis. Both masks can be

rotated independently by separate drives. The system

is shown in Figure 1.

Figure 1 and Figure 2: Semi-circular mask in tantalum-foil

for the fabrication of SPPs with a diameter of 100 µm (l.)

and developed double rotation system with two servo drives

for independent and separate movement of the masks (r.).

The micro structuring process starts with the cal-

culation of the sector angle and the step angle from

the topological charge (TC), which represents the

number of 2π phase jumps within the structure. Fur-

thermore, the number of levels N

defines the step an-

gle of the target structure. The masks are in congruent

position after the referencing of the system. Follow-

ing, one of the masks is twisted toward the other until

the sector angle is reached. This position is the initial

state for the microstructuring of each sector, inde-

pendently from the sector angle. In consideration of

the TC, the orientation of the resulting mask changes

Fabrication of Micro Spiral Phase Plates in Fused Silica using F2-Laser Microstructuring

115

for each sector. Starting from this initial state, the sec-

tor angle is reduced by the step angle after every laser

pulse. This process is repeated until the number of re-

quired steps is reached. In this way the SPPs were fab-

ricated sector by sector. The process is realized in a

sequence of loops and can be influenced by the TC,

the level number and the laser pulse fluence. The lat-

ter defines the ablation depth per pulse, which defines

the vertical step size. One advantage of these tech-

nique is, that we are able to fabricate irregular SPPs.

However, a disadvantage is, that the topological

charge has to be at least two and the process is limited

by the resolution of the imaging system in general and

accuracy of the mechanic components as well. After

the fabrication, we removed the remained debris by

etching the sample 30 min in a 1.7 molar KOH solu-

tion, followed by 15 min ultrasonic cleaning.

3 RESULTS AND DISCUSSION

3.1 Geometrical Properties of the

Fabricated SPPs

The fabrication of SPPs in fused silica with different

TCs is possible by changing the number of sectors N

and the corresponding sector angle. For regular SPPs

the sector angle is an integer fractional part of 360 de-

gree. A set of fabricated SPPs with different TCs and

level numbers are shown in Figure 3. As can be seen

in this Figure, the sectors of the SPPs in the upper row

are well fabricated.

Figure 3: Three dimensional micrographs (top view) of fab-

ricated SPPs in Corning 7980 with m = 1, a TC of 2, 3, 4, 5

and 6 (left to right) and a level number of 8, 16 and 32 (top

to bottom).

This is caused by the higher laser pulse fluence

and the appropriate ablation depth per pulse. The

SPPs in the middle and lower row got an uneven

depth within the sectors. The Reason for this is the

inhomogeneity of the energy distribution of the laser

beam. The used laser system is currently not in tune.

Because of a low damage threshold of some optical

components, the homogenizer is de-adjusted. Due to

this, the energy distribution of the laser beam is

slightly in-homogenous. The fabrication of SPPs with

a higher level number requires a lower step size and

thereby a lower laser pulse fluence. The fabrication of

SPPs with 32 levels requires an ablation depth per

pulse of 24.27 nm. Due to this, the used laser pulse

fluence is H = 0.77 J/cm², which is just a little more

than the ablation threshold fluence of

= 0.56 J/cm² of the material. Because of this, the

error of the ablation depth within the ablation area in-

crease and summed up by the number of pulses. In

this way, the inhomogeneity of the laser beam is

transferred to the surface and in particular to the mi-

crostructure. Nevertheless, it is possible to fabricate

left-handed SPPs (see Figure 4).

Figure 4: Three dimensional micrographs (top view) of fab-

ricated SPPs in Corning 7980 with m = -1, a TC of 2, 3, 4,

5 and 6 (left to right) and a level number of 8, 16 and 32

(top to bottom).

In this case, the calculations and starting condi-

tions are the same. However, the motion of the axis

were interchanged and the feed direction is inverted.

As a result, the microstructuring depth increase in the

counter clockwise direction, as can be seen. In Fig-

ure 5 the circular profile sections of the 8-level SPPs

are shown. The radius of the circular section was set

to R

= 25 µm. As can be seen, the single slope within

one SPP is nearly equal. In general the microstructur-

ing depth is in the range of 900 nm which is slightly

more than the required 776.72 nm. Furthermore, the

last step is significantly deeper than the previous

steps.

The reason for this is the accumulation of radia-

tion, which is reflected at the steep edge of the struc-

ture. Moreover, the lateral step size become smaller

by increasing the TC. An increase of this lead to a re-

duction of the sector angle as well as the step angle

and the corresponding lateral step size. Furthermore,

it can be seen that the arc length of the sectors are not

equal. The reason for this, is possibly a malfunction

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

116

of the rotation system. This problem can maybe

solved by some constructive changes. The compari-

son of one sector of an 8-, 16- and 32-level SPPs with

a topological charge of 2 shows the influence of the

level number and the required reduction of the verti-

cal step size (see Figure 6).

Figure 5: Circular profile section of the 8 level SPPs with

different TCs.

Figure 6: Circular profile section of one sector of an 8-, 16-

and 32-level SPP with a TC of 2.

The increase of the numbers of levels once more

lead to the reduction of the lateral step size. Due to

this the profile section of the 32-level SPP is more

continuous than the section of the 8- and 16-level

SPPs. In consideration of the radial dependencies of

this, it is not possible to fabricate a complete contin-

uous surface with this technique. Furthermore, it can

be seen that the steep edge of the structure also be-

come flattened by increasing the number of levels.

Thereby the gained efficiency is affected by geomet-

rical inaccuracies. One option to avoid these, is to in-

crease the modulation depth. The SPPs, which are

shown in Figure 7, were fabricated with a laser pulse

fluence of 1.97 J/cm².

Figure 7: Three dimensional micrographs (top view) of fab-

ricated SPPs in Corning 7980 with a m of -1, -2 and -4, a

TC of 2, 3, 4, 5 and 6 (left to right), a level number of 8, 16

and 32 (top to bottom) and constant vertical step size.

Figure 8: Circular profile section of the 8, 16 and 32 level

SPPs with a modulation depths m of -1, -2 and -4.

To increase the modulation depth, the number of lev-

els were increased only. The SPPs which were shown

in Figure 7 are left handed, with an m of -1 (upper

row), -2 (middle row) and -4 (lower row). The in-

crease of the OAM by increasing the level number,

lead to a surface profile with a more continuous

course, as can be seen in Figure 8.

3.2 SPPs with Lens Term

To show further opportunities of this fabrication tech-

nique, we calculated some different kinds of masks.

One calculated mask pair is shown in Figure 9. Re-

garding to this, the left mask is the semi-static mask,

which defines a constant sector angle. Because of the

asymmetric geometry of the rotation mask (right), it

is not possible to influence the sector angle like using

the semi-circular masks. At the beginning of the pro-

cess the masks have to be in congruent position with

Fabrication of Micro Spiral Phase Plates in Fused Silica using F2-Laser Microstructuring

117

regard to their rotation center and lower edges. This

kind of masks enables the fabrication of SPPs with an

additional radius of curvature (ROC) and straight sec-

tor edges, as can be seen in Figure 10.

Figure 9: Semi-static mask (left) and rotary mask (right) for

SPP fabrication with additional radius of curvature (ROC).

Figure 10: Three dimensional micrographs (top view) of

three fabricated SPPs in Corning 7980 with an m of -1, -2

and -4, a TC of 3 and a level number of 8, 16 and 32 (left to

right).

Figure 11: Three dimensional micrograph of a SPP with ad-

ditional ROC.

But this combination got also a big disadvantage.

It is not possible to get the whole sector structured, as

can be seen in Figure 11. To solve this problem, the

micro structuring process has to be divided in two

processes.

In a first sequence one sector of the SPP has to be

fabricated like described in the previous chapter. In a

second sequence, the fabricated staircase structure

has to be structured again, using the corresponding

mask geometry for lens fabrication. The calculation

method for this and the parameter dependencies were

subject of previous investigations. For this setup,

there are different ways to solve this problem. The

first is to reduce the sector angle of the semi-static

mask to the half of the rotation mask. The second is

to enlarge the mask aperture angle of the rotation

mask to the twice angle of the semi-static mask. One

of these configurations allows the described proce-

dure. This can lead to a microstructuring process

where the level number, the OAM and the ROC can

be influenced independently. Only the TC is given by

the mask itself. The third method is to calculate two

nearly identical masks with curved radial edges of the

sector. But the one mask has to be reversed to the

other because they are placed in opposite of each

other. Due to the curved edges of the mask, the edges

of the sectors of the SPPs become also curved. The

advantages of this configuration are the same like the

semi-circular masks. But the ROC is not inde-

pendently adjustable with regard to the level number,

the handedness and also the vertical step size. How-

ever, we calculated two semi-circular masks with de-

fined curved sector edges, as can be seen in Figure 12.

Figure 12: Set of semi-circular masks with curved edges.

Figure 13: Three dimensional micrographs (top view) of

SPPs with an m of -1, -2 and -4 (top to bottom), an addi-

tional ROC, curved sector edges and different level num-

bers (8, 16 and 32 from top to bottom).

And as intended, using these masks lead to curved

sector edges. This is shown in Figure 13. The calcu-

lated ROCs of the structures are in the range of 1 to

16 mm, depending on the TC and the level number.

But we are currently not able to measure the ROC of

these structures. For this we need to develop a special

evaluation algorithm which separates the spherical

from the helical structural percentage. This should be

done in consideration of some well selected and de-

fined boundary conditions, which we did not defined

yet. Furthermore, we have to take some fabrication

defects into account, which we cannot separate from

the structure easily.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

118

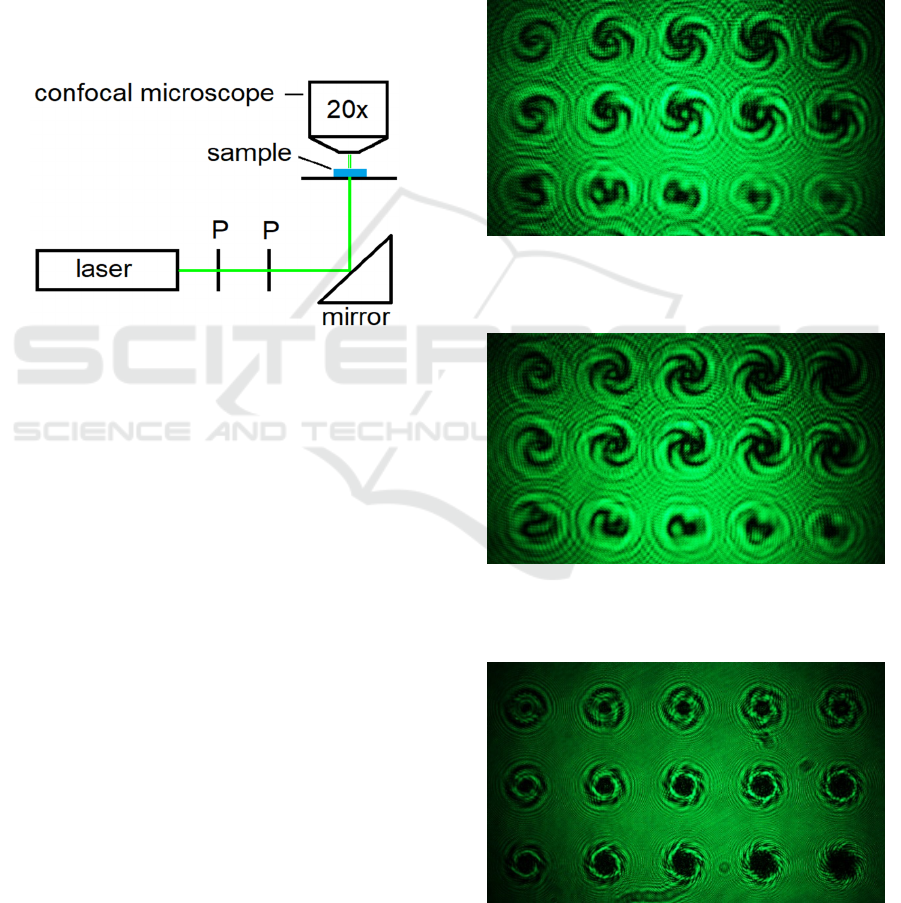
3.3 Testing the Optical Function

To prove the optical function of these elements, we

set up a simple measurement system, where the sam-

ple is illuminated by a frequency doubled Nd:YAG

laser. The intensity of the laser beam can be adjusted

by two polarizers (P). For the detection of the radia-

tion, we used a confocal microscope. A schematic il-

lustration of the measurement setup is shown in

Figure

14. With this we are able to measure the relative in-

tensity distribution of a set of SPPs in a defined plane

behind the sample. Because of some geometrical lim-

itations, we can capture the diffraction image in a

maximum distance of 3 mm.

Figure 14: Illustration of the measurement setup.

As can be seen in Figure

15 and Figure 16 the

number of intensity maxima increase with the number

of TCs. The distributions which are generated by

SPPs in the lower rows, are very different. This is

caused by the fabrication errors, which were dis-

cussed in chapter 3.1. Moreover, there are some

smaller intensity maxima in the center of the shown

distributions in the upper and the middle row. The

reason for this is the unstructured area in the center of

the SPPs. This is mainly a result of the limited reso-

lution of the imaging system of the micro machining

station in combination with adjusting and imaging er-

rors. Furthermore, it can be seen that the intensity dis-

tributions of the SPPs with the same configuration but

different handedness is the inverted of each other.

However, with this measurement setup it is not

possible to see a significant influence of the level

number. Furthermore, there are interfering effects be-

tween adjacent distributions. To prevent this, the spot

of the laser beam has to be reduced. If this is not suf-

ficient a pinhole could be placed on axis to the SPP.

The relation of the pinhole and beam diameter should

be selected in a right way, to avoid any diffraction ef-

fects. In comparison to the level number, the influ-

ence of the modulation depth can be seen clearly. The

diffraction image in Figure 17 is generated by the

SPPs which are shown in Figure 7. The increase of

the modulation depth lead to a circular formation of

the intensity maxima. Moreover, the maxima are lat-

erally reduced in radial direction. The diffraction im-

ages in the lower row show also a subdivision of the

ring distribution. The reason for this could be the in-

teraction of the lateral step size (and corresponding

level number) and the TC. In this case, the higher

level number could lead to a very small lateral step

size. These steps may act as a circular phase grating,

in superposition with the helical phase.

Figure 15: Confocal microscope image of the intensity dis-

tribution 3 mm above the SPPs are shown in Figure 3

(OAM

Figure 16: Confocal microscope image of the intensity dis-

tribution 3 mm above the SPPs are shown in Figure 4

(OAM

Figure 17: Confocal microscope image of the intensity dis-

tribution 0.49 mm above the SPPs with different modula-

tion depth.

Fabrication of Micro Spiral Phase Plates in Fused Silica using F2-Laser Microstructuring

119

In addition, the SPPs which were fabricated with

the curved semi-circular masks were also optically

examined. As can be seen in

Figure 18, the curved

steps and sectors lead to a further reduction of the

maxima size in rotation direction.

Figure 18: Intensity distribution of transmitting radiation

through SPPs 0.49 mm above, with different modulation

depth and additional ROC (SPPs shown in Figure 13).

As a result, the optical response of the SPPs in-

cludes a defined number of intensity maxima depend-

ing on the TC. The ROC decrease by the increase of

the TC and the level number. This could lead to a re-

duction of the maxima size and thereby an increase of

the intensity too. Like in the previous investigations,

the influence of the level number is not apparent. This

could be solved by upgrading the measurement sys-

tem for single SPP characterization with optimized

measurement conditions.

4 CONCLUSIONS

The fabrication of SPPs with different TCs, level

numbers, handedness and modulation depths is possi-

ble using the fluorine laser microstructuring tech-

nique. For this, a double mask rotation system was

developed and installed.

The fabrication of simple SPPs can be done using

two semi-circular masks. Furthermore, these allows

the fabrication of SPPs with different configurations

by changing the process and programming parame-

ters. This enables the fabrication of SPPs with a TC

of 2 to 6. The number of intensity maxima within the

optical response of the SPPs is equal to the TC. In

general, the fabrication of SPPs with an irregular TC

is possible. Due to some little inaccuracies in the arc

length of the sectors, the rotation system should be

optimized.

An increase of the level number lead to a more

continuous surface profile and enhance the efficiency

of the SPPs but requires a very low laser pulse fluence

for a 2π modulation depth. As a result, the slightly in-

homogeneous energy distribution of the laser beam is

transferred into the microstructure. This affect the op-

tical function of the SPPs. To solve this problem the

modulation depth can be increased. But this also got

an influence on the OAM and lead to the reduction of

the size of the intensity maxima in radial direction.

In addition to this, the SPPs can be fabricated in-

cluding a ROC in two different ways. The first is to

calculate a set of masks for the fabrication of a de-

fined SPP. The other way is to calculate two semi-

circular masks with curved edges. Using the latter

lead to a more flexible process in comparison to the

first. But for this the ROC cannot be influenced inde-

pendently from the other parameters. However, an ad-

ditional ROC lead to a further reduction of the size of

the intensity maxima. The influence of the step size

should be the subject of further investigations and

supported by some theoretical studies. For the im-

provement of the optical characterization, the meas-

urement system should be improved too.

Moreover, we want to build up an optical link us-

ing some lenses first, followed by using a fiber as a

transfer medium. Depending on the results, further in-

vestigations will be done in the field of OAM multi-

plexing using integrated optics.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the financial sup-

port of the present work by the European Union and

the Free State of Saxony.

REFERENCES

Allen, L., Beijersbergen, M.W., Spreeuw, R.J.C. and

Woerdman, J.P. (1992). Orbital angular momentum of

light and the transformation of Laguerre-Gaussian laser

modes. In Physical Review A, 45(11), pp. 8185-8189.

Allan, L. and Padgett, M. (2011). The Orbital Angular Mo-

mentum of Light: An Introduction, In: Twisted Photons,

eds. Torres J.P and Torner L., pp. 1-12.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

120

Bozinivic, N., Yue, Y., Ren, Y., Tur, M., Kristensen, P.,

Huang, H., Willner, A.E. and Ramachandran, S. (2013).

Terrabit-Scale Orbital Angular Momentum Mode Divi-

sion Multiplexing in Fibers. In Science, 340 (6140), pp.

1545-1548.

Buettner, S., Pfeifer, M., and Weissmantel, S. (2019). Man-

ufacturing of Cylindrical Micro Lenses and Micro Lens

Arrays in Fused Silica and Borosilicate Glass using F

Laser Microstructuring. 7th International Conference

on Photonics, Optics and Laser Technology.

Kasztelanic, R., Kujawa, I., Stępień, R., Haraśny, K., Pysz,

D. and Buczyński, R. (2013). Molding of soft glass re-

fraction mini lens with hot embossing process for

broadband infrared transmission systems. In Infrared

Physics & Technology, 61, pp. 299-305.

Neitz, M., Wöhrmann, M., Zhang, R., Fikry, M., Marx, S.

and Schröder, H. (2017). Design and Demonstration of

a Photonic Integrated Glass Interposer for Mid-Board-

Optical Engines, 67

Electronic Components and Tech-

nology Conference.

O’Shea, D.C., Suleski, Th.J., Kathman, A.D. and Prather,

D.W. (2004). Diffractive Optics. Design, Fabrication,

and Test. Bellingham, Washington USA: SPIE, pp. .

Pfeifer, M., Büettner, S., Zhang, R., Serbay, M. and

Weißmantel, S. (2015). F2-Lasermikrostrukturierung

von Mikro-Fresnel-Linsen, In Journal of the University

of Applied Sciences Mittweida, pp. 127-130.

Pfeifer, M., Jahn, F., Kratsch, A., Steiger, B. and

Weissmantel, S. 2014. F

-Laser Microfabrication of

Diffractive Optical Elements, 2nd International

Conference on Photonics, Optics and Laser

Technology.

Pfeifer, M., Weissmantel, S. and Reisse, G. 2013. Direct

laser fabrication of blaze gratings in fused silica. In

Applied Physics A 112, pp. 61-64.

Qiu, J., Li, M., Ye, H., Yang, C., and Shi, C. (2018).

Fabrication of high fill factor cylindrical microlens

array with isolated thermal reflow. In Applied Optics,

57(25), pp. 7296-7302.

Richardson, D. J. (2010). Filling the Light Pipe. In Science,

330 (6002), pp. 327-328.

Xie, Z., Gao, S., Lei, T., Feng, S., Zhang, Y., Li, F. Zhang,

J., Li, Z. and Yuan, X. (2018). Integrated

(de)multiplexer for orbital angular momentum fiber

communication. In Photonics Research, 6 (7), pp. 743-

749.

Xing, J., Rong, W., Sun, D., Wang, L. and Sun, L. (2016).

Extrusion printing for fabrication of spherical and

cylindrical microlens arrays. In Applied optics, 55 (25),

pp. 6947–6952.

Fabrication of Micro Spiral Phase Plates in Fused Silica using F2-Laser Microstructuring

121