
A Technique for Automata-based Verification with Residual Reasoning
Shaun Azzopardi
a
, Christian Colombo and Gordon Pace
Department of Computer Science, Faculty of ICT, University of Malta, Msida, Malta
Keywords:
Verification, Model-based Analysis, Residual, Static Analysis, Partial Verification.
Abstract:
Analysing programs at a high-level of abstraction reduces the effort required for verification, but may ab-
stract away details required for full verification of a specification. Working at a lower level, e.g. through
model checking or runtime verifying program code, can avoid this problem of abstraction, at the expense of
much larger resource requirements. To reduce the resources required by verification, analysis techniques at
decreasing levels of abstraction can be combined in a complementary manner through partial verification or
residual analysis, where any useful partial information discovered at a high-level is used to reduce the verifi-
cation problem, leaving an easier residual problem for lower-level analyses. Our contribution in this paper is
a technology-agnostic symbolic-automata-based framework to project verification effort onto different verifi-
cation stages. Properties and programs are both represented as symbolic automata, with an event-based view
of verification. We give correctness conditions for residual analysis based on equivalence with respect to veri-
fication of the original problem. Furthermore we present an intraprocedural residual analysis to identify parts
of the property respected by the program, and parts of the program that cannot violate the property.
1 INTRODUCTION
Verification techniques are used to attempt to prove
that a program satisfies or violates a certain specifi-
cation. Such an attempt may fail to give a verdict
when not enough resources have been allocated, or
when the analysis ignores pertinent details necessary
for the problem at hand. Traditionally in the face of
such a failure the only option is to attempt a differ-
ent kind of verification technique on the same prob-
lem. Often however failing verification attempts can
be used to reduce the original problem, leaving a
smaller (and hopefully easier) problem for subsequent
attempts (Dwyer and Purandare, 2008).
Techniques for this kind of partial verification
fall largely into two categories: program-based and
property-based. Program-based techniques identify
parts of the program proven safe, leaving a smaller
part of the program to be explored by subsequent
techniques. Property-based techniques instead trans-
form the property that the program should be com-
pliant with, encoding certain aspects of the specific
program being verified to reduce the problem.
These two categories are dual to each other. Con-
sider that a model checker may exhaust all the re-
sources available before traversing all the program
a
https://orcid.org/0000-0002-2165-3698
state space. One can then take a program-based ap-
proach and slice the verified partial state space away,
leaving a reduced program exhibiting only the possi-
bly unsafe behaviour (Beyer et al., 2018; Lal et al.,
2007). Dually, a property-based approach can pred-
icate the original property by a condition that only
holds true for program states that have not yet been
verified safe (Beyer et al., 2012). This work exists
largely for state-based specification formalisms that
can specify predicates about the acceptable concrete
variable state of the program.
Another popular approach for verification, espe-
cially for runtime verification(Falcone et al., 2018),
abstracts program state changes in terms of events.
Event-based specifications specify properties in terms
of program actions (e.g. program function calls or
state modification), with verification involving event
instrumentation of the program and properties com-
pared in some manner with this instrumented program
to determine compliance. Program-based approaches
in this context remove instrumentation from proven
safe parts of the program. CLARA is one such ap-
proach (Bodden and Lam, 2010; Azzopardi et al.,
2020), analysing Java source code with finite-state
properties using control-flow analysis (ignoring data
aspects of the program), with extensions for symbolic
automata (Azzopardi et al., 2017). Property-based ap-
proaches for event-based formalisms are limited, fo-
Azzopardi, S., Colombo, C. and Pace, G.
A Technique for Automata-based Verification with Residual Reasoning.
DOI: 10.5220/0008981902370248
In Proceedings of the 8th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2020), pages 237-248
ISBN: 978-989-758-400-8; ISSN: 2184-4348
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
237

cused on Java and involving only summarisation of
deterministic parts of the program (Dwyer and Puran-
dare, 2007), or refining of pre- and post-conditions of
events (Ahrendt et al., 2012).
We can then identify gaps in literature with re-
gards to existing event-based approaches to partial
verification: (i) they are largely technology-specific;
and (ii) no approaches combine both control-flow
and data-oriented aspects of a program. In this pa-
per we seek to remedy these gaps by a technology-
agnostic approach that encodes both control-flow and
data-oriented aspects of the program in a symbolic
automata-based model. We give appropriate condi-
tions for reductions of verification problems in this
framework, and present three such novel complemen-
tary intraprocedural residual analyses. We evaluate
the approach in a Solidity smart contract case study
by measuring the reduction of resources required by a
subsequent runtime verification phase.
In Section 2 we present a technology-agnostic
framework for verification with forms of symbolic au-
tomata acting both as models for programs and prop-
erties. In Section 3 we discuss correctness condi-
tions for residual analysis in the presented framework,
and present three novel residual operations illustrated
through examples. In Section 4 we present an eval-
uation of these approaches, while discussing the pre-
sented results in Section 5. We further consider re-
lated work in Section 6 and conclude in Section 7.
2 PROGRAM VERIFICATION
Verification is the process of checking that a pro-
gram satisfies a property. Here we are interested in
event-based verification techniques, where program
behaviour and properties can both be represented as
a set of event traces, and verification being the pro-
cess of checking that the program traces are a sub-
set of the property traces. However working directly
with programs represented by sets of traces, as in pre-
vious work (Azzopardi et al., 2017), ignores both the
program structure and data-based decisions, which di-
rectly determine the sequences of events produced.
Here we attempt to remedy this.
In this section we present our formalisms for pro-
grams and properties, both being similar forms of
symbolic automata, with program automata produc-
ing events that drive property automata. As a running
example we use the Solidity (a language designed to
write smart contracts for the Ethereum blockchain)
smart contract in Listing. 1, which implements an in-
terface for an auction house. We also assume an event
set Σ, in this paper containing two kinds of program
1 c o n t r a c t Sm ar t Au c ti o nH ou s e {
2 a d dr e s s owne r ;
3 u i n t g o i n g s = 0 ;
4 bo ol o ng oi n g ;
5 mapping ( i n t => boo l ) f i n i s h e d ;
6 mapping ( i n t => add re s s p a ya b l e ) w i n ne r ;
7 mapping ( i n t => u i n t ) o f f e r s ;
8 i n t i d ;
9
10 c o n s t r u c t o r ( ) p u b l i c {
11 ow ner = msg . s en d er ;
12 }
13 m o d i f i e r isO w n er ( ) {
14 r eq u i r e ( owner == msg . se n de r ) ;
15 ;
16 }
17 f u n c t i o n s t a r t ( i n t itemID , u i n t s t a r t O f f e r )
p u b l i c i s Owner {
18 r eq u i r e ( ! o ng oi n g ) ;
19 r eq u i r e ( ! f i n i s h e d [ i d ] ) ;
20 o f f e r s [ i t em I D ] = s t a r t O f f e r ;
21 i d = it e mID ;
22 o n g oi n g = tr ue ;
23 }
24 f u n c t i o n o f f e r ( ) p u b l i c pa y ab l e {
25 r eq u i r e ( o n go in g ) ;
26
27 i f ( o f f e r s [ i d ] < msg . v a l u e ) {
28 i f ( w i n ne r [ i d ] ! = a d d re s s ( 0 ) ) {
29 w i nn er [ i d ] . t r a n s f e r ( o f f e r s [ i d ] ) ;
30 }
31 wi nn e r [ i d ] = msg . s en d er ;
32 o f f e r s [ i d ] = msg . v al ue ;
33 }
34 }
35 f u n c t i o n d e c l a r e ( ) p u b l i c i s Owner {
36 r eq u i r e ( o n go in g ) ;
37 r eq u i r e ( g o i n g s >= 3 ) ;
38 f i n i s h e d [ i d ] = t r u e ;
39 o n g oi n g = f a l s e ;
40 i d = −1;
41 g o i n g s = 0 ;
42 }
43 f u n c t i o n g oi ng ( ) p u b l i c i s Ow ner {
44 r eq u i r e ( o n go in g ) ;
45 g o i n g s ++ ;
46 }
47 }
Listing 1: Auction smart contract implementation.
events: (i) events wrapping around a function call, ei-
ther before (e.g. before(function)) or after (e.g. af-
ter(function)); and (ii) we use the notation @var to
match after a variables modification (we also allow
reference to the previous value of a variable through
var
pre
). We also assume Σ contains an empty event ε.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
238

2.1 Control-flow Automata
A common representation for programs is the corre-
sponding control-flow graph, with transitions repre-
senting execution of statements or conditional branch-
ing. Based on this notion, here we define control-flow
automata (CFAs). To represent statement execution,
we tag transitions by a statement (st : STMT), while to
represent conditions on the state (required to repre-
sent if-then-else and looping constructs) we guard
these by a condition (c : Cond). Here we are inter-
ested in event-based verification, which assumes the
program emits events that are processed by the mon-
itor, thus we let transitions trigger an event (e : Σ). A
transition is then of the form s
cstIe
−−−−→ s
0
.
To keep the semantics technology-agnostic we as-
sume a set of symbolic states Ω, with conditions as
predicates over Ω and statements as transformations
of Ω. Moreover, consider that a well-designed pro-
gram is not often a single monolothic piece but con-
sists of different methods
1
. To model this we allow
concrete CFA states to be call states, which encapsu-
late other CFAs, allowing for a form of hierarchy. We
characterise this formally.
Definition 2.1. A control-flow automaton (CFA) is
parametrised by a type of symbolic program states Ω;
and a finite set of concrete program states S.
A CFA, of type CFA, is a tuple hs
0
, E, calls, →i,
where:
(a) s
0
∈ S is the initial concrete program state;
(b) E ⊆ S is the set of end states, we use s
E
for an
element of this set;
(c) calls : S 7→ (Ω → CFA) identifies states associated
with dynamic method calls; and
(d) →: S × Cond × STMT × Σ → S is the deterministic
transition relation (where Cond = Ω → Bool, and
STMT = Ω → Ω).
We write s
cstIe
−−−−→ s
0
for (s, c, st, e, s
0
) ∈→. We use
P or M for CFAs. We use the function methods : CFA →
2
CFA
for the set of methods transitively called by M
2
.
Figure. 2 illustrates CFAs corresponding to meth-
ods in Listing. 1. In these examples we use several
shorthands: (i) ∗ is used in place of the otherwise
3
transition; and (ii) we leave out the true condition, the
identity statement, and ε (and their markers).
An interesting aspect of Listing. 1 is that it does
not have a main method but instead simply offers a set
1
We use the term methods to refer to program functions,
to distinguish them from the formal object.
2
In this paper we will be limiting our analysis to when
this is finite.
3
Corresponding to the transition with the negation of the
disjunction of the alternate transitions’ conditions.
s
1
start
s
E
s
start
s
offer
s
going
s
declare
s
5
Figure 1: Automata modelling the interface of the smart
contract, with shaded states marking call states.
s
0
start
revert
s
1
s
2
s
3
s
4
s
5
s
E
*
owner = msg.sender
*
!ongoing
!finished[id]
*
offers[itemID]
= startOffer;
id = itemID;
I @id
ongoing = true;
I after(start)
(a) start method.
s
0
start
revert
s
1
s
2
s
3
s
4
s
5
s
E
*
ongoing
I before(offer)
offers[id]
< msg.value
* I after(offer)
winner[id] != address(0)
winner[id]
.transfer(offers[id])
I @winner
*
winner[id] = msg.sender;
I @winner
offers[id] = msg.value;
I @offer[id]
I after(offer)
(b) offer method.
Figure 2: CFAs of methods from Listing. 1 and the under-
lying interface
4
.
of methods that can be called in any sequence, while
a CFA expects a single entry-point in the program.
Consider that such a single entry-point can be mod-
eled with a CFA based on the automaton in Figure. 1,
with appropriate transition labels that allow the inter-
face methods to be called in any sequence with arbi-
trary inputs depending on the initial symbolic state.
To be able to reason about CFAs we give the for-
malism an operational semantics that produces the
execution traces associated with the CFA. This se-
mantics traverses a CFA given an initial symbolic
state. This symbolic state evolves based on the avail-
able transitions, producing a symbolic event pair from
Σ × Ω. When at call states there are two different
behaviours. If an end state can be reached in the
called method then control is yielded back to the call-
4
Here events in gray will be removed by applying the
residual techniques presented in Section 3.
A Technique for Automata-based Verification with Residual Reasoning
239

ing CFA, encoding the produced execution trace on a
transition. If on the other hand the called method can-
not reach an end state (with the input symbolic state)
control is yielded back with no recorded events. For
example, looking at Figure. 2a note how a revert
state is not an end state (and cannot reach an end
state), and thus any trace ending at this state is not
recorded as an execution trace of the program.
To model method calls, states are extended with a
direction (S
↑↓
def
= S × {↑, ↓} ): s
↑
denotes exiting from
a call of s, and s
↓
denotes entering into a call of s.
Transitions in the semantics are tagged by traces
containing pairs of events and symbolic states (to be
consumed by the monitor). For simplicity we abuse
notation and assume the transitive closure of the op-
erational semantics transition is also tagged by these
traces, rather than traces of traces, i.e. →, ⇒: (S
↑↓
×
Ω) × (Σ × Ω)
∗
× (S
↑↓
× Ω), with this corresponding to
the standard transitive closure with concatenation of
the traces.
Definition 2.2. The intraprocedural operational se-
mantics of a CFA is given with configurations as a
pairs of directed states and symbolic states (S
↑↓
×Ω),
transitions labeled by traces of pairs of events and
symbolic states ((Σ ×Ω)
∗
), and characterised by:
(i) Given a transition s
1
cstIe
−−−−→ s
2
, with c holding on
ω, and s
2
not being an end state, then a con-
figuration (s
↑
1
, ω) transitions to (s
↓
2
, st(ω)) with
he, st(ω)i:
s
1
cstIe
−−−−→ s
2
s
2
6∈ E c(ω)
(s
↑
1
, ω)
he,st(ω)i
−−−−−→ (s
↓
2
, st(ω))
(ii) If s
1
is not a call state, then a configuration with a
state s
↓
1
simply transitions to a configuration with
the same symbolic state and the exiting state s
↑
1
:
s
1
6∈ dom(calls)
(s
↓
1
, ω)
hi
−→ (s
↑
1
, ω)
(iii) If s
1
is a call state, then a configuration (s
↓
1
, ω)
transitions with ews to a configuration (s
↑
1
, ω
0
) if
the method called by s
1
reaches an end configura-
tion with ω
0
when starting with ω:
s
1
∈ dom(calls) M = calls(s
1
)(ω)
∃s
E
∈ E
M
, ω
0
∈ Ω · (s
0
M
, ω)
ews
⇒ (s
E
, ω
0
)
(s
↓
1
, ω)
ews
−−→ (s
↑
1
, ω
0
)
(iv) If s
1
is a call state, then a configuration (s
↓
1
, ω)
transitions with hi to a configuration (s
↑
1
, ω) if the
method called by s
1
reaches no end configuration
when starting with ω:
s
1
∈ dom(calls) M = calls(s
1
)(ω)
@s
E
∈ E
M
, ω
0
∈ Ω · (s
0
M
, ω) ⇒ (s
E
, ω
0
)
(s
↓
1
, ω)
hi
−→ (s
↑
1
, ω
0
)
From this operational semantics we can charac-
terise the execution behaviour of a CFA by identifying
the prefixes induced by an initial symbolic state.
Definition 2.3. The behaviour of CFA P starting with
symbolic state ω of length i ∈ N is the trace t
P,ω,i
de-
fined formally as follows
5
:
t
P,ω,i
def
=
(
pre(ews, i) (s
↓
0
P
, ω)
ews
⇒ (s
↑
E
P
, ω
0
) ∧ i < len(ews)
hi otherwise
We use CFAs to represent the actual behaviour
of a program, in fact note how in CFAs there is a
direct one-to-one correlation with states and lines in
code. Its low-level nature however makes it unviable
for high-level specification. In the next section, we
consider a more appropriate variant for specification.
2.2 Dynamic Event Automata
Common formalisms for property specification
largely fall into logic-based or automata-based. Here
we focus on dynamic event automata (DEAs), expres-
sive symbolic automata encoding allowed behaviour
both through control-flow and data-oriented aspects,
allowing for more succinct representations and power
than the more traditional finite-state automata. DEAs
are similar to CFAs, with symbolic states (Θ), and
transitions tagged by events (e), guards (g) on both the
program and property symbolic states, and actions (a)
on the property symbolic state, written q
e|g7→a
−−−−→ q
0
.
Definition 2.4. A dynamic event automaton (DEA) is
parametrised by: (i) a type of symbolic monitor states
Θ; (ii) a type of symbolic program states Ω; and (iii)
a finite set of concrete states Q.
A DEA is then a tuple π
def
= hq
0
, θ
0
, B, A, →i, where:
(a) q
0
∈ Q is the initial concrete monitor state;
(b) θ
0
∈ Θ is the initial monitor symbolic state;
(c) B, A ⊆ Q are respectively the set of concrete bad
and accepting states, we use q
B
for a bad state;
and
(d) →: Q × (Σ \ {ε})× Guard × Act → Q is the set of
transitions (where Guard = Θ × Ω → Bool, and
Act = Θ × Ω → Θ).
We write q
e|g7→a
−−−−→ q
0
for (q, e, g, a, q
0
) ∈→.
Figure. 3 illustrates some DEAs for Listing. 1.
Monitors at runtime evolve depending on the be-
haviour of the program. Here the behaviour of the
program at runtime is encoded as a trace of pairs of
events and program symbolic states. Then we define
5
Where pre : (Σ ×Ω)
∗
×N is the prefix of the input trace
of the input length if existent, otherwise the empty trace,
and len : (Σ × Ω)
∗
→ N gives the length of a trace.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
240
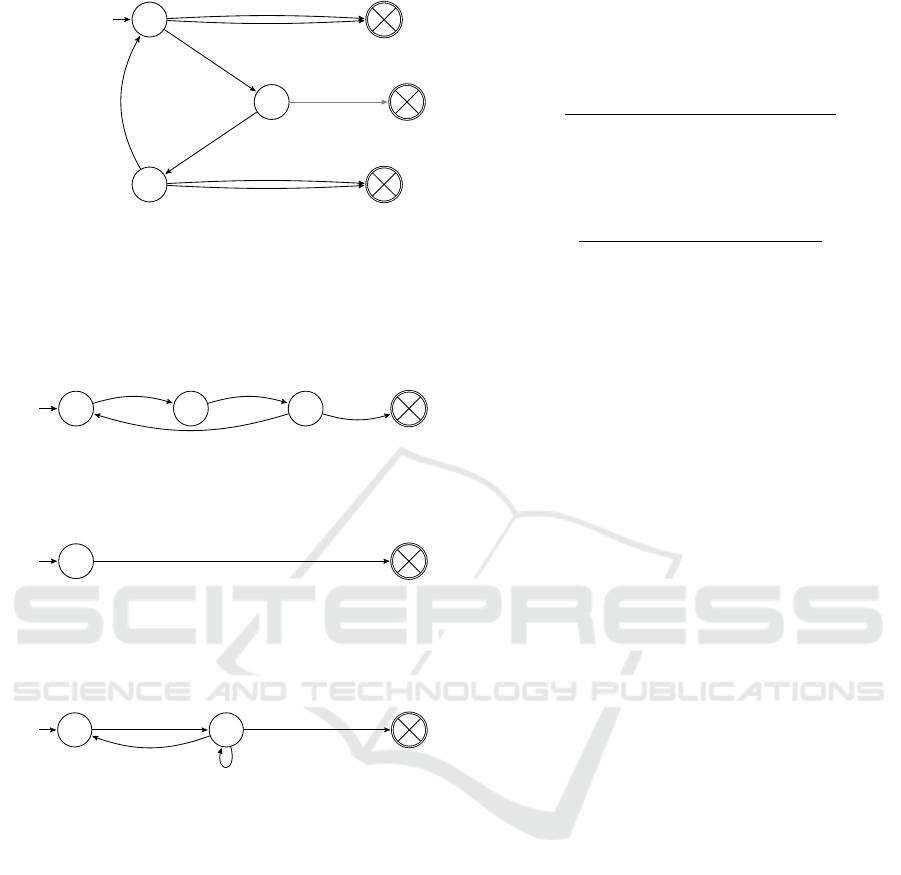
q
1
start
q
2
q
3
@goings | goings
pre
!= goings
after(offer)
after(start)
after(declare)
| goings < 3;
before(declare)
| goings >= 3
after(offer)
@winner[id]
after(declare)
| goings == 0
(a) The business process of an auction smart contract: (i)
no offers can be made before an auction is started; (ii) dur-
ing an auction the winner cannot be declared before going
thrice; (iii) no offer can be made and no winner set just as
the auction is declared; and (iv) after the auction has been
declared the goings reset.
q
1
start
q
2
q
3
before(offer)
| ongoing
@id{true}
after(start)
@winner
(b) When an offer is made during an ongoing action and the
item being auctioned is changed, no winner is set until the
auction starts.
q
1
start
@offers[id] | offers[id]
pre
≥ offers[id]
(c) Whenever the current winning offer for an item is modi-
fied, the new value must be larger than the old value.
q
1
start
q
2
after(start(itemID,startOffer))
7→ lid := itemID;
bidder := msg.sender;
o := startOffer
before(offer(o’)) | o’ > o
7→ o := o’;
highest := msg.sender;
after(declare)
| winner[lid] 6= bidder
∨ offers[lid] = o
after(declare) | ∗
(d) Keep track of the current highest bid. This should be the
winning bid at the end of an auction.
Figure 3: Several properties expected of the auction smart
contract in Listing. 1, with bad states marked with a cross.
the operational semantics of DEAs to allow DEAs to
evolve based on these symbolic events. A transition
is taken if its event matches the event triggered while
the guard holds on the symbolic states. While it trans-
forms the monitoring symbolic state with the action
accordingly. The semantics halts once a verdict (a bad
or accepting state) has been reached.
Definition 2.5. The operational semantics of a DEA
is given with configurations of type Q×Θ, with transi-
tions labeled by elements of Σ ×Ω, and characterised
by the following rules:
(i) A configuration (q, θ), given a transition q
e|g7→a
−−−→
q
0
, evolves to a configuration (q
0
, a(ω, θ)) only if
the guard g holds on θ:
q
e|g7→a
−−−−→ q
0
q 6∈ A ∪ B g(ω, θ)
(q, θ)
e,ω
−−→ (q
0
, a(ω, θ))
(ii) if the previous rule does not hold, then the config-
uration does not evolve:
@q
0
, θ
0
· θ
0
6= θ ∧ (q, θ)
e,ω
−−→ (q
0
, θ
0
)
(q, θ)
e,ω
−−→ (q, θ)
We overload ⇒ for the transitive closure of →.
We use DEAs to explicitly specify the behaviour
that the program is prohibited from exhibiting, char-
acterised as the set of traces reaching a bad state.
Definition 2.6. The bad traces of property π are those
traces that reach a bad state in π: B(π)
def
= {t ∈ (Σ)× Ω |
∃q
B
∈ B, θ ∈ Θ · (q
0
, θ
0
)
t
⇒ (q
B
, θ)}.
Looking at the operational semantics consider that
states unreachable from the initial state cannot partic-
ipate in a violation. Moreover states that cannot reach
a bad state can be marked as accepting, since when
reaching such states any continuation cannot violate.
We can reduce a DEA accordingly.
Definition 2.7. A DEA is in optimal form if: (i) there
are no states unreachable from the initial state: @q ∈
Q·q
0
6⇒ q; and (ii) states that cannot reach a bad state
are accepting and have no outgoing transitions: ∀q ∈
Q, q
B
∈ B · q 6⇒ q
B
=⇒ (q ∈ A∧@q
0
∈ Q · q ⇒ q
0
∧ q 6= q
0
).
We assume every DEA used here is optimal.
Finally, we can characterise compliance of a pro-
gram with a property when every execution prefix ex-
hibited at runtime is not in the property bad language.
Definition 2.8. A CFA P is said to satisfy a property π
if every execution prefix it generates is not a bad trace
of π: P ` π
def
= ∀ω ∈ Ω, i ∈ N·t
P,ω,i
6∈ B(π).
Based on this background, we introduce our
framework for partial verification of event-based
properties in the next section. Our objective is to
prove P ` π or to reduce it to another problem P
0
` π
0
.
3 RESIDUAL STATIC ANALYSIS
Exploring the whole runtime state space of a program
exhaustively is expensive for large enough programs.
An alternative is to perform sound static analysis, by
over-approximating the behaviour of a program and
verifying this sound abstraction rather than the actual
A Technique for Automata-based Verification with Residual Reasoning
241

program behaviour. We can then conclude satisfac-
tion when no violating prefix is found in the abstrac-
tion. However the lack of completeness means that
locating a violating prefix does not allow us to con-
clude that the program is violating, leaving an incon-
clusive result. This motivates the need for partial ver-
ification techniques where instead, inconclusive re-
sults are framed as a residual version of the original
problem.
Here we discuss and give correctness condi-
tions for reducing the verification problem, and then
present an intraprocedural program-property analysis
combining both control- and data-flow abstractions
upon which we define three novel residual analyses
that soundly: (i) silence CFA events; (ii) remove DEA
transitions; and (iii) remove DEA transition guards.
The full proofs of the claims in this section can be
found in a corresponding technical report (Azzopardi
et al., 2019).
3.1 Residual Correctness
Reducing the verification problem involves transfor-
mations of the program instrumentation and of the
property. Care must be taken to ensure that these
transformations do not cause a change in verdict to
the program, i.e. that they are equivalent. There are
different levels to which this can be ensured.
The most basic condition that is required of a
residual analysis is to simply ensure that the origi-
nal verification problem (P ` π) is equivalent to the
residual verification problem (P
0
` π
0
). However this
may be considered too weak. Consider that we may
be interested in runtime verifying the residual prob-
lem, where each trace is analysed individually. Con-
sider that P may violate π with multiple traces, and
then a sufficient P
0
is one that exhibits only one of the
original violating traces and a sufficient π
0
is π. This
means that there is some input with which P violates π
but with which P
0
does not violate π
0
, although P ` π
is still equivalent to P
0
` π
0
.
Instead we can characterise a deeper level of
equivalence, one that exists at the level of inputs.
This ensures that at runtime an execution trace of P
will violate iff the corresponding execution trace of P
0
will violate. However, consider that P
0
may be trans-
formed such that its execution trace violates later than
that of P. In applications such as enforcement, this
behaviour would not be ideal since detecting a viola-
tion as early as possible is ideal. To ensure that P and
P
0
violate at the same time, we consider also prefixes
of the CFAs of the same length. We term this equiv-
alence at the level of input and prefix length lockstep
verification equivalence.
Definition 3.1. (P, π) is said to be in lockstep with
the pair (P
0
, π
0
) iff execution traces of P and P
0
from
the same symbolic state ω are given the same verdict
by π and π
0
for every prefix length i:
∀ω ∈ Ω, i ∈ N ·t
P,ω,i
∈ B(π) ⇐⇒ t
P
0
,ω,i
∈ B(π
0
).
Our objective is then to create residual analyses
that produce a verification problem that is in lockstep
with the original, ensuring detection of a violating
trace occurs at the same point. Note how this leaves
us open to detect non-violating traces before the orig-
inal monitor.
3.2 Intraprocedural Analysis
The problem of verification here is the checking that
the language of the program is not contained in the
bad language of the property, as defined in Defini-
tion. 2.8. A standard manner of checking this is
to analyse the composition of the program with the
property (Vardi, 2007). In our case CFAs may con-
tain calls to other CFAs, making composition non-
straightforward. Moreover, for complex programs,
dealing with interprocedural behaviour (i.e. the way
data- and control- flows through multiple procedures)
can prove to be expensive. Instead the analyses
we present here are intraprocedural, considering the
behaviour of each method individually, while over-
approximating outside behaviour. Working at this
level allows for less resource-intensive analysis. An-
other aspect necessary for this analysis is that execu-
tion traces depend on the manner data flows through a
CFA, which is determined by the transitions and their
labels. A viable analysis then does not only take into
account the control-flow structure of a CFA, but also
the conditions that determine data-flow, and the state-
ments that determine how data is transformed.
In this section we present both data- and control-
flow abstractions of a program. We first characterise
data abstractions of runtime symbolic states using
conditions, and then define an intraprocedural com-
position of CFAs and DATEs that takes into account
a data abstraction to avoid impossible runtime paths.
This composition will be the basis upon which we de-
fine our residuals.
3.3 Data Abstraction
In an attempt to maintain a light analysis, we shall
not be enumerating all the possible runtime config-
urations of a CFA. Instead, we shall be abstracting
these configurations by the corresponding concrete
program state (e.g. state s abstracts runtime config-
uration (s, ω)). To determine which transitions from s
can actually be taken at runtime, we wish to associate
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
242

Table 1: A data abstraction for the offer CFA in Figure. 2b.
State Data Abstraction
s
0
true
s
1
ongoing
s
2
ongoing & offers[id] < msg.value
s
3
ongoing & offers[id] < msg.value
s
4
ongoing & offers[id] < msg.value
& winner[id] == msg.sender
s
5
ongoing & offers[id] == msg.value
& winner[id] == msg.sender
s
E
ongoing
with s some information about the symbolic states it
can be associated with at runtime. We characterise
such a data abstraction as a function that associates
a condition with a state that holds true on every cor-
responding symbolic state at runtime. We keep this
intraprocedural.
Definition 3.2. A function ∼: S → Cond is said to be
a data abstraction of a CFA if for any explicit state
s, it associates with s a condition that is always true
on symbolic states associated with configurations of s
that are reachable from the initial configuration and
reaching an end configuration: ∀ω
0
, ω, ω
E
∈ Ω, s ∈
S
↑↓
· (s
↓
0
, ω
0
) ⇒ (s , ω) ⇒ (s
↑
E
, ω
E
) ∧ s ∼ c =⇒ c(ω).
A data abstraction here essentially is a state in-
variant relation. Consider that a trivial abstraction
is one that associates true with every state. Another
more useful abstraction that we use in a prototype of
this work is created by intraprocedurally propagating
statement effects. For example, if a state s is only ac-
cessible through a transition that performs a statement
x = 7 then s ∼ (x == 7) is an appropriate abstraction
for s. See Table. 1 for this logic applied to offer
(Figure. 2b).
To utilise these abstractions during our analysis,
we can employ an SMT solver (specifically the Z
3
solver (de Moura and Bjørner, 2008)) that can be ex-
ploited to check whether a DEA guard is compatible
(>), or not (⊥) with a condition. We assume this is
sound, i.e. it may be inconclusive, since certain back-
ground theories for symbolic states may be undecid-
able.
Definition 3.3. A satisfaction procedure sat :
Guard × Cond → {>, ⊥, ?} is a procedure that sat-
isfies the following conditions:
(i) Compatibility If the procedure returns > then
whenever the condition is true on a symbolic state,
the guard is also true on the same state:
sat(g, c) = > =⇒ (∀ω ∈ Ω, θ ∈ Θ ·c(ω) =⇒ g(θ, ω));
and
(ii) Incompatibility If the procedure returns ⊥, then
whenever the condition is true on a symbolic state,
the guard is false on the same state:
sat(g, c) =⊥ =⇒ (∀ω ∈ Ω, θ ∈ Θ ·c(ω) =⇒ ¬g(θ, ω)).
For example, we can easily conclude that for any
guard y, sat(ongoing ∨ y, ongoing) = > for any y,
while for a guard y independent of the CFA symbolic
state, sat(y, c) =?.
Furthermore consider that a DEA transition
q
e|g7→a
−−−−→ q
0
may only execute after a CFA transition
s
cstIe
−−−−→ s
0
. To check whether the DEA transition may
be triggered, we have the option of checking whether
g is incompatible with the data abstraction of s
0
. How-
ever the data abstraction of s
0
may be very weak, since
s
0
may have multiple incoming transitions (consider
s
E
in Table. 1). Instead, since here we know which
transition is being taken, we can compute a stronger
abstraction, by updating the abstraction of s with the
transition taken, i.e. with the condition c and state-
ment st.
Definition 3.4. A procedure that computes the data
abstraction of a state with respect to a certain tran-
sition, update : S × Cond × STMT → Cond, obeys the
condition that the produced predicate holds at run-
time on the symbolic state after the transition is taken:
∀ω, ω
E
∈ Ω · (s
↓
0
, ω
0
) ⇒ (s
↑
, ω) ⇒ (s
↑
E
, ω
E
) ∧ c(ω) =⇒
update(s, c, st)(st(ω)).
Consider that a valid value for update(s
5
, true,
skip) is the abstraction of s
5
. This allows us to con-
sider the effect of taking the transition from s
5
to s
E
(see Figure. 2b), rather than using the weaker abstrac-
tion associated with s
E
(see Table. 1).
We shall be using this data abstraction of states to
identify on-the-fly incompatible transitions in a CFA-
DEA composition, as presented in the next section.
3.3.1 Control-flow Abstraction
Since we have limited ourselves by intraprocedural-
ity, in the interest of tractability, we cannot simply
unfold P and compose it against the property. Instead
our approach is based on the intuition that if an exe-
cution trace of P is violating, then the violation must
occur in some method M of P. Our analysis then will
involve attempting to find such an M, by composing
each method against the property, while abstracting
the behaviour before and after the method is called,
and during calls of the method.
The composition will give us a view of every pos-
sible execution of P that contains an execution of M.
To achieve this we can abstract the behaviour before
the method is called chaotically, allowing any event
to occur before the initial state of M. This models any
possible call to M from any method. With similar jus-
tification, we can do the same for end and call states.
Consider however that a method M may con-
tain special events that only it can trigger, e.g. only
A Technique for Automata-based Verification with Residual Reasoning
243

the start method triggers the before(start) event.
Then, a more precise abstraction only allows initial,
end, and call states to behave chaotically with events
that may occur outside of M, while allowing end and
call states to re-enter M with artificial transitions to
its initial state. This re-entering will allow us to make
more precise inferences about execution traces of the
program.
We then proceed by comparing transitions of M
with those of π such that: (i) any available DEA tran-
sition with the same event and compatible guard is
taken synchronously (a concrete match); and (ii) if the
guards are not mutually exclusive with the abstracted
CFA state, or if the transition’s event is ε, then the
configuration evolves asynchronously in M. This re-
flects the CFA and DEA operational semantics.
Definition 3.5. The abstract intraprocedural compo-
sition of a CFA M and a property π is the transition
system with states of type S × Q, transitions labeled
by pairs of CFA and DEA transition labels, with pos-
sibly one label missing represented by the symbol:
((Cond×STMT ×Σ)∪{})×((Σ×Guard×Action)∪{}),
and characterised by the following rules:
1. Initial and end configurations take any available
DEA transition with events used outside of M
6
,
while end and call configurations may transition
into M and back:
s ∈ {s
0
} ∪ E e ∈ out(M)
q
e|g7→a
−−−−→ q
0
(s
0
, q)
−−−−→
e|g7→a
(s
0
, q
0
)
s ∈ E ∪ dom(calls)
q, q
0
∈ Q
(s, q)
−→
(s
0
, q)
(s
E
, q
0
)
−→
(s, q
0
)
2. (s, q) transitions to (s
0
, q
0
) if there are transitions
between the respective states in the CFA and DEA,
with the same event, and if the abstraction of s up-
dated with the CFA transition is not incompatible
with the DEA guard:
s
cstIe
−−−−→ s
0
q
e|g7→a
−−−−→ q
0
sat(update(s, c, st), g) 6=⊥
(s, q)
cstIe
−−−−→
e|g7→a
(s
0
, q
0
)
3. (s, q) transitions to (s
0
, q) if there are transitions
between the respective CFA states, and if the data
abstraction of s updated with the CFA transition
is not incompatible with the conjunction of the
negation of each guard associated with a transi-
tion from q:
s
cstIe
−−−−→ s
0
sat(update(s, c, st),
^
q
e|g
0
7→a
−−−−→q
0
¬g
0
) 6=⊥
(s, q)
cstIe
−−−−→
(s
0
, q)
6
out : CFA → 2
Σ
is the function that returns the set of
events used shallowly in CFAs’ of P that are not the input
CFA.
4. Any configuration with a program state with an
outgoing ε-transition asynchronously transitions
with that CFA transition:
s
cstIε
−−−−→ s
0
(s, q)
cstIε
−−−−→
(s
0
, q)
We overload ⇒ as its transitive closure. We call
a transition that does not use a concrete transition,
and use 6 for a label that is not .
Note how we are using as a placeholder value
whenever either a DEA transition does not match or a
CFA transition is not used.
As described before, we want to use this compo-
sition to identify when DEA transitions can be used
on the way to a violation. We will do this by iterat-
ing over all concrete transitions of a composition, and
gathering those whose source configurations is reach-
able from both the initial configuration, and directly
from a configuration that can reach a bad end con-
figuration. This will allow to choose all those DEA
transitions that may be used on the way to a violation,
i.e. those DEA transitions that may both be used as
part of a violating trace and those transitions that may
be used to avoid a violating verdict.
Definition 3.6. We write (s, q)
x
−→
y
→(s
0
, q
0
), when:
(i) the transition is in the composition:
(s, q)
x
−→
y
(s
0
, q
0
); and
(ii) (s, q) is reachable from the initial configuration and can
reach a bad end configuration:
(s
0
, q
0
) ⇒ (s, q) ⇒ (s
E
, q
B
).
Note how we require (s, q) to reach a bad end con-
figuration and not (s
0
, q
0
) since q
0
may be effectively
accepting and then (s, q)
x
−→
y
→(s
0
, q
0
) would be used on the
way to an accepting verdict.
Then we claim that if we cannot find a method of a
program P for which there is no such useful transition,
we can conclude that P satisfies the DEA in question.
Theorem 3.1. ∀π ∈ Π ·@M ∈ methods(P), s, s
0
∈ S
M
, q
B
∈
B, q ∈ Q \ B · (s, q)
6
−→
6
→(s
0
, q
B
) =⇒ P ` π.
Proof Sketch. Synchronous steps of the CFA P and
DEA π at runtime have corresponding transitions in a
composition of π with a method of P. This allows to
conclude that if at runtime there is a point at which the
program is not violating and takes a step that causes a
violation, then this step must be reflected in concrete
transition of some composition.
This is a strong requirement for satisfaction, given
the chaotic abstraction we are using, and often will
fail. Instead we can produce residuals.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
244

3.3.2 Residual Analysis
The characterising features of residual problems are
twofold, they are: (i) reductions of the original prob-
lem; and (ii) in lockstep with the original problem.
The first is required to ensure that the residual prob-
lem requires the same or less work than the original
problem, rather than increasing the workload. To en-
sure the second, we must be careful in the way we
choose sub-structures of a DEA to remove. Our prin-
ciple here will be that we only remove objects that
cannot affect the verdict of a given trace. We will
present three residuals that obey this principle, all re-
lying on the notion of a useful transition.
Looking at Theorem. 3.1, consider that any prop-
erty transitions not participating in a useful transition
are either unused or used when an accepting verdict
has already been given. This ensures that removing
them will not cause a runtime verdict to change.
Definition 3.7 (Control-Flow Residual). π\P is the
property with the transitions of π participating in a
useful transition in a method of P:
→
π\P
def
=
q
e|g7→a
−−−−→ q
0
|
∃M ∈ methods(P), s, s
0
∈ S
M
·
(s, q)
6
−−−−→
e|g7→a
→(s
0
, q
0
)
.
Consider for example that in a composition of
start (Figure. 2a) and Figure. 3b a bad state is never
reached — a change in id is always followed by
a before(start) event that avoids reaching the bad
state. Moreover, since these events only occur in
this method, the respective transitions can be removed
from Figure. 3b. Note how the limitation for end
states in the first composition rule is essential to prove
this.
Dually, we can re-formulate this for CFA transi-
tions. Consider that any CFA transition not used in a
useful transition can be silenced (i.e. transformed into
ε-transitions), since the events they trigger are only
triggered when a verdict can already be given.
Definition 3.8. P\π is the program:
(i) with transitions of P participating in a concrete
transition:
→
0
def
=
(
s
cstIe
−−−−→ s
0
|
∃M ∈ methods(P), s, s
0
∈ S
M
·
(s, q)
cstIe
−−−−→
6
→(s
0
, q
0
)
)
;
and
(ii) with the rest of the transitions of P silenced:
→
1
def
=
n
s
cstIε
−−−−→ s
0
| (s, c, st, e, s
0
) ∈→
π
\ →
0
o
.
Then →
P\π
def
=→
0
∪ →
1
. The reduction applies tran-
sitively to calls: calls
P\π
= λs, ω · calls(s)(ω)\π.
Consider that in Figure. 2a we can turn off the id
modification event between state s
4
and s
5
since as de-
termined previously, the transition can never be used
towards a violation.
We can show that the residual problem pair thus
created is equivalent to the original problem.
Theorem 3.2. (P\π, π\P) is in lockstep with (P, π).
Proof Sketch. Consider that any step towards a vio-
lation at runtime must be reflected in a composition.
These steps are exactly those that have corresponding
useful transitions in a composition, and thus remain
in the residual problem. Any transitions removed or
silenced had no effect on the verdict in the original
problem and being removed in the residual problem
thus does not affect the verdict given, allowing us to
easily conclude the theorem.
Using the composition, we can furthermore de-
fine another residual operation that operates on DEA
guards. Consider that looking at the composition we
have an over-approximation of when DEA transitions
match CFA transitions. A special case is when we
find that a certain DEA transition may always be used
when it is an option, i.e. from any configuration that
can trigger such a transition then all outgoing transi-
tions concretely match that transition. In this case,
since the composition is sound, we can conclude that
this also holds at runtime and thus we can avoid com-
puting the guard of such a transition by transforming
it into the true guard.
Definition 3.9 (Guard Residual). π P is the property
with the union of the following transition sets:
(i) the DEA transitions that are not always activated:
→
0
def
=
q
e|g7→a
−−−→ q
0
|
∃M ∈ methods(P), s, s
0
, s
00
∈ S
M
,
q
00
∈ Q · (s, q)
cstIe
−−−−→
e|g7→a
→(s
0
, q
0
)∧
∃l 6= (e, g, a) · (s, q)
cstIe
−−−−→
l
→(s
00
, q
00
)
and
(ii) the DEA transitions that are always activated
with silenced guards:
→
1
def
=
q
e|true7→a
−−−−−→ q
0
|
(q, e, g, a, q
0
) ∈→
π\P
∧
(q, e, g, a, q
0
) 6∈→
0
.
Then →
πP
def
=→
0
∪ →
1
.
Consider Figure. 3b: We can easily determine
that ongoing is always true when before(offer) oc-
curs, consider Table. 1, and similarly for the silenced
guards in Figure. 3a. Note how in the definition of
the guard residual, we are analysing the control-flow
residual and not the original property (see (ii)). This
is necessary since considering the transitions of π can
lead us to create a non-deterministic DEA or a DEA
with different behaviour. Consider using π na
¨
ıvely
instead of π\P in condition (ii): This would lead us
to have to consider transitions never activated in the
A Technique for Automata-based Verification with Residual Reasoning
245

composition. Silencing their guards could change the
behaviour at runtime or clash with transitions from
the same state. Using π\P avoids this.
Theorem 3.3. (P, π P) is in lockstep with (P, π).
Proof Sketch. Consider how the composition makes
explicit any possible intraprocedural behaviour, in-
cluding no matching (see rule (iii) of the composi-
tion). Then, weakening a guard when there is no alter-
native transition from the same property state in any
composition is sound since then there are no alterna-
tives at runtime either.
This finishes our presentation of our framework
for residual analysis using symbolic automata, while
we have introduced several residual operators that we
evaluate in the next section.
4 EVALUATION
To evaluate the techniques in this paper, we consid-
ered the running example and the various properties
we defined over it. We runtime verified these prop-
erties both before and after residual analysis, measur-
ing the overheads in each case, using the CONTRACT-
LARVA tool (Azzopardi et al., 2018).
Traditionally these overheads are measured in
terms of two aspects: (i) the time taken in both setups;
and (ii) the memory consumed by both setups. These
are both measures of different aspects of the compu-
tation required for monitoring. The running example
we use here, Listing. 1, is a smart contract written
in the Solidity language intended for the Ethereum
blockchain(Wood, 2014). In Ethereum any compu-
tation requested has to be paid for according to a pre-
set deterministic unit called gas, which has a variable
real-world cost. Thus reducing the computation per-
formed on the blockchain is imperative, to reduce the
cost of a service running off the blockchain. Gas is
also intended to be proportional to the effort required
to store and compute on the blockchain. We then use
this measure to evaluate our residual techniques here.
Table. 2 illustrates the results of the evaluation,
listing the percentage of gas overheads that (i) moni-
toring the original property adds; (ii) monitoring the
residual property adds; and (iii) savings of the latter
over the former. Consider how there are significant
reductions to gas costs associated with deployment,
except in the last case since no reductions could be
made to the property. The results with function calls
vary, with significant reductions for the offer method
in the first partially proven property, with little reduc-
tions in the other cases.
Table 2: Evaluation of analysis with running example
7
.
DEA
Monitored % of Residual % of Savings % of
original gas original gas monitored gas
Deploy.
Figure. 3a 65.87% 36.33% 28.58%
Figure. 3b 32.55% 0% 100%
Figure. 3c 21.40% 0% 100%
Figure. 3d 48.69% 48.69% 0%
start
Figure. 3a 0.92-25.07% 0.92-25.07% 0%
Figure. 3b 0.02-9.36% 0% 100%
Figure. 3c 1.30-24.17% 0% 100%
Figure. 3d 0.94-93.63% 0.94-93.63% 0%
offer
Figure. 3a 3.87-5.68% 2.63-4.01% 27.71-31.89%
Figure. 3b 14.86-72.15% 0% 100%
Figure. 3c 1.43-31.65% 0% 100%
Figure. 3d 0.2-1.40% 0.2-1.40% 0%
declare
Figure. 3a 40.30% 37.75% 6.32%
Figure. 3b 87.56% 0% 100%
Figure. 3c 0.62% 0% 100%
Figure. 3d 26.58% 26.58% 0%
goings
Figure. 3a 3.01-77.57% 3.01-77.57% 0%
Figure. 3b 0.86-1.33% 0% 100%
Figure. 3c 0.85-1.33% 0% 100%
Figure. 3d 0.86-1.33% 0.86-1.33% 0%
These result shows how analysing properties be-
fore runtime verification can help avoid some runtime
overheads, however these reductions in overheads de-
pend significantly on how much of the property and
instrumentation was removed. An issue this evalua-
tion does not tackle is how useful these analyses are
when combined with more precise static analyses.
5 DISCUSSION
In this work we made the decision to use a represen-
tation of programs that is similar to our specification
language, begging the question: why not simply use
DEAs as both our program and specification models?
The response is that DEAs cannot be used elegantly
to represent the actual behaviour of a program. Con-
sider that there are several differences between DEAs
and programs: (i) DEAs are passive (they wait for
events to occur) whereas programs are active (they
trigger events); (ii) programs call other programs se-
quentially whereas DEAs are monolithic; and (iii) it
is not clear how DEAs can be extracted from pro-
grams while maintaining a one-to-one connection to
program code necessary to turn off some instrumenta-
tion as required. CFAs on the other hand are easily ex-
tractable from common programming languages like
Java while they allow for calls to other CFAs. How-
ever CFAs are not appropriate for high-level specifi-
cations that intersect across different modules, unlike
DEAs. What is missing from our analysis here is the
consideration of concurrency, which we leave for fu-
ture work.
We also made a choice in the definition of CFA
7
Using remix.ethereum.org to simulate deployment
and transactions with reasonable function calls.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
246

operational semantics to define the semantics of calls
recursively. Another option would have been to use
a stack-based approach, with configurations as pairs
of symbolic states and a stack (or sequence) of ex-
plicit states. Upon a call, the initial state of the called
method is pushed onto stack, and popped upon reach-
ing an end state. Here we avoided this for simplicity,
although we do require a form of interprocedurality to
prove our results (Azzopardi et al., 2019).
The residual analyses here are quite weak on two
fronts: (i) they are intraprocedural; and (ii) they de-
pend on universal observations about the program (i.e.
a transition’s guard is removed if it is always ac-
tivated). Adding efficient interprocedurality can be
done using some form of weighted pushdown system
(Reps et al., 2007). Moreover the current approach
can be extended by easily obtainable interprocedu-
ral information, e.g. limiting the chaos at call states
by computing the alphabet of the transitively called
methods. Analysis of the composition can be further
extended to allow for existential observations about
the program. This would allow us, perhaps through
special transitions, to determine points in the program
for which a certain side-effect-free guard can be pre-
computed. This proposed approach has similarities
with work of (Dwyer and Purandare, 2007).
The work presented here can also be extended
with a notion of typestate, i.e. a property replicated
for each object (or a binding of multiple objects) of a
certain kind, which we do not detail here for concise-
ness. The extension for typestate is straightforward:
(i) associate events in CFA transitions with objects
(dynamic on the program symbolic state); (ii) intro-
duce a pointer analysis to identify equivalence classes
of events according to the runtime objects they may
be associated with; and (iii) project analysis onto each
possible event equivalence class.
An observation about partial verification is that it
can be seen as an extension of usual verification. Con-
sider that verification is usually framed as an opera-
tion that either returns a satisfying, violating, or un-
known verdict: ver : P × Π → {>, ⊥, ?}. Partial ver-
ification extends this by instead returning a new pro-
gram and property pair: partialVer : P ×Π → P ×Π.
To signal violation the residual property can be the
always violating property π
⊥
, while to signal satis-
faction we can use the always satisfying property π
>
.
6 RELATED WORK
We find several approaches towards partial verifica-
tion in literature. (Bodden and Lam, 2010) introduce
a tool for the control-flow analysis of Java programs
against finite-state automata properties. This tool in-
corporates several analyses that safely turn off event
instrumentation in the program. An interesting anal-
ysis this performs takes into account continuation-
equivalency (Bodden, 2010), where backwards and
forwards analyses are used to determine different
points in the program that have the same continua-
tion with respect to the property, allowing the turning
off of any redundant events whose silencing does not
change the continuation. This analysis proves to be
useful for finite-state automata, however given that
DEAs contain guarded events it is not clear if this
would be as useful. This approach is different from
ours in that the focus is solely on reducing instrumen-
tation, while we also encode inconclusive results in a
residual property. Differently from our approach this
tool takes into account typestate.
Another approach is STARVOORS (Ahrendt
et al., 2012) that deals with DEAs extended with pre-
and post-conditions for methods called when at cer-
tain concrete states. In this work, a theorem prover
is used to prove these conditions, where they are ei-
ther pruned away or refined. This analysis ignores the
control-flow of the property, unlike our approach.
A different summary-based approach is taken by
(Dwyer and Purandare, 2007). Instead of remov-
ing transitions from the property and instrumentation
from the program, (Dwyer and Purandare, 2007) anal-
yse the program to identify sequences of statements
that always start and end at the same property states.
Instrumentation in this sequence is removed, with
new special events added signaling entry and exit into
the sequence. A transition is added accordingly in the
property. Unlike our approach, the residual property
and program here are transformations of the original
rather than structural reductions.
(Beyer et al., 2018) also use automata they call
control-flow automata, similar to ours, with transi-
tions corresponding to operations on a program’s vari-
able state. However they take a state-based approach,
where they are interested in verifying assertions at
certain points in the program. They encode what is
learned about a program in a condition automaton,
that represents both the safe and potentially unsafe
program paths. These automata are used to create
residual programs with safe parts pruned away. This
approach is quite general and can be applied to the
problem of verifying against a DEA. The motivation
here is different from our approach since we are inter-
ested in residual monitoring of the whole program.
A Technique for Automata-based Verification with Residual Reasoning
247

7 CONCLUSIONS
Partial verification is an approach to verification
where on analysis failing, its partial results are used
to produce a simpler residual problem for subse-
quent passes. In this paper we have presented an
event-based framework that can be used as the basis
to produce residuals verification problems, while we
have presented novel residual operators that analyse
the program intraprocedurally to identify unnecessary
event instrumentation, property transitions, and prop-
erty event guards. We evaluated this with a Solid-
ity smart contract, showing some gains depending on
how much of a property was proven.
We are working on an implementation
8
of this
approach for CONTRACTLARVA (Azzopardi et al.,
2018), a tool for runtime verification on the Ethereum
blockchain. A next logical step is to consider exten-
sions of our work to when parts of the program are
unknown or dynamic at runtime. We believe our ap-
proach to dealing with intraprocedural analysis, i.e.
by considering call states as chaotic, can be re-used
for this purpose. Missing from literature is also resid-
uals of temporal logic based specifications, which are
popular formalisms for verification.
REFERENCES
Ahrendt, W., Pace, G. J., and Schneider, G. (2012). A
unified approach for static and runtime verification:
Framework and applications. In Margaria, T. and
Steffen, B., editors, Leveraging Applications of For-
mal Methods, Verification and Validation - 5th Inter-
national Symposium, ISoLA 2012, Heraklion, Crete,
Greece, Proceedings, Part I, volume 7609 of LNCS,
pages 312–326. Springer-Verlag.
Azzopardi, S., Colombo, C., and Pace, G. (2019). A tech-
nique for automata-based verification with residual
reasoning. Technical Report CS-2019-02, Department
of Computer Science, University of Malta.
Azzopardi, S., Colombo, C., and Pace, G. J. (2017).
Control-flow residual analysis for symbolic automata.
In Francalanza, A. and Pace, G. J., editors, Proceed-
ings Second International Workshop on Pre- and Post-
Deployment Verification Techniques, Torino, Italy, 19
September 2017, volume 254 of Electronic Proceed-
ings in Theoretical Computer Science, pages 29–43.
Open Publishing Association.
Azzopardi, S., Colombo, C., and Pace, G. J. (2020).
CLARVA: Model-based residual verification of java
programs. In Model-Driven Engineering and Software
Development - 8th International Conference, MOD-
ELSWARD 2020, Valletta, Malta, February 25-27,
2020.
8
https://www.github.com/shaunazzopardi/solidity-
static-analysis
Azzopardi, S., Ellul, J., and Pace, G. J. (2018). Monitoring
smart contracts: CONTRACTLARVA and open chal-
lenges beyond. In The 18th International Conference
on Runtime Verification.
Beyer, D., Henzinger, T. A., Keremoglu, M. E., and
Wendler, P. (2012). Conditional model checking: A
technique to pass information between verifiers. In
Proceedings of the ACM SIGSOFT 20th International
Symposium on the Foundations of Software Engineer-
ing, FSE ’12, pages 57:1–57:11, New York, NY, USA.
ACM.
Beyer, D., Jakobs, M.-C., Lemberger, T., and Wehrheim,
H. (2018). Reducer-based construction of conditional
verifiers. In Proceedings of the 40th International
Conference on Software Engineering, ICSE ’18, pages
1182–1193, New York, NY, USA. ACM.
Bodden, E. (2010). Efficient hybrid typestate analysis by
determining continuation-equivalent states. In ICSE
’10: International Conference on Software Engineer-
ing, pages 5–14, New York, NY, USA. ACM.
Bodden, E. and Lam, P. (2010). Clara: Partially Evaluat-
ing Runtime Monitors at Compile Time. In 1st In-
ternational Conference on Runtime Verification (RV),
volume 6418 of LNCS, pages 183–197. Springer. Tu-
torial.
de Moura, L. and Bjørner, N. (2008). Z3: An efficient smt
solver. In Ramakrishnan, C. R. and Rehof, J., editors,
Tools and Algorithms for the Construction and Anal-
ysis of Systems, pages 337–340, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Dwyer, M. B. and Purandare, R. (2007). Residual dynamic
typestate analysis exploiting static analysis: Results
to reformulate and reduce the cost of dynamic analy-
sis. In Proceedings of the Twenty-second IEEE/ACM
International Conference on Automated Software En-
gineering, ASE ’07, pages 124–133, New York, NY,
USA. ACM.
Dwyer, M. B. and Purandare, R. (2008). Residual checking
of safety properties. In Havelund, K., Majumdar, R.,
and Palsberg, J., editors, Model Checking Software,
pages 1–2, Berlin, Heidelberg. Springer Berlin Hei-
delberg.
Falcone, Y., Krsti
´
c, S., Reger, G., and Traytel, D. (2018). A
taxonomy for classifying runtime verification tools. In
Colombo, C. and Leucker, M., editors, Runtime Verifi-
cation, pages 241–262, Cham. Springer International
Publishing.
Lal, A., Kidd, N., Reps, T., and Touili, T. (2007). Abstract
error projection. In Proceedings of the 14th Interna-
tional Conference on Static Analysis, SAS’07, pages
200–217, Berlin, Heidelberg. Springer-Verlag.
Reps, T., Lal, A., and Kidd, N. (2007). Program analy-
sis using weighted pushdown systems. In Arvind, V.
and Prasad, S., editors, FSTTCS 2007: Foundations
of Software Technology and Theoretical Computer
Science, pages 23–51, Berlin, Heidelberg. Springer
Berlin Heidelberg.
Vardi, M. Y. (2007). Automata-theoretic model checking
revisited. In Proceedings of the 8th International Con-
ference on Verification, Model Checking, and Abstract
Interpretation, VMCAI’07, pages 137–150, Berlin,
Heidelberg. Springer-Verlag.
Wood, G. (2014). Ethereum: A secure decentralised gen-
eralised transaction ledger. Ethereum Project Yellow
Paper, 151:1–32.
MODELSWARD 2020 - 8th International Conference on Model-Driven Engineering and Software Development
248
