
Adapting the Markov Chain based Algorithm M-DBScan to Detect
Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
Eldane Vieira J
´
unior, Rita Maria Silva Julia and Elaine Ribeiro Faria
Computer Department, Federal University of Uberl
ˆ
andia, Uberl
ˆ
andia, Minas Gerais, Brazil
Keywords:
Novelty Detection, Markov Chain, StarCraft, M-DBScan Algorithm.
Abstract:
Digital games represent an appropriate test scenario to investigate the agents’ ability to detect changes in
the behavior of other agents trying to prevent them from fulfilling their objectives. Such ability allows the
agents to adapt their decision-making process to adequately deal with those changes. The Markov Chain
based algorithm M-DBScan is a successful tool conceived to detect novelties in data stream scenarios. Such
algorithm has been validated in artificially controlled situations in games in which a single set of features and a
single Markov Chain are sufficient to represent the data and to detect the occurrence of novelties, which usually
is not enough to make the agents able to adequately perceive the environment changes in real game situations.
The main contribution of the present work is then to investigate how to improve the use of M-DBScan as a
tool for detecting behavior changes in the context of real and dynamic StarCraft games by using distinct sets
of features and Markov Chains to represent the peculiarities of relevant game stages. Further, distinctly from
the existing researches, here M-DBScan is validated in situations in which the timestamp, between successive
novelties, is not constant.
1 INTRODUCTION
Intelligent agents have been increasingly used to solve
a great variety of practical problems, such as dis-
ease diagnosis, medical image analysis, natural lan-
guage processing, robot navigation, games, Internet
of Things (IoT), etc (Gubbi et al., 2013; Norvig and
Intelligence, 2002).
In order to cope with such problems, frequently
the agents have to face opponents that try to prevent
them from succeeding in their tasks. In these situ-
ations, it becomes crucial that the agents map their
opponents’ behavior, being aware of eventual occur-
rence of strategic changes. In general, these changes
can be analyzed through the novelties that the oppo-
nents’ actions provoke in the environment.
The attempt to identify novelties in data streams
has to cope with difficulties such as the followings:
the data obtained from the data streams is potentially
infinite; the lack of control in the data arrival order;
the data already processed must be discarded; the
data can arrive in very high frequency; the data can
go through changes (Krawczyk et al., 2017; Babcock
et al., 2002).
The learning process of an agent in a data stream
scenario must be incremental since it must reflect the
most recent changes observed. Then, the set of fea-
tures used to represent the data must be defined to
allow the perception of the agent over any data alter-
ations.
In Real-time Strategy (RTS) games, for example,
the detection of the alterations in the opponent’s be-
havior is essential to adapt the agent decision-making
to such changes. In these cases, the alterations may be
perceived through the analysis of novelties detected in
the data stream(Yannakakis and Maragoudakis, 2005;
Vallim et al., 2013).
The Markov Chain based proceeding Micro-
Clustering DBScan (M-DBScan) has excelled in the
context of researches regarding the detection of nov-
elties in data stream scenarios (Vallim et al., 2013).
In such researches, M-DBScan has been validated us-
ing artificially controlled situations related to some
games, without compromising the accuracy of the al-
gorithm. The datum is represented by a unique set
of features and only one Markov Chain (MC) was
used to detect the occurrence of novelties (Vallim
et al., 2013; Vieira et al., 2019). Further, in the sit-
uations investigated by the existing researches with
M-DBScan, the timestamp between every successive
214
Vieira Júnior, E., Julia, R. and Faria, E.
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft Player Agent.
DOI: 10.5220/0008985802140223
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 214-223
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

novelty is constant. However, in many practical prob-
lems treated by Artificial Intelligence (AI), the agents
deal with extremely dynamic environments, whose
intense changes require distinct sets of features to rep-
resent them over time. It happens, for example, in
many RTS games, in which there is a great variety
of game scenarios in the course of a real match. In
these cases, it is practically impossible that the agents
can adequately perceive the novelties occurred in the
environment through a unique set of features.
Considering the arguments aforementioned, the
main contribution of the present work is to investi-
gate how to use M-DBScan to detect novelties in data
stream scenarios in which the environment undergo
changes associated with the moment of the process,
requiring distinct sets of features to represent the pe-
culiarities of the data over time. The study here, using
the StarCraft RTS game as a case study, also differs
from other existing works for taking into considera-
tion situations in which the timestamp between suc-
cessive novelties is not constant. More specifically,
the purpose here is to use M-DBScan to capture nov-
elties in the successive game scenarios that appear
throughout a real match and, based on such novel-
ties, to investigate eventual changes in the opponents’
behavior. The hypothesis of this approach is the fol-
lowing: as the opponent’s decision-making directly
impacts the game scenario, its profile can be investi-
gated through continuous analysis of the dynamic en-
vironment over the successive game stages.
To cope with such purpose, the authors defined
the following game stages as being relevant to pursue
their objectives (based on the game characteristics):
the Beginning Stage of the Battle (BSB); the Middle
Stage of the Battle (MSB); finally, the Final Stage of
the Battle (FSB). Further, in order to represent the
game scenarios, the authors used sub-sets of features
extracted from a universe set of 16 features (related to
the units that compose the StarCraft armies), which is
able to appropriately represent the specificities of the
three stages, being such selection based on their own
experience with the game.
To evaluate the gains obtained from the approach
proposed herein, in which M-DBScan takes into ac-
count and fits the specificities of every stage of the
environment, this work calculates and compares the
results produced by such algorithms through two dis-
tinct test scenarios: first, MDBScan is used in real
game situations of StarCraft matches in the same way
as it had been tested in the related works, that is, in the
course of a complete StarCraft game, a unique set of
features is used to represent the game scenarios and a
unique MC is constructed to detect the changes in the
opponents’ behavior; second, MDBScan is used ac-
cording to the approach proposed herein, that is, over
real StarCraft contests, a distinct set of features and a
distinct MC are used to represent every game stage. In
this case, some set of features corresponds to a sub-set
of the 16 features aforementioned. The results con-
firm the advances produced by the approach proposed
in the present work.
The main motivations for choosing StarCraft as
a case study are the followings: 1) Game problems
frequently involve challenges that are very similar to
those found in real-world problems, including situ-
ations in which opponents try to minimize the suc-
cess of agents that try to cope with such problems
(Neto and Julia, 2018); 2) The StarCraft game sce-
narios are very dynamic over time, requiring distinct
sets of features to perceive their peculiarities in differ-
ent game stages (for example, the feature Dead enemy
unit, in spite of being essential to represent novelties
in endgame scenarios, FSB stage, it is irrelevant at the
beginning of the game, BSB stage); 3) In StarCraft
games, any novelty must be identified in a short pe-
riod of time, so as to allow that any action in response
to a detected novelty is taken within the time period
in which the current set of features is still adequate to
represent the game scenario.
This paper is organized as following: in section 2,
the theoretical foundations are presented; section 3 re-
sumes the related works; section 4 describes how the
M-DBScan based novelty detection process can be
used to cope with the dynamic environment of Star-
Craft; section 5 presents the experiments and the re-
sults; finally, section 6 summarizes the conclusion and
points out some possible future works.
2 THEORETICAL
FOUNDATIONS
This section presents a short description of some con-
cepts and techniques used in the development of the
work presented in this paper.
2.1 Player Modeling
Player modeling is defined as the study of computa-
tional models of game players. It is focused on the
way that a player interacts with a game, which may in-
clude the detection and prediction of its features, and
also how to model and express these features (Yan-
nakakis et al., 2013).
Player modeling is used in human-computer inter-
action, and it has also been used in the context where
the player is an agent, and in this case, player model-
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
215

ing can be used to improve these agents as described
in (Weber and Mateas, 2009).
The present paper aims at identifying changes in
the playing style of the adversary in different mo-
ments of the game. A model is created using the al-
gorithm M-DBScan and it will be adapted over time,
in order to reflect recent information. The algorithm
M-DBScan was improved in this study by the use of
different MCs for different moments of the game.
2.2 Novelty Detection in Data Stream
Novelty detection is an efficient process to identify
an instance of data that differs in a significant man-
ner from some already known concepts. This research
area has received a great deal of attention in machine
learning and data mining (Faria et al., 2016).
Novelty detection has been used in researches re-
lated to the context of a data stream, which can be
defined as a sequence of data instances that arrives
continuously, with specific characteristics as the fol-
lowing (Gama and Gaber, 2007): the data arrives on-
line; the order that data arrives can not be controlled;
the size of a data stream is unlimited; a data already
processed is usually discarded, once there are limited
resources as memory.
2.3 M-DBScan
The algorithm M-DBScan is an approach to detect
changes in data streams in which the data is not la-
beled (Vallim et al., 2013). This algorithm has an
incremental clustering process, based on DenStream
(Cao et al., 2006), which is a clustering technique ap-
plied in a data stream. The clustering process is fol-
lowed by a mechanism to detect novelties, which can
be used to identify behavior change (Vallim, 2013).
The clustering step proposed by M-DBSCAN
is composed of two phases, online and offline.
While the online phase keeps a statistical sum-
mary of the dataset, based on micro-clusters, which
are used to maintain compact information as ra-
dius, center, and weight, considering the data that
arrives from the stream. The micro-clusters can
be classified as potential-micro-cluster (p-micro-
cluster), outlier-micro-cluster (o-micro-cluster) and
core-micro-cluster (c-micro-cluster), and each of
them has its own requirements, as described in (Cao
et al., 2006). The offline phase generates clusters
based on the result produced by the online phase, and
it uses the concepts of density and connectivity (Cao
et al., 2006).
Once the offline phase has been concluded, the
clusters generated in the offline phase are used in a
novelty detection module, that aided by a sliding win-
dow, is capable to indicate the occurrence of changes.
The novelty detection module uses MC, and in this
process, each state in the MC represents a group pro-
duced in the offline phase, and the transitions between
the states follow the dynamics observed in the arrivals
of new data and how the assignment of this data to a
micro-cluster occurred.
2.3.1 Novelty Detection Module
In order to detect novelties, the M-DBScan algorithm
uses two entropy measures, named spatial entropy and
temporal entropy. The dynamics of how to calculate
the entropies, and how to update them follows the
specifications presented in (Vieira et al., 2019; Vallim
et al., 2013).
Since the states in the MC are the representation
of groups produced in the offline clustering step of
M-DBScan, the probabilities in the MC transitions are
updated every time that a data arrives from the stream.
A weighting factor η
t
is used to control the intensity
of each probability update. The sum of probabilities
linked to transitions with the same origin state has 1
as its maximum value when a transition is no longer
activated, it will suffer a value deterioration.
In order to identify a novelty, at least one of the en-
tropies must surpass its pre-defined threshold. The al-
gorithm M-DBScan requires that a minimum amount
of novelty must be identified in an interval of time
represented by a sliding window with size k, to char-
acterize a behavior or strategy change. Every novelty
occurrence is registered in the sliding window, where
it is necessary to verify if the amount of registered
novelties has reached the minimum amount necessary
to declare, decisively, a change. A novelty that oc-
curred in a certain moment can disappear from the
window if it has slided k times, considering as the ini-
tiation, the moment that this novelty was registered.
However, if a behavior change was detected, from this
point on every novelty will be ignored for a period of
time equal to k. This process is used to discard nov-
elties linked to the same change that has already been
identified (Vallim et al., 2013).
3 RELATED WORKS
Among the related works, some applied machine
learning techniques to RTS games, to optimize strate-
gic tasks, these are those tasks that carry an influence
throughout the game, such as the order of construc-
tions and what to construct. A study presented in
(Justesen and Risi, 2017), for example, describes a
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
216

way of dealing with the task that decides which struc-
tures must be constructed in the game StarCraft, using
the algorithm Continual Online Evolutionary Plan-
ning (COEP). There are related works that try to im-
prove battle skills of RTS automatic players, as in
the study presented in (Shao et al., 2017), which de-
scribes the development of a decision module for the
game StarCraft, based on a neural network with re-
inforcement learning, that can point out an action for
each living unit. In (Stanescu and
ˇ
Certick
`
y, 2016) an-
other study is presented that tries to improve an au-
tomatic player specialized in battles, this study uses
a prediction method to indicate the most likely com-
bination of units produced by the enemy in an RTS
game like StarCraft. In the work described in (Niel
et al., 2018) has developed a simple custom RTS
game, in which the main goal of the players is to de-
fend their bases and destroy the enemy’s base. In this
work was used reinforcement learning (RL) combined
with a multi-layer perceptron (MLP) to determine
how the agent will perform the tasks in the game. The
Q-learning was tested against Monte Carlo learning as
reinforcement learning algorithms, and two different
methods for assigning rewards to agents were tested,
the individual and the sharing reward. The results
showed that the combination of Q-learning and indi-
vidual rewards presented the best win-rate. The works
presented in (Justesen and Risi, 2017; Shao et al.,
2017; Stanescu and
ˇ
Certick
`
y, 2016; Niel et al., 2018)
do not deal with novelty identification and there is no
attempt to represent different moments of the game
using appropriate features, to improve the strategy de-
tection, which are great differences to the present pa-
per.
The work in (
´
Alvarez Caballero et al., 2017) used
supervised learning techniques as MLP, Random For-
est and Logistic Regression, over a big amount of
data obtained from StarCraft replays. The objective
of this work is to predict the winner of a match in the
game StarCraft. This work proved that the use of ap-
propriate StarCraft features will increase the accuracy
of this prediction, which can occur at a very satisfy-
ing level after 10 minutes of gameplay. In (Synnaeve
et al., 2012), a method is presented for discovering
tactics and strategies in the game StarCraft. A cre-
ated dataset was analyzed by the technique Gaussian
Mixture Model, to identify every single cluster (army
formation) that will indicate the details of each army
composition, and these details go on to provide a way
of finding the best army formation. In (Weber and
Mateas, 2009), a study is put forward that tries to cre-
ate a model that represents a general enemy based on
several others, in order to be used in the prediction of
strategic action. In (Weber and Mateas, 2009) was
used techniques for classification as K-Nearest Neigh-
bor, Non-Nested generalized exemplars and Additive
Logistic Regression. The works described in (
´
Alvarez
Caballero et al., 2017; Synnaeve et al., 2012; Weber
and Mateas, 2009) show significant differences to the
present paper, since they do not select attributes for
a better representation of the game phases, and they
apply a supervised learning process, which is not the
case in the present paper.
In (Vallim, 2013), the authors use M-DBScan to
detect player behavior changes in RTS game, in first
person shooter game and in artificial datasets, show-
ing the diversity and success in the usage of this
technique. However, such work differs from the ap-
proach presented herein for the following reasons: it
deals with artificially controlled situations in which
the timestamp between every pair of successive nov-
elties is constant; and it only copes with game sce-
narios for which the dynamics can be appropriately
represented by a unique set of features, using just
one MC to investigate eventual changes. In the study
presented in (Vieira et al., 2019) the algorithm M-
DBScan was used with data from the game StarCraft
to show that the technique works in controlled test
scenarios that, like (Vallim, 2013), just used one MC.
4 DYNAMIC NOVELTY
DETECTION IN StarCraft
The main contribution of the approach proposed in
this study is to adapt the use of the algorithm M-
DBScan to improve its capacity in detecting novelties
in the game StarCraft. Such novelties concern sig-
nificant alterations on the game scenarios that even-
tually may point out an opponent’s strategic change.
As presented in this section, the basis of this approach
consists on using distinct and appropriate sets of fea-
tures to represent the game scenarios according to the
peculiarities of the following game stages: Beginning
Stage of the Battle (BSB), in which the adversaries
begin the conflict; MSB Middle Stage of the Battle
(MSB), in which deaths begin to occur in one of the
armies involved in the battle; and, finally, FSB Final
Stage of the Battle (FSB), which can be characterized
by the significant reduction in the number of battle
units that compose the armies involved in the contest.
In order to represent the game scenarios, the authors
use sub-sets of features extracted from a universe set
of 16 features, being such selection based on their
own experience with the game. In this way, during
the process of detecting eventual changes in the op-
ponent’s strategy, the present approach has to build 3
distinct MCs, one for each game stage. This approach
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
217

also differs from other existing works for taking into
consideration situations in which the timestamp be-
tween successive novelties is not constant.
The Figure 1 illustrates the process of assigning
the data to the correct MC.
Figure 1: Selecting the correct instance of MC.
4.1 StarCraft: General Description
StarCraft is an RTS game released by Blizzard Enter-
tainment in 1998 (Entertainment, 1998), being used
specifically the expansion StarCraft: BroodWar in
this work. This engine is based on rules that define
the dynamics in the game to assign tasks for units as
combat, locomotion and how to gather resources from
the environment. In the game, players can control one
of three races: Terran, Protons and Zerg. Each race
has its peculiarities related to the aspects of weak-
nesses and strengths. There are differences among
the units, some are appropriate on building structures
and collecting resources from the environment, others
are more appropriate for combat. However, the army
must be analyzed considering all the units that com-
pose it, which makes it possible to have an overview
concerning how good that army is, considering the ef-
fective level of damage that it can cause or its level of
defense.
In the game StarCraft, some challenges emphasize
it as a case study with characteristics of a data stream
scenario. For example, the data is obtained in a very
high frequency, and the uncertainty about how long
the game will last makes it impossible to guess how
much data can be obtained from the stream. The area
in the map that has not been explored is kept hidden,
making it impossible to know what exists in this un-
known area of the map, which makes applying strate-
gies to the game difficult.
4.2 Feature Extraction
In this work, sub-sets of a set composed of 16 features
are used to describe the game stages. In particular, the
features used in the process of novelty detection can
make the process of identification easier. As such, in
this work, features were empirically selected for dif-
ferent moments of the game, to better represent the
specificities of distinct game stages that are strategi-
cally relevant.
Each instance of the data set, created by the au-
thors, corresponds to an accumulated perception (rep-
resented by the aforementioned features) of the last 15
seconds of the game. These features can be summa-
rized as three groups: i) hit point (HP), which repre-
sents the amount of life of each unit. This group of
features is used to represent the intensiveness and ef-
fectiveness of the agent and opponent attack. ii) army
power, which represents the damage/defense that the
enemy army can cause; iii) amount of damage, rep-
resented by the number of dead units of the enemy
and score of damage to the structures. Concerning
the types of the units, we can consider that: i) Unit
1 has low attack power; ii) Unit 2 has medium attack
power; and iii) Unit 3 has high attack power. The 16
features are described as follows:
• Feature 1 (Dead enemy unit): provides the num-
ber of deaths in the enemy army.
• Feature 2 (Low HP Agent Unit 1): provides the
number of units type 1 in the agent army with low
hit points.
• Feature 3 (Low HP Agent Unit 2): provides the
number of units type 2 in the agent army with low
hit points.
• Feature 4 (Low HP Agent Unit 3): provides the
number of units type 3 in the agent army with low
hit points.
• Feature 5 (High HP Agent Unit 1): provides the
number of units type 1 in the agent army with high
hit points.
• Feature 6 (High HP Agent Unit 2): provides the
number of units type 2 in the agent army with high
hit points.
• Feature 7 (High HP Agent Unit 3): provides the
number of units type 3 in the agent army with high
hit points.
• Feature 8 (Attack power): represents the damage
that the enemy army can cause.
• Feature 9 (Defense power): represents the defense
power of the enemy army.
• Feature 10 (Damage in construction): provides a
score for the damage that the enemy caused to
structures.
• Feature 11 (Low HP Enemy Unit 1): provides the
number of units type 1 in the enemy army with
low hit points.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
218
• Feature 12 (Low HP Enemy Unit 2): provides the
number of units type 2 in the enemy army with
low hit points.
• Feature 13 (Low HP Enemy Unit 3): provides the
number of units type 3 in the enemy army with
low hit points.
• Feature 14 (High HP Enemy Unit 1): provides the
number of units type 1 in the enemy army with
high hit points.
• Feature 15 (High HP Enemy Unit 2): provides the
number of units type 2 in the enemy army with
high hit points.
• Feature 16 (High HP Enemy Unit 3): provides the
number of units type 3 in the enemy army with
high hit points.
The subset of features selected to represent the
BSB game stage, named as V
1
, is composed of the
following features: 5, 6, 7, 8, 9, 14, 15 and 16; the
MSB moment is represented by the universe set of
16 features, named as V ; and, finally, the FSB game
stage is represented by the subset whose elements are
the features 2, 3, 4, 5, 6, 7, 11, 12, 13, 14, 15 and
16, named as V
2
. All the features were empirically
selected considering what is reasonable at each mo-
ment, for example, units with low HP will not exist at
the beginning of the battles.
4.3 M-DBScan
The M-DBScan algorithm has been used to detect
changes in the opponent’s strategy in two distinct
manners: the game scenarios were represented by the
universe set V ; and subsets of V was used represent
different game stage.
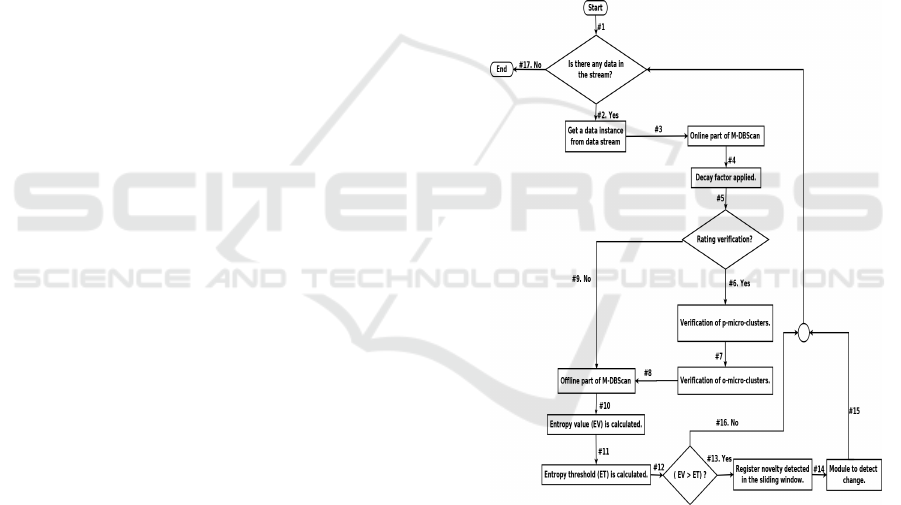
The algorithm M-DBScan is illustrated in the
flowchart presented in Figure 2 (Vieira et al., 2019).
Initially, the algorithm M-DBScan checks if there is
a data sample in the stream (arrow #1): if so, the al-
gorithm retrieves the datum (arrow #2) that will be
presented as an input to the online part of the algo-
rithm M-DBScan (arrow #3), which will recalculate
all the concerning parameters related to the assigned
micro-cluster for this datum. In sequence, a decay
factor is applied to all remaining micro-clusters (ar-
row #4). Step (arrow #5) checks if it is time to per-
form a rating verification: if so, this verification is ex-
ecuted (arrow #6), transforming into o-micro-clusters
all p-micro-clusters that do not satisfy anymore the p-
micro-cluster constraints (Cao et al., 2006) (due to the
use of the decay factor). In the same way, in this rating
verification, all o-micro-clusters that do not present
anymore the requirement for an o-micro-cluster will
be deleted (arrow #7). Next, the offline part of M-
DBScan is run (arrow #8). Otherwise, if in step (ar-
row #5) it is not time to perform the rating verifica-
tion, the offline part of M-DBScan will be directly
run (arrow #9). Then, the entropy value (temporal en-
tropy or spatial entropy) and its corresponding thresh-
old are calculated (arrow #10 and #11). If the entropy
exceeds its threshold, then a novelty is detected and
registered in the sliding window (arrow #13). Next,
a module for detecting change is used (arrow #14),
which verifies if the minimum amount of novelties
has been reached. The module for detecting change
is also responsible for controlling the sliding window.
Next, upon detecting a novelty or not, the algorithm
tries to retrieve a new data sample from the stream (ar-
row #15 and #16). The execution of M-DBScan ends
when there is no more data from the stream (arrow
#17).
Figure 2: M-DBScan flowchart.
5 EXPERIMENTS AND RESULTS
The conducted experiments aim to show the impact of
the use of a distinct set of features and distinct MCs to
represent every game stage in the M-DBSCAN algo-
rithm, in contrast to the use of a unique set of features
and unique MC.
Different datasets were created to represent differ-
ent game scenarios, and among them, there are those,
in which the interval of time between novelties are not
constant.
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
219

Table 1: Description of Datasets.
Dataset Novelty ID Timestamp Game Moment Strategy
Dataset 1
1 500 BSB D1S1
2 1000 MSB D1S2
3 1500 FSB D1S3
Dataset 2
1 500 BSB D2S1
2 1000 MSB D2S2
3 1500 MSB D2S3
4 2000 MSB D2S4
5 2500 MSB D2S5
6 3000 MSB D2S6
7 3500 FSB D2S7
Dataset 3
1 149 BSB D3S1
2 468 MSB D3S2
3 528 MSB D3S3
4 626 MSB D3S4
5 1019 MSB D3S5
6 1196 MSB D3S6
7 1901 MSB D3S7
8 3413 FSB D3S8
Dataset 4
1 206 BSB D4S1
2 676 MSB D4S2
3 1546 MSB D4S3
4 1774 MSB D4S4
5 2734 MSB D4S5
6 5605 MSB D4S6
7 6067 MSB D4S7
8 7648 MSB D4S8
9 7772 FSB D4S9
5.1 Datasets
The tools used to generate the dataset are the engine
UAlbertaBot (Churchill and Buro, 2011; Churchill
et al., 2012), a playing bot that won the 2013 AI-
IDE StarCraft AI Competition, and the Brood War
Application Programming Interface (BWAPI), a way
for programmers to interact with and control the full
game StarCraft.
For the experiments, four datasets were gen-
erated
1
. These datasets were collected from real
matches in the game StarCraft. Each data instance
represents 15 seconds of the game playing and con-
tains 16 features. A novelty is characterized when a
change of opponent’s strategy occurs.
The datasets are described in Table 1. In this ta-
ble, the columns Novelty ID is a sequential number to
identify each novelty of the dataset; Timestamp indi-
cates how many data samples arrived from the begin-
ning of the stream until the novelty occurrence; Game
Moment indicates in which game moment the novelty
1
https://drive.google.com/open?
id=1nqndc7E3ru1sEb r3Q7NLmySCiepbOgu
occurred (BSB, MSB, or FSB); Strategy indicates the
code of a strategy used in the novelty. Each strategy
used is based on one of the following: the increase of
attack power; the increase of defense power; army im-
provement with stronger units; defensive endurance
for the endgame.
Although the datasets are composed of 16 fea-
tures, a subset containing 8 and 12 features, here
named V
1
and V
2
, are used in the BSB and FSB mo-
ments of the game, respectively. In the MSB moment,
the 16 features (V ) are used.
5.2 Settings
The parameters used in the experiments were selected
based on empirical tests. The parameters for the clus-
tering process are: µ, which is a minimum amount
of points in a micro-cluster, ε is a radius limit for
micro-cluster, β is an outlier threshold and λ is a de-
cay factor. The parameter used in the entropy process
are: the weighting factor η
t
, which is used to control
the intensity of each probability update; the weighting
factors γ and δ used in the process of threshold cal-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
220
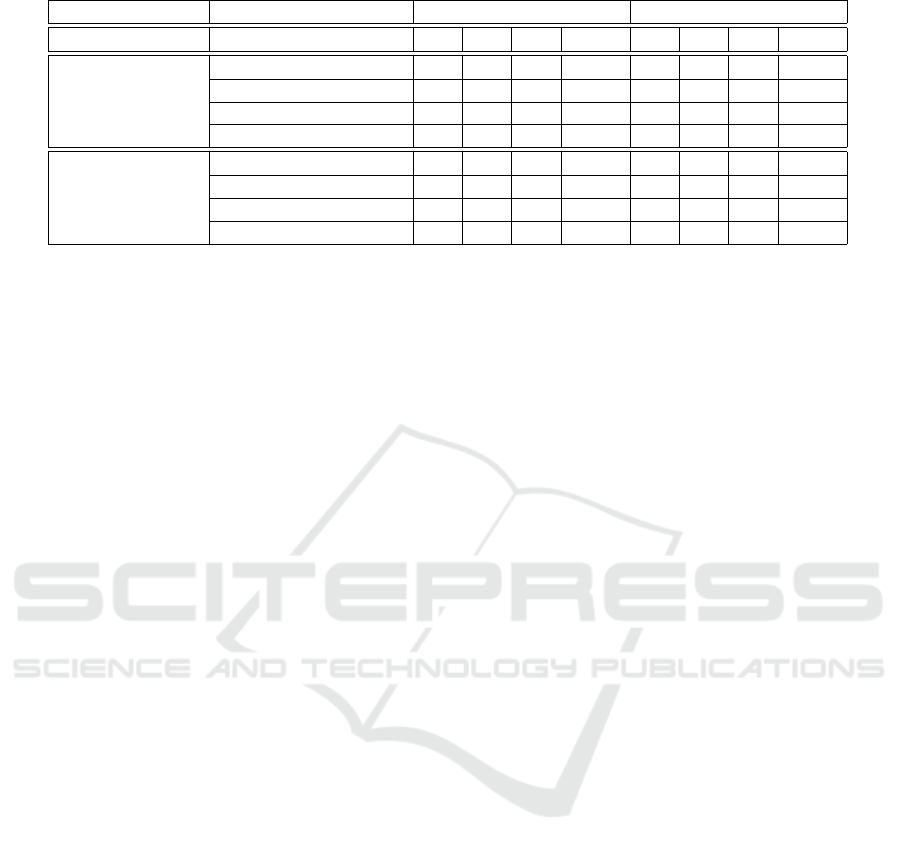
Table 2: Results of the experiments using 1 MC and 3 MCs.
Amount of MCs Dataset Temporal Entropy Spatial Entropy
TP FP FN F1 TP FP FN F1
1 MC
Dataset 1 (3 changes) 2 1 1 0.666 3 1 0 0.857
Dataset 2 (7 changes) 3 3 4 0.461 4 1 3 0.666
Dataset 3 (8 changes) 3 4 5 0.4 3 2 5 0.461
Dataset 4 (9 changes) 4 4 5 0.47 5 2 4 0.625
3 MCs
Dataset 1 (3 changes) 3 1 0 0.857 3 0 0 1
Dataset 2 (7 changes) 4 3 3 0.571 5 1 2 0.769
Dataset 3 (8 changes) 4 2 4 0.571 5 2 3 0.666
Dataset 4 (9 changes) 6 4 3 0.631 6 1 3 0.75
culation; and the constant parameter θ, which is the
number of standard deviations used to define a nor-
mal distribution for entropy values.
The experiments were run using the following val-
ues of parameters:
• The parameters used in the clustering process: µ
is 9; β is 0.1; ε is 20; λ is 0.03.
• The parameters used in the experiments for tem-
poral entropy: minimum amount of novelties is 2;
size of sliding window is 20; η
t
is 0.05; γ is 0.05;
δ is 0.03; θ is 3.
• The parameters used in the experiments for spatial
entropy: minimum amount of novelties is 2; size
of sliding window is 20; η
s
is 0.05; γ is 0.09;δ is
0.002; θ is 3.
The measures false positives (FP), false negatives
(FN), true positives (TP), and F1 are used to evaluate
the experiments. These measures are presented for
each entropy strategy (temporal and spatial).
Table 2 show the results of the proposed approach
in contrast to the original M-DBSCAN, considering
the four datasets and the temporal and spatial en-
tropies. Table 2 presents the results of the M-DBScan
using only 1 MC and the results of the M-DBScan us-
ing 3 different MCs, each one built from a different set
of attributes for a different moment of the game (V for
MSB, V
1
for BSB and V
2
for FSB). Based on the re-
sults, it is possible to notice that the best results for all
measures were achieved using the M-DBSCAN with
3 different MCs. Also, the spatial entropy achieved
the best results in both scenarios.
Every false positive detected in the experiments
occurred at the moment MSB. The MSB phase is a
moment of the game when the player can perform ac-
tions with some effect over the dynamics of the MC,
but not necessarily sufficient to characterize a novelty
in the strategy.
Considering that the spatial entropy presented bet-
ter results than the temporal entropy, the Figure 3
presents a comparison between the real occurrence of
changes, and its corresponding detections by the al-
gorithms using the spatial entropy. In this figure, it
is pointed out the exact moment that a behavior nov-
elty occurred, and the moment that each approach of
M-DBScan identified the novelty or indicated a false
positive. In the graphs in this figure, there are high-
lighted lines indicating the separation of the BSB,
MSB and FSB phases, which always occur in this or-
der. It is possible to observe in Figure 3 that the false
positives occur when the detection of a novelty had
a considerable delay, and when a novelty is pointed
out by the algorithm in a moment that none novelty is
expected.
Analyzing the Figure 3, all three novelties in
dataset 1 were detected by our approach. However,
the third novelty, which occurs in the FSB phase,
was not detected by the M-DBSCAN with 1 MC.
For dataset 2, among seven novelties, four were de-
tected by our approach, and three were detected by
M-DBSCAn with 1 MC. Again, a novelty which oc-
curred in the FSB game moment was detected by M-
DBSCAN with 3 MCs, but not by M-DBSCAN with
1 MC. For dataset 3, among eight novelties, four of
them were identified by M-DBSCAN with 3 MCs and
three by M-DBSCAN with 1 MC. Over again, the dif-
ference between the approaches is in the detection of
novelties in the FSB game moment. Considering the
dataset 4 in which occurs nine novelties, six of them
were detected by our approach, and only four were
detected by M-DBSCAN with 1 MC. For this dataset,
the differences between the approaches occurred in
the FSB and MSB stages.
The Wilcoxon test was applied over the four
datasets, comparing the performance of the M-
DBscan using temporal and spatial entropies in both
scenarios, first using only one MC to detect the
changes, and then, three MCs are used, each for a dif-
ferent moment of the game (BSB, MSB, and FSB).
The tool KEEL (Alcal
´
a-Fdez et al., 2011) was used to
perform the Wilcoxon test.
The results obtained by the Wilcoxon test for M-
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
221

Figure 3: Graphics indicating the moment of a behavior novelty detection using Spatial Entropy.
DBScan with spatial entropy, comparing the approach
using three MCs to that using one MC, are R
+
equal
to 10 and R
−
equal to 0, with an asymptotic p-value
equal to 0.04461. For M-DBScan with temporal en-
tropy, also comparing the approach using three MCs
to that using one MC, the results obtained by the
Wilcoxon test are R
+
equal to 10 and R
−
equal to 0,
with an asymptotic p-value close to 0.04461. In both
situations the null hypothesis can be rejected.
6 CONCLUSION AND FUTURE
WORKS
This paper presents an approach to improve the abil-
ity of the MC based algorithm M-DBScan to detect
behavior changes in the dynamic StarCraft game en-
vironment. To cope with such objective, here dis-
tinct sets of features and MCs were used to capture
the game scenario peculiarities over time. Further,
this study also takes into consideration situations in
which the timestamp between successive novelties is
not constant.
The results confirm the advances produced by the
approach proposed herein.
Noteworthy here is that both, spatial and temporal
entropy, produced satisfactory results, but the former
presented a superior performance.
In future works, the authors intend to use Genetic
Algorithms to automate the feature selection process,
and to incorporate the module for detecting changes
in the opponent’s strategy into the decision-making
module of StarCraft player agent, allowing this agent
to adapt their decision making to the opponent profile.
REFERENCES
Alcal
´
a-Fdez, J., Fern
´
andez, A., Luengo, J., Derrac, J.,
Garc
´
ıa, S., S
´
anchez, L., and Herrera, F. (2011). Keel
data-mining software tool: data set repository, integra-
tion of algorithms and experimental analysis frame-
work. Journal of Multiple-Valued Logic & Soft Com-
puting, 17.
Babcock, B., Babu, S., Datar, M., Motwani, R., and
Widom, J. (2002). Models and issues in data stream
systems. In Proceedings of the twenty-first ACM
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
222

SIGMOD-SIGACT-SIGART symposium on Principles
of database systems, pages 1–16. ACM.
Cao, F., Estert, M., Qian, W., and Zhou, A. (2006). Density-
based clustering over an evolving data stream with
noise. In Proceedings of the 2006 SIAM international
conference on data mining, pages 328–339. SIAM.
Churchill, D. and Buro, M. (2011). Build order optimiza-
tion in starcraft. In AIIDE, pages 14–19.
Churchill, D., Saffidine, A., and Buro, M. (2012). Fast
heuristic search for rts game combat scenarios. In AI-
IDE, pages 112–117.
Entertainment, B. (1998). Starcraft: Brood war. PC.
Level/area: Episode IV, mission, 2.
Faria, E. R., Gonc¸alves, I. J., de Carvalho, A. C., and Gama,
J. (2016). Novelty detection in data streams. Artificial
Intelligence Review, 45(2):235–269.
Gama, J. and Gaber, M. M. (2007). Learning from data
streams: processing techniques in sensor networks.
Springer.
Gubbi, J., Buyya, R., Marusic, S., and Palaniswami, M.
(2013). Internet of things (iot): A vision, architec-
tural elements, and future directions. Future genera-
tion computer systems, 29(7):1645–1660.
Justesen, N. and Risi, S. (2017). Continual online evolu-
tionary planning for in-game build order adaptation
in starcraft. In Proceedings of the Genetic and Evo-
lutionary Computation Conference, pages 187–194.
ACM.
Krawczyk, B., Minku, L. L., Gama, J., Stefanowski, J.,
and Wo
´
zniak, M. (2017). Ensemble learning for
data stream analysis: A survey. Information Fusion,
37:132–156.
´
Alvarez Caballero, A., Merelo, J. J., S
´
anchez, P. G.,
and Fern
´
andez-Ares, A. (2017). Early prediction
of the winner in starcraft matches. In Proceedings
of the 9th International Joint Conference on Com-
putational Intelligence - IJCCI,, pages 401–406. IN-
STICC, SciTePress.
Neto, H. C. and Julia, R. M. S. (2018). Ace-rl-checkers:
decision-making adaptability through integration of
automatic case elicitation, reinforcement learning, and
sequential pattern mining. Knowledge and Informa-
tion Systems, 57(3):603–634.
Niel, R., Krebbers, J., Drugan, M. M., and Wiering, M. A.
(2018). Hierarchical reinforcement learning for real-
time strategy games. In Proceedings of the 10th In-
ternational Conference on Agents and Artificial In-
telligence - Volume 2: ICAART,, pages 470–477. IN-
STICC, SciTePress.
Norvig, P. R. and Intelligence, S. A. (2002). A modern ap-
proach. Prentice Hall.
Shao, K., Zhu, Y., and Zhao, D. (2017). Cooperative rein-
forcement learning for multiple units combat in star-
craft. In Computational Intelligence (SSCI), 2017
IEEE Symposium Series on, pages 1–6. IEEE.
Stanescu, M. and
ˇ
Certick
`
y, M. (2016). Predicting oppo-
nent’s production in real-time strategy games with an-
swer set programming. IEEE Transactions on Com-
putational Intelligence and AI in Games, 8(1):89–94.
Synnaeve, G., Bessiere, P., et al. (2012). A dataset for star-
craft ai & an example of armies clustering. In AIIDE
Workshop on AI in Adversarial Real-time games, vol-
ume 2012.
Vallim, R. M., Andrade Filho, J. A., De Mello, R. F., and
De Carvalho, A. C. (2013). Online behavior change
detection in computer games. Expert Systems with Ap-
plications, 40(16):6258–6265.
Vallim, R. M. M. (2013). Minerac¸
˜
ao de fluxos cont
´
ınuos de
dados para jogos de computador. PhD thesis, Univer-
sidade de S
˜
ao Paulo.
Vieira, E., Julia, R. M. S., and de Faria, E. R. (2019). Min-
ing data stream to detect behavior change in a real-
time strategy game. In Proceedings of Machine Learn-
ing and Data Mining in Pattern Recognition. ibai pub-
lishing.
Weber, B. G. and Mateas, M. (2009). A data mining ap-
proach to strategy prediction. In Computational In-
telligence and Games, 2009. CIG 2009. IEEE Sympo-
sium on, pages 140–147. IEEE.
Yannakakis, G. N. and Maragoudakis, M. (2005). Player
modeling impact on player’s entertainment in com-
puter games. In International Conference on User
Modeling, pages 74–78. Springer.
Yannakakis, G. N., Spronck, P., Loiacono, D., and Andr
´
e,
E. (2013). Player modeling. In Dagstuhl Follow-Ups,
volume 6. Schloss Dagstuhl-Leibniz-Zentrum fuer In-
formatik.
Adapting the Markov Chain based Algorithm M-DBScan to Detect Opponents’ Strategy Changes in the Dynamic Scenario of a StarCraft
Player Agent
223
