
First Steps for Determining Agent Intention in Dynamic Epistemic Logic
Nathalie Chetcuti-Sperandio
1
, Alix Goudyme
1
, Sylvain Lagrue
2 a
and Tiago de Lima
1
1
CRIL, Artois University and CNRS, France
2
HEUDIASYC, Universit
´
e de Technologie de Compi
`
egne, France
Keywords:
Dynamic Epistemic Logic, Intention, Epistemic Games.
Abstract:
Modeling intention is essential to explain decisions made by agents. In this work, we propose a model of
intention in epistemic games, represented in dynamic epistemic logic. Given a property and a sequence of
actions already performed by a player in such a game, we propose a method able to determine whether the
player had the intention to obtain the property. An illustration of the method is given using a simplified version
of the collaborative game Hanabi.
1 INTRODUCTION
Being able to determine the purpose of an agent or a
group of agents from his knowledge would be of inter-
est in areas such as economics, games and, of course,
artificial intelligence. Our aim in this article is to be
able to discover the agents’ intention from, on the one
hand, their knowledge of the actions at their disposal
and, on the other hand, the actions they have finally
carried out. We chose to restrict the study to epistemic
games. The game world allows us to work within
a defined framework and to have total control over
the players’ knowledge and actions. Epistemic games
are games of incomplete information in which success
depends mainly on the players’ knowledge about the
state of the game and about the other players’ knowl-
edge. Examples of this type of games are Cluedo or
Hanabi.
Dynamic epistemic logic is a logic that deals with
the knowledge of agents and its evolution as a result
of events (Baltag and Moss, 2004), (van Ditmarsch
et al., 2007). It thus appears as a formalism adapted to
the logical modelling of intention in epistemic games,
in this case in Hanabi, a game on which we chose to
evaluate our work.
Our modelization of the intention differs from the
Belief-Desire-Intention theory and it is closer to the
intention developed by M.E. Bratman in Intention,
Plans, and Practical Reason (Bratman, 1987). Our
modelization is somehow also a generalization of the
a
https://orcid.org/0000-0001-9292-3213
utility function described by T. Agotnes and H. van
Ditmarsch (Agotnes and van Ditmarsch, 2011).
In the remainder of this article, we will first
present the dynamic epistemic logic, then the Hanabi
game, before detailing our work on intention mod-
elling in this game.
2 DYNAMIC EPISTEMIC LOGIC
2.1 Epistemic Logic
Epistemic logic (EL) is a modal logic that models
the notions of agents knowledge and beliefs (Fagin
et al., 2003). Let N be a finite set of agents. It con-
tains the standard operators of classical propositional
logic (CPL) >,⊥,¬,∧,∨,→,↔ plus a new operator
K representing the knowledge of each agent in N. For
example, the formula K
α
¬(φ ↔ ψ) means “agent α
knows that φ and ψ are not equivalent”.
Formulas in this logic are interpreted using epis-
temic models. Let P be the set of propositions, and
let N = {1, ..., n} be a set of n agents. An epistemic
model is a tuple of the form U = (M,{R
i
}
i∈N
,h),
where each R
i
is an equivalence relation on M and h
is a valuation function. The relations R
i
are called in-
distinguishability relations and define the worlds that
are indistinguishable for each agent. The valuation
function associates a set of possible worlds in M to
each proposition in P. A possible world can then be
seen as a model of CPL. We note possible worlds M
n
Chetcuti-Sperandio, N., Goudyme, A., Lagrue, S. and de Lima, T.
First Steps for Determining Agent Intention in Dynamic Epistemic Logic.
DOI: 10.5220/0008991207170724
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 717-724
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
717

(where n is an integer) and M represents the set of all
the worlds M
n
. Let α ∈ N, we use use I
U
M
i
α
to denote
the set {M
j
∈ M | (M
i
,M
j
) ∈ R
α
}
The satisfaction relation of epistemic logic is the
same as for CPL plus the following:
• |=
U
M
j
K
α
ψ iff for all worlds M
i
∈ M we have
M
j
R
α
M
i
|=
U
M
i
ψ
• |=
U
M
j
ˆ
K
α
ψ iff for some world M
i
∈ M we have
M
j
R
α
M
i
|=
U
M
i
ψ
Agents can reason about the knowledge of other
agents. They can imagine worlds that they know are
false but potentially true for other agents. For ex-
ample, the formula K
1
K
2
p ∧ ¬K
2
K
1
K
2
p means that
agent 1 knows that agent 2 knows p but agent 2 does
not know that agent 1 knows that agent 2 knows p.
Note that we use the notion of knowledge in this
article, instead of belief. Indeed, in games, if one fol-
lows the rules, players can only believe truths, even
for games where lying is allowed. In the latter case,
players, knowing that others may lie, do not take the
claims of other players as truth. The only way for an
assertion to be false is if the rules have not been re-
spected.
2.2 Actions
Dynamic epistemic logic (DEL) extends EL by
adding actions (for more details, see (Plaza, 1989),
(Gerbrandy and Groeneveld, 1997), (Baltag and
Moss, 2004), (van Ditmarsch et al., 2007)).
Definition 1. An atomic action is a pair
formed by a precondition and postcondition
a = (pre(a), post(a)), where pre(a) is a for-
mula in EL and post(a) is a partial function with
signature P → {>,⊥, p,¬p}.
In particular, action “nop” is the pair (>,
/
0). This
action represents the action of “doing nothing”, which
has no precondition (i.e., it can be executed at any
time) and does not change the state of the world (i.e.,
the value of each proposition p remains the same).
Let A be the set of possible actions and U =
(M,R,h) the current epistemic model. Executing
the action a ∈ A, in U generates the model U
|a
=
(M
|a
,R
|a
,h
|a
) where:
• M
|a
= {M
i
∈ M such that |=
U
Mi
pre(a)} is the re-
striction to the set of the worlds satisfying the pre-
condition of a.
• R
|a
= R∩(M
|a
×M
|a
) is the restriction of relations
to the worlds of M
|a
.
• h
|a
(p) = {M
i
∈ M such that |=
U
Mi
post(a)(p)} ∩
M
|a
is the restriction of the valuation to the worlds
of M
|a
along with the reassignment of the values
of propositional variables.
In our setting, agents can execute indeterminate
actions. This means that a player may not know what
action he is actually performing. For example, in
Hanabi, a player can place a card without knowing
which one it is. The effects of this action are not de-
termined for the player. To deal with that, we allow in
our setting actions of the form AI = a
1
∪ a
2
∪ · ·· ∪ a
k
,
where each a
i
is an atomic action. The operator ∪ thus
behaves as a non-deterministic choice. And, for each
pair (a
i
,a
j
), we have pre(a
i
) ∧ pre(a
j
) ≡ ⊥, i.e., the
atomic actions are mutually exclusive. The execution
of AI in a universe U is defined as follows.
Definition 2. Let U
M
0
be a pointed universe, where
U = (M,R, h) is a universe and M
0
∈ M is the actual
world in U. The execution of an indeterminate action
AI in U
M
0
is as follows:
• if there is a
i
∈ AI such that |=
U
M
0
M
0
pre(a
i
), then
execute action a
i
in U
M
0
,
• otherwise, execute action (⊥,
/
0) in U
M
0
Therefore, the result of the execution of an inde-
terminate action is a non-deterministic choice among
the actions that are executable in the actual possible
world. If none of the atomic actions composing the
indeterminate action is executable in the actual world,
then we obtain an empty universe.
In what follows, we use A
∗
to denote the set of all
indeterminate actions.
Definition 3. Let A be a finite set of actions, U
M
0
=
(M,R,h) a pointed universe and α an agent of N. We
call complete indeterminate action for agent i in U
M
0
all the elements AI of A
∗
such that ∀a ∈ AI,∃M
j
∈ M
such that M
0
R
α
M
j
such that |=
U
M
j
pre(a) and for all
M
j
∈ M
j
∈ M such that M
0
R
α
M
j
∃a ∈ AI such that
|=
U
M
j
pre(a). We denote A
∗α
the set of all complete
indeterminate actions for agent α in U
M
0
.
Many games are turn based. Adding the concept
of game turn to dynamic epistemic logic can be com-
plicated and constraining. Introducing simultaneous
actions of all the players (joint actions) was preferred.
Game turns are then modelled using the nop action:
on each turn, one player plays while the others per-
form the nop action (do nothing). The following def-
inition of joint action is based on the ATDEL logic
(de Lima, 2014).
Definition 4. Let A be a set of atomic actions, and
let N = {1,... n} be a set of n players (agents). A
joint action a j is an element of the set A
n
, one atomic
action for each player in N. We associate, to each
joint action a j, a joint pre-condition pre
j
(a j) and a
joint post-condition post
j
(a j), defined by:
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
718

p=T
p=T
T=
d
T=
d
T=
d
M
0
M
1
M
2
M
0
M
2
pre(a)=p
post(a)(p)=
U
|a
U
T
Figure 1: Example of an action.
• pre
j
(a j) =
V
n
i=1
pre(a
i
)
• ∀p ∈ P post
j
(a j)(p) =
>, if ∃a
i
, post(a
i
)(p) = >
and ∀a
i
post(a
i
)(p) = > or is undefined
⊥, if ∃a
i
, post(a
i
)(p) = ⊥
and ∀a
i
post(a
i
)(p) = ⊥ or is undefined
¬p, if ∃a
i
, post(a
i
)(p) = ¬p
and ∀a
i
post(a
i
)(p) = ¬p or is undefined
p, otherwise
However, the joint actions defined above are built
from atomic actions and not from indeterminate ac-
tions. For this case, we have the following definition.
Definition 5. Let A be the set of atomic actions, and
let N = {1, . ..,n} the set of agents. Let the indetermi-
nate action AI
i
, for each agent i ∈ N, be of the form:
AI
1
= (a
1,1
∪ ··· ∪ a
1, j
i
). The indeterminate joint ac-
tion is a non-deterministic choice of joint actions, i.e.,
it is of the form X = X
1
∪ X
2
∪ ··· ∪ X
m
, where each
X
j
= (a
1,k
,. . .,a
n,`
) is a tuple of atomic actions, one
for each agent.
In other words, an indeterminate joint action is a
non-deterministic choice between joint actions, one
for each agent, each one formed by atomic actions.
The execution of the indeterminate joint action X in
U is given as in Definitions 2 and 4 above.
Example
In the example presented in Figure 1, the initial epis-
temic state U is on the left. There are three worlds
and a propositional variable p. The world M
0
is cir-
cled twice: it is the actual world. The actual world is
the one that represents reality (that is, what is true at
the moment). The worlds M
0
and M
2
belong to h(p),
the world M
1
does not belong to h(p). Let a be an
action defined by the precondition pre(a) = p and the
postcondition post(a)(p) = ⊥, the result of the exe-
cution of the action a on the universe U is shown on
the right: the worlds M
0
and M
2
satisfy the precondi-
Figure 2: Presentation of the game Hanabi.
tion, they are thus kept and the propositional variable
acquires a new value, the one of the post-condition.
3 HANABI
We will use the game Hanabi in several examples of
this article. Hanabi is a cooperative turn-based card
game where 2 to 5 players aim at scoring a maximum
number of points (see Figure 2). The cards are of five
different colors (blue, green, red, yellow and white)
and five different numbers (1 to 5). For each color,
there are three cards with number 1, two cards with
number 2, two cards with number 3, two cards with
number 4 and one card with number 5. There are three
clue tokens and also eight life tokens.
To score points, the players must join forces to pile
up cards on the table. Each stack has cards of one and
same color and they must be numerically ordered. For
example, a stack of white cards must start with a white
1 and then it can have a white 2 over it etc., until the
white 5. The stack may be incomplete. One point is
scored for each card in the table, for a maximum score
of 25 points (i.e. five stacks of five cards each).
The players start with 4 to 5 cards each (depending
on the total number of players). The remaining cards
are piled up face down on a deck. The particularity of
Hanabi is that the players cannot see their own cards,
but they can see the other players’ cards. The actions
available for the player are: (i) give a clue; (ii) discard
a card; (iii) try to place a card on a stack or on the
table.
Give a Clue. On his turn, a player a can give a clue
to only one other player b. The clue covers all player’s
b cards. It must be complete and can relate to only one
of the 10 characteristics that cards can have (color or
number). For example, if player 1 tells player 3 ”Your
1st and 4th cards are blue” then the other cards must
not be blue. Finally, when a player gives a clue, a
First Steps for Determining Agent Intention in Dynamic Epistemic Logic
719
clue token is consumed. This action is only possible
if there are clue tokens available.
Discard a Card. On his turn, a player can take a
card from his hand and put it on the discard pile, face
up. Then, the player can draw a new card from the
deck, if any, and regains a clue token.
Place a Card. When the player chooses to place
one of her cards, there are two possibilities: either
(i) the card can be placed on one of the stacks or the
table or (ii) it cannot. A card can be placed on the
stack of its color, if the card at the top of this stack
is the previous card (preceding number). A card of
number 1 can be placed directly on the table if there
is no stack of that color on the table. Placing a card of
number 5 makes it possible to complete a stack and to
gain a token of life. When a card cannot be placed on
a stack or on the table, the card ends up in the discard
pile, face up, and the players loose one life token.
End of the Game. The game ends if there are no
more life tokens, or if the maximum number of points
is reached, or after a complete turn following the draw
of the last card of the deck.
4 INTENTION
4.1 Principles
The purpose of our work is to determine, a posteri-
ori, the intentions that a player had during a game. In
other words, we would like to explain the actions per-
formed by a player during a game. Our idea is based
on the following principle: compared to all the po-
tential results imagined by the player, did he perform
the action that led him to the best expected result? In
the following, we will explain this idea in more detail.
Let a player and a property p, expressed as a formula
in CPL, be given.
First Principle. We associate, to each universe U
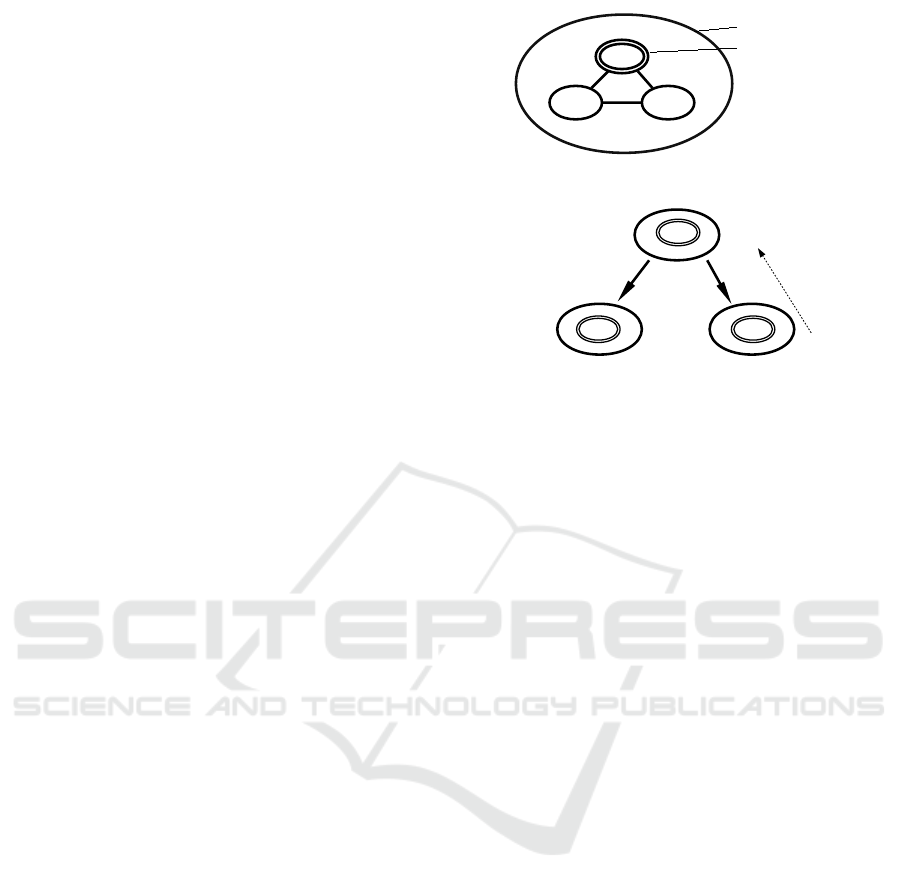
and a proposition p, a value v(U, p) called frequency
of the property p which, as its name suggests, is
equal to the frequency of the worlds satisfying p, in-
distinguishable from the actual world for the player
(see Figure 3). This idea was originally proposed by
Markus Eger in his thesis (Eger, 2018).
Second Principle. Suppose the player imagines
only one possible world, the actual world, and has two
p
p
Actual world
Universe
Value of the universe
v=2/3
Figure 3: Illustration of the first principle.
a
b
U
U
|a
U
|b
v=0
v=1
v=1
p
Figure 4: Illustration of the simple second principle.
possible actions a and b (see Figure 4). The action a
leads to a universe of value 0 and the action b to a
universe of value 1. The best action for the property p
is therefore the action b. If the player performed the
action b, then he intended to get the property p, oth-
erwise he did not had that intention. The value of the
universe obtained by the best action is assigned to the
initial universe.
Suppose now that the player imagines two possi-
ble worlds, still with two actions a and b (see Fig-
ure 5). In the first world, the action a leads to a uni-
verse with value 0.5 and the action b to a universe
with value 1. In the second world, the action a leads
to a universe with value 0.5 and the action b to a uni-
verse with value 0. The worlds being equivalent for
the player, there is as much chance for him to be in
one as in the other. Actions are therefore associated
with the average values of the universes to which they
lead. The value of a is therefore 0.5 and the value of
b is 0.5 as well. As before, we assign to the initial
universe the value of the best action (or best actions
like here). In this case, no matter what action was
performed, getting the property p cannot be consid-
ered intentional since all the actions make it possible
to obtain it with the same chances. It’s a difference
with the Belief-Desire-Intention theory within the in-
tention operator is a normal operator. In particular, in
the BDI theory there is the intention of tautology, this
is not the case here.
On the other hand, the intention to obtain a prop-
erty is clear in the case where there is only one best
action for that. For other percentages of best actions
among all actions, it is more difficult to measure in-
tention. So if it still seems relevant to talk about inten-
tion when there are 2 best actions among 10 actions
to obtain a property, for 5 best actions out of 10 one
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
720
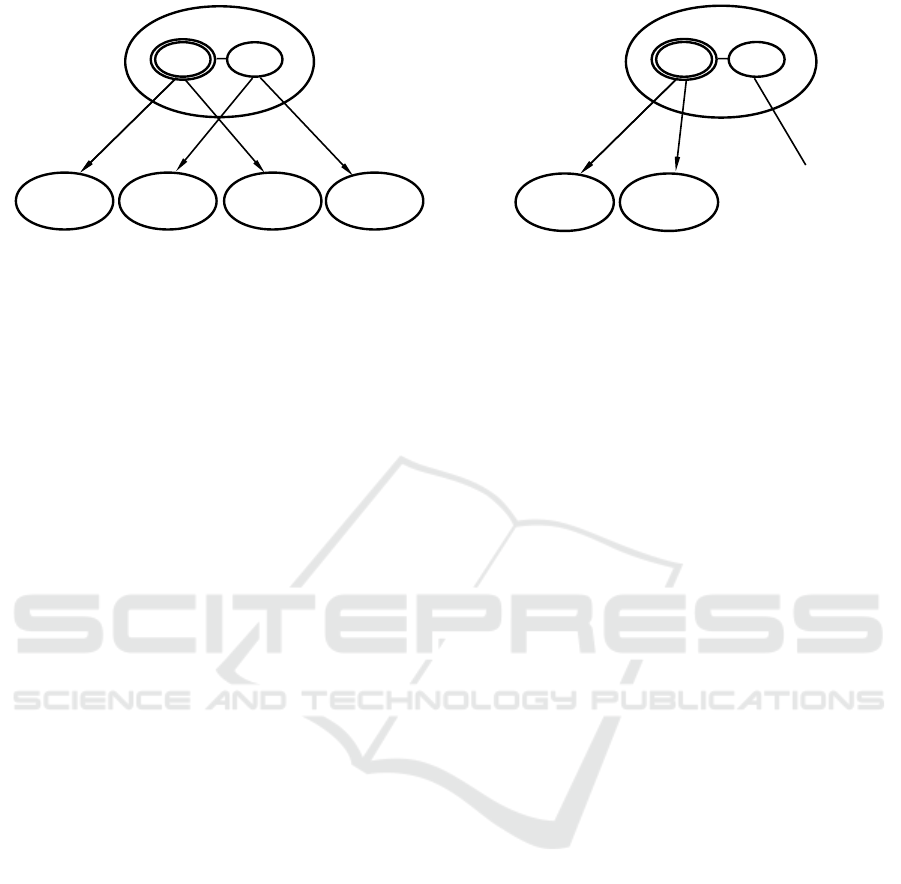
U
1
U
2
U
3
U
4
a
a b
b
v=0,5
v=1
v=0,5
v=0
v
a
=0,5
v
b
=0,5
v=0,5
U
Figure 5: Illustration of the second principle.
could speak of randomness. And at 9 best actions out
of 10, it is hard to talk about intention to get the prop-
erty. However, in the latter case, we then have one
best action out of 10 to obtain the non-propriety. We
are considering establishing thresholds of intention to
take it into account more finely.
Third Principle. In a third example, the player
imagines two worlds again, but this time it is up to
another player to play and this one has three possi-
ble actions: a, b and c (see Figure 6). Since the sec-
ond player has his own goals, the different actions are
more or less interesting in terms of his personal objec-
tives and the measure of this interest is called utility.
However, what will be taken into account here is not
the utility defined by the second player but what the
first player imagines to be the utility for the second
player.
First, suppose that the first world is the actual
world, the first player imagines the utility of the ac-
tions, for example u(a) = 0.6, u(b) = 0.6 and u(c) =
0.3. The first player assumes that the second player is
rational and therefore will perform a maximum utility
action. Since the two actions a and b have maximum
utility, the first player thinks that the second player
will perform one of these two actions with equiprob-
ability. These two actions lead to two different uni-
verses whose values are 0.8 and 0.6. The average
value of these two actions, which is 0.7, is assigned
to the first world. The same reasoning is done with
the second world. The actions have different utilities,
the universes thus generated have different values and,
eventually, the value for this second world is 0.3. Fi-
nally, the average value of both worlds is 0.5 and it is
assigned to the current universe.
The method of determining the intention of a
player proposed here is based on these 3 principles.
Example. Consider 3 players and some property p.
We want to determine the best action for player 1 to
get the property p in 3 turns. We begin by develop-
U
1
U
2
v=0,8 v=0,6
v
M0
=0,7
v
M1
=0,3
v=0,5
U
a
b
v=0,3
M
0
M
1
Figure 6: Illustration of the third principle.
ing the tree of the universes as described previously
but on 3 turns; this tree has 4 levels. The first level is
composed of the initial universe. The second level is
composed of the set of universes imagined by player
1 after his turn. The third level is composed of the set
of possible universes for player 1 after his turn and
player 2’s turn. The fourth level is composed of the
set of possible universes for player 1 after the turns
of player 1, 2 and 3. The values of the universes of
the fourth level are calculated using the first principle.
Then the values of the universes of the third and sec-
ond level can be calculated by means of the third prin-
ciple. Finally the value of the universe of the first level
is calculated using the second principle. This makes
it possible to check whether the action performed by
player 1 is the one that, from the point of view of the
player in question, had the best chance of obtaining
the property p.
Note. The notion of the value of a universe is close
to that of utility. Actually, for the simplest exam-
ples, the value of the universe is simply the frequency
of occurrence of the desired property within the uni-
verse, in other words, the probability of obtaining it.
Since a universe is linked to the action that makes
it possible to reach it, each action can be assigned
a measure of its utility to obtain the property. This
therefore defines a utility. However, we prefer not to
use this term because we give values to states and not
to actions.
4.2 Intention in Epistemic Games
First, we define a utility function that will associate,
to each world, each action and each player, a value.
Definition 6. Let A be a finite set of actions, N a finite
set of players, and U a universe. A utility function u is
a function that associates a real number x ∈ R to each
triple (AI,α,M
i
) ∈ A
∗
× N × M. A Measured Action-
able Universe (MAU) Ω is a triple (U, A,u).
First Steps for Determining Agent Intention in Dynamic Epistemic Logic
721

Definition 7. Let Ω = (U,A,u) be a measured ac-
tionable universe, M
i
∈ M a world and α ∈ N an
agent. A
Ω
M
i
,α
= {a ∈ A
∗α
| ∀b ∈ A
∗α
,u(a, α, M
i
) ≥
u(b,α, M
i
)} is the set of the most useful actions for
α in the world M
i
.
Now we will formally define the first principle,
that is, the calculation of the frequency of a propo-
sitional variable within the worlds that the player can-
not distinguish from the actual world.
Definition 8. Let U
M
0
be a universe, p an epistemic
formula and α ∈ N an agent. We note H(p) = {M
i
∈
M/ |=
U
M
0
M
i
p} The presence ratio of p for α is
pr
U
M
0
α
(p) =
|I
U
M
0
α
∩ H(p)|
|I
U
M
0
α
|
, if I
U
M
0
α
6=
/
0
0, otherwise
The value of a universe, according to a property p,
for k game turns can now be defined.
Definition 9. Let Ω = (U
M
0
,A, u) be a measured ac-
tionable universe, α ∈ N an agent, p an epistemic
formula and k a positive integer. Also let A
α
M
i
=
A
Ω
M
i
,1
× A
Ω
M
i
,α−1
× A
Ω
M
i
,α+1
× A
Ω
M
i
,n
. The value of the
universe U
M
0
for the agent α to the order k is:
v(U
M
0
,A, u,α, p, k ≥ 1) = max
a∈A
∗α
v
a
(U
M
0
,A, u,α, p, k)
where:
v
a
(U
M
0
,A, u, α, p,k ≥ 1) =
∑
M
i
∈I
U
M
0
α
avg
action
×
1
|I
U
α
|
where:
avg
action
=
∑
(a
1
,..,a
α−1
,a
α+1
,a
n
)∈A
α
M
i
value ×
1
|A
α
M
i
|
where:
value = v(U
M
i
|(a
1
,..,a
n
)
,A, u, α, p,k − 1)
and
v(U
M
0
,A, u, α, p,0) = pr
U
M
0
α
(p)
The function max in the formula characterizes the
second principle, while the double sum characterizes
the third principle. When it is the turn of a specific
player, the only action performed by the other players
is the action nop. The second sum then has only one
element, so there is no average on the actions of other
players, which corresponds to the second principle.
When it is the turn of one of the other players, the only
action maximum for the specific player is the action
nop, his other actions giving empty universes and thus
null values.
Definition 10. Let Ω = (U
M
0
,A, u) be a measured ac-
tionable universe, α ∈ N an agent, p an espistemic
formula and k a positive integer. The set of the best
actions to obtain property p at the k-th turn for the
player α, is the set:
Best(Ω, p,α,k) = {a ∈ A
∗α
| ∀b ∈ A
∗α
,
v
a
(U
M
0
,A, u, α, p,k) ≥ v
b
(U
M
0
,A, u, α, p,k)}
These last two definitions are used to character-
ize the best actions according to the player to get
a property k game turns in advance. Thus, given a
property p, one can check if the player has made the
best sequence of actions to obtain it. If this is the
case, then obtaining p was intentional, otherwise we
consider that p was obtained by accident. For ex-
ample, if the agent α performed the action a and if
a ∈ Best(Ω, p,α, k) then this was intentional. This be-
comes false if all the actions are among the best ac-
tions (Best(Ω, p,α, k) = A), in which case no action is
intentional.
4.3 Utility
The calculation of the best action requires defining a
utility for the actions, or more precisely, a utility from
the point of view of the player for the actions of the
other players. Finding the best way to model utility
for a game is a research work in itself and it is not
what we were aiming at. Therefore we propose a util-
ity definition based on the end-of-game reward that is
calculable by any player for any other player as long
as the end-of-game reward information is accessible
to all the players.
A player imagines several possible worlds and for
each world he imagines, the other players can imag-
ine other worlds. In Figure 7, for player 1, the world
M
0
and the world M
1
are indistinguishable from the
actual world M
0
. As for player 2, the worlds M
0
and
M
5
are indistinguishable and the worlds M
1
and M
2
are indistinguishable.
We start by defining the utility of the actions for
player 2 according to player 1. Player 1 knows that
player 2 hesitates between either the clique of worlds
M
0
and M
5
, or the clique of worlds M
1
and M
2
. So
these two cliques must be treated separately. We fo-
cus first on the first clique. To calculate the utility of
an action of the player 2 according to a world of the
clique, the following reasoning is made:
• this world is supposed to be the actual world;
• the maximum score that could be reached at the
end of the game after having performed the joint
action of player 2 and the other players (here
player 1 only) is computed;
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
722
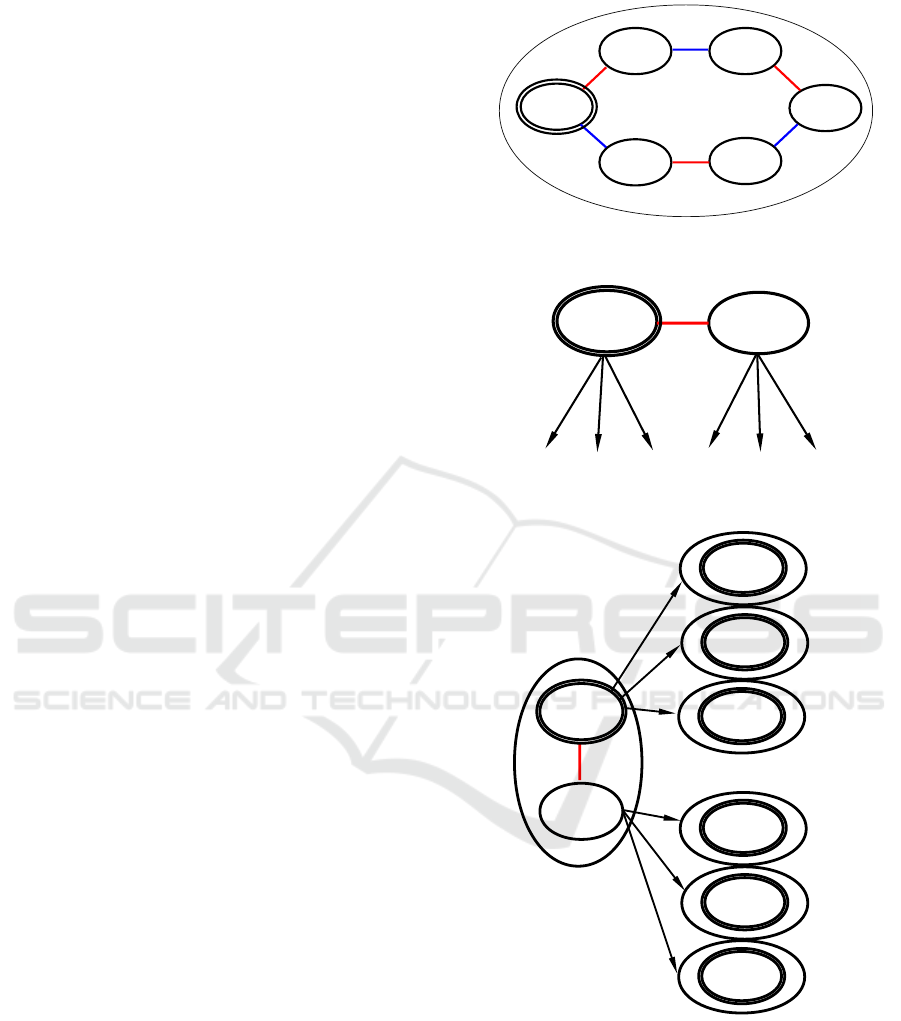
• the average over all the other players’ actions
(here player 1 only) is calculated;
• this average is defined as the utility of the action
for this world.
As the players consider these worlds equiproba-
bly, to compare the actions, it is necessary to calcu-
late the average utility of all the worlds of the clique.
This provides the utility of the action for this clique.
Finally, we define the utility of an action of player 2
from a world possible for player 1 as being equal to
the utility of the clique that it generates for player 2.
For the other worlds, the value of utility, having no
importance, is set arbitrarily.
As regards the utilities of player 1 for himself they
do not matter, so they are also arbitrarily set.
For turn-based games, only the nop action does
not give an empty universe when it is not up to the
player to play. Therefore it is not possible to give val-
ues to the utilities of the other actions. Giving an iden-
tical value to each empty universe would not change
the order of the values of the utilities of the actions.
One can also skip this step of averaging on the ac-
tions of other players. In both cases, the action of the
greatest utility will be the same.
4.4 Example
We will use the game Hanabi in a simplified ver-
sion to illustrate the use of the previously given def-
initions. In the simplified game, there are only red
cards of numbers 1, 2 and 3 and two players. There
are eight clue tokens and three life tokens. There are
only three actions (D, P and C): discard a card, place
a card, give a clue (which corresponds here to giv-
ing the value of the other player’s card). After deal-
ing the cards, player 1 has the card of number 1 and
player 2 has the card of number 2, so the deck con-
sists of the car of number 3. Figure 7 shows the
initial universe. The game is over: player 1 started
by giving the clue “you have the card of number 2”
and, after player 2’s turn, player 1 knew her card
and the card of number 2 had not been discarded.
We will check if the property “player 2 has not dis-
carded her card and the player 1 knows her card”,
noted p = ¬D : 2 ∧ (B
1
J1 : 1 ∨ B
1
J1 : 2 ∨ B
1
J1 : 3),
was obtained intentionally.
In the initial universe (Figure 7), player 1 imag-
ines two possible worlds: M
0
and M
1
. Then two cases
must be considered: one is where the actual world is
M
0
and the other one is where the actual world is M
1
(see Figure 8). The value of the action “give a clue”
must be calculated. Player 1 declares “you have the
card of number 2”. As a consequence, all the worlds
that do not satisfy “player 2 holds the card of number
P1: 1
P2: 2
Deck: 3
P1: 1
P2: 3
Deck: 2
P1: 3
P2: 2
Deck: 1
P1: 3
P2: 1
Deck: 2
P1: 2
P2: 3
Deck: 1
P1: 2
P2: 1
Deck: 3
1
2
1
1
2
2
U
M0
M
0
M
1
M
2
M
3
M
4
M
5
Figure 7: Initial universe.
P1: 1
P2: 2
Deck: 3
P1: 3
P2: 2
Deck: 1
1
M
0
M
1
Discard Clue Place
Discard Clue
Place
Figure 8: Initialization of the calculation of the value of the
actions of player 1.
P1: 1
P2: 2
Deck: 3
P1: 3
P2: 2
Deck: 1
1
M
0
M
1
P1: 3
P2: 1
Deck: 2
P1: 3 P2: 1
Deck: 2
L=1
P1: 1
P2: 3
Deck: 2
P1: 1 P2: 3
Deck: 2
L=1
D: Discard
P: Put
C: Give a clue
L=1: lost 1 life
token
D
P
C
D
P
C
P1: 1
P2: 2
Deck: 3
P1: 3
P2: 2
Deck: 1
u=1
pr
1
U
(p)=0
u=1
pr
1
U
(p)=0
u=3
pr
1
U
(p)=1
u=1
pr
1
U
(p)=0
u=1
pr
1
U
(p)=0
u=1
pr
1
U
(p)=1
Maximum utility: D, P, C
Maximum utility: C
U
|C
M0
Figure 9: Calculation of the value of the action “give a clue”
in world M
0
.
2” disappear. In this example, performing this action
in M
0
(respectively in M
1
) yields the universe U
M
0
|C
(respectively U
M
1
|C
, where the actual world differs),
presented in Figure 9. In this universe U
M
0
|C
, player 2
has the same three possible actions. If the world M
0
is
the actual world, the actions D and P have a utility of 1
First Steps for Determining Agent Intention in Dynamic Epistemic Logic
723

and the action C has a utility of 3. Therefore, player 1
thinks that player 2 will perform this action, which
means we obtain the property p with frequency of 1.
If the world M
1
is the actual world, the three actions
D, P and C have a utility of 1. For player 1, player 2
will perform one of these three actions equiprobably.
The property is not true after performing actions D or
P, whereas it is true with a frequency of 1 after per-
forming action C. Thus, this universe value is:
1
1
+
1
3
2
.
The same reasoning is used for U
M
1
|C
which, in this
example, has the same computations as U
M
0
|C
. By cal-
culating the average value of these two universes, the
value of the action ”give a clue” is:
v
Clue
(U
M
0
,A, u, 1, p,2) =
1
1
+
1
3
2
+
1
1
+
1
3
2
2
=
2
3
Similarly, v
Discard
(U
M
0
,A, u, 1, p,2) =
1
3
and
v
Place
(U
M
0
,A, u, 1, p,2) =
2
3
. Hence, the best actions
are giving a clue and placing a card. Consequently,
the player intended to get the property ”I know my
card, and player 2 did not discard his” after two turns.
5 CONCLUSION
We defined here a modelling of intention. This is
not the first work integrating intention and epistemic
logic. Lorini and Herzig (Lorini and Herzig, 2008)
model intention via operators of successful or failed
attempts. However, their logic models time linearly
(i.e. there is only one possible future). It is therefore
much less natural to capture game semantics.
Note that, in our approach, the more a formula is
specific to a target universe, the more certain it is that
the actions will be considered intentional. Therefore,
a more general formula would, a priori, result in a bet-
ter characterization of intention. We intend, in future
contributions, to define the generality of a fomrmula
within a set of universes.
Also note that worlds are considered here as
equiprobable. It might be interesting, in a future
work, to integrate weighted logics such as the one pre-
sented by Legastelois (Legastelois, 2017).
Our modelling takes into account players able to
imagine all the possible worlds and all the universes
that would result from them following the actions they
think most relevant. If a machine already has limited
resources, this same job for a human is even more
difficult. One of the ways to take this limitation into
account would be to consider an action as one of the
best when its value exceeds a given threshold (for ex-
ample, 80% of the real maximum value).
Finally, a multi-valued logic such as the one in
(Yang et al., 2019) could be used to reduce the size
of epistemic models. Integration of this in our work
seems feasible.
REFERENCES
Agotnes, T. and van Ditmarsch, H. (2011). What will they
say? public announcement games. Synthese, 179:57–
91.
Baltag, A. and Moss, L. (2004). Logic for epistemic pro-
grams. Synthese, 139(2):165–224.
Bratman, M. E. (1987). Intention, Plans, and Practical Rea-
son. CSLI Publications.
de Lima, T. (2014). Alternating-time temporal dynamic
epistemic logic. Journal of Logic and Computation,
24(6):1145–1178.
Eger, M. (2018). Intentional Agents for Doxastic Games.
PhD thesis, North Carolina State University.
Fagin, R., Halpern, J., Moses, Y., and Vardi, M. (2003).
Reasoning about knowledge. MIT Press.
Gerbrandy, J. and Groeneveld, W. (1997). Reasoning about
information change. Journal of Logic, Language, and
Information, 6(2):147–169.
Legastelois, B. (2017). Extension pond
´
er
´
ee des logiques
modales dans le cadre des croyances graduelles. PhD
thesis, Universit
´
e Pierre et Marie Curie - Paris VI.
Lorini, E. and Herzig, A. (2008). A logic of intention and
attempt. Synthese, 163(1):45–77.
Plaza, J. (1989). Logics of public communications. In IS-
MIS, pages 201–216.
van Ditmarsch, H., van der Hoek, W., and Kooi, B. (2007).
Dynamic Epistemic Logic. Springer.
Yang, S., Taniguchi, M., and Tojo, S. (2019). 4-valued logic
for agent communication with private/public informa-
tion passing. In ICAART, pages 54–61.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
724
