
The Role of Plasma Kinetic Processes during High Intense THz
Pulses Generation
A.V. Bogatskaya
1,2,3 a
, N. E. Gnezdovskaia
1,3 b
and A. M. Popov
1,2,3 c
1
D. V. Skobeltsyn Institute of Nuclear Physics, Moscow State University, 119991, Moscow, Russia
2
P. N. Lebedev Physical Institute, RAS, 119991, Moscow, Russia
3
Department of Physics, Moscow State University, 119991, Moscow, Russia
Keywords: Two-color Laser Fields, Terahertz Generation from Plasma, Plasma Waves, Plasma Kinetics, Electron
Velocity Distribution Function.
Abstract: This article is devoted to the theoretical study of THz radiation emission from plasma taking into account the
kinetic properties of nonequilibrium electron velocity distribution function (EVDF) formed in the process of
tunnel ionization by the two-color laser femtosecond pulse. The dispersive equation for longitudinal
oscillations was solved within the framework of elementary and kinetic models of plasma volume. It was
shown that the accounting of plasma kinetics can lead to essential variation of the spectral characteristics of
generated pulse thus leading to a change in signal duration.
1 INTRODUCTION
The continuing over the years interest in sources of
terahertz radiation is caused by manifold of their
applications in various fields, such as spectroscopy,
material science, biology, medicine, security systems
and so on (Tonouchi, 2007; Nagai et al, 2006; Liu et
al, 2010; Fischer et al, 2002; Kampfrath et al, 2013).
Two-color schemes providing strong THz pulses with
a very broad spectrum are the most popular among
the plasma methods of THz generation (Thomson et
al, 2010; Clerici et al, 2013; Oh et al, 2014; Andreeva
et al, 2016). In this article we provide the
generalization of the well-known transient
photocurrent model of THz generation (Kim et al,
2007; Gildenburg and Vvedenskii, 2007; Silaev and
Vvedenskii et al, 2009) by considering the kinetic
approach for the electron ensemble relaxation during
the THz waves emission. According to (Kim et al,
2007; Silaev and Vvedenskii et al, 2009) THz signal
occurs in a region of the focal waist of two-color or
ultrashort single-color laser field (it could be Ti-Sa or
some other mid-IR laser source) caused by the
residual electric photocurrent and polarization arising
a
https://orcid.org/0000-0002-1538-3433
b
https://orcid.org/0000-0001-9891-3235
c
https://orcid.org/0000-0002-7300-3785
from the angular asymmetry of the photoionization
process.
2 THz PULSE FORMATION IN
PLASMA IN FRAMES OF
ELEMENTARY MODEL
Let us start from the considering the emission from
plasma within the elementary model. To produce
plasma in our simulations we took two-color Ti-Sa
laser pulse with the sine-squared envelope consisting
of fundamental and second harmonics (400 + 800 nm)
and gas xenon. The intensity of fundamental
harmonic was chosen to be about 3.3 ∙10
W/cm
2
(for the 2nd harmonic this value was four times less),
pulse duration is about 100 fs, phase shift between the
harmonics is π/2. The ionization process was
considered in frames of tunnel ionization model
(Delone and Krainov, 1998; Tong and Lin, 2005)
(authors believe that this model is valid for xenon
atom as well due to the proximity of xenon and
hydrogen ionization potentials). The rate of ionization
52
Bogatskaya, A., Gnezdovskaia, N. and Popov, A.
The Role of Plasma Kinetic Processes during High Intense THz Pulses Generation.
DOI: 10.5220/0009005200520057
In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 52-57
ISBN: 978-989-758-401-5; ISSN: 2184-4364
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
per unit of time in dependence of electric field
strength 𝑤(𝐸) can be written in a form :
𝑤
(
|𝐸
(
𝑡
)
|
)
=
4𝜔
(
𝐸
𝐸
⁄)
exp
(
−2𝐸
3|𝐸
(
𝑡
)
|
⁄
−
12|𝐸
(
𝑡
)
|𝐸
⁄)
.
(1)
Here 𝐸
=5.14∙10
V cm
⁄
and 𝜔
=4.13∙
10
𝑠
are the atomic units of electric field and
frequency, respectively. The temporal dynamics of
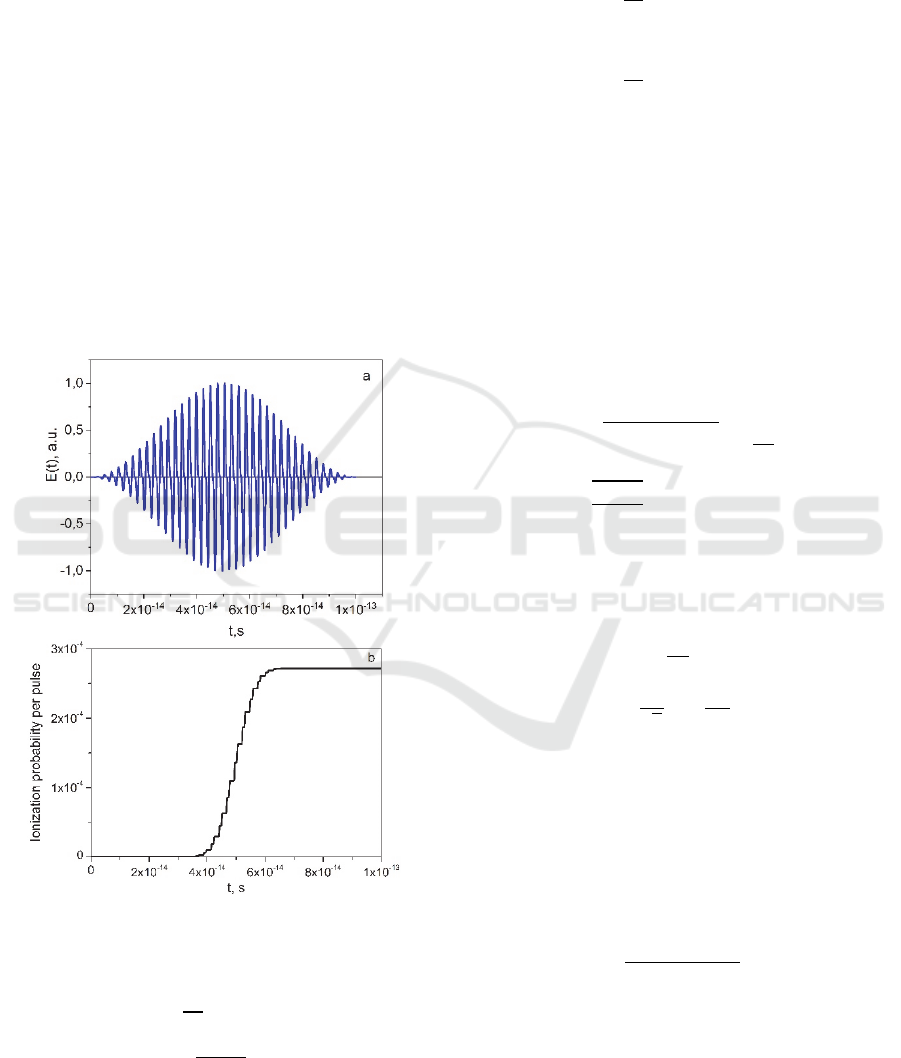
the ionization process for the given two-color laser
pulse is represented in Fig.1 for the xenon at
atmospheric pressure. Thus, by the end of the laser
pulse ionization is about 2.7 ∙ 10
which leads to the
electron concentration about 𝑁
≅7∙10
cm
-3
.
The asymmetry of the ionization process in the
two-color pulse leads to the formation of longitudinal
plasma oscillations. To obtain the frequency domain
of these oscillations one should solve the dispersive
equation for longitudinal plasma waves:
Figure 1: Time dependence of the ionization probability in
xenon (b) under the action of the two-color Ti-Sa laser pulse
(a). The parameters of laser pulse are listed in the text.
0=
𝜀(𝜔),
(2)
where 𝜀
(
𝜔
)
=1+𝑖
(
)
is the plasma
permittivity at frequency 𝜔 and 𝜎(𝜔) is the plasma
conductivity. It should be mentioned that equation (2)
is written for the longitudinal waves in free space.
Considering the geometry of plasma volume where
oscillations occur will lead to the following disperse
equations (Landau and Lifshitz,1981):
0=
(
𝜀
(
𝜔
)
+1
)
(3)
in the case of cylindrical plasma formation and
0=
(
𝜀
(
𝜔
)
+2
)
(4
)
for the spherical one.
In the frames of elementary model of plasma all
electrons have equal velocities and 𝜎
(
𝜔
)
=
𝑒
𝑁
𝑚(𝜈
−𝑖𝜔)
⁄
, where 𝜈
denotes the transport
collisional frequency of electrons in the focal volume
which is assumed to have constant value and 𝑁
is
electron density in plasma. For typical laser plasma
parameters the longitudinal plasma oscillations occur
in the THz frequency band and, hence, can produce
the seed THz pulse. By considering the cylindrical
shape of plasma (this seems to be closer to the real
shape of laser focal waist) and resolving equation (3)
with respect to 𝜔, one derives
𝜔=
𝜔
/2 − 𝜈
4
⁄
−𝑖
.
(5)
Here 𝜔
=
is the plasma (Langmuir)
frequency which is about 5∙10
𝑠
for the above
given electron density and belongs to THz frequency
range. In order to produce signal of several periods of
oscillations, attenuation in plasma should be less than
the Langmuir frequency, thus in the first order with
respect to the parameter
<1 one obtains from (5):
𝜔≈
√
−𝑖
.
(6
)
Real parts of the expressions (5) and (6) represent
the frequency of electronic gas oscillations and it can
be observed that taking into account the geometry of
plasma volume leads to the shifting of this frequency
while the imaginary part stands for the collisional
attenuation of plasma wave. Evolution of plasma
oscillations after the two-color laser pulse action can
be described by plasma polarization:
𝑃
(
𝑧,𝑡
)
=
𝑃
𝑒
⁄
𝑐𝑜𝑠
𝜔
/2 − 𝜈
4
⁄
𝑡𝑒
∙
.
(7)
Here 𝑃
is the value of residual polarization after the
two-color pulse action, 𝑎 is the size of focal waist of
two-color laser pulse where the plasma waves are
effectively excited (in our calculations we assume 𝑎
is around 0.01 cm). Expression (7) was written under
The Role of Plasma Kinetic Processes during High Intense THz Pulses Generation
53
the assumption that in the region of pulse focal waist
plasma oscillations take place with the same phase.
Indeed, as the group velocity of the two-color pump
pulse in plasma is close to the speed of light (here we
neglect the walk-off between the fundamental and
second pulse harmonics), one can consider the
simultaneous excitation of plasma volume after the
two-color pulse action. In case of proximity of plasma
frequency and collisional frequency 𝜈
the THz
emission spectrum is wide consisting of different
(both short and long) waves so the plasma can not be
considered as a point-like source (especially for short
waves). To obtain the emission of the seed pulse we
are going to solve wave equation with the polarization
(7) as the sourсe:
(
,
)
=
(
,
)
+
(
,
)
.
(8)
By applying double Fourier transform to the equation
(8): 𝐸
,
=
𝐸(𝑧,𝑡)𝑒𝑥p (𝑖𝜔𝑡 − 𝑖𝑘𝑧)𝑑𝑧𝑑𝑡
,
𝑃
,
=
𝑃
(𝑧,𝑡)𝑒𝑥p (𝑖𝜔𝑡− 𝑖𝑘𝑧)𝑑𝑧𝑑𝑡
one obtains
the following relation between the Fourier
components of the polarization and the wave field:
𝐸
,
(
𝑘
−𝜔
𝑐
⁄)
=
𝜔
𝑃
,
,
(9)
where
𝑃
,
=−𝑖𝑃
√
𝜋exp
−
×
1 𝜔−
𝜔
−𝜈
4
⁄
+
+
+1 𝜔+
𝜔
−𝜈
4
⁄
+
(10)
From (9) the spatial evolution of the plasma emission
spectrum reads:
𝐸
(
𝑧
)
=
4𝜋
,
⁄
𝑒𝑥𝑝
(
𝑖𝑘𝑧
)
𝑑𝑘
.
(11)
The solution 𝐸
(
𝑧
)
of equation (9) for 𝑧=0 will
represent the spectrum which is formed from the
oscillations of polarization vector (7). Expression
(11) can be resolved by means of residue theory. By
choosing only the wave propagating in positive
direction for the pulse spectrum we finally have:
𝐸
(𝑧)
|
=𝑃
𝑎𝜋
𝑒𝑥𝑝
−
×
1 𝜔−
𝜔
−𝜈
4
⁄
+
+
1𝜔+
𝜔
−𝜈
4
⁄
+
.
(12)
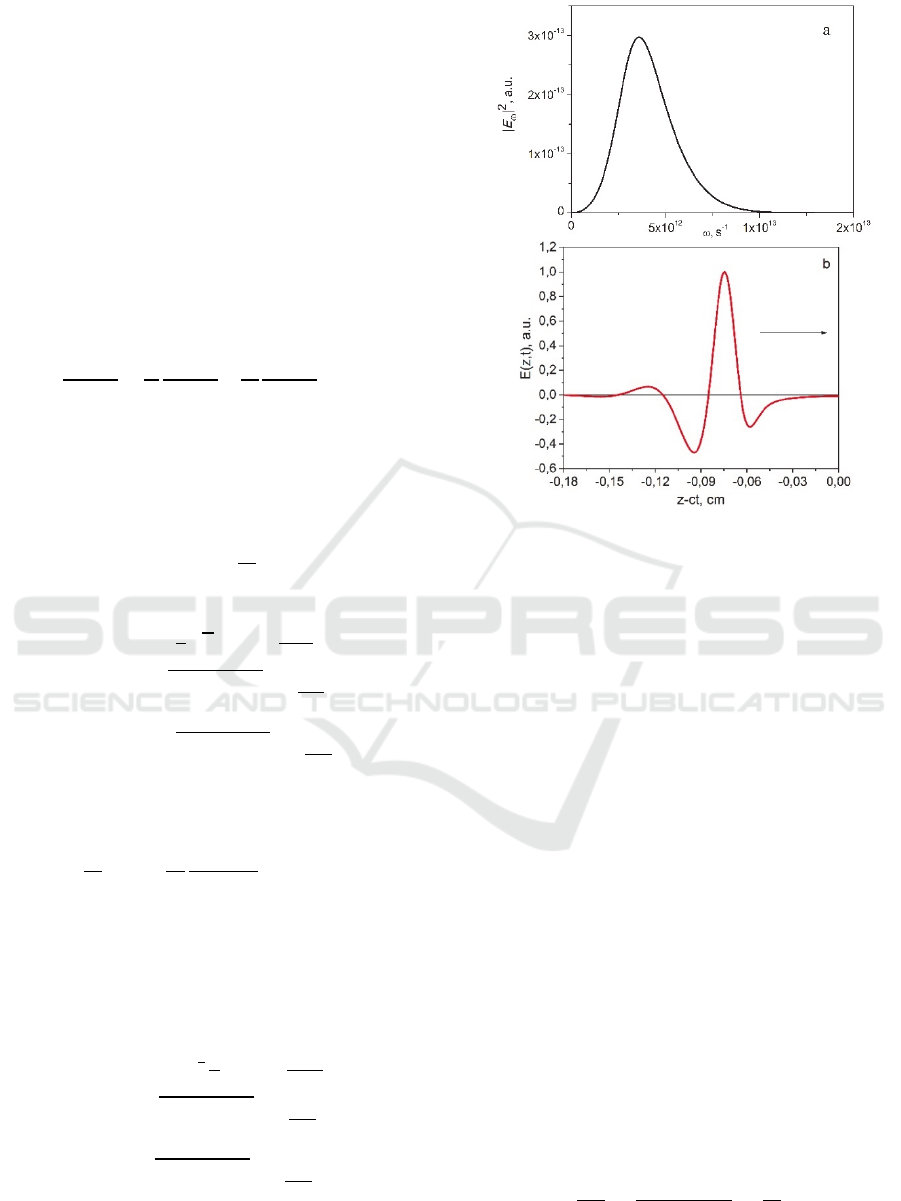
Figure 2: Spectrum (a) and spatial-temporal distribution (b)
of emitted signal in plasma within the elementary model.
Plasma electron concentration 𝑁
=7∙10
cm
-3
.
Transport frequency in plasma 𝜈
=3.75∙10
s
-1
.
Arrow shows the direction of pulse propagation.
Typical spectrum of emission
|
𝐸
|
and spatial-
temporal distribution of the produced pulse are shown
in Figure 2 for the plasma frequency 𝜔
=5∙10
s
-1
(which corresponds to the electron concentration
𝑁
=7∙10
cm
-3
), 𝜈
=3.75∙10
s
-1
(for
estimates we selected gas xenon at atmospheric
pressure and the velocity of electrons was chosen to
be about 10
cm/s).
3 THz PULSE FORMATION
UNDER THE INFLUENCE OF
KINETIC PROPERTIES OF
NONEQUILIBRIUM PLASMA
The main issue of this section is the study of influence
of plasma kinetic properties on the THz pulse
formation. Within the framework of the two-term
expansion for Boltzmann kinetic equation the plasma
conductivity can be expressed as (Ginzburg and
Gurevich, 1960; Raizer, 1977):
𝜎
(
𝜔
)
=
(
(
)
)
(
−
𝑑𝑣,
(13)
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
54
where 𝑓(𝑣) stands for electron distribution function
over absolute value of velocity normalized by
𝑓
(
𝑣
)
𝑣
𝑑𝑣
=1/4𝜋 . Substituting (13) in
dispersive equation (3) for the cylindrical plasma
geometry one obtains the following integral equation
for longitudinal plasma oscillations:
ω=−
𝑖
𝜔
(
(
)
)
(
−
𝑑𝑣.
(14)
Solution of the equation (14) provides the spectrum
of plasma waves for the given electron velocity
distribution function (EVDF) and in general terms
should be solved numerically. In case of 𝜔
>
〈
𝜈
〉
,where
〈〉
means averaging over the distribution
function, it is possible to write the analytical solution
in the first order over parameter
〈
𝜈
〉
/𝜔:
𝜔≅
𝜔
√
2
−
𝑖
2
∙(<𝜈
(𝑣)>+
+
<𝑣
()
>).
(15)
It can be seen that accounting of plasma kinetics
leads to additional term in the imaginary part of 𝜔
compared to (6) which could be both positive or
negative depending on the sign of the derivative
function
()
and the expression for the EVDF.
Thus, taking into account both the velocity
dependence of transport scattering cross section and
distribution of electrons enables to describe the
spectrum of emitted radiation from plasma more
correctly.
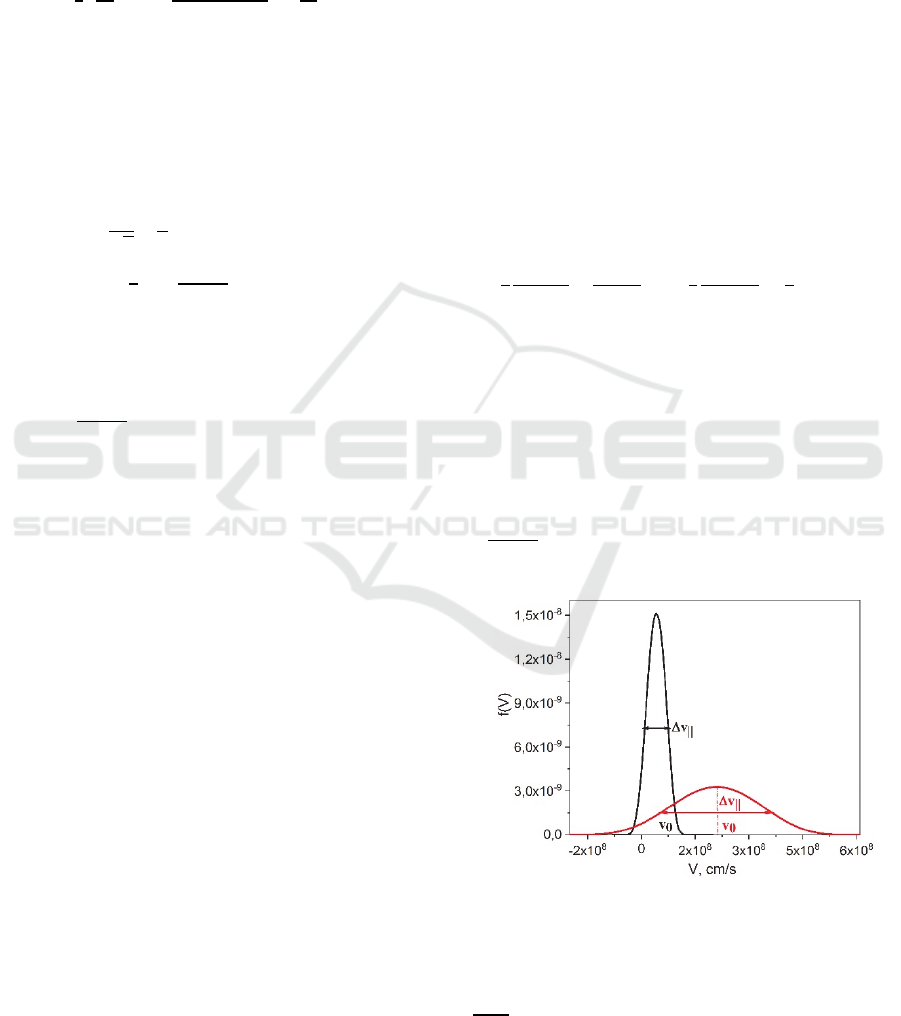
Figure (3) demonstrates the electron velocity
distribution functions formed along the polarization
axis during the tunnel ionization of xenon by two-
color femtosecond laser pulses with fundamental
wavelengths of 800 and 3900 nm. The duration of
3900 nm pulse and the intensities of fundamental and
second harmonics were chosen to be the same as for
the 800 nm pulse which was considered in the Section
I. Both obtained distributions are highly
nonequilibrium and have sharp angular distribution
along the direction of the electric field of the pulse.
Below we will call them EVDF
1
for the distribution
formed by the (400+800) nm laser pulse and EVDF
2
for the distribution formed by the (1950+3900) nm
laser pulse. According to the plasma kinetic theory,
elastic collisions lead to the isotropization of angular
distribution of electrons, while the domination of
electron-electron collisions determines fast
maxwellization of EVDF. Duration of the
maxwellization process can be estimated as 𝜏
~𝜈
,
where 𝜈
is the frequency of electron - electron
collisions. By estimating electron-electron collisional
cross section as 𝜎
≈(𝜋𝑒
𝜀
)×𝐿
⁄
(here 𝜀
is the
electron energy and 𝐿≈10 is the Coulomb
logarithm) for 𝜀
~ 0.5 eV which corresponds to
maximum of EVDF
1
(see fig.4) and 𝜀
~ 12.4 eV for
the EVDF
2
, one obtains 𝜏
~1.4 × 10
s
-1
and
𝜏
~1.6 × 10
s
-1
. Here 𝑁
was chosen to be
7×10
cm
-3
(obtained by the formula (1) ionization
degree is approximately the same for both cases). The
above estimates lead to the fact that for the EVDF
1
fast maxwellization will take place, while for the
EVDF
2
elastic collisions will redistribute electrons
rather quickly (within the time interval of several
collisions) leading to the isotropic distribution in
velocity space. For the transport collisional
frequencies we derive 𝜈
≈10
s
-1
and 𝜈
≈
6.6 × 10
s
-1
.
To estimate the temperature T of the maxwellized
EVDF
1
one can write the following relation
∆
∥
+
(
)
+2∙
(
∆
)
=
𝑇.
(16)
which has the sense of energy conservation law
during the isotropization process in three-
dimensional velocity space. Here 𝑣
,Δ𝑣
||
are taken
from Fig. 3, Δ𝑣
stands for the transverse distribution
of photoelectrons formed in the tunnel ionization,
which is usually assumed to be small compared with
the electron velocities along the pulse polarizations
(Delone and Krainov, 1998). In Fig. 4 the obtained
isotropic distributions are plotted with the function
𝑣
()
for xenon to analyse the contribution of
kinetic effects to the imaginary part of solution (15),
Figure 3: One-dimensional electron velocity distribution
functions (EVDF) along the polarization of two-color laser
field with fundamental wavelengths 800 nm (black curve)
and 3900 nm (red curve). Here 𝑣
,Δ𝑣
||
are the mean
velocity and velocity dispersion correspondingly.𝑣
=4.2∙
см
,Δ𝑣
||
=5.3∙10
cm/s for 800 nm; 𝑣
=2.09∙10
cm/s, Δ𝑣
||
=2.46∙10
cm/s for 3900 nm. Distribution
functions are normalized to unity.
The Role of Plasma Kinetic Processes during High Intense THz Pulses Generation
55
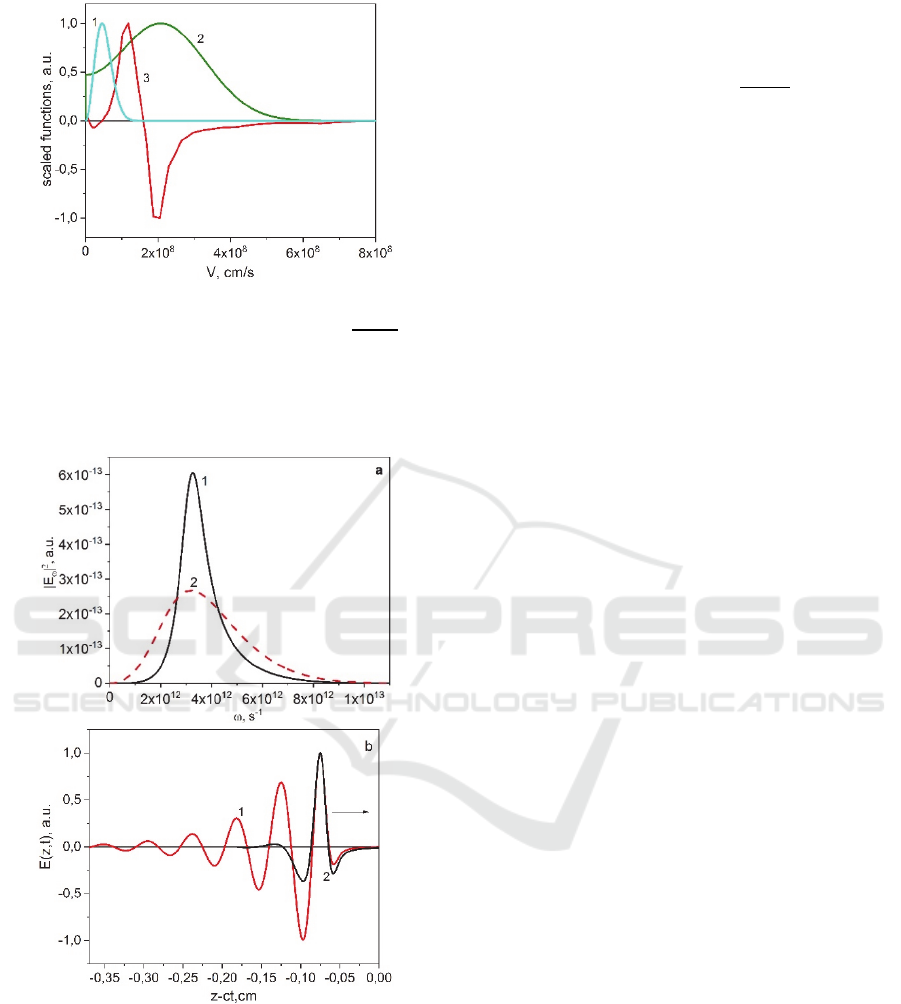
Figure 4: EVDF
1
after the Maxwellization process (1),
EVDF
2
after the isotropization process (2) and 𝑣
()
(3).
All the functions are scaled (divided by maximum values).
EEDF
1
and EEDF
2
represent the velocity distribution in
three-dimensional velocity space and normalized by
condition
𝑓
(
𝑣
)
𝑣
𝑑𝑣=1/4𝜋.
Figure 5: Spectra of emission (a) and spatial-temporal
distributions of electric field strength (b) for plasma
characterized by the distribution functions EVDF
1
(1) and
EVDF
2
(2).
which determines the collisional damping of plasma
waves. The value of transport scattering cross section
for xenon atom was taken from (Hayashi, 1983). As
for distribution (2) in Fig. 4 it comes from the
distribution formed by the (1950+3900) nm laser
pulse replotted for the velocity module and
renormalized in three-dimensional velocity space.
One can see, for example, that for the distribution (2)
the negative value of function 𝑣
()
can decrease
the value of damping coefficient in (15), thereby
leading to the formation of longer THz pulses with
narrower spectrum.
In case of our consideration plasma frequency is
close to the transport collisional frequency, so we
apply numerical methods to the solution of (14).
Equation (14) was solved by the iterative method, and
for obtained distribution functions we have the
following results:
𝜔≈3.3∙ 10
−4.3∙
10
𝑖s
-1
for the EVDF
1
𝜔≈2.5∙ 10
−1.9∙
10
𝑖 s
-1
for the EVDF
2
.
The spectra of emission
|
𝐸
|
and spatial-
temporal distributions of electric field strength
𝐸(𝑧,𝑡) for both distribution functions are shown in
Fig.5.
4 CONCLUSIONS
This article considers the THz pulse generation
through the longitudinal plasma oscillations arising
from gas ionization by two-color femtosecond laser
pulse. The obtained analytical and numerical results
demonstrate that due to the strong velocity
dependence of transport scattering cross section of
gas atoms various velocity distributions of plasma
electrons can provide sufficiently different spectra of
emission, which can lead to generation of THz pulses
with different spectral and spatial widths. The
performed research will play important role for the
new approach to obtain high intense THz pulses in
nonequilibrium plasma of noble gases proposed and
developed by the authors [Bogatskaya and Popov,
2013; Bogatskaya et al, 2014; Bogatskaya and Popov,
2018]. The approach consists in additional
amplification of seed THz pulse which arises under
the action of two-color (mid)IR laser in photoionized
plasma channel formed by femtosecond eximer KrF
laser pulse.
ACKNOWLEDGEMENTS
This work was supported by the Russian Science
Foundation (project no. 18-72- 00125).
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
56

REFERENCES
Andreeva, V., A., Kosareva, O., G., Panov, N., A., Shipilo,
D., E., Solyankin, P., M., Esaulkov, M., N., González,
P., Shkurinov, A., P., Makarov, V., A., Bergé, L., Chin,
S. L., 2016. Phys. Rev. Lett., 116, 063902.
Bogatskaya, A., V., Popov, A., M., 2013. JETP Lett. 97,
388
Bogatskaya, A., V., Popov, A., M., Smetanin, I., V., 2014.
J. Rus. Las. Res., 35, 437.
Bogatskaya, A., V., Popov, A., M., 2018. Las. Phys., 28,
115301
Clerici, M., et al 2013. Phys. Rev. Lett., 110, 253901.
Delone, N., B., Krainov, V., P., 1998. Phys. Usp., 41, 469.
Fischer, B., M., Walther. M., Jepsen.,P., U., 2002. Phys.
Med. Biol., 47, 3807.
Gildenburg, V., B., Vvedenskii N., V., 2007. Phys. Rev.
Lett. 98, 245002.
Ginzburg, V., L., Gurevich, A., V., 1960. Usp. Fiz. Nauk,
70, 201.
Hayashi, M., 1983. J. Phys. D., 16, 581.
Kampfrath, T., Tanaka, K., Nelson, K., A., 2013. Nat.
Photonics, 7, 680.
Kim, K., Y., Glownia, J., H., Taylor, A., Rodriguez, J., G.,
2007. Opt. Express, 15, 4577.
Landau, L., D., Lifshitz, L., M., 1981. Quantum Mechanics:
Non-Relativistic Theory, Butterworth Heinemann, 3rd
Edition.
Liu, J., Dai J, Chin, S., L., Zhang, X., C., 2010. Nat.
Photon., 4, 627.
Nagai, N., Sumitomo, M., Imaizumi, M., Fukasawa, R.,
2006. Semicond. Sci. Technol., 21, 201.
Oh, T., I., Yoo, Y., J., You Y., S., Kim, K., Y., 2014. Appl.
Phys. Lett., 105, 041103.
Raizer, Yu., P., 1974. Laser-Induced Discharge
Phenomena, Consultants Bureau, New York, London.
Silaev, A., A., Vvedenskii, N., V., 2009. Phys. Rev. Lett.,
102, 115005.
Thomson, M., D., Blank, V., Roskos, H., G., 2010. Opt.
Express, 18, 23173.
Tong, X., M., Lin, C., D., 2005. J. Phys. B, 38, 2593.
Tonouchi, M., 2007. Nat. Photon., 1, 97.
The Role of Plasma Kinetic Processes during High Intense THz Pulses Generation
57
