Evaluation of Simulator Incorporating Non-equilibrium

Green’s Function and Improvement of Quantum Cascade

Lasers Output using the Simulator

Shigeyuki Takagi

, Hirotaka Tanimura

, Tsutomu Kakuno

, Rei Hashimoto

Kei Kaneko

and Shinji Saito

Department of Electrical and Electronics Engineering, School of Engineering, Tokyo University of Technology,

1404-1 Katakura-cho, Hachioji-city, Tokyo, Japan

Corporate Manufacturing Engineering Center, Toshiba Corporation, 8 Shinisogo-cho, Isogo Ward,

Yokohama-city, Kanagawa, Japan

Keywords: Quantum Cascade Lasers, QCLs, Non-equilibrium Green’s Function, Electron Scattering, Quantum Well.

Abstract: We applied a simulator incorporating a non-equilibrium Green’s function (NEGF) to quantum cascade laser

(QCL) wavelength prediction, and confirmed its validity including its temperature dependence. In addition,

the electroluminescence (EL) intensity of the QCL was increased by a factor of 1.4 by including a structure

that made the light-emitting layer barrier thin calculated using the simulator. The NEGF is used to calculate

the electron density existing in the QCL and the laser gain. To examine the validity of wavelength calculation,

we calculated the oscillation wavelengths for the seven types of film structure in the 3 to 9 µm band in our

references, and compared them with the experimental results. As a result, the difference between them was

well below 0.36 µm. Furthermore, the film structure for increasing the gain was calculated on the basis of the

structure reported in one of the references. The gain was increased 1.17 to 1.28 times by reducing the

thicknesses of the barriers by 10%. The QCLs with this film structure were prototyped and their EL output

intensity was measured. It was confirmed that the EL output intensity output was improved and the film

structure design obtained using the simulator was effective.

1 INTRODUCTION

Quantum cascade lasers (QCLs) are n-type

semiconductor lasers in which two types of

semiconductor film are alternately stacked, and the

laser light in the infrared region can be obtained (Faist

et al., 1994). Conventional semiconductor lasers

(LDs) are limited to visible part of the spectrum and

infrared wavelengths below 3 μm. QCLs oscillate in

the infrared region, and the desired wavelength can be

obtained simply by changing the thickness of a

multilayer film using two kinds of materials.

Since the QCL wavelength is in the infrared

region, QCLs are expected to be applied in trace gas

analysis and remote gas detection. To realize this, a

QCL with a wavelength suitable for such

measurements is required. Furthermore, with such

trace substance detection and remote gas detection,

https://orcid.org/0000-0002-7653-4602

higher sensitivity is expected by increasing the

output. Since the amount of laser absorption is

measured in the detection of trace substances, it is

necessary for the laser to propagate a long optical

path. To develop a laser with such a high output and

a wavelength suitable for measurement, it is effective

to use a simulator that can predict the oscillation

wavelength and gain.

In the current simulators, the Schrödinger

equation is solved to calculate the wave function, and

the laser light intensity is calculated from the

lifetimes of the upper and lower levels and the

transition probabilities between the upper and lower

levels semi-classically (Jirauschek and Kubis, 2014).

On the other hand, in the calculation using a non-

equilibrium Green’s function (NEGF), the electron

density distribution and the transition of electrons

from the upper level to the lower level can be

Takagi, S., Tanimura, H., Kakuno, T., Hashimoto, R., Kaneko, K. and Saito, S.

Evaluation of Simulator Incorporating Non-equilibrium Green’s Function and Improvement of Quantum Cascade Lasers Output using the Simulator.

DOI: 10.5220/0009101100580063

In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 58-63

ISBN: 978-989-758-401-5; ISSN: 2184-4364

calculated quantum mechanically. Furthermore, by

determining the self-energy of electron scattering, we

can easily add the effect of electron scattering on the

electron distribution. Not only can the gain be

calculated accurately, it is also possible to reflect the

effects of operating temperature and film stress.

Then, we introduced a simulator that incorporates

NEGF for the calculation of electron density (Grange,

2015). Oscillation wavelengths were calculated for

structures with wavelengths of 3 to 9 µm reported so

far, and compared with the wavelengths actually

measured in previous study. To investigate the

temperature dependence of the simulator, the

oscillation wavelength from 77 to 293K was

calculated for a film structure QCL with an oscillation

wavelength of 4 µm, and the temperature dependence

was consistent with the wavelength of the prototype

QCL. Furthermore, the active layer was designed to

increase the gain using a simulator, and it was shown

that the output could be improved by reducing the

barrier of the light-emitting layer. As a result of

evaluating the QCL with this structure, the EL

emission intensity was increased 1.4-fold compared

with the previous structure QCL, and it was shown

that the simulator design method is effective for the

structure design of QCLs.

2 SIMULATOR

INCORPORATING NEGF

2.1 Composition of Simulator

Nextnano.QCL (Nextnano GmbH) was used for

calculating the oscillation wavelength of QCLs.

Figure 1 shows the calculation flow in the simulator.

Assuming that the unperturbed Hamiltonian is H

and

the electron scattering is the perturbation term

Hamiltonian H

scatt

in the Schrödinger equation, the

Hamiltonian H is expressed by Eq. (1).

H = H

+ H

cat

(1)

Next, the Poisson equation is solved to find the

mean-field electrostatic potential, and the retarded

self-energy Σ

and the lesser self-energy Σ

describing electron scattering are calculated. The

density of States (DOS) is obtained from the retarded

Green’s function G

using the Dyson equation shown

in Eq. (2).











Σ



(2)

Figure 1: Calculation flow of NEGF simulator.

Using the Keldysh equation shown in Eq. (3), we

obtained the electron density matrix from the lesser

Green’s function G















(3)

where G

is an advanced Green’s function. In the

NEGF, the above calculations are repeated until G

converges below the set threshold. That is, G

obtained by a self-consistent method. On the basis of

the obtained electron density matrix, the current and

the gain of the QCL are calculated.

From a series of calculations, the relationship

between the energy (wavelength) and the gain is

calculated. The oscillation wavelength of the laser is

determined as the wavelength that maximizes the

gain. By using the NEGF, we can add the effects such

as the crystal lattice and electron scattering to the

simulation. In this way, it is possible to perform the

calculation while taking into consideration of the

influence on the film stress and electrons scattering to

the crystal lattice corresponding to the operating

temperature of the QCL.

2.2 Structure and Oscillation

Wavelength

We selected seven papers in which oscillation in the

3 to 9 μm band was reported (Kirch et al, 2015, Yu et

al., 2010, Wang et al, 2009, Faist et al., 1996, Evans

et al., 2007, Faist et al., 1998, Aldukhayel et al.,

2009), and the oscillation wavelength in each film

structure was calculated using the simulator. The

wavelengths in the references and those obtained by

simulation are shown in Fig. 2. The left side of the

dotted line is the material InAlAs/InGaAs, and the

right side (G) is the film material AlAs(Sb) / InGaAs.

The differences between the simulations and the

Evaluation of Simulator Incorporating Non-equilibrium Green’s Function and Improvement of Quantum Cascade Lasers Output using the

Simulator

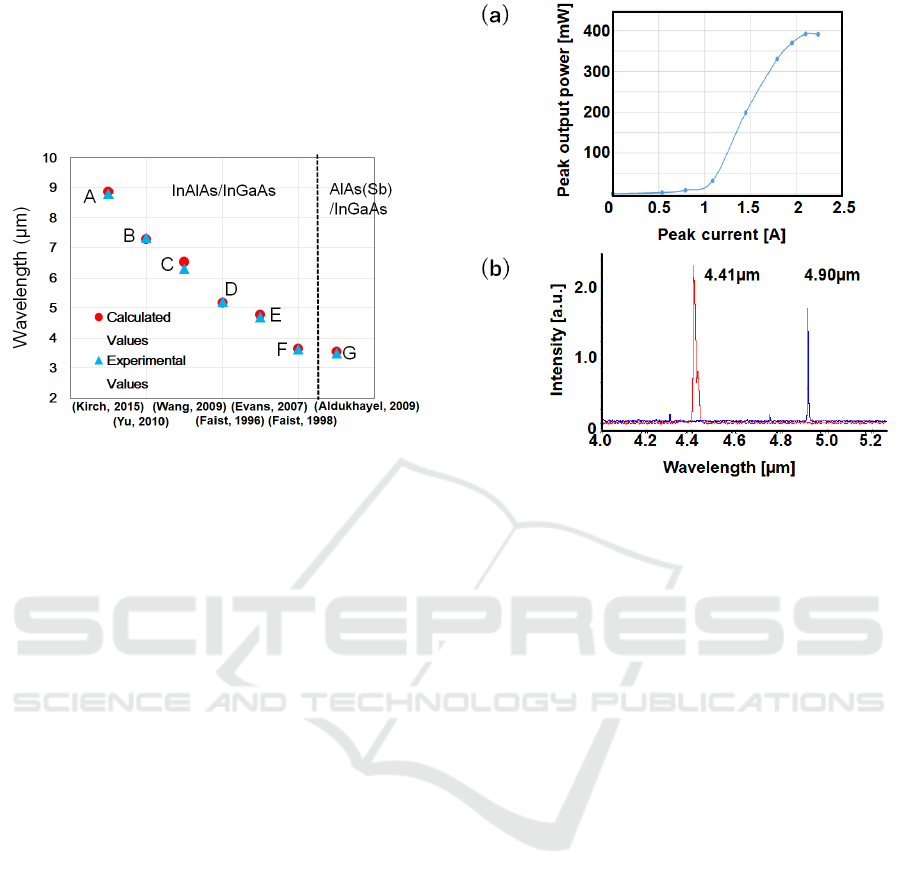
experiment are less than 0.4 μm except for B of 0.59

in the QCL with the film material InAlAs/InGaAs. In

the case of G, the difference is 0.045 μm, and it is

shown that the calculated values reproduce the

experimental values well even if the film material is

changed.

A: Kirch, D. et al. “Highly temperature insensitive, low threshold-

current density (λ = 8.7–8.8 μm) quantum cascade lasers”

B: Yu, J S. et al. “Injector doping level-dependent continuous-wave

operation of InP-based QCLs at λ ~ 7.3 μm above room

temperature”

C: Wang, C. et al. ”Mode-locked pulses from mid-infrared

quantum cascade lasers”

D: Faist, J. et al. ”High power mid-infrared (λ ~ 5 μm) quantum

cascade lasers operating above room temperature”

E: Evans, A. et al. “Buried heterostructure quantum cascade lasers

with high continuous-wave wall plug efficiency”

F: Faist, J. et al. “Short wavelength quantum cascade laser based

on strained compensated InGaAs/AlInAs”

G: Aldukhayel, A. et al. “Investigations of carrier scattering into L-

valley in λ = 3.5 μm InGaAs/AlAs(Sb) quantum cascade lasers

using high hydrostatic pressure”

Figure 2: Comparison of wavelengths reported in papers

and wavelengths obtained by simulation.

In parallel with the simulation, we fabricated two

QCLs with an oscillation wavelength in the 4 μm

band. The QCL has 30 cycles of active layers, whose

structure is the same as that used by Evans et al. The

device length is 4 mm and the ridge width is 12 μm.

The QCLs were operated at 100 kHz with a pulse

width of 300 ns at room temperature (293 K). The

oscillation wavelength of the prototype QCL is shown

in Fig. 3 (a). The two prototype devices oscillated at

wavelengths of 4.41 and 4.90 μm, respectively. The

differences between the calculated wavelengths and

the measured wavelengths, including our

experimental results, are within 0.36 μm. The output

characteristics of the QCL with an oscillation

wavelength of 4.41 μm are shown in Fig. 3 (b). A

peak output of about 400mW is obtained.

Figure 3: QCL output characteristics (a) and oscillation

wavelength (b).

2.3 Temperature Dependence

To investigate the temperature dependence of the

simulation results, the operating temperature was

changed from 84 to 241 K in the simulation. The

temperature dependence was also measured with our

QCL with an oscillation wavelength of 4.41 µm

fabricated as described in Sec 2.2. The simulation

results were compared with the experimental results of

the prototype QCL and the measurement results Wen

et al., 2011) of Wen et al. The active layer structures

are all the same as those used by Evans et al. The

temperature ranges at which the oscillation wavelength

was measured are from 84 to 241 K in the work by Wen

et al. and from 77 to 294 K in our experiment.

The simulation results, our experimental results,

and the results of Wen et al. are shown in Fig. 4. The

oscillation wavelength of the simulation is slightly

longer than those obtained by Wen et al. and with our

prototype QCL. The simulation results reproduce the

tendency that the wavelength increases with

increasing temperature. The change in wavelength

with the temperature (the tuning coefficient of the

wavelength) is as follows. The tuning coefficients are

0.58 nm/K in the simulation, 0.81 in the experiment

by Wen et al. and 0.50 nm/K in our experiment. The

tuning coefficients in the simulations are between that

obtained by Wen et al. and that obtained with our

QCL, and the temperature dependence of the QCL

oscillation wavelength can be well reproduced.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

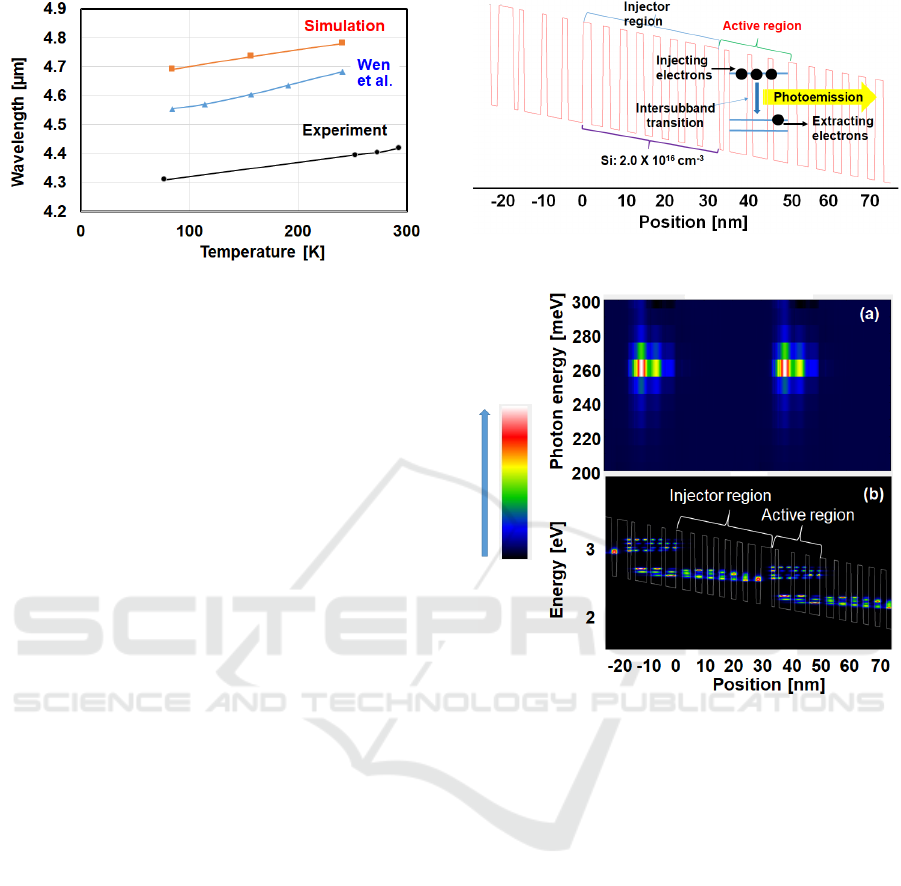
Figure 4: Wavelength dependence on operating

temperature.

3 HIGH QCL OUTPUT USING

SIMULATOR

3.1 Investigation of High Output by

Simulation

Since it was found that the wavelength can be

calculated accurately by our simulator as shown in

Sec 2.2, we attempted to design a high-power active

region for QCLs using this simulator. The design was

based on the structure shown in Fig. 5 (Evans et al.,

2007). The material is Ga

0.331

0.669

As for the wells

and Al

0.638

0.362

As for the barriers. In this structure,

one period consists of 22 layers, the injection region

is from the 1st to 14th layers, and the active region is

from the 15th to 22nd layers. The injection region is

doped with 2.0  10

−3

Si. Electrons are injected

from the injection region into the upper subband of

the active region, and they drop to the lower subband

through the intersubband transition. Photoemission

occurs at that time. This structure is denoted as

APL91. Many cases were calculated while adjusting

parameters related to net strain, calculation range, and

convergence condition.

Figure 6 shows the gain contour diagram and DOS

for APL91. The maximum gain of 91.33968 cm

-1

with

a photon energy of 260 meV (wavelength of 4.767 μm)

can be seen in the second well of the active region

(around the horizontal axis of -10, 40 nm) in the gain

contour diagram. Since the experimental wavelength is

4.705 μm, the calculated value is in good agreement

with the experimental one. In the DOS diagram, the

DOS is larger in the well next to the thick barrier of the

injection region. Electrons are injected from this well

into the active region. In addition, large values of DOS

are distributed in the upper and the lower subbands of

the active region. Strong luminescence is generated by

these DOS distributions.

Figure 5: Conduction band of APL91.

Figure 6: Gain contours (a) and density of states (b) of

APL91.

First, simulations with various parameters were

performed on the basis of physical considerations.

The film structure with the noticeable change in gain

was the structure in which the thicknesses of the

barriers in the active region were varied. The

calculated gains of this design are shown in Fig. 7.

When the barriers in the active region were made

thinner, the gain increased, and a maximum gain that

is 1.61 times that in APL91 was seen. On the other

hand, in the structures in which the thicknesses of

barriers are increased, the gains are lower than those

in APL91.

High outputs can be expected from “the structure

with thin barriers in the active region”, but if the

structure is markedly changed, fabricating the

prototype becomes difficult. Figure 8 shows the net

strain of the structures in which the barrier thicknesses

of the active region are varied. Since the net strain

increases as the thickness decreases, the wavelength

was calculated for a structure with 10 % thinner

barriers and a structure with 10 % thicker barriers.

Evaluation of Simulator Incorporating Non-equilibrium Green’s Function and Improvement of Quantum Cascade Lasers Output using the

Simulator

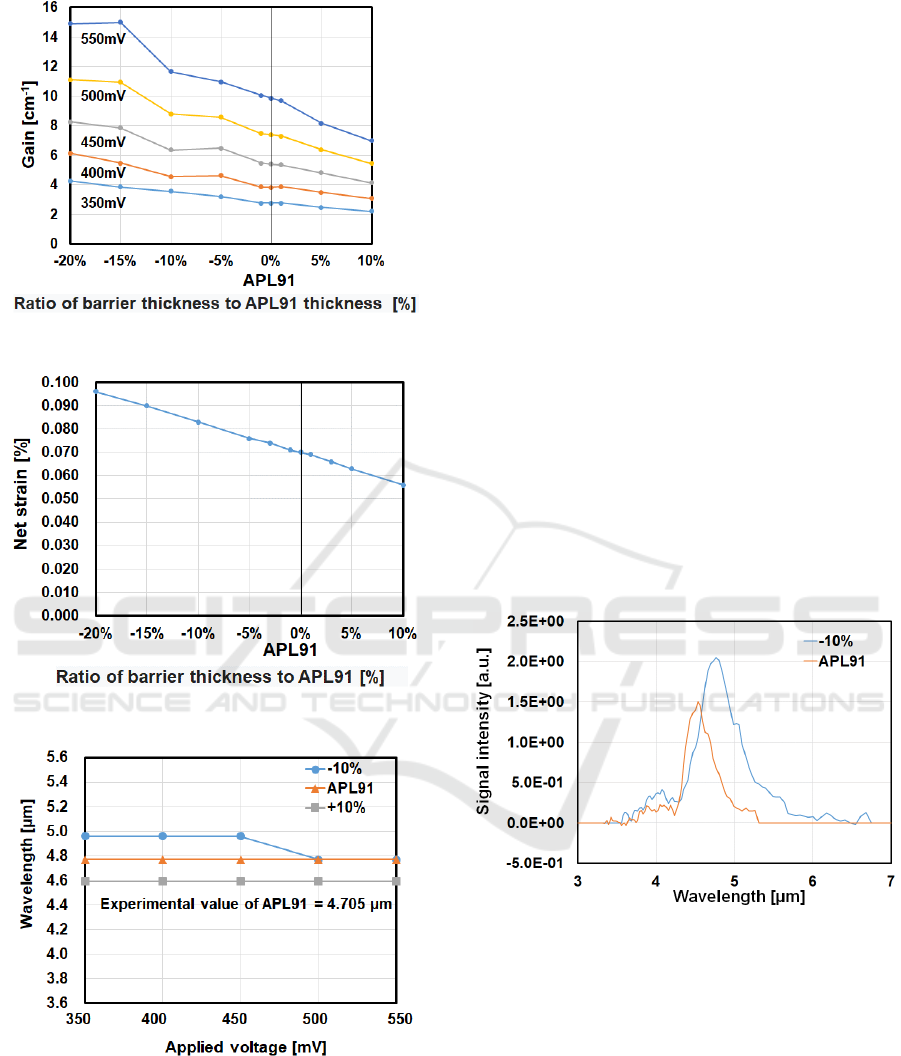
Figure 7: Dependence of gain on barrier film thickness.

Figure 8: Dependence of net stress on barrier film thickness.

Figure 9: Oscillation wavelength dependence on barrier

film thickness.

Figure 9 shows the calculated wavelengths. The

structure with 10% thinner barriers in the active

region had a slightly longer wavelength than APL91.

This is because the difference in energy between

quantum levels contributing to photoemission

became narrow owing to the decreased thickness of

the barriers. On the other hand, the wavelength was

shortened in the structure with 10% thicker barriers in

the active region, because the energy difference of the

quantum levels that contributes to photoemission

became wide with increasing thickness of the barriers

in the active region.

3.2 Characteristics of Laser Output

On the basis of calculation results, we fabricated

devices for measuring EL with 10 % thinner barriers

(10% device) in the active region. The device length

is 4 mm and the ridge width is 15 μm. The device is

mounted on an NS mount by In evaporation and flux

without a submount. The device was operated at a

frequency of 100 kHz, a pulse width of 300nm (duty

3%), and a cooling temperature of 273 K.

Figure 10 shows the EL spectra of the prototypes.

The horizontal axis represents wavelength and the

vertical axis represents EL intensity. Good emission

was observed in the 10 % EL device. The emission

wavelength is about 4.8 µm, which is in good

agreement with the calculated value in Fig. 9. We also

observed that the EL intensity of the 10 % device

was 1.4 times that of APL91.

Figure 10: EL spectra of APL91 and prototype with 10 %

thinner barriers.

4 CONCLUSIONS

We calculated the QCL wavelengths and the

temperature dependence of the wavelength with a

simulator using NEGF, and compared them with the

experimental results reported in the literatures and our

prototype QCLs. The difference between the

oscillation wavelength of QCL and the oscillation

wavelength obtained by the simulation was less than

0.36µm, and the wavelength dependences on the

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

active layer structure and the operating temperature

were in good agreement with those obtained in the

experiments in the references and those obtained with

our QCLs.

Furthermore, the active layer was designed to

increase the gain using a simulator, and it was shown

that the output could be improved by reducing the

barrier thicknesses in the active layer. We fabricated

QCLs with this structure and evaluated their output

wavelength and power. As a result, the EL emission

intensity was increased to 1.4 times that of the

previous structure QCL, and it was shown that the

simulator design method is effective for the structure

design of QCLs.

ACKNOWLEDGEMENTS

This work was supported by Innovative Science and

Technology Initiative for Security, ATLA, Japan.

REFERENCES

Faist, J., Capasso, F., Sivco, D. L., Sirtori, C., Hutchinson,

A., & Cho, A. Y. (1994). Quantum cascade laser.

Science, 264, 553–556.

Jirauschek, C., & Kubis, T. (2014). Modeling techniques

for quantum cascade lasers. Appl. Phys. Rev., 1, 011307.

Grange, T. (2015). Contrasting influence of charged

impurities on transport and gain in terahertz quantum

cascade lasers. Phys. Rev. B, 92, 241306–31–5.

Kirch, D., Chang, C.-C., Boyle, C., Mawst, L. J., Lindberg,

D., Earles, T., & Botez, D. (2015). Highly temperature

insensitive, low threshold-current density (λ = 8.7–8.8

μm) quantum cascade lasers. Appl. Phys. Lett., 106,

151106–1–5.

Yu, J. S., Slivken, S., & Razeghi, M. (2010). Injector

doping level-dependent continuous-wave operation of

InP-based QCLs at λ ~ 7.3 μm above room temperature.

Semicond. Sci. Technol., 25, 125015–1–5.

Wang, C. Y., Kuznetsova, L., Gkortsas, V. M., Diehl, L.,

Kärtner F. X., Belkin, M. A., Belyanin, A., Li, X., Ham,

D., Schneider, H., Grant, P., Song, C. Y., Haffouz, S.,

Wasilewski, Z. R., Liu, H. C., & Capasso, F. (2009).

Mode-locked pulses from mid-infrared quantum

cascade lasers. Opt. Express, 17 (15), 12929–12943.

Faist, J., Capasso, F., Sirtori, C., Sivco, D. L., Baillargeon,

J. N., Hutchinson, A. L., Chu, S. N. G., & Cho, A. Y.

(1996). High power mid-infrared (λ ~ 5 μm) quantum

cascade lasers operating above room temperature. Appl.

Phys. Lett., 68, 3680–3682.

Evans, A., Darvish, S. R., Slivken, S., Nguyen, J., Bai, Y.,

& Razeghi, M. (2007). Buried heterostructure quantum

cascade lasers with high continuous-wave wall plug

efficiency. Appl. Phys. Lett., 91, 071101–1–3.

Faist, J., Capasso, F., Sivco, D. L., Hutchinson, A. L., Chu,

S.-N. G., & Cho, A. Y. (1998). Short wavelength

quantum cascade laser based on strained compensated

InGaAs/AlInAs. Appl. Phys. Lett., 72, 680–682.

Aldukhayel, A., Jin, S. R., Marko, I. P., Zhang, S. Y., Revin,

D. G., Cockburn, J. W., & Sweeney, S. J. (2013).

Investigations of carrier scattering into L-valley in λ =

3.5 μm InGaAs/AlAs(Sb) quantum cascade lasers using

high hydrostatic pressure. Phys. Status Solidi B, 250

(4), 693–697.

Wen, Y., Quanyong, L., Wanfeng, L., Jinchuan, Z., Lijun,

W., Junqi, L., Lu, L., Fengqi, L., & Zhanguo, W.

(2011). Porous waveguide facilitated low divergence

quantum cascade laser. Semicond., 32 (6), 064008.

Evaluation of Simulator Incorporating Non-equilibrium Green’s Function and Improvement of Quantum Cascade Lasers Output using the

Simulator