One Step Ahead Optimal Control of a Single Echelon Supply Chain

using Mathematical Programming

Amit Bhaya

, Eugenius Kaszkurewicz

and Luiz Carlos de Barros Roth

COPPE, Federal University of Rio de Janeiro, PO Box 68504, Rio de Janeiro, Brazil

Keywords:

Supply Chain, Mathematical Programming, Optimal Control, Discrete-time Dynamical System.

Abstract:

A single echelon supply chain model problem, consisting of a store with known inventory and shipping ca-

pacities, a known delivery delay or lead time and a random demand for a product at the store is formulated

as an optimal control problem. In the practical case when only current and past demands are known, using

the concept of one step ahead optimal control, the problem is reformulated as the mathematical programming

problem of maximizing economic value added (EVA), subject to the dynamics and constraints, such as inven-

tory size. Illustrative examples are given and performance indices are proposed to evaluate the performance

of the proposed controller, which exhibits good efﬁciency and no bullwhip effect.

1 INTRODUCTION

(McGarvey and Hannon, 2004) describe a simple sup-

ply chain problem in the following terms: “One of

our most difﬁcult issues involves understanding the

complex way in which the world of the customer con-

nects with the world of retail business. The vagaries

of pleasing customers on the one hand while dealing

with suppliers on the other can sometimes seem over-

whelming. Charge too much or not have the article

in stock, and you may never see the customer again.

Order too much or too often, and you may run up the

inventory cost, causing proﬁts to vanish. This is a bal-

ancing act if ever there was one. How can you walk

that tightrope and survive? Reliance on mental mod-

els of a process fraught with randomness, feedbacks,

and delays makes the most astute of mental manage-

ment models unreliable.”

In this paper we will formulate the single echelon

supply chain control problem discussed in (McGar-

vey and Hannon, 2004, p.179-187) as an optimal

control problem, when the demand is known over the

entire planning horizon and then propose feedback

controllers for unknown demands, based on this

approach. There is a large and ever-growing literature

on control of supply chains and a brief review is given

https://orcid.org/0000-0002-3144-1242

https://orcid.org/0000-0001-5471-9596

https://orcid.org/0000-0002-0481-4728

in the following section, focusing only on the papers

most relevant to the approach proposed here.

1.1 Literature Review

(Ivanov et al., 2018) in their recent survey write

“Modern production and logistics systems, supply

chains, and Industry 4.0 networks are challenged by

increased uncertainty and risks, multiple feedback cy-

cles, and dynamics. Control theory is an interesting

research avenue which contributes to further insights

concerning the management of the given challenges

in operations and supply chain management.” They

also identify one of the main contributions of control

theory as being the application of dynamic feedback

control to production-inventory systems and point out

that a wide range of control-theoretic tools have been

used in this context, ranging from the classical PID

control to model predictive control. We also point

the reader to the recent survey (Lin et al., 2017) on

control-theoretic approaches to the inventory control

problem.

In the speciﬁc area of feedback control of a sup-

ply chain, based on a state model of its dynamics,

most of the literature has been devoted to models that

apply standard control ideas such as set point con-

trol, which involves choosing set points or targets for

system variables, such as inventory level. These ap-

proaches can be viewed as parametrized versions of

several standard algorithms from the SCM literature,

such as order-up-to-inventory control. A large class of

Bhaya, A., Kaszkurewicz, E. and Roth, L.

One Step Ahead Optimal Control of a Single Echelon Supply Chain using Mathematical Programming.

DOI: 10.5220/0009130702330240

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 233-240

ISBN: 978-989-758-396-4; ISSN: 2184-4372

233

such controllers is known by the acronym IOBPCS,

which stands for inventory and order based produc-

tion control system. Various preﬁxes, such as AP (for

automatic pipeline) and MP (for matched parameter)

identify variants of the basic IOBPCS scheme. Papers

in this area also assume linear models and study the

effect of the controller on the bullwhip effect and on

stability with regard to, for example, step changes in

the demand: see, for example, (Lin et al., 2019; Lin

and Naim, 2019; Hoberg et al., 2007).

The model predictive control (MPC) approach

uses a model of the real plant, as well as past and cur-

rent system data to successively predict on some hori-

zon; optimize some suitable performance index, on

a (possibly different) horizon, using the predictions;

and, ﬁnally, apply one or more of the computed op-

timal controls to the plant, before beginning a new

predict-optimize-control sequence. For examples of

this approach, see (Wang et al., 2007) and references

therein. If the performance index takes economic fac-

tors into account, the MPC approach is referred to as

economic MPC and a recent example in the supply

chain context is (Subramanian et al., 2014).

This paper uses an approach that is related to the

MPC approach; however, it uses only past values of

the demand and system state, does not use a predic-

tor, and uses a stage cost that is economic: it is the

so called Economic Value Added (EVA) performance

index, commonly used in the business and ﬁnancial

world (McGarvey and Hannon, 2004). The main idea,

which can be described by the term greedy control

(Lavretsky, 2000), is to optimize EVA using past de-

mands, for just one step ahead of the current time, ap-

ply this optimal control to the system, update its state

and repeat the cycle of one step ahead optimization

of EVA, until the end of the horizon. Note that the

control scheme just described is set up to compute an

ordering decision (or control) in real time, although it

can also be used in a planning mode. The main differ-

ences between the approach of this paper and existing

results are as follows: (i) an economic stage cost func-

tion is used, similar to the one in (Subramanian et al.,

2014), but also including discounting of the proﬁt to

its present value and not including any target or track-

ing costs, (ii) using only past demands and the current

demand to compute the present value of the control,

not involving any prediction, in contrast with (Wang

et al., 2007). The result is a real-time control that is

computationally cheap and, as will be shown, efﬁcient

when compared with the globally optimal omniscient

control, which will be deﬁned in the sequel.

2 DISCRETE-TIME SUPPLY

CHAIN DYNAMICS

The supply chain considered in this paper is that of a

store, the example being taken from (McGarvey and

Hannon, 2004). It has two main components: a de-

lay between ordering and receiving, corresponding to

a block named conveyor or pipeline and an accumu-

lator, which receives the ordered items after the stip-

ulated delay, corresponding to the store. Selling of

items in the store occurs in accordance with the de-

mand and it is assumed that all but w items (the ones

in the display windows) in the store can be sold. The

store manager’s objective is to choose an ordering se-

quence, in response to the demand, that maximizes

cumulative proﬁt over a given time horizon, assuming

that there are costs associated to handling, shipping,

storage and shortage (being out-of-stock affects sales

negatively, since customers are turned away). Finally,

proﬁts (=sales revenues minus costs) are discounted

using a ﬁxed interest rate and then added over the

given horizon to obtain the cumulative proﬁt, referred

to as economic value added (EVA). The following

notation will be used to formulate the mathematical

model.

– k: discrete time counter.

– x

(k): quantity of items in the ith stage of shipping,

i = 1,...,D, where i = 1 corresponds to receiving and

i = D + 1 to ordering.

– D: delay between receiving and ordering.

– s

(k): stock level in store at discrete time instant k.

– d(k): customer demand at store at time k.

– s

(k): sales (selling) at time k.

– p: price per unit of material sold.

– w: quantity of items to be displayed in the store win-

dow (and not sold), also called display stock.

– c

(k): out-of-stock cost at time k.

– α

(k): out-of-stock cost per unit of demand not met

at time k.

– c

(k): handling cost at time k.

– α

: handling cost per unit of material handled.

– c

(k): cost of maintaining stock level in store at

time k.

– α

: storage cost per unit of material stored.

– c

(k): shipping cost of material in transit.

– α

: shipping cost per unit of material being

shipped.

– c

(k): total cost at time k.

– d

(k): discounted proﬁt at time k.

– ρ: discount rate.

– L(k): cumulative proﬁt at time k.

– K

: horizon over which cumulative proﬁt is to be

maximized.

The delay between ordering and receiving is writ-

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

234

ten by introducing a string of D one unit delays as

follows:

(k + 1) = x

i+1

(k), i = 1,...,D (1)

D+1

(k) = o(k) (2)

Thus the quantity of material in transit (i.e., being

shipped) at time k, denoted by s

(k), can be written

as:

(k) =

∑

i=1

(k), (3)

while the quantity of material being received at the

store is x

(k) and corresponds to an order placed D

time units in the past, so that the variable ordering,

denoted o(k) is just x

D+1

(k).

Evolution of the stock level in the store at time

k is determined by the quantity of material being re-

ceived (x

(k)) plus the quantity currently in the store

(k) (setting aside a quantity w to be put in the display

window and not sold) less the quantity sold (s

(k)) in

response to the demand. The corresponding equation

is as follows.

(k + 1) = s

(k) − w + x

(k) − s

(k) (4)

In order to describe the sales s

(k) at time k, observe

that sales can only occur if the store level s

(k) plus

the received material x

(k) less the quantity in the dis-

play window w is greater than the demand d(k). Thus

sales can be written as follows:

(k) = d(k) + min{0, s

(k) − w + x

(k) − d(k)}. (5)

Thus the quantity of sales matches the demand d(k) if

it is less than the effective available store level s

(k) −

w + x

(k), otherwise it is just equal to the latter.

The costs are expressed as follows:

(k) = α

(d(k) − s

(k)) (out of stock cost) (6)

(k) = α

(k) (storage cost) (7)

(k) = α

(k) + o(k)) (handling cost) (8)

(k) = α

∑

i=1

(k) (shipping cost) (9)

(k) = c

(k) + c

(k) (total cost)

(10)

Discounted proﬁt is the revenue from sales less the

total cost (all at time k), appropriately discounted:

(k) = (ps

(k) − c

(k))e

−ρk

. (11)

The cumulative proﬁt L(k) accumulates the dis-

counted proﬁt:

L(k + 1) = L(k) + d

(k). (12)

The objective function is simply the cumulative proﬁt

at the end of the time horizon and thus, given the de-

mand d(k),k = 1,...,K

− 1 over the whole plan-

ning horizon, the optimization problem to be solved

is an optimal control problem, which will be referred

to as the omniscient optimal control problem (since

the demand over the entire planning horizon is as-

sumed to be known), and can be written as follows:

max

{o(k)}

−1

k=1

L(K

) (13)

In optimal control terminology, this is a problem of

choosing an optimal ordering sequence that maxi-

mizes the ﬁnal cumulative proﬁt L(K

). More real-

istically, the following constraints are also needed:

o(k) ≥ 0, k = 1, ...,K

− 1 (14)

(k) ≤ C

max ship

, k = 1,...,K

− 1 (15)

(k) ≤ C

max store

, k = 1,...,K

− 1 (16)

For future reference, the state vector of the supply

chain at instant k is denoted as z(k) and deﬁned as:

z(k) = [x

(k), ...,x

(k), s

(k)] (17)

3 ONE STEP AHEAD OPTIMAL

CONTROL

In practice, of course, only current and past demands

are known to the supply chain manager, who has to

make the ordering decision based on this information

and observation of the current variables, such as in-

ventory or store level, amount of goods in the ship-

ping pipeline, sales levels, etc. This section formu-

lates the so called one step ahead optimal control

(OSAOC) problem that respects this practical infor-

mation constraint.

Given the delay D between ordering and receiv-

ing, it is clear that, at time instant k, the value

of the objective function L(k + 1) (the cumulative

proﬁt) at the next time instant k + 1 is dictated by

the ordering o(k − D). This means that, since the

past demands and the current demand are assumed

known, one can optimize over the backward hori-

zon {k − D, k − D + 1,...,,k} (the past), to obtain the

optimal sequence {o

∗

(i)}

i=k−D

, assuming the state

z(k) = [x

(k), ...,x

(k), s

(k)] to be given. Note that,

from (1)-(2), the state z(k) can also be expressed as

z(k) = [o(k − D),...,o(k − 1),s

(k)]. Thus, after the

optimization step is carried out, the state is updated to

z(k + 1) = [o(k − D + 1), ...,o

∗

(k), s

(k + 1)], intro-

ducing only the current input and discarding the older

ones, which are given and cannot be changed. Now

a new optimization step can be carried out, from this

One Step Ahead Optimal Control of a Single Echelon Supply Chain using Mathematical Programming

235

new initial condition. In other words, at each step k,

although the entire vector {o

∗

(i)}

i=k−D

is determined,

only the ﬁrst element of the sequence o

∗

(k) is used: it

is injected into the sytem state and its effect on the ob-

jective function is only observed D instants later. The

OSAOC problem just described is denoted OS(z(k))

and written formally as follows:

max

{o(i)}

i=k−D

L(k + 1)

subject to (1)-(12)

and z(k) = [x

(k), ...,x

(k), s

(k)] (speciﬁed i.c.)

(18)

Let the optimal control computed as the solution

to (18) be denoted as follows:

∗

(k − D),...,o

∗

(k)] := argmax

{o(i)}

i=k−D

L(k + 1)

(19)

With this notation in place, the iterative one step

ahead control (OSAOC) scheme can be written as

shown (Algorithm 1):

Algorithm 1: One step Ahead Optimal Control (OSAOC).

1: Initial state z

:= z(k

), k

= D given

2: while D ≤ k ≤ K

− 1 do

3: z(k) := z

= [o(k − D),..., o(k −1),s

(k)]

4: solve OS(z(k)) defined in (18)

5: to get [o

∗

(k − D);...;o

∗

(k)]

6: z

← [o(k − D + 1),...,o

∗

(k), s

(k + 1)]

7: k ← k + 1

8: end while

Remark: Algorithm 1 bears a resemblance to a model

predictive control (MPC) scheme. Note, however,

that it relies only on past values of the demand and

uses no prediction.

4 IMPLEMENTATION OF THE

ALGORITHM

The MATLAB implementation uses the Optimization

Toolbox, which is set up to carry out black box opti-

mization of a function, using interior-point, sequential

quadratic programming (SQP) and active set meth-

ods, amongst others. The black box in question is

the system model (1)-(5) of the supply chain dynam-

ics. In the examples presented in Sec. 5, the MAT-

LAB Optimization Toolbox fmincon command was

used to optimize, with the algorithm being chosen as

interior point.

5 SIMULATION EXAMPLES

In this section, an example of a simple demand curve

is ﬁrst given to highlight the differences between om-

niscient and one step ahead optimal control. This is

followed by a more realistic example of a demand

generated from a Poisson distribution. In all cases,

the comparison is between the ﬁnal value of the cu-

mulative proﬁt attained by the OSAOC (L

OSA

) and

the omniscient control (L

omni

) for the same demand

sequence. The ratio between L

OSA

omni

is referred

to as the efﬁciency η.

5.1 Demand with Step Change

The simple demand used to illustrate the differences

in behavior between the omniscient and OSAO con-

trol is constant, with one step change. The parame-

ters used in the simulation are as follows: α

= 20,

= 5, α

= 10, α

= 5, p = 100, ρ = 0.005,

max store

= 30, C

max ship

= 50, s

(0) = 10, D = 7,

= 37, s

(0) = 0. Finally the demand is as fol-

lows: constant at value 4 from k = 0 to k = 20, after

which a step change to the value 6 occurs. The cumu-

lative proﬁts L

OSA

and L

omni

attained by the OSAOC

and omniscient algorithms at the end of a 30 day

period are, respectively, 7288.7 and 8605.9, so that

the OSAOC achieves an efﬁciency η = 84.6%, with

respect to the globally optimum (omniscient) result.

Figures 1 to 3 show the main results for the demand

with step change and their captions provide additional

details and observations.

5.2 Demand with Poisson Distribution

Experiments in this subsection are carried out with

a demand d that has a Poisson distribution with

λ = 1 shifted by 1 (to eliminate demands equal to

zero), generated by the MATLAB command d =

poissrnd(1,37,1)+1. The parameters used in the

simulation are as follows: α

= 20, α

= 5, α

10, α

= 5, p = 100, ρ = 0.005, C

max store

= 30,

max ship

= 50, s

(0) = 10, D = 7, K

= 37, s

(0) = 0.

The cumulative proﬁts L

OSA

and L

omni

attained by the

OSAOC and omniscient algorithms at the end of a

30 day period are, respectively, 2107.6 and 2598.6,

so that the OSAOC achieves an efﬁciency η = 81.1%

with respect to the globally optimum (omniscient) re-

sult. Figures 4 to 9 show the main results for the Pois-

son demand and their captions provide additional de-

tails and observations.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

236

5.3 Comparison of Average

Performance of OSAOC versus

Omniscient Control

Ten samples each of Poisson and uniformly dis-

tributed demands were generated and the average ef-

ﬁciency (resp. standard deviation) were found to be

78.25%(3.28%) (Poisson) and 73.52%(5.77%) (uni-

form).

The coefﬁcient of variation is a measure of relative

variability, deﬁned as the ratio of the standard devia-

tion to the mean of the variable under consideration.

Thus, a measure of ampliﬁcation of demand variabil-

ity, also known as bullwhip, is the ratio of the coef-

ﬁcients of variation of the ordering and the demand,

and is denoted B

, where the subscript od refers to

the ratio being calculated and the superscript x can be

os (resp. om) for one step (resp.omniscient). A related

measure is the ratio of the coefﬁcients of variation of

the inventory (store) level and the demand, denoted

std

. For the Poisson demand of sec. 5.2, the calcu-

lations, carried out over the interval [D,K

− D] so as

to exclude both initial transient due to pipeline ini-

tialization, and ﬁnal transient due to the turnpike ef-

fect for the omniscient case, yield: B

= 0.43,B

std

0.32,B

= 0.70,B

std

= 0.28. Since all these mea-

sures are less than unity, the conclusion is that the

proposed one step ahead controller does not cause

ampliﬁcation of the demand uncertainty. This should

be contrasted with the behavior of controllers of the

IOBPCS family (Lin and Naim, 2019) and the MPC

family with targets (Subramanian et al., 2014).

6 CONCLUDING REMARKS

This paper proposed a one step ahead optimal control

scheme for a single echelon supply chain that does

not require prediction but only the solution of a low-

dimensional (in terms of the number of decision vari-

ables) optimization problem at each time step, thus

being perfectly adequate for real time supply chain

control. This one step ahead or greedy control is

shown to be quite efﬁcient, attaining, for Poisson or

uniformly distributed demands, at least 70% of the

(unattainable) omniscient global optimum. In addi-

tion, experiments show that the proposed OSAO con-

trol scheme does not cause ampliﬁcation of the de-

mand uncertainty or bullwhip, which is attributable to

the fact that no target levels for inventory or pipeline

are used. Another important observation is that the

model (1)-(12), with the exception of (5), consists

of linear equations. It is easy to write (5) in piece-

wise linear form, which means that both the omni-

scient (13) and OSAOC optimization problems (18)

can be rewritten as linear programming problems,

which, from a computational viewpoint, implies that

the simple examples in Sec. 5, can easily be scaled to

much larger dimension. It should also be noted that a

large number of supply chain problems, including the

multi-echelon case, are described by linear or piece-

wise linear dynamics. Thus, the proposed scheme is

scalable and can: (i) be generalized to large multi-

echelon supply chains, which will be the subject of fu-

ture work, and (ii) used in a planning mode, to choose

inventory size, shipping capacity requirements and

prices that ensure proﬁt margins, since these choices

can be recast as feasibility problems. This is also the

subject of ongoing work, to be reported in a future

version of this paper.

REFERENCES

Hoberg, K., Bradley, J. R., and Thonemann, U. W. (2007).

Analyzing the effect of the inventory policy on or-

der and inventory variability with linear control the-

ory. European Journal of Operational Research,

176:1620–1642.

Ivanov, D., Sethi, S., Dolgui, A., and Sokolov, B. (2018).

A survey on control theory applications to operational

systems, supply chain management, and industry 4.0.

Annual Reviews in Control.

Lavretsky, E. (2000). Greedy optimal control. In Amer-

ican Control Conference (ACC), pages 3888–3892,

Chicago,IL.

Lin, J. and Naim, M. (2019). Why do nonlinearities

matter? the repercussions of linear assumptions

on the dynamic behaviour of assemble-to-order sys-

tems. International Journal of Production Research,

57(20):6424–6451.

Lin, J., Naim, M., Purvis, L., and Gosling, J. (2017). The

extension and exploitation of the inventory and order

based production control system archetype from 1982

to 2015. International Journal of Production Eco-

nomics, 194:135–152.

Lin, J., Naim, M., and Spiegler, V. (2019). Delivery time

dynamics in an assemble-to-order inventory and order

based production control system. International Jour-

nal of Production Economics.

McGarvey, B. and Hannon, B. (2004). Dynamic Modeling

for Business Management: An Introduction. Springer,

New York.

Subramanian, K., Rawlings, J. B., and Maravelias, C. T.

(2014). Economic model predictive control for inven-

tory management in supply chains. Computers and

Chemical Engineering, 64:71–80.

Wang, W.-L., Rivera, D. E., and Kempf, K. G. (2007).

Model predictive control strategies for supply chain

management in semiconductor manufacturing. Int. J.

Production Economics, 107:56–77.

One Step Ahead Optimal Control of a Single Echelon Supply Chain using Mathematical Programming

237

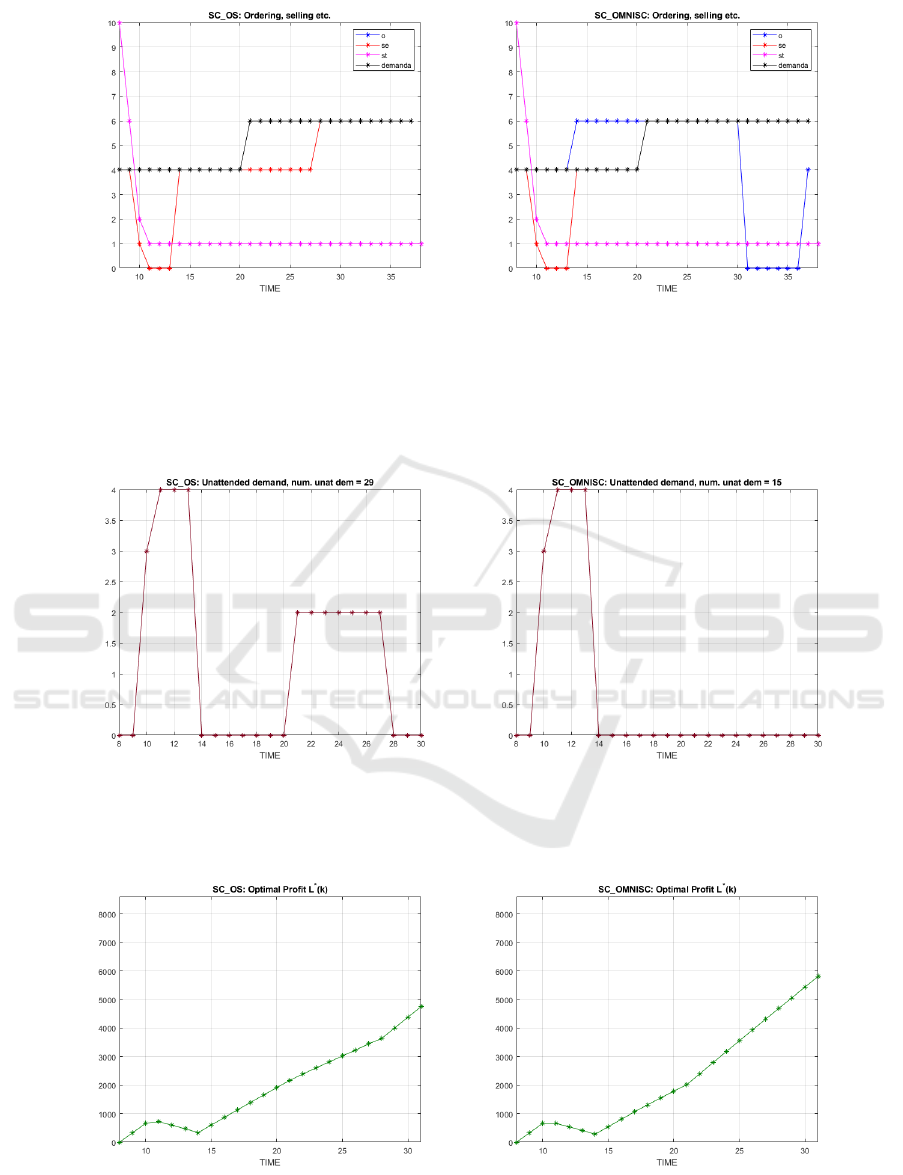
Figure 1: Showing ordering and selling over the horizon k = 0 to k = K

= 37, with a step increase in the constant demand at

k = 20: OSAOC (left), omniscient control (right). Note the turnpike effect for omniscient control over the horizon k

= 37,

with the ordering dropping to zero D instants before the end of the horizon is reached, because the demand will be met with

the orders in the pipeline. For this reason, all simulation examples are run till K

= 37, but the efﬁciency η is calculated

at k = 30 (in order to exclude the turnpike effect). Also note that, the omniscient control, with complete knowledge of the

demand, anticipates ordering in order to meet the demand perfectly, given a sufﬁciently large initial inventory, and maintains

the inventory at the minimum, which is the speciﬁed display stock of 1, thus operating in just-in-time mode.

Figure 2: Showing lost sales: OSAOC (left) and omniscient control (right), until k = 30. Observe that both controllers lead

to lost sales in the initial segment, between k = 9 and k = 14, because the pipeline is initially empty. However, the OSAO

controller also results in lost sales when the step increase in demand occurs, since it is causal (non-anticipative) and this, of

course, does not occur with the omniscient noncausal controller, which is able to anticipate the future demand.

Figure 3: Showing evolution of cumulative proﬁt: OSAOC (left), omniscient control (right), with the OSAO controller

attaining an efﬁciency η = L

OSA

omni

= 84.6%. Note that, after the end of the transient caused by the zero initial pipeline

(0) = 0), the cumulative proﬁt curve is monotonically increasing.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

238

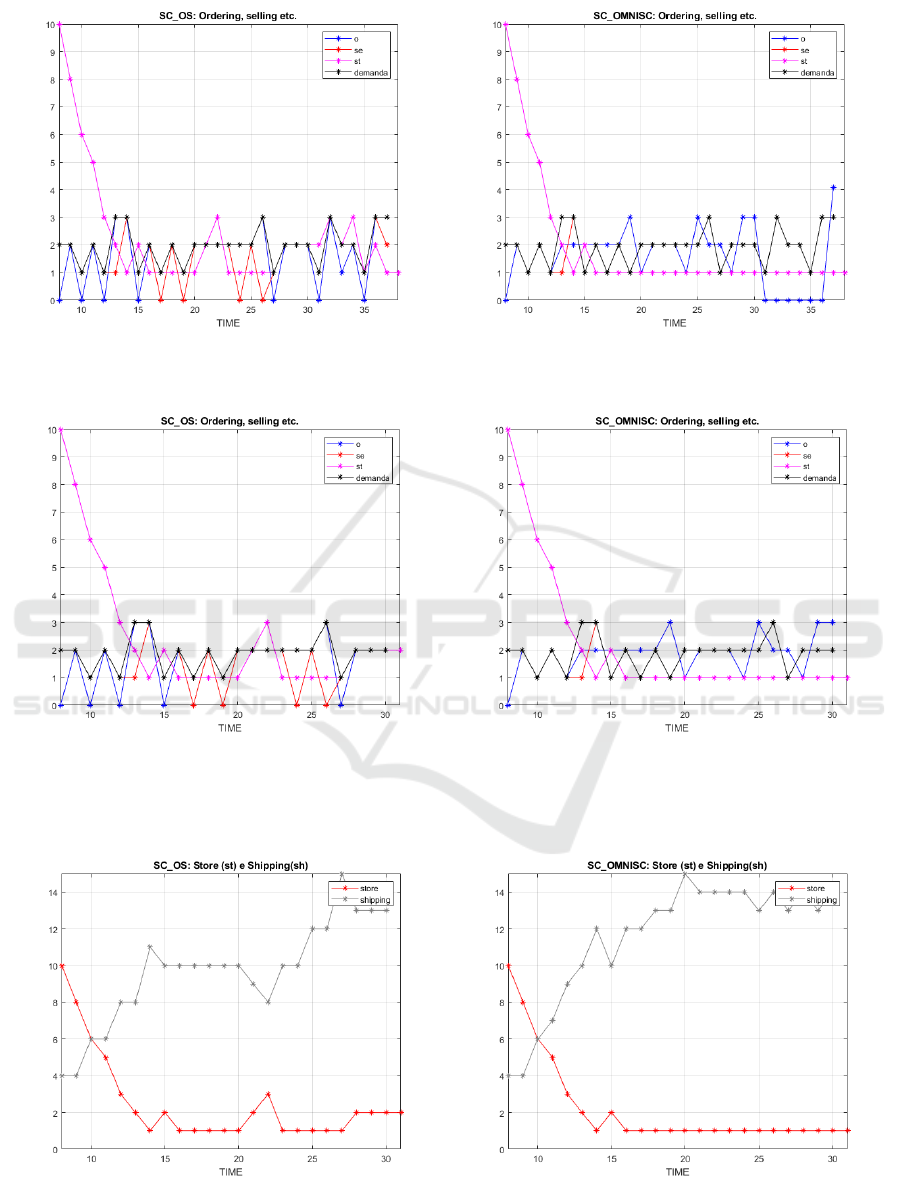
Figure 4: Showing the evolution of ordering, selling, store for a Poisson demand: OSAOC (left), omniscient (right) for the

horizon k = 0 to k = K

= 37, with the turnpike effect for the omniscient control starting from k = 30.

Figure 5: Showing the evolution of ordering, selling, store variables for a Poisson demand, with the graphs plotted from

instant k = 8 to k = 30, in order to start from the ﬁrst computed ordering, assuming that demands from k = 1 to k = 7 are used

as the initial past demands, and also, for purposes of comparison, truncating the horizon at k = 30 to avoid the turnpike effect,

which occurs at the end of the horizon, for the omniscient case: OSAOC (left), omniscient (right).

Figure 6: Showing the evolution of the store and shipping variables, for a Poisson demand, for a 30 day period: OSAOC (left),

omniscient (right). Note that, after the initial transient (i.e., k ≥ 16), the OSAOC is not able keep the inventory level at the

minimum, which is the speciﬁed display stock of 1, unlike the anticipative omniscient controller.

One Step Ahead Optimal Control of a Single Echelon Supply Chain using Mathematical Programming

239

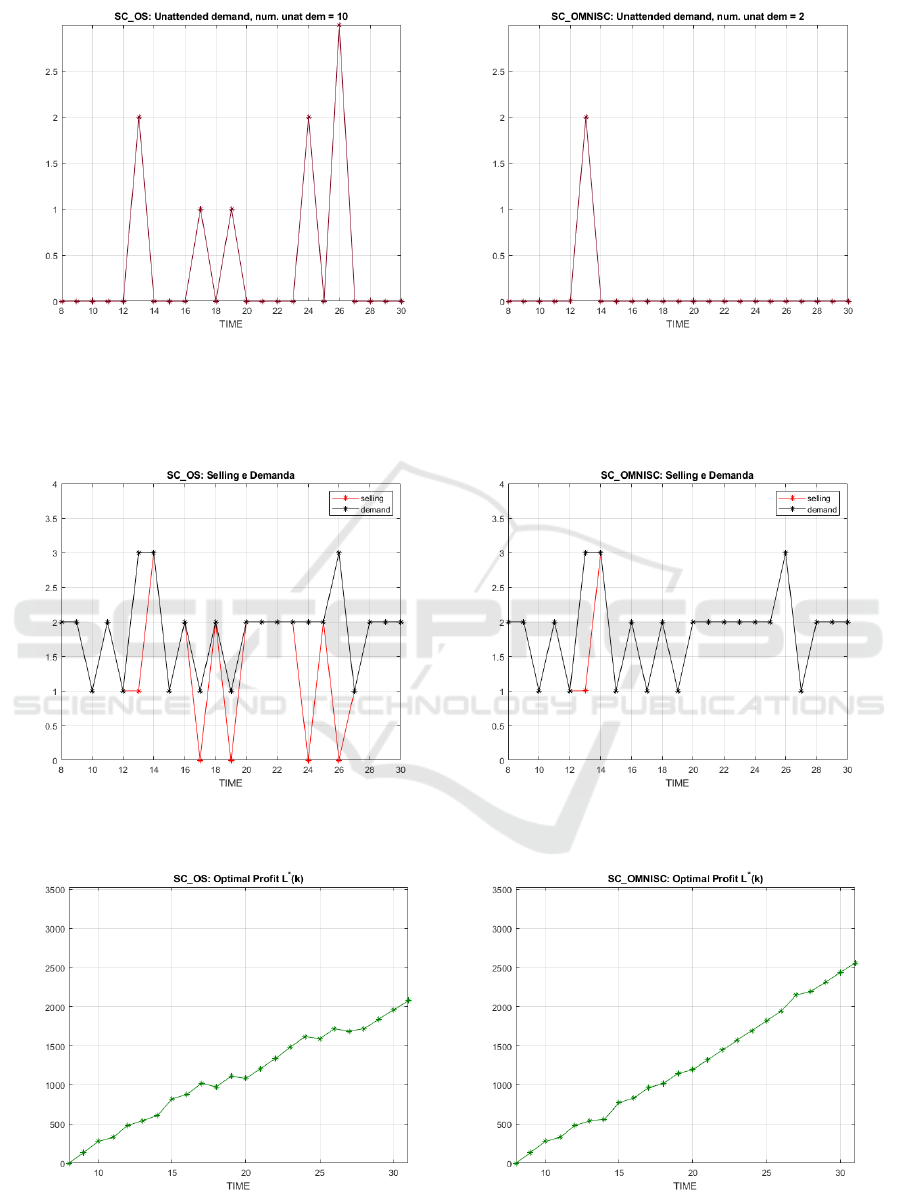
Figure 7: Showing the evolution of lost sales, for a Poisson demand: OSAOC (left), omniscient (right). Note that, lost sales

occur at k = 17, 19,24,26 only for OSAOC after the initial transient, but not for the omniscient controller. This means that,

in Figure 6, the OSAOC is at minimum store level at these instants, since it is unable to meet the demand. In contrast, the

omniscient controller, also at the minimum store level, is meeting demand with the orders being received, in the just-in-time

mode.

Figure 8: Showing the evolution of selling for a Poisson demand: OSAOC (left), omniscient (right). Note that, after the initial

transient, the omniscient selling matches the demand perfectly, operating, as explained in the caption to Fig. 7.

Figure 9: Showing the evolution of the cumulative discounted proﬁt (EVA): OSAOC (left), omniscient (right), with the OSAO

controller attaining an efﬁciency η = L

OSA

omni

= 81.1%. Despite the zero initial pipeline, the initial store level is able to

meet the initial demands during the lead time of D = 7.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

240