Securing Industrial Production from Sophisticated Cyberattacks

Andrew Sundstrom

, Damas Limoge

, Vadim Pinskiy

and Matthew Putman

Nanotronics Imaging, Brooklyn, NY, U.S.A.

Keywords:

Cyberattack, Malicious Attack, Man-in-the-Middle, Stuxnet, Statistical Process Control, Machine Learning,

Artiﬁcial Intelligence, Innovation Error, Deep Reinforcement Learning.

Abstract:

Sophisticated industrial cyberattacks focus on machine level operating systems to introduce process variations

that are undetected by conventional process control, but over time, are detrimental to the system. We pro-

pose a novel approach to industrial security, by treating suspect malicious activity as a process variation and

correcting for it by actively tuning the operating parameters of the system. As threats to industrial systems

increase in number and sophistication, conventional security methods need to be overlaid with advances in

process control to reinforce the system as a whole.

1 INTRODUCTION

The past 30 years of cyberattacks have witnessed a

startling degree of proliferation, adaptation, speci-

ﬁcity, and sophistication

(see Figure 1). Industrial

and military security is the study of walls, physi-

cal and digital, which limit malicious insertion or re-

moval of information. For high-security factories and

military installations, this means creating systems that

are removed from the global computer network and

often removed from internal networks. Minuteman

ICBM silos, for example, are entirely isolated sys-

tems whose launch protocols are seldom updated and

whose launch directives are delivered over the Strate-

gic Automated Command and Control System

—

both protocol and directive systems have relied

3,4

, un-

til recently

5,6

, on data stored on 8-inch ﬂoppy disks,

employing an effective combination of network iso-

lation, obsolete IBM Series/1 computing hardware,

and low-capacity digital media that is too small for

a sophisticated modern cyberattack with a large code

footprint. Factory systems (e.g. PLC (Laughton and

https://orcid.org/0000-0002-3378-4513

https://orcid.org/0000-0002-4963-0500

https://orcid.org/0000-0002-5899-1172

https://orcid.org/0000-0002-1045-1441

https://bit.ly/36BjOkt

https://bit.ly/3041w91

https://bit.ly/2tDxtZE

https://wapo.st/2FvgNGp

https://bit.ly/2QXUJJR

https://nyti.ms/2QAojWP

Warne, 2003) and SCADA (Boyer, 2009)) operate on

static code that has been validated and is assumed to

be immutable, if not by foreign manipulation. In this

study, we focus on an industrial setting to describe our

approach.

Although computer methods can be used for vali-

dation and security veriﬁcation prior to deployment,

the actual evidence of malicious code installation

comes from in-ﬁeld testing of the entire production

line. If malicious code is installed, conventional the-

ory says its effects should manifest themselves in the

overall yield of the production line. This method of

statistical detection is typically successful in catch-

ing direct cyberattacks on single nodes, but it fails

against more sophisticated, systemic cyberattacks.

The best known example of the new breed of so-

phisticated cyberattacks

7,8

is Stuxnet

(Karnouskos,

2011), which surfaced in 2010

. The effects on the

centrifuges infected by Stuxnet were not statistically

signiﬁcant with respect to expected baseline behavior,

and so each piece of hardware passed nominal Statis-

tical Process Control (SPC) standards. Even if one

machine—a single node—starts to behave atypically,

https://bit.ly/39P5gQ9

https://bit.ly/2s6iaIt

https://bit.ly/36zw056

For a detailed account, refer to the Repository of Indus-

trial Security Incidents (RISI) database, which records “in-

cidents of a cyber security nature that have (or could have)

affected process control, industrial automation or Super-

visory Control and Data Acquisition (SCADA) systems.”

https://www.risidata.com/

Sundstrom, A., Limoge, D., Pinskiy, V. and Putman, M.

Securing Industrial Production from Sophisticated Cyberattacks.

DOI: 10.5220/0009148206630670

In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 663-670

ISBN: 978-989-758-399-5; ISSN: 2184-4356

663

the effects would manifest in the outputs of that node,

measured against historical averages, and the machine

would be immediately taken ofﬂine, before the entire

process can be affected or before other machines can

be similarly infected.

In sophisticated modern cyberattacks, however,

SPC is ill-suited to detect subtle changes in the op-

eration of many system elements, which individu-

ally have small changes, and are thus undetected,

but when integrated over time, have major and often

catastrophic effects on the entire system. To counter

this vulnerability, we propose several methods for de-

tection or correction, based on learning distributions

of the system and identifying anomalous behavior. In

the corrective case, an agent continuously runs the

feedback and feed-forward controls of the system, si-

multaneously correcting for nominal process varia-

tions (e.g. those that occur as a result of process or

raw material quality ﬂuctuations) and preventing ma-

licious cyberattacks.

Figure 1: The growth in the number of distinct cyberattacks

in the past 30 years, as depicted by Kaspersky Labs.

2 STATISTICAL PROCESS

CONTROL

Statistical Process Control (SPC), as popularized by

William Edwards Deming in post-war Japan (Dem-

ing and Renmei, 1951), (Deming, 1986), (Denton,

1991), (Delsanter, 1992), calls for process standards

to be established for each step in the manufacturing

process and monitored throughout the production life

cycle. The goal is to continuously improve the pro-

cess through the life cycle.

It is assumed that as long as each node is oper-

ating within speciﬁcation, the ﬁnal product will also

be within speciﬁcation. The speciﬁcations are set

based on subject matter expertise and historical per-

formance. The dependability and impact of one node

onto the next or subsequent nodes is not directly ad-

justed in SPC, but rather, each sub-process is exam-

ined as an independent entity. This leads to wider

margins for the operating condition of each node, pre-

venting the system from ever operating in the absolute

highest efﬁciency or stability.

From a security perspective, this margin can be

targeted by sophisticated process cyberattacks. If a

single node or several nodes in a system start to op-

erate at the upper bounds (or lower bounds) of their

speciﬁcation, individual alarms will not be triggered,

but the overall process quality will be affected. This

especially holds for man-in-the-middle cyberattacks,

where reported sensor signals, for example, are faked

by the malicious code. The life cycle of the node will

also be affected, requiring increased downtime for re-

pair. Several layers of downstream nodes will also be

affected and over time, the continual drift of the sys-

tem will tend toward non-compliance. By that point,

the correction needed to recover the system would be

massive and cost-prohibitive.

3 A MATHEMATICAL MODEL

OF PROCESS CONTROL

DISRUPTION

A factory can be deﬁned using to a wide variety of

topological schemes, including feedback and feed-

forward organization. Here we give a simple model

of a factory, offering just enough complexity to facili-

tate a rigorous presentation of the approaches outlined

below, which can operate on system topologies of ar-

bitrary complexity.

Accordingly, we deﬁne a factory, F, as a strictly

linear sequence of n processing nodes, labeled

1,...,n, connected in a forward-linked chain.

F :→ 1 →2 →···→i → ···→ n

The processing done by each node i has two at-

tribute distributions, an expected distribution, Q

, and

an observed distribution, P

. Q

is characterized by µ

and σ

. If Q

= N(µ

,σ

), then Q

is completely

characterized. P

is characterized by µ

and σ

. If

= N(µ

,σ

), then P

is completely characterized.

We deﬁne the damage caused by node i to be the

Kullback–Leibler divergence (Kullback and Leibler,

1951), (Kullback, 1959) of P

with respect to Q

= D

||Q

) =

∑

x∈χ

(x)log



(x)



. (1)

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

664

For this simple, illustrative model, we assume

damage is cumulative, more speciﬁcally additive,

across F, and so

∑

i=1

. (2)

Consider the Statistical Process Control (SPC)

protocol, which uses µ

and σ

to determine if pro-

cessing at node i is in or out of control on the basis of

whether x ∈P

falls within µ

±3σ

Now consider two adversarial cases for node i,

where Q

= N(µ

,σ

) and P

= N(µ

,σ

• Case 1 (max-burn): µ

= µ

+ 3σ

− ε

and

• Case 2 (min-burn): µ

= µ

−3σ

+ε

and σ

By setting σ

, we ensure 99.99943% of the

observed events stay in control.

This gives a deﬁnition of SPC satisfaction:

SPCSAT = 1(

∑

i=1

1({x :x ∈ P

±5σ

and

x 6∈Q

±3σ

} = ∅) > τ

(3)

for some ratio τ

∈(0, 1], typically 1, meaning the pro-

cessing of all nodes 1,...,n is in control.

By deﬁnition, Cases 1 and 2 satisfy SPC; their P

burn at, but are safely contained within, the upper and

lower bounds of the Q

, respectively.

Despite satisfying SPC, Cases 1 and 2 do accu-

mulate measurable damage. This is the essence of

how a cyberattack like Stuxnet works; it causes pro-

cessing nodes to operate within established statistical

tolerances, while accumulating damage to the manu-

factured products.

Consider Case 1. The probability density func-

tions for Q

and P

are given by

(x) =

2πσ

−

(x−µ

)

2σ

(4)

and

(x) =

2π(

)

−

(x−(µ

+3σ

−ε

))

)

, (5)

respectively.

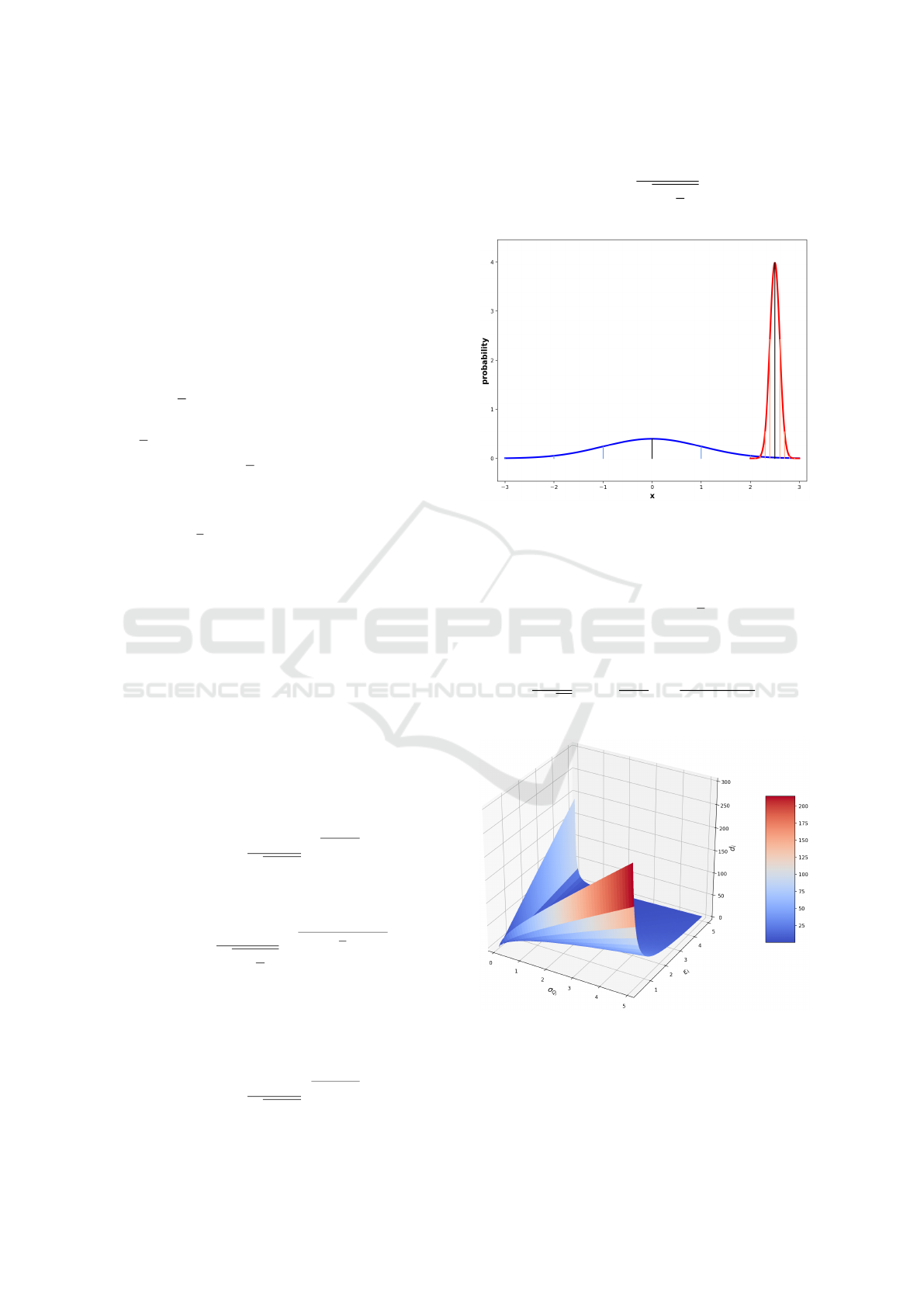
Since most of the probability mass of P

is near

x = µ

+ 3σ

−ε

and is otherwise close to 0 (see

Figure 2), we ﬁnd

(x) ≈

2πσ

(3σ

−ε

)

2σ

(6)

and

(x) ≈

2π(

)

. (7)

Figure 2: Example expected distribution Q

(blue) and ex-

ample observed distribution P

(red) for a given node i in

Case 1: P

is designed to occupy the rightmost extreme

subrange of Q

, where the probability mass of P

for x ∈

±5σ

is entirely contained within x ∈ [µ

+ 3σ

−

2ε

,µ

+ 3σ

]. Shown here: {µ

= 0, σ

= 1}, {ε

0.5,µ

= µ

+ 3σ

−ε

= 2.5, σ

= 0.1}.

Substituting these into the deﬁnition of d

, we derive

√

2π



log



5σ



(ε

−3σ

)

2σ



. (8)

Figure 3: Damage, d

, as a function of expected standard de-

viation, σ

and proximity to SPC tolerance, ε

, for a given

node i in Cases 1 and 2, as given by (8).

We depict (8) in Figure 3. Here we see that as ex-

pected variance, σ

, shrinks to 0 while proximity to

Securing Industrial Production from Sophisticated Cyberattacks

665

SPC tolerance, ε

, grows, then damage, d

increases

exponentially. Similarly, as ε

shrinks to 0 while σ

grows, then d

increases exponentially. These two

maxima represent two intuitively undesirable situa-

tions, neither of which are detected by SPC: {σ

→

0,ε

→ ∞} =⇒ the stringency of Q

outstrips the

proximity of P

to the extrema of Q

; and {σ

→

∞,ε

→ 0} =⇒ P

occupies an ever-narrowing sub-

range of Q

Consider Case 2. The only difference from Case

1 is the probability density function for P

, given by

(x) =

2π(

)

−

(x−(µ

−3σ

+ε

))

)

. (9)

Since most of the probability mass of P

is near

x = µ

−3σ

+ε

and is otherwise close to 0, we ﬁnd

(x) is identical to Case 1, so the remaining deriva-

tion follows identically, as one expects from the sym-

metric normal distribution.

Hence, in Cases 1 and 2, we have an expression

that deﬁnes a measurable damage for each node i in F

despite their having satisﬁed SPC. Sufﬁciently large

cumulative damage implies process control disrup-

tion:

> τ

. (10)

4 FORMULATING THE DAMAGE

RECOVERY PROBLEM

SPC is a static, non-interventional approach to pro-

cess control, where well-deﬁned statistical properties

are passively observed to pass or fail at each node,

and only after the last node’s processing is a decision

made as to whether to keep or discard the manufac-

tured product.

By contrast, we consider a dynamic, interven-

tional approach to process control, where each node

subsequent to the node causing detected damage is

woven into an optimization problem—the damage re-

covery problem–and actively controlled to instantiate

a solution to it. This is done near real-time and while

each cycle is ongoing, rather than at the end of a given

cycle.

If a control system detects node k has caused

damage (i.e., has produced a damaged or distorted

distribution), then intuitively, we want to employ a

control strategy that samples from P

, and generates

all subsequent resulting distributions ﬂowing from it,

k+1

,...,P

, such that the remaining cumulative dam-

age, d

k+1

+ ···+ d

, is minimized. Accordingly, we

formulate the damage recovery problem as

argmin

k+1

,...,P

}

(

∑

i=k+1

||Q

)

. (11)

5 PROPOSED SOLUTION

ARCHITECTURES

In the interest of minimizing the damage, D

, as

deﬁned in (11), one might consider simply applying

more stringent controls to each node of the process,

effectively minimizing the σ

, or attempt to idealize

the situation by assuming zero (or nearly zero) ob-

servable variance in practice, effectively minimizing

the σ

. More stringent controls translate into expo-

nential increases in expense in the number of nodes,

n, and observing ideally low levels of variance may

very well be impossible over long time spans for any

realistic manufacturing process.

As a counter to the trivial solution above, several

advanced methods for detection or correction are con-

sidered. One naturally follows the other, though a

correction method may include only implicit detec-

tion. Three potential solutions to the correction of

damage are outlined below, though their efﬁcacy will

be explored later. The ﬁrst uses adaptive methods

to control a system with an unknown disturbance, in

the simplest case, a constant disturbance. To gener-

alize the distribution description from (1), a single-

input, single-output system is established in state-

space form as

= A

+ B

ε,i

(t)

(t) = C

(12)

for ~x

deﬁned as arbitrary states of the system, y de-

ﬁned as the output of the system, and A, B and C

are system matrices deﬁning the ordinary differential

equation of the underlying dynamics. The input of

this system, u

, is a noisy input signal deﬁned by

ε,i

= u

(t) + ε

, (13)

where ε

is additive noise contributed by ε

∼

N (µ

ε,i

) Additionally, the observed output, y

, is

a function of the system output in (12) as

ν,i

= y

(t) + ν

(14)

for a similarly noisy signal measurement, with ν

∼

N (µ

ν,i

,σ

ν,i

). This notation is reconciled with that of

Sections 3 – 4 by establishing that y

ν,i

∼Q

for a given

node, i, of a process. In an unaffected system, the

mean of the noise contributions are zero, such that

ε,i

= µ

ν,i

= 0. In a malicious cyberattack, however,

the deviation manifests as non-zero mean input noise.

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

666

5.1 Innovation Error Distribution via

Kalman Filter State Estimation

A common approach to estimating states within a sys-

tem similar to (12) is a Kalman Filter (Kalman, 1960)

(KF), which can be extended to nonlinear systems as

well. The formulation of the KF is generally reliant

on zero mean noise, but in the case of a malicious

cyberattack, the offset of the input instruction would

manifest as a non-zero mean additive noise. There-

fore, a KF can be constructed for the presumed linear

time-invariant system described in (12). The ﬁlter is

constructed using measurements of output, y

ν,i

(t) for

a node of a process, and the canonical, untouched in-

put instructions u

(t). If the process is correctly cali-

brated, the input/output sensor measurements should

have zero mean noise, but in the case of a malicious

cyberattack there would be a non-zero bias, as de-

picted in Figure 2. The ﬁlter (Thrun et al., 2005) is

constructed as

i,k

= A

i,k−1

+ B

i,k

= A

i,k−1

+ R

i,k

+ σ

ν,i

)

−1

i,k

+ K

i,k

ν,i,k

−C

i,k

)

i,k

= (I −K

i,k

)

i,k

(15)

for the k

sample of a process node, i, where ¯· is

the measurement update notation, Σ

i,k

is the covari-

ance of the state prediction, R

is the covariance of

the input noise, ε

, and K

i,k

are the Kalman gains.

With a large enough sample, the innovation distribu-

tion, ˜y

i,k

= y

ν,i,k

−C

i,k

should be ˜y

i,k

∼ N (µ

˜y,i,k

0,C

i,k|k−1

). However, with a malicious cyber-

attack, µ

˜y,i,k

6= 0, but this can occur naturally with

minimal samples. Once a sample threshold is met,

k > k

min

, an alarm can be established for ˜y

i,k

> γ

where γ

can be tuned for a process node. If the in-

novation error is non-zero and above the threshold γ

a malicious cyberattack might be occurring. Figure 4

shows a schematic of the ﬁlter described in (15). It

should be noted that a twin controller must be main-

tained and isolated from the primary PLC controllers.

This is used as an unbiased reference for the kalman

ﬁlter. The limitations of this method are requiring a

known system, of the form A, B, and C. Addition-

ally, the duplicated controller represent an additional

challenge for maintaining software links. To alleviate

these issues, agnostic inferential methods can be used

as abstract representations of the system node.

A(s)

−

C(s) G(s)

ν,i,k

H(s)

C(s) KF

˜y

i,k

Figure 4: A block diagram of the systems described in (12),

incorporating the Kalman ﬁlter of (15) for innovation error

distribution. The controller, C(s), the plant, G(s), and the

measurement, H(s), represent the basic constituents of the

nodal control, while the Kalman ﬁlter, KF, produced an in-

novation error. The attack is represented by the block A(s).

5.2 Inferential Methods for Detection

and Correction

Artiﬁcial Intelligence (AI) (Russell and Norvig,

2010) in the form of Deep Learning (DL) (Goodfel-

low et al., 2016) has revolutionized image processing

(Krizhevsky et al., 2012), machine translation (John-

son et al., 2017), and many other forms of classiﬁca-

tion (Goodfellow et al., 2014). Speciﬁcally, the abil-

ity to form complex and non-obvious associations be-

tween image pixels and labels, has allowed for higher

accuracy of detection than conventional computer vi-

sion (Krizhevsky et al., 2012). These methods are also

not constrained by the same matching conditions of

classical ﬁlter methods, such as approach suggested

in Section 5.1. This enables more availability for sys-

tems that have undetermined or hard to model dynam-

ics.

5.2.1 Autoencoding for Unsupervised Anomaly

Detection

Signiﬁcant attention has been paid to autoencoders

trained to detect anomalies (An and Cho, 2015),

(Sakurada and Yairi, 2014), (Zhou and Paffenroth,

2017), which, when paired with a Long Short-

Term Memory (LSTM) (Hochreiter and Schmidhu-

ber, 1997) block in both the encoder and decoder,

has been shown to be applicable to anomaly detec-

tion. In (Malhotra et al., 2016), an autoencoder was

constructed with these LSTM blocks which maintain

a state memory of the sequence. For a sequence of

measured outputs, ~y

ν,i

, an unsupervised autoencoder

training can be instantiated to map the entropy of out-

put observations on to a parameter set, θ

, such that

ν,i

= f (~y

ν,i

,θ

). (16)

The error of this autoencoder is deﬁned as

ν,i

=~y

ν,i

−

ν,i

, (17)

Securing Industrial Production from Sophisticated Cyberattacks

667

and for a normal operation,

ν,i

∼N (µ

˜y,i

,Σ

˜y,i

), where

˜y

and Σ

˜y,i

are ﬁt to the distribution using maximum

likelihood. Subsequently, an anomaly score, a

, for a

sequence can be deﬁned as

= A



ν,i

,µ

˜y,i

,Σ

˜y,i



= (

ν,i

−µ

˜y,i

)

−1

˜y,i

(

ν,i

−µ

˜y,i

(18)

Similarly to the Kalman Filter formulation in Section

5.1, when the anomaly score, a

> γ

, an anomaly is

detected and an alarm is sounded. Figure 5 shows a

block diagram of the autoencoder system. The limi-

A(s)

−

C(s) G(s)

ν,i,k

H(s)

Figure 5: A block diagram of the systems described in (16)–

(18), incorporating the autoencoder for anomaly detection.

The controller, C(s), the plant, G(s), and the measurement,

H(s), represent the basic constituents of the nodal control,

while the autoencoder, AE, detects errors, wherein a sufﬁ-

cient anomaly score triggers alarm A. The attack is repre-

sented by the block A(s).

tations of the autoencoder approach are a reliance on

node-speciﬁc training of trajectory prediction models,

ignoring the complete factory output. It is possible

that while one node is operating appropriately, a pre-

vious node has already created damage, and the out-

put of the node in question will already be affected.

To correct for this, a more complete system would

consider states of each nodal output as an entire tra-

jectory, and adjust the set-point input of each subse-

quent node accordingly. Such an approach could be

accomplished through online optimization methods,

such as reinforcement learning.

5.2.2 Deep Reinforcement Learning

In Sections 5.1 and 5.2.1, malicious cyberattack de-

tection was discussed, but no implicit correction was

established. However, the deﬁnition of damage, d

given in (1) suggests a natural structure to formu-

late a delayed reward function for a reinforcement

learning agent seeking to construct a set of distri-

butions, P

k+1

,...,P

, to solve the damage recovery

problem given in (11), through its actions,

( j)

, for i =

k + 1,. . . , n, over some set of iterations, j = 1,. . . , m:

( j)

) =

∑

i=k+1

(

( j)

), (19)

for

(

( j)

) = P

(

( j)

)log

(

( j)

)

(

( j)

)

(20)

In (Lillicrap et al., 2015a), an agent is trained in an

actor-critic modality, such that one network produces

an action, α

i,k

, given a state, ~x

i,k

for the k

sample of

the i

node of a process, and another network makes

a prediction of Q-value, Q

i,k

(~x

i,k

,α

i,k

|θ

Q,i

), learned

over parameters θ

Q,i

, where π

(~x

i,k

,θ

π,i

) is a learned

policy over parameters θ

π,i

. The reward is calculated

using a Bellman formulation such that

(~x

i,k

,α

i,k

) = r

i,k

+ γ

(~x

i,k+1

,π

(~x

i,k+1

)|θ

π,i

(21)

Most reinforcement learning agents use an update

law corresponding to maximizing the expected return.

However, given the formulation in (11), our update

law will be

−∇

π,i

J =

−E

i,k

∼ρ

[∇

(~x

i,k

,α

i,k

|θ

Q,i

)∇

(~x

i,k

|θ

π,i

)].

(22)

This update law will minimize the Q-value, thereby

minimizing damage, and will manifest in actions

aimed at returning the distribution to its canonical

shape. One formulation of action could be

i,k

= α

i,k

∗

i,k

, (23)

where u

i,k

is the input of (12), α

i,k

is an instruction

modiﬁer, and u

∗

i,k

is the instruction read for a partic-

ular sample, k, of node i. If this instruction is cor-

rupted, and that corruption manifests in the states, the

policy, π

i,k

, will act to correct it. Figure 6 shows a

scheme to operate the agent within a factory setting,

acting as an outer-loop for the control set-point. An

alternative version would directly vary the gain of the

control effort from the C

(s) controllers, subverting

the set-point input.

Reinforcement learning has proven effective in

complex environments (Sutton and Barto, 2018), (Lil-

licrap et al., 2015b), (Schulman et al., 2017), (Fuji-

moto et al., 2018), but requires signiﬁcant samples to

converge. It is recommended that an agent is tuned

on simulation data ﬁrst, then subsequently reﬁned on

observed data, before it is deployed in a live system.

Moreover, this approach offers a new way to ad-

dress system security by bundling process-based ma-

licious cyberattacks into nominal process variations

and offers direct control and correction for those vari-

ations. The approaches is not simply a method of de-

tection or passive prevention; rather, a cyberattack is

assumed to manifest as a routine (e.g. probable) sys-

tem variation, such as a machine tuning out of norm or

a raw material stock moving out of tight speciﬁcation.

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

668

A(s)

s,0,k

s,i,k

s,N,k

−

(s)

ν,0,k

ν,i,k

ν,N,k

π(S

)

Figure 6: A block diagram of a potential scheme for reinforcement learning based manufacturing control of multiple nodes,

i = 0,. . . , N. For each node i, the controller, C

(s), the plant, G

(s), and the measurement, H

(s), represent the basic constituents

of the nodal control. Together, the nodes are embedded in a policy-learning feedback loop governed by the state of the system

at time k, S

, sampled from data store Y , and the policy taking the current state as input, π(S

). The attack is represented for

a single node, i, by the block A(s).

One would not know that the system was infected,

but as long as the agent is making active controls, the

ﬁnal product would be unchanged and the effect of

the cyberattack nulliﬁed. This also creates latency for

nominal IT process to take place and detect intrusion.

By focusing on active process control, rather than re-

active models, this approach takes advantage of time

series data throughout the manufacturing process and

not just a single data point for each ﬁnished good.

6 CONCLUSION

Physical and digital detachment, which has largely

shielded industrial equipment from immediately

catastrophic malicious cyberattacks, is no longer suf-

ﬁcient for cyber-defense. In order to enable dis-

tributed manufacturing measurement, analysis and

feedback, process nodes must be networked, present-

ing a cyberattack vector for nefarious actors. Even

with sophisticated ﬁrewalls and real-time alarms to

detect corrupted process trajectories, an opportunity

persists for minimally invasive alterations to process

instructions to operate within acceptable statistical

tolerances while damaging the ﬁnal product irrepara-

bly. The answer is not to deprecate the functional-

ity of modern factories in the interest of safeguard-

ing their output, nor is it to pour immense capital into

process nodes to ensure their operation ﬁts within an

impenetrable distribution of operation.

More sophisticated cyberattacks are able to pen-

etrate standalone equipment, inserting process varia-

tions and commands, causing subtle, non-trivial er-

rors that are difﬁcult to detect through conventional

process control methods. These cyberattacks can

be planned months or years before the actual effect

on the instrumentation—possibly within the supply

chain of the equipment—making detection and pre-

vention difﬁcult to impossible. The effects they intro-

duce are time and process-state integrative over long

scales and across multiple nodes, making detection

and correction difﬁcult. We present several alterna-

tive approaches for a generalized manufacturing set-

ting that offer not only complete standalone operation,

but also active correction for all types of process vari-

ation. A sophisticated cyberattack on a speciﬁc node

or a change in the raw material is corrected by ac-

tively changing the processing conditions of subse-

quent nodes. This agent is continually operational,

regardless of the cyberattack, and prevents malicious

attempts to alter the steady-state processing from hav-

ing a noticeable effect on the ﬁnal quality of the sys-

tem. This approach increases quality and yield of the

Securing Industrial Production from Sophisticated Cyberattacks

669

system by actively correcting for all types of nomi-

nal variations, while offering increased resistance to

possible cyberattacks on the process equipment.

REFERENCES

An, J. and Cho, S. (2015). Variational autoencoder based

anomaly detection using reconstruction probability.

Special Lecture on IE, 2(1).

Boyer, S. A. (2009). SCADA: Supervisory Control And

Data Acquisition. International Society of Automa-

tion, USA, 4 edition. ISBN 1936007096.

Delsanter, J. (1992). Six sigma. Managing Service Quality,

2(4).

Deming, W. E. (1986). Out of Crisis. MIT Center for Ad-

vanced Engineering Study, Cambridge, MA, USA.

Deming, W. E. and Renmei, N. K. G. (1951). Elementary

Principles of the Statistical Control of Quality; a Se-

ries of Lectures. Tokyo, Nippon Kagaku Gijutsu Rem-

mei, Tokyo, Japan.

Denton, D. (1991). Lessons on competitiveness: Motorola’s

approach. Production and Inventory Management

Journal, 32(3).

Fujimoto, S., van Hoof, H., and Meger, D. (2018). Ad-

dressing function approximation error in actor-critic

methods. arXiv preprint arXiv:1802.09477.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press, Cambridge, MA, USA. ISBN

0262035618. http://www.deeplearningbook.org.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In

Proceedings of the 27th International Conference on

Neural Information Processing Systems - Volume 2,

NIPS’14, pages 2672–2680, Cambridge, MA, USA.

MIT Press.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural Computation, 9(8):1735—-1780.

Johnson, M., Schuster, M., Le, Q. V., Krikun, M., Wu, Y.,

Chen, Z., Thorat, N., Vi

egas, F., Wattenberg, M., Cor-

rado, G., Hughes, M., and Dean, J. (2017). Google’s

multilingual neural machine translation system: En-

abling zero-shot translation. Transactions of the Asso-

ciation for Computational Linguistics, 5:339–351.

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Journal of basic Engineer-

ing, 82(1):35–45.

Karnouskos, S. (2011). Stuxnet worm impact on indus-

trial cyber-physical system security. In 37th Annual

Conference of the IEEE Industrial Electronics Society

(IECON 2011), Melbourne, Australia. http://papers.

duckdns.org/ﬁles/2011 IECON stuxnet.pdf.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).

Imagenet classiﬁcation with deep convolutional neu-

ral networks. In Pereira, F., Burges, C. J. C., Bot-

tou, L., and Weinberger, K. Q., editors, Advances

in Neural Information Processing Systems 25, pages

1097–1105. Curran Associates, Inc. https://bit.ly/

39PWOAb.

Kullback, S. (1959). Information Theory and Statistics.

John Wiley & Sons.

Kullback, S. and Leibler, R. (1951). On information

and sufﬁciency. Annals of Mathematical Statistics,

22(1):79–86.

Laughton, M. and Warne, D., editors (2003). Electrical En-

gineer’s Reference Book, chapter 16. Newnes, 16 edi-

tion. ISBN 0750646373.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015a). Contin-

uous control with deep reinforcement learning. arXiv

preprint arXiv:1509.02971.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez,

T., Tassa, Y., Silver, D., and Wierstra, D. (2015b).

Continuous control with deep reinforcement learning.

arXiv preprint arXiv:1509.02971.

Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agar-

wal, P., and Shroff, G. (2016). LSTM-based encoder-

decoder for multi-sensor anomaly detection. arXiv

preprint arXiv:1607.00148.

Russell, S. and Norvig, P. (2010). Artiﬁcial Intelligence: A

Modern Approach. Prentice Hall, Upper Saddle River,

NJ, USA, 3 edition. ISBN 0136042597. http://aima.

cs.berkeley.edu/.

Sakurada, M. and Yairi, T. (2014). Anomaly detection

using autoencoders with nonlinear dimensionality re-

duction. In Proceedings of the MLSDA 2014 2nd

Workshop on Machine Learning for Sensory Data

Analysis, page 4. ACM.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement

Learning: An Introduction. MIT Press, Cambridge,

MA, USA, 2 edition. ISBN 0262039249. http://

incompleteideas.net/book/the-book-2nd.html.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

robotics. MIT press.

Zhou, C. and Paffenroth, R. C. (2017). Anomaly detec-

tion with robust deep autoencoders. In Proceedings of

the 23rd ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 665–

674. ACM.

ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy

670