Supervised Hardware/Software Partitioning Algorithms for FPGA-based

Applications

Belhedi Wiem and Hannachi Marwa

Department of Research, Altran Technologies, France

Keywords:

Hardware/Software Partitioning, Linear Regression, Logistic Regression, Support Vector Machine (SVM),

Linear Discriminant Analysis (LDA), Deep Neural Network (DNN).

Abstract:

Real time systems require the cooperation of the reconﬁgurable hardware and the software in order to boost

the application performance in terms of both energy and time. However, the integration of these systems

presents a hardware/software co-design challenges in terms of both time minimization and autonomy; hence,

the importance of hardware/software partitioning algorithms.

Here, we present a selection of artiﬁcial intelligence based-approaches that we apply in order to solve the

hardware/software classiﬁcation task in real-time systems. For this, the used database consists of a collection

of real experiments that were conducted in Altran Technologies. The tested classiﬁcation algorithms include

Linear Regression model optimized with gradient descent, logistic regression, Support vector machine (SVM),

Linear Discriminant Analysis (LDA), and deep neural network (DNN).

Results show the applicability of these methods and the high accuracy of the task type decision.

1 INTRODUCTION

The rapid evolution of industrial applications poses

a unique challenge requiring high computing perfor-

mance, ﬂexibility, energy efﬁciency, autonomy, and

real-time processing in order to meet the require-

ments. For this, numerous solutions were proposed to

solve the tradeoff between high computational com-

plexity and time/energy consumption for real-time ap-

plications.

In fact, processors are very efﬁcient in data man-

agement and control, but they are less efﬁcient in

computation and data processing because of their

sequential architecture. On the other hand, hard-

ware solutions such as Field-Programmable Gate Ar-

ray (FPGAs), Application-Speciﬁc Integrated Circuit

(ASICs) have a parallel architecture that allows them

to achieve high computing power. However, their per-

formance in the management and data control is out-

performed by the processors. Hence, the cooperation

of these hardware and software solutions in hetero-

geneous systems would boost the application perfor-

mance in terms of both energy and time (Mohamed

et al., 2018)

The heterogeneous nature of this type of systems

makes it possible to use resources adapted to each

type of request. When heavy processing is required,

such as video processing, dedicated hardware blocks

may be used while the processor is used for lighter

tasks. Unlike dedicated hardware blocks, the pro-

cessor has the advantage that it can be programmed

easily, thus making the system scalable. We there-

fore see a rivalry between performance and scalabil-

ity. Indeed, they allow effective treatment of certain

requests while retaining the programmable aspect of

the processor. However, they remain dedicated to

one type of treatment. Heterogeneous systems have

been successfully employed for different tasks includ-

ing real-time locating systems (Alawieh et al., 2015),

video processing (Hoozemans et al., 2019), and for

matrix multiplication, watermarking, ﬁltering, near-

est neighborhood, and AES decryption (Rethinagiri

et al., 2015).

Despite the effectiveness of these systems, they

still require the optimization of several parameters,

such as hardware/software tasks partitioning in order

to minimize time and energy consumption.

In this paper, we propose to apply several ma-

chine learning algorithms in order to optimize Hard-

ware/Software partitioning. The selected algorithms

are the linear regression, logistic regression, support

vector machine (SVM), linear discriminant analysis

(LDA), and the deep neural network (DNN).

The remainder of this paper is organized as fol-

860

Wiem, B. and Marwa, H.

Supervised Hardware/Software Partitioning Algorithms for FPGA-based Applications.

DOI: 10.5220/0009149708600864

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 860-864

ISBN: 978-989-758-395-7; ISSN: 2184-433X

lows. Section 2 introduces the used database, and

overviews and discusses the classiﬁcation algorithms.

Section 3 presents our preliminary results. Section

4 outlines our conclusions and describes our current

and future work.

2 HARDWARE/SOFTWARE

CLASSIFICATION

2.1 Database

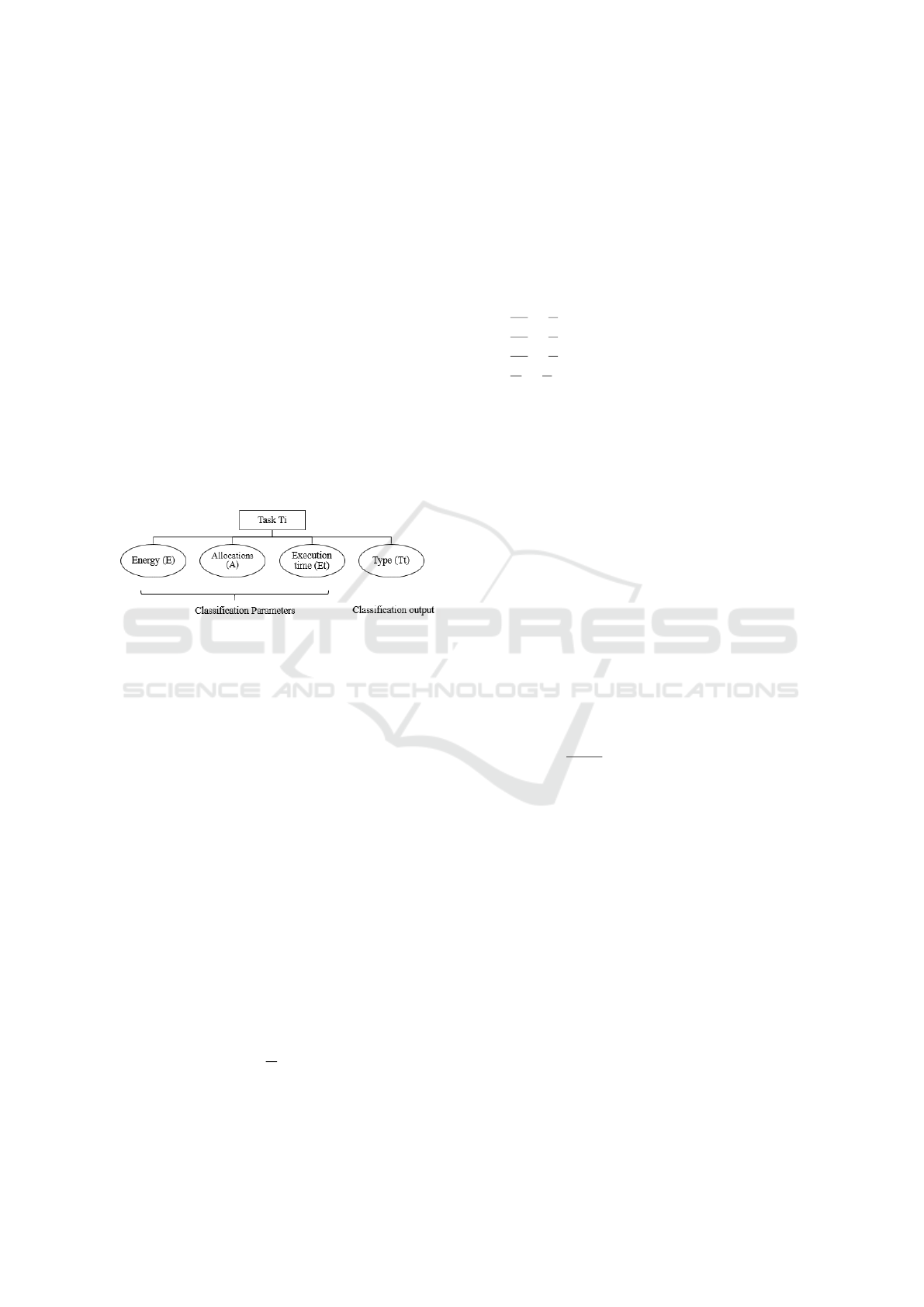
The database is of a collection of experiments on

FPGA tasks that were conducted in Altran Technolo-

gies. As illustrated in Figure 1, it consists of several

tasks with their respective Execution time (ET), En-

ergy, Allocations together with their respective types

(Hardware or Software).

Figure 1: Database Architecture.

In the Task type (Tt), the value ”1” denotes that

the task is mapped as hardware, and ”0” denotes that

the task is software.

2.2 Linear Regression Model Optimized

with Gradient Descent

In this paper, we admit that the task type (Tt) can

be modeled as a linear function of the execution time

(ET), the energy (E), and the allocation (A) as:

y = α

+ α

+ b (1)

where x

is the execution time (ET), x

is the energy

(E), x

is the allocations (A), y is the task type (Tt),

, α

are the mixing coefﬁcients, and b is the in-

tercept. While training the regression model, it calcu-

lates the cost function which measures the Root Mean

Squared error between the predicted task type ¯y and

true one. The model targets, therefore, to minimize

the cost function deﬁned as:

RMSE =

∑

i=1

( ¯y

− y

)

(2)

In order to minimize the cost function, the best coefﬁ-

cient must be found. For this, initial values of have to

be set randomly and then the model iteratively update

these values in order to minimize the cost function

until it reaches the minimum. The best values will be

then employed to predict the task type in the most ac-

curate manner it can. To do so, the gradient descent

algorithm is employed. This latter consists of a com-

monly used optimization function that adjusts weights

according to the cost error (Ruder, 2016) as:











dα

∑

i=1

−x

(α

+ α

+ b))

dα

∑

i=1

−x

− (α

+ α

+ b))

dα

∑

i=1

−x

− (α

+ α

+ b))

∑

i=1

−(y

− (α

+ α

+ b))

(3)

2.3 Logistic Regression

Logistic regression is the statistical technique used to

predict the relationship between inputs, that can be ei-

ther continuous or categorical, and predicts the prob-

ability that an observation falls into one of two cate-

gories (Maxwell, 2015). The logistic regression is an

extension of linear regression for classiﬁcation prob-

lems. In fact, it models the probabilities for classiﬁ-

cation problems with two possible outcomes.

The interpretation of the weights in logistic regression

differs from the interpretation of the weights in linear

regression, since the outcome in logistic regression is

a probability between 0 and 1. Hence, the weighted

sum is transformed by a logistic function to a proba-

bility.

Mathematically, logistic regression estimates a

multiple linear regression function deﬁned as:

log(

1 − P

) = α

+ α

(4)

where

= P

(y = 1|x = x

) (5)

2.4 Linear Discriminant Analysis

(LDA)

The Linear Discriminant Analysis (LDA) aims to ﬁnd

linear combinations of features that characterize or

separate two or more classes (Antuvan and Masia,

2019). In fact, it projects a dataset onto a lower-

dimensional sub-space with good class separability in

order to reduce computational costs and to avoid over-

ﬁtting.

Hence the ﬁrst step of the LDA algorithm is to cal-

culate the separability between different classes. This

latter is the distance between the mean of different

classes deﬁned as:

∑

i=1

( ¯x

− ¯x

)( ¯x

− ¯x

)

(6)

Supervised Hardware/Software Partitioning Algorithms for FPGA-based Applications

861

where x is a sample (i.e., row) and g is the total num-

ber of samples within a given class.

After that, the distance between the mean and

sample of each class, also called the within class vari-

ance, is calculated as:

∑

i=1

− 1)S

∑

i=1

∑

j=1

( ¯x

i, j

− ¯x

)( ¯x

i, j

− ¯x

)

(7)

Then the lower dimensional space P

LDA

is con-

structed so that the between class variance is maxi-

mized and the within class variance is minimized. Let

P be the lower dimensional space projection, the P

LDA

is determined as:

LDA

= argmax

(8)

2.5 Support Vector Machine (SVM)

For a number N of features, support vector machine

(SVM) algorithm aims to ﬁnd a hyperplane in an N-

dimensional space that distinctly classiﬁes the data

(Gola et al., 2019). In fact, given a labeled training

data, SVM outputs an optimal hyperplane that cate-

gorizes new examples (Maxwell, 2015). In fact, it can

be summed up as an optimization problem depending

only on the multipliers α











max

(α) =

∑

i=1

−

∑

i=1

∑

, y

, x

s.t α

≥ 0 ∀i

and

∑

i=1

= 0

(9)

and y

are respectively the input and output observa-

tions,

, x

is the inner product of the observations

i and i

, α

are the ponderation coefﬁcients that deﬁne

the support points.

2.6 Deep Neural Network (DNN)

As indicated in the DNN architecture illustrated in

Figure 2 the DNN model consists of four layers, two

of which are hidden layers. In the input layer, three

variables are set as independent inputs, including the

execution time (TE), the energy (E), and the alloca-

tion (A), while the task type label is set as the output

(Hw/Sw decision). Hence, the values of the three-

neurons of the input layer are passed through two hid-

den layers that have multiple neurons with activation

function in all neurons. The ﬁnal output layer, which

indicates of the task type, has one neuron.

In the proposed architecture, the Relu function is used

as the activation function in all layers except in the

last layer (output layer) where the Sigmoid function

is used in order to map the output to the [0, 1] (Nie

et al., 2019).

Firstly, the input data should be vectorized and fed

into the network. A series of matrix operations is op-

erated on the input data layer by layer through the

two hidden layers. Each input sample is multiplied by

weights and added to bias that are updated after every

epoch. Finally, the activation functions are applied to

the result (Agostinelli et al., 2014).

Figure 2: DNN Architecture.

3 RESULTS AND DISCUSSION

In this work, the point is to describe what qualities

in a partitioning task contributes to decide whether it

is hardware or software. In other words: If the task

is, for instance, of a certain execution time, energy

and allocations, there probability that a certain task is

a hardware. In order to quantify the probability of a

task regarding software or hardware, several classiﬁ-

cation approaches were used. Performance results are

reported in terms of training and test accuracy as well

as minimum mean-square error (MMSE) deﬁned as

(Wiem et al., 2018):

MMSE =

∑

i=1

( ¯y(k) − y(k)) (10)

The comparative results are shown in Tables 1 and 2.

The predicted classes were compared with the true

ones for the training set of 70% randomly chosen

data from the dataset. The remaining data constitute

the test set. The training is conducted through 100

epochs, where an epoch corresponds to a learning on

all the data. In this work, the number of epochs was

chosen to satisfy the trade-off between the estimation

accuracy and the training time. To test and evaluate

the network, the test set was used ( population of 30%

of the whole database).

In the classiﬁcation process, we observed that al-

most all the learning models grouped tasks under cer-

tain characteristics. For example, tasks that possess

high execution time and high energy in one group

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

862

Table 1: Training/Test accuracies.

Classiﬁcation Method Training accuracy Test accuracy

LR 0.53 0.52

BR 0.87 0.60

LDA 0.93 0.40

SVM 0.87 0.80

DNN 0.86 0.80

Table 2: Classiﬁcation results in terms of MMSE.

Classiﬁcation Method MMSE

LR 0.3404

BR 0.6324

LDA 0.7745

SVM 0.3638

DNN 0.4472

(hardware tasks). The observation on the classi-

ﬁcation results favors SVM learning algorithm for

classiﬁcation problems since the correctness percent-

age is high compared to the competitive algorithms.

Though, the differences are not much.

The results reported in Tables 1 and 2, therefore,

prove the success of these approaches recognize task

type through the implicit relationships between input

and output variables. From these results, both DNN

and SVM are the most successful approaches to pre-

dict the task type with the highest accuracy and with-

out complex procedure.

4 CONCLUSION AND FUTURE

WORK

In this paper, we investigated the feasibility of su-

pervised learning algorithms for hardware/software

partitioning. Experiments were conducted using a

database that were collected from real tasks within

Altran technologies.

In fact, In general, this paper talks about classiﬁ-

cation of functions in terms of their implementation

through hardware or software to raise the efﬁciency

of the system in terms of time and energy consump-

tion for FPGA-based Applications. Basically, it in-

troduces hardware/software partitioning algorithms in

order to solve the classiﬁcation task in real-time sys-

tems. Such a system consists of 6 parts. First , the

database where we contain several tasks with 3 pa-

rameters, Energy, Allocations, Execution time and all

together with their types. Second, Linear Regression

model as the task type is represented linearly with the

three database parameters each multiplied by coefﬁ-

cient. This model aims to minimize the cost by ﬁnd-

ing the best proper coefﬁcient value for each parame-

ter. Third, Logistic Regression, where it differs from

the linear regression model as the calculation of the

weight based on the probability that falls into one of

two categories. Mainly, it is the statistical technique

that used to predict the relationship between inputs.

Fourth, Linear Discriminant Analysis (LDA), where it

aims to characterize or separate different classes that

share linear features in order to optimize the compu-

tations. Fifth, Support Vector Machine (SVM), as it

used to classify the data by ﬁnding a hyperplane in an

N-dimensional space where N is the number of fea-

tures. Finally, the last part of this paper is Deep Neu-

ral Network (DNN). DNN consists of 4 layers where

2 are hidden. The inputs of the trained DNN are the

three database parameters and the output is the item

type. Each layer have number of neurons with acti-

vation function. After applying these algorithms on

real experimentations on FPGA and CPU, we found

that they are efﬁcient especially DNN and SVN algo-

rithms where they were more accurate in classifying

task type.

Hence, we prove the applicability of these meth-

ods and the high accuracy of the task type decision.

The tested models were trained ofﬂine based on

the collected data from real experimentations on

FPGA and CPU. The evaluation results show the ef-

fectiveness of AI in solving the partitioning prob-

lem. For real-time applications, it is important for the

tested methods to have a good generalization ability

so that they can still work effectively when the con-

ditions of online deployment could not be satisﬁed in

the training stage (Mohammad and Hannachi, 2019) ,

(Mohamed, 2019). Hence, motivated by the promis-

ing results, future work may address the unsupervised

learning for a hardware/software partitioning in order

to achieve a fully autonomous real-time system.

REFERENCES

Agostinelli, F., Hoffman, M., Sadowski, P., and Baldi, P.

(2014). Learning activation functions to improve deep

neural networks. arXiv preprint arXiv:1412.6830.

Alawieh, M., Kasparek, M., Franke, N., and Hupfer, J.

(2015). A high performance fpga-gpu-cpu platform

for a real-time locating system. In 2015 23rd Eu-

ropean Signal Processing Conference (EUSIPCO),

pages 1576–1580. IEEE.

Antuvan, C. W. and Masia, L. (2019). An lda-based

approach for real-time simultaneous classiﬁcation of

movements using surface electromyography. IEEE

Transactions on Neural Systems and Rehabilitation

Engineering, 27(3):552–561.

Gola, J., Webel, J., Britz, D., Guitar, A., Staudt, T., Winter,

M., and M

ucklich, F. (2019). Objective microstructure

classiﬁcation by support vector machine (svm) using

Supervised Hardware/Software Partitioning Algorithms for FPGA-based Applications

863

a combination of morphological parameters and tex-

tural features for low carbon steels. Computational

Materials Science, 160:186–196.

Hoozemans, J., van Straten, J., Viitanen, T., Tervo, A.,

Kadlec, J., and Al-Ars, Z. (2019). Almarvi execution

platform: Heterogeneous video processing soc plat-

form on fpga. Journal of signal processing systems,

91(1):61–73.

Maxwell, R. (2015). The Routledge companion to labor and

media. Routledge.

Mohamed, K. (2019). Model order reduction method

for large-scale rc interconnect and implementation

of adaptive digital pi controller. IEEE Transac-

tions on Very Large Scale Integration (VLSI) Systems,

27(10):2447–2458.

Mohamed, K., Mehdi, A., and Abdelkader, M. (2018).

Lyapunov-global-lanczos algorithm for model order

reduction & adaptive pi controller of large scale elec-

trical systems. Scientia Iranica, 25(3):1616–1628.

Mohammad, N. and Hannachi, M. (2019). Optimized place-

ment approach on reconﬁgurable fpga. In Interna-

tional Journal of Modeling and Optimization 9.

Nie, X., Cao, J., and Fei, S. (2019). Multistability and

instability of competitive neural networks with non-

monotonic piecewise linear activation functions. Non-

linear Analysis: Real World Applications, 45:799–

821.

Rethinagiri, S. K., Palomar, O., Moreno, J. A., Unsal, O.,

and Cristal, A. (2015). Trigeneous platforms for en-

ergy efﬁcient computing of hpc applications. In 2015

IEEE 22nd International Conference on High Perfor-

mance Computing (HiPC), pages 264–274. IEEE.

Ruder, S. (2016). An overview of gradient de-

scent optimization algorithms. arXiv preprint

arXiv:1609.04747.

Wiem, B., Mowlaee, P., Aicha, B., et al. (2018). Unsuper-

vised single channel speech separation based on opti-

mized subspace separation. Speech Communication,

96:93–101.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

864