
Influence of Sampling Point Setting on Fitting Error of Ideal
Gaussian Beam
Yan Baozhu, Liu Wenguang, Zhou Qiong, Sun Quan and Yang Yi
College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha, Hunan, P.R. China
Keywords: Gaussian Beam, Least Square Fitting, Fitting Error, Sampling Point.
Abstract: The setting of sampling points on the detector array will affect the fitting error of Gaussian beam. Based on
MATLAB and least square method, the fitting of ideal Gaussian beam in one dimension and two dimensions
was simulated, and the influence of sampling point interval on the fitting error of characteristic parameters,
such as facula center, facula radius and center power density, were studied. The results show that, the number
of sampling points in the two-dimensional simulation is greater, so the fitting accuracy is better than that in
the one-dimensional simulation under the same condition of sampling point interval. In the range of initial
conditions of simulation calculation, the interval of sampling points shall be d≤50mm, then the fitting error
would be controlled within the range of admissible one.
1 INTRODUCTION
Generally, the detector array is used to measure the
power density distribution of the facula(C. Higgs,
P.C. Grey, J.G. Mooney. 1999; J. Thomas Knudtson,
Kenneth L. Ratzlaff. 1983). The characteristic
parameters of the facula are acquried by the least
square fitting. The setting of sampling points on
detector array will affect the fitting error of facula. It
can be predicted that, the smaller the interval between
sampling points, and the larger the sampling range,
the smaller the fitting error of facula. In the design of
detector array, due to the limitation of single detector
size and data processing capacity, the sampling point
interval cannot be small infinitely, and the sampling
range cannot be large infinitely, so it is necessary to
make a balance between sampling point setting and
fitting error. It is great to use as few sampling points
as possible to obtain the fitting error that meets the
requirements. In this paper, based on MATLAB and
least square method, one-dimensional and two-
dimensional simulation are carried out for the
sampling point setting on the Gaussian facula, and the
influence of sampling point interval on the fitting
error is studied.
2 ONE-DIMENSIONAL
SIMULATION
2.1 Calculation Method of
One-dimensional Simulation
The general expression of power density distribution
function of one-dimensional Gaussian beam is
(Bingkun Zhou, Yizhi Gao, Tirong Chen, et al.. 2000):
()
2
0
0
2
0
2
() exp
xx
Ix I
w
−
=⋅ −
(1)
Where x
0
is the facula center, w
0
is the facula radius,
and I
0
is the center power density.
First of all, equation (1) is transformed by
logarithm operation on both sides of the equal
sign(Bing Kong, Zhao Wang, Yusan Tan, 2002), then:
2
0
2
0
2
0
2
0
0
2
0
2
,
4
ln ( ) ,
2
ln
a
w
x
zIxaxbxcb
w
x
cI
w
=−
==++=
=−
(2)
The coefficients of a, b and c can be obtained by the
second order polynomial fitting of the transformed
140
Baozhu, Y., Wenguang, L., Qiong, Z., Quan, S. and Yi, Y.
Influence of Sampling Point Setting on Fitting Error of Ideal Gaussian Beam.
DOI: 10.5220/0009150901400145
In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 140-145
ISBN: 978-989-758-401-5; ISSN: 2184-4364
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
function. According to the relationship between the
transformed function and the original Gaussian
function, the corresponding parameters of the Gaussian
function can be obtained as follow:
2
000
2
exp , ,
42
bb
Icx w
aaa
=− =− =−
(3)
The position of the sampling point on the actual
detector array is given, and the facula wobbles within
a certain range. For the convenience of calculation, it
is assumed that the facula is fixed, and sampling points
are set uniformly. In this way, three parameters are
involved in the distribution of sampling points, as
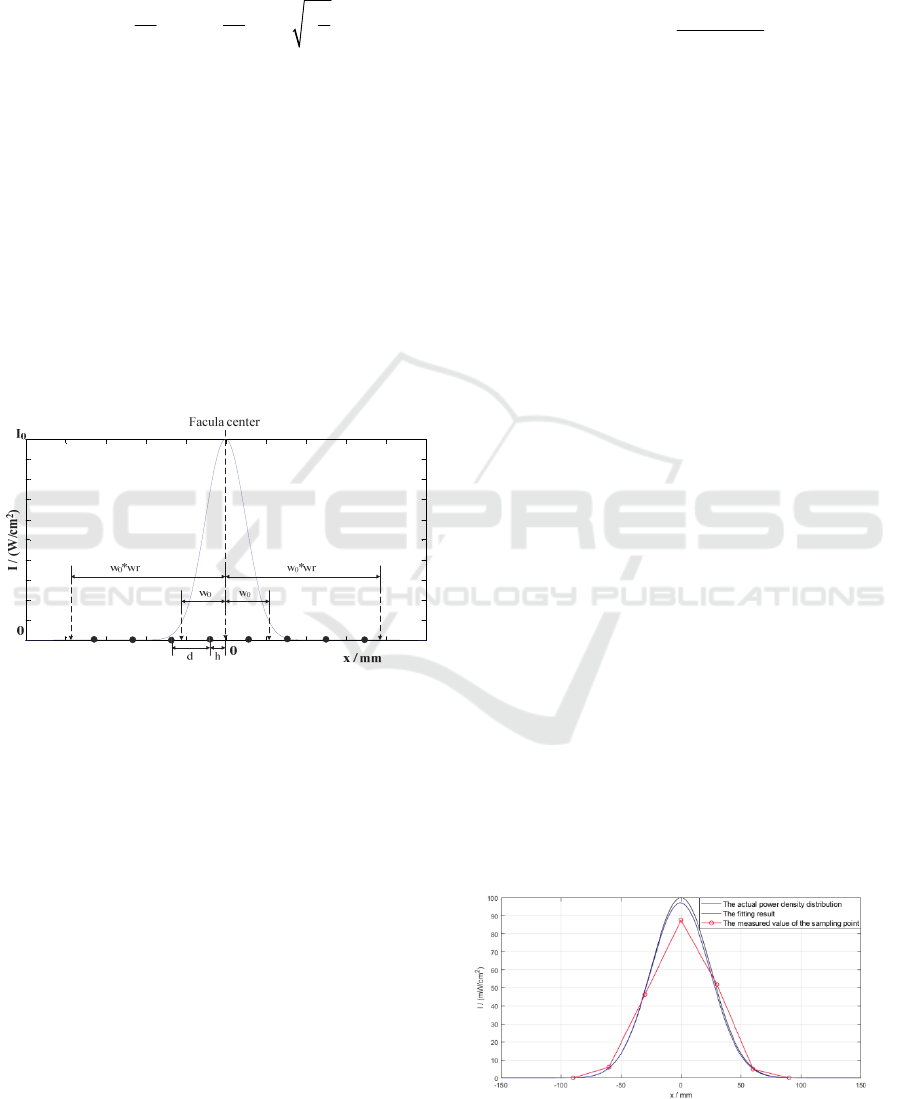
shown in Figure 1. They are d, wr, and h, which stand
for the interval of sampling points, the ratio of
sampling point range to facula diameter, and the
distance between the facula center and the sampling
point on the left side of it. Parameters of d and wr are
related to the design of detector array. Parameter of h
changes randomly in the actual measurement, with the
range of 0~d/2.
Figure 1: Physical meaning of parameters in simulation
calculation.
For each set of d, wr and h, the coordinates x
i
of each
sampling point can be determined. Then the true value
I(x
i
) of each sampling point can be obtained by
substituting x
i
to formula (1). There is a certain
measurement error for each sampling points, which
follows the normal distribution with the mean value of
0 and the standard deviation of δ
0
. A group of random
error values δ
i
(i=1, 2, … , n, n is the number of
sampling points) that meet the above normal
distribution are selected, so the measured value of each
sampling point is I'(x
i
)= I(x
i
)*(1+δ
i
). Substituting it
into formula (2), z'(x
i
)=ln(I'(x
i
)) is obtained. In
MATLAB, the least square fitting of (x
i
,z'(x
i
)) is
carried out using the polyfit function (Shenyong Ruan,
Yongli Wang, Qunfang Sang, 2004), and three
coefficients of a
1
, b
1
and c
1
are obtained. Then, the
fitting coefficients x
01
, w
01
and I
01
are calculated
according to formula (3). Here, the subscript "1"
represents the fitting result.
Therefore, the power density distribution function
obtained by fitting is:
()
2
01
101
2
01
2
() exp
xx
Ix I
w
−
=⋅ −
(4)
Compared with the true value in formula (1), the fitting
error values of facula center (x
01
-x
0
), facula radius
(w
01
-w
0
), and center power density (I
01
-I
0
) are obtained.
A number of m groups of random error are selected,
and a group of fitting error, such as (x
01
-x
0
)
j
, (w
01
-w
0
)
j
and (I
01
-I
0
)
j
, j = 1, 2, ... , m, is obtained for each group
of random error according to the above process. Then
the fitting error under the conditions of d, wr and h is
acquired by the standard deviation of m groups of
fitting error values is calculated.
2.2 Initial Conditions of
One-dimensional Simulation
The initial conditions used in the calculation are:
1) The facula center x
0
=0. The facula radius w
0
=50mm.
The center power density I
0
=100mW/cm
2
.
2) The ratio of the sampling point range to the facula
diameter wr=2. The sampling point interval d is
changed from 30mm to 60mm, and the step is 1mm.
The distance between the facula center and the
sampling point on the left side of it h is changed from
0 to d/2, and the step is d/8.
3) the standard deviation of sampling point error is
δ
0
=15%.
4) The number of groups of random error m = 10000.
2.3 Results of One-dimensional
Simulation
When d=30mm, wr=2, h=0mm, a group of random
error of sampling points is selected, and the fitting
result for the measured values of sampling points is as
Figure 2:
Figure 2: Result of one-dimensional fitting.
0
0
0
0
0
0
0
0
0
0
0
Influence of Sampling Point Setting on Fitting Error of Ideal Gaussian Beam
141

In the figure, the black line represents the actual power
density distribution, the red circle represents the
measured value of the sampling point, and the blue line
represents the power density distribution obtained by
fitting the measured value of the sampling points,
where x
01
=0.46mm, w
01
=49.80mm and
I
01
=97.18mW/cm
2
, and the fitting errors are (x
01
-
x
0
)=0.46mm, (w
01
-w
0
)=-0.20mm, and (I
01
-I
0
)=-
2.82mW/cm
2
.
A number of m=10000 groups of random error
values are selected, and a number of m=10000 groups
of the fitting error is obtained. Then the fitting error
under the conditions of d=30mm, wr=2 and h=0mm is
obtained: the fitting error of the facula center is
δ
x0
=0.61mm, the fitting error of the facula radius is
δ
w0
=0.59mm, and the fitting error of the center power
density is δ
I0
=8.73mW/cm
2
.
When d and h change in the calculation range, the
simulation results of the fitting errors are as shown in
Figure 3 ~ Figure 5.
Figure 3: Fitting error of the facula center for one-
dimensional simulation.
Figure 4: Fitting error of the facula radius for one-
dimensional simulation.
It can be seen from the figure:
1) The relationship between fitting error and sampling
interval is not monotonous increasing or decreasing,
but segmented. With the increase of d, the overall
errors of the next section is higher than that of the
Figure 5: Fitting error of the center power density for one-
dimensional simulation.
previous section. While in a certain section, it is
basically monotonic decreasing. This is because in a
certain
range, the number of sampling points is
constant. The larger d is, the wider the distribution of
sampling points is, the more information is detected,
and the smaller the fitting error is. When d increases to
a certain value, because wr is limited to 2, the number
of sampling points decreases, so the detection
information decreases, and the fitting error suddenly
increases. Taking h=0 as an example, the range of
sampling points is limited to w
0
*wr=50*2=100mm.
When d=30-33mm, there are three sampling points on
both sides of the facula center. When d=34-50mm,
there are two sampling points on both sides of the
facula center. When d=51-60mm, there is one
sampling point on both sides of the facula center.
Therefore, the boundary between segments are
between d=33mm and d=34mm, d=50mm and
d=51mm.
2) It is assumed that, the admissible errors of the facula
center, facula radius and center power density are 1mm,
2.5mm (5%) and 10mW/cm
2
(10%), respectively,
which are represented by solid red lines in the figures.
When selecting the interval of sampling points d, the
fitting errors should not exceed the admissible ones
under all h conditions. It can be seen from the figures
that, within the initial condition range of simulation
calculation, the fitting error of facula radius is smaller
than the admissible one, and the fitting errors of facula
center and center power density do not exceed the
admissible ones when d ≤ 40mm and d ≤ 33mm
respectively. Therefore, d≤33mm should be selected
to ensure the fitting accuracy.
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 6
0
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
error of x
0
/ mm
d / mm
h/d=0
h/d=1/8
h/d=1/4
h/d=3/8
h/d=1/2
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
0.3
0.6
0.9
1.2
1.5
1.8
2.1
2.4
2.7
h/d=0
h/d=1/8
h/d=1/4
h/d=3/8
h/d=1/2
error of w
0
/ mm
d / mm
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
8
9
10
11
12
13
14
15
16
h/d=0
h/d=1/8
h/d=1/4
h/d=3/8
h/d=1/2
error of I
0
/ (mW/cm
2
)
d / mm
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
142

3 TWO-DIMENSIONAL
SIMULATION
3.1 Calculation Method of
Two-dimensional Simulation
The general expression of the power density
distribution function of the two-dimensional Gaussian
beam cross-section facula is as follows:
()()
22
00
0
22
00
22
(, ) exp
xy
xx yy
Ixy I
ww
−−
=⋅ − −
(5)
Where (x
0
, y
0
) is the facula center, (w
0x
, w
0y
) is the
facula radius in the X and Y directions, and I
0
is the
center power density.
Similar to the one-dimensional simulation
calculation, equation (5) is transformed by logarithm
operation on both sides of the equal sign.
2
0
0
2
0
22
2
0
0
2
0
22
00
0
22
00
2
,
4
2
ln ( , ) ,
4
22
ln
x
x
y
y
xy
a
w
x
b
w
z I x y ax bx cy dy e c
w
y
d
w
x
y
eI
ww
=−
=
==++++=−
=
=−−
(6)
The coefficients a, b, c, d and e can be obtained by the
second order polynomial fitting of the transformed
function. According to the relationship between the
transformed function and the original Gaussian
function, the corresponding parameters of the Gaussian
function can be obtained as follow:
22
00
000
exp , ,
44 2
22
,,
2
xx
bd b
Ie x
ac a
d
wyw
ac c
=−− =−
=− =− =−
(7)
Similar to the one-dimensional simulation calculation
shown in Figure 1, four parameters are involved in the
two-dimensional distribution of sampling points.They
are the interval of sampling points d, the ratio of
sampling point range to facula diameter wr, the
distance between the facula center and the sampling
point on the left side of it hx, and the distance between
the facula center and the sampling point under it
hy.Parameters of d and wr are related to the design of
detector array. Parameters of hx and hy change
randomly in the actual measurement, with the range of
0~d/2.
For each set of d, wr, hx and hy, the coordinates (x
i
,
y
j
) of each sampling point can be determined, where
i=1, 2,... , nx, j=1, 2,... , ny, nx and ny represent the
number of columns and rows of sampling points
respectively. The true value I(x
i
, y
j
) of each sampling
point is obtained by substituting (x
i
, y
j
) to formula (5).
A group of random error values δ
ij
are selected, and the
measured value of each sampling point is I'(x
i
, y
j
)= I(x
i
,
y
j
)*(1+δ
ij
). Substituting it into formula (6), z'(x
i
,
y
j
)=ln(I'(x
i
, y
j
)) is obtained. Then the least square fitting
of ((x
i
, y
j
) , z'(x
i
, y
j
)) is carried out, and five
coefficients of a
1
, b
1
, c
1
, d
1
and e
1
are obtained. So, the
fitting coefficients (x
01
, y
01
), (w
0x1
, w
0y1
) and I
01
are
calculated according to formula (7).
So far, the power density distribution function of
the two-dimensional Gaussian beam cross-section
facula is obtained by fitting:
()()
22
01 01
101
22
01 01
22
(, ) exp
xy
xx yy
Ixy I
ww
−−
=⋅ − −
(8)
Compared with the true value in formula (5), the fitting
errors of facula center (x
01
-x
0
, y
01
-y
0
), facula radius
(w
0x1
-w
0x
, w
0y1
-w
0y
), and center power density (I
01
-I
0
)
are obtained.
A number of m groups of random error are selected,
and a group of fitting error, such as (x
01
-x
0
, y
01
-y
0
)
j
,
(w
0x1
-w
0x
, w
0y1
-w
0y
)
j
and (I
01
-I
0
)
j
, j = 1, 2, ... , m, is
obtained for each group of random error according to
the above process. Then The fitting error under the
conditions of d, wr hx and hy is acquired by the
standard deviation of m groups of fitting error values is
calculated.
3.2 Initial Conditions of
Two-dimensional Simulation
The initial conditions used in the calculation are:
1) The facula center (x
0
,y
0
)=(0,0). The facula radius
w
0x
=w
0y
=50mm. The center power density
I
0
=100mW/cm
2
.
2) The ratio of the sampling point range to the facula
diameter wr=2. The sampling point interval d is
changed from 30mm to 60mm, and the step is 1mm.
The distance between the facula center and the
sampling point on the left side of it hx is changed from
0 to d/2, and the step is d/4. The distance between the
facula center and the sampling point under it hy is
changed from 0 to hx, and the step is d/4.
3) the standard deviation of sampling point error is
δ
0
=15%.
Influence of Sampling Point Setting on Fitting Error of Ideal Gaussian Beam
143
4) The number of groups of random error m = 10000.
3.3 Results of Two-dimensional
Simulation
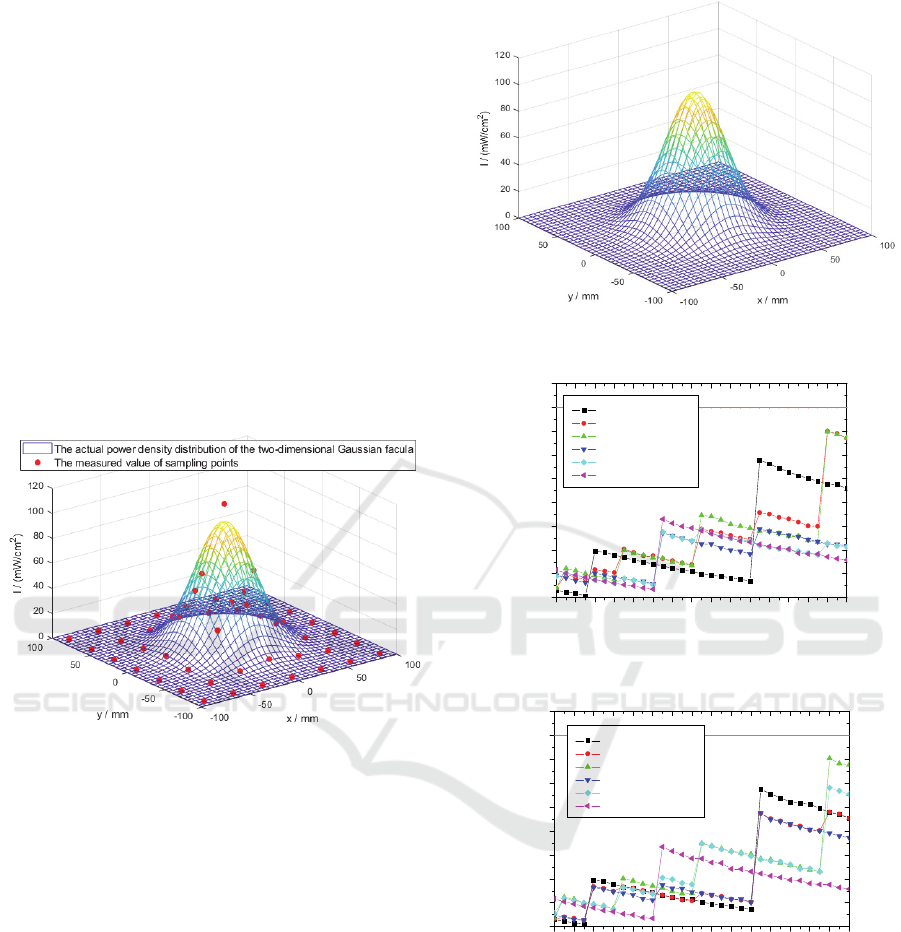
The actual distribution of the power density of the two-
dimensional Gaussian facula is shown in Figure 6.
When d=30mm, wr=2, hx=hy=0mm, a group of
random error of sampling points is selected, and the
measured value of sampling points is obtain as shown
in the red dot in Figure 6. The power density
distribution obtained by fitting the measured value of
the sampling points is shown in Figure 7, where
x
01
=0.30mm, w
0x1
=49.82mm, y
01
=0.32mm,
w
0y1
=49.98mm and I
01
=101.00mW/cm
2
, and the fitting
errors are (x
01
-x
0
)=0.30mm, (w
0x1
-w
0x
)=-0.18mm, (y
01
-
y
0
)=0.32mm, (w
0y1
-w
0y
)=-0.02mm and (I
01
-
I
0
)=1.00mW/cm
2
, respectively.
Figure 6: Gaussian facula and measured value of sampling
points.
A number of m=10000 groups of random error values
are selected, and a number of m=10000 groups of the
fitting errors (x
01
-x
0
)
j
, (w
0x1
-w
0x
)
j
, (y
01
-y
0
)
j
, (w
0y1
-w
0y
)
j
and (I
01
-I
0
)
j
are obtained. Then the fitting errors under
the conditions of d=30mm, wr=2 and hx=hy=0mm are
obtained: the fitting error of the facula center is (δ
xo
,
δ
y0
)=(0.23mm, 0.23mm), the fitting error of the facula
radius is (δ
w0x
, δ
w0y
)=(0.22mm, 0.22mm), and the
fitting error of the center power density is
δ
I0
=4.16mW/cm
2
.
When d, hx and hy change in the calculation range,
the simulation results of the fitting errors are as shown
in Figure 8 ~ Figure 12.
It can be seen from the above data:
1) Within the range of initial conditions of simulation
calculation, the fitting error of two-dimensional
simulation is less than that of one-dimensional
simulation. The reason is: there are more sampling
points
distributed in two-dimensional, and more
Figure 7: Result of two-dimensional fitting.
Figure 8: Fitting error of the facula center x
0
for two-
dimensional simulation.
Figure 9: Fitting error of the facula center y
0
for two-
dimensional simulation.
information is detected, then the fitting error is smaller.
2) The relationship between the fitting error and the
interval of sampling points is not monotonous
increasing or decreasing, but segmented. Because the
number of sensors has changed. With the increase of d,
the overall error of the next section is higher than that
of the previous section. While in a certain section, it is
basically monotonic decreasing. This is consistent with
one-dimensional simulation.
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
hx/d=0 hy/d=0
hx/d=1/4 hy/d=0
hx/d=1/4 hy/d=1/4
hx/d=1/2 hy/d=0
hx/d=1/2 hy/d=1/4
hx/d=1/2 hy/d=1/2
error of x
0
/ mm
d / mm
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
hx/d=0 hy/d=0
hx/d=1/4 hy/d=0
hx/d=1/4 hy/d=1/4
hx/d=1/2 hy/d=0
hx/d=1/2 hy/d=1/4
hx/d=1/2 hy/d=1/2
error of y
0
/ mm
d / mm
PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology
144

Figure 10: Fitting error of the facula radius w
0x
for two-
dimensional simulation.
Figure 11: Fitting error of the facula radius w
0y
for two-
dimensional simulation.
Figure 12: Fitting error of the center power density for two-
dimensional simulation.
3) It is assumed that, the admissible errors of the facula
center, facula radius and center power density are
1mm, 2.5mm (5%) and 10mW/cm
2
(10%),
respectively, which are represented by solid red lines
in the figure. When selecting the interval of sampling
points d, the fitting errors should not exceed the
admissible ones under all hx and hy conditions. It can
be seen from the figure that, in the initial condition
range of the simulation calculation, the fitting errors of
the facula center and the facula radius are smaller than
the admissible ones, and the fitting error of the center
power density exceeds the admissible one when
d>50mm. Therefore, in the design, d≤50mm should
be selected to ensure that all fitting errors do not exceed
the admissible ones. The interval range of sampling
points is larger than that allowed by one-dimensional
simulation.
4 CONCLUSIONS
Based on MATLAB and least square method, the one-
dimensional and two-dimensional fitting of Gaussian
distribution facula are carried out. The influence of
sampling point layout on fitting error is studied, and the
relationship between the fitting error and sampling
point interval is analyzed. The results show that, the
number of sampling points in the two-dimensional
simulation is larger, and the fitting accuracy is better
than that in the one-dimensional simulation under the
same sampling point interval. Because the actual facula
is a two-dimensional Gaussian distribution, the two-
dimensional simulation results shall be prioritized.
In the range of initial conditions of simulation
calculation, the interval of sampling points should be d
≤50mm, so that the fitting errors of facula center,
facula radius and center power density can be
controlled within the admissible ones.
REFERENCES
Bingkun Zhou, Yizhi Gao, Tirong Chen, et al.. 2000. Laser
principle(4th edition), National Denfense Industry Press,
Beijing.
Shenyong Ruan, Yongli Wang, Qunfang Sang, 2004.
MATLAB program design, Publishing house of
electronics industry, Beijing.
Lili Wang, Zhongwen Hu, Hangxin Ji, 2012. Laser facula
center location algorithm based on Gaussian fitting,
Journal of Applied Optics, 33(5), 985.
Bing Kong, Zhao Wang, Yusan Tan, 2002. Gaussian fitting
technique of laser facula, Laser Technology, 26(4),277.
C. Higgs, P.C. Grey, J.G. Mooney. 1999. Dynamic target
board for ABL ACT performance characterization,
Proceeding of SPIE, 3706, 216
J. Thomas Knudtson, Kenneth L. Ratzlaff. 1983. Laser beam
spatial profile analysis using a two-dimensional
photodiode array, Rev.Sci.Instrum, 54(7),856
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
0.0
0.5
1.0
1.5
2.0
2.5
3.0
hx/d=0 hy/d=0
hx/d=1/4 hy/d=0
hx/d=1/4 hy/d=1/4
hx/d=1/2 hy/d=0
hx/d=1/2 hy/d=1/4
hx/d=1/2 hy/d=1/2
error of w
0x
/ mm
d / mm
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 6
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
hx/d=0 hy/d=0
hx/d=1/4 hy/d=0
hx/d=1/4 hy/d=1/4
hx/d=1/2 hy/d=0
hx/d=1/2 hy/d=1/4
hx/d=1/2 hy/d=1/2
error of w
0y
/ mm
d / mm
30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60
4
5
6
7
8
9
10
11
12
error of I
0
/ (mW/cm
2
)
d / mm
hx/d=0 hy/d=0
hx/d=1/4 hy/d=0
hx/d=1/4 hy/d=1/4
hx/d=1/2 hy/d=0
hx/d=1/2 hy/d=1/4
hx/d=1/2 hy/d=1/2
Influence of Sampling Point Setting on Fitting Error of Ideal Gaussian Beam
145
