
An Optimization Method for a Multi-day Distribution Problem with
Shortage Supplies
Netiphan Amphaiphan
1
and Wasakorn Laesanklang
1,2
1
Department of Mathematics, Faculty of Science, Mahidol University, Rama VI Road,
Ratchathewi, Bangkok, 10400, Thailand
2
Centre of Excellence in Mathematics, CHE, Thailand
Keywords:
Multi-period Vehicle Routing Problem, Shortage Supplies, Distribution, Mixed Integer Programming Model.
Abstract:
We investigated a multi-day distribution problem while supplies are limited. This scenario can be found
in post-natural disasters or economic crisis such as floods, earthquakes, palm oil shortage crisis, etc. The
objective function of this problem is to minimize total traveling distance, unsatisfied cost, and variance of
supply delivery proportion. In order to solve this multi-day problem optimally, it requires large computing
memory and takes a long computational time. Therefore, we divided these large problems into multiple daily
sub-problems and solved the sub-problems with the exact method. The sub-problems were solved sequentially
for which the prior daily sub-problem is to be tackle first and the following daily sub-problems are defined
based on the prior daily sub-problem solution. Changes were applied to update demands and to adjust delivery
priority. There are three delivery priority setups proposing in this paper. Also, we present an experiment using
the three proposed methods to solve modified Solomon’s vehicle routing problem datasets which extended a
single period vehicle routing problem with time windows to be seven-day routing problems.
1 INTRODUCTION
This paper proposes an exact-heuristic hybrid method
to solve a multi-day distribution problem with short-
age supplies. Normally, supply distribution in normal
situation is an operation which has been studied for
many years. The problem has been shown in many
paper and text books such as N-location distribution
problem (Karmarkar and Patel, 1977) and produc-
tion distribution problem (Boudia et al., 2007). How-
ever, there are situations where supplies are limited in
which a normal distribution operation is not practical
because there are too many demands that cannot be
filled. Supplies shortages are not normally occur in
high or medium income countries. Although, emer-
gency and disaster situations may cause the supply
shortages. For example, in 2011, Thailand encoun-
tered an extreme flood triggered by Tropical Storm
Nock-Ten. There were 13.6 million people stuck
in the disaster area. Thai government transformed
government buildings, schools, university buildings
to be temporally shelters because majority of houses
were unable to occupied. People in these relieve care
needed food, medicine and other supplies so that they
could survive the day. Meanwhile, these commodi-
ties could not reproduce in the disaster area, they were
transported from other part of Thailand to a distribu-
tion center. The operation at distribution center was
indeed challenging as it must fill demands in remote
area, at which might not have road access. In some
case, the operation may have a limitation due to the
number of vehicles and their capacity rather than a
limitation of supplies. Recently, in 2019, there was
another tropical storm hit the northeastern of Thai-
land. There were reports of insufficient relieve goods
and distribution problem in post-disaster event. This
has shown that there were no efficient plan to deal
with the distribution problem with limited supplies in
Thailand.
An example of the real-life supply shortages were
the case when Thailand faced the palm oil crisis in
2011. Palm oil production was decrease and there
were no supplies in the market. An immediate policy,
which was order from the Thai government to limit
palm oil purchase per transaction to three liters. The
policy applies in order to prevent consumer to stock-
pile palm oil. Similarly, distributor cannot apply nor-
mal distribution operation because the best possible
solution is to have the palm oil products to sell near
distribution center. This plan will indeed effect cus-
356
Amphaiphan, N. and Laesanklang, W.
An Optimization Method for a Multi-day Distribution Problem with Shortage Supplies.
DOI: 10.5220/0009154703560363
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 356-363
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tomers who live very far from the distribution center
that they cannot have excess to the product in a rea-
sonable price. Therefore, these rare events needs a
special operation plan.
This paper proposes a method to find supply dis-
tribution plan especially when all demands cannot be
fulfilled. The solution of this problem gives a plan
to distribute supplies with one vehicle mode in multi-
ple periods. The plan should ration supplies equally
among the demand points. We present a mathematical
programming model for a multi-day distribution prob-
lem with shortage supplies. However, this model can-
not be solved as our sample problems are very com-
putationally expensive. Therefore, we implement a
method utilizing a mixed integer programming model
to tackle this problem by solving the problem in a
daily basis and to have demand information passing to
the next day problem to balance supplies distribution.
The goal is to generate routing plans for the whole
time period and to have an equal supply distribution.
The remaining of the paper is organized as fol-
lows. We discuss related research in Section 2. Sec-
tion 3 describes the problem and its assumptions.
It also present our weekly quadratic programming
model. Section 4 gives a daily problem and how our
plan is recalculated. Section 5 describes the dataset
used in this work and the results from our method.
Section 6 presents our conclusions.
2 LITERATURE REVIEW
There were several literature for transportation prob-
lem in post natural disasters. (
¨
Ozdamar et al., 2004)
proposed a model that generated an emergency logis-
tic plan for natural disaster. They investigated a sce-
nario when supplies were limited and there were pre-
diction of demands. (Liu et al., 2007) studied large-
scale emergency plans and proposed a mathematical
model to minimize the total unsatisfied demands. (Af-
shar and Haghani, 2012) developed a comprehensive
model for pick up and delivery schedule for natu-
ral disasters. (Hsueh et al., 2008) studied a vehicle
routing problem for disasters with two-phase deci-
sions, tactical decisions and routing decisions. (He
and Zhang, 2016) determined priority allocation co-
efficient for post-disaster relief supplies using set the-
ory. (Qin et al., 2017) investigated insufficient emer-
gency supplies in the initial period right after a dis-
aster event with uncertain demands of affected loca-
tions. This proposed solution method was split into
two stages, determining the serviced demand point
and optimizing the related factors such as a number of
used vehicles, supplies and routes. (Liu et al., 2019)
studied a location-routing problem for the early post-
earthquake where relief goods were insufficient. The
goal was to find a fair distribution plan using a de-
mand loss function.
Emergencies and disasters mainly create short
term insufficient supply situations. However, there
were researches dealing with long term supply short-
ages such as a distribution problem with limited in-
ventory (Chien et al., 1989) and blood supply chain
in Thailand (Chaiwuttisak et al., 2014).
There were many ways to solve large-scale prob-
lems such as local search, neighborhood search, ge-
netic algorithm, etc. Problem decomposition is a
technique that can be applied to make a large prob-
lem become smaller sub-problem so that the solver
find a solution faster. (Kim and Kim, 1999) decom-
posed a multi-period vehicle scheduling problem into
N single-retailer problems to generate delivery sched-
ule. (Cheng and Wang, 2009) investigated VRP with
time window constraints using decomposition tech-
nique to reduce the problem size. (Laesanklang and
Landa-Silva, 2017) also applied decomposition and
repair methods for home healthcare planning to ob-
tain a feasible solution.
There were a few research works in the litera-
ture tackled multi-period supplies shortage problem
such as blood supply chain in Thailand (Chaiwutti-
sak et al., 2014) and multi-depot production planning
(Parthanadee and Logendran, 2006). The studies on
general multi-period VRP with shortage supplies are
relatively rare. Our work investigates a multi-period
VRP with supply shortages while splitting the prob-
lem into multiple daily sub-problems.
3 MULTI-DAY DISTRIBUTION
WITH SHORTAGE SUPPLIES
This section describes the quadratic programming
model for the multi-day distribution problem with
shortage supplies. The problem is to generate a trans-
portation plan over a multi-day period with supply
shortage event. Therefore, solutions for this trans-
portation plan should distribute the products equally
to all demand nodes. This may differ from the normal
distribution operation for which it is to find the min-
imum operation cost. The assumptions for the multi-
day distribution problem with shortage supplies are
listed below.
1. Transportation costs and travel times are propor-
tional to travel distances. Also, transportation cost
from any location i to j in all periods are identical.
2. Distance from location i to location j equals to
An Optimization Method for a Multi-day Distribution Problem with Shortage Supplies
357

distance from location j to location i.
3. Each customer must be visited no more than once
a day.
4. The total delivered commodities must not exceed
vehicle capacity.
5. Each location must be visited no more than once
per day but that visit may have not fill the demand
in full.
6. All vehicles are homogeneous.
7. Demands are given for all locations for the whole
time horizon. Although, demands may accumu-
late if the demand point has not been visited.
Ideally, to have the best possible solution, the multi-
day problem should be solved as a whole. We may
present this problem using a quadratic programming
model.
3.1 Weekly Problem
As we mentioned in Section 1, we would like to find
delivery plans that have equally supply distribution
for every demand node. Therefore, the quadratic pro-
gramming model was proposed for this problem.
Table 1 presents notations to be used in this paper.
The notations can be grouped as sets, parameters, and
variables.
The decision is to assign a set of vehicles V to
make visit at a set of locations C at time period in a set
of time T. Each vehicle v ∈ V has maximum capacity
q
v
and each location i ∈ C also has demands on day
t ∈ T , represented by s
t
i
. We considered a distribution
with single depot so that c
0
and c
0
0
are artificial start
and end nodes where the two artificial nodes represent
one physical depot.
The problem is constructed based on graph where
nodes or vertices are locations to visit and the edges
are routes between the two locations. A variable x
v,t
i,l
is
a binary decision variable in which x
v,t
i,l
= 1 represents
that a vehicle v must make a visit at location l after
location i at day t, and x
v,t
i,l
= 0 otherwise. An assign-
ment to travel between location i and location j has
corresponding distance d
i, j
and travel time α
i, j
. Also,
an integer variable δ
v,t
i
is the arrival time of the vehi-
cle v ∈ V at location i ∈ C on day t ∈ T . y
t
i
is a binary
decision variable where its value is 1 when no vehicle
make visit at location i ∈ C on day t ∈ T , and y
t
i
= 0
indicates otherwise. A variable p
v,t
j
is a variable be-
tween 0 to 1 for determining delivery proportion. In
this problem, it is possible to delivery partial demands
as the supplies are very limited and rationing must
be enforce to distribute the commodity equally for all
Table 1: Notations for the multi-day distribution problem
with shortage supplies.
Sets
C A set of locations.
V A set of vehicles.
T A set of time period. ( T = {1, 2, ..., 7})
Parameters
d
i, j
Distance between node i and j.
M Penalty cost of not assigning visit a node.
α
i, j
Travel time from node i to j.
γ
t
i
Weight for each location i at time t.
q
v
Vehicle capacity of vehicle v
s
t
i
Demand of location i on day t
ω
1
A weight associated to total transportation cost.
ω
2
A weight associated to unsatisfied cost.
ω
3
A weight associated to variance of
proportion of delivered supply.
Variables
x
v,t
i, j
Binary decision variable with value 1 indicating
that vehicle v is assigned to visit i and then
move to visit j on day t, and 0 otherwise.
y
t
i
Binary decision variable with value of 1
indicating that visit i on day t is unassigned,
and 0 otherwise.
δ
v,t
i
Arrival time at node i assigned to vehicle v
on day t
p
v,t
i
Delivery proportion delivered to customer i by
vehicle v on day t (0 ≤ p
v,t
i
≤ 1)
demand points. Therefore, we define β
i
as the pro-
portion of delivered supplies and the total demands at
location i for the whole time horizon. This proportion
β
i
can be written as
β
i
=
∑
t∈T
∑
v∈V
p
v,t
i
· s
t
i
∑
t∈T
s
t
i
.
In order to measure equal distribution, we then mini-
mize the variance of β
i
. Note that we use
¯
β as a nota-
tion of an average of all β
i
.
From the above notation, we present the mathe-
matical model for the multi-day distribution problem
with shortage supplies below.
Min. ω
1
∑
t∈T
∑
i, j∈C
∑
v∈V
d
i, j
· x
v,t
i, j
+ ω
2
∑
t∈T
∑
i∈C
∑
v∈V
(s
t
i
− s
t
i
· p
v,t
i
)
+ ω
3
·
∑
j∈C
(β
j
−
¯
β)
2
|C|
(1)
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
358

Subject to
∑
v∈V
∑
i∈C∪{c
0
}
x
v,t
i,l
+ y
t
l
= 1 ∀l ∈ C, t ∈ T (2)
∑
i∈C∪{c
0
0
}
x
v,t
c
0
,i
= 1 ∀v ∈ V, t ∈ T (3)
∑
i∈C∪{c
0
}
x
v,t
i,c
0
0
= 1 ∀v ∈ V, t ∈ T (4)
∑
i∈C∪{c
0
}
x
v,t
i,r
=
∑
j∈C∪{c
0
0
}
x
v,t
r, j
∀v ∈ V, r ∈ C, t ∈ T (5)
∑
i∈C
s
t
i
· p
v,t
i
≤ q
v
∀v ∈ V, t ∈ T (6)
∑
i∈C∪{c
0
}
x
v,t
i, j
≥ p
v,t
j
∀v ∈ V, j ∈ C, t ∈ T (7)
∑
i∈C∪{c
0
}
x
v,t
i, j
≤ M · p
v,t
j
∀v ∈ V, j ∈ C, t ∈ T (8)
s
t
j
· p
v,t
j
≥ 0.05 · q
v
· x
v,t
i, j
∀v ∈ V, i, j ∈ C ∪ {c
0
}, t ∈ T
(9)
x
v,t
i, j
+ x
v,t
j,i
≤ 1 ∀v ∈ V, i, j ∈ C, i 6= j, t ∈ T (10)
δ
v,t
i
+α
i, j
−(1−x
v,t
i, j
)·M ≤ δ
v,t
j
∀v ∈ V, i ∈C∪{c
0
},
j ∈ C ∪ {c
0
0
}, i 6= j, t ∈ T (11)
The objective function of the proposed multi-day dis-
tribution with shortage supplies is to minimize a sum-
mation of three weighted costs (1). The first cost is the
total travelling distances for the whole time horizon.
The second cost is the unsatisfied cost, which is mea-
sured from the number of accumulated demands that
have not been served at the end of the time horizon.
The third cost is to have equal supply distribution,
which is measured by the percentage of delivered sup-
ply variance. The percentage delivered supply vari-
ance is to measure differences between delivery pro-
portion, in which the ideal solution should be the case
where all locations get the same proportion of supply
or the delivery proportion variance should equal to 0.
Therefore, the proposed model is to minimising the
percentage supply variance should provide a fair dis-
tribution plan. There are corresponding weights to the
above objective function costs which are ω
1
, ω
2
, and
ω
3
, respectively.
We set the variance as the highest priority to min-
imize. Hence, the weight ω
3
is the highest in this
objective function. The second priority is to mini-
mize the cost of unsatisfied demands where the cor-
responding weight is ω
2
. The lowest priority is to
minimize the cost of travelling distances, where the
weight is ω
1
. We followed weight parameter setting
from (Rasmussen et al., 2012). These weights are set
by ω
1
= 1, ω
2
=
∑
i∈B
∑
j∈B
d
i, j
and ω
3
= ω
2
|C| max
i∈C,t∈T
γ
t
i
.
The proposed mathematical model has the follow-
ing constraints to complete the multi-day distribution
problem with shortage supplies. First, constraint (2)
ensures that a visit l ∈ C is either assigned to a ve-
hicle v ∈ V by having one of x
v,t
i,l
= 1 or left unas-
signed by having y
t
l
= 1 for every time period t ∈ T .
For each day, a vehicle must leave a depot from con-
straint (3) and it must return to depot at the end of
the day (4). During the day, a vehicle must travel to
visit a list of locations, where the flow conservation
constraint guarantees the condition such that a vehi-
cle v arrives at a location l, it must leave that location
(5). Constraint (6) defines maximum vehicle capacity
for which the total delivery must not exceed. Con-
straints (7) and (8) control that the p
v,t
j
can be more
than 0 only if the sum of x
v,t
i, j
is 1. Furthermore, a visit
to be made must delivery supplies at least 5 % of the
vehicle capacity. Constraint (10) prevents vehicle v to
return to a location i ∈C if it has been left the location.
Constraint (11) is a sub-tour elimination constraint in-
dicating that the arrival time at location j ∈ C must be
more than the arrival time at location i ∈ C, given that
the vehicle v ∈ V must visit location j after location i
(x
v,t
i, j
= 1) (Moshref-Javadi and Lee, 2016).
The mathematical programming model for the
multi-day distribution problem with shortage supplies
above is a quadratic programming model as it ap-
plies variance as one of the objective function. The
problem is a np-hard so that applying exact method
to solve this problem may not be the best approach.
Therefore, we propose a method to sequentially solve
daily sub-problems using a mixed integer program-
ming model and mathematical solver to tackle this
problem.
4 SOLUTION METHOD
This section explains our proposed method to solve
the multi-day distribution problem with shortage sup-
plies. We formulate a MIP model for a daily problem
and use it to solve the multi-day problem. The multi-
day problem is then split into multiple daily problems.
Each daily problem is then solved by the exact solver
to get the best solution with a limited computation
time. A next day problem is then updated with de-
mands and historical supplies to adjust the next day
delivery plan.
Algorithm 1 illustrates the steps of our proposed
method. A multi-period vehicle routing problem can
be denoted by P = (V, B), where V is the set of ve-
hicles and B is the set of locations. The goal is to
assign vehicles to make visits at multiple locations
within the time horizon. Our proposed method has
An Optimization Method for a Multi-day Distribution Problem with Shortage Supplies
359

three steps, which are decomposing problem, solving
sub-problems and updating parameters. At the updat-
ing parameter step, demands and delivery priority of
a problem at period t depend on the solution of the
problem at period t − 1. This step allows us to solve
the problem as a day-by-day in sequential basis. The
updating parameter step is the key to balance the sup-
ply delivery.
Algorithm 1: Algorithm for solution method.
Data: Problem P=(V,B), V is the set of
vehicles and B is the set of all
locations
Result: {SolutionPath} sub sol
1 begin
2 {Problem} T=ProblemDecomposition
(V,B);
3 SortSubProblem(t);
4 for day t ∈ T do
5 sub sol (t)=cplex.solve (t, s
t
i
, γ
t
i
);
6 Update data (d
t
i
, γ
t
i
);
7 end
8 end
4.1 Problem Decomposition
Our proposed method tackles this problem in a day-
by-day basis. Therefore, we split this one week
problem into seven daily sub-problems. These sub-
problems will be solved sequentially, such that the
sub-problem at period t will be processed before the
sub-problem at period t + 1. Structure of each sub-
problem is identical with the full problem such that
it has a set of vehicles and a set of locations with all
constraints applied.
The daily sub-problems will be formulated as a
mixed integer programming model and to be solved
by a mathematical solver.
4.2 Daily Sub-problem
We implement a mixed integer programming model
for the daily sub-problems. Originally, our multi-day
problem is a quadratic programming problem as it
is required to have balance supply distribution. In
this daily problem, we re-implement the quadratic
term into linear factor. Hence, we replace the term
∑
j∈C
(β
j
−
¯
β)
2
|C|
with a weighted delivered demands γ
t
k
j
·
s
t
k
j
· p
v,t
k
j
. To balance delivery priority, we use weight
adjustment step which will be explained in the next
subsection.
Therefore, mixed integer programming model for
the daily problem is presented below. Note that at
time period t
k
∈ T , all variables are considered at time
t
k
.
Min.
∑
i, j∈C∪{c
0
,c
0
0
}
∑
v∈V
d
i, j
· x
v,t
k
i, j
+
∑
i∈C
M ·y
t
k
i
−
∑
v∈V
∑
j∈C
γ
t
k
j
· s
t
k
j
· p
v,t
k
j
(12)
Subject to
∑
v∈V
∑
i∈C∪{c
0
}
x
v,t
k
i, j
+ y
t
k
j
= 1 ∀ j ∈ C (13)
∑
j∈C∪{c
0
0
}
x
v,t
k
c
0
, j
= 1 ∀v ∈ V (14)
∑
i∈C∪{c
0
}
x
v,t
k
i,c
0
0
= 1 ∀v ∈ V (15)
∑
i∈C∪{c
0
}
x
v,t
k
i,r
=
∑
j∈C∪{c
0
0
}
x
v,t
k
r, j
∀v ∈ V, r ∈ C (16)
∑
j∈C
s
t
k
j
× p
v,t
k
j
≤ q
v
∀v ∈ V (17)
∑
i∈C∪{c
0
}
x
v,t
k
i, j
≥ p
v,t
k
j
∀v ∈ V, j ∈ C (18)
∑
i∈C∪{c
0
}
x
v,t
k
i, j
≤ M · p
v,t
k
j
∀v ∈ V, j ∈ C (19)
s
t
k
j
· p
v,t
k
j
≥ 0.05 ·v
v
· x
v,t
k
i, j
∀v ∈ V, i ∈ C ∪ {c
0
}, j ∈ C
(20)
x
v,t
k
i, j
+ x
v,t
k
j,i
≤ 1 ∀v ∈ V, i, j ∈ C, i 6= j (21)
δ
v,t
k
i
+ α
i, j
− (1 − x
v,t
k
i, j
) · M ≤ δ
v,t
k
i
∀v ∈ V,
i ∈ C ∪{c
0
}, j ∈ C ∪ {c
0
0
}, i 6= j (22)
4.3 Updating Parameters
Updating parameter step is to balance delivery distri-
bution. The problem assumption does not require that
all locations have to be visited in one day, but visits
may distribute for the whole horizon. For one day
plan, it is possible that some locations left unassigned
or some locations may be visited but they are received
partial demands.
Table 2 presents settings for γ
t
j
parameter. The
parameter sets delivery priority for which the assign-
ments should prioritise a visit j over the other visits at
day t when the visit has the highest γ
t
j
. In this paper,
we propose three parameter settings. The first setting
is the case where the γ
t
j
remains the same for every
time period. The second setting is to double the prior-
ity value to locations that have not been visited in the
time period t − 1. The third setting is to double the
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
360

Table 2: Three setups for changing weight of locations.
Setup Description
1 γ
t
j
= γ
t−1
j
for all locations.
2 γ
t
j
= 2γ
t−1
j
for all locations that have not
been visited on day t −1.
3 γ
t
j
= 2γ
t−1
j
for some locations that have
not been visited on day t −1.
priority value for some locations that have not been
visited on day t −1.
For all these cases, we assume that their demands
are accumulated if the needs have not been delivered.
Therefore, the demand parameter is to be changed by
d
t
i
= d
t−1
i
+ d
t−1
i
· (1 − p
v,t−1
i
). For example, location
a has ordered 10 units of product every day. On the
first day, this location may receive the commodity for
6 units. Thus, on day 2, the location a may request
this product for another 10 units. Hence, an updated
demand for location a on day 2 is equal to 10+(10-
6)=14.
The method was implemented in JAVA with a
well-known commercial mathematical solver, IBM
ILOG CPLEX Optimization Studio (CPLEX) in a
process to solve the daily MIP model.
5 EXPERIMENTS AND
COMPUTATIONAL RESULTS
In this section, we explain our modified datasets, ex-
perimental setups and results of the experiment.
5.1 Datasets
We use modified Solomon’s datasets in our experi-
ment. The datasets have three instance types which
are randomly generated type (R), clustered type (C),
and mixed type (RC). Originally, Solomon’s datasets
are created for a single period vehicle routing prob-
lem with time windows. The objective function of the
original datasets are to find a routing plan which has
the lowest number of assigned vehicles and the short-
est total travel distances. The constraints of the orig-
inal problem are vehicle capacity, delivery time win-
dows and the demands for each location which every
location must be served.
In our modified Solomon’s dataset, a single pe-
riod VRPTW is expanded to be a seven-day schedul-
ing problem. There are four instances for each origi-
nal dataset type. Each new instance has 25 visit loca-
tions and the original demands are requested repeat-
edly for seven days. The modified problems do not
require delivery time window, in which the delivery
can be made anytime in a day. Therefore, we created
12 modified seven-day instances for our experiment.
We also set initial location visiting priority randomly,
which had range between 1 to 3.
5.2 Results
In this section, we present results from our experi-
ments. This experiment compared solutions of the
modified Solomon’s datasets which obtained from the
proposed algorithm. We set the computational time to
return the best feasible solution if the daily computa-
tional time exceed five minutes. Thus, the maximum
computation times for a weekly problem is 35 min-
utes.
Table 3 presents objective values of solutions from
three visiting priority setups. Each setup in the ta-
ble presents four objective values, which are total
travel distance (Distance), unsatisfied cost (Unsat-
isfied), supply distribution variance (Variance), and
the total weekly cost (Weekly cost). There are 12
modified Solomon’s instances presented in the table.
Bold texts in the table present the best objective value
among the three setups.
Consider the number of the cheapest weekly cost
solutions, there are 3, 2, and 7 best solutions from
Setup 1, Setup 2, and Setup 3, respectively. The
weighted summation of objective values shows that
the unsatisfied cost is the most influential value, fol-
lowed by the percentage of delivered supply variance,
and the total travel distance.
We analyze the result based on the original
Solomon’s dataset types which are randomly gener-
ated dataset (R), clustered generated dataset (C), and
mixed generated dataset (RC).
For dataset type R, Setup 3 provided the best over-
all solutions, in which the Setup 3 found the lowest
weekly cost solutions for three instances. The main
contribution was that the Setup 3 had the lowest over-
all unsatisfied delivery plan. Setup 1 provided one
solution with the lowest weekly cost. Also, Setup 1
had the lowest travel distances for every solution for
this dataset type. On the other hand, Setup 2 did not
find the best solution and had the highest weekly cost.
For data type C, Setup 2 had the best solution for
two instances when comparing the weekly cost while
Setup 1 and Setup 3 had the best solution for one in-
stance for each setup. Setup 3 also had solution with
the shortest distance for three instances.
For data type RC, Setup 3 provided the minimum
unsatisfied cost, variance and weekly cost of three
datasets. Setup 1 and Setup 2 had two solutions pro-
viding the shortest distances. From the result, Setup 2
An Optimization Method for a Multi-day Distribution Problem with Shortage Supplies
361
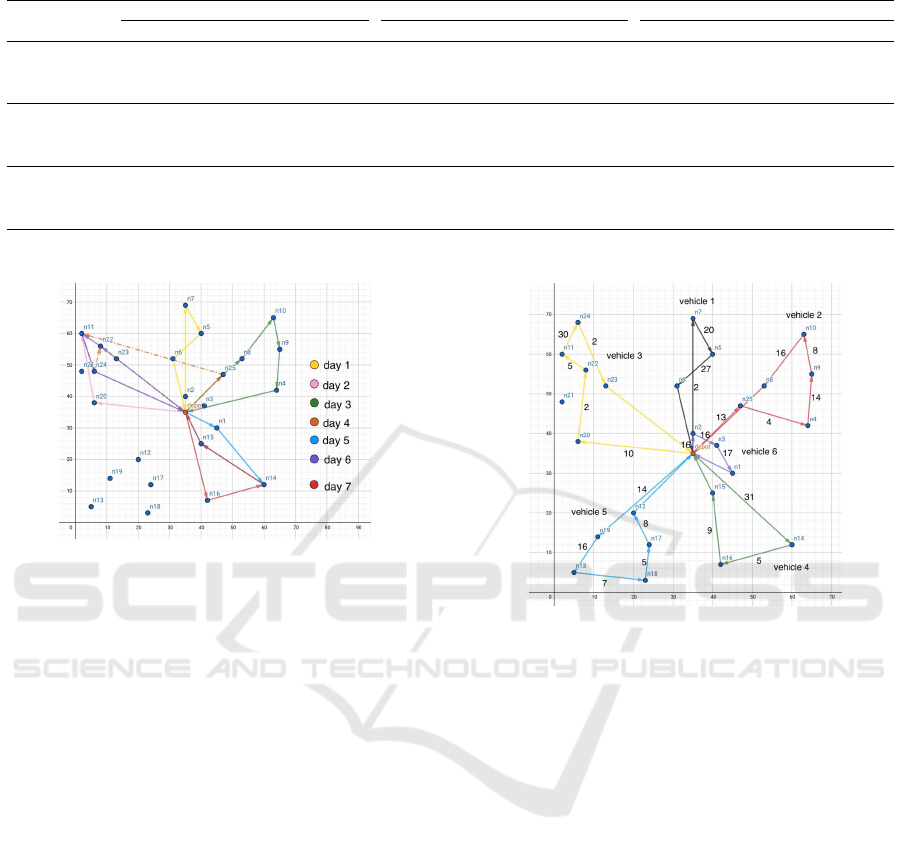
Table 3: Solution weighted costs for the modified Solomon’s Dataset.
Setup 1 Setup 2 Setup 3
Datasets Distance Unsatisfied Variance Weekly cost Distance Unsatisfied Variance Weekly cost Distance Unsatisfied Variance Weekly cost
Dataset 1-Type R 3,717 5,257,411 39,755 5,300,883 3,789 6,519,331 53,007 6,576,127 3,999 4,849,787 26,504 4,880,290
Dataset 2-Type R 3,751 11,555,526 92,762 11,652,039 4,709 12,321,124 92,762 12,418,595 4,036 11,780,452 92,762 11,877,251
Dataset 3-Type R 3,465 8,486,067 66,259 8,555,791 4,058 8,170,676 79,511 8,254,244 4,091 7,094,634 53,007 7,151,732
Dataset 4-Type R 2,670 9,910,719 66,259 9,979,648 3,467 11,361,697 106,014 11,471,178 3,042 9,741,450 119,266 9,863,757
Dataset 1-Type C 2,510 19,648,281 159,021 19,809,813 2,460 19,660,473 145,769 19,808,702 2,320 19,682,029 172,273 19,856,622
Dataset 2-Type C 2,276 12,176,945 119,266 12,298,487 2,760 13,080,714 106,014 13,189,488 2,627 12,211,753 92,762 12,307,142
Dataset 3-Type C 3,482 24,555,669 172,273 24,731,424 3,445 24,554,433 172,273 24,730,150 3,393 24,610,267 172,273 24,785,932
Dataset 4-Type C 3,791 18,510,574 145,769 18,660,135 3,696 19,305,326 145,769 19,454,791 3,595 18,402,617 145,769 18,551,981
Dataset 1-Type RC 3,603 29,517,301 185,525 29,706,428 3,636 29,551,403 198,776 29,753,815 4,789 29,610,417 172,273 29,787,479
Dataset 2-Type RC 4,550 18,110,902 159,021 18,274,473 4,554 17,572,174 159,021 17,735,749 4,899 15,971,893 145,769 16,122,561
Dataset 3-Type RC 3,779 6,944,624 66,259 7,014,661 3,560 6,980,138 66,259 7,049,957 3,625 6,907,342 66,259 6,977,226
Dataset 4-Type RC 3,504 12,491,983 92,762 12,588,249 3,468 13,007,388 106,014 13,116,870 3,551 12,118,460 145,769 12,267,781
where ω
1
= 1, ω
2
= 17669 and ω
3
= 1325175
Remark: Bold texts present the best objective value among the three setups.
Figure 1: A routing plan of vehicle 1 for dataset 2 type R.
did not perform well when considered weekly costs,
unsatisfied demands and supply distribution variance.
Overall, Setup 3 found solutions with the lowest
weekly cost, which contributed from low unsatisfied
demands and delivered supply variance. Setup 1 had
the shortest total distance.
As we mention that we preferred a solution with
equal supplies distribution. From this view, we can
conclude that Setup 3 is the best setup because it pro-
vided the best solution for seven instances. From Ta-
ble 3, we recommended that the dataset type R should
be solved by applying Setup 1 because it provides the
best overall costs. Next, we present a solution from
using Setup 1 to solve Dataset 2-Type R.
Figure 1 illustrates a 7-day vehicle scheduling so-
lution for vehicle 1 applying setup 1 to solve Dataset
2-Type R. The instance has 25 visiting locations and
one service depot. There are six vehicles, each has
capacity of 50 units. From the figure, vehicle 1 is de-
ployed every day. There are locations where the vehi-
cle has visited multiple days such as a path from lo-
cation n
14
to location n
15
and return to depot on day 5
and day 7. The solution also shows the case where the
visiting order may not so efficient in term of travelling
distances, such as a route on day 1 (yellow path). This
is because the sub-problem solution is not the optimal
solution because the mathematical solver reaches the
Figure 2: A routing plan of all vehicles on the first period
using Setup 1.
computation time limit.
Figure 2 displays a one-day plan of all vehicles.
Each line represents a vehicle path to delivery com-
modities. Numbers on each line represent the number
of commodity to delivery at destination location. For
example, the plan for vehicle 5 is to delivery 14 units
at location n
19
, 16 units at location n
13
, 7 units at lo-
cation n
18
, 5 units at location n
17
, 8 units at location
n
12
and return to depot. From this one-day plan, six
vehicles make visits to 24 locations and only one lo-
cation, n
21
, has not been visited on day 1. The plan to
visit location n
21
is on day 3 and day 6.
6 CONCLUSIONS AND FUTURE
WORK
This paper explains a multi-day distribution problem
while supplies are shortage or there are transporta-
tion difficulties limiting supply delivery. The aim is
to build visiting plans having fair supply distribution
over planning horizon. We assume a constant de-
mand from every location every day, which then accu-
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
362

mulated with unsatisfactory demands from previous
days.
We propose a hybrid heuristic method to tackle
this multi-day problem as multiple daily sub-
problems. Each sub-problem was solved by a mixed-
integer programming model. We applied heuristic de-
livery priority distribution, so that the locations that
had not been visited on previous days had higher vis-
iting priority. There were three priority distribution
setups applied in our experiment, which were dou-
ble the priority every locations that had not been vis-
ited, double the priority for some locations that had
not been visited, and no priority changes as a control
group. We tested our proposed method with 12 mod-
ified Solomon’s instances.
Our future works includes expanding problem
cases, improving the current algorithm and exploring
other solution approaches. To expand problem cases,
we may added due date and time window constraints
can be included as our future works. It is necessary to
improve the current algorithm to obtain an optimal so-
lution. Our proposed algorithm can also be improved
to tackle larger problems. Also, our future works will
apply other heuristic methods to this problem, such
as neighbourhood search, genetic algorithm, and con-
structive heuristic methods to compare results with
this hybrid heuristic approach.
ACKNOWLEDGEMENTS
We would like to thank Science Achievement Schol-
arship of Thailand (SAST) for financial support.
REFERENCES
Afshar, A. and Haghani, A. (2012). Modeling integrated
supply chain logistics in real-time large-scale disaster
relief operations. Socio-Economic Planning Sciences,
46(4):327–338.
Boudia, M., Louly, M. A. O., and Prins, C. (2007). A
reactive grasp and path relinking for a combined
production–distribution problem. Computers & Op-
erations Research, 34(11):3402–3419.
Chaiwuttisak, P., Smith, H., Wu, Y., and Potts, C. (2014).
Blood supply chain with insufficient supply: a case
study of location and routing in thailand. Lecture
Notes in Management Science, 6:23–31.
Cheng, C.-B. and Wang, K.-P. (2009). Solving a vehicle
routing problem with time windows by a decomposi-
tion technique and a genetic algorithm. Expert Sys-
tems with Applications, 36(4):7758–7763.
Chien, T. W., Balakrishnan, A., and Wong, R. T. (1989).
An integrated inventory allocation and vehicle routing
problem. Transportation science, 23(2):67–76.
He, S. and Zhang, L. (2016). Location-routing model
for post-disaster initial stage relief supplies based on
priority level. Chemical Engineering Transactions,
51:973–978.
Hsueh, C.-F., Chen, H.-K., and Chou, H.-W. (2008). Dy-
namic vehicle routing for relief logistics in natural dis-
asters. In Vehicle routing problem. IntechOpen.
Karmarkar, U. S. and Patel, N. R. (1977). The one-period,
n-location distribution problem. Naval Research Lo-
gistics Quarterly, 24(4):559–575.
Kim, J.-U. and Kim, Y.-D. (1999). A decomposition ap-
proach to a multi-period vehicle scheduling problem.
Omega, 27(4):421–430.
Laesanklang, W. and Landa-Silva, D. (2017). Decomposi-
tion techniques with mixed integer programming and
heuristics for home healthcare planning. Annals of
Operations Research, 256(1):93–127.
Liu, C., Kou, G., Peng, Y., and Alsaadi, F. E. (2019).
Location-routing problem for relief distribution in the
early post-earthquake stage from the perspective of
fairness. Sustainability, 11(12):3420.
Liu, D., Han, J., and Zhu, J. (2007). Vehicle routing for
medical supplies in large-scale emergencies. Lecture
Notes in Operations Research, 8:412–419.
Moshref-Javadi, M. and Lee, S. (2016). The customer-
centric, multi-commodity vehicle routing problem
with split delivery. Expert Systems with Applications,
56:335–348.
¨
Ozdamar, L., Ekinci, E., and K
¨
uc¸
¨
ukyazici, B. (2004). Emer-
gency logistics planning in natural disasters. Annals of
operations research, 129(1-4):217–245.
Parthanadee, P. and Logendran, R. (2006). Periodic product
distribution from multi-depots under limited supplies.
Iie Transactions, 38(11):1009–1026.
Qin, J., Ye, Y., Cheng, B.-r., Zhao, X., and Ni, L. (2017).
The emergency vehicle routing problem with uncer-
tain demand under sustainability environments. Sus-
tainability, 9(2):288.
Rasmussen, M. S., Justesen, T., Dohn, A., and Larsen, J.
(2012). The home care crew scheduling problem:
Preference-based visit clustering and temporal depen-
dencies. European Journal of Operational Research,
219(3):598–610.
An Optimization Method for a Multi-day Distribution Problem with Shortage Supplies
363
