
Q-Credit Card Fraud Detector for Imbalanced Classification using
Reinforcement Learning
Luis Zhinin-Vera
a
, Oscar Chang
b
, Rafael Valencia-Ramos
c
, Ronny Velastegui
d
,
Gissela E. Pilliza
e
and Francisco Quinga Socasi
f
School of Mathematical and Computational Sciences, Yachay Tech University, 100650, Urcuqui, Ecuador
Keywords:
Agents, Credit Card Fraud Detector, Deep Learning.
Abstract:
Every year, billions of dollars are lost due to credit card fraud, causing huge losses for users and the financial
industry. This kind of illicit activity is perhaps the most common and the one that causes most concerns in the
finance world. In recent years great attention has been paid to the search for techniques to avoid this significant
loss of money. In this paper, we address credit card fraud by using an imbalanced dataset that contains
transactions made by credit card users. Our Q-Credit Card Fraud Detector system classifies transactions
into two classes: genuine and fraudulent and is built with artificial intelligence techniques comprising Deep
Learning, Auto-encoder, and Neural Agents, elements that acquire their predicting abilities through a Q-
learning algorithm. Our computer simulation experiments show that the assembled model can produce quick
responses and high performance in fraud classification.
1 INTRODUCTION
Currently, fraud is the number one enemy in the busi-
ness world. It affects industries and organizations and
accounts for the big money invested in fraud predic-
tion researching. The constant grow of this problem
has strongly promoted the development of new tech-
nologies to counteract fraudsters. The last advances
in credit card fraud detection include top technologies
themes such as Artificial Neural Network (ANN),
Deep Learning and Intelligent Agents. In particular
the implementation of agents has become important
since it produces effective, quick acting monitoring
of credit card fraud transactions, reducing the risk of
fraud or other financial traps that could signify losses.
A quick response is essential because fraudsters are
constantly creating new elaborated treachery mecha-
nisms.
In terms of a robust functional system the main
goal is to detect the highest possible number of
fraudulent transactions using a finite dataset, in
a
https://orcid.org/0000-0002-6505-614X
b
https://orcid.org/0000-0002-4336-7545
c
https://orcid.org/0000-0002-1036-1817
d
https://orcid.org/0000-0001-8628-9930
e
https://orcid.org/0000-0001-6386-9254
f
https://orcid.org/0000-0003-3213-4460
our case treated by Principal Component Analysis
(PCA) approaches to anonymize the user and min-
imizes/maximize data correlation. Since frauds oc-
curs with more frequency than regular transactions,
databases are always imbalanced. This paper de-
velops a fraud detection methodology that resolves
the problem of imbalanced classification by combin-
ing the processing capacities of neural agents and
Q-learning, establishing a promising way to satisfy
quick acting and high precision requirement. The
Reinforcement Learning method slightly outperforms
neural networks while a similar representation is used
(Wiering et al., 2011).
2 RELATED WORK
2.1 Credit Card Fraud Detection
An approach called Long Short-term Memory Recur-
rent Neural Network (LSTM) is used. Authors imple-
ment an ANN for detecting credit card fraud, taking
into account sequences of transactions occurred in the
past, in order to determine whether a new transaction
is legitimate or fraudulent (Wiese and Omlin, 2009).
Checking the usage patterns of a user in previous
transactions to detect a credit card frauds is suggested
Zhinin-Vera, L., Chang, O., Valencia-Ramos, R., Velastegui, R., Pilliza, G. and Socasi, F.
Q-Credit Card Fraud Detector for Imbalanced Classification using Reinforcement Learning.
DOI: 10.5220/0009156102790286
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 279-286
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
279

(Dighe et al., 2018). They compare the usage pattern
and current transaction, to classify it as either fraud
or a legitimate transaction. Among the techniques
implemented are KNN, Na
¨
ıve Bayes, CFLANN, M-
Perceptron and DTrees.
Credit cards frauds have no constant patterns is
stated (Pumsirirat and Yan, 2018). Therefore, the use
of an unsupervised learning is necessary. They take
account that the frauds are committed once through
online mediums and then the techniques change. To
solve this issue, they implement a deep Auto-encoder
model and a restricted Boltzmann machine, that can
reconstruct normal transactions to find anomalies in
the patterns.
An intelligent agent can obtain a high rate of fraud
transaction with low false alarm rate, providing a con-
venient way to detect frauds (Chukwuneke, 2018).
Their implementation of the intelligent agent is focus
on detect the fraud when transaction is in progress,
taking into account the costumers pattern, and any de-
viation from the regular pattern is considered to the
fraudulent transaction.
2.2 Imbalanced Classification
Research work in imbalanced data classification is fo-
cused on two levels: data level and algorithmic level.
In data level, the objective is balance the class dis-
tribution by manipulating the training samples, tak-
ing into account the over-sampling minority class,
the under sampling majority class and their combi-
nations. The authors takes into account that the over-
sampling can lead to overfitting while under-sampling
lose valuable information on the majority class. On
the other hand, the objective of the algorithmic level
methods, is increase the importance of minority class
by improving algorithms by decision threshold ad-
justment, cost-sensitive learning and ensemble learn-
ing (Lin et al., 2019). An alternative loss function in
deep neural network that can capture the classification
errors from both minority class and majority class is
established (Wang et al., 2016). Extracting hard sam-
ples of minority classes and improved the bootstrap-
ping sampling algorithm which ensure the training
data in each mini-batch, by batch-wise optimization
with Class Rectification Loss function (Dong et al.,
2019).
2.3 Reinforcement Learning in
Classification
Recently, the deep reinforcement learning has had ex-
cellent results, because it can assist classifiers to learn
important features or select good instances from noisy
data. The authors understand the classification task as
sequential decision-making process, that uses a multi-
ple agents interacting with the environment to obtain
the optimal policy of classification. However, the in-
teraction between agents and environment, generate
an extremely high time complexity (Lin et al., 2019).
Establishing a deep reinforcement learning model di-
vided into instance selector and relational classifier, to
learn the relationship classification in noisy text data.
The instance selector part, implements an agent se-
lects high quality sentence from noisy data while the
relational classifier part learns from the previous se-
lected data and give a reward to the instance selector.
The finally model obtains a better classifier and high-
quality data set (Feng et al., 2018). A deep reinforce-
ment learning framework for time series data classi-
fication is established. This framework use a specific
reward function and a clearly formulated Markov pro-
cess (Martinez et al., 2018). The information avail-
able about imbalanced data classification with rein-
forcement learning is quite limited.
3 TECHNICAL BACKGROUND
3.1 Q-Learning
Q-Learning is one far-reaching reinforcement learn-
ing techniques that does not require a model of the
environment to learn to execute complex tasks. Es-
sentially Q-Learning makes possible for an algorithm,
to learn a sequential task, where rewards are re-
leased in a step by step fashion, until a journey called
”Episode” is completed. After training the ”educated”
agent develops a road map memory called ”policy”,
usually represented by a matrix Q, which optimizes
rewards capture trajectories in any definable environ-
ment. Q(s
t
,a
t
) gives the value of taking action a
t
in
a state s
t
. Equation 1 is the leading actor of the Q-
learning algorithm, derived from the Bellman equa-
tion by considering the first and second term of an
infinite series (Watkins and Dayan, 1992):
Q
obs
(s
t
,a
t
) = r + γmax
a
Q(s
t+1
,a
t+1
), (1)
where γ is the discount factor which manages the bal-
ance between immediate and future rewards. In this
equation the value of Q(s
t
,a
t
) of state and action is
given by the sum of the reward r with the discounted
maximum future expected reward after moving to the
next state S
t+1
. The value of Q
obs
(s
t
,a
t
) is com-
puted by an agent and then is updated with its the
own estimate of Q
∗
(s
t
,a
t
) in a Q-table. The term
max
a
Q(s
t+1
,a
t+1
) gives the maximum value for all
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
280
actions in the following state. Q-learning is an off-
policy algorithm since during training it updates the
Q-values without making any assumptions about the
actual policy being followed (Li et al., 2019).
It should be noted that in low-dimensional finite
state spaces, Q-functions are recorded by a table (ma-
trix). However in high-dimensional continuous state
spaces, Q functions cannot be resolved unless a deep
Q-learning algorithm is used as mediator to fit the Q-
function with a deep neural network producing fea-
ture rich data (Lin et al., 2019).
3.2 Data Description
The dataset contains transactions made by credit cards
in September 2013 by European cardholders, it repre-
sents transactions that occurred in two days, where we
have 492 frauds out of 284,807 transactions (MLG-
Kaggle, 2015), notice the strong unbalancing between
fraud and legal trades, typical of this kind of big
business. The database contains numerical variables
which have been hidden using PCA (Principal Com-
ponent Analysis) transformation. These 28 features
named V1,V 2, ...,V 28 contain confidential data of the
users and are non-reversible, thus protecting the orig-
inal characteristics of the data. There are two special
features that have not been transformed using PCA,
these are Time and Amount. There is also an im-
portant variable called Class, which is a fundamental
value in the database.
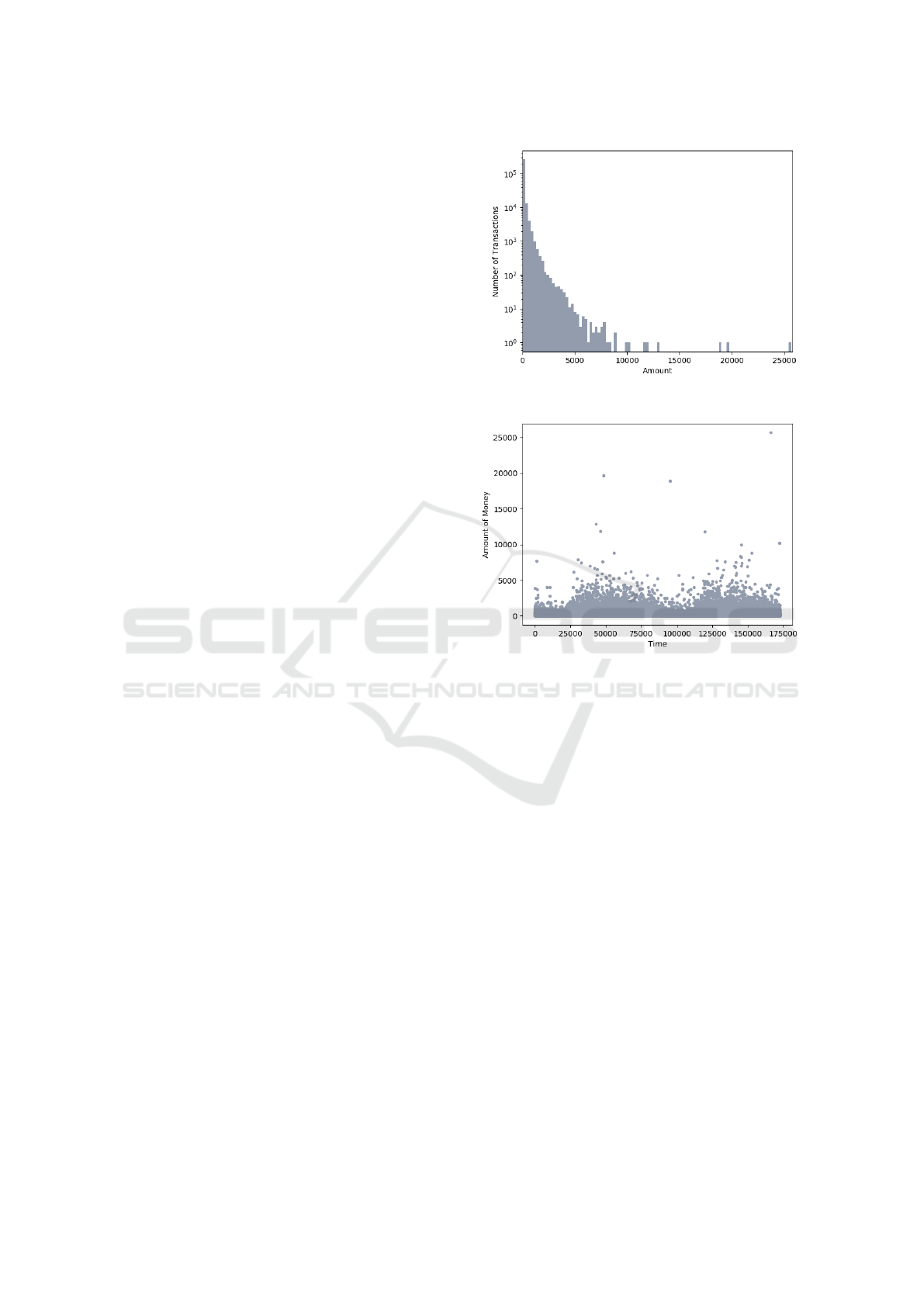
The feature called Amount is the amount of
money in each transaction. The largest transaction
that has this data set is $25,691.16 while the aver-
age of the transactions is $88.35. Figure 1 shows that
the data is mostly concentrated at very small values
close to zero while only a few transactions approxi-
mate the maximum value found. On the other hand,
the representation of the amount of money for each
transaction (see Figure 2) shows some values that dif-
fer from the others. These are called outliers and in
this case they are transactions in which a large amount
of money is transferred. Logically, these values at-
tract the attention of being possible frauds, however
this is something that fraudsters want to totally avoid.
Existing information shows that fraudsters frequently
transferred small amounts of money to continue steal-
ing in an undetectable manner.
The class feature is what gives information that
if the transactions are fraudulent or not, this variable
takes value 1 in case of fraud and 0 otherwise. This
feature shows that there is a minimum percentage of
fraudulent cases which represent 0.17% of all data.
While non-fraudulent cases equal 99.83%. It is con-
cluded that the data is highly imbalanced, which re-
Figure 1: Distribution of Monetary Value Feature.
Figure 2: Money per Transaction.
quires choosing appropriate measures to divide the
data and make the training of the system effective.
4 PROPOSED SOLUTION
This Section describes the proposed intelligent sys-
tem, which learns to detect fraudulent transactions ef-
ficiently. The Q-Credit Card Fraud Detector (Q-
CCFD) is composed of three different artificial intel-
ligence techniques related to each other.
The first is an Auto-encoder (AE), which allows
to extract important features from the unlabeled data.
The hidden layer of this unsupervised network is the
input to another Mediator Network (MN) designed
to classify each input with its respective label gen-
uine/fraud. The intermediate layer of the Mediator
becomes the input to an Agent which is responsible
for the final real time classification of the transaction
being processed.
This Section is divided in two sections: Section
4.1 presents all the design and architecture of this pro-
posed system and Section 4.2 which describes algo-
Q-Credit Card Fraud Detector for Imbalanced Classification using Reinforcement Learning
281

rithm specifications used by these 3 artificial intelli-
gence techniques.
4.1 Network Architectures
The system is the result of learning three main com-
ponents which were adjusted individually. Figure 3
presents a general scheme of Q-CCFD in order to
have a complete overview and simplify the definition
of each component.
To set hyper-parameters to a convenient point is
a common problem in neural networks, usually there
exist a large number of possible combinations of
which only few give the best results. Finding this op-
timal configuration requires effort but it is a unavoid-
able task. For this work, after some trial and error the
following hyper-parameters are chosen.
4.1.1 Auto-encoder
This first component extracts important characteris-
tics from the database, which is essential to facilitate
the learning of the system and the detection of signif-
icant transactions that could harm the entire process.
Normalization. The Auto-encoder inputs are the 28
features V 1,V 2,...,V 28 of the database. This data
must be re-scaled so that they have a standard normal
distribution with a mean of 0 and standard deviation
of 1, this is compatible with sigmoid used as trans-
fer function. As usual normalizing carried out before
starting to train a model.
Before each X transaction is given as input of the
AE, the maximum and minimum value of the 28 fea-
tures is found and then the following equation is used:
X
0
=
X −X
min
X
max
− X
min
, (2)
where each X transaction is rescaled at the interval
[0,1].
Number of Hidden Neurons and Layers. An
Auto-encoder reproduces in its output the same data
received in its inputs and has therefore the same num-
ber of neurons in both layers. On the other hand, the
number of neurons in the hidden layer is a free choice
element and it generally depends on the complexity of
the relations in the database. The number of neurons
per layers should be carefully chosen since too many
or too few neurons will cause underfitting/overfitting
problems.
We made comparative tests to determine the best
number of hidden neurons for reliable representa-
tions; however, the definitive metric is determined
based on the performance of the next operative net-
work that is fed by the Auto-encoder. Finally, an AE
with 38 neurons in a single hidden layer is chosen be-
cause with this numbers the output presents a mini-
mum error value.
4.1.2 Mediator Network
A neural network is used to classify transactions. The
input is given by the hidden layer of the Auto-encoder,
therefore it does not require data normalization.
The output layer is given by 2 neurons, which cor-
respond to the 2 possible cases: fraud or genuine.
This is the base for a metric to measure the perfor-
mance and find the best structure of the hidden layer,
which will become important by defining the input for
the next component.
After performing some tests which include pass-
ing information to other downstream components the
best found possible structure was a hidden layer with
11 neurons.
4.1.3 Agent
The final component of the entire system is an agent
who is responsible for accurately classifying in real
time each one of the incoming transactions.
The agent input is the hidden layer of the MN. The
output layer are 2 neurons corresponding to the two
classes of the database. After some accuracy evalu-
ation the amount of neurons in this hidden layer was
set to 11.
4.2 Parameter Setting
This Section details system specifications such as the
learning algorithm, the transfer functions, loss func-
tions and other fundamental characteristics tuned to
obtain good performance.
4.2.1 Auto-encoder
An auto-encoder uses an unsupervised learning.
Backpropagation algorithm while setting the target
values to be equal to the inputs. The transfer function
that computes the weighted sum of inputs is sigmoid
function and the loss function is Mean Squared Error.
The best found learning rate value is 0.9.
4.2.2 Mediator Network
This supervised learning network uses Backpropaga-
tion algorithm with MSE and learning rate equal to
0.9. Sigmoid is the activation function that takes the
input and compresses the output in the interval [0.1].
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
282

Figure 3: General Architecture of Q-Credit Card Fraud Detector.
4.2.3 Agent
The utilized Agent is based in reinforcement learn-
ing. Its activation function is the learning sigmoid
and the algorithm is a novel version of Deep Q-
learning (Mnih et al., 2015). Concerning framework
our method solves classification problems using Re-
inforcement learning and an agent which receives re-
wards depending on the class to which it classifies in-
coming data. A positive reward is given it classifies
a transaction correctly, otherwise a negative reward is
assigned.
Imbalanced Classification Markov Decision Pro-
cess (Lin et al., 2019) decomposes the task of clas-
sification into a sequential decision-making problem.
The input received by the agent is each of the weights
x
i
of the hidden layer of the neural network with its
respective label l
i
. Therefore the training data set is
D = (x
1
,l
1
),(x
2
,l
2
),...,(x
i
,l
i
). The ICMDP uses a
five-tuple (S , A,T ,R , E ) with the following defini-
tions:
• State S: Each state is defined by the input, with x
1
being the initial state s
1
. It goes to the next state
with the next transaction given by hidden layer of
NN.
• Action A: The action a
t
that the agent will take is
given by the dataset label. In database used, the
action is given by A = {0, 1} being 1 for cases of
fraud and 0 for non-fraud.
• Transition probability T : The agent moves from
one state s
t
to the next state s
t+1
according to the
order in which the data is read. Transition proba-
bility is defined by p(s
t+1
|s
t
,a
t
).
• Reward R : the value of the reward r
t
depends on
the action the agent takes. Two different rewards
are defined for each class. The reward function is
given by:
R(s
t
,a
t
,l
t
) =
+1 a
t
= l
t
and s
t
∈ D
F
−1 a
t
6= l
t
and s
t
∈ D
F
+λ a
t
= l
t
and s
t
∈ D
N
−λ a
t
6= l
t
and s
t
∈ D
N
where D
F
represents the set of fraudulent transac-
tions, D
N
is the set of non-fraudulent transactions
and λ is a value in the interval [0,1] that is the
reward when the agent correctly classifies a non-
fraudulent transaction, which are part of the class
with the largest samples of the entire imbalanced
dataset. The reward of 1/ − 1 is greater than λ
since being the minority class the impact of cor-
rectly classifying significantly affects the perfor-
mance of the system.
• Terminal E: Set to indicate that training must be
stopped by the appearance of some terminal state.
These states can arise in any training episode.
Episode is a concept in reinforcement learning,
which is a transition trajectory from initial state
to terminal state {s
1
,a
1
,r
1
,s
2
,a
2
,r
2
,...,s
t
,a
t
,r
t
}.
Episode ends when all training data is classified
or when the agent misclassifies the sample from
minority class (Lin et al., 2019) and then the ter-
minal variable changes its value, to start a new
episode.
Q-Credit Card Fraud Detector for Imbalanced Classification using Reinforcement Learning
283

• Policy π
θ
: This is a mapping function π
:
S →
A where π
θ
denotes the action a
t
performed by
agent in state s
t
. The policy π
θ
in ICMDP can
be considered as a classifier with the θ parameter
(Lin et al., 2019).
The above-mentioned definitions are an essential part
of formally raising the problem and seeking to opti-
mize the classification policy π
∗
:
S → A which max-
imized rewards in ICMDP.
The final value with the best accuracy value of λ
is 0.1. The memory replay size M used is 200000 and
γ value is equal to 0.9.
The above-mentioned definitions are an essential
part of formally raising the problem and seeking to
optimize the classification policy π
∗
:
S → A which
maximized rewards in ICMDP.
The final value with the best accuracy value of λ
is equal to 0.1. The memory replay size M used is
200000 and γ value is equal to 0.9.
5 IMPLEMENTATION
This Section describes the implementation of Q-
Credit Card Fraud Detector, which makes possible to
tune various parameters and then evaluate the perfor-
mance of the overall system. Section 5.1 specifies the
programming language and libraries used and Section
5.2 specifies the process of implementation.
5.1 Technology
The language used is C/C++ because it is flexible
and implemented code is easy to read, understand and
edit.
The working software runs in a C++ compiler
with minimum graphic capacities and IDE, including
our own neural and Q-Learning libraries.
5.2 Code Structure
Algorithm 1 shows an implementation of the general
scheme that presents the Figure 3, in which each of
the components of the proposed system is described,
so that the three main techniques of artificial intelli-
gence used can be distinguished.
The function Train Auto-encoder (D) receives the
normalized database as an input parameter and begins
modifying its weights of the hidden layer θ
AE
until
the best representation of its input is obtained in its
output. While Train Mediator Network (θ
AE
) starts
to train a MN using as input the θ
AE
values. Set the
targets using the label of each transaction {0,1}.
Algorithm 1: Q-CCFD.
Input : T = {1,2,3,...,284807}
x
i
= {v1, v2, ...v28}, with i ∈ T
Read Training Data
Normalize x
i
∈ D
D = {(x
1
,..,l
1
),(x
2
,l
2
),...,(x
T
,L
T
)}
Randomly initialize weights θ
IHO
while Key not pressed do
θ
AE
=Train Auto-encoder(D)
θ
MN
=Train Mediator Network(θ
AE
)
Train Agent(θ
MN
)
end
Testing: Data unlabeled
Agent learning uses Train Agent(θ
MN
) the algo-
rithm 2, this is an implementation base on Deep Q-
learning for Imbalanced Classification Markov Deci-
sion Process (Lin et al., 2019).
In each iteration, the agent uses policy a
t
= π
θ
(s
t
)
to choose the action and then obtains the reward using
REWARD function in Algorithm 3.
Algorithm 2: Train Agent.
Input : θ
MN
D = {(θ
1
MN
,l
1
),(θ
2
MN
,l
2
),...,(θ
T
MN
,L
T
)}
Episode number K.
Initialize replay memory D with M capacity
Randomly initialize parameters θ
Initialize simulation environment ε
for episode k = 1 to K do
Shuffle D
Initialize state s
1
= θ
1
MN
for t = 1 to T do
Pick an action: a
t
= π
θ
(s
t
)
r
t
,terminal
t
= REWARD(a
t
,l
t
)
Set s
t+1
= θ
t+1
MN
Store (s
t
,a
t
,r
t
,s
t+1
,terminal
t
) to M
Randomly sample
(s
j
,a
j
,r
j
,s
j+1
,terminal
j
) from M
Set y
j
=
(
r
j
, terminal
j
=1
r
j
+ γmax
a
0
Q(s
j+1
,a
0
;θ),terminal
j
=0
Perform a gradient descent step:
L(θ) = (y
j
− Q(s
j
,a
j
;θ))
2
if terminal
t
=1 then
break
end
end
end
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
284

Table 1: General specifications of Q-Credit Card Fraud Detector.
Auto-encoder Mediator Network Agent
Input Layer 28 56 25
Hidden Layer 56 25 15
Output Layer 28 2 2
Learning Algorithm Backpropagation Backpropagation Deep Q-learning
Transfer Function Sigmoid Sigmoid Sigmoid
Loss Function MSE MSE (y
j
− Q(s
j
,a
j
;θ))
2
Learning Rate 0.9 0.9 0.9
Discount factor (γ) N/A N/A 0.9
Lambda value (λ) N/A N/A 0.1
Size replay memory (M) N/A N/A 200000
Algorithm 3: Environment Simulation.
D
F
represents the fraud class
D
N
represents the non-fraud class
Function: REWARD(a
t
∈ A,l
t
∈ L)
Initialize terminal
t
= 0
if s
t
∈ D
F
then
if a
t
= l
t
then
Set r
t
= 1
else
Set r
t
= −1
terminal
t
= 1
end
else
if a
t
= l
t
then
Set r
t
= λ
else
Set r
t
= −λ
end
end
return r
t
,terminal
t
6 RESULTS
Figure 4 shows the proposed system interface, a
friendly and simple software that allows the user to
have an easy interaction. Table 1 show a general sum-
mary of the Sections 4.1 and 4.2, which defines the
best parameter settings for the system.
Table 2 shows the best result, which is given by
the accuracy of the system. These values were mea-
sured in training and testing phase using whole im-
balanced database. There are other algorithms that
use the same dataset to detect fraud. The difference
with Q-CCFD is that they use methods to balance
the database: hybrid sampling and random sampling
(Dighe et al., 2018). Q-CCFD when using the imbal-
anced dataset is more adaptable to the real problems
that arise in bank transactions. Table 3 shows a com-
parison of the accuracy values obtained between these
algorithms.
Table 2: Results of Q-Credit Card Fraud Detector.
Accuracy
Training Testing
Auto-encoder 99.9 96.4
Mediator Network 98.2 96.7
Agent 98.9 98.1
Table 3: Comparison with other existing algorithms.
*Balanced dataset.
Classifiers Accuracy
Logistic Regression 96.2*
Naive Bayes 96.9*
Decision Tree 96.4*
K-Nearest Neighbour 99.1*
Q-Credit Card Fraud Detector 98.1
7 CONCLUSIONS
This paper presents a credit card fraud detector based
on deep networks and reinforcement learning. It uses
an auto-encoder and neural agent trained with a Q-
learning algorithm working on imbalanced data set,
treated by PCA and containing real credit card trans-
actions. The system performs credit cards transaction
classification by combining supervised, unsupervised
and reinforcement learning. The proposed solution
works as a quick acting intelligent agents and can
identify frauds with remarkably accuracy.
The future scope is to adjust our solution to work
in real-time banking systems. For this, a more com-
plex database should be obtained (e.g., credit card
holder id, where the transaction was realized, sales-
man id) and improve the solution if necessary.
Q-Credit Card Fraud Detector for Imbalanced Classification using Reinforcement Learning
285
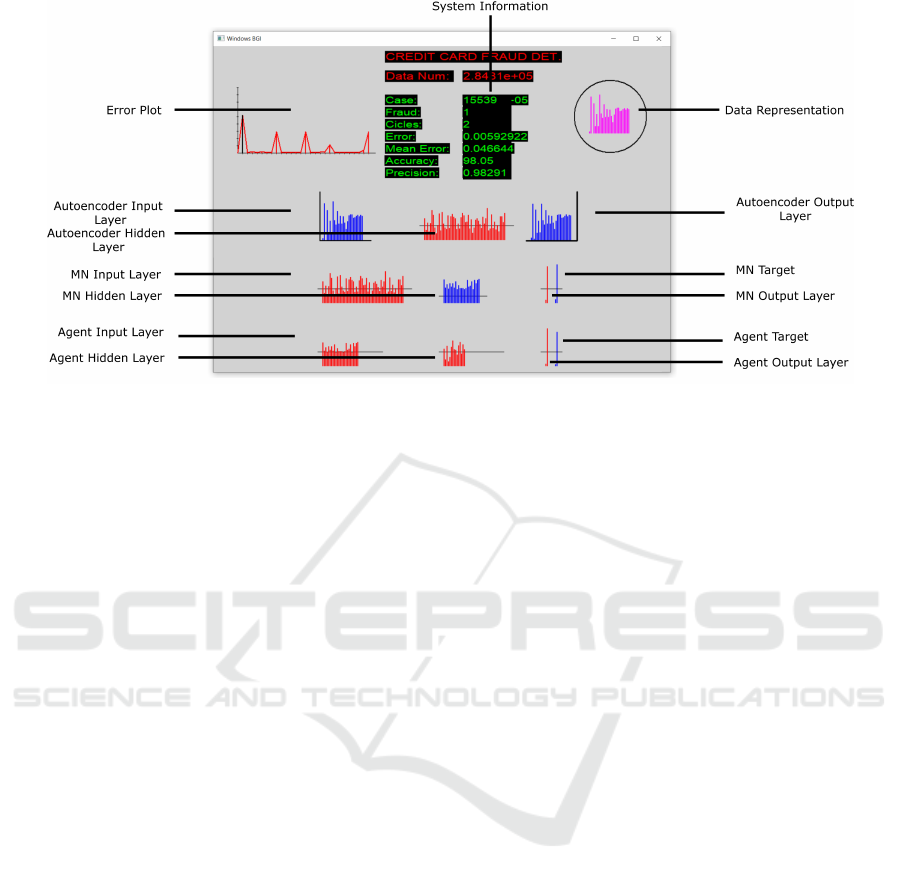
Figure 4: Interface of Q-Credit Card Fraud Detector.
ACKNOWLEDGEMENTS
Authors thank to the SDAS Research Group
(www.sdas-group.com) for its valuable support.
REFERENCES
Chukwuneke, C. (2018). Credit card fraud detection system
using intelligent agents and enhanced security fea-
tures.
Dighe, D., Patil, S., and Kokate, S. (2018). Detection of
credit card fraud transactions using machine learning
algorithms and neural networks: A comparative study.
pages 1–6.
Dong, Q., Gong, S., and Zhu, X. (2019). Imbalanced deep
learning by minority class incremental rectification.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 41(6):1367–1381.
Feng, J., Huang, M., Zhao, L., Yang, Y., and Zhu, X.
(2018). Reinforcement learning for relation classifi-
cation from noisy data.
Li, M.-J., Li, A.-H., Huang, Y.-J., and Chu, S.-I. (2019). Im-
plementation of deep reinforcement learning. In Pro-
ceedings of the 2019 2Nd International Conference on
Information Science and Systems, ICISS 2019, pages
232–236, New York, NY, USA. ACM.
Lin, E., Chen, Q., and Qi, X. (2019). Deep reinforce-
ment learning for imbalanced classification. CoRR,
abs/1901.01379.
Martinez, C., Perrin, G., Ramasso, E., and Rombaut, M.
(2018). A deep reinforcement learning approach for
early classification of time series. In 2018 26th Eu-
ropean Signal Processing Conference (EUSIPCO),
pages 2030–2034.
MLG-Kaggle (2015). Credit card fraud detection dataset.
Retrieved June 5, 2019.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller,
M., Fidjeland, A. K., Ostrovski, G., Petersen, S.,
Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-
maran, D., Wierstra, D., Legg, S., and Hassabis, D.
(2015). Human-level control through deep reinforce-
ment learning. Nature, 518(7540):529–533.
Pumsirirat, A. and Yan, L. (2018). Credit card fraud detec-
tion using deep learning based on auto-encoder and
restricted boltzmann machine. International Journal
of Advanced Computer Science and Applications, 9.
Wang, S., Liu, W., Wu, J., Cao, L., Meng, Q., and Kennedy,
P. (2016). Training deep neural networks on imbal-
anced data sets. pages 4368–4374.
Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-
chine Learning, 8(3):279–292.
Wiering, M., Van Hasselt, H., Pietersma, A.-D., and
Schomaker, L. (2011). Reinforcement learning algo-
rithms for solving classification problems. pages 91 –
96.
Wiese, B. and Omlin, C. (2009). Credit Card Transactions,
Fraud Detection, and Machine Learning: Modelling
Time with LSTM Recurrent Neural Networks, volume
247, pages 231–268.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
286
