
A Homomorphic Proxy Re-authenticators based Efficient Multi-client
Non-interactive Verifiable Computation Scheme
Shuaijianni Xu
1,2
and Liang Feng Zhang
1
1
School of Information Science and Technology, ShanghaiTech University, Shanghai, China
2
Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai, China
Keywords:
Outsourcing Computation, Multi-client Verifiable Computation, Homomorphic Proxy Re-authenticator.
Abstract:
In TCC 2013, Choi, Katz, Kumaresan, and Cid introduced a multi-client verifiable computation (MVC) model
for outsourcing computations to cloud. MVC allows multiple non-communicating clients to outsource the
computation of a function f over a series of joint inputs to a powerful but untrusted cloud server, ensuring that
the input of each client will be secret from all the other entities and rejects any incorrect results from the server.
They also proposed a construction of MVC, which heavily depends on fully homomorphic encryption (FHE)
and garbled circuits (GCs), thus lacks practical relevance. In this paper, we propose a general transformation
from the homomorphic proxy re-authenticator (HPRA) of Derler, Ramacher and Slamanig (FC 2017) to MVC.
Our MVC schemes will be significantly more efficient, as long as the underlying HPRA is free of FHE and
GCs. By applying the transformation to an HPRA scheme of Derler, Ramacher and Slamanig, we obtained
an MVC scheme for computing the linear combinations of vectors. Our implementation shows that the new
MVC scheme is significantly more efficient, both in terms of client computation and server computation. To
our best knowledge, this is the first implementable MVC scheme to date.
1 INTRODUCTION
The past years have witnessed an increasing amount
of attention spent on the problem of securely out-
sourcing computations, due to the popularity of cloud
computing and the proliferation of mobile devices.
Outsourcing computation allows clients (e.g. mo-
bile devices or sensors) to offload the computation of
a function to powerful cloud servers. However, the
servers are not always trusted and various security
concerns arise. For example, the servers may have
strong financial incentives to run quick but incorrect
computations to minimize the consumption of their
computing resources; the servers may also abuse the
client’s data (e.g., function, input and output), as long
as the data is not encrypted. How to guarantee the
correctness of the server’s results and how to protect
the clients’ data have been two fundamental security
problems in the field of outsourcing computations.
In the single-client scenario, (Gennaro et al.,
2010) introduced a model of non-interactive verifi-
able computation (VC) for ensuring the correctness
of the server’s results. The VC scheme of (Gennaro
et al., 2010) allows a computationally weak client to
outsource the computation of a function f on many
inputs x
1
,x
2
,··· , x
n
to a server, but only results in
impractical constructions due to their dependance on
expensive cryptographic primitives such as FHE and
GCs. (Benabbas et al., 2011; Parno et al., 2013; Ben-
Sasson et al., 2013; Ben-Sasson et al., 2014; Braun
et al., 2013; Cormode et al., 2012; Setty et al., 2013;
Wahby et al., 2015; Papamanthou et al., 2013) pro-
vided significantly more efficient constructions for re-
stricted classes of functions.
The model of (Gennaro et al., 2010) has been
extended for outsourcing computation problems in
many different scenarios. One of them allows mul-
tiple clients to outsource computations on their joint
inputs to a cloud server. Such an extension is mean-
ingful. For example, due to the lack of infrastructure
(e.g., very limited cell coverage), n sensor nodes may
be unable to directly connect to each other but are able
to communicate with a central server. The sensors are
likely to outsource the computation of a function f
over a series of their joint data. The server is respon-
sible to collect the data and then reports the results,
based on which the sensors determine the data should
be further observed.
(Choi et al., 2013) extended the single-client VC
model of (Gennaro et al., 2010) to a multi-client non-
Xu, S. and Zhang, L.
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme.
DOI: 10.5220/0009158101950206
In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 195-206
ISBN: 978-989-758-399-5; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
195

interactive verifiable computation (MVC) model. An
n-client MVC scheme allows n non-communicating
clients to outsource the computation of a function f
over a series of joint inputs (x
(1)
1
,··· , x
(1)
n
),··· to a
powerful cloud server, ensuring that the input of each
client will be secret from all the other entities and
the clients will reject any incorrect results from the
server. (Choi et al., 2013) also proposed a construc-
tion of MVC for outsourcing the computation of any
boolean circuit f . However, their scheme still heavily
depends on FHE and GCs and thus is impractical.
To move toward more practical MVC schemes, a
very intuitive idea would be replacing these expensive
cryptographic primitives(i.e., FHE, GCs) with more
practical algorithms. Unfortunately, if we are lim-
ited to the outsourcing of functions as generic as any
boolean circuits and want to ensure the confidential-
ity of the client’s data, then the tools such as FHE are
somehow indispensable. In this paper, we mainly fo-
cus on the construction of efficient MVC schemes for
outsourcing specific computations, and in particular,
computing the linear combination of vectors over a
finite field.
Our Contribution. Our first contribution is a gen-
eral transformation from the homomorphic proxy re-
authenticator (HPRA) of (Derler et al., 2017), a
tool that adds security and verifiability guarantees to
multi-user data aggregation scenarios, to MVC. We
modified definition of some MVC algorithms, and en-
sure that these changes affect neither the functionality
nor the security of MVC. Our transformation results
in MVC schemes with the following properties:
• No malicious server is able to convince the honest
clients to accept an incorrect output.
• Each client’s input is hidden from the server and
other clients; the result of the computation is hid-
den from the server.
• The involved parties do not need to communicate
with each other or share a secret key. Instead, they
use independent secret keys to both encrypt and
authenticate their respective inputs.
• Comparing with the HPRA, the scheme introduce
no extra computations; it is free of FHE/GCs and
thus significantly more efficient, as long as the un-
derlying HPRA is free of FHE/GCs.
• Comparing with the HPRA, the security of the
scheme requires no extra assumptions.
Our second contribution is the implementation of a
specific MVC scheme, which can be obtained by ap-
plying the general transformation to a specific HPRA
scheme of (Derler et al., 2017). Our MVC allows n
clients, each has a vector of dimension `, to jointly
compute a linear combination of their vectors. To
our best knowledge, this is the first implementable
MVC scheme to date. If we treat the multiplication
of two matrices as a set of linear combination com-
putations, then our scheme is applicable to outsource
matrix multiplications. For the purpose of compari-
son, we consider the multiplication of two 100 ×100
matrices. (Parno et al., 2013) established a model for
evaluating the efficiency of the FHE+GCs based VC
schemes such as (Gennaro et al., 2010; Choi et al.,
2013). The analysis of (Parno et al., 2013) shows
that, in order to multiply two 100 ×100 matrices, the
MVC scheme of (Choi et al., 2013) would take ≥10
11
seconds at the client. The experiments show that the
clients and the server in our MVC scheme only need
≈ 10
3
seconds. Our MVC is significantly faster at
both the clients and the server.
Our Techniques. The HPRA scheme is a protocol
between three types of parties: a set of signers, an
aggregator and a receiver. It allows the signers to au-
thenticate their data under their own keys and allows
an aggregator to transform these signatures to a MAC
under the receiver’s key. Most importantly, the ag-
gregator can evaluate f on the inputs and produce an
aggregate authenticated message vector correspond-
ing to the function’s output, which allows the receiver
to perform necessary verifications. A main difference
between MVC and HPRA is that: in HPRA, there is
a receiver who obtains the result of the computation
and performs the verification; while in MVC, the first
client is responsible for verification. In order to con-
struct MVC from HPRA, a very natural idea is to es-
tablish a mapping from the parties in HPRA to those
in MVC. We merge the receiver with the first signer
in HPRA and regard them as the first client in MVC;
let the remaining signers in HPRA play the roles of
all other clients in MVC; let the aggregator in HPRA
play the role of a cloud server in MVC. In Section 3,
we show that given an aggregator unforgeable, input
private and output private HPRA scheme, our trans-
formation yields an MVC scheme that satisfies all the
properties of correctness, soundness, privacy against
the first client and privacy against the server.
Related Work. (Gennaro et al., 2010) introduced
a single-client non-interactive verifiable computation
model and constructed a scheme that heavily depends
on FHE and GCs. (Benabbas et al., 2011) constructed
more efficient verifiable computation schemes for re-
stricted classes of functions. Following this line, the
up-to-date implementations of efficient (single-client)
systems (Parno et al., 2013; Ben-Sasson et al., 2013;
Ben-Sasson et al., 2014; Braun et al., 2013; Cormode
et al., 2012; Setty et al., 2013; Wahby et al., 2015;
Papamanthou et al., 2013) for outsourcing computa-
tions shows that in this area we are on the verge of
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
196

achieving practical efficiency.
(Choi et al., 2013) extended the single-client VC
model of (Gennaro et al., 2010) to a setting where
the inputs are provided by multiple clients. They pro-
vided an FHE-based construction for outsourcing any
boolean circuits, which did not settle the efficiency
problem, either. Moreover, the soundness may be bro-
ken when the server is allowed to send ill-formed re-
sponses to the first client and then see if that client re-
jects. This problem was addressed in (Gordon et al.,
2015) with a scheme having stronger security guaran-
tees against a malicious server or an arbitrary set of
malicious colluding clients. However, their scheme
also requires FHE and GCs. In particular, their on-
line phase efficiency was sacrificed in order to achieve
the stronger security guarantees.
(Goldwasser et al., 2014) gave a construction of
multi-input functional encryption (MIFE) based on
indistinguishability obfuscation (iO). Their scheme
allowed multiple clients to delegate computations to
an untrusted server and could achieve better effi-
ciency. However, MIFE inherently required the exis-
tence of iO, which is a stronger assumption. (Fiore
et al., 2016) constructed a multi-key homomorphic
authenticator (multi-key HA), which allowed multi-
ple clients to store data on a cloud server and del-
egate a computation on the data to the server. But
the multi-key HAs never guaranteed the privacy of
the clients’ data. Based on multi-key HAs, (Derler
et al., 2017) introduced the notion of homomorphic
proxy re-authenticators (HPRA), which allowed dis-
tinct clients to authenticate their data under their own
keys and verifies the correctness of the computation
result under a re-authenticator key. Also based on
multi-key HAs, (Schabh
¨
user et al., 2019) constructed
a multi-key support outsourced computation, which
was claimed to be context-hiding. However, they did
not provide a proper encryption scheme hence cannot
effectively protect input privacy.
Organization. Section 2 highlights the preliminar-
ies including MVC and HPRA. Section 3 presents
our HPRA to MVC transformation. In section 4, we
present a implementation of a concrete instantiation
and discuss the experimental results. Finally, section
5 concludes the work.
2 PRELIMINARIES
In this section we recall the models and definitions
of multi-client verifiable computation (MVC) and ho-
momorphic proxy re-authenticator (HPRA).
2.1 MVC
The notion of multi-client non-interactive verifiable
computation was introduced in (Choi et al., 2013). In
an n-party MVC there are n clients P
1
,P
2
,...,P
n
who
wish to outsource the computations of f over a series
of joint inputs to a server multiple times. For every
i ≥ 1, in the i-th evaluation the clients P
1
,P
2
,...,P
n
’s
inputs are denoted as x
(i)
1
,x
(i)
2
,...,x
(i)
n
respectively. P
1
is designated to learn y
(i)
= f (x
(i)
1
,x
(i)
2
,...,x
(i)
n
). MVC
guarantees both the secrecy of each client’s input and
the correct reconstruction of all function values.
Figure 1: Multi-client Verifiable Computation.
Definition 1. (MVC) An n-party MVC scheme Π =
({KeyGen
j
}
n
j=1
,EnFunc, {EnInput
j
}
n
j=1
,Compute,
Verify) for a function family F consists of 2n + 3
polynomial-time algorithms as below and shown in
Figure 1.
• (pk
1
,sk
1
) ← KeyGen
1
(pp). The client P
1
will run
this algorithm on a set pp of public parameters to
obtain a public key pk
1
and a private key sk
1
.
• (pk
j
,sk
j
) ← KeyGen
j
(pp, pk
1
). For j = 2,··· ,n,
the client P
j
will run this algorithm to obtain a
public key pk
j
and a private key sk
j
.
• (φ,ξ) ←EnFunc(
−→
pk, sk
1
, f ). The client P
1
will run
this algorithm with
−→
pk = (pk
1
, pk
2
,..., pk
n
) and
sk
1
to encode any f ∈ F as an encoded function
φ, which will be sent to the server, and generate
a decoding secret ξ, which will be kept private by
the client.
• (χ
(i)
1
,τ
(i)
) ← EnInput
1
(i,
−→
pk, sk
1
,ξ,x
(i)
1
). When
outsourcing the i-th computation to the server, P
1
will run this algorithm to convert its input x
(i)
1
as
an encoded input χ
(i)
1
, which will be sent to the
server, and generate a decoding secret τ
(i)
, which
will be kept private by the client.
• χ
(i)
j
←EnInput
j
(i,
−→
pk, sk
j
,x
(i)
j
). When outsourcing
the i-th computation to the server, each client P
j
( j 6= 1) will run this algorithm to convert its input
x
(i)
j
as an encoded input χ
(i)
j
, which will be sent to
the server. We denote
−→
χ
(i)
= (χ
(i)
1
,··· , χ
(i)
n
).
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme
197

• ω
(i)
← Compute(i,
−→
pk, φ,
−→
χ
(i)
). The server will
run this algorithm to get an encoded output ω
(i)
.
• y
(i)
∪{⊥} ← Verify(i, ξ, τ
(i)
,ω
(i)
). The client P
1
will run this algorithm to output either a value y
(i)
= f (x
(i)
1
,···x
(i)
n
), or a symbol ⊥indicating that the
server attempted to cheat.
We modify the definition of some MVC algo-
rithms, and ensure that: (1) these changes do not
affect the functionality of MVC, that is, the modi-
fied MVC can still solve the same question; (2) these
changes do not affect the security of MVC, as each
participant does not get any additional information.
• We replace all security parameter 1
κ
in inputs with
a public parameter pp which contains both infor-
mation of 1
κ
and function f , as f is public.
• We run client P
1
’s algorithm KeyGen
1
first and let
pk
1
be an input of client P
j
’s algorithm KeyGen
j
, for j = 2, . . . , n. This change causes other clients
to wait for client P
1
finish KeyGen
1
, but does not
affect security. As (Choi et al., 2013) has assumed
that there was a public-key infrastructure (PKI),
such that all clients had public keys known to each
other in MVC scheme.
• Our EnFunc needs sk
1
as input, which is also a
reasonable change as EnFunc is run by client P
1
.
Required by (Choi et al., 2013; Gordon et al., 2015),
an MVC scheme should be correct, sound and input
private. An MVC scheme is correct if all algorithms
of the scheme are faithfully executed, then the verifi-
cation algorithm will always produce the correct func-
tion output.
An MVC scheme is sound if no malicious server
can convince the honest clients to accept an incorrect
output, even if it is given access to Oracle I N , which
generates multiple input encodings as follows.
Oracle I N (x
1
,··· , x
n
)
• i := i + 1;
• record (x
(i)
1
,...,x
(i)
n
) := (x
1
,...,x
n
);
• (χ
(i)
1
,τ
(i)
) ← EnInput
1
(i,
−→
pk, sk
1
,ξ,x
(i)
1
);
• for j = 2,...,n : χ
(i)
j
← EnInput
j
(i,
−→
pk, sk
j
,x
(i)
j
);
• output (χ
(i)
1
,...,χ
(i)
n
).
Definition 2. (Soundness) For the scheme Π, con-
sider an experiment Exp
sound
A
[Π, f ,κ,n] with respect
to an adversarial server A: For j = 1,...,n, pub-
lic/private key pairs (pk
j
,sk
j
) are generated, an en-
coded function φ and decoding secret ξ are generated.
The adversary A is given inputs
−→
pk, φ and access to
Oracle I N , and outputs a forge ω
∗
. The challenger
runs Verify and gets y
∗
, if y
∗
/∈ {⊥, f (x
(i)
1
,...,x
(i)
n
)},
the output of the experiment is defined to be 1; and
0 otherwise. The scheme Π is sound if for any
n = poly(κ), any function f ∈ F , and any proba-
bilistic polynomial-time adversary (PPT) adversary
A, there is a negligible function negl(·) such that
Pr[Exp
sound
A
[Π, f ,κ, n] = 1] ≤negl(κ).
An MVC scheme is private if every client’s input
is kept private from the server as well as the other
clients. In MVC scheme, clients other than the first
client clearly do not learn anything about each others’
inputs. Therefore, the input privacy of MVC consists
of two parts: privacy against the first client and pri-
vacy against the server.
Definition 3. (Privacy against the First Client) The
scheme Π achieves the privacy against the first client
if for any input vectors ~x
0
= (x
1
,x
2
,···,x
n
),~x
1
=
(x
1
,x
0
2
,···,x
0
n
) with f (~x
0
) = f (~x
1
), the view of P
1
when running an execution of Π with all clients hold-
ing ~x
0
is indistinguishable from the view of P
1
when
running an execution with all clients holding~x
1
.
The definition of privacy against the server re-
quires that the encoded inputs from two distinct inputs
should be indistinguishable to the server, even when
malicious server is given access to the encoded inputs
generation oracle Oracle I N .
Definition 4. (Privacy against the Server) Consider
an experiment Exp
priv
A
(Π, f ,κ, n, b) with respect to a
stateful adversarial server A: For j = 1, . . . , n, pub-
lic/private key pairs (pk
j
,sk
j
) are generated, an en-
coded function φ and decoding secret ξ are gener-
ated. The adversary A is given inputs
−→
pk, φ and ac-
cess to Oracle I N , and outputs a pair of jointly in-
puts (x
0
1
,···,x
0
n
),(x
1
1
,···,x
1
n
). The challenge cipher-
text (χ
b
1
,···,χ
b
n
) is computed and given to A. A con-
tinues to have oracle access to I N , and outputs a
guess b
0
of b. We define the advantage of A in the
experiment above as:
Adv
priv
A
(Π, f ,κ, n) =
Pr[Exp
priv
A
(Π, f ,κ, n, 0) = 1]−
Pr[Exp
priv
A
(Π, f ,κ, n, 1) = 1]
.
The MVC scheme Π is private against the server if for
any n = poly(κ), any function f ∈ F , and any PPT
adversary A, there is a negligible function negl(·)
such that Adv
priv
A
(Π, f ,κ, n) ≤negl(κ).
2.2 HPRA
The notion of homomorphic proxy re-authenticator
was introduced in (Derler et al., 2017). An HPRA
scheme involves three types of parties: a set of sign-
ers, an aggregator and a receiver. It allows n signers
to authenticate data items ~m
1
,~m
2
,. .. ,~m
n
with signa-
tures under their own keys, and allows the aggregator
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
198
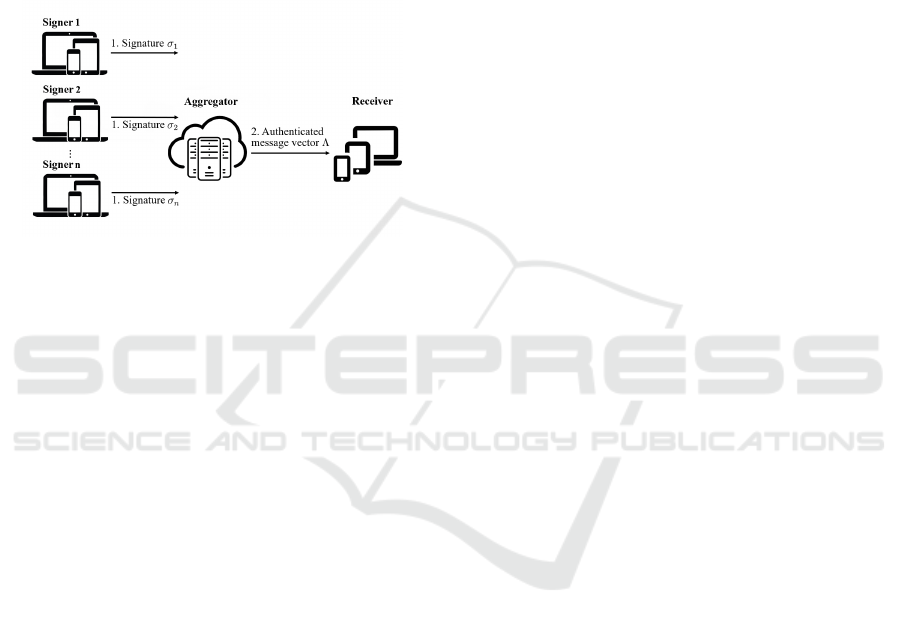
to transform these signatures to a signature under the
receiver’s key. In addition, the aggregator can eval-
uate a function f on the inputs so that the resulting
signature corresponds to the evaluation of f , and pro-
duce an aggregate authenticated message vector Λ.
Definition 5. (HPRA) A homomorphic proxy re-
authenticator scheme Σ = (Gen,SGen,VGen,Sign,
Verify,SRGen,VRGen,Agg,AVerify ) consists of nine
polynomial-time algorithms as below and shown in
Figure 2.
Figure 2: Homomorphic Proxy Re-Authenticator.
• pp ← Gen(1
κ
,`): Given a security parameter 1
κ
and a constant `, outputs a set of public parame-
ters pp, which explicitly defines a message space
M
`
, a function family F = {f |f : (M
`
)
n
→M
`
},
and a tag space.
• (id,sk,pk) ← SGen(pp): Each signer P
i
will run
this algorithm on public parameters pp to output
a signer key consist of an identifier id, a private
key sk and a public key pk.
• (mk,aux) ←VGen(pp): The receiver will run this
algorithm on public parameters pp to output a
MAC key mk and auxiliary information aux.
• σ ← Sign(sk,~m,µ): Each signer will run this al-
gorithm to sign its input ~m as a signature σ, which
will be sent to the aggregator. For all the sign-
ers P
1
.. .P
n
, we denote their signatures as
−→
σ =
(σ
1
.. .σ
n
).
• b ← Verify(pk,~m,µ,σ): Any entity who knows ~m
can run this algorithm to verify the validation of
a signature σ, and outputs a bit b.
• rk
i
← SRGen(sk
i
,aux): Each signer will run this
algorithm to generate a re-encryption key rk
i
.
• ak
i
← VRGen(pk
i
,mk,rk
i
): The receiver will run
this algorithm to generate an aggregation key ak
i
,
which will be sent to the aggregator.
• Λ ← Agg
−→
ak,
−→
σ ,µ, f
: The aggregator will run
this algorithm to compute an aggregate authenti-
cated message vector Λ. Here
−→
ak = (ak
1
,...,ak
n
).
• (~m,µ)/(⊥,⊥) ← AVerify(mk,Λ, ID, f ): The re-
ceiver will run this algorithm to output a pair
(~m,µ), otherwise output (⊥,⊥) indicating that the
server attempts to cheat.
Required by (Derler et al., 2017), an HPRA
scheme should be correct, input private, signer un-
forgeable, and aggregator unforgeable. Correctness
of an HPRA requires that if all algorithms of the
scheme are executed faithfully, then the Λ will always
verify successfully and decode to the correct output
~m = f (~m
1
,~m
2
,. .. ,~m
n
).
The input Privacy of HPRA captures the require-
ment that an aggregate authenticated message vector
Λ should leak no more information about the signers’
data ~m
1
,~m
2
,. .. ,~m
n
beyond what can be inferred from
~m = f (~m
1
,~m
2
,. .. ,~m
n
) and the description of f .
Definition 6. (Input privacy) The HPRA scheme Σ
for F is input private if for all κ ∈ N, all f ∈ F ,
all tags µ, and all (~m
11
,. .. ,~m
n1
),(~m
12
,. .. ,~m
n2
) ∈
(M
`
)
n
with f (~m
11
,. .. ,~m
n1
) = f (~m
12
,. .. ,~m
n2
), all
pp ← Gen(1
κ
,`), all (mk, aux) ← VGen(pp), for i =
1,. .. , n, (sk
i
,pk
i
) ← SGen(pp), ak
i
← VRGen(sk
i
,
aux,SRGen(pk
i
,mk)).The following distributions are
identical:
Agg
−→
ak, Sign(sk
i
,~m
i1
,µ)
i∈[n]
,µ, f
,
Agg
−→
ak, Sign(sk
i
,~m
i2
,µ)
i∈[n]
,µ, f
.
The signer unforgeability of an HPRA scheme re-
quires that, as long as the aggregator remains honest,
no coalition of dishonest signers can produce a valid
Λ with respect to the function f ∈ F such that Λ is
outside of the range of f evaluated on arbitrary com-
binations of the actually signed vectors. The aggrega-
tor unforgeability is the natural counterpart of signer
unforgeability, where the aggregator is dishonest and
the signers are honest.
Let T stand for “Signer” or “Aggregator”. In both
definitions we allow the adversary to access a set O
T
of oracles, where O
T
:= {SG,SKey, SR, VR, A} for
T = “Signer” and O
T
:= {SG, Sig,SR,VR,VRKey}
for T = “Aggregator”. The oracles maintain some
sets S, AK, RK and SIG which are initially empty, and
work as below, here i = 1, . . . , n represents the index
of client P
i
and we do not consider the corruption be-
tween signers:
• SG(i): Works as SGen, sets S [i] ← (id, sk, pk), re-
turns (id,pk).
• Skey(i): Returns S[i].
• Sig({1,. . . , n}, (~m
i
)
i∈[n]
): Works as Sign, sets SIG
[µ] ← SIG[µ] ∪{~m
i
,S[i]} for i = 1,...,n, returns
−→
σ = (σ
1
.. .σ
n
) and µ.
• SR(i): Works as SRGen, returns RK[i] = rk
i
.
• VR(i): Works as VRGen but without returning
anything, sets AK[i] = ak
i
.
• VRKey(i): Returns AK[i]
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme
199

• A(
−→
σ ,{1, . . . , n}, µ, f ): Works as Agg, returns Λ
Definition 7. (T-Unforgeability) For the HPRA
scheme Σ, consider an experiment Exp
T-unforge
A
(Σ,κ,
n,`) with respect to a PPT adversary A: Public
parameter pp is generated by running Gen(1
κ
,`),
MAC key and auxiliary information (mk, aux) are
generated by running VGen(pp). A is given inputs
pp and aux and access to oracle O
T
, and outputs
a forge (Λ
?
,ID
?
, f
?
). The challenger runs AVerify
(mk,Λ
?
,ID
?
, f
?
) and gets (~m,µ), if (~m, µ) 6= (⊥, ⊥
) and (@(~m
j
)
j∈[n]
: (∀j ∈ [n] : (~m
j
,id
∗
) ∈ SIG[µ]) ∧
f
?
(~m
1
.. .,~m
n
) = ~m), outputs 1; otherwise outputs 0.
The HPRA scheme Σ is T-unforgeable, if for all PPT
adversaries A there is a negligible function negl(·)
such that: Pr[Exp
T-unforge
A
(Σ,κ, n, `) = 1] ≤ negl(κ).
An HPRA scheme may provide output privacy,
which models the situation that the aggregator learns
neither the inputs nor the function’s output. The for-
mal definition of output privacy requires an oracle
RoS, which is defined as below:
• RoS(i,(~m
i
)
i∈[n]
,b): If S[i] =⊥, returns ⊥. Other-
wise samples µ uniformly at random and if b =
0 computes (σ
i
← Sign(S[i][2],~m
i
,µ))
i∈[n]
. Else
randomly chooses (~r
i
)
i∈[n]
← (M
`
)
n
and com-
putes (σ
i
← Sign(S[i][2],~r
i
,µ))
i∈[n]
and returns
−→
σ = (σ
1
.. .σ
n
).
Definition 8. (Output Privacy) For the HPRA
scheme Σ, consider an experiment with Exp
outpriv
A
(Σ,κ, n, `) respect to a PPT adversaries A: Public pa-
rameter pp is generated by running Gen(1
κ
,`), MAC
key and auxiliary information (mk, aux) are gener-
ated by running VGen(pp). A is given input pp and
access to oracle O. A random bit b ← {0,1} is cho-
sen by challenger, and a challenge ciphertext
−→
σ is
computed and given to A. A continues to have oracle
access to O, and outputs a guess b
0
of b. Where the
oracle O := {SG,SKey, RoS(b), SR, VR, VRKey}. An
HPRA for a family of function classes F , is output pri-
vate, if for all PPT adversaries A there is a negligible
function negl(·) such that: Pr[Exp
outpriv
A
(Σ,κ, n, `) =
1] ≤
1
2
+ negl(κ).
3 OUR TRANSFORMATION
In this section, we show the general transformation
from HPRA to MVC. As described in Section 2, an
n-client MVC scheme involves two types of parties:
n clients and a server. An n-signer HPRA schemes
involves three types of parties: n signers, an aggre-
gator and a receiver. Simple comparisons give us the
following observations: (1) Both the clients in MVC
and the signers in HPRA are responsible to provide
inputs; (2) Both the server in MVC and the aggrega-
tor in HPRA are responsible to compute an encoded
output and a proof; (3) Both the first client in MVC
and the receiver in HPRA are responsible to perform
the verification and the decryption.
Based on the above observations, a very natural
idea of transforming HPRA to MVC is via the follow
mapping between the participants of two schemes: (1)
let the aggregator in HPRA play the role of the server
in MVC; (2) let the first signer and the receiver in
HPRA play the role of the first client in MVC; (3) for
every j = 2,3,...,n, let the j-th signer in HPRA play
the role of the j-th client in MVC. This natural idea
gives a scheme in the standard MVC model, which
can be depicted with Figure 3.
It remains to understand why the above transfor-
mation gives an MVC scheme with the desired prop-
erties of correctness, soundness, privacy against the
first client, and privacy against the server, provided
that the underlying HPRA scheme satisfies the prop-
erties of correctness, T-Unforgeability, input privacy
and output privacy:
Figure 3: Idea of Transformation.
• The aggregator unforgeability (Definition 7) of
HPRA requires that no dishonest aggregator can
persuade the receiver to both accept and output a
wrong function value, which naturally gives the
soundness (Definition 2) of MVC.
• The output privacy (Definition 8) of HPRA re-
quires that the aggregator should not be able to
learn any information about the signers’ inputs or
the function’s output. This property implies the
property of privacy against the server (Definition
4) in MVC.
• The input privacy (Definition 6) of HPRA gives
the privacy against the first client (Definition 3)
in MVC. Our transformation would give an MVC
scheme where the server learns the first client’s
information, including its private keys and inputs.
However, these additional information will not af-
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
200

fect the security. In Definition 3, the first element
of two challenge input vectors ~x
0
and ~x
1
must be
equal, which prevents a malicious server from us-
ing the first client’s information to gain any ad-
vantage in the security experiment.
Let Σ = (Gen,SGen,VGen,Sign,Verify,SRGen,
VRGen,Agg,AVerify ) be an HPRA scheme for a
function family F . Our general transformation from
Σ to Π = ({KeyGen
j
}
n
j=1
,EnFunc,{EnInput
j
}
n
j=1
,
{EnInput
j
}
n
j=1
,Compute,Verify), an MVC scheme
for F , will be detailed in the remaining part of this
section. Let pp ← Σ.Gen (1
κ
,`) be a set of public
parameters. In the proposed MVC scheme we con-
sider the computation of a function f on the input
(~x
(i)
1
,. .. ,~x
(i)
n
) , where each client P
j
’s input ~x
(i)
j
∈ M
`
is a vector over a finite field. Our MVC scheme works
as follows:
• (pk
1
,sk
1
) ← KeyGen
1
(pp). On input public pa-
rameter pp, the client P
1
runs HPRA’s signer’s
key generation algorithm Σ.SGen(pp) and obtains
an identifier id
1
and a public/private key pair
(sk
1
,pk
1
). Client P
1
runs receiver’s key gener-
ation algorithm Σ.VGen(pp) obtains a MAC key
mk and auxiliary information aux. On private key
sk
1
and auxiliary information aux, client P
1
runs
signer’s re-encryption key generation algorithm
Σ.SRGen(sk
1
,aux), and obtains re-encryption key
rk
1
. The client P
1
sets pk
1
= (id
1
,pk
1
,aux,rk
1
),
sk
1
= (sk
1
,mk).
• (pk
j
,sk
j
) ← KeyGen
j
(pp, pk
1
). On inputs pub-
lic parameter pp and client P
1
’s public key pk
1
,
for j = 2...n each client P
j
runs HPRA’s signer’s
key generation algorithm Σ.SGen(pp) and obtains
an identifier id
j
and a public/private key pair
(sk
j
,pk
j
). On inputs private key sk
j
and auxil-
iary information aux, client P
j
runs signer’s re-
key generation algorithm Σ.SRGen(sk
j
,aux), and
obtains re-encryption key rk
j
. Client P
j
individu-
ally sets pk
j
= (id
j
,pk
j
,rk
j
), sk
j
= sk
j
.
• (φ,ξ) ← EnFunc(
−→
pk, sk
1
, f ). For j = 1 ...n, takes
a signer public key pk
j
and client P
1
’s private key
sk
1
, client P
1
runs Σ.VRGen(pk
j
,mk,rk
j
) and ob-
tains an aggregation key ak
j
. The client P
1
sets the
encoded function φ = ( f ,
−→
ak) and decoding secret
ξ = ∅.
• (χ
(i)
1
,τ
(i)
) ← EnInput
1
(i,
−→
pk, sk
1
,ξ,~x
(i)
1
). When
outsourcing the i-th computation to the server,
takes a time period i, the public keys
−→
pk, client
P
1
’s private key sk
1
, an input message vector ~x
(i)
1
,
the decoding secret ξ, the first client P
1
gets a tag
µ ∈ G, runs the sign algorithm Σ.Sign(sk
1
,~x
(i)
1
,µ),
gets a signature σ
1
, set χ
(i)
1
= σ
1
, τ
(i)
= mk.
• χ
(i)
j
← EnInput
j
(i,
−→
pk, sk
j
,~x
(i)
j
). When outsourc-
ing the i-th computation to the server, takes a time
period i, the public keys
−→
pk, client P
j
’s signer se-
cret key sk
j
and input message vector ~x
(i)
j
, each
client P
j
(with j 6= 1) gets a tag µ ∈ G, then he
runs the algorithm Σ.Sign(sk
j
,~x
(i)
j
,µ), gets signa-
ture σ
j
, sets χ
(i)
j
= σ
j
.
• ω
(i)
← Compute(i,
−→
pk, φ,
−→
χ
(i)
). Given the pub-
lic keys
−→
pk , the encoded function φ, and the en-
coded inputs
~
χ
(i)
, the server runs the aggregate al-
gorithm Σ.Agg(
−→
ak,
−→
χ
(i)
,µ,φ), gets aggregate au-
thenticated message vector Λ and set ω
(i)
= Λ.
• y
(i)
∪{⊥} ← Verify(i,
−→
pk, ξ, τ
(i)
,ω
(i)
). Take the
public keys
−→
pk, the decoding secrets (ξ,τ
(i)
), and
an encoded output ω
(i)
, the first client P
1
runs
receiver’s verification algotithm Σ.AVerify(mk,Λ,
ID, f ) which outputs a message vector and a tag
(~m,µ) on success and (⊥,⊥) otherwise. Sets
y
(i)
= ~m on success and returns ⊥ otherwise.
The scheme Π should satisfy the properties of cor-
rectness, soundness and privacy. While the correct-
ness property is easy to verify, proofs for the follow-
ing theorems can be found in Appendix.
Theorem 1. If Σ is a T-unforgeable HPRA scheme,
here T = “Aggregator”, then Π described above is a
sound MVC scheme.
Theorem 2. If Σ is an input private HPRA scheme,
then Π is an MVC scheme with the privacy against
the first client property.
Theorem 3. If Σ is an output private HPRA scheme,
then Π is an MVC scheme with the privacy against
the server property.
4 IMPLEMENTATION
To evaluate the efficiency of our transformation, we
apply our transformation on a concrete instantiation
of HPRA, scheme 3 in (Derler et al., 2017), and con-
duct several experiments. The experiments is tested
on personal computer with a Intel Core i7-4790K
CPU running at 3.60GHz, 8GB of RAM running on
Windows 10. And we use VMware Workstation Pro
12.0 to help us setup a build environment on ubuntu-
16.04.1. The entire implementation is completely
done in C programming language. We use the PBC
(Pairing-Based Cryptography) library
1
to help us
1
https://crypto.stanford.edu/pbc/
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme
201
generating suitable bilinear-map groups. More specif-
ically, we use the type A curve defined in PBC li-
brary: y
2
= x
3
+x over F
q
for prime q = 3 mod 4 with
|q| = 512.
We omit simulating the communication between
the clients and server, as our work does not focus
on the communication process and this simplification
will not affect our analysis on computational com-
plexity.
4.1 Client Computation
There are three variables that have a major impact on
runtime: the length ` of the input vector, the max-
imum size of input vector element, denoted as x
max
(any element of client P
j
’s input vector ~x
(i)
j
is smaller
than 2
x
max
) and the total number n of the clients. We
will first give a theoretical analysis on how these vari-
ables affect the clients’ and server’s runtime and then
verify the correctness of the analysis through some
carefully designed experiments described as follows.
We define some symbols for simplification:
Mul
G
: Multiplication operation time in G.
Exp
G
: Exponentiation operation time in G.
Mul
G
T
: Multiplication operation time in G
T
.
Exp
G
T
: Exponentiation operation time in G
T
.
Pair
G
: Pairing operation time in G.
Log: Time to solve the discrete log problem.
Pre-processing. The pre-processing is a process
consist of KeyGen (including both KeyGen
1
and
KeyGen
j
) and EncFunc. The theoretical analysis of
pre-processing runtime is shown in Table 1. Here we
set x
max
to 20 bits, the experimental results shown in
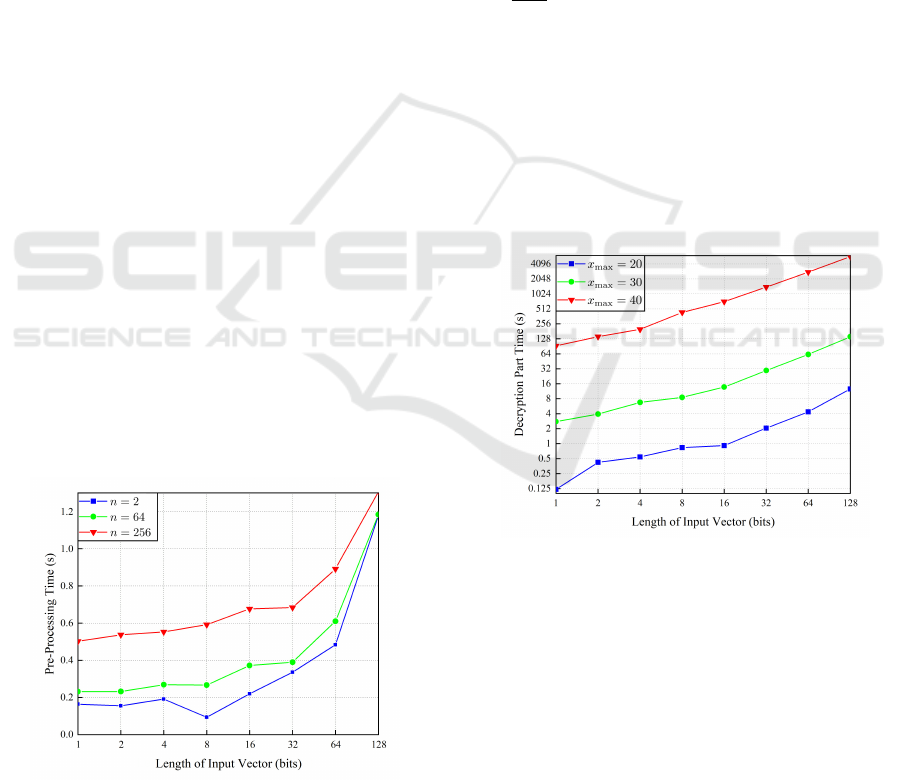
the Figure 4 depicts that:
Figure 4: Client’s Pre-processing Time.
• When the total number n of the clients is fixed,
pre-processing time is proportional to the length `
of the input vector.
• When the length ` of the input vector is fixed, pre-
processing time is proportional to n.
• As ` and n increase, ` has a greater impact on run-
time than n.
Input Encoding. We omit the experiment on the
clients’ encoding process which only includes EnIn-
put, as it is a efficient algorithm whose runtime only
relates to length ` of the input vector as Table 1 re-
vealed.
Verification Process. The verification process in-
cluding only Verify algorithm which acctually con-
sist of two parts: decryption part and verification part.
We used the Pollard’s kangaroo algorithm (Pollard,
1978) which is the fastest known way to break dis-
crete log for a general elliptic curve with complexity
O(
√
x
max
), to help us solving the discrete log prob-
lem in decryption part. Thus, the complexity of the
decryption part is related to the maximum size x
max
of input vector element and the length ` of the input
vector as Table 1 revealed. The runtime of the verifi-
cation part becomes negligible compared to the time
required for decryption as x
max
increase. Here we fix
n to 2 for it has very little impact on the runtime, the
experimental results shown in the Figure 5 with log2
type Y axis indicates that:
Figure 5: Client’s Decryption Time.
• When the maximum size x
max
of input vector el-
ement is fixed, the runtime verification process is
proportional to the length ` of the input vector.
• When the length ` is fixed, the runtime of verifi-
cation process is proportional to x
max
.
• As x
max
and ` increase, x
max
has a greater impact
on runtime than `.
4.2 Server Computation
As shown in Table 1, the server’s runtime is related to
the length ` of the input vector and the total number
n of the clients. Here we set x
max
to 20 bits for sim-
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
202

Table 1: Computational Complexity of Our MVC.
Mul
G
Exp
G
Mul
G
T
Exp
G
T
Pair
G
Log
Pre-processing 0 2` + 2n + 4 0 ` + 1 0 0
Input Encoding ` + 1 ` + 3 ` 2` 0 0
Decryption Part 0 0 ` + 1 ` + 1 0 ` + 1
Verification Part ` −1 ` + n n + 1 3 ` + n 0
Server Computation 0 n (2` + 3)(n −1) + 1 (2` + 2)n ` + n + 1 0
plicity, the experimental results shown in the Figure 6
below further demonstrate our theory:
• When the total number n of the clients is fixed,
server’s runtime is proportional to the length ` of
the input vector.
• When the length ` is fixed, server’s runtime is pro-
portional to n.
Figure 6: Server’s runtime.
4.3 Analysis and Comparisons
Efficiency Analysis. In some cases, the client com-
putation time is even higher than server computation
time, and we are trying to avoid it. Below we analyze
under what circumstances this concrete instantiation
is an efficient solution from both theory and experi-
ments. We assume that the time required for all group
operations is constant. And
p
x
max
+ log
2
n −1 repre-
sents the expected value of the sum of n clients’ input
vector elements with maximum size x
max
.
Theoretically speaking, the total runtime of client P
1
:
T
client
= 12` + 5n + 12 + (` + 1)
p
x
max
+ log
2
n −1.
In general, we hope that any client takes will less time
than the server needs in the process, otherwise, this
MVC scheme will not be efficient, that is:
T
client
≤ 7n + (4n −1)` −1.
By observing the inequality above, when the total
number n of the clients grows big enough and the
maximum size x
max
stays rather small, server’s run-
time will exceed client’s runtime.
The experimental results shown in the Figure 7 be-
low further demonstrate our theory. Here we fixed ` to
128, and set x
max
= 20 bits which is rather small. As
n grows, the server’s runtime will exceed the clients’
total runtime, and the gap between these two will be-
come more and more significant.
Figure 7: Total runtime.
Comparisons with Previous Work. As MVC is a
extend non-interactive verifiable computation scheme
(Gennaro et al., 2010) where inputs are provided by
multiple clients, both MVC and non-interactive ver-
ifiable computation use the expensive FHE and GCs
technology in the same way, each client runs the en-
cryption and decryption algorithm only once in one
round computing. (Parno et al., 2013) established a
model for evaluating the efficiency of the FHE+GCs
based VC schemes such as (Gennaro et al., 2010;
Choi et al., 2013). More specifically, they simulated
an experiment on two matrices with parameter t, takes
as input two (t ×t) matrices M
1
and M
2
, and outputs
the t ×t matrix M
1
·M
2
, each component in M
1
and
M
2
is at most 32 bits.
In order to fit experiment in (Parno et al., 2013),
we set both the total number of the clients n and length
of the input vector ` equal to t, the maximum size of
input vector component equals to 32 bits, and t clients
will jointly outsource t linear combination functions
in order to get the result of matrix multiplication.
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme
203

Here we plot the time necessary for the verify pro-
cess, as showing in Figure 8, our verify algorithms is
much more efficient than the original MVC scheme.
We believe these numbers show that our protocol is
applicable in a practical setting.
Unfortunately, since we used the Pollard’s kanga-
roo algorithm (Pollard, 1978) to solve the discrete log
problem in the decryption. The time we spend in the
decryption process is still relatively long, it is accept-
able when the input length is shorter than 50-bit.
Figure 8: Comparison with (Choi et al., 2013).
5 CONCLUSION
In this paper, we provide a general transformation
from HPRA to MVC. We also implemented an MVC
scheme for computing the linear combinations of vec-
tors over a finite field. To our best knowledge, this is
the first implementable MVC scheme for outsourcing
specific computation to date. Our implementation re-
quires the computation of discrete logarithms. How
to avoid the the expensive operations of computing
discrete logarithms is an open question for further re-
search.
ACKNOWLEDGEMENTS
This work is supported by National Natural Science
Foundation of China (Grant No. 61602304). The
authors thank Zidong Lu for useful helping provided
in experiment environment configuration and C pro-
gramming.
REFERENCES
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., and
Virza, M. (2013). Snarks for c: Verifying program ex-
ecutions succinctly and in zero knowledge. In Annual
Cryptology Conference, pages 90–108. Springer.
Ben-Sasson, E., Chiesa, A., Tromer, E., and Virza, M.
(2014). Succinct non-interactive zero knowledge for a
von neumann architecture. In 23rd USENIX Security
Symposium, pages 781–796.
Benabbas, S., Gennaro, R., and Vahlis, Y. (2011). Veri-
fiable delegation of computation over large datasets.
In Annual Cryptology Conference, pages 111–131.
Springer.
Braun, B., Feldman, A. J., Ren, Z., Setty, S., Blumberg,
A. J., and Walfish, M. (2013). Verifying computations
with state. In Proceedings of the Twenty-Fourth ACM
Symposium on Operating Systems Principles, pages
341–357. ACM.
Choi, S. G., Katz, J., Kumaresan, R., and Cid, C. (2013).
Multi-client non-interactive verifiable computation. In
Theory of Cryptography Conference, pages 499–518.
Springer.
Cormode, G., Mitzenmacher, M., and Thaler, J. (2012).
Practical verified computation with streaming interac-
tive proofs. In Proceedings of the 3rd Innovations in
Theoretical Computer Science Conference, pages 90–
112. ACM.
Derler, D., Ramacher, S., and Slamanig, D. (2017). Ho-
momorphic proxy re-authenticators and applications
to verifiable multi-user data aggregation. In Inter-
national Conference on Financial Cryptography and
Data Security, pages 124–142. Springer.
Fiore, D., Mitrokotsa, A., Nizzardo, L., and Pagnin, E.
(2016). Multi-key homomorphic authenticators. In In-
ternational Conference on the Theory and Application
of Cryptology and Information Security, pages 499–
530. Springer.
Gennaro, R., Gentry, C., and Parno, B. (2010). Non-
interactive verifiable computing: Outsourcing com-
putation to untrusted workers. In Annual Cryptology
Conference, pages 465–482. Springer.
Goldwasser, S., Gordon, S. D., Goyal, V., Jain, A., Katz, J.,
Liu, F.-H., Sahai, A., Shi, E., and Zhou, H.-S. (2014).
Multi-input functional encryption. In Annual Interna-
tional Conference on the Theory and Applications of
Cryptographic Techniques, pages 578–602. Springer.
Gordon, S. D., Katz, J., Liu, F.-H., Shi, E., and Zhou, H.-
S. (2015). Multi-client verifiable computation with
stronger security guarantees. In Theory of Cryptog-
raphy Conference, pages 144–168. Springer.
Papamanthou, C., Shi, E., and Tamassia, R. (2013). Signa-
tures of correct computation. In Theory of Cryptogra-
phy Conference, pages 222–242. Springer.
Parno, B., Howell, J., Gentry, C., and Raykova, M. (2013).
Pinocchio: Nearly practical verifiable computation. In
2013 IEEE Symposium on Security and Privacy, pages
238–252. IEEE.
Pollard, J. M. (1978). Monte carlo methods for index
computation mod p. Mathematics of computation,
32(143):918–924.
Schabh
¨
user, L., Butin, D., and Buchmann, J. (2019). Con-
text hiding multi-key linearly homomorphic authenti-
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
204

cators. In Cryptographers Track at the RSA Confer-
ence, pages 493–513. Springer.
Setty, S., Braun, B., Vu, V., Blumberg, A. J., Parno, B., and
Walfish, M. (2013). Resolving the conflict between
generality and plausibility in verified computation. In
Proceedings of the 8th ACM European Conference on
Computer Systems, pages 71–84. ACM.
Wahby, R. S., Setty, S. T., Ren, Z., Blumberg, A. J., and
Walfish, M. (2015). Efficient ram and control flow in
verifiable outsourced computation. In NDSS.
APPENDIX
Proof of Theorem 1
We show that if there exists a polynomial-time ad-
versary (PPT) A for which break soundness of MVC
(Definition 2), that is, Pr[Exp
sound
A
[Π, f ,κ, n] = 1] ≥
non-negl(κ) then we can construct a PPT adversary
B that breaks the T-unforgeability of Σ when T =
“Aggregator”. B is given inputs (1
κ
,n,`) and an ora-
cle O
T
:= {SG, Sig, SR,VR,VRKey}. In detail:
Experiment Exp
T-unforge
B
[Σ,κ, n, `] :
1. The challenger runs pp ← Gen(1
κ
,`), (mk,
aux) ← VGen(pp), sends pp and aux to B.
2. For j = 1, . . . n, B queries the following ora-
cles and gets (id
j
,pk
j
) ← SG( j), rk
j
← SR
( j), B also queries the oracle VR( j) to gen-
erate ak
j
, and queries ak
j
← VRKey( j).
3. B then sets pk
1
= (id
1
,pk
1
,aux,rk
1
), for
j = 2 . . . n, pk
j
= (id
j
,pk
j
,rk
j
), φ =
( f ,(ak
j
)
j∈[n]
) and sends them to A. Here f
is the function on which A can break MVC
soundness.
4. B initializes a counter i := 0.
5. Whenever A queries its encryption oracle
I N with input (~x
1
,. .. ,~x
n
), B answers the
queries in following way:
a. Sets i := i + 1.
b. Records (~x
(i)
1
,. ..~x
(i)
n
) := (~x
1
,. .. ,~x
n
).
c. Queries the oracle and gets (
−→
σ
(i)
,µ) ←
Sig(( j)
j∈[n]
,(~x
(i)
j
)
j∈[n]
).
d. Sets and returns
−→
χ
(i)
:=
−→
σ
(i)
.
6. When A outputs ω
?
, B sets Λ
?
:= ω
?
and
sends (Λ
?
,ID
?
, f
?
) to the challenger, here
ID
?
:= (id
1
,. .. , id
n
), f
?
= f .
7. The challenger runs AVerify(mk,Λ
?
,ID
?
, f
?
).
8. If (~m,µ) 6= (⊥,⊥) and (@(~x
j
)
j∈[n]
: (∀j ∈
[n] : (~x
j
,id
∗
) ∈ SIG[µ]) ∧ f
?
(~x
1
.. .,~x
n
) = ~m)
(i.e., 1. f
?
(~x
1
,. .. ,~x
n
) = ~m , and at least one
~x
j
have not been queried by A in the i-th
querry or 2. f
?
(~x
1
,. .. ,~x
n
) 6= ~m), outputs 1;
otherwise outputs 0.
If a PPT adversary A can break MVC with non-
negl(κ), then A can find a ω
?
, such that chal-
lenger gets y
∗
/∈ {⊥, f (x
(i)
1
,. .. , x
(i)
n
)} when run-
ning Verify. As Π.Verify in our transformation
directly calls Σ.AVerify, if A produces such a
ω
∗
, then B can directly take ω
∗
as an input of
Σ.AVerify. Clearly, when A can cheat Π.Verify and
let Exp
sound
A
[Π, f ,κ, n] = 1, B can definitely cheat
Σ.AVerify and let Exp
T-unforge
B
(Σ,κ, n, `) = 1. Then
We successfully construct such a B which breaks
T-unforgeability when T = “Aggregator” with non-
negl(κ): Pr[Exp
T-unforge
B
(Σ,κ, n, `) = 1] ≥Pr[Exp
sound
A
(Π, f
∗
,κ,n) = 1] ≥ non-negl(κ). However, as the T-
unforgeability has been proven in HPRA, this makes
a contradiction. Therefore, there is no PPT adversary
A for which soundness of MVC does not hold.
Proof of Theorem 2
The privacy against first client can be intuitively de-
rived from the input privacy of HPRA. Recall the
Definition 6, an HPRA Π scheme is called input pri-
vate if for all (~m
11
,. .. ,~m
n1
) and (~m
12
,. .. ,~m
n2
) where
f (~m
11
,. .. ,~m
n1
) = f (~m
12
,. .. ,~m
n2
), the following dis-
tributions are identical:
Λ
1
←Π.Agg
−→
ak,
−→
σ
1
,µ, f ), Λ
2
←Π.Agg
−→
ak,
−→
σ
2
,µ, f ).
Where
−→
σ
1
is the signatures of (~m
11
,. .. ,~m
n1
)
from Σ.Sign algorithm,
−→
σ
2
is the signatures of
(~m
12
,. .. ,~m
n2
) from Σ.Sign algorithm.
Recall the Definition 3, an MVC scheme Σ is
called privacy against the first client if the view of the
first client when running Σ with clients holding in-
puts (~x
1
,~x
2
,. .. ,~x
n
) is indistinguishable from the view
of the first client when running Σ with clients hold-
ing inputs (~x
1
,~x
0
2
,. .. ,~x
0
n
). As the first client P
1
has no
other opportunity to access information from all other
entities when running Σ, except when running Verify
algorithm: P
1
gets an encoded output ω
(i)
which may
reveals some information. Therefore, we only need to
prove that the following distributions are identical:
ω
(i)
← Σ.Compute
i,(pk
j
)
j∈[n]
,φ,
−→
χ
(i)
,
ω
0
(i)
← Σ.Compute
i,(pk
j
)
j∈[n]
,φ,
−→
χ
0
(i)
.
Here
−→
χ
(i)
is the encoded from (~x
1
,~x
2
,. .. ,~x
n
) us-
ing Π.EnInput
1
and Π.EnInput
j
, and
−→
χ
0
(i)
is the
encoded from (~x
1
,~x
0
2
,. .. ,~x
0
n
) using Π.EnInput
1
and
Π.EnInput
j
.
Without loss of generality, we can set (~m
11
,
.. .,~m
n1
) := (~x
1
,~x
2
,. .. ,~x
n
) and (~m
12
,. .. ,~m
n2
) := (~x
1
,
A Homomorphic Proxy Re-authenticators based Efficient Multi-client Non-interactive Verifiable Computation Scheme
205

~x
0
2
,. .. ,~x
0
n
), be any two vectors with same first com-
ponent and f (~x
1
,~x
2
,. .. ,~x
n
) = f (~x
1
,~x
0
2
.. .,~x
0
n
). Very
intuitively speaking, Π.EnInput
1
and Π.EnInput
j
both directly call the algorithm Σ.Sign, except that
Π.EnInput
1
returns mk additionally, i.e.,
−→
χ
(i)
=
−→
σ
1
,
−→
χ
0
(i)
=
−→
σ
2
. Furthermore, Π.Compute algorithm ex-
actly calls Σ.Agg, ω
(i)
and ω
0
(i)
are calculate exactly
the same way as in the definition of input privacy of
HPRA, i.e., ω(i) = Λ
1
and ω
0
(i)
= Λ
2
. Due to the input
privacy of HPRA, ω
(i)
and ω
0
(i)
are clearly identical.
Therefore, we proved that MVC scheme Σ is privacy
against the first client.
Proof of Theorem 3
We show that if there exists a PPT adversary A for
which privacy against the server of MVC on func-
tion f does not hold, then we can construct a PPT
adversary B that break the output privacy of HPRA.
B is given input 1
κ
,n,` and access to an oracle O :=
{SG,SKey,RoS(b),SR,VR,VRKey }. We follow the
assumption of MVC that all the clients are honest but
curious, in detail:
Experiment Exp
outpriv
B
[Σ,κ, n, `] :
1. The challenger runs pp ← Gen(1
κ
,`), (mk,
aux) ← VGen(pp) and chooses a random
bit b ← {0, 1}, then sends pp and aux to B.
2. For j = 1,...n, B queries the following
oracles and gets (id
j
,pk
j
) ← SG( j), ⊥←
SKey( j), rk
j
← SR( j). B also queries the
oracle VR( j) to generate ak
j
, and queries
ak
j
← VRKey( j).
3. B then sets pk
1
= (id
1
,pk
1
,aux,rk
1
), for
j = 2 . . . n, pk
j
= (id
j
,pk
j
,rk
j
), φ = ( f ,
−→
ak)
and sends them to A. Here f is the function
on which A can break MVC soundness.
4. B initializes a counter i := 0.
5. Whenever A queries its encryption oracle
I N with input (~x
1
,. .. ,~x
n
), B answers the
queries in following way:
a. Sets i := i + 1.
b. Records (~x
(i)
1
,. ..~x
(i)
n
) := (~x
1
,. .. ,~x
n
).
c. Queries the oracle and gets ((
−→
σ
(i)
,µ) ←
Sig({1,...,n},(~x
(i)
j
)
j∈[n]
).
d. Sets and returns
−→
χ
(i)
:=
−→
σ
(i)
to A.
6. When A outputs (~x
0
1
,. .. ,~x
0
n
),(~x
1
1
,. .. ,~x
1
n
), B
chooses a random bit b
0
← {0, 1} and
works as following:
a. Queries RoS( j,~x
b
0
1
,. .. ,~x
b
0
n
,b) and ob-
tains ((σ
b
0
1
,c
b
0
1
),. . . , (σ
b
0
n
,c
b
0
n
)).
b. Returns the challenge ciphertext
−→
χ
b
0
:=
−→
σ
b
0
to A.
7. When A returns a bit b
1
to B, B outputs 1,
if b
0
= b
1
, otherwise, outputs 0.
Intuitively speaking, when b
0
= b
1
, A figures out
which one of inputs (~x
0
1
,. .. ,~x
0
n
),(~x
1
1
,. .. ,~x
1
n
) is signed,
and B tends to believe that RoS(b) does sign one of
the inputs, and outputs a guess for the value of b, b
0
=
1. Otherwise, when A cannot figure out which one of
inputs is signed, B tends to believe that RoS(b) signs
a random string. Then B will outputs a guess for the
value of b, b
0
= 0.
Recall the definition of private against the server
in Section 2 Definition 3, we can figure out that when
the privacy against the server of MVC against A does
not hold:
Adv
priv
A
(Π, f ,κ, n) =
Pr[Exp
priv
A
(Π, f ,κ, n, 0) = 1]−
Pr[Exp
priv
A
(Π, f ,κ, n, 1) = 1]
≥ non-negl(κ).
Without loss of generality, we assume that the prob-
ability Pr[Exp
priv
A
[Π, f ,κ, n, 1] = 1] is bigger than
the probability Pr[Exp
priv
A
[Π, f ,κ, n, 0] = 1]. If b =
0, RoS(b) encrypts (~x
b
0
1
,. .. ,~x
b
0
n
), then the view
of A when run as a sub-routine by B is dis-
tributed identically to the view of A in experiment
Exp
priv
A
[Π, f ,κ, n, b
0
] . Thus,
Pr[Exp
outpriv
B
[Σ,κ, n, `] = 1|b = 0] = Pr[b
0
= 0]
−Pr[b
0
= 0] ·Pr[Exp
priv
A
(Π, f ,κ, n, 0) = 1]
+Pr[b
0
= 1] ·Pr[Exp
priv
A
(Π, f ,κ, n, 1) = 1].
Since b
0
is randomly chosen by B, Pr[b
0
= 0] =
Pr[b
0
= 1] = 1/2, we have:
Pr[Exp
outpriv
B
[Σ,κ, n, `]=1|b=0]≥
1
2
+
1
2
·non-negl(κ).
If b = 1, RoS(b) encrypts a string of random num-
bers, then the view of A when run as a sub-routine by
B is distributed identically to the view of A in an ex-
periment of guessing random numbers. Thus,
Pr[Exp
outpriv
B
(Σ,κ, n, `) = 1|b = 1] = 1/2.
Combining the above two equations, since b is
randomly chosen by challenger, Pr[b = 0] = Pr[b =
1] = 1/2, if the output privacy of MVC can be broken
by A with non-negligible probability non-negl(κ), we
have:
Pr[Exp
outpriv
B
(Σ,κ, n, `) = 1] = 1/2 ·Pr[b
0
= 1|b = 0]
+1/2 ·Pr[b
0
= 1|b = 1] ≥1/2 + 1/4 ·non-negl(κ).
However, as the output privacy has been proven
in HPRA, makes a contradiction. Thus, if the output
privacy is hold, then our MVC scheme also maintains
the privacy against the server.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
206
