
Learning Efficient Coordination Strategy for Multi-step Tasks in
Multi-agent Systems using Deep Reinforcement Learning
Zean Zhu
a
, Elhadji Amadou Oury Diallo
b
and Toshiharu Sugawara
c
Department of Computer Science and Communication Engineering,
Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo 169-8555, Japan
Keywords:
Multi-agent System, Deep Reinforcement Learning, Coordination, Cooperation.
Abstract:
We investigated whether a group of agents could learn the strategic policy with different sizes of input by
deep Q-learning in a simulated takeout platform environment. Agents are often required to cooperate and/or
coordinate with each other to achieve their goals, but making appropriate sequential decisions for coordinated
behaviors based on dynamic and complex states is one of the challenging issues for the study of multi-agent
systems. Although it is already investigated that intelligent agents could learn the coordinated strategies using
deep Q-learning to efficiently execute simple one-step tasks, they are also expected to generate a certain co-
ordination regime for more complex tasks, such as multi-step coordinated ones, in dynamic environments. To
solve this problem, we introduced the deep reinforcement learning framework with two kinds of distributions
of the neural networks, centralized and decentralized deep Q-networks (DQNs). We examined and compared
the performances using these two DQN network distributions with various sizes of the agents’ views. The
experimental results showed that these networks could learn coordinated policies to manage agents by using
local view inputs, and thus, could improve their entire performance. However, we also showed that their
behaviors of multiple agents seemed quite different depending on the network distributions.
1 INTRODUCTION
Learning efficient coordination and cooperation strat-
egy in solving the problems in a complex environment
is a central issue in a multi-agent system. To achieve
this sort of learning, agents are expected to observe
the surrounding environment combined with their in-
ternal states to make appropriate decisions. Although
a number of studies such as (Miyashita and Sugawara,
2019) showed that agents could learn coordinated pol-
icy well for the execution of a simple one-step task
in the environment using the deep Q-learning, intelli-
gent agents need to learn to execute tasks consisting
of a few steps in a cooperative manner. For example,
in a takeout platform environment, such as Uber Eats
and Talabat, delivery agents have to locate restaurants
to pick up ordered dishes firstly and then deliver them
to the destinations where customers wait. Besides,
being aware of their current state is very important
because they will be unable to take any other future
order for a while if they get a contract of the current
a
https://orcid.org/0000-0001-9541-4270
b
https://orcid.org/0000-0001-6441-7719
c
https://orcid.org/0000-0002-9271-4507
order. To achieve desirable cooperative behavior, all
agents should know what they need to do in the cur-
rent situation; otherwise, agents might be affected by
other agents that have inappropriate behaviors.
The deep reinforcement learning (DRL) has been
proved working in many fields such as video games
(Mnih et al., 2013) and traffic control (Li et al.,
2016). Because it is impractical to learn appropri-
ate actions in the environment in which a vast num-
ber of observable states exist with traditional algo-
rithms like Q-learning, we also attempt to apply the
DRL to the multi-agent system in our experiments
to solve the coordination/cooperation problems in the
dynamic environment. In addition, Markov game
model (Littman, 1994) has been widely used as a uni-
versal model in the multi-agent deep reinforcement
learning (MADRL) (Egorov, 2016). Training a model
for the multi-agent system is still challenging because
the states of agents and their appropriate actions are
mutually and dynamically affected with each other.
Therefore, we examine whether the DRL can gen-
erate a coordination regime for multi-step tasks, like
takeout problems, without conflicting their behaviors.
The function of MADRL used to tackle these prob-
Zhu, Z., Diallo, E. and Sugawara, T.
Learning Efficient Coordination Strategy for Multi-step Tasks in Multi-agent Systems using Deep Reinforcement Learning.
DOI: 10.5220/0009160102870294
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 287-294
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
287

lems in this paper is to learn to generate appropriate
actions for specific states to maximize the numerical
rewards for all or individual agents depending on the
deployment of the deep Q-networks (DQNs) for the
DRL. To examine from these perspectives, we intro-
duce two types of training in MADRL; centralized
training, in which a manager has a DQN to be trained
to generate actions for all agents, and decentralized
training, in which individual agents are trained to gen-
erate better actions for themselves. Our contribution
is to examine the performance of these two training
methods and compare the agents’ behavior for multi-
step tasks (i.e., orders) constantly occurring in the en-
vironment.
Furthermore, we also changed the observable
views of each agent for training to see the differences
in the emerging collective behaviors. We developed a
takeout platform simulator in which multi-step tasks
are generated continuously and investigated the effect
of the DQN distribution on the entire performance.
Note that although the size of our simulation environ-
ment is not so large, the number of states for learning
is enormous and the rules in the environment are com-
plex. Nevertheless, our experimental results indicate
that learning by MADRL converged to efficient be-
haviors of multiple agents but their behaviors were
quite different depending on the distribution of the
DQNs.
2 RELATED WORKS
In general, multi-agent reinforcement learning
(MARL) is used so that multiple agents appropriately
cooperate, coordinate or compete with each other
through taking joint actions with the associated
rewards in the given environment. We focus on
the most related and recent work for multi-agent
systems, especially cooperation and coordination,
to accomplish sophisticated coordinated tasks. The
Q-learning algorithm explained in (Watkins and
Dayan, 1992) is the most fundamental method for
MARL problems. (Tan, 1993) showed that the agents
could learn cooperative behaviors independently
with Q-learning in a simulated social environment in
which independent agents did not perform well with
Q-learning in (Matignon et al., 2012). Unfortunately,
traditional learning approaches such as Q-learning
or policy gradient (Silver et al., 2014) result in poor
performance in our study due to the large size of
observable states of our environment.
Meanwhile, (Mnih et al., 2013) indicated that
the online Q-learning method based on deep learn-
ing models could be used to overcome the problems
x
1
x
2
r
1
c
1
x
1
c
1
x
2
x
2
x
1
r
1
x
1
x
2
time t = 0
time t = 2
time t = 10
Figure 1: Example Environment with an execution of an
Order.
caused by dynamic environments. Furthermore, sev-
eral ideas have been introduced to make the DQNs
more stable during training procedures. For example,
the experience replay shown in (Mnih et al., 2015)
lets multiple agents remember and reuse experiences
from the past and is the practical method to reduce the
number of transitions required to learn strategies. The
learning algorithms such as DQN and double DQN
(DDQN) (Van Hasselt et al., 2016) architectures are
also used to improve the learning abilities, for exam-
ple, a distributed DDQN framework was applied to
train agents cooperatively move, attack and defend in
various geometric formations (Diallo and Sugawara,
2018).
Moreover, (Lin et al., 2018) used centralized neu-
ral networks to solve the relocation problem in the
large-scale online ride-sharing platform. They pro-
posed a contextual MARL framework in which the
neural network was given additional environment in-
formation when making decisions. However, we have
to mention that the goal of their study was to pre-
dict where agents could take more tasks and agents
would be relocated to destinations instead of explor-
ing destinations by themselves. (Miyashita and Sug-
awara, 2019) compared the coordination regimes as
well as the learning performance with different view
sizes for independent agents. They claim that agents
could learn coordination structures without conflicts
with a partial view of the environment, although the
tasks they introduced were the simple one-step tasks,
unlike ours.
3 PROBLEM
We consider a multi-agent problem in which a group
of agents learn the coordinated behavior for delivering
ordered dishes in an online takeout platform. Deliv-
ering tasks are continuously generated by restaurants
according to customers’ requests. When one of the
agents picks up an order from the restaurant and de-
livers the ordered dishes to the customer’s location,
the order is completed. The goal of this problem is to
maximize the order completion rate by agents’ coor-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
288

dinated behaviors learned with deep neural networks.
Note that a task in our problem consists of two-step
and ordered subtasks; pickup and delivery. An exam-
ple of our problem environment is shown in Fig. 1,
in which the environment is a grid world, red trian-
gles are restaurants, yellow stars are customers, and
blue circles are delivery agents. The possible actions
of agents are one of A = {up, right, down, left}. We
assume that each grid cell has a certain size in which
there can be up to five agents in it.
When the ordered dishes are almost ready, the
restaurant broadcasts order information to nearby
agents in the broadcast area, which is expressed by
a yellow area in Fig. 1. The restaurant selects and
makes a contract with one of the delivery agents in
this area according to a particular rule, and the se-
lected agent would be guided to this restaurant to
pick up the order. Then, the order will be marked
as the finished state when the agent arrives at the cus-
tomer’s cell. The agent is expected to learn policy
π that decides where it should wait for future orders
from restaurants, and its actions to deliver the ordered
dishes along with the appropriate path.
We model this problem as a Markov game
h
N, K, S, A, R
i
, where N, K, S, A, R are the set of n
agents, the set of restaurants, the set of all local states,
the joint action space, and the reward functions, re-
spectively. The details are given as follows:
• Agent i ∈ N = {1, ..., n}: Agent i is an robot or
delivery person for delivering orders in the take-
out platform.
• Restaurant j ∈ K: Restaurant j will broadcast
orders information to agents in the M × M area
whose center is itself when j has an order to de-
liver. Parameter M is called the broadcast area
size.
• State s
t
∈ S: Each state is expressed by s
t
=
s
1
t
× · · · × s
n
t
, where s
i
t
is the local state observed
by agent i at time t and contains the information
about the position of itself, the local restaurants
and customers at time t.
• Action a
t
∈ A: Joint action a
t
∈ A at time t can be
denoted by the product of all actions a
t
= (a
1
t
×
··· × a
n
t
) ∈ A
1
× ··· × A
n
, where A
i
is the action
space of agent i.
• Reward Function R : R is the function R : S ×
A −→ R, which expresses the reward for joint ac-
tion a
t
∈ at state s
t
∈ S
t
and whose value R(s
t
, a
t
)
may be a positive or negative real number.
Fig. 1 shows an example process of delivering an
order. At time t = 0, agent1 (which is denoted by x
1
in
this figure) takes the action to go up and agent2 (x
2
)
takes action to go left. Then restaurant1 (which is
denoted by r
1
) broadcasts the request signal about or-
der1 to nearby agents in the yellow area. Both x
1
and
x
2
report their positions to r
1
. Then, r
1
selects x
1
to
deliver this order because the distance between x
1
and
r
1
is the shortest. From time t = 1 to 2, x
1
will be nav-
igated by r
1
to the r
1
’s cell and given a certain reward
(this reward is +5 in an experiment below) for picking
the order up at t = 2. From time t = 3, x
1
starts to lo-
cate customer1 (which is denoted by c
1
in this figure)
with actions from the deep networks (or random ac-
tions because we will use the ε-greedy learning strat-
egy) until it arrives at c
1
’s cell. Note that x
1
cannot
pick up any other order before it completes the cur-
rent order. At time t = 10 in this example, x
1
reaches
c
1
and receives a certain reward (which is +10 in our
experiment below).
4 PROPOSED METHOD
This section describes the methods that were taken in
our experiments to analyze the performance and the
emerging coordinated behaviors by the DQNs. We
applied the centralized DQN and the decentralized
DQNs for learning the agents’ behaviors in a multi-
agent system.
4.1 Decentralized DQNs
The decentralized DQNs mean that agents have their
own deep neural networks whose structures are the
DDQN to generate actions for themselves on the ba-
sis of the local information, in order to achieve their
goals independently. We think that agent i ∈ N will
learn a coordinated strategy through this learning pro-
cess because the appropriate coordination allows it to
maximize its cumulative discounted future reward R
i
t
at time t. Note that R
i
t
is calculated by
R
i
t
=
T
∑
t
0
=t
γ
t
0
−t
· r
i
t
0
, (1)
where T is the time step at which the simulation envi-
ronment terminates and γ ∈ [0, 1] is the discount factor
that weights the importance of rewards.
Then, the action value of Q for agent i with policy
π
i
is defined as
Q
π
i
(s
i
, a
i
) = E[R
i
t+1
|s = s
i
t
, a = a
i
t
], (2)
and the optimal Q
∗
is defined as
Q
∗
(s
i
, a
i
) = max
π
i
E[R
i
t+1
|s = s
i
t
, a = a
i
t
]. (3)
The action-value function for agent i is defined as
Q
∗
(s
i
, a
i
) = E[R
i
t+1
+ γmax
a
i
Q
∗
(s
i
t+1
, a
i
)|s, a]. (4)
Learning Efficient Coordination Strategy for Multi-step Tasks in Multi-agent Systems using Deep Reinforcement Learning
289

Moreover, the optimal policy of an agent depends not
only on its own states but also on the policies of other
agents. To be more concrete, agents should observe
other agents’ locations and restaurants in their views
to avoid the conflicts and redundant activities, such as
gathering in one restaurant, so that they could cooper-
ate to finish more orders from various restaurants.
At time t, the neural network weight θ
i
t
is updated
to minimize the loss function L
t
(θ
i
t
) for agent i, which
is defined as:
L
t
(θ
i
t
) = E
(s
i
,a
i
,r
i
,s
i
t+1
)
y
i
t
− Q
i
(s
i
, a
i
;θ
i
t
)
2
, (5)
where y
i
t
is the target Q-value of agent i from target
network (Mnih et al., 2015) with parameters θ
i,−
t
:
y
i
t
= R
i
t+1
+ γQ
s
i
t+1
, argmax
a
i
Q(s
i
t+1
, a
i
;θ
i,−
t
)
(6)
The Q-value for each agent is independent in this
method, and therefore, agents can modify their own
behaviors on the basis of the individual observations.
The state of agent i at time t, s
i
t
, is concatenated
with the observations and the distance information.
Note that we use the target Q-network with parame-
ters θ
i,−
updated every P steps to improve the stability
of DQN. P is called the update rate, after this.
4.2 Centralized DQN
The centralized DQN means that there is only one
deep neural network generating actions for all agents
in the environment. In this paper, we consider the case
in which a manager is trained by a neural network
with DDQN structure whose inputs are the collection
(or tensor) of the local states observed by all agents.
Then, the manager attempts to maximize the sum
of the discounted future rewards earned by all agents
R
t
at time t, which is defined as
R
t
=
n
∑
i=1
T
∑
t
0
=t
γ
t
0
−t
· r
i
t
0
, (7)
where T and γ are identical to those in Section 4.1.
The action value of Q for all agents with policy π is
calculated by
Q
π
(s, a) = E[R
t+1
|s = s
t
, a = a
t
], (8)
and the optimal Q
∗
for all agents is defined as
Q
∗
(s, a) = max
π
E[R
t+1
|s = s
t
, a = a
t
]. (9)
The action-value function for all agents is defined as
Q
∗
(s, a) = E[R
t+1
+ γmax
a
Q
∗
(s
t+1
, a)|s, a]. (10)
When optimizing the policy, it should observe the ac-
tions, rewards, and states of all agents. The challenge
Input 1
Input 2
CONV 1 CONV 2 Pooling Flatten FNC 1
FNC 2
Output
(a) Decentralized DQN.
Agent 1
Agent
n
FCN
a
1
FCN
a
n
FCN 3 FCN 4
Output 1
Output
n
CONVs
Pooling
Flatten
CONVs
Pooling
Flatten
(b) Centralized DQN.
Figure 2: Neural network architecture.
is to consider and select useful information as input
for training to make all agents work efficiently with-
out predefined precise control.
The Q-function is estimated by the network func-
tion approximator with the collection of weights θ of
the network. The network parameters can be updated
by minimizing the loss function L
t
(θ
t
) at time t for all
agents:
L
t
(θ
t
) = E
(s,a,r,s
t+1
)
y
t
−
n
∑
i=0
Q
i
(s
i
, a
i
;θ
t
)
2
, (11)
where y
t
is the target Q-value of all agents which is
generated from the target network with parameters
θ
−
:
y
t
= R
t+1
+ γ
n
∑
i=0
Q
s
i
t+1
, argmax
a
i
Q(s
i
t+1
, a
i
;θ
−
t
)
(12)
The target network whose parameters θ
−
are up-
dated from the online target network only every P
steps to improve the stability of the output from the
DQN. Two kinds of states, which includes the agent
observations and distance information, are stored to-
gether in the memory pool. In this method, the Q
value is the sum of rewards from all agents to make
sure that all agents can receive appropriate actions
from the manager. When one or a few agents do
not work correctly, the total value of rewards will de-
crease; thus, the deep neural network should be ad-
justed in time.
4.3 Structure of Deep Q Networks
The architecture of the decentralized DQNs used in
our experiments is shown in Fig. 2a. It is composed of
convolution network layers, max-pooling layer, flat-
ten layer, and fully connected network (FCN) layers.
Input1 includes the local view observation by the in-
dividual agents, the order distribution, and the cus-
tomer locations, while Input2 includes the associated
information, such as the distance from the agent to the
customer. The output is four values of actions, i.e., up,
right, down, or left, and the action with the maximum
value is selected (with possibility 1 − ε).
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
290

Fig. 2b shows the centralized DQN architecture
used in our experiments. The convolution layers are
used to maintain spatial relationships between the
states of all agents. The observations from all agents
are collected and processed with the same network
structure shown in Fig. 2a. Then, all of them will be
concatenated into FCN layers (FCNs 3 and 4). Fi-
nally, n outputs which include the values of actions
for all agents, will be generated for the corresponding
agents.
4.4 Reward Structure
We design a reward scheme to encourage agents to be-
have reasonably as well as to accelerate the learning
process. Each time when agents move one step, they
receive a small negative reward −0.01. If they get
stuck in the border of the grid world, which means
they try to get out of the environment, they receive
a negative reward −0.1. When they pick up an or-
der from the restaurant, they receive a positive reward
+5.0. Because it is more difficult for them to deliver
the dishes to the customers’ positions, they will be
given a bigger positive reward +10.0 when they suc-
ceed in arriving in customers’ cells.
4.5 Exploration and Exploitation
Exploration means that agents explore new states by
random actions to improve the policy. On the other
hand, with exploitation, agents select the most opti-
mal action based on past memory. We use ε-greedy
(0 ≤ ε ≤ 1) to make a balance between exploration
and exploitation. At the time t, agents take a random
action with the possibility ε
t
and take an optimal ac-
tion according to current policy with the possibility
1 − ε
t
. ε
t
can be calculated by
ε
t
= max(ε
init
· φ
t
, ε
min
),
where ε
init
is the initial value at time t = 0 and ε
min
is
the lower bound.
5 EXPERIMENTS
5.1 Experimental Settings
We conducted a number of experiments to compare
the performances of the learned behaviors by us-
ing both the centralized DQN and the decentralized
DQNs with different view sizes of inputs for the neu-
ral networks. The parameters used in our experiments
are listed in Table 1. We set the local view size to
Table 1: Experimental parameters.
Parameter Value
Size of environment 20 × 20
Number of agents (n) 12
Number of restaurants (|K|) 10
Broadcast area size (M) 5
Time steps in one episode 720 time steps
Total number of orders 344 per episode
Initial value of ε (ε
init
) 1.0
Lower bound of ε (ε
min
) 0.1
Decay rate (φ) 0.9999995
Update rate (P) 7200 time steps
Discount factor (γ) 0.95
Figure 3: Training loss value.
(2 × V + 1, 2 ×V + 1) and changed V in the experi-
ments. The takeout simulation environment was ter-
minated when the time step increased to 720, even if
there were remaining orders in the restaurants. The
positions of the agent were scattered in the envi-
ronment randomly at the beginning of each episode
while the positions of restaurants were fixed in all
episodes. Customers whose positions were randomly
determined in the grid world were generated together
with their orders. The positions of customers were
only shown to the agents that have picked up the cor-
responding ordered dishes at the restaurants. Then,
the customers disappeared right after agents arrived
at the customers’ positions. The number of orders in
each episode was 344 because we expect each agent
could complete one order within 25 time steps after
sufficient training. All orders in the experiment had
no time limitation and restaurants would broadcast
orders information when the orders were generated.
All experimental results of the learning methods pre-
sented here are averaged over three runs.
Learning Efficient Coordination Strategy for Multi-step Tasks in Multi-agent Systems using Deep Reinforcement Learning
291
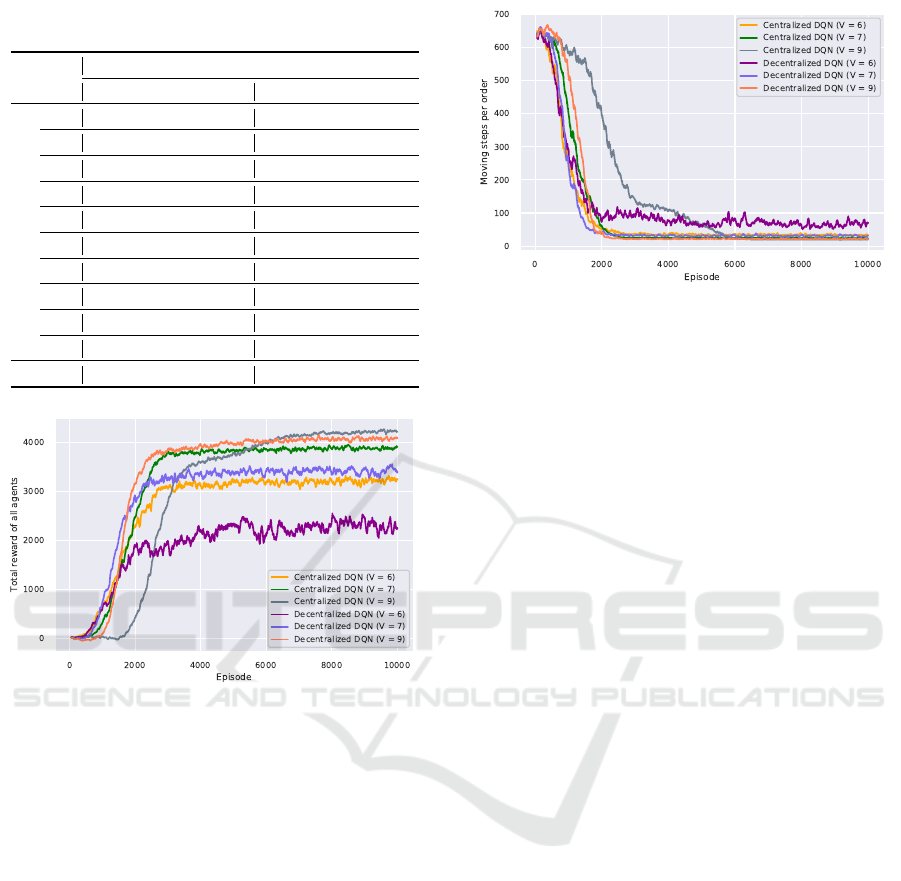
Table 2: Order completion rate in percentage (%) with all
methods for each restaurant.
Centralized DQN Decentralized DQN
V = 6 V = 7 V = 9 V = 6 V = 7 V = 9
Restaurant ID
1 48.16 73.52 86.38 11.81 37.91 54.60
2 98.49 98.12 98.99 75.30 95.48 96.56
3 97.69 97.80 100.00 69.39 98.24 99.26
4 72.83 89.69 97.61 22.78 65.82 76.95
5 98.56 98.62 97.23 78.17 96.70 97.10
6 85.54 95.78 99.38 38.50 86.78 95.63
7 97.89 95.48 97.33 73.14 96.62 98.70
8 93.47 98.48 95.83 78.46 95.90 98.82
9 97.47 95.91 97.27 47.54 88.07 96.01
10 97.76 99.49 98.23 61.30 96.36 97.12
Average 88.79 94.29 96.82 55.64 85.79 91.08
Figure 4: Reward.
5.2 Learning Convergence and Loss
Values
The loss values obtained in our experiments is shown
in Fig. 3. This figure clearly shows that the learning
process by centralized DQN and decentralized DQNs
with various local view sizes (where V = 6, 7, and 9)
could converge around 2,500 to 4,000 episodes. The
centralized DQN required more time to learn the pol-
icy π probably because the input contains the obser-
vations from all agents, but the loss values of the cen-
tralized DQN became much smaller than those of the
decentralized DQNs. As the value of V increased, the
loss values converged to lower values in both DQNs.
Note that when V = 9, the local view size was 19×19,
which means they could almost see the whole envi-
ronment.
5.3 Rewards
The rewards reflecting the results of doing tasks is an
essential factor to investigate the performance of all
Figure 5: Average steps to finish one order.
agents. Fig. 4 shows the total rewards that all agents
received. As the results of the loss functions in the
previous section, agents with centralized DQN per-
formed better than agents with decentralized DQNs
when V was identical. It is evident that when V = 6,
the performance of agents with decentralized DQNs
was the lowest. Each agent believed that their actions
were appropriate, but the total rewards were lower
than those with the centralized DQN. Besides, they
were more likely to gather in the same area as shown
in Table 2 which is listed the completion rates of order
deliveries requested by restaurants; this is probably
due to the limited observations (V = 6).
When the agents’ view size was large (V = 9), al-
though the learning using the centralized DQN took
longer time to converge, the centralized DQN learned
a better policy π to make most agents cooperate to
achieve more rewards in the environment after 6,000
episodes (Fig. 4). Note that the manager with cen-
tralized DQN could not always learn a good policy
to generate appropriate actions for all agents, while
agents with the decentralized DQNs could always
learn the individual policies, which might not be bet-
ter than those with the centralized DQN, to generate
actions for our problems.
5.4 Behaviors of Agents
Fig. 5 plots the steps to finish one order during the
training process. At first, all of them needed around
650 time steps, which was almost one episode, to fin-
ish an order. Then, most DQNs could generate better
actions to execute orders, resulting in less than 100
time steps per order after around 2000 episodes. Note
that ε ≈ 0.15 around 2000 episodes. As we mentioned
in Section 5.3, agents controlled by the centralized
DQN (V = 9) took more time steps (approximate 5800
episodes) for learning to pick up and deliver ordered
dishes. The agents with centralized DQN required
fewer time steps to complete the orders than those by
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
292

6
2
3
8
9
5
7
1
4
10
6
2
3
8
9
5
7
1
4
10
6
2
3
8
9
5
7
1
4
10
6
2
3
8
9
5
7
1
4
10
6
2
3
8
9
5
7
1
4
10
6
2
3
8
9
5
7
1
4
10
Figure 6: Locations of agents movement from the evaluation experiment.
the decentralized DQNs when their local view sizes
are identical.
After training, we conducted the three experimen-
tal runs using the trained DQNs to observe the emerg-
ing behaviors of all agents. The parameter ε was
set to 0.1 in these experiments. Each experimental
run consisted of five episodes, and actions taken by
these agents were generated by the resulting neural
networks or the random method. Fig. 6 shows the lo-
cation heat maps of all agents’ movements, meaning
that how many times agents were at each cell. The
color of the cell becomes darker if agents moved to
the cell more times. The red triangles with integers in-
dicate the restaurants with their IDs. We can see that
the right-bottom corner in Fig. 6d, Fig. 6e and Fig. 6f
are much darker than other cells in the environment
when agents used the decentralized DQNs.
We found that a few agents were wandering in this
corner and waiting for requesting signals from two
restaurants nearby. The agents that wait around this
corner for a long time were different in each episode.
This means that all policies learned from the decen-
tralized DQNs could not perform well if agents found
restaurants in the corner. However, this phenomenon
did not appear in the heat maps of the centralized
DQN experiments; agents were trained well and not
suffering from getting stuck in corners. We can also
observe that the agents with both methods learned
strategies to avoid passing through the areas where
there were no restaurants.
The average order completion rate (in percentage)
with all methods for each restaurant are listed in Ta-
ble 2. Because restaurant1 and restaurant4 were lo-
cated near a corner and therefore, it has slightly lower
chances to receive the order from them and the aver-
age length from them to customers were likely to be
longer; thus, their order completion rates were rela-
tively low. On the other hand, other restaurants, such
as restaurants5 and 8, which are located in the cen-
ter of the environment, have higher order completion
rates. The order completion rates always increased if
the local view size V increased in both centralized and
decentralized DQNs.
5.5 Discussion
We can find a few interesting phenomena from our
experimental results. First, both the centralized DQN
and decentralized DQNs with partial observations
could be trained well to learn strategies to complete
the established two-step tasks. It is known that the
small size of inputs could accelerate the convergence
speed for DRL but their solution qualities were lower.
When V = 7, the local view size covers around 56% of
the whole environment, the manager with the central-
ized DQN still could learn a good policy π to manage
all agents well.
Second, the quality of learned behaviors by the
centralized DQN was better than that of the decentral-
ized DQNs in terms of total rewards and the resulting
Learning Efficient Coordination Strategy for Multi-step Tasks in Multi-agent Systems using Deep Reinforcement Learning
293

coordinated strategy. One reason is that states of all
agents were observed and aggregated as the inputs to
the central neural network. Thus, it tries to learn the
policy π to help all agents by avoiding to gather in
one place. Agents using the centralized DQN could
cooperate efficiently because they could find nearby
restaurants and pick up orders immediately after de-
livering orders to customers by helping and receiv-
ing orders from any restaurants. In contrast, although
agents with decentralized DQNs still can learn poli-
cies for executing the tasks, it is hard for them to learn
such coordinated strategy by mutual cooperation, es-
pecially when they only have a small size of obser-
vations. Instead, they focused on a few restaurants to
receive the orders shown and this is the main differ-
ence in their coordinated behaviors by the centralized
and decentralized DQNs.
6 CONCLUSION
We investigated that a certain coordination strategy
could be learned by multi-agent in a dynamic takeout
platform problem. Our experiment results show that
agents with both DQN methods can learn the cooper-
ation strategy efficiently, especially for the centralized
DQN method. With the centralized DQN method,
agents controlled by a manager that could get the
states of all agents could have cooperative behaviors
by receiving the orders from any restaurant flexibly.
On the other hand, agents with decentralized DQNs
could also learn strategies for picking up and deliv-
ering orders, but their behaviors were quite different;
they focused on a few specific restaurants to receive
orders. However, there was an obvious problem that
agents could not learn well with too small observation
area. This is a pivotal issue which we want to focus
on and solve in the future.
We want to extend the size of the simulation envi-
ronment and the number of agents for our future work.
For example, agents are divided into a few teams in a
large environment, and agents are controlled by vari-
ous team leaders. Different teams are expected to be
responsible for an inevitable part of the region with
coordinated strategies.
ACKNOWLEDGEMENTS
This work is partly supported by JSPS KAKENHI,
Grant number 17KT0044.
REFERENCES
Diallo, E. A. O. and Sugawara, T. (2018). Learning strategic
group formation for coordinated behavior in adver-
sarial multi-agent with double dqn. In International
Conference on Principles and Practice of Multi-Agent
Systems, pages 458–466. Springer.
Egorov, M. (2016). Multi-agent deep reinforcement learn-
ing. CS231n: Convolutional Neural Networks for Vi-
sual Recognition.
Li, L., Lv, Y., and Wang, F.-Y. (2016). Traffic signal timing
via deep reinforcement learning. IEEE/CAA Journal
of Automatica Sinica, 3(3):247–254.
Lin, K., Zhao, R., Xu, Z., and Zhou, J. (2018). Efficient
large-scale fleet management via multi-agent deep re-
inforcement learning. In Proceedings of the 24th
ACM SIGKDD International Conference on Knowl-
edge Discovery & Data Mining, pages 1774–1783.
ACM.
Littman, M. L. (1994). Markov games as a framework
for multi-agent reinforcement learning. In Machine
learning proceedings 1994, pages 157–163. Elsevier.
Matignon, L., Laurent, G. J., and Le Fort-Piat, N. (2012).
Independent reinforcement learners in cooperative
markov games: a survey regarding coordination prob-
lems. The Knowledge Engineering Review, 27(1):1–
31.
Miyashita, Y. and Sugawara, T. (2019). Cooperation and co-
ordination regimes by deep q-learning in multi-agent
task executions. In International Conference on Arti-
ficial Neural Networks, pages 541–554. Springer.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M.
(2013). Playing atari with deep reinforcement learn-
ing. arXiv preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness,
J., Bellemare, M. G., Graves, A., Riedmiller, M., Fid-
jeland, A. K., Ostrovski, G., et al. (2015). Human-
level control through deep reinforcement learning.
Nature, 518(7540):529.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and
Riedmiller, M. (2014). Deterministic policy gradient
algorithms.
Tan, M. (1993). Multi-agent reinforcement learning: Inde-
pendent vs. cooperative agents. In Proceedings of the
tenth international conference on machine learning,
pages 330–337.
Van Hasselt, H., Guez, A., and Silver, D. (2016). Deep re-
inforcement learning with double q-learning. In Thir-
tieth AAAI conference on artificial intelligence.
Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-
chine Learning, 8(3):279–292.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
294
