Secure Comparison and Interval Test Protocols based on Three-party
MPC
Wataru Fujii
1
, Keiichi Iwamura
1
and Masaki Inamura
1,2
1
Graduate School of Engineering, Tokyo University of Science, Tokyo, Japan
2
Center for Research and Collaboration, Tokyo Denki University, Tokyo, Japan
Keywords:
Secret Sharing, Multiparty Computation, Secure Comparison, Secure Interval Test.
Abstract:
Multiparty Computation (MPC) is a technology that enables computations to be performed without exposing
private data. Three main approaches are employed to construct an MPC: secret-sharing schemes, homomor-
phic encryption, and garbled circuit. Although secret-sharing based MPC involves lower communication cost
generally, it requires more round communications for concrete protocols such as comparisons or interval tests.
Herein, we propose a five-round secure comparison protocol and a five-round interval test protocol using a
shuffling protocol based on a three-party secret-sharing scheme. Additionally, we compare our protocols with
existing protocols based on rounds and multiplications.
1 INTRODUCTION
Recently, multiparty computation (MPC) has at-
tracted significant attention as a technique to obtain
statistics without exposing private data. In general, an
MPC is a computation between N parties P
1
,...,P
N
having private inputs x
1
,...,x
N
. These parties com-
pute outputs (y
1
,...,y
N
) = f (x
1
,...,x
N
) such that P
i
derives only output y
i
.
Three main techniques have been developed for
MPC: secret-sharing schemes, homomorphic encryp-
tion, and garbled circuit. In general, secret-sharing-
based MPC involves relatively lower computational
and communication costs but requires more round
communications for concrete protocols such as com-
parisons or interval tests. Therefore, it is important for
secret-sharing-based MPC to reduce the round com-
munications of these protocols. Herein, we focus on
Shamir’s (2,3) secret-sharing (Shamir, 1979)-based
MPC, which is an algorithm that divides a secret s
into three shares. The original secret s can be restored
by collecting two of three shares.
Damg
˚
ard et al. demonstrated the first constant-
round comparison protocol based on secret-sharing
schemes (Damg
˚
ard et al., 2006); Nishide and Ohta
proposed more efficient constant-round protocols
such as comparisons or interval tests (Nishide and
Ohta, 2007) by improving the idea thereof. Further-
more, Reistad and Toft proposed an eight-round com-
parison protocol based on the limited compared val-
ues (Reistad and Toft, 2007).
Herein, we propose a five-round secure compari-
son protocol based on Shamir’s (2,3) secret-sharing
scheme using a shuffling protocol (Laur et al.,
2011; Chida et al., 2019). Moreover, we construct a
five-round interval test protocol using our proposed
comparison protocol and the interval test protocol of
(Nishide and Ohta, 2007).
Related Works. Many studies regarding se-
cure constant-round comparison protocols based on
secret-sharing schemes have been conducted, e.g.,
(Damg
˚
ard et al., 2006; Nishide and Ohta, 2007; Reis-
tad and Toft, 2007; Reistad, 2009). Moreover, studies
regarding logarithmic-round secure comparison pro-
tocols have been introduced (Garay et al., 2007; Cat-
rina and De Hoogh, 2010). Recently, Morita et al.
proposed an efficient-round secure comparison proto-
col based on the client-server model, which enables
communication rounds to be reduced by the precom-
putation of clients (Morita et al., 2018).
2 PRELIMINARIES
In this section, we introduce some notations and
known techniques. Herein, we denote p to represent
an odd prime number, l the bit length of p, and Z
p
a
prime field. In addition, we assume that all protocols
are computed over Z
p
.
698
Fujii, W., Iwamura, K. and Inamura, M.
Secure Comparison and Interval Test Protocols based on Three-party MPC.
DOI: 10.5220/0009161406980704
In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 698-704
ISBN: 978-989-758-399-5; ISSN: 2184-4356
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2.1 Shamir’s (2,3) Secret-sharing
Scheme
Let s ∈ Z
p
be the secret shared by three parties P
1
, P
2
,
P
3
. Every parity P
i
has a unique identification value
x
i
∈ Z
p
\{0}.
Share. A dealer builds a random polynomial f (x)
with a randomly chosen a ∈ Z
p
, as follows:
f (x) = s + ax mod p
and sends a share [s]
i
= f (x
i
) to P
i
.
Reveal. A restorer collects two or more shares of s
and recovers s by reconstructing the random polyno-
mial f (x).
2.2 Addition, Multiplication and XOR
We assume that three parties possess two secret
shared values a, b as [a] = ([a]
1
,[a]
2
,[a]
3
), [b] =
([b]
1
,[b]
2
,[b]
3
), and c ∈Z
p
, which is a value known to
all parties. [a + b], [a] + c, and c[a] can be computed
locally by computing [a]
i
+ [b]
i
, c + [a]
i
, and c[a]
i
, re-
spectively. Therefore, these operations do not require
communication.
Meanwhile, the multiplication of shared values
[a], [b] requires the parties to communicate with each
other. We assume that the parties perform the mul-
tiplication proposed by (Gennaro et al., 1998). Ac-
cording to (Gennaro et al., 1998), when the number
of parties is n, the multiplication requires n(n −1)
shared values to be sent in parallel. In our settings,
six shared values must be sent in parallel.
The XOR operation of two secret shared bits [b
1
],
[b
2
] ∈{0,1}⊂Z
p
is constructed as [b
1
]⊕[b
2
] = [b
1
]+
[b
2
] −2[b
1
][b
2
]. [b
1
] + [b
2
] can be performed locally
and the communication costs of this operation equal
those of the multiplication. When b
2
is a public value,
this operation do not require communication.
2.3 Complexity
Similar to other studies, we used two metrics: round
complexity and number of multiplication invocations,
to evaluate the communication costs of the protocols.
The round complexity means the numbers of sequen-
tial rounds of the multiplications. If we compute [a][b]
and [c][d], two operations can be performed in paral-
lel. Therefore, the complexity is one round and two
multiplications.
We assume that the complexity of sharing and re-
vealing is negligible compared with that of multipli-
cation, as in other studies. However, we determine
the complexity of the shuffling protocols. For more
details, see Section 5.4.
3 SUBPROTOCOLS
In this section, we introduce a number of subproto-
cols. These protocols are related to the generation of
random values.
Random Number Sharing (RNS). This protocol, de-
scribed in Algorithm 1, outputs a sharing [r] of a
uniformly random, unknown value r ∈ Z
p
(Damg
˚
ard
et al., 2006). The complexity is one round and one
multiplication.
Algorithm 1: RNS Protocol.
Output: [r] (r ∈ Z
p
).
1: P
i
shares a uniformly random shared value [r.i].
2: [r] ← [r.1] + [r.2] + [r.3].
3: Output [r].
Random Non-zero Number Sharing (RNNS). This
protocol, described in Algorithm 2, outputs a sharing
[r] of a uniformly random, unknown non-zero value
r ∈ Z
p
\{0} (Damg
˚
ard et al., 2006). The complexity
is two rounds and three multiplications.
Algorithm 2: RNNS Protocol.
Output: [r] (r ∈ Z
p
\{0}).
1: [r],[s] ← 2 ×RNS.
2: [v] ← [r] ×[s]
3: v ← Reveal([v]).
4: If v = 0, abort. Otherwise, output [r].
Random Bit Sharing (RBS). This protocol, de-
scribed in Algorithm 3, outputs a sharing [b] of a
uniformly random unknown bit b ∈ {0,1} (Damg
˚
ard
et al., 2006). The complexity is two rounds and two
multiplications.
Algorithm 3: RBS Protocol.
Output: [b] (b ∈ {0,1}).
1: [r] ← RNS.
2: [a] ← [r] ×[r]
3: a ← Reveal([a]).
4: a.1,a.2 ←
√
a
5: c ← min(a.1,a.2).
6: If c = 0, abort. Otherwise, proceed as follows
7: [d] ← [r]/c.  d ∈ {−1,1}
8: [b] ← ([d] + 1)/2.
9: Output [b].
Secure Comparison and Interval Test Protocols based on Three-party MPC
699

Random Bitwise Values Sharing (RBVS). This pro-
tocol, described in Algorithm 4, outputs bitwise shar-
ings [r
0
],...,[r
l−1
] of a uniformly random, unknown
value r such that 0 ≤ r =
∑
l−1
i=0
2
i
r
i
< p. In Algorithm
4, (p −1)
i
denotes the i’th bit of p −1, and r < p
occurs only when a vector

d does not contain any 0
elements. We assume that two attempts are required
to compute r < p for an arbitrary odd p, as in (Reistad
and Toft, 2007; Reistad, 2009). Therefore, the com-
plexity is three rounds and 8l multiplications. When
p = 2
l
−c, where c is a small integer, only one at-
tempt is required, and the multiplications can be re-
duced to 2l. For more details, see (Reistad and Toft,
2007; Reistad, 2009).
Algorithm 4: RBVS Protocol.
Output: [r
0
],...,[r
l−1
], (r
i
∈ {0,1}).
1: For i = 0,...,l −1 in parallel do
[r
i
] ← RBS
[s
i
] ← RNS.
2: For i = 0,...,l −1 in parallel do
[d
i
] = [s
i
](1 + (p −1)
i
−[r
i
] +
∑
l−1
j=i+1
((p −1)
j
⊕
[r
j
])).
3: [

d ] = ([d
0
],...,[d
l−1
]).
4:

d ← Reveal([

d ]).
5: If a vector

d contains a 0 element then abort. Oth-
erwise, proceed as follows.
6: Output [r
0
],...,[r
l−1
].
4 EXISTING COMPARISON
PROTOCOL
The secure comparison protocol is a protocol that
computes a shared bit [a < b ] from shared values
[a],[b] ∈Z
p
. Reistad and Toft proposed an eight-round
comparison protocol based on compared values that
were limited to less than
p−1
2
(Reistad and Toft, 2007;
Reistad, 2009).
Their protocols comprise two subprotocols. The
first subprotocol converts the comparison [a < b] into
a comparison [r] > c, where [r] is a random bitwise-
shared value, and c is a value known to all parties.
The second subprotocol computes the comparison
[r] > c. This subprotocol is based on the homomor-
phic encryption comparison protocol (Damg
˚
ard et al.,
2007).
4.1 Conversion of the Comparison
This protocol, described in Algorithm 5, has inputs
[a], [b] <
p−1
2
and outputs ([a] < [b]) = c
o
⊕[r
0
] ⊕
([r] > c), where c
o
is the least-significant bit of c and
[r
0
] is the least-significant bit of [r]. For more details
on this protocol, see (Reistad and Toft, 2007; Reistad,
2009).
Algorithm 5: Conversion Protocol.
Input: [a], [b] < (p −1)/2.
Output: ([a] < [b]) = c
o
⊕[r
0
] ⊕([r] > c).
1: ([r
0
],...,[r
l−1
]) ← RBV S.
2: [r] ←
∑
l−1
i=0
2
i
[r
i
].
3: [c] ← 2([a] −[b]) + [r].
4: c ← Reveal([c]).
5: Output ([a] < [b]) = c
o
⊕[r
0
] ⊕([r] > c).
The cost of the conversion protocol equals to one
RBVS protocol and one XOR operation. Therefore,
the complexity is four rounds and 8l + 1 multiplica-
tions. When p = 2
l
−c, where c is a small integer, the
multiplications can be reduced to 2l + 1.
4.2 Computing ([r ] > c)
Given random bitwise-shared values ([r
0
],...,[r
l−1
])
and a value c, vector [e] = ([e
0
],...,[e
l−1
]) is com-
puted as follows:
[e
i
] = [s
i
] 1 + (c
i
−[r
i
])[s] +
l−1
∑
j=i+1
(c
j
⊕[r
j
])
!
(1)
In equation (1), [s
i
] are uniformly random non-zero
values and [s] is a uniformly random shared value of
s ∈ {−1, 1}. By revealing vector [e], we can obtain
the comparison ([r] > c) as follows. It is noteworthy
that e = 1 if vector e has a 0 element, and e = 0 oth-
erwise.
([r] > c) = e ⊕

−
[s] −1
2

(2)
When vector e does not have any 0 elements, each e
i
is masked by s
i
, and e
i
does not leak any information
regarding shares. However, the equation r
i
= c
i
holds
for i > m when e
m
= 0 exists in vector e. Therefore,
information regarding r is leaked.
To solve this problem, the parties compute a vec-
tor [ ˜e
i
] shifted by a random unknown value v ∈
{0,...,l −1}, as follows:
[ ˜e
i
] = [e
(i+v) (mod l)
] (3)
In equation (3), the location of the 0 is hidden by v.
Therefore, revealing [ ˜e
i
] does not leak any informa-
tion regarding r.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
700

The round complexity of computing ([r] > c) is
five rounds. In total, the comparison protocol con-
tains nine rounds. However, one round can be reduced
by computing equation (1) before [r] < p is verified.
Thus, the round complexity can be reduced to eight
rounds.
5 OUR PROTOCOLS
5.1 Reducing the Round Complexity
In existing comparison protocols, the computation of
([r] > c) requires five of eight rounds. This is be-
cause the computation of a shifted vector requires
many rounds. Hence, we present two proposals as
follows:
• We compute [e] with fewer rounds.
• For permuting [e], we apply a shuffling protocol
instead of computing a shifted vector.
By using these two proposals, we can construct a
five-round secure comparison protocol.
5.2 Computing [e] with Fewer Rounds
More round-efficient vector [e ] = ([e
0
],...,[e
l−1
]) are
shown below. This equation is based on the ho-
momorphic encryption comparison protocol (Veugen,
2012), which is the improved protocol of (Damg
˚
ard
et al., 2007).
[e
i
] = [s
i
] [s] + (c
i
−[r
i
]) + 3
l−1
∑
j=i+1
(c
j
⊕[r
j
])
!
(4)
Equation (4) requires only one round and l
multiplications in contrast to equation (1), which
requires two rounds and 2l multiplications.
Security. As in equation (1), When vector e does
not have any 0 elements, each e
i
is masked by s
i
,
and e
i
does not leak any information regarding shares.
However, the equation r
i
= c
i
holds for i > m when
e
m
= 0 exists in vector e, and information regarding r
is leaked. Thus, [e
i
] must be permuted.
5.3 Subprotocols for Shuffling Protocol
In this section, we describe (2,2)-additive secret shar-
ing and share conversion, which are subprotocols of
a shuffling protocol. The shuffling protocol cannot
be constructed efficiently on Shamir’s (2,3) secret-
sharing scheme. Thus, we execute the shuffling proto-
col after converting shares from Shamir’s (2,3) secret
sharing to (2,2)-additive secret sharing.
5.3.1 (2,2)-Additive Secret-sharing Scheme
For the sake of simplicity, we assume that the secret
s ∈ Z
p
is shared by two parities P
1
, P
2
. We denote
[[s]]
i
as P
i
’s share of s and [[s]] = ([[s]]
1
,[[s]]
2
) as the
shorthand.
Share. randomly choose r ∈ Z
p
; let [[s]]
1
= r and
[[s]]
2
= s −r.
Reveal. Output s = [[s]]
1
+ [[s]]
2
.
5.3.2 Share Conversion
Share conversion from Shamir’s (2,3) secret shar-
ing to (2,2)-additive secret sharing can be performed
without communication (Cramer et al., 2005). Let λ
i
(for i = 1, 2) be coefficients of the Lagrange interpo-
lation and compute as follows:
[[s]]
i
= λ
i
[s]
i
(5)
λ
1
= −
x
2
x
1
−x
2
λ
2
= −
x
1
x
2
−x
1
5.4 Shuffling Protocol
Notations and Definitions. We define the notations
used in the shuffling protocol as follows:
• π: a random permutation.
• π
12
: a random permutation shared by P
1
,P
2
.
• π
3
: a random permutation known to only P
3
.
• π ◦

s: l vectors permuted by π.
• π ◦[[

s]]
i
: P
i
’s (2,2) - additive secret shared l vec-
tors permuted by π.
•

β
12
: l vectors of random values less than p shared
by P
1
,P
2
.
Random Permutation. Herein, random permutation
π is written as follows:
π =

0 1 ... l −1
π(0) π(1) ... π(l −1)

Whenx represents l vectors, π◦x denotes thatx is ran-
domly permuted by π, that is,x = (x
0
,...,x
l−1
) are re-
arranged into (´x
0
,..., ´x
l−1
) such that ´x
j
= x
π( j)
. Simi-
larly, π◦[[x]]
i
denotes that [[x ]]
i
= ([[x
0
]]
i
,...,[[ x
l−1
]]
i
)
Secure Comparison and Interval Test Protocols based on Three-party MPC
701

are reordered into ([[ ´x
0
]]
i
,...,[[ ´x
l−1
]]
i
) such that
´x
j
= x
π( j)
.
Algorithm. We describe the shuffling protocol in Al-
gorithm 6, which is the protocol based on (Laur et al.,
2011; Chida et al., 2019). This protocol has inputs of
shared vector [e] = ([e
0
],...,[e
l−1
]) and outputs ran-
domly permuted vector π ◦e = π
3
◦π
12
◦e.
Algorithm 6: Shuffling Protocol.
Input: [e] = ([e
0
],...,[e
l−1
]).
Output: π ◦e = π
3
◦π
12
◦e.
1: P
1
shares π
12
and

β
12
with P
2
.
2: Convert [e ] into [[e ]]
1
, [[e ]]
2
.
3: P
1
sends [[

´e]]
1
= π
12
◦[[e]]
1
−

β
12
to P
3
.
4: P
2
sends [[

´e]]
2
= π
12
◦[[e]]
2
+

β
12
to P
3
.
5: P
3
computes π
3
◦([[

´e]]
1
+ [[

´e]]
2
) = π
3
◦π
12
◦e.
6: P
3
outputs π ◦e = π
3
◦π
12
◦e.
Security. π
3
is known to only P
3
, and π
12
is shared
by only P
1
,P
2
. Therefore, π = π
3
◦π
12
is the un-
known random permutation, and π ◦e does not leak
any information regarding r because e is randomly
permuted by π.
Complexity. Similar to other studies, we ignore the
complexity of sharing and revealing. However, we
determine the communication costs of sending some
vectors and random permutations. One multiplication
cost is equivalent to sending six values. Therefore,
the complexity of sending one value is one round and
1/6 multiplications. [[

´e]]
1
, [[

´e]]
2
and

β
12
are l vectors
and π
12
is a 2 ×l matrix. Thus, this protocol requires
5l ×1/6 = 5l/6 multiplications. π
12
and

β
12
can be
shared in parallel, whereas [[

´e]]
1
and [[

´e]]
2
can be sent
in parallel. Thus, the round complexity is two rounds.
However, the sharing of π
12
and

β
12
can be exe-
cuted simultaneously with other protocols in advance
because π
12
and

β
12
are random values unrelated to
the inputs. Therefore, the actual round complexity is
one.
5.5 Secure Comparison Protocol
We describe our secure comparison protocol in
Algorithm 7. This protocol has inputs [a], [b] <
p−1
2
and outputs [a < b], where (a < b) = 1 if a < b and
(a < b) = 0 otherwise.
Complexity. The complexities of our comparison
protocol are as follows: three rounds and 8l multi-
plications for the RBVS protocol, two rounds and 3l
Algorithm 7: Secure Comparison Protocol.
Input: [a],[b] <
p−1
2
.
Output: [a < b]
1: ([r
0
],...,[r
l−1
]) ← RBV S.
2: [r] ←
∑
l−1
i=0
2
i
[r
i
].
3: [c] ← 2([a] −[b]) + [r].
4: c ← Reveal([c]).
5: For i = 0,...,l −1 in parallel do
[s
i
] ← RNNS.
6: Compute [s].  s ∈ {−1,1}
7: For i = 0,...,l −1 in parallel do
[e
i
] = [s
i
]

[s] + (c
i
−[r
i
]) + 3
∑
l−1
j=i+1
(c
j
⊕[r
j
])

.
8: [e] = ([e
0
],...,[e
l−1
]).
9: π ◦e ← Shuffling([e]).
10: If vector π ◦e contains a 0 element then e = 1;
otherwise, e = 0.
11: ([r] > c) = e ⊕

−
[s]−1
2

.
12: Output ([a] < [b]) = c
o
⊕[r
0
] ⊕([r] > c).
multiplications for [s]
i
, two rounds and two multipli-
cations for [s], one round and l multiplications for
[e]
i
, one round and 5l/6 multiplications for the shuf-
fling protocol, and one round and one multiplication
for c
o
⊕[r
0
] ⊕([r] > c). The total complexity is 10
rounds and (12 +5/6)l + 3 multiplications. However,
the computations of [s]
i
and [s] can be executed simul-
taneously with RBVS protocols in advance because
[s]
i
and [s] are random values unrelated to the inputs.
Therefore, we can ignore these round complexities.
In addition, one round can be reduced by computing
[e]
i
before [r] < p is verified. We assume that two at-
tempts are required to compute r < p for an arbitrary
odd p. Therefore, we require an additional of 4l + 2
multiplications for two sets of [e]
i
, [s]
i
, and [s]. In to-
tal, the complexity is five rounds and (16 + 5/6)l + 5
multiplications.
When p = 2
l
−c, where c is a small integer, only
one attempt is required and the multiplications of the
RBVS protocol is 2l. Thus, the multiplications can be
reduced to (6 + 5/6)l + 3.
5.6 Secure Interval Test Protocol
The secure interval test protocol has inputs of public
constants c
1
, c
2
and shared value [a] ∈ Z
p
; it outputs
[c
1
< a < c
2
] without revealing (c
1
< a < c
2
). We
construct a five-round secure interval test protocol us-
ing our proposed comparison protocol and the interval
test protocol of (Nishide and Ohta, 2007).
Subprotocol. We describe the subprotocol of our se-
cure interval test protocol in Alogrothm 8. This proto-
col has inputs of bitwise shared value ([r
0
],...,[r
l−1
])
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
702

and a public constant c; it outputs [c < r], where
(c < r ) = 1 if c < r and (c < r) = 0 otherwise. The
complexity is two rounds and (4+5/6)l +2 multipli-
cations, excluding rounds complexities of [s] and [s]
i
.
Algorithm 8: Subcomparison Protocol.
Input: ([r
0
],...,[r
l−1
]), a public constant c.
Output: [c < r]
1: For i = 0,...,l −1 in parallel do
[s
i
] ← RNNS.
2: Compute [s].  s ∈ {−1,1}
3: For i = 0,...,l −1 in parallel do
[e
i
] = [s
i
]

[s] + (c
i
−[r
i
]) + 3
∑
l−1
j=i+1
(c
j
⊕[r
j
])

.
4: [e] = ([e
0
],...,[e
l−1
]).
5: π ◦e ← Shuffling([e]).
6: If vector π ◦e contains a 0 element then e = 1;
otherwise, e = 0.
7: [c < r] = e ⊕

−
[s]−1
2

.
8: Output [c < r].
Secure Interval Test Protocol. We describe our se-
cure interval test protocol in Algorithm 9. This pro-
tocol has inputs of public constants c
1
, c
2
, and shared
value [a] ∈ Z
p
; it outputs [c
1
< a < c
2
], where (c
1
<
a < c
2
) = 1 if c
1
< a < c
2
and (c
1
< a < c
2
) = 0 oth-
erwise.
Algorithm 9: Secure Interval Test Protocol.
Input: public constants c
1
, c
2
, shared value[a].
Output: [c
1
< a < c
2
]
1: ([r
0
],...,[r
l−1
]) ← RBV S.
2: [r] ←
∑
l−1
i=0
2
i
[r
i
].
3: [c] ← [a] +[r].
4: c ← Reveal([c]).
5: if c
2
5 c then
r
1
← c −c
2
and r
2
← c −c
1
.
6: else if c 5 c
1
then
r
1
← c + p −c
2
and r
2
← c + p −c
1
.
7: [c
1
< a < c
2
] ← [r
1
< r] ×[r < r
2
].
8: else if c
1
< c < c
2
then
r
1
← c −c
1
−1 and r
2
← c + p −c
2
+ 1.
9: [c
1
< a < c
2
] ← 1 −([r
1
< r] ×[r < r
2
]).
10: Output [c
1
< a < c
2
].
When c
2
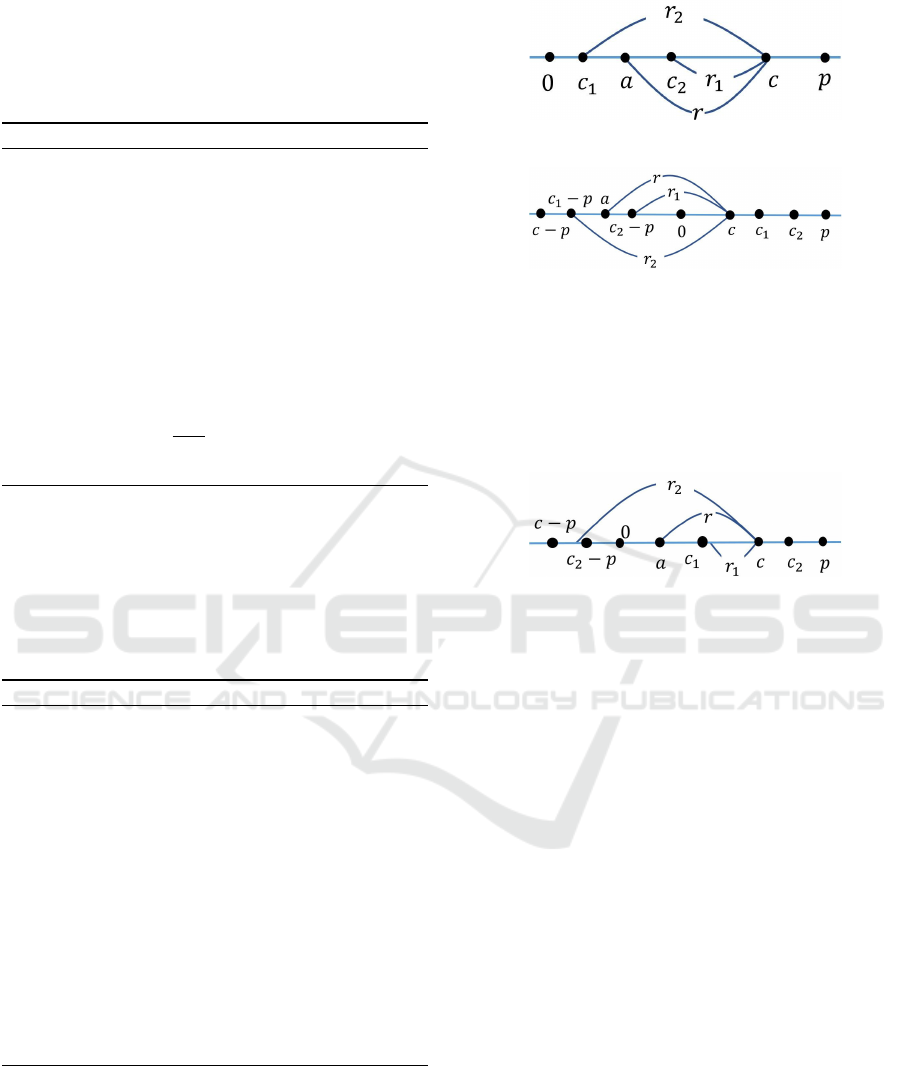
5 c, as shown in Figure 1, the shared bit
[c
1
< a < c
2
] equals to 1 if r
1
= (c −c
2
) < r < r
2
=
(c −c
1
). Similarly, when c 5 c
1
, as shown in Figure
2, the shared bit [c
1
< a < c
2
] equals to 1 if r
1
= (c +
p −c
2
) < r < r
2
= (c + p −c
1
). Therefore, the shared
bit [c
1
< a < c
2
] can be obtained by computing [r
1
<
r] ×[r < r
2
] in these two cases.
Figure 1: The case of c
2
5 c.
Figure 2: The case of c 5 c
1
.
When c
1
< c < c
2
, as shown in Figure 3, the shared
bit [c
1
< a < c
2
] equals to 0 if r
1
= (c −c
1
−1) <
r < r
2
= (c + p −c
2
+ 1). Therefore, the shared bit
[c
1
< a < c
2
] can be obtained by computing 1 −[r
1
<
r] ×[r < r
2
] in this case.
Figure 3: The case of c
1
< c < c
2
.
Complexity. [r
1
< r] and [r < r
2
] can be computed
in parallel by Algorithm 8. Thus, the complexities
of our interval test are as follows: three rounds and
8l multiplications for the RBVS protocol, two rounds
and 2 ×((4 + 5/6)l + 2) multiplications for [r
1
< r]
and [r < r
2
], and one round and one multiplication for
[r
1
< r] ×[r < r
2
]. The total complexity is six rounds
and (16 + 5/3)l + 5 multiplications. However, one
round can be reduced by computing [e]
i
before [r] < p
is verified, as in the comparison protocol. We assume
that two attempts are required to compute r < p for an
arbitrary odd p. Therefore, we require an additional
of 8l + 4 multiplications for four sets of [e]
i
, [s]
i
, and
[s]. In total, the complexity is five rounds and (24 +
5/3)l + 9 multiplications.
When p = 2
l
−c, where c is a small integer, only
one attempt is required and the multiplications of the
RBVS protocol is 2l. Thus, the multiplications can be
reduced to (10 + 5/3)l + 5.
6 COMPARISON WITH OTHER
STUDIES
In this section, we compare our comparison and in-
terval test protocols with existing protocols based on
Secure Comparison and Interval Test Protocols based on Three-party MPC
703

rounds and multiplications to evaluate the communi-
cation costs of the protocols.
In comparison protocols, for the sake of simplic-
ity, we assume that the compared values are restricted
to less than
p−1
2
and p = 2
l
−c, where c is a small
integer. Therefore, only one attempt is required to
compute r < p in RBVS protocol. In interval test
protocols, inputs are arbitrary values in Z
p
, and two
attempts are required.
Table 1: Complexities of comparison protocols.
Rounds Multiplications
(Damg
˚
ard et al., 2006) 44 148l + 188llog
2
l
(Nishide and Ohta, 2007) 13 36l + 1
(Reistad and Toft, 2007) 8 20l + 36llog
2
l + 6
(Reistad, 2009) 6 7.5l + 11
Proposed 5 (6 + 5/6)l + 3
Table 2: Complexities of interval test protocols.
Rounds Multiplications
(Nishide and Ohta, 2007) 13 72l + 1
Proposed 5 (24+ 5/3)l + 9
7 CONCLUSIONS
The main results obtained in this study are as follows.
• By using a shuffling protocol, we proposed a five-
round secure comparison protocol .
• We constructed a five-round secure interval test
protocol by applying our secure comparison pro-
tocol.
• We showed that proposed protocols have less
communication costs than existing protocols.
In future studies, we will consider methods to further
reduce the communication costs of our protocols.
REFERENCES
Catrina, O. and De Hoogh, S. (2010). Improved primitives
for secure multiparty integer computation. In Interna-
tional Conference on Security and Cryptography for
Networks, pages 182–199. Springer.
Chida, K., Hamada, K., Ikarashi, D., Kikuchi, R., Kiribuchi,
N., and Pinkas, B. (2019). An efficient secure three-
party sorting protocol with an honest majority. Cryp-
tology ePrint Archive, Report 2019/695.
Cramer, R., Damg
˚
ard, I., and Ishai, Y. (2005). Share conver-
sion, pseudorandom secret-sharing and applications to
secure computation. In Theory of Cryptography Con-
ference, pages 342–362. Springer.
Damg
˚
ard, I., Fitzi, M., Kiltz, E., Nielsen, J. B., and Toft,
T. (2006). Unconditionally secure constant-rounds
multi-party computation for equality, comparison, bits
and exponentiation. In Theory of Cryptography Con-
ference, pages 285–304. Springer.
Damg
˚
ard, I., Geisler, M., and Krøigaard, M. (2007). Effi-
cient and secure comparison for on-line auctions. In
Australasian Conference on Information Security and
Privacy, pages 416–430. Springer.
Garay, J., Schoenmakers, B., and Villegas, J. (2007). Prac-
tical and secure solutions for integer comparison. In
International Workshop on Public Key Cryptography,
pages 330–342. Springer.
Gennaro, R., Rabin, M. O., and Rabin, T. (1998). Simpli-
fied vss and fast-track multiparty computations with
applications to threshold cryptography. In podc, vol-
ume 98, pages 101–111. Citeseer.
Laur, S., Willemson, J., and Zhang, B. (2011). Round-
efficient oblivious database manipulation. In Proceed-
ings of the 14th International Conference on Informa-
tion Security, ISC’11, pages 262–277, Berlin, Heidel-
berg. Springer-Verlag.
Morita, H., Attrapadung, N., Teruya, T., Ohata, S., Nuida,
K., and Hanaoka, G. (2018). Constant-round client-
aided secure comparison protocol. In ESORICS.
Nishide, T. and Ohta, K. (2007). Multiparty computa-
tion for interval, equality, and comparison without
bit-decomposition protocol. In International Work-
shop on Public Key Cryptography, pages 343–360.
Springer.
Reistad, T. I. (2009). Multiparty comparison-an improved
multiparty protocol for comparison of secret-shared
values. In SECRYPT, pages 325–330.
Reistad, T. I. and Toft, T. (2007). Secret sharing compar-
ison by transformation and rotation. In International
Conference on Information Theoretic Security, pages
169–180. Springer.
Shamir, A. (1979). How to share a secret. Communications
of the ACM, 22(11):612–613.
Veugen, T. (2012). Improving the dgk comparison protocol.
In 2012 IEEE International Workshop on Information
Forensics and Security (WIFS), pages 49–54. IEEE.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
704