Co-Op Advertising with Two Competing Retailers:

A Feedback Stackelberg-Nash Game

ul Selin Savas¸kan

and Suresh P. Sethi

Department of Economics, C¸ anakkale Onsekiz Mart University, C¸ anakkale, Turkey

Naveen Jindal School of Management, The University of Texas at Dallas, Richardson, TX 75080, U.S.A.

Keywords:

Differential Games, Distribution Channels, Cooperative Advertising, Retail Competition, Participation Rate,

Feedback Stackelberg-Nash Game.

Abstract:

A nearly explicit feedback Stackelberg-Nash equilibrium is obtained in a dynamic distribution channel con-

sisting of a manufacturer and two competing asymmetric retailers engaged in promoting the manufacturer’s

product to be sold through the retailers. The manufacturer decides on its support for the retailers’ advertising

activities by announcing cooperative advertising subsidies called “participation rates.” The retailers compete

for market share by selecting advertising efforts. We formulate the problem as a Stackelberg-Nash differential

game and reduce it to merely solving a set of algebraic equations. We ﬁnd that the manufacturer should offer

the cooperative advertising policy to only one retailer and even then, only when a “participation threshold”

depending on the model parameters is exceeded. We identify the levers that determine the optimal participa-

tion rate. Furthermore, we obtain important insights into how sensitive the optimal solution is with respect to

the parameters. Moreover, we show that retail-level competition induces the manufacturer to offer a higher

level of support to the supported retailer and over a wider range of parameters when compared to the results

obtained in a one-manufacturer, one-retailer setting studied in the literature.

1 INTRODUCTION

Manufacturer-retailer relationships concern about the

decisions of each channel member affect the other’s

proﬁtability and strategy choices. For example, the

retailer advertises the manufacturer’s product to in-

crease its sales, but it may not do so to the extent that

the manufacturer might prefer. Then, the manufac-

turer might provide incentives to the retailer. The situ-

ation is complicated even further if there is more than

one retailer with common customer base carrying the

manufacturer’s product. This case is not uncommon

in situations where territories are not exclusive. The

manufacturer and the retailers make an effort to max-

imize their individual proﬁts.

Manufacturers often use cooperative advertising

to inﬂuence their retailers’ advertising decisions. Co-

operative advertising is an arrangement whereby a

manufacturer agrees to reimburse a portion of the ad-

vertising expenditures incurred by retailers for selling

its product (Bergen and John 1997).

Cooperative advertising programs can be a signif-

icant part of the advertising budgets of manufactur-

ers. By some estimates, more than $25 billion was

spent on cooperative advertising in 2007, compared to

$15 billion in 2000 and $900 million in 1970 (Nagler

2006), and approximately 25-40% of all manufactur-

ers used this arrangement (Dant and Berger 1996).

The importance of understanding cooperative adver-

tising programs in manufacturer-retailer relationships

is based on these ﬁgures.

Dutta et al. (1995) conduct an empirical analy-

sis of cooperative advertising plans offered by man-

ufacturers to their retailers and report that the aver-

age participation rate over all product categories is

74.6%. More importantly, they ﬁnd that the partic-

ipation rate differs from industry to industry—it is

88.38% for consumer convenience products, 69.85%

for consumer nonconvenience products, and 69.02%

for industrial products. In this paper, we make a theo-

retical contribution to the cooperative advertising lit-

erature by endogenously determining the optimal par-

ticipation rate in the face of competition as a function

of various ﬁrm- and industry-level parameters and an-

alyzing how these parameters affect a manufacturer’s

participation rate policy.

We model a dynamic distribution channel in

which a manufacturer sells a product through one or

Sava¸skan, G. and Sethi, S.

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game.

DOI: 10.5220/0009165200190029

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 19-29

ISBN: 978-989-758-396-4; ISSN: 2184-4372

both of two independent and competing retailers. The

retailers choose their advertising efforts after the man-

ufacturer decides the extent of its support for each re-

tailer’s advertising activity. This is called “participa-

tion rate,” i.e., the portion of the retailer’s advertis-

ing expenditures that the manufacturer will subsidize.

The manufacturer ﬁrst chooses its participation rates.

Taking the participation rates into consideration, the

two retailers simultaneously choose their local adver-

tising levels. Sales are then realized based on the ad-

vertising efforts.

As our dynamics, we use a competitive exten-

sion of the Sethi (1983) advertising model along the

lines suggested by Sorger (1989) and Prasad and Sethi

(2004). The leader-follower sequence in the chan-

nel is formulated as a Stackelberg differential game.

Stackelberg differential games are quite difﬁcult to

solve, even without the competition among the fol-

lowers involving a Nash differential game amongst

them. Often, only an open-loop solution is obtained,

which is, in general, time inconsistent; e.g., see Dock-

ner et al. (2000).

We provide a nearly explicit (time-consistent)

feedback Stackelberg equilibrium for a cooperative

advertising problem with retail competition. Further-

more, the equilibrium is reduced to merely solving

a set of algebraic equations. We identify the levers

that determine the optimal participation rate and ob-

tain important insights into how sensitive the optimal

solution is with respect to the parameters. Impor-

tantly, it makes possible to study the effect of retail-

level competition on the behavior of the manufacturer.

The proofs of the results in the paper are relegated to

Appendix.

2 RELATED LITERATURE

In the context of cooperative advertising, we ﬁrst re-

view static models in the literature; e.g., see Berger

(1972), Berger and Magliozzi (1992), Dant and

Berger (1996), Bergen and John (1997), Kali (1998),

Kim and Staelin (1999), Huang et al. (2002). In an

early paper, Berger (1972) models cooperative adver-

tising as a wholesale-price discount and make out that

the manufacturer can use cooperative advertising to

make higher proﬁts. Dant and Berger (1996) extend

the Berger (1972) model to study the role of cooper-

ative advertising in franchising systems. They obtain

that the franchisor and the franchisee would be bet-

ter off if both of them jointly determine their coop-

erative advertising contributions than if they were to

maximize their proﬁts separately. Bergen and John

(1997) explore the impact of advertising spillover and

manufacturer and retailer differentiation on the par-

ticipation rate. They show that the participation rate

should be higher for less differentiated retailers, more

differentiated brands, and more upscale products in

a product category. For understanding how brand

name advertising, local advertising, and the partici-

pation rate effect in cooperative advertising, Huang et

al. (2002) analyze two models—a traditional model

with the manufacturer as the Stackelberg leader and

another where the manufacturer and the retailer form

a cooperative advertising partnership. These results

show that the total channel proﬁts and the investments

in national and local advertising are higher in the part-

nership setting than in the traditional case. There are

many dynamic models of cooperative advertising in

the literature (e.g., Jørgensen et al. 2000, 2001, 2003,

Jørgensen and Zaccour 2003, Karray and Zaccour

2005, He et al. 2007, He et al. 2009). Jørgensen et

al. (2000) consider a setting in which a manufacturer

and an exclusive retailer decide on advertising that has

both long-term and short-term effects on sales. They

ﬁnd that both channel members attain higher proﬁts

when the manufacturer supports both types of retail

advertising than if it were to provide only partial ad-

vertising support. Jørgensen and Zaccour (2003) an-

alyze a goodwill model of advertising in which there

is no natural channel leader. Using a dynamic incen-

tives approach, they show that the use of cooperative

advertising can generate a Pareto-optimal joint proﬁt

maximization outcome. Jørgensen et al. (2003) ana-

lyze a model with a manufacturer, who invests in na-

tional advertising to promote the brand’s image, and

a retailer, who invests in local advertising that dam-

ages the brand’s image. They show that it is optimal

for the manufacturer to use cooperative advertising if

the brand’s image is sufﬁciently low, or if the harm to

the brand’s image from the retailer’s advertising ef-

forts is low. Karray and Zaccour (2005) model ad-

vertising at both the manufacturer and retailer levels.

They consider a retailer that sells two products—the

manufacturer’s product and a private label at a lower

price—and show that the manufacturer can use coop-

erative advertising to mitigate the negative impact of

the retailer’s private label. The papers most related to

our work are He et al. (2011,2012) and Chutani and

Sethi (2012). We will specify how these are related

to the paper in the next section where we develop our

model.

3 MODEL

We consider a distribution channel with a single man-

ufacturer who sells a product to one or both of two

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

independent and competing retailers, Retailer 1 and

Retailer 2. Let x(t) denote the market share of Re-

tailer 1 at time t ≥ 0, which depends on its own and

its competitor’s advertising efforts. Accordingly, the

market share of Retailer 2 at time t is 1 −x(t). The

manufacturer supports the retailers’ advertising activ-

ities by sharing a portion of the retailers’ advertising

expenditures. This support, termed the participation

rate, for Retailer i is denoted θ

In Table 1, we list the notation above and the re-

maining notation used in this paper.

Table 1: Notation.

t Time t, t ≥0

x (t) ∈ [0, 1] Retailer 1’s proportion of the market

at time t

Initial market share of Retailer 1

(t) ≥ 0 Retailer i’s advertising effort rate

at time t, i = 1,2

(t) ≥ 0 Manufacturer’s participation rate for

Retailer i at time t

> 0 Advertising effectiveness parameter

≥ 0 Market share decay parameter

r > 0 Discount rate of the two retailers and

the manufacturer

> 0 Gross margin of Retailer i

≥ 0 Gross margin of the manufacturer

from Retailer i

, V Value functions of Retailer i and the

manufacturer, respectively

(x) or f

d f /dx for a differentiable function f (x)

f (x)

or f

max{f (x),0} for a function f (x)

We will assume M

≥M

≥0 without loss of gen-

erality. The case M

= M

≥ 0 reduces our model to

that of Prasad and Sethi (2004). Thus, we contribute

by studying the case M

> M

≥ 0, without loss of

generality, since the case M

> M

≥0 can be treated

simply by re-labeling the ﬁrms.

The special case M

> M

= 0 arises when the

manufacturer sells only through Retailer 1, and Re-

tailer 2 represents an independent competing channel,

and it has been studied in He et al. (2011). Since

their aim was to examine simply the effect of com-

petition from an independent retailer, they did so un-

der the simplifying assumption that ρ

= ρ

, m

, and δ

= δ

. We relax these assumptions in this

paper.

Another related paper is He et al. (2012) that as-

sumes M

= M

, whereas we generalize their model

by relaxing this requirement. We should however

mention that they also study the case of three retailers

each giving the same margin to the manufacturer.

Finally, Chutani and Sethi (2012) have studied

a retail market oligopoly with N retailers. How-

ever, their sales-advertising dynamics is represented

by an extension of the 1983 Sethi model by Erickson

(2009).

The advertising expenditure is quadratic in the

advertising effort u

(t), i = 1,2, and the manufac-

turer’s and Retailer i’s advertising expenditure rates

at time t are given by θ

(t)u

(t) + θ

(t)u

(t) and

(1 −θ

(t))u

(t), i = 1,2, respectively. The assump-

tion of a quadratic cost function is common in the lit-

erature and implies diminishing marginal returns to

advertising expenditure; e.g., see Deal (1979), Sorger

(1989), Chintagunta and Jain (1992), Prasad and Sethi

(2004), Bass et al. (2005), He et al. (2009).

The market share dynamics of Retailer 1 is given

˙x (t) = ρ

(t)

1 −x (t) −ρ

(t)

x (t) −δ

x (t)

+δ

(1 −x (t)), x (0) = x

∈ [0, 1],

(1)

where the advertising response constant ρ

determines

the effectiveness of Retailer i’s advertising activity,

i = 1,2, and the market share decay constants δ

and

determine the rate at which its consumers are lost

and gained, respectively, due to churn. This speciﬁ-

cation, characterized by the square-root feature intro-

duced in the Sethi (1983) model, has the same desir-

able properties of concave response with saturation as

the Vidale-Wolfe (1957) model. Note that the market

share is non-decreasing in the retailer’s own adver-

tising effort and non-increasing in the competitor’s

advertising effort. Moreover, the speciﬁed concave

response has been validated in empirical studies by

Chintagunta and Jain (1992), Naik et al. (2008), and

Erickson (2009).

The present-valued proﬁts of Retailer 1, Retailer 2

and the manufacturer can be expressed, respectively,

∞

−rt



x (t) −(1−θ

(t))u

(t)



dt, (2)

∞

−rt



(1 −x (t)) −(1 −θ

(t))u

(t)



dt, (3)

and

π = max

(t), θ

(t), t≥0

∞

−rt

[(M

x(t) + M

(1 −x(t))

−θ

(t)(u

(t))

−θ

(t)(u

(t))

]dt (4)

subject to the state equation (1).

In a feedback Stackelberg-Nash equilibrium for

our inﬁnte-horizon problem, the manufacturer deter-

mines his strategy in the feedback form as θ

(x) :

[0,1] → [0,1],i = 1,2, and the retailer i’s strategy is

based on the state as well as the manufacturer’s deci-

sion, and is therefore of the form u

(x,θ

(x),θ

(x)) :

[0,1]

→ [0,∞], i = 1,2.

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game

Let Θ

and U

, i = 1,2, denote the spaces of such

strategies of the manufacturer and the retailers, re-

spectively. Then given θ

∈ Θ

and u

∈U

, i = 1, 2,

we denote by x

t,y

(s;θ

,θ

), s ≥ t, the solution

of the equation

˙x(s) = ρ

(x(s))

1 −x(s) −ρ

(x(s))

x(s),

x(t) = y. (5)

Let

t,y



(·),θ

(·),u

(·,θ

(·),θ

(·)),u

(·,θ

(·),θ

(·))



∞

exp

−r(s−t)



t,y

(s;θ

,θ

)

−(1 −θ

t,y

(s;θ

,θ

)))

t,y

(s;θ

,θ

),θ

,θ

)}



ds, i = 1, 2 (6)

and

t,y



(·),θ

(·),u

(·,θ

(·),θ

(·)),u

(·,θ

(·),θ

(·))



∞

exp

−r(s−t)



−M

t,y

(s;θ

,θ

)

−

∑

i=1

t,y

(s;θ

,θ

)))

t,y

(s;θ

,θ

),θ

,θ

)}



ds, (7)

where we should stress that θ

(·), u

(·,θ

(·),θ

(·))

evaluated at any state z are θ

(z), u

(z,θ

(z),θ

(z)),

i = 1,2.

We can now deﬁne the feedback Stackelberg-Nash

equilibrium for the problem.A quadruple of strate-

gies (θ

∗

,θ

∗

) ∈ Θ

×Θ

×U

is called a

Stackelberg-Nash equilibrium if the following holds

t,y



∗

(·),θ

∗

(·),u

∗

(·,θ

∗

(·),θ

∗

(·)),u

(·,θ

∗

(·),θ

∗

(·))



≥ Π

t,y



(·),θ

(·),u

∗

(·,θ

(·),θ

(·)),u

∗

(·,θ

(·),θ

(·))



∀(θ

,θ

) ∈ Θ

×Θ

, ∀(t, y) ∈ [0, ∞) ×[0,1],

t,y



∗

(·),θ

∗

(·),u

∗

(·,θ

∗

(·),θ

∗

(·)),u

∗

(·,θ

∗

(·),θ

∗

(·))



≥ Π

t,y



∗

(·),θ

∗

(·),u

(·,θ

∗

(·),θ

∗

(·)),u

∗

(·,θ

∗

(·),θ

∗

(·))



∀u

∈ U

, ∀(t, y) ∈ [0, ∞) ×[0,1],

t,y



∗

(·),θ

∗

(·),u

∗

(·,θ

∗

(·),θ

∗

(·)),u

(·,θ

∗

(·),θ

∗

(·))



≥ Π

t,y



∗

(·),θ

∗

(·),u

∗

(·,θ

∗

(·),θ

∗

(·)),u

(·,θ

∗

(·),θ

∗

(·))



∀u

∈ U

, ∀(t, y) ∈ [0, ∞) ×[0,1].

For further details on feedback Stackelberg-Nash

equilibrium, see Bensoussan et al. (2019, 2014). Also

speciﬁed there is a procedure that obtains such an

equilibrium. In this paper, we shall use that procedure

to solve our problem (2)-(5) to obtain the strategies

(x) and u

(x,θ

,θ

), i = 1,2.

Note that the feedback Stackelberg-Nash equilib-

rium obtained for the problem (2)-(5), is time consis-

tent, as opposed to the open-loop Stackelberg equilib-

rium, which, in general, is not; See Bensoussan et al.

(2015) for details.

Upon examining the Stackelberg differential game

described in equations (2)-(5), we can immediately

see that if M

= M

= M ≥ 0, then

∞

−rt

x(t) +M

(1 −x(t)))dt =

∞

−rt

Mdt = M/r,

and the objective function of the manufacturer in

equation (4) can be written as M/r plus the negative

advertising terms inside the integral. It is clear then

that the objective is maximized when θ

∗

= θ

∗

= 0,

and thus V (x

) = M/r. Before beginning our analysis

of the case M

> M

≥ 0, we note from an inspection

of the manufacturer’s objective function in equation

(4) that only one of the retailers will be supported in

all cases.

Proposition 1. It is never optimal for the manufac-

turer to support both retailers. In particular, M

≥ 0 implies θ

∗

≡ 0.

4 ANALYSIS AND RESULTS

We now begin our study of the case M

> M

≥

0. In view of Proposition 1, we set θ

∗

≡ 0.

The next two propositions deal with solving the

Stackelberg differential game (2)-(5). For this, let

), V

(x) and V (x) denote the value function of

retailer 1, retailer 2 and the manufacturer, respec-

tively. These will be obtained in the course of our

analysis.

Proposition 2. The feedback Stackelberg equilibrium

of the game (2-5) is characterized as follows:

(a) The optimal advertising decisions of the retailers

are given by

(x,θ

,0) =

√

1 −x

2(1 −θ

)

(x,θ

,0) = −

√

(8)

(b) The optimal participation rate of the manufacturer

has the form

(x) =

(x) −V

(x)

(x) +V

(x)

. (9)

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

, V

, and V for Retailer 1,

Retailer 2, and the manufacturer, respectively, satisfy

the following three simultaneous differential equa-

tions:

= m

x +





1 −



−V



(1 −x)

x −V

(δ

x −δ

(1 −x)) (10)

= m

(1 −x) +





1 −



−V



(1 −x) (11)

−V

(δ

x −δ

(1 −x))

rV = M

x + M

(1 −x) −







−V



(1 −x)





−V



−1



−

(1 −x)





−V



−1



−δ

x + δ

(1 −x) (12)

At this point, we conjecture linear value func-

tions, which work for our formulation since it has

the square-root feature in the dynamics (5). Specif-

ically, we set V

= α

+β

x, V

= α

+β

(1 −x), and

= α

+ β

x in equations (10-12), where the un-

known parameters α

, β

, α

, β

, α

, and β

are

constants. Then, by equating the coefﬁcients of x on

both sides of equations (10-12), we get six simultane-

ous algebraic equations that can be solved to obtain

the six unknown parameters. The results are provided

in Proposition 3.

Proposition 3. (a) The retailers’ optimal advertising

decisions are given by

∗

(x,θ

∗

(x),0) =

√

1 −x

2(1 −(

2β

−β

2β

+β

)

∗

(x,θ

∗

(x),0) =

√

. (13)

(b) The optimal participation rate of the manufacturer

is a constant given by

∗

(x) =



2β

−β

2β

+ β



. (14)

manufacturer are linear in market share, i.e., V

+ β

x, V

= α

+ β

(1 −x), and V

= α

+ β

where the parameters α

, β

, α

, β

, α

, and β

are

obtained from the following system of equations:

rα



1 −



2β

−β

2β

+β





+ β

(15)

rβ

= m

−



1 −



2β

−β

2β

+β





−

−β

(δ

+ δ

) (16)

rα

+ β

, (17)

rβ

= m

−



1 −



2β

−β

2β

+β





−β

(δ

+ δ

), (18)

rα

= M

−



2β

−β

2β

+β





1 −



2β

−β

2β

+β







1 −



2β

−β

2β

+β





+ δ

, (19)

rβ

= M

−M



2β

−β

2β

+β





1 −



2β

−β

2β

+β





−



1 −



2β

−β

2β

+β





−(δ

+ δ

)β

, (20)

There are now two cases to consider: θ

∗

= 0 and

∗

> 0.

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game

4.1 Case θ

∗

= 0

Whenever this case arises, and we will, later in Propo-

sition 4, determine the precise conditions on the prob-

lem parameters when it does, we must have the

value-function coefﬁcients that satisfy the condition

2β

−β

2β

+β

≤0, and these coefﬁcients must solve the fol-

lowing system of equations obtained from (15-20) by

setting



2β

−β

2β

+β



= 0:

rα

+ β

, (21)

rβ

= m

−

−β

(δ

+ δ

),(22)

rα

+ β

, (23)

rβ

= m

−

−β

(δ

+ δ

),(24)

rα

= M

+ β

, (25)

rβ

= M

−M

−

−β

(δ

+ δ

). (26)

Given these equations, we can state the following

result that presents the participation threshold, i.e.,

the point at which the manufacturer moves from θ

∗

0 to θ

∗

> 0.

Proposition 4. The participation threshold S is given

S = 2(M

−M

) −m

−

, (27)

where β

is the unique positive solution of

+ κ

−κ

= 0 (28)

with κ

16(r+δ

+δ

)

3ρ

16(r+δ

+δ

)

−8m

+16m

3ρ

, and κ

16m

3ρ

. The

manufacturer chooses θ

∗

> 0 when S > 0 and θ

∗

= 0

when S ≤ 0. Furthermore, ∂S/∂(M

−M

) = 2 > 0 at

S ≤0.

Note that S is computed by solving the system of

equations in (21-26) for θ

∗

= 0, in which case S ≤ 0.

From the result ∂S/∂(M

−M

) > 0 at S = 0, we can

immediately see that when S = 0, a decrease in (M

−

) will keep θ

∗

= 0, whereas an increase in (M

−

) will make it optimal for the manufacturer to set

∗

> 0. This is because an increase in the difference

in the manufacturer’s margins from Retailers 1 and 2

offers the manufacturer a greater incentive to provide

promotional support to Retailer 1.

Next, we state Corollary 1, which provides the

solutions to equations (21-26) for the case when the

two retailers are symmetric, i.e., δ

= δ, ρ

= ρ, r

r, m

= m, α

= α, and β

= β, i = 1,2.

Corollary 1.

(a) The value-function coefﬁcients of the two retailers

in the symmetric case are given by

α =

4mρ

−(r −δ)



(r + 2δ)

+ 3mρ

−(r + 2δ)



9rρ

β =

(r + 2δ)

+ 3mρ

−(r + 2δ)

3ρ

. (29)

(b) The value-function coefﬁcients of the manufac-

turer are given by

2rM



βρ

+ 2δ



+ M

)

2r (βρ

+ r + 2δ)

−M

βρ

+ r + 2δ

, (30)

where β is speciﬁed by (29).

for S w.r.t. the model parameters: ∂S/∂(M

−M

) =

2 > 0, ∂S/∂m < 0, ∂S/∂ρ < 0, ∂S/∂r > 0, ∂S/∂δ > 0.

(d) At the manifold S = 0, we have the following

comparative statics results for the model parameters:

∂(M

−M

)/∂m > 0, ∂ρ/∂m < 0, ∂(M

−M

)/∂δ <

0, ∂m/∂δ > 0, ∂ρ/∂δ > 0, ∂r/∂δ = −2 < 0.

Corollary 2. When r = δ = 0, S in (27) reduces to

S =

3mρ

(3(M

−M

) −2m). (31)

Thus, S in (31) can be used as an approximate par-

ticipation threshold when r and δ are small compared

to m, M

, M

, and ρ.

4.2 Case θ

∗

> 0

When the solution in Section 4.1 results in S > 0, we

know θ

∗

> 0. Then, by substituting



2β

−β

2β

+β



2β

−β

2β

+β

into equations (15-20), we have the following

system of equations to solve for the value-function co-

efﬁcients:

rα

(2β

+ β

) + β

, (32)

rα

+ β

, (33)

rα

= M

(2β

+ β

)

+ β

, (34)

rβ

= m

−

(2β

+ β

) −

−β

(δ

+ δ

) (35)

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

rβ

= m

−

(2β

+ β

) −

−β

(δ

+ δ

), (36)

rβ

= M

−M

−

(2β

+ β

)

−

−β

(δ

+ δ

). (37)

This requires numerical analysis. Figure 1 illus-

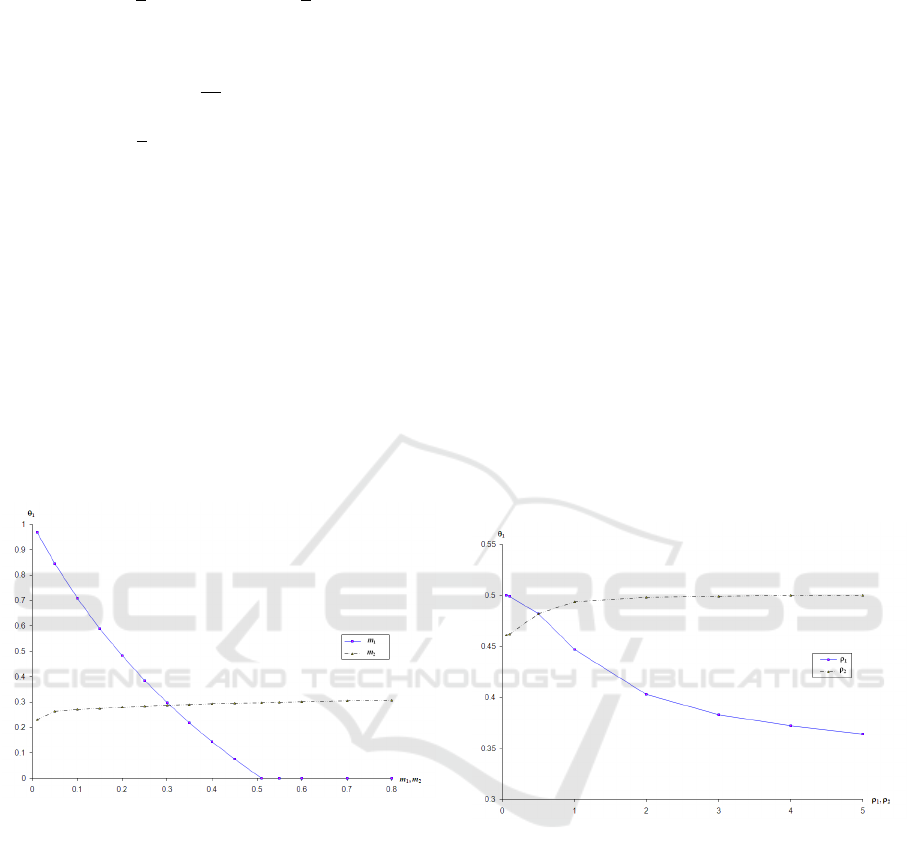
trates the effect of the retailer’s margin on the man-

ufacturer’s participation rate. We use the following

sample parameter values: r = 0.03, ρ

= ρ

= 0.5,

= 0.07, δ

= 0.1, M

= 0.5, M

= 0.2. Further-

more, for the effect of Retailer 1’s margin, we set Re-

tailer 2’s margin to m

= 0.5, and vice versa.

We already know from Corollary 1(c) that

∂S/∂m < 0 at S ≤ 0 in the symmetric case. The result

shown in Figure 1—that θ

∗

decreases, and at a de-

ceasing rate, as the margin m

of the supported retailer

increases—is consistent with our ﬁnding in the sym-

metric case and represents its generalization to the

asymmetric case. The reason behind this result is that

Figure 1: Effect of Retailers’ Margins on the Optimal Par-

ticipation Rate.

with low margin m

, Retailer 1 will under-advertise

and the manufacturer’s proﬁt will suffer. So, then, it

is in the interest of the manufacturer to participate so

as to encourage the retailer to advertise more. As m

increases, Retailer 1 has its own incentive to adver-

tise, and, therefore, the manufacturer does not need

to offer as much in the way of participation. As m

keeps increasing, the manufacturer ceases to partici-

pate altogether. We see from Figure 1 that θ

∗

indeed

becomes zero at m

≈0.5, where the switch from “co-

operative advertising” to “no cooperative advertising”

takes place. A more precise value can be obtained by

using (27), and we ﬁnd this to be m

= 0.50925. Thus,

we have generalized to the competitive environment

the result obtained in He et al. (2009) in the absence

of competition.

The effect of the margin of the non-supported re-

tailer, i.e., Retailer 2, on the offer of cooperative

advertising to Retailer 1, the supported retailer, ap-

pears to be weak. Note that at m

= 0.3, the two

curves in Figure 1 cross. At this point, as m

in-

creases ceteris paribus, θ

∗

decreases sharply whereas

as m

increases, θ

∗

increases but slowly. This means

that as m

increases, Retailer 1 faces greater advertis-

ing competition from the competing retailer and this

induces the manufacturer to support Retailer 1 at a

slightly higher rate. On the other hand, as m

in-

creases, as has already been mentioned, it increases

the incentive of Retailer 1 to advertise of its own ac-

cord, and thus the manufacturer reduces its support

signiﬁcantly. Even though m

has a weak effect on

∗

, it may still make a difference between the manu-

facturer supporting or not supporting Retailer 1. Nu-

merical analysis shows that when m

= m

= 0.5,

then θ

∗

= 0.012. But as m

decreases from 0.5 (e.g.,

= 0.25), the manufacturer stops offering promo-

tional support to Retailer 1. On the other hand, as m

increases from 0.5 to 0.80, θ

∗

increases from a sup-

port of 1.2% to only 3.2%.

Figure 2: Effect of Advertising Effectiveness on the Opti-

mal Participation Rate.

In Figure 2, the ﬁxed parameter values are m

0.2, m

= 0.5, r = 0.03, ρ

= 0.5, δ

= 0.07, δ

= 0.1,

= 0.5, M

= 0.2. Consistent with the comparative

statics result for the symmetric case in Corollary 1(c)

that ∂S/∂ρ < 0, this ﬁgure shows that as the advertis-

ing effectiveness of the supported retailer increases,

the degree of support by the manufacturer diminishes.

The reason is that, given the greater effectiveness of

advertising, the retailer has an incentive to advertise

at a higher level even without the support of the man-

ufacturer. The unsupported retailer’s advertising ef-

fectiveness does not have a great impact, but as it in-

creases, it slowly raises the participation rate.

Finally, Figure 3 shows that as the sum of the mar-

ket share decay rates for the two retailers increases,

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game

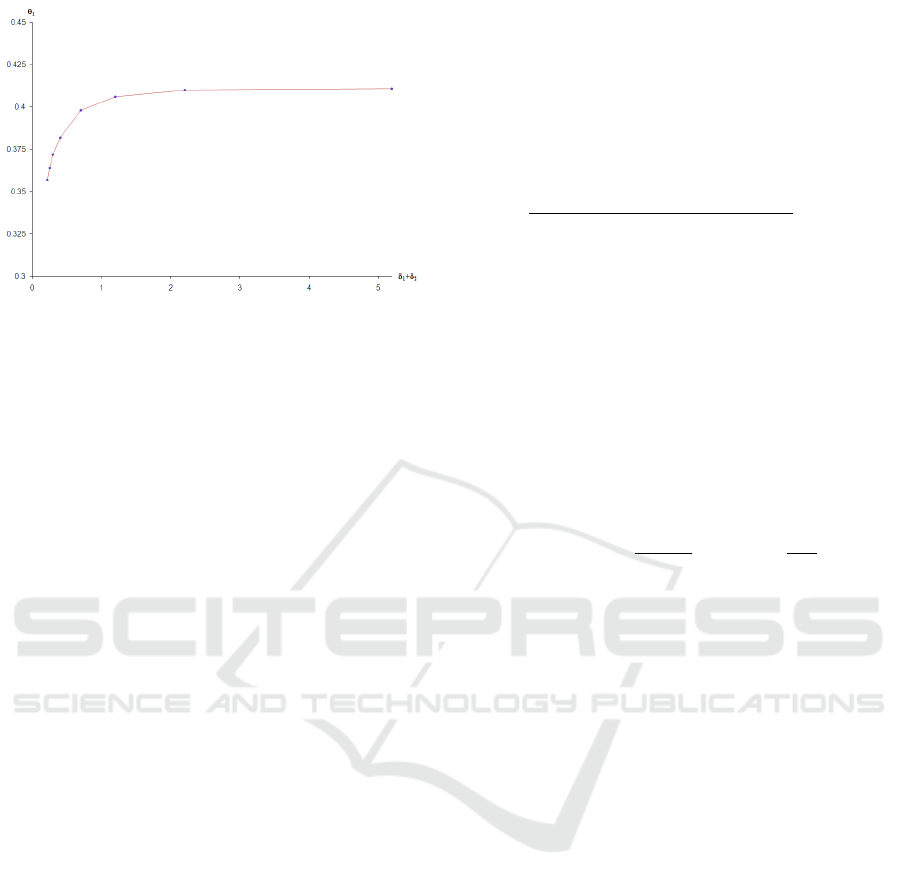
Figure 3: Effect of Decay on the Optimal Participation Rate.

the participation rate to the supported retailer, i.e.,

Retailer 1, increases. For this ﬁgure, the remaining

parameter values are m

= 0.5, m

= 0.2, r = 0.03,

= 0.5, ρ

= 0.5, M

= 0.8, M

= 0.2. Note that

we have plotted θ

∗

against the sum of the decay rates

since it is clear from the dynamics in (1) that the de-

cay rate for Retailer 1 is (δ

+ δ

). It is for this rea-

son that we can easily see from equations (32-37) that

, β

, and β

, and, therefore, θ

∗

, are affected by the

sum (δ

+δ

) and not by the decay rates individually.

The result can be explained intuitively since the in-

crease of (δ

+ δ

) is similar to increasing the speed

of the treadmill with which the advertising must keep

up. Thus, as (δ

+ δ

) increases, Retailer 1 ﬁnds it

more expensive to maintain its market share and the

manufacturer must offer a higher participation rate to

Retailer 1 to adequately promote the product. This

ﬁnding generalizes to the asymmetric case the analyt-

ical result obtained for the symmetric case in Corol-

lary 1(c) that ∂S/∂δ < 0. Finally, note that the effect

of the decay rates is most pronounced at their lower

values and does not have much effect on the partici-

pation rate at higher values.

5 EXTENSIONS

The model can be extended to include retail price

competition. In the case where the retail price, de-

noted p

, is endogenously determined in addition to

the advertising decision u

, Retailer i’s discounted

proﬁt maximization problem is given by

) = max

(t), p

(t)

∞

−rt

Ωdt i = 1, 2, (38)

subject to (1), where

Ω = D

(t), p

3−i

(t))(p

(t) −c

(t)

−(1 −θ

(x(t)))u

(t),

(t) is the price charged by Retailer i,

(t), p

3−i

(t)) = (1 −b

(t) + d

3−i

(t))

is the demand function expressed as a function of the

prices of the two retailers, c

is the marginal cost of

Retailer i, and b

and d

are demand parameters. Solv-

ing for the retailers’ optimal prices yields

ˆp

3−i

+ b

3−i

(2 + 2b

+ d

3−i

)

−d

, i = 1,2.

(39)

Using the parameter m

to denote

(t), p

3−i

(t)))(p

(t) −c

) in equation (38),

where p

= ˆp

from equation (39), results in equations

(2-3).

The demand parameters affect price, which, in

turn, affects the proﬁt margins. Thus, the results in

Section 4 remain unchanged except that we can now

add that the demand parameters affect the participa-

tion rate θ

∗

via m

, i =1, 2.

As in Prasad and Sethi (2004), one could extend

the model to include a stochastic term in the dynamic

equation in (1) as follows:

dx (t) =



(t)

1 −x(t) −ρ

(t)

x (t)



+(−δ

x (t) +δ

(1 −x(t)))dt

+σ(x(t))dz (t) (40)

where σ(x (t)) represents a variance term and z(t),

t ≥ 0, is the standard Wiener process.

6 CONCLUSIONS

In this paper, we consider a manufacturer who sells a

product to one or both of two independent and com-

peting retailers. The retailers invest in local adver-

tising effort, while the manufacturer decides whether

or not to support the retailers’ advertising activities

through a participation rate. We use differential game

theory to solve the Stackelberg game between the

manufacturer and the two retailers.

We derive the optimal advertising levels of the

two retailers and the participation rates of the man-

ufacturer, and ﬁnd that the manufacturer will provide

strictly less than 100% participation rate, and that the

manufacturer will offer a non-zero participation rate

to the retailer from whom the manufacturer earns the

higher margin. We then analyzed several special cases

of the general model, including the case of symmetric

retailers. Compared to He et al. (2009), who do not

model retail competition, we ﬁnd that the presence of

a competing retailer induces the manufacturer to pro-

vide a higher level of cooperative advertising support

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

to its retailer, and for a greater range of parameter val-

ues, than if that retailer were a monopolist.

There remain open issues for future research. To

preserve tractability, we did not model the manufac-

turer’s wholesale price decision in this paper, as was

done in He et al. (2009). Future research could extend

the model to also include the manufacturer’s whole-

sale price. It would also be interesting to explore deci-

sions in a retail oligopoly, along the lines of Fruchter

(1999).

Finally, this paper opens up a fruitful avenue for

future empirical research. Since we have provided

the optimal participation rates as well as their de-

pendence on various ﬁrm- and industry-level param-

eters, it would now be possible to empirically ex-

amine whether our results can explain the participa-

tion rates in different industries as reported in Dutta

et al. (1995). This would of course require estima-

tion of the ﬁrm- and industry-level parameters, pos-

sibly employing the techniques used in Naik et al.

(2008). Provided an appropriate data set can be found

or collected, an empirical study to validate our results

would undoubtedly deepen our understanding of the

cooperative advertising practices in different indus-

tries.

REFERENCES

F. M., A. Krishnamoorthy, A. Prasad, S. P. Sethi. 2005.

Generic and brand advertising strategies in a dynamic

duopoly. Marketing Science 24 556-568.

A., S. Chen, S. P. Sethi, 2014. Feedback Stackelberg

Solutions of Inﬁnite-Horizon Stochastic Differential

Games. Models and Methods in Economics and Man-

agement Science, Essays in Honor of Charles S.

Tapiero, F.E. Ouardighi and K. Kogan (Eds.), Interna-

tional Series in Operations Research & Management

Science, Vol. 198, Springer 3-15.

A., S. Chen, S. P. Sethi, 2015. The Maximum Principle for

Global Solutions of Stochastic Stackelberg Differen-

tial Games. SIAM Journal on Control and Optimiza-

tion 53(4) 1956-1981.

A., S. Chen, S. P. Sethi, A. Chutani, C. C. Siu, S. C.

P. Yam. 2019 (forthcoming). Feedback Stackelberg–

Nash Equilibria In Mixed Leadership Games With an

application to cooperative advertising. SIAM Journal

on Control and Optimization.

M., G. John. 1997. Understanding cooperative advertising

participation rates in conventional channels. Journal

of Marketing Research 34 357-369.

P. D. 1972. Vertical cooperative advertising ventures. Jour-

nal of Marketing Research 9 309-312.

Berger P. D., T. Magliozzi. 1992. Optimal cooperative ad-

vertising decisions in direct-mail operations. Journal

of the Operational Research Society 43 1079-1086.

Chintagunta P. K., D. C. Jain. 1992. A dynamic model

of channel member strategies for marketing expendi-

tures. Marketing Science 11 168-188.

Dant R. P., P. D. Berger. 1996. Modeling cooperative adver-

tising decisions in franchising. Journal of the Opera-

tional Research Society 47 1120-1136.

Deal K. R. 1979. Optimizing advertising expenditures in a

dynamic duopoly. Operations Research 27 682-692.

Dockner E. J., S. Jørgensen, N. V. Long, and G. Sorger.

(2000). Differential Games in Economics and Man-

agement Science, Cambridge University Press, Cam-

bridge, UK.

Dutta S., M. Bergen, G. John, A. Rao. 1995. Variations in

the contractual terms of cooperative advertising con-

tracts: Am empirical investigation. Marketing Letters

6 15-22.

Erickson G. M. 2009. An oligopoly model of dynamic ad-

vertising competition. European Journal of Opera-

tional Research 197 374-388.

Fruchter G. E., 1999. The many-player advertising game.

Management Science 45 1609-1611.

He X., A. Krishnamoorthy, A. Prasad, S. P. Sethi. 2011.

Retail competition and cooperative advertising. Oper-

ations Research Letters 39 11-16.

He X., A. Krishnamoorthy, A. Prasad, S. P. Sethi. 2012. Co-

Op Advertising in Dynamic Retail Oligopolies. Deci-

sion Sciences Journal 43 73-105.

He X., A. Prasad, S. P. Sethi, G. Gutierrez. 2007. A sur-

vey of Stackelberg differential game models in supply

chain and marketing channels. Journal of Systems Sci-

ence and Systems Engineering 16 385-413.

He X., A. Prasad, S. P. Sethi. 2009. Cooperative advertis-

ing and pricing in a dynamic stochastic supply chain:

Feedback Stackelberg strategies. Production and Op-

erations Management 18 78-94.

Huang Z., S. X. Li. V. Mahajan. 2002. An analysis of

manufacturer-retailer supply chain coordination in co-

operative advertising. Decision Sciences 33 469-494.

Jørgensen S., S. P. Sigue, G. Zaccour. 2000. Dynamic coop-

erative advertising in a channel. Journal of Retailing

76 71-92.

Jørgensen S., S. Taboubi, G. Zaccour. 2001. Cooperative

advertising in a marketing channel. Journal of Opti-

mization Theory and Applications 110 145-158.

Jørgensen S., S. Taboubi, G. Zaccour. 2003. Retail promo-

tions with negative brand image effects: Is coopera-

tion possible? European Journal of Operational Re-

search 150 395-405.

Jørgensen S., G. Zaccour. 2003. Channel coordination over

time: Incentive equilibria and credibility. Journal of

Economic Dynamics and Control 27 801-822.

Karray S., G. Zaccour. 2005. A differential game of adver-

tising for national brand and store brands. In: A. Hau-

rie and G. Zaccour (Eds.), Dynamic Games: Theory

and Applications, Springer, 213-229.

Kim S. Y., R. Staelin. 1999. Manufacturer allowances and

retailer pass-through rates in a competitive environ-

ment. Marketing Science 18 59-76.

Nagler M. G. 2006. An exploratory analysis of the deter-

minants of cooperative advertising participation rates.

Marketing Letters 17 91-102.

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game

Naik P. A., A. Prasad, S. P. Sethi. 2008. Building brand

awareness in dynamic oligopoly markets. Manage-

ment Science 54(1) 129-138.

Prasad A., S. P. Sethi. 2004. Competitive advertising under

uncertainty: A stochastic differential game approach.

Journal of Optimization Theory and Applications 123

163-185.

Sethi S. P. 1983. Deterministic and stochastic optimization

of a dynamic advertising model. Optimal Control Ap-

plications and Methods 4 179-184.

Sorger G. 1989. Competitive dynamic advertising: A mod-

iﬁcation of the Case game. Journal of Economic Dy-

namics and Control 13 55-80.

Vidale M. L., H. B. Wolfe. 1957. An operations-research

study of sales response to advertising. Operations Re-

search 5 370-381.

APPENDIX

Proof of Proposition 1

First, note that if M

> M

, then the

manufacturer’s objective function in equa-

tion (4) can be organized as follows:

∞

−rt



+ (M

−M

)x −θ

(x) −θ

(x)



dt.

This suggests that the manufacturer should encourage

Retailer 1 to increase its advertising to increase x

(and discourage Retailer 2 to decrease advertising

and (1 −x) by setting θ

∗

= 0) as much as possible.

xspace 

Proof of Proposition 2

The Hamilton-Jacobi-Bellman (HJB) equation (Sethi

and Thompson 2000) for Retailer i is given by:

= max

x −(1 −θ



√

1 −x



−V



√

x −δ

x + δ

(1 −x)



, (41)

= max



(1 −x) −(1 −θ



√

1 −x



−V



√

x −δ

x + δ

(1 −x)



.(42)

The ﬁrst-order conditions for maximization yield the

optimal advertising levels in equation (8) in Proposi-

tion 2(a). Substituting these solutions into the above

HJB equations for the two retailers yields equations

(10-11) in Proposition 2(c).

The HJB equation for the manufacturer is given

by:

rV = max

, θ











x + M

(1 −x) −θ

(x|θ

,θ

)

−θ

(x|θ

,θ

)



(x|θ

,θ

)

√

1 −x



−V

(ρ

(x|θ

,θ

)

√

x −δ

x + δ

(1 −x)).

(43)

Substituting the optimal advertising efforts of the

two retailers into the above equation and simplifying

yields

rV = max

, θ











x + M

(1 −x) −





(1−x)

(1−θ

)





(1−θ

)

−

(1−θ

)ρ

x+(1−θ

)



2(δ

x−δ

(1−x))(1−θ

)−ρ

(1−x)



2(1−θ

)(1−θ

)

(44)

Solving the ﬁrst-order conditions for the partici-

pation rates, and noting that M

> M

implies θ

∗

= 0,

yields equation (9) in Proposition 2(b). Substituting

these solutions into equation (44) and simplifying, we

obtain equation (12) in Proposition 2(c). xspace 

Proof of Proposition 3

With V

= α

+β

x and V

= α

+β

(1 −x), we have

= β

and V

= β

. Inserting these into (10) and

(11), we have

r (α

+ β

x) = m

x +

(1 −x)



1 −



−β

+β





−

−β

(δ

x −δ

(1 −x)), (45)

r (α

+ β

(1 −x)) = m

(1 −x) +

−

(1 −x)



1 −



−β

+β





+ β

(δ

x −δ

(1 −x)). (46)

With V = α

+ β

x, we have V

= β

. Substi-

tution into equations (8) and (9) yields (13) in Propo-

sition 3(a) and (14) in Proposition 3(b), respectively.

Substituting these into the HJB equation in (12) and

simplifying yields

r (α

+ β

x) = M

x + M

(1 −x) −

−



2β

−β

2β

+β



(1 −x)



1 −



2β

−β

2β

+β





−

(1 −x)



1 −



2β

−β

2β

+β





−δ

x + δ

(1 −x). (47)

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

Equating the powers of x in (47), we obtain equa-

tions (19-20) in Proposition 3(c). Substituting V

into (45-46) and equating the powers of x and

(1 −x) yields equations (15-18) in Proposition 3(c).

xspace 

Proof of Proposition 4

Solving equation (22) for β

yields

−β



+ 4(r + δ

+ δ

)



2β

. (48)

Substituting the above solution into equation (24) and

simplifying yields the quartic equation (28).

As detailed in Prasad and Sethi (2004), it can be

shown that there exists a unique β

> 0 that solves the

above quartic equation. This is the unique equilibrium

of the Stackelberg differential game. That solution

can then be substituted into (48) to yield the solution

for β

. We know from (26) that

2(M

−M

)

+ β

+ 2(r + δ

+ δ

)

. (49)

Substituting the solutions for β

and β

into (49)

yields β

Since β

> 0 from equation (20), the participation

threshold is obtained as 2β

−β

as follows;

4(M

−M

) −β

−β

−2β

(r + δ

+ δ

)

+ β

+ 2 (r + δ

+ δ

)

. (50)

We know from equation (22) that

+ 2β

(δ

+ δ

) =



−4rβ

−β



Using this in the numerator of (50) and simplify-

ing gives the participation threshold S in (27).

Since β

is independent of (M

−M

), we have

∂S/∂(M

−M

) = 2 > 0. xspace 

Proof of Corollary 1

The solutions for α

and β

, i = 1,2, in Corollary 1(a),

are the same as in the symmetric analysis in Prasad

and Sethi (2004) in the absence of uncertainty.

For the manufacturer, as before, the linear value

function V = α

+β

x solves the HJB equation. Set-

ting θ

= θ

= 0, imposing symmetry in the model

parameters, and simplifying the HJB equation results

r(α

+ β

x) = M



βρ

+ 2δ





−M

−



βρ

+ 4δ



x. (51)

Equating the coefﬁcients of x in equation (51)

yields the solutions in equation (30) in Corol-

lary 1(b). Note that this can be interpreted as

∞

−rt

x + M

(1 −x))dt given the solution ob-

tained with θ

= θ

= 0.

For the comparative statics, imposing symmetry

in the participation threshold from equation (27), we

have S(.) = 2(M

−M

) −m −

= 0. Substitut-

ing the solution for β from equation (29), this can be

rewritten as

S(.) = 2(M

−M

) −

2(r + 2δ)



(r + 2δ)

+ 3mρ

−(r + 2δ)



9ρ

. (52)

Taking the derivative of S in equation (52) w.r.t.

the model parameters yields the comparative statics

in Corollary 1(c): ∂S/∂(M

−M

) > 0, ∂S/∂m < 0,

∂S/∂ρ < 0, ∂S/∂r > 0, ∂S/∂δ > 0.

Proof of Corollary 2

We know that V

= β

and β

= β

= β, where

β =

√

(r+2δ)

+3mρ

−(r+2δ)

3ρ

. Moreover, β

−M

βρ

+r+2δ

with the aforementioned β.

Since θ

−β

+β

2β

−β

2β

+β

, we need 2β

−β > 0

for θ

> 0. Substituting the value of β into β

and

simplifying 2β

−β, we have

S = 2β

−β =

6(M

−M

)

r + 2δ + 2

(r + 2δ)

+ 3mρ

−



3mρ

+ (r + 2δ)

−(r + 2δ)



3ρ

. (53)

Therefore, θ

∗

> 0 when S > 0 from above. With

r = δ = 0 in (53), we obtain equation (31) as the ap-

proximation of (53). xspace 

Co-Op Advertising with Two Competing Retailers: A Feedback Stackelberg-Nash Game