Hybrid Fuzzy Binning for Near-duplicate Image Retrieval:

Combining Fuzzy Histograms and SIFT Keypoints

Afra’a Ahmad Alyosef and Andreas N

urnberger

Department of Technical and Business Information Systems, Faculty of Computer Science,

Otto von Guericke University Magdeburg, Germany

Keywords:

Near-duplicate Image Retrieval, Fuzzy Histogram, HSV Color Histogram, SIFT Keypoints.

Abstract:

Near-duplicate image retrieval is still a challenging task, especially due to issues with matching quality and

performance. Most existing approaches use high dimensional vectors based on local features such as SIFT

keypoints to represent images. The extraction and matching of these vectors to detect near-duplicates are time

and memory consuming. Global features such as color histograms can strongly reduce the dimensionality of

image vectors and signiﬁcantly accelerate the matching process. On the other hand, they strongly decrease the

quality of the retrieval process. In this work, we propose a hybrid approach to improve the quality of retrieval

and reduce the computation time by applying a robust ﬁltering process using global features optimized for

recall followed by a ranking process optimized for precision. For efﬁcient ﬁltering we propose a fuzzy partition

hue saturation (HS) histogram to retrieve a subset of near-duplicate candidate images. After that, we re-rank

the top retrieved results by extracting the SIFT features. In order to evaluate the performance and quality of

this hybrid approach, we provide results of a comparative performance analysis using the original SIFT-128D,

the HS color histogram, the fuzzy HS model (F-HS), the proposed fuzzy partition HS model (FP-HS) and

the combination of the proposed fuzzy partition HS histogram with the SIFT features using large scale image

benchmark databases. The results of experiments show that applying the fuzzy partition HS histogram and

re-rank the top results (only 6%) of the retrieved images) using the SIFT algorithm signiﬁcantly outperforms

the use of the individual state of art methods with respect to computing efﬁciently and effectively.

1 INTRODUCTION

Several major issues of image near-duplicate retrieval

(NDR) have been discussed in a lot of previous contri-

butions (Chum et al., 2007; Chu et al., 2013; Xu et al.,

2010) to reduce the size of image datasets by ﬁnd-

ing out images that belong to the same scene but are

taken of different perspectives, lightness conditions,

cameras, or scales. Furthermore, NDR has been in-

troduced in (Auclair et al., 2009), to detect copyright

violations and in (Alyosef and N

urnberger, 2019) to

identify the relation between zoomed-in images and

whole scene (i.e., zoomed-in retrieval (ZIR)). Key-

point features are extracted upon local distinct regions

of an image. The main research in NDR has focused

on using highly discriminative image features speciﬁ-

cally, the scale-invariant feature detector and descrip-

tor (SIFT). Since they are invariant to a number of im-

age deformations such as afﬁne transformation, view-

point or lightness change and adding noise or blur

to images. The descriptors of these features are high

dimensional vectors. Therefore, their extraction and

matching are time and memory consuming. Global

features such as color features represent images using

vectors of ﬁxed length. The extraction and match-

ing of global features are faster than keypoints but

they produce lower performance than keypoint fea-

tures in solving retrieval tasks. In this work, we con-

struct our hybrid approach by combining the beneﬁts

of the HSV color features and SIFT features. The

advantage of this hybrid approach is decreasing the

required memory, accelerating the matching process

and improving the performance of NDR and ZIR.

The remainder of this paper is organized as fol-

lows. Section 2 reviews the relevant works to accel-

erate the NDR. Section 3 details the proposed hybrid

method. Section 4 presents the settings and results of

our experiments. Section 5 concludes the work.

Alyosef, A. and Nürnberger, A.

Hybrid Fuzzy Binning for Near-duplicate Image Retrieval: Combining Fuzzy Histograms and SIFT Keypoints.

DOI: 10.5220/0009169602410248

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 241-248

ISBN: 978-989-758-397-1; ISSN: 2184-4313

241

2 STATE OF ART

SIFT features have high dimensional descriptors (the

dimensionality of each descriptor is 128D). There-

fore, their extraction and matching are time and

memory consumption speciﬁcally for a large image

dataset. To overcome this problem, two varieties

of optimization have been discussed in the previous

works. The ﬁrst optimization is to downscale the di-

mensionality of a SIFT descriptor to get a lower di-

mension descriptor and consequently accelerate the

matching process (Khan et al., 2011; Ke and Suk-

thankar, 2004; Alyosef and N

urnberger, 2016). The

second optimization suggests accelerating the process

of feature indexing and matching. To achieve this,

the concept of a bag of features has been proposed

in (Li et al., 2014; Grauman and Darrell, 2007; Jiang

et al., 2015; Nist

er and Stew

enius, 2006). The fuzzy

c3 c4

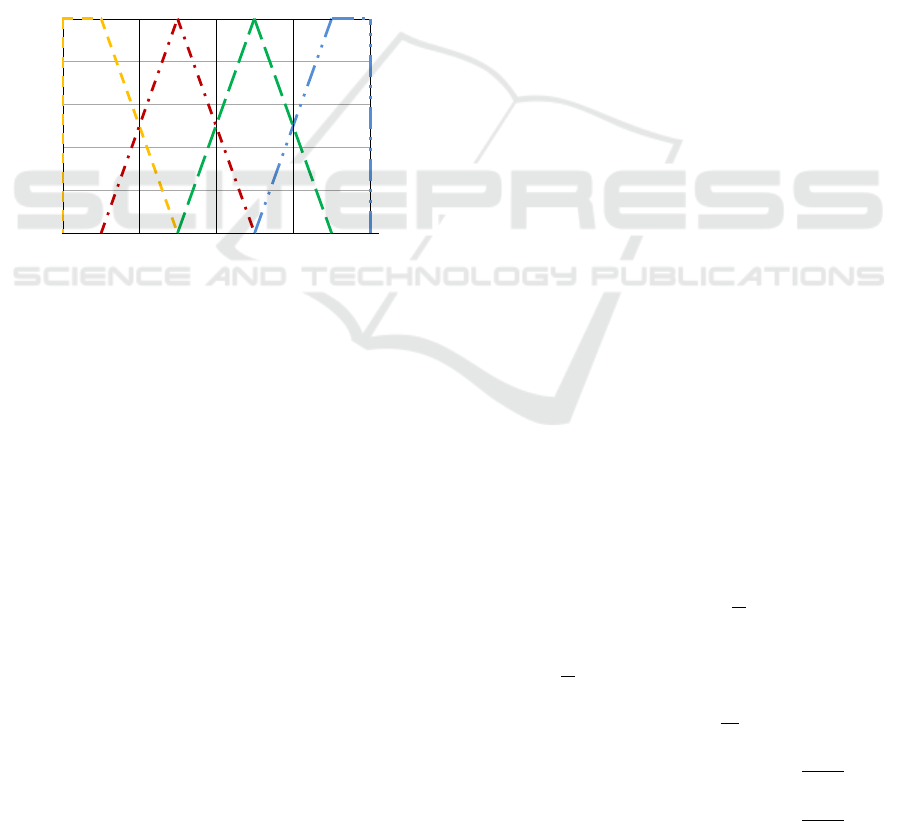
Figure 1: Comparison of crisp clusters and fuzzy clusters of

histogram bins.

color histogram has been introduced by (Han and Ma,

2002), which built the fuzzy histogram by processing

the three channels of the RGB histogram simultane-

ously. The idea is to compute the distance between the

color value of each pixel of an image and all clusters.

To improve the performance of the SIFT algorithm in

ﬁelds of object detection and image retrieval the idea

of the color descriptor (instead of the grayscale de-

scriptor) has been introduced in (Bosch et al., 2008;

van de Sande et al., 2010). However, these methods

increase the dimensionality of the SIFT descriptor. In

this work, we aim to accelerate the matching process

to improve the performance of image NDR and ZIR

tasks.

3 HYBRID APPROACH

To accelerate and improve the retrieval performance

of image NDR and ZIR, we proposed our hybrid ap-

proach by ﬁrst applying the fuzzy color histogram.

Second, re-rank the results using their SIFT features.

The following subsections detail our method.

3.1 Fuzzy HSV & Partition Fuzzy HSV

This section details our method in building the fuzzy

HSV histogram (F-HSV). To improve the retrieval

performance, we suggest dividing each image into

sub-images and constructing the fuzzy partition HSV

histogram (FP-HSV). The following subsections de-

tail our proposed model to build F-HSV and FP-HSV.

3.1.1 Fuzzy HSV Histogram

The HSV color space is created by merging the three

channels of RGB color space to get hue, saturation

and value channels (HSV). Hue deﬁnes the type of

color and its value belongs to the range [0

, 360

Saturation describes pureness of color and value de-

scribes the amount of light in color. The values of

saturation and value belong to the range [0, 255]. To

build the 3D HSV color histogram, we divide each

color channel into a speciﬁc number of clusters. Af-

ter that, we assign the HSV values of each pixel to the

closest cluster centers. Theses clusters produce bins

of the HSV color histogram. Based on this, we split

the hue channel into 30 clusters (bins) and each of

Saturation and value channels into 32 clusters. The

way of building clusters produce crisp clusters i.e.

each sample color contributes only in one bin (clus-

ter). Consider c

; k = 1, ...,L are centers of clusters,

where L is the number of clusters and r the radius of

cluster. The crisp clustering is deﬁned as:

p(x|c

) =

(

1, if |x − c

| ≤ r

0, otherwise

(1)

Since the clusters here stand for the bin of the HSV

histogram, all clusters have the same radius r. To

build the fuzzy clusters, we apply the following steps:

• for each sample x, determine the cluster where the

sample belongs to using crisp clustering.

• compute the absolute distance between the sample

and all centers c

; k = 1, ..., L.

• assign the probability 1 −

to the cluster c

where d

= |x − c

| ≤ r. Based on the location of

a sample to the center of cluster, assign the prob-

ability

to c

k−1

or c

k+1

i.e.:

p(x|c

) = 1 −

if x ≤ c

: p(x|c

k−1

) = 1 −

1 − d

else if x > c

: p(x|c

k+1

) = 1 −

1 − d

(2)

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

242

• for samples that belong to the ﬁrst cluster and sat-

isfy d

= |x − c

| ≤ r, we assign the both proba-

bility computed in Equation 2 to the ﬁrst cluster.

• the same idea for the last cluster i.e. contribu-

tions are assigned to the last center for samples

that they belong to the last cluster and satisfy

= |x − c

| ≥ r.

• normalize the clusters of F-HSV utilizing the area

of the input image.

Figure 1 explains the difference between crisp and

fuzzy clustering in case of having four clusters.

3.1.2 Construction of 2D Fuzzy Histogram

In our practice study, we notice that the third dimen-

sion of HSV histogram, which is the value dimension,

decreases the performance of image NDR. The value

dimension measures the amount of lighting in color

therefore; any change in the lightness of colors causes

a signiﬁcant change in the bins of value dimension.

Based on this, we consider only the hue and saturation

dimensions when we construct the color histogram

i.e., we construct the F-HS and FP-HS histograms in-

stead of F-HSV and FP-HSV. Section 4.3.1 shows the

comparison between the F-HSV and the F-HS mod-

els.

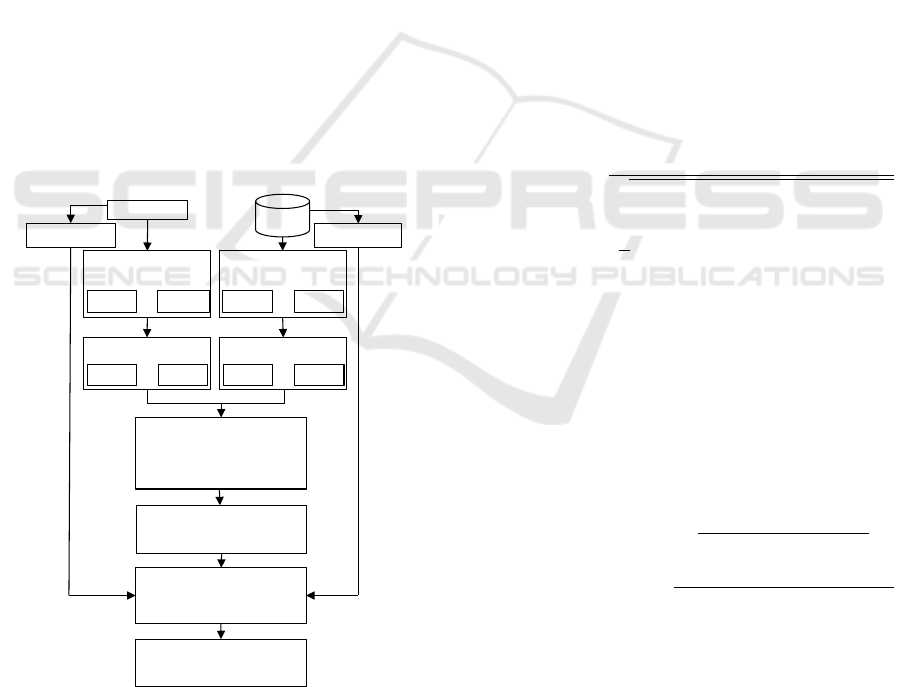
Image

dataset

Query Image

Extract SIFT features

Divide each image into

sub-images

sub-img

i_1

sub-img

i_m

…

Construct FP-HSV

FP-HSV

i_1

FP-HSV

i_m

…

Divide query image

into

sub-images

sub-img

q_1

sub-img

q_m

…

Construct FP-HSV

FP-HSV

q_1

FP-HSV

q_m

…

Compute the average correlation

avg_corr=

avg(corr(FP-HSV

q_j

,FP-HSV

i_j

)

Rank results based on decreasing

avg_corr

Compare SIFT features of Q and

the

top retrieved images

Extract SIFT features

Re-rank top

results based on

SIFT features

Figure 2: Flowchart of our proposed method.

3.1.3 Fuzzy Partition HS Histogram

To improve image NDR and ZIR by employing the

F-HS histogram, we suggest dividing each image into

a set of sub-images P. After that, we compute the

F-HS histogram for the whole image and for each

sub-image as described in Subsection 3.1.1. The set

of all F-HS histograms for all sub-images builds the

fuzzy partition HS histogram (FP-HS). The FP-HS

improves the performance of image NDR and ZIR

because it presents additional information about the

distribution of colors in images. Since the FP-HS

model considers the spatial distribution of colors, it

decreases the retrieving of non-relevant images.

3.1.4 Histogram Similarity Measures

Many methods have been suggested to measure the

similarity between two color histograms such as in-

tersection, Chi-Square, correlation and Earth mover

distance (P. Marin-Reyes, 2016). The idea of correla-

tion measure is to compare the distribution of two his-

tograms instead of the bin to bin comparison. There-

fore, we use in this work the correlation measure

by computing the mean µ and standard deviation σ

over all bins. The correlation Corr between two his-

tograms H

and H

is deﬁned as (P. Marin-Reyes,

2016):

Corr(H

, H

) =

∑

i=1

1,i

− µ

)(H

2,i

− µ

)

∑

i=1

1,i

− µ

)

∑

i=1

2,i

− µ

)

where µ =

∑

i=1

(3)

The values of Corr belong to the rang [−1, +1]. The

value of −1 means that there is no correlation be-

tween the histograms. Whereas, the value +1 implies

that histograms are identical. The complexity of this

measure is O(L) (P. Marin-Reyes, 2016). The cor-

relation between two fuzzy partitions HS histograms

of two near-duplicate images FP-HS

and FP-HS

deﬁned as:

Corr(FP-HS

, FP-HS

) =

Corr(F-HS

, F-HS

)

P + 1

∑

i=1

Corr(F-HS

, F-HS

)

P + 1

(4)

In the case of zoomed-in / whole scene retrieval, we

compute the correlation between the F-HS

of the

zoomed-in image and both F-HS

and the set FP-

;i = 1, ..., P of a whole scene. After that, we mea-

sure the correlation between the zoomed-in and whole

scene images as the average of the highest two corre-

lations. Equation 5 describes the average correlation

in case of zoomed-in / whole scene retrieval, where

Hybrid Fuzzy Binning for Near-duplicate Image Retrieval: Combining Fuzzy Histograms and SIFT Keypoints

243

max

zw1

, max

zw2

are the highest two correlations.

avg-Corr(z, w) =

avg(max

zw1

, max

zw2

)

where

{max

zw1

, max

zw2

} = max{Corr(F-HS

, F-HS

{Corr(F-HS

, FP-HS

); i = 1, ..., P}}

(5)

3.1.5 Complexity of F-HS & FP-HS

We compare the computation time of the traditional

HS, the F-HS and the FP-HS models to build color

histograms using the Ukbench dataset (the details of

this dataset are described in Subsection 4.1). Table 1

shows that the F-HS and FP-HS require a longer time

to generate their histograms than the crisp HS model.

However, the F-HS and FP-HS models signiﬁcantly

improve the performance of image NDR (see Subsec-

tion 4.3.1) comparing to the HS histogram. Moreover,

F-HS and FP-HS still too faster than the SIFT algo-

rithm (which needs hours to complete the feature ex-

traction for the same image dataset). In addition, the

F-HS and the FP-HS models produce a lesser amount

of features than the SIFT algorithm. Hence, they ac-

celerate the matching process.

Table 1: Time computation of HS, F-HS and FP-HS his-

tograms using the Ukbench dataset.

Method HS F-HS FP-HS

Sub-images - - P = 3 P = 9

Time (Sec.) 151 273 381 530

3.2 SIFT Feature Extraction

In this work, we aim to present the effect of us-

ing the F-HS and FP-HS in improving the perfor-

mance of image NDR and ZIR. Therefore, in the

step of extracting the SIFT features we are not going

to discuss the optimized SIFT methods (Alyosef and

urnberger, 2017a; Alyosef and N

urnberger, 2017b;

Alyosef and N

urnberger, 2016; Khan et al., 2011) in-

stead, we apply the original SIFT algorithm (Lowe,

2004) to extract the SIFT keypoints and build their

128 dimensions descriptors. The original SIFT algo-

rithm (Lowe, 2004) extracts features using grayscale

color space i.e. the color information play no role

in the building of descriptors. To match the key-

points, we utilize the Kd-tree and the best-bin-ﬁrst

algorithm as described in (Lowe, 2004). However,

this method of matching obtains duplicate matches

i.e. a keypoint of one image may match with many

keypoints in the other one. To overcome this prob-

lem, we eliminate all duplicate matches except the

one which has the best matching score. This ﬁltering

of matched features is important to reduce the number

of mismatched features. Further discussion to ﬁlter

the matched features have been discussed in (Alyosef

and N

urnberger, 2019)

3.3 Re-rank the Top N Results

To optimize the NDR results obtained by the F-HS

and the FP-HS models, we apply the SIFT algorithm

on the top N retrieved results. Consequently, no need

to compare the SIFT features of a query image with

all SIFT features of dataset images. Instead, we com-

pare the features of a query image with only the top

N retrieved results where size(N) << size(Dataset).

In the Section 4, we discuss the suitable values for the

top N results. Figure 2 details the step of our method.

4 EVALUATION

We evaluate the performance of our hybrid model to

solve image NDR and ZIR tasks. We describe our

experiments as in the following subsections.

4.1 Datasets

In this work, since we aim to solve two tasks (i.e.

image NDR and ZIR), we decide to use two image

datasets. The ﬁrst one is UKbench dataset which con-

tains 10200 images of 2550 various scenes (Nist

er and

Stew

enius, 2006). For each scene, there are four near-

duplicate images. We pick the ﬁrst image as query

image and keep the rest three images in the dataset.

So we get 2550 queries. The second is the Oxford

building dataset to solve the ZIR task (Philbin et al.,

2007). This dataset contains images of the same sight

but not necessarily the same scene i.e. the images

present inside and outside parts of sights. To use this

dataset for solving the ZIR task, we generate three

sets of zoomed-in images by cropping and rescal-

ing the images of the oxford building dataset. These

datasets are Oxford-Zoomed-in-50, Oxford-Zoomed-

in-25 and Oxford-Zoomed-in-10 where the zoomed-

in images cover 50%, 25% and 10% of the original

scene respectively. We use these three constructed

datasets as queries to solve the task of the whole scene

(original images of oxford buildings) retrieval.

4.2 Evaluation Measures

To evaluate the performance of the proposed F-HS,

FP-HS models and the hybrid approach, we compute

the recall, MAP and VR (Alyosef and N

urnberger,

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

244

2019). Given are a set of Q query images, M

number

of relevant image to a query image q, then the mean

recall MR is deﬁned as:

MR =

∑

q=1

Recall(q) ; Recall(q) =

(6)

To present the distribution of recalls of individual

query images around the MR, we compute the vari-

ance of the recall values V R as follow:

V R =

∑

q=1

(Recall(q) − MR)

(7)

To present the positions of relevant images in the set

of retrieved results, we compute the mean average

precision MAP as:

MAP =

∑

q=1

Ap(q)

; AP(q) =

∑

i=1

p(i) × r(i)

(8)

Where Ap(q) is the average precision for image q and

r(i) = 1 if the i

retrieved image is one of the relevant

images otherwise r(i) = 0, p(i) is the precision at the

element, J is the number of retrieved results.

4.3 Results of Image NDR

The results of the original HSV, HS, SIFT and the

proposed F-HS and FP-HS and the hybrid method

are compared and evaluated to solve the image NDR

tasks.

Table 2: MR of the crisp HSV, the crisp HS, the F-HSV, and

the F-HS methods for the top 3, 10 and 500 results.

Method MR3% MR10% MR500%

HSV 34.87 44.44 82.38

HS 38.49 48.01 87.52

F-HSV 37.09 47.76 86.38

F-HS 41.87 51.62 87.52

4.3.1 Comparison of F-HSV, F-HS & HSV, HS

As we mentioned in Subsection 3.1.2, using 2D HS

histogram performs better than the 3D HSV his-

togram. To justify this idea, we compare the perfor-

mance of crisp HSV, F-HSV to the performance of

crisp HS, F-HS histograms to solve image NDR tasks.

We apply this experiment on the Ukbench dataset.

Table 2 shows that the crisp HS and the F-HS mod-

els perform better than the crisp HSV and the F-HSV

models in solving the image NDR task. Table 3 clar-

iﬁes that the ignoring of the value domain improves

the MAP and the VR by solving image NDR tasks.

Table 3: MAP and VR of crisp HSV, crisp HS, F-HSV and

F-HS methods on top 3 and 10 results.

Method MAP3 MAP10 VR3 VR10

HSV 31.40 33.52 11.65 16.02

HS 35.57 36.47 12.01 13.81

F-HSV 33.40 35.02 11.19 15.65

F-HS 37.32 40.39 12.07 13.28

4.3.2 Results of F-HS for NDR Task

As shown in Table 2 the F-HS outperforms the crisp

HSV, F-HSV and the HS models. Therefore, we re-

ranked the results of the F-HS using their SIFT fea-

tures. Table 2 presents that the top 500 retrieved im-

ages using FH-SH retrieves about 87% of the rele-

vant images. Therefore, we suggest to re-rank the top

500 results using their SIFT features. Table 4 presents

that applying the hybrid method (i.e., ﬁrst F-HS and

then re-rank the top 500 results) obtains better results

than the extraction and matching of only SIFT fea-

tures to solve image NDR task. Moreover, our hy-

brid approach accelerates the matching process since

it compares SIFT features of a query image with only

the top 500 retrieved results i.e., with only 6.5% of

total images in the dataset. Table 4 explains that our

hybrid method obtains better MAP than the SIFT al-

gorithm. In addition, it presents that the distribution

of the individual recalls around the MR is better by

our method than by the SIFT algorithm.

Table 4: The MR of the SIFT algorithm and the F-

HS+SIFT for the top 3, 10 and 50 results.

Method MR3% MR10% MR50%

SIFT 49.32 54.31 58.70

F-HS+SIFT 55.77 64.61 72.78

Table 5: MAR and VR of the SIFT & the F-HS+SIFT mod-

els.

Method MAP3 MAP10 VR3 VR10

SIFT 47.46 51.07 15.08 15.17

F-HS+SIFT 53.76 57.46 14.75 14.60

4.3.3 Results of FP-HS for NDR Task

Table 6 presents the performance of the FP-HS model

when both query and dataset images are divided into

three (P = 3) and then nine (P = 9) sub-images. The

results illustrate that the using of nine sub-images im-

proves the MR of the FP-HS model. Moreover, as pre-

sented in Table 7, the FP-HS model produces a small

Hybrid Fuzzy Binning for Near-duplicate Image Retrieval: Combining Fuzzy Histograms and SIFT Keypoints

245

VR when P = 9 too. As displayed in Table 6, the MR

obtained by nine sub-images is around 80% on the top

50 results while it is more than 90% when the top 500

results are retrieved. Therefore, we can improve the

performance of image NDR by re-ranking the top 50

or 500 results, i.e., only 0.65% or 6.5% of the size of

the dataset respectively.

Table 6: MR of the FP-HS model for P = 3 and P = 9.

FP-HS MR3 MR10 MR50 MR500

P = 3 52.27 59.32 73.53 89.32

P = 9 55.71 66.22 78.44 91.32

Table 7: The MAP and VR of the FP-HS model.

FP-HS MAP3 MAP10 VR3 VR10

P = 3 46.74 50.39 13.42 15.73

P = 9 52.68 56.71 13.24 14.29

4.3.4 Re-rank FP-HS Results for NDR Task

We improve the ranking of results by matching the

SIFT features of a query with the top 300 images. Ta-

bles 8 and 9 introduce the re-ranked results of the FP-

HS model. The hybrid model obtains the best MR

when P = 9 is utilized to construct the FP-HS. More-

over, the best MAP and VR are obtained concerning

the hybrid model and P = 9 (Table 9). The hybrid

model (when P = 9) improves the results of image

NDR by 22% more than the SIFT algorithm, 30%

more than F-HS, and 4% more than the hybrid model

using P = 3. In this work, we do not resume the evalu-

ation concerning more sub-images since the partition

of images into smaller sub-images is once again time

and memory consuming. Figure 3 presents a compari-

son between the SIFT algorithm, the F-HS model, the

FP-HS, and the hybrid approach. The SIFT algorithm

and the F-HS model retrieve only one of the three rel-

evant images in the top three results. Whereas, the

FP-HS model retrieves two of the relevant images in

top results. However, re-ranking the results utilizing

SIFT features obtains all relevant results in the top

three results.

Table 8: The MR of the hybrid approach on the top 300

found by the FP-HS model.

Re-ranked results: hybrid approach

Partitions MR3% MR10% MR50%

P = 3 68.52 73.73 75.44

P = 9 72.77 81.79 87.59

Table 9: The MAP and the VR of the hybrid approach on

the top 300 results of the FP-HS model.

Re-ranked: hybrid approach

Partitions MAP3 MAP10 VR3 VR10

P = 3 67.12 70.57 13.11 12.05

P = 9 71.06 75.20 12.64 11.16

Query image:

Retrieved results by the SIFT algorithm:

Retrieved results by the F-HS model:

Retrieved results by the FP-HS model:

Retrieved results by our hybrid approach:

Figure 3: Comparison of the top three retrieved images em-

ploying the SIFT, the F-HS, the FP-HS, and the hybrid ap-

proach to solve the image NDR task.

4.4 Result of Zoomed-in Retrieval

Zoomed-in images retrieval is a part of image NDR

when the zoomed-in image covers the most relevant

details in the whole scene. If the zoomed-in image

covers only a very small part of the whole scene and

differs in resolution, then the justiﬁcation of zoomed-

in / whole scene relation is challenging even for the

human visual system. Therefore, in this work, we dis-

cuss the case of ZIR separately. We use the Oxford

buildings dataset to compare the performance of the

F-HS, the SIFT, the FP-HS, and the hybrid approach.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

246

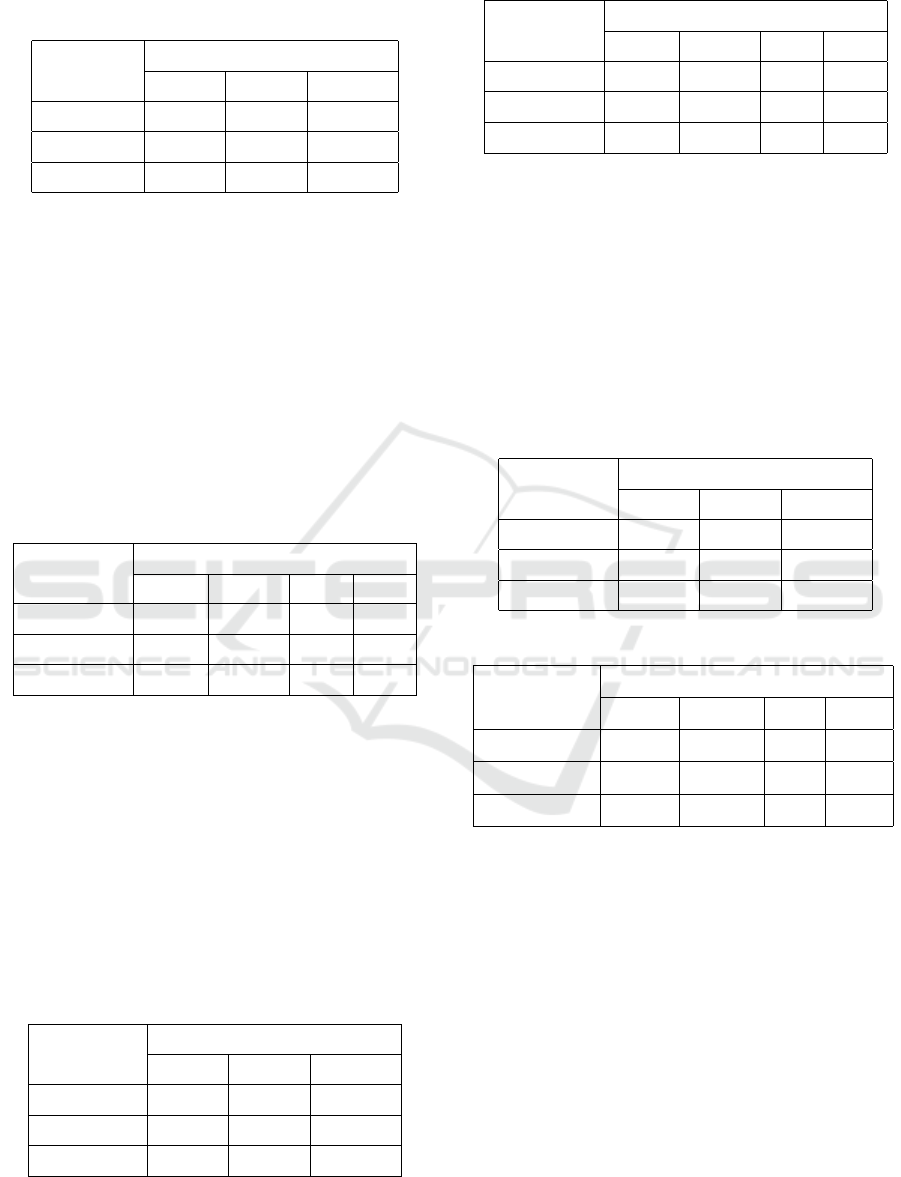
Table 10: MR values for various zoomed-image datasets to

solve the ZIR task. The results are computed concerning

the top 1, 5, and 50 results.

Oxford- F-HS

Zoomed-in MR1% MR5% MR50%

50% 77.63 83.86 95.41

25% 49.17 57.13 78.49

10% 29.93 36.79 59.63

4.4.1 Zoomed-in Retrieval using F-HS

Tables 10, 11 explain that the best performance of

the F-HS model is achieved for the Oxford-Zoomed-

in-50. When zoomed-in images cover only 10% of

whole scenes, the MR and the MAP of the F-HS

model decrease very strongly since the color distri-

bution in zoomed-in images differs dramatically from

whole scenes. We do not present the MAP for the

ﬁrst result since it is equal to the MR. The best VR is

obtained for the Oxford-Zoomed-in-50.

Table 11: The MAP and VR of the F-HS model for the top

5 and 50 results.

Oxford- F-HS

Zoomed-in MAP5 MAP50 VR5 VR50

50% 70.93 72.64 11.41 12.41

25% 37.25 39.35 11.83 13.21

10% 19.58 21.46 14.64 15.21

4.4.2 Zoomed-in Retrieval using FP-HS

We present the performance only for (P = 9) since

the utilizing of nine sub-images outperforms the us-

ing of only three sub-images. Tables 10 and 12 show

that the FP-HS model obtains MR 3%, 14%, and 23%

better than the F-HS model for Oxford-Zoomed-in-

50, Oxford-Zoomed-in-25, and Oxford-Zoomed-in-

10 respectively. As described in 12 and 13, the best

MR and MAP are obtained for the Oxford-Zoomed-

in-50 dataset. The VR is small for all query datasets.

Table 12: MR of the FP-HS model to solve ZIR task.

Oxford- F-HS

Zoomed-in- MR1% MR5% MR50%

50% 79.10 85.40 96.20

25% 63.48 73.77 92.02

10% 53.10 61.44 82.39

Table 13: The MAP and VR of the FP-HS model.

Oxford- F-HS

Zoomed-in MAP5 MAP50 VR5 VR50

50% 66.39 66.98 16.92 3.65

25% 48.52 50.84 23.94 7.33

10% 39.80 41.99 25.81 14.50

4.4.3 Re-rank FP-HS Result

To improve the ZIR, we re-rank the top 100 results

utilizing their SIFT features. Table 14 presents that

our hybrid approach improves the MR even when the

zoomed-in image covers a small part (i.e. 10%) of

the whole scene. Moreover, it improves the VR of

re-ranked results (see Table 15). The MAP for our

approach is about the same for the top ﬁve and ten

results.

Table 14: The MR results of the hybrid approach.

Oxford- F-HS

Zoomed-in- MR1% MR5% MR10%

50% 95.92 96.24 96.24

25% 91.56 92.07 92.07

10% 79.66 81.55 82.06

Table 15: The MAP and VR of the hybrid approach.

Oxford- F-HS

Zoomed-in MAP5 MAP50 VR5 VR50

50% 96.08 96.08 3.91 3.61

25% 91.80 91.80 7.29 7.02

10% 80.48 80.55 16.20 15.04

5 CONCLUSIONS

In this work, we introduced a method to accelerate the

extraction and matching of features to improve image

NDR and ZIR. To accelerate the extraction of fea-

tures and reduce the usage of memory, we proposed

the F-HS and FP-HS models. The purpose of these

models is to construct the fuzzy 2D hue and satura-

tion histogram of an image. To enhance the perfor-

mance of the FP-HS model, we re-rank the top N re-

trieved results utilizing their SIFT features. Hence,

we avoid the comparison of SIFT features with the

whole dataset images. The results indicated that the

hybrid method has a better performance than applying

the SIFT algorithm or the FP-HS model individually.

Hybrid Fuzzy Binning for Near-duplicate Image Retrieval: Combining Fuzzy Histograms and SIFT Keypoints

247

REFERENCES

Alyosef, A. A. and N

urnberger, A. (2016). Adapted sift

descriptor for improved near duplicate retrieval. In

Proc. ICPRAM, pp. 55-64.

Alyosef, A. A. and N

urnberger, A. (2017a). The effect

of sift features properties in descriptors matching for

near-duplicate retrieval tasks. In ICPRAM.

Alyosef, A. A. and N

urnberger, A. (2017b). Near-duplicate

retrieval: A benchmark study of modiﬁed sift descrip-

tors. In Springer, pp. 121-138.

Alyosef, A. A. and N

urnberger, A. (2019). Detecting sub-

image replicas: Retrieval and localization of zoomed-

in images. In CAIP.

Auclair, A., Vincent, N., and Cohen, L. D. (2009). Hash

functions for near duplicate image retrieval. In WACV.

Bosch, A., Zisserman, A., and oz, X. M. (2008). Scene

classiﬁcation using a hybrid generative/discriminative

approach. In Trans. PAMI.

Chu, L., Jiang, S., Wang, S., Zhang, Y., and Huang, Q.

(2013). Robust spatial consistency graph model for

partial duplicate image retrieval. In IEEE Trans. on

Multimedia, pp. 1982-1996.

Chum, O., Philbin, J., Isard, M., and Zisserman, A. (2007).

Scalable near identical image and shot detection. In

Proc. CIVR, pp. 549-556.

Grauman, K. and Darrell, T. (2007). The pyramid match

kernel: Efﬁcient learning with sets of features. In

Journal of Machine Learning Research.

Han, J. and Ma, K. K. (2002). Fuzzy color histogram and

its use in color image retrieval. In IEEE TRANS. ON

IMAGE PROCESSING.

Jiang, M., Zhang, S., Li, H., and Metaxas, D. N. (2015).

Computer-aided diagnosis of mammographic masses

using scalable image retrieval. In IEEE Trans.

Biomedical Engineering.

Ke, Y. and Sukthankar, R. (2004). Pca-sift: A more dis-

tinctive representation for local image descriptors. In

CVPR, pp. 506-513.

Khan, N., McCane, B., and Wyvill, G. (2011). Sift and surf

performance evaluation against various image defor-

mations on benchmark dataset. In DICTA, pp. 501-

506.

Li, J., Qian, X., Li, Q., Zhao, Y., Wang, L., and Tang,

Y. Y. (2014). Mining near duplicate image groups.

In Springer, pp. 655-669.

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. In Computer Vision.

Nist

er, D. and Stew

enius, H. (2006). Scalable recognition

with a vocabulary tree. In Conf. CVPR.

P. Marin-Reyes, J. Lorenzo-Navarro, M. C. S. (2016). Com-

parative study of histogram distance measures for re-

identiﬁcation. In CoRR.

Philbin, J., Chum, O., Isard, M., Sivic, J., and Zisserman, A.

(2007). Object retrieval with large vocabularies and

fast spatial matching. In IEEE Conf. on CVPR.

van de Sande, K., Gevers, T., and Snoek, C. (2010). Eval-

uating color descriptors for object and scene recogni-

tion. In IEEE Trans. on PAMI.

Xu, D., Cham, T., Yan, S., Duan, L., and Chang, S. (2010).

Near duplicate identiﬁcation with spatially aligned

pyramid matching. In IEEE Trans. Circuits and Sys-

tems for Video Technology.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

248