Classification of Visual Strategies in Physics Vector Field Problem-solving
Saleh Mozaffari
1,2,3
, Mohammad Al-Naser
1,2
, Pascal Klein
1,2
, Stefan K
¨
uchemann
1
, Jochen Kuhn
1
,
Thomas Widmann
3
and Andreas Dengel
1,2
1
Technische Universit
¨
at Kaiserslautern, Kaiserslautern, Germany
2
German Research Center for Artificial Intelligence (DFKI GmbH), Kaiserslautern, Germany
3
WidasConcepts GmbH, Wimsheim, Germany
Keywords:
Eye Tracking, Classification, Physics, Education.
Abstract:
In this study, we taught 20 physics students two different visual strategies to graphically interpret the physical
meaning of vector field divergence. Using eye-tracking technology, we recorded students’ eye-movement
behavior of both strategies when they were engaged in graphical vector field representations. From the eye-
tracking data we extracted the number of fixations and saccadic direction and proposed a linear SVM model
to classify strategies of problem-solving in the vector field domain. The results show different gaze patterns
for the two strategies, and the influence of vector flow orientation on gaze-patterns. A high accuracy of
81.2%(0.11%) has been achieved by testing the algorithm using cross-validation, i.e. that the algorithm is
able to predict the strategy the student applies to judge the divergence of a vector field. The results provide
guiding tools for learning-effective instruction design and teachers gain benefit from monitoring the students’
non-verbal level of performance and fluency using each strategy. Apart from that, students would receive the
objective feedback on their progress of learning.
1 INTRODUCTION
Learning of fundamental science such as physics is
crucial to develop the students’ skills which is con-
sidered as an important gateway to their future em-
ployment and life opportunities. Education aims to
provide an effective system to enhance the quality of
learning. Such system needs to investigate how the
students explore, perceive, process, and interpret a
different kind of information. In the physics educa-
tion, the visual system plays the most important role
to explore and capture the information from different
sort of representations. Many problems in upper di-
vision physics and other scientific disciplines require
students to relate abstract concepts to multiple ex-
ternal representations (MERS), including diagrams,
equations, graphics or data tables. From an educa-
tional perspective, it is well known that multiple rep-
resentations of abstract concepts have the potential to
substantially promote learning (Meltzer, 2005). How-
ever, the acquisition of this skill requires instructional
support, especially when concepts become more so-
phisticated. In this context, a great deal of uncertainty
rises when the eyes scan the representations for visu-
ally informative clues. This fact roots in the individ-
ual differences, education background, ethnicity, cul-
ture, environment, and many other factors. Moreover,
in many physics concepts, the myriad ways of visual
strategies are available for interacting with the differ-
ent types of representations(Mozaffari et al., 2016a;
Mozaffari et al., 2016b; Mozaffari et al., 2018a).
However, some physics domains have distinct visual
strategy rules. One example which has recently been
studied consists of the visual interpretation of two-
dimensional vector field plots with respect to diver-
gence (Maries and Singh, 2013; Bollen et al., 2016;
Ishimaru et al., 2016; Klein et al., 2018; Klein et al.,
2019).
When students are instructed with multiple rep-
resentations, eye tracking offers unique possibilities
to track the students’ processing of text, equations,
diagrams, etc. it gives the opportunity to analyze
and computationally model the eye-gaze data in order
to objectively evaluate the students visually cognitive
performance. This objective evaluation helps to im-
prove the quality of learning in that particular physics
domain. The educators could assess the students’
non-verbal cognitive performance and on another
hand, the students benefit from the feedback on their
gaze-driven approach. Despite the vast attention paid
Mozaffari, S., Al-Naser, M., Klein, P., Küchemann, S., Kuhn, J., Widmann, T. and Dengel, A.
Classification of Visual Strategies in Physics Vector Field Problem-solving.
DOI: 10.5220/0009173902570267
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 257-267
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
257

Figure 1: Vector field plot representations used in this study.
eye-tracking research community to the data analy-
sis, fewer studies address the classification of eye-
movements patterns in education (Holmqvist et al.,
2011). Thus, the modeling of the strategic-based eye
movement behavior sounds promising to increase the
learning quality in the physics domain. This research
investigated student’s visual understanding of vector
field plots, which are an important tool for learning
theoretical physics and which occur in the introduc-
tory and upper-division university physics curricula.
Prior research has shown that most students and even
graduates fail to connect the concept of divergence to
graphical vector field representations (Pepper et al.,
2012; Bollen et al., 2016). Basically, there are two
equivalent but yet different approaches to this prob-
lem, requiring different visual strategies; integral and
differential approaches. The contribution of this pa-
per is two-fold: Firstly, it explores and investigates
the context-related eye-tracking features. Secondly,
presents and evaluates a supervised model of the two
approaches upon the derived features. Before present-
ing the methodology and the data collection phase, the
brief explanation of eye-tracking basics and the sub-
ject content are provided. They are required to under-
stand the underlying methodological approach.
1.1 Eye-tracking
Eye-tracking is a non-intrusive method to obtain in-
formation about visual attention and cognitive pro-
cessing. The most often used eye-tracking features
are derived from fixations (relatively long periods,
usually lasting between 100 and 600 ms, in which
the eye is almost still) and saccades (very fast eye
shifts between fixations, lasting less than 100 ms):
Fixation duration, number of fixations, and saccade
length. According to the theory of long-term working
memory, the information-reduction hypothesis, and
the holistic model of image perception, these three
measures are associated with information processing,
selective attention allocation, and visual span, respec-
tively (Gegenfurtner et al., 2011). Even though these
measures are fundamental to general eye-tracking
methodology, they are not enough to evaluate spatio-
temporal gaze patterns. In the Methodology section,
the more sophisticated eye-tracking features are intro-
duced.
1.2 Subject Background
In simplified cases that we consider in this study, stu-
dents must decide whether vector fields have zero or
non-zero divergence. The vector fields used in this
study are displayed in Fig. 2. This task is challenging
even for graduate students (Maries and Singh, 2013)
and requires the interpretation of the mathematical
definition and its application to the vector field. To
judge whether a vector field has zero or non-zero di-
vergence, one of the following two conditions can be
used. The differential strategy (DS):
div
~
F =
∂F
x
∂x
+
∂F
y
∂y
(1)
Or the integral strategy (IS):
div
~
F = lim
V →0
1
V
Z
∂V
~
F · d~n. (2)
Application of Eq. 1 to a graphical vector field
plot means that one must inspect the change of the x-
component of the field in the x-direction and change
of the y-component in y-direction (see Fig. 2 cen-
ter). Vividly speaking, we must perform horizontal
and vertical eye movements to judge the change of
the vector field in horizontal and vertical directions,
respectively, making this visual task perfectly suitable
for eye-tracking methodology.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
258

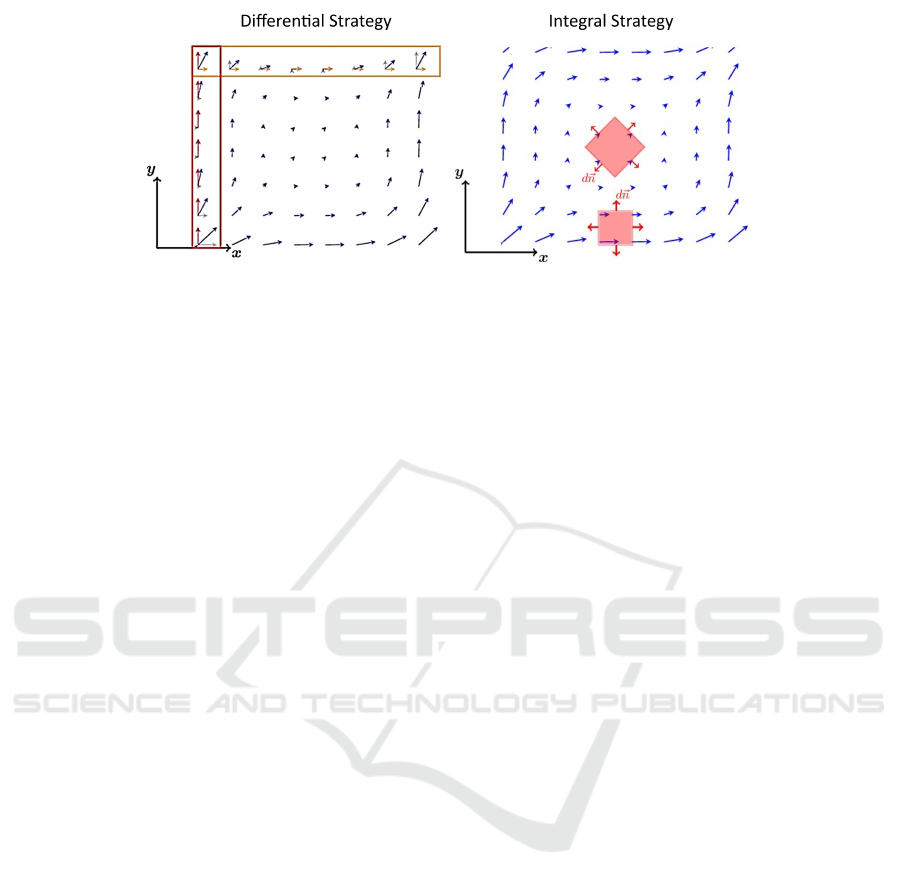
Figure 2: Graphical representation of a two-dimensional vector field. The left panels displays the procedure of the differential
strategy. To judge whether y-component of the vector field (red arrows) changes in y-direction the students need to focus
on the red box. Similarly, in order to judge whether x-component of the vector field (yellow arrows) changes in x-direction
the students only need to focus on the yellow box. Combining both information, the students are able to conclude on the
divergence of the vector field. The right panel shows the procedure of the integral strategy. To determine the divergence, the
students need to quantify the arrows entering and exiting certain areas (here red squares).
In contrast, application of Eq. 1 to a graphical vector
field plot means that we determine the divergence us-
ing the flux through the boundary ∂V of a test volume
V in the field (or test areas in the two-dimensional
case), see Fig.2 right. For instance, qualitative reason-
ing is simple if the outer surface normal d~n is either
parallel or perpendicular to the field vector
~
F (e.g.,
cuboids or spheres in 3D and rectangles or circles
in 2D). When students use this strategy, we expect
a higher number of fixations, longer fixation duration
and shorter saccade lengths as compared to the appli-
cation of Eq. 1 to the field(Klein et al., 2018).
2 METHODOLOGY
This section provides the underlying methodology
used in this paper. First, the preprocessing step is
introduced. Second, the approach to investigate the
implication of vector field orientation is presented.
Then, the feature extraction procedure followed by
the classification approach has been presented.
2.1 Preprocessing
We proposed an approach to cluster the distributed
gaze-driven sequences in the vector field plot. The
saccadic codification and transition matrix calculation
are also explained.
2.1.1 Attentive Region Clustering
It is inevitable having noise and outliers in an eye-
tracking experiment. Besides, depending on an exper-
iment design, not all of the collected gaze patterns are
relevant to the research. For instance, in this study,
we ignored the fixations outside of the desired Area
of Interest (AOI), which is the area of the vector field
(see Fig. 1). Furthermore, in particular, this algorithm
tends to find attentive region(s) in the vector fields 1—
8 for both DS and IS. The inattentive regions could
bias the dispersion-based features. Hence, we pro-
pose a novel approach, here termed Attentive Region
Clustering Algorithm (ARCA), to cluster the attentive
region(s) inside the vector field. The Attentive Region
Clustering Algorithm is presented in Algorithm 1.
Identifying the visual strategies instructed in this
study, the ARCA (Algorithm 1) provides the fixations
during problem-solving whereas inattentive fixations
are mostly scattered broadly inside the vector repre-
sentation. Using the filtered fixations, in the next sec-
tion, we propose a similarity measure to evaluate di-
vergence of the vector field representations.
2.1.2 Saccadic Codifications
The visual strategies indicated in Fig. 2 offer either
axis-wise evaluation in the differential problem or ob-
serving the vector flow through an arbitrary rectangle
inside the vector field. Hence, eye movement direc-
tions during the problem-solving task reveal the qual-
ity of visual approaches made by the students based
on the instructions. Selection of the axis side left or
right, and up or down is optional to solve differen-
tial (DS) problems. It is somehow similar to integral
(IS) tasks’ visual strategy where the position of the
rectangle with any rotation inside the vector field rep-
resentation is flexible. Hence, we group the saccades
into X for the x-axis, Y for the y-axis, M for diagonal,
and N for anti-diagonal directions. To group saccades
into X, Y, M, and N, the absolute saccadic angular-
ity is used for the labeling. In this sense, all saccades
within in the angular range of 337.5
◦
−22.5
◦
com-
Classification of Visual Strategies in Physics Vector Field Problem-solving
259

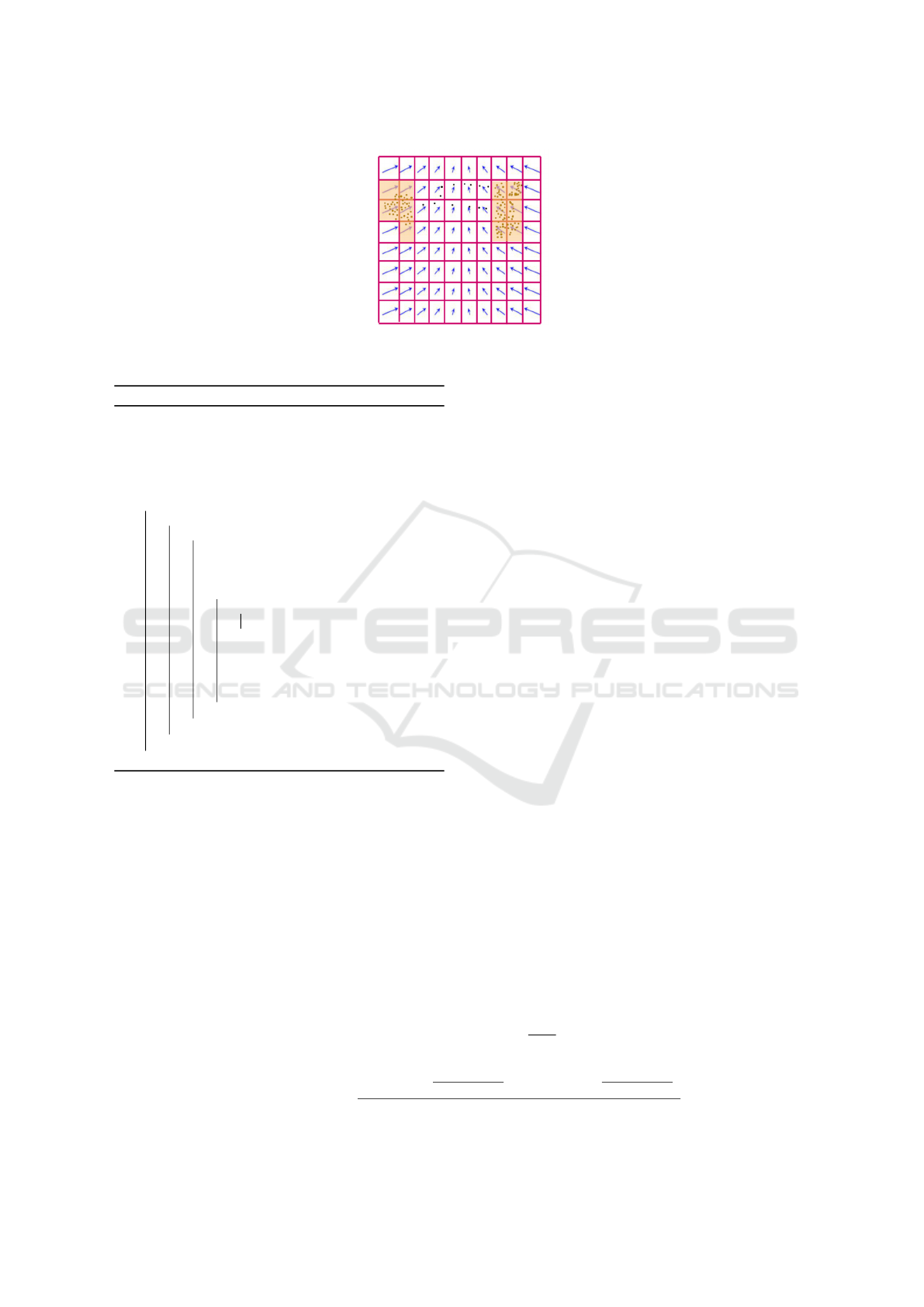
Figure 3: Illustration of the identification of tiles (yellow) which are regions within the 10 × 10 grid which received more
fixations (black dots) then the threshold (here 3 fixations).
Algorithm 1: Attentive Region Clustering.
Result: Write here the result
calculate f ixations from raw gaze samples ;
define AOI in the stimuli as the representative region
for the vector field area;
omit the fixations out of the AOI box;
threshold = 3 fixations;
for strategies : (DS, IS) do
for participants : [1 : 20] do
for stimulus : [V 1 : V 8] do
M = split AOI into 10x10 grid;
create attention map: calculate the
fixation population on M tiles;
for tile : M[1 : 10,1 : 10] do
if |tile| < threshold then
discard tile;
end
label-connected tiles: finding
islands in M;
intersect fixations of AOI area with
M;
end
end
end
end
bined with those from 157.5
◦
− 202.5
◦
are labeled as
X, the ones from 22.5
◦
− 67.5
◦
combined with those
from 202.5
◦
−247.5
◦
are labeled as M, the ones from
67.5
◦
− 112.5
◦
combined with those from 253.5
◦
−
297.5
◦
are labeled as Y and the ones from 22.5
◦
−
67.5
◦
combined with those from 202.5
◦
− 247.5
◦
are
labeled as N.
2.1.3 Calculate Transition Matrix
The sequence of saccades constructs a string for each
trial. The elements of the string are associated with
the corresponding saccadic labels. Consequently, 320
sequences from 320 trials were constructed. These
sequences are fundamental to calculate the transition
matrices. The transition matrices are used for transi-
tional analysis, feature extraction, and classification.
A transition matrix is 4 × 4 2-D array as an alter-
native representation of the corresponding sequence.
For instance, Table 1 presents an exemplary transition
matrix for the sequence ”XXXMYYYNYX”.
2.2 Implication Vector Field
Orientation
Vector field flows in the different directions as in-
dicated in Fig. 1. As explained in section 2.1.2,
because of the freedom of choice in direction and
area in both visual strategies, it raises question about
the impact of vector flow on students decision about
the area and processing direction. Due to the men-
tioned freedom, the higher level of uncertainty is ex-
pected. As a measure of uncertainty, we investi-
gated Jensen-Shannon divergence(JSD) in the tran-
sition matrices. JSD is an Shannon Entropy-based
method to measure the similarity between two prob-
ability distributions (Holmqvist et al., 2011). It
is an extended version of Kullback-Leibler diver-
gence(KLD). As KLD fails to fulfill the triangle in-
equality which leads to asymmetric results, we pre-
ferred to apply the JSD (Holmqvist et al., 2011) for
our purpose. The JSD results range in [0..1] intervals
where the higher value indicates the larger the diver-
gence. The Kullback-Leibler divergence and Jensen-
Shannon divergence are defined as following:
KLD(p||q) =
∑
X
p(x)log
2
(
p(x)
q(x)
) (3)
JSD(p(x)||q(x) =
KLD(p(x)||
p(x) + q(x)
2
) + KLD(q(x)||
p(x) + q(x)
2
)
2
(4)
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
260

Table 1: An exemplary transition matrix for the sequence ”XXXMYYYNYX”. For example, X −→ X transition two times
happened in the beginning of the sequence.
X Y M N
X 2 0 1 0
Y 1 2 0 1
M 0 1 0 0
N 0 1 0 0
Input data—p(x) and q(x)—have the form of
probability density functions, i. e., the normalized
transition matrices.
Separated for both IS and DS strategies, for all
we calculated the normalized transition matrix of each
participant. Then for each group (IS and DS), the JSD
similarity measure applied.
2.3 Feature Extraction
Appropriate feature selection is a highly important
stage to construct a robust machine learning model.
Both dispersion-based and sequential-based features
are necessary to build a robust model for classification
of the visual strategies defined in section 1.2. In this
study, we calculated the following features for each
trial (N = 320) to build up our model:
2.3.1 Stationary Entropy (H
s
)
Entropy is a measure in information theory to describe
the information in a variable in terms of ordering.
This measure is called Shannon entropy and it is de-
fined as:
H
s
= −
∑
i
p(r
i
)log
2
(r
i
),r
i
> 0 (5)
where H
s
is the stationary entropy in bits and p(r
i
) is
the proportion of saccadic label r
i
. r
i
replaced with
1e−9 in case r
i
= 0. We normalized the stationary
entropy by dividing the result with the maximum pos-
sible entropy. In our case, four labels construct the se-
quence. Therefore,
∑
4
i=1
1
4
log
2
(
1
4
) = 2.0, is the max-
imum possible bits. Hence, all stationary entropy re-
sults divided by 2.0.
2.3.2 Transition Entropy (H
t
)
The entropy can be calculated for a transition ma-
trix (Mozaffari et al., 2016b; Krejtz et al., 2014). The
lowest possible value is zero when there is no uncer-
tainty about what type of transition will occur. The
maximum value for entropy is when all the cells in
the transition matrix carry different values.
H
t
= −
∑
i, j
p(r
i
)
∑
p
i j
log
2
(p
i j
),r
i
&p
i j
> 0 (6)
r
i
and p
i j
replaced with 1e−9 in case of 0.
where H
t
is the transition entropy, p(r
i
) is the pro-
portion of saccadic label r
i
, and p
i j
is the value of
normalized transition matrix in row i and column j.
2.3.3 Relative Saccade Angularity (A
r
)
The average of relative saccade angles shows the ten-
dency of the students to drive their visual attention to
the same direction. Relative saccade angularity is de-
fined as the angle between a saccade and the previous
saccade
1
.
2.3.4 Fixation Duration (F
d
)
Fixation duration (Holmqvist et al., 2011) is a classi-
cal metric in eye-tracking research. It is a dispersion-
based measure indicating the density of visual atten-
tion.
2.3.5 Attention Score (F
s
)
We calculate the attention score(F
s
) by dividing the
number of fixations in the attentive region calculated
with ARCA by all the fixations in the AOI. This mea-
sure approximates the focus on the instructed strategy.
2.3.6 Direction Rank Entropy (H
d
)
In section 2.2, the freedom of selecting areas and di-
rections in the vector field representation has already
been explained. However, tracing one direction, e. g.
moving the visual attention simply up and down yield
the same saccadic code (Y). Discriminating IS and DS
visual strategies requires information about opposite
direction movements. The procedure to calculate H
d
is the following:
1. In each sequence, directions to the left, down,
down-left, and down-right weighted with −1 and
the rest with +1. For instance, label X in the left
directions becomes -X and +X Vice versa.
2. Then we add all the labels and get the absolute
weight for each label. For example, -2X, -4Y, and
2M yields [2, 4, 2, 0].
1
Absolute saccade angularity defines as the angle be-
tween the saccade and horizon
Classification of Visual Strategies in Physics Vector Field Problem-solving
261

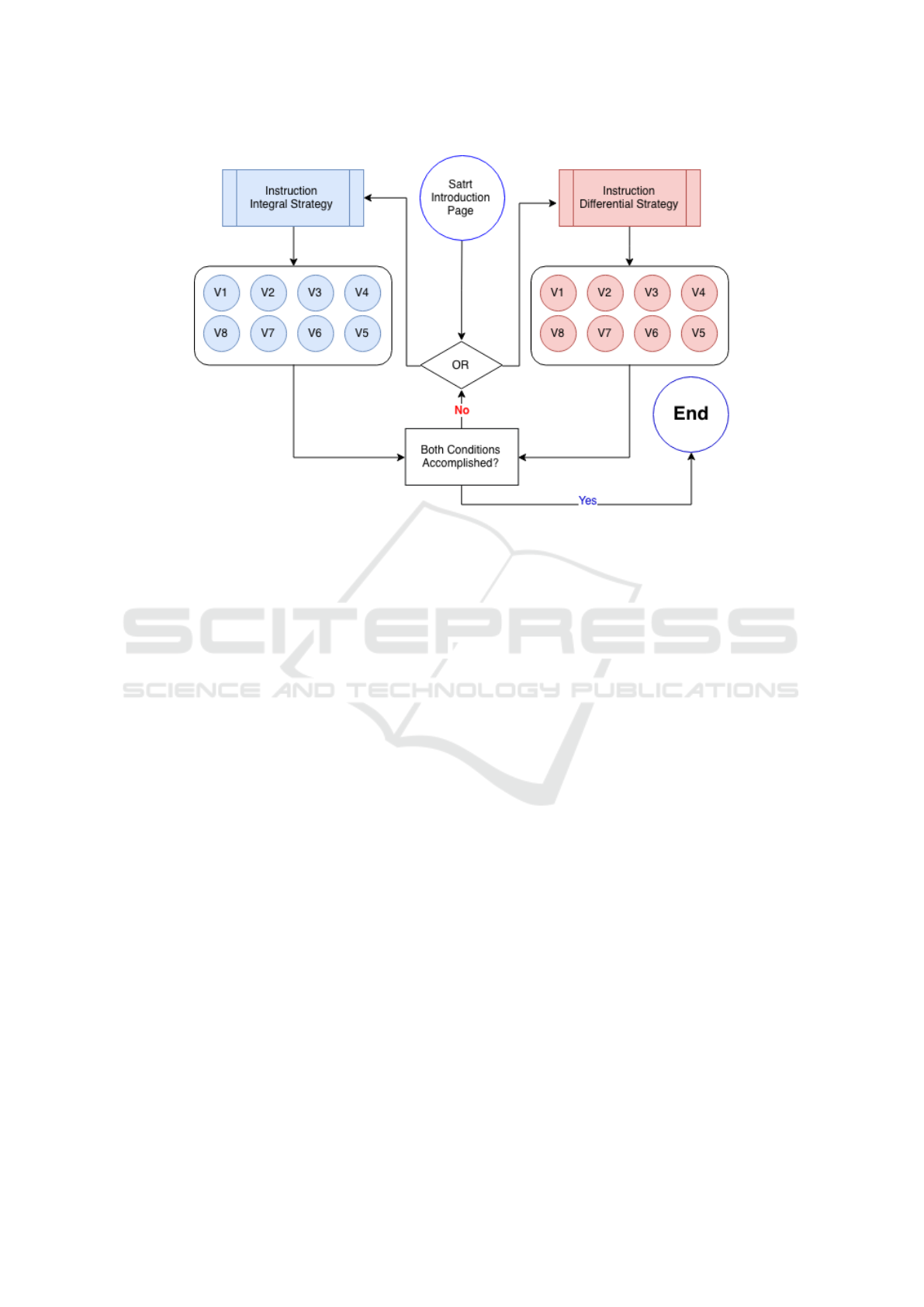
Figure 4: The procedure of the experiment. The students started with an introduction about the concept of Vector Divergence
Problem displayed on a computer screen. Then, students started with the DS strategy (see Fig. 2 left panel) or with the IS
strategy (see Fig. 2 right panel). Both instructions, DS and IS, covered 250 words and included a step-by-step description
with visual cues about the application. In each instruction period, students applied the prevailing strategy to eight vector fields
(V1—V8) 1 which were presented one after another.
3. Divide the weighted vector with the length of the
sequence.
4. Normalize the weighted vector with the l1 norm.
5. Replace zero values with 1e−9.
6. Calculate entropy of the weighted vector using
Eq. 5.
2.3.7 Attentive Cluster Numbers (C
r
)
The attentive region acquired by ARCA could distin-
guish the visual strategies. To elaborate more, stu-
dents may like to assume multiple rectangles in the
vector field area to solve the integral problem. There-
fore, in the IS, the number of attentive regions is rel-
atively higher (mean = 2.65, std = 0.36) compared to
the axis-based strategy for DS (mean = 1.71,std =
0.23).
2.4 Classification
In order to classify two visual strategies in the VFD
domain (IS and DS), in this stage of the research,
the Support Vector Machine (SVM) was employed to
build up the binary classifier. Using 10-fold cross val-
idation, 65% of data was selected randomly for train-
ing and the rest was used for testing. Also, the best-
tuned parameters (C, γ, and kernel) were selected by
performing grid search accompanied with the cross-
validation. The model trained with the feature vector
presented in section 2.3. Investigating other machine
learning models left for the future work.
3 DATA COLLECTION
This section demonstrates the data collection phase.
The participants, the study design, as well as the ex-
periment’s procedure, are presented here.
3.1 Participants
Twenty major physics students of the University of
ANONYMOUS (15 male, 5 female) aged 19–24 (av-
erage 20.6 years) took part in the experiment. All
participants were about to attend an introductory elec-
tromagnetism course and had successfully completed
two mechanics lectures (calculus-based mechanics
and experimental physics). Divergence has been in-
troduced in both mechanics lectures and has also been
recapitulated in the electromagnetism course before
the experiment was conducted. Participation was vol-
untary, took 30 min in total (survey and experiment),
and was compensated with 10$.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
262

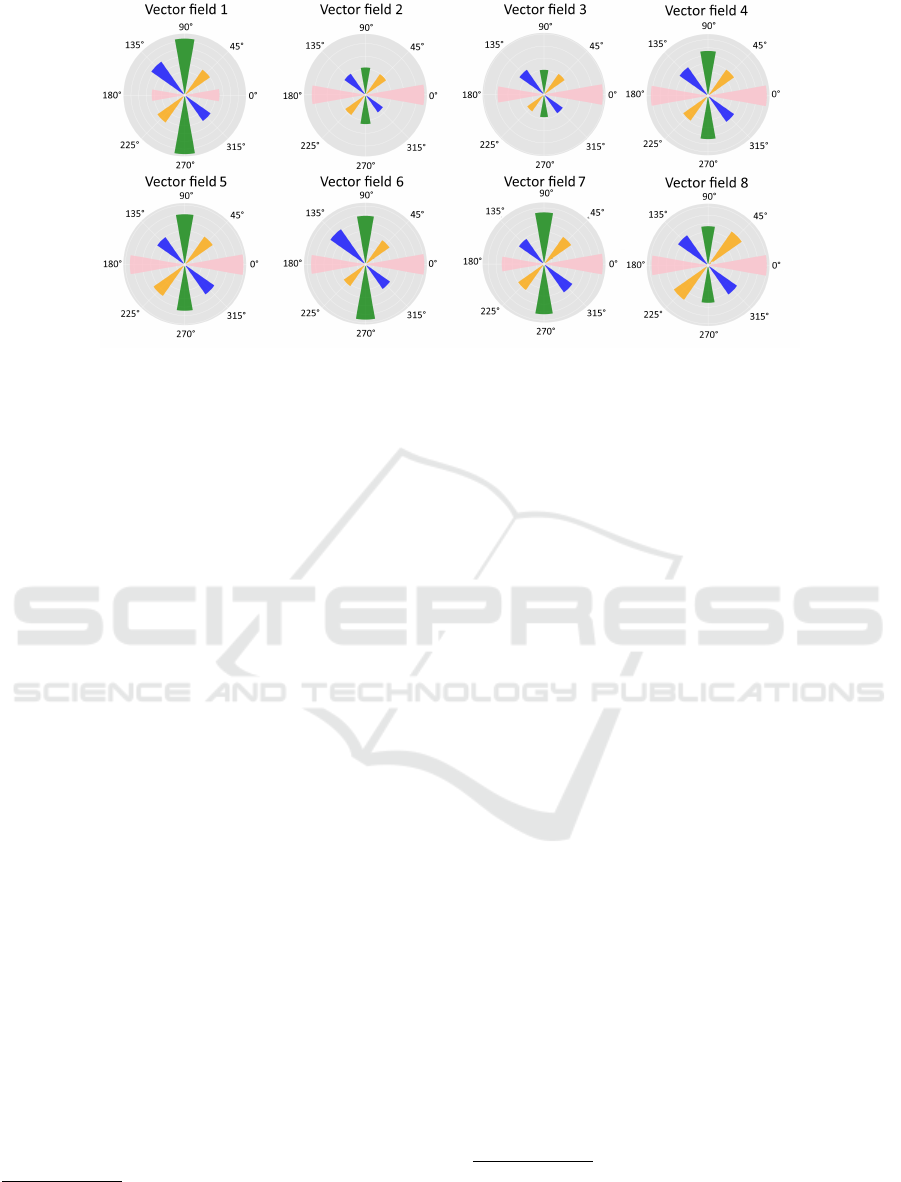
Figure 5: The saccadic direction when students applying the IS to judge whether a vector field has zero or non-zero divergence.
The colors indicate the angular interval labeled with X (light red) indicating horizontal saccades, Y (green) meaning vertical
saccades, M (yellow) diagonal saccades and N (blue) anti-diagonal saccades. Exploring diagonally and anti-diagonally is
more evident in this approach compared to DS.
3.2 Study Design and Material
The students started with an introduction to the con-
cept of vector field divergence displayed on a com-
puter screen. The sequence of the experiment is il-
lustrated in Fig. 4. All students started with strat-
egy 1 (Figure. 2 left); the derivative strategy, DS) or
strategy 2 (Figure. 2 right; the integral strategy, IS).
Both instructions, DS and IS; covered 250 words (1
textbook page), respectively, and included a step-by-
step description with visual cues about the applica-
tion (worked-out example). In each instruction pe-
riod, students applied the prevailing strategy to eight
vector fields shown in Fig. 1 which were presented
one after another. The vector fields used in the study
are presented in Fig. 1. Students did not receive any
feedback after completing a VDP and were unable to
revisit the instruction page.
3.3 Eye-tracking Procedures
We obtained gaze data for all twenty students using a
Tobii X3-120
2
eye-tracker installed on a 24” LCD
screen with an aspect ratio of 16:9 as they worked
with the VDP. All students had normal or correct-
to-normal vision. The device has an accuracy of 0.4
degrees
3
and allows a relatively high freedom of head
movement. The sampling frequency was 120 Hz.
Gaze recording was accomplished using the Tobii Pro
2
https://www.tobiipro.com/product-listing/tobii-pro-x3-
120/
3
reported by the manufacturer
Studio
4
. The eye-tracking measures, including fix-
ations and saccades, are calculated with the anony-
mous
5
library written in Python.
4 RESULTS
4.0.1 Vector Orientation Implication
Fig. 5 and 6 show the saccadic directions preferred
by students in integral and differential approaches, re-
spectively. The axis-wise tendency is more evident in
the DS. However, horizontal or vertical movements
are varied in different movements. The similarity
measure based on Jensen-Shannon divergence for the
vector flows is presented in Figure 7. For the purpose
of the significant test, we added pairwise results of
within JSD similarity measure in a dedicated array for
each vector of DS and IS. The results suggest in some
vector field—but not all— that there is a tendency to
choose various options of selecting the area or sac-
cadic direction. This could be interpreted as dynami-
cally fitting the strategy to the vector flows in order to
get the right answer. For the purpose of the significant
test, we added pairwise results of within JSD similar-
ity measure in a dedicated array for each vector of DS
and IS. The one-way ANOVA significant test shows
the significant differences between some vector fields
as shown in Tab. 2.
4
https://www.tobiipro.com/product-listing/tobii-pro-
studio/
5
Due to the blind review will be added for the camera-
ready version
Classification of Visual Strategies in Physics Vector Field Problem-solving
263

Figure 6: The saccadic direction when students applying the DS to judge whether a vector field has zero or non-zero diver-
gence. The colors indicate the angular interval labeled with X (light red) indicating horizontal saccades, Y (green) mean-
ing vertical saccades, M (yellow) diagonal saccades and N (blue) anti-diagonal saccades. Horizontal (X) and vertical eye-
movements are more pronounced in this approach compared to the IS.
Table 2: Vector fields having significant differences in the one-way ANOVA test with a p-value<0.05 and d f = 189.
Strategy Vector Fields F p-value
DS 2 8 14.64 0.0001
DS 4 5 9.22 0.0025
DS 4 6 8.77 0.0032
DS 5 7 5.84 0.0160
DS 5 8 13.5 0.0002
DS 6 7 5.17 0.0235
DS 6 8 13.35 0.0002
IS 1 4 8.74 0.0033
IS 1 7 5.84 0.02
IS 2 4 8.12 0.004
IS 4 5 56.24 0
IS 6 7 18.96 0.0017
IS 7 8 109.85 0
4.0.2 Classification Results
The best model selected by grid search and cross val-
idation is an SVM with linear kernel, C = 10, and
γ = 0.001 for the vectors presented in section 2.3.
Table 3 indicates the precision and recall of the
model on testing set. An accuracy of 81.2%(0.11%)
has been achieved by the linear SVM model.
Considering on uncertainty in human behavior,
in particular, eye movements, the results of the bi-
nary classification is promising to model experts gaze
pattern in order to evaluate the real-world problem-
solving task in an intelligent e-learning user inter-
face. However, there is several room for improvement
which is discussed in the next section.
5 DISCUSSION AND FUTURE
WORK
Considering the Dreyfus model of skill acquisition
perspective (Benner, 2004; Dreyfus, 2004; Dreyfus
and Dreyfus, 1980), this contribution of this work is
twofold: First, it helps to offer the novice learners by
providing appropriate instruction needed for concep-
tual learning. The awareness of visual behavior of
the students by monitoring of a particular problem-
solving strategy might be highly beneficial for them.
Although not all of the problems in physics are based
on graphical representations such as the divergence of
a vector field plot, it opens the door for an investiga-
tion how to address certain missed instructions. Thus,
the second contribution is from another point of view:
”How to detect non-verbal patterns of the skilled per-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
264

Figure 7: The Jensen-Shannon divergence in vector field representations.
Table 3: The score of the linear SVM model with C = 10 and γ = 0.001.
precision recall f1-score support
DS 0.89 0.70 0.78 59
IS 0.73 0.91 0.81 53
avg / total 0.81 0.81 0.79 112
sons and transfer it heuristically to the novices?”. For-
tunately, with the rising of deep learning in recent
years, those associated visual patterns for solving and
comprehending the related problem can be exploited
and encoded with modern technologies (Kise et al.,
2017). According to these concerns, we start to use
a simple linear model to have proof for the future in-
vestigations of more sophisticated machine-learning
techniques. The classification score provides an indi-
cation of the right path to pursue although there are
some constraints on data in both terms of quality and
quantity. Jenson-Shanon Divergence (JSD) score is
intentionally used in this research because of its appli-
cation to design an autoencoder for learning transfer.
An autoencoder is an unsupervised type of artificial
neural network used to learn efficient data codings.
To have an efficient representation of data, the aim of
autoencoders is to minimize the degree of uncertainty
e.g., JSD. Hence, to give a picture for further research,
the one-way ANOVA test is performed to statistically
check the significance of the difference between the
JSD score means of two independent groups, which
are DS and IS. The classification results are promis-
ing to develop gaze-based pattern classification mod-
els. In this study, we trained linear SVM model for
our purpose. However, other machine learning tech-
niques can be investigated. For instance, Recurrent
Neural Networks are highly suitable for sequential-
based gaze data. The problem of deep networks is
to have an adequate training set. Such an amount of
data is very cumbersome to collect in the eye-tracking
studies. Considering the rising interest in using gen-
erative models, the main idea of future work is to cre-
ate a generative model from recorded data. Synthetic
domain-specific eye movement data then can be used
and evaluated with an appropriate deep network ar-
chitecture (Mozaffari et al., 2018b).
The results also showed the effect of vector flow to
form the strategy. Deeper data analysis in this regard
leads to develop a more generic model in VDP. For
instance, the correlation of the direction of the vec-
tor in the vector field plot with saccadic direction is
worthy to explore. Conducting a none-instruction-
based experiment with the same vector field stimuli
is in our agenda of research. In particular, evaluat-
ing and quantifying the performance of students’ task-
related the gaze behavior (IS and DS) with the model
has been achieved in this study. Furthermore, inves-
tigation of gaze-patterns in reading—reading speed,
regression rate, and reading depth—and find the re-
lations to the comprehensibility of problem-solving
technique is another area of future work. The meth-
ods and ideas used in this research are plausible to
apply in other domains of eye-tracking research. Fi-
nally, the concept idea of this paper connects machine
learning and human-computer interaction (Ishimaru
et al., 2016; Ishimaru et al., 2018) to develop an in-
telligent user interface to advance education in funda-
mental science such as physics and mathematics.
6 CONCLUSION
In this paper, we explored the eye-movement pattern
of 20 students in instruction-based problem solving
for integral and differential approaches in the domain
Classification of Visual Strategies in Physics Vector Field Problem-solving
265

of vector field divergence in physics. The results show
that the flow orientations of the vectors have an in-
fluence on students attention areas in the vector field
representation and on the pursue of different saccadic
directions. Using a 10-fold cross-validation and grid
search parameter we tune the Support Vector Machine
in order to classify the visual strategies (DS and IS),
a linear kernel SVM with C = 10, and γ = 0.001 has
achieved an accuracy of 81.2%(0.11%). This means,
that besides large individual variations in eye-gaze
patterns among students, the algorithm is able to clas-
sify strategic gaze-patterns in a specific problem do-
main. On one hand, the results are helpful for im-
proving the quality of learning and teaching since they
provide a valid and detailed feedback for teachers on
the effectiveness of their instructions to teach a cer-
tain strategy from monitoring the student’s non-verbal
performance. On the other hand, the algorithm may
be used to give students an objective immediate feed-
back on their progress of learning.
ACKNOWLEDGEMENT
This paper was partially supported by DFKI GmbH,
and WidasConcepts GmbH.
REFERENCES
Benner, P. (2004). Using the dreyfus model of skill acqui-
sition to describe and interpret skill acquisition and
clinical judgment in nursing practice and education.
Bulletin of science, technology & society, 24(3):188–
199.
Bollen, L., van Kampen, P., Baily, C., and De Cock, M.
(2016). Qualitative investigation into students’ use of
divergence and curl in electromagnetism. Physical Re-
view Physics Education Research, 12(2):020134.
Dreyfus, S. E. (2004). The five-stage model of adult skill
acquisition. Bulletin of science, technology & society,
24(3):177–181.
Dreyfus, S. E. and Dreyfus, H. L. (1980). A five-stage
model of the mental activities involved in directed
skill acquisition. Technical report, California Univ
Berkeley Operations Research Center.
Gegenfurtner, A., Lehtinen, E., and S
¨
alj
¨
o, R. (2011). Ex-
pertise differences in the comprehension of visualiza-
tions: A meta-analysis of eye-tracking research in pro-
fessional domains. Educational Psychology Review,
23(4):523–552.
Holmqvist, K., Nystr
¨
om, M., Andersson, R., Dewhurst, R.,
Jarodzka, H., and Van de Weijer, J. (2011). Eye track-
ing: A comprehensive guide to methods and measures.
OUP Oxford.
Ishimaru, S., Bukhari, S. S., Heisel, C., Kuhn, J., and
Dengel, A. (2016). Towards an intelligent textbook:
eye gaze based attention extraction on materials for
learning and instruction in physics. In Proceedings
of the 2016 ACM International Joint Conference on
Pervasive and Ubiquitous Computing: Adjunct, pages
1041–1045. ACM.
Ishimaru, S., Großmann, N., Dengel, A., Watanabe, K.,
Arakawa, Y., Heisel, C., Klein, P., and Kuhn, J.
(2018). Hypermind builder: Pervasive user interface
to create intelligent interactive documents. In Pro-
ceedings of the 2018 ACM International Joint Confer-
ence and 2018 International Symposium on Pervasive
and Ubiquitous Computing and Wearable Computers,
pages 357–360. ACM.
Kise, K., Augereau, O., Utsumi, Y., Iwamura, M., Kunze,
K., Ishimaru, S., and Dengel, A. (2017). Quantified
reading and learning for sharing experiences. In Pro-
ceedings of the 2017 ACM International Joint Con-
ference on Pervasive and Ubiquitous Computing and
Proceedings of the 2017 ACM International Sympo-
sium on Wearable Computers, pages 724–731. ACM.
Klein, P., Lichtenberger, A., K
¨
uchemann, S., Becker, S.,
Kekule, M., Viiri, J., Baadte, C., Vaterlaus, A., and
Kuhn, J. (2019). Visual attention while solving the
test of understanding graphs in kinematics: An eye-
tracking analysis. European Journal of Physics.
Klein, P., Viiri, J., Mozaffari, S., Dengel, A., and Kuhn, J.
(2018). Instruction-based clinical eye-tracking study
on the visual interpretation of divergence: How do
students look at vector field plots? Physical Review
Physics Education Research, 14(1):010116.
Krejtz, K., Szmidt, T., Duchowski, A. T., and Krejtz,
I. (2014). Entropy-based statistical analysis of eye
movement transitions. In Proceedings of the Sym-
posium on Eye Tracking Research and Applications,
pages 159–166. ACM.
Maries, A. and Singh, C. (2013). Exploring one aspect
of pedagogical content knowledge of teaching assis-
tants using the test of understanding graphs in kine-
matics. Physical Review Special Topics-Physics Edu-
cation Research, 9(2):020120.
Meltzer, D. E. (2005). Relation between students’ problem-
solving performance and representational format.
American journal of physics, 73(5):463–478.
Mozaffari, S., Klein, P., Al-Naser, M., Bukhari, S. S.,
Kuhn, J., and Dengel, A. (2016a). A study on rep-
resentational competence in physics using mobile eye
tracking systems. In Proceedings of the 18th In-
ternational Conference on Human-Computer Interac-
tion with Mobile Devices and Services Adjunct, pages
1029–1032. ACM.
Mozaffari, S., Klein, P., Bukhari, S. S., Kuhn, J., and Den-
gel, A. (2016b). Entropy based transition analysis
of eye movement on physics representational compe-
tence. In Proceedings of the 2016 ACM International
Joint Conference on Pervasive and Ubiquitous Com-
puting: Adjunct, pages 1027–1034. ACM.
Mozaffari, S., Klein, P., Viiri, J., Ahmed, S., Kuhn, J., and
Dengel, A. (2018a). Evaluating similarity measures
for gaze patterns in the context of representational
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
266

competence in physics education. In Proceedings of
the 2018 ACM Symposium on Eye Tracking Research
& Applications, page 51. ACM.
Mozaffari, S. S., Raue, F., Hassanzadeh, S. D., Agne, S.,
Bukhari, S. S., and Dengel, A. (2018b). Reading type
classification based on generative models and bidirec-
tional long short-term memory.
Pepper, R. E., Chasteen, S. V., Pollock, S. J., and Perkins,
K. K. (2012). Observations on student difficulties with
mathematics in upper-division electricity and mag-
netism. Physical Review Special Topics-Physics Ed-
ucation Research, 8(1):010111.
Classification of Visual Strategies in Physics Vector Field Problem-solving
267