Reinforcement Learning Considering Worst Case and Equality within

Episodes

Toshihiro Matsui

Nagoya Institute of Technology, Gokiso-cho Showa-ku Nagoya 466-8555, Japan

Keywords:

Reinforcement Learning, Path-ﬁnding, Equality, Leximin.

Abstract:

Reinforcement learning has been studied as an unsupervised learning framework. The goal of standard rein-

forcement learning methods is to minimize the total cost or reward for the optimal policy. In several practical

situations, equalization of the cost or reward values within an episode may be required. This class of problems

can be considered multi-objective, where each part of an episode has individual costs or rewards that should

be separately considered. In a previous study this concept was applied to search algorithms for shortest path

problems. We investigate how a similar criterion considering the worst-case and equality of the objectives

can be applied to the Q-learning method. Our experimental results demonstrate the effect and inﬂuence of the

optimization with the criterion.

1 INTRODUCTION

Reinforcement learning has been studied as an un-

supervised learning framework (Sutton and Barto,

1998). The goal of standard reinforcement learning

methods is to minimize the total cost or reward for the

optimal policy. In several practical situations, equal-

ization of the cost or reward values within an episode

might be required. For example, in mobile robot

navigation or adaptive routing in communication net-

works, the equalization of lifetime or peak load of in-

dividual facilities in a paths might be required. This

class of problems can be considered multi-objective,

where each part of an episode has individual costs or

rewards that should be separately considered. Such

episodes relate to situations where a sequence of an

agent’s behavior should be determined so that its risk

or beneﬁt is equalized in the sequence.

As a criterion for multiple objectives, we use lex-

imin, which is deﬁned as a dictionary order on objec-

tive vectors sorted in ascending order. The maximiza-

tion problem with leximin improves the worst-case

cost and equality among objectives. Previvous studies

show that optimization with leximin can be decom-

posed in the manner of dynamic programming (Mat-

sui et al., 2014; Matsui et al., 2015).

This concept has been applied to search algo-

rithms based on dynamic programming for shortest

path problems with similar criterion (Matsui et al.,

2018). Since the problem resembles reinforcement

learning for minimization problems that optimize se-

quences from a start state to a goal state, a similar

technique can be applied to a part of the reinforce-

ment learning.

We investigate how a similar criterion consider-

ing the worst-case and equality of the objectives can

be applied to the Q-learning method. For this goal,

we extend the criterion to meet the weighted average

operation for different lengths of cost/reward vectors

corresponding to episodes, and consider the require-

ments and limitations of the extended Q-learning. Our

experimental results demonstrate the effect and inﬂu-

ence of the optimization with our criterion.

The remainder of this paper is organized as fol-

lows. In the next section, we describe the prelim-

inary aspects of our study including standard rein-

forcement learning, a criterion that considers multi-

ple objectives and a shortest path problem with this

criterion. Then, we propose a reinforcement learning

method with a similar criterion in Section 3. The pro-

posed approach is experimentally evaluated and dis-

cussed in Sections 4 and 5. Finally, we conclude our

study in Section 6.

2 PRELIMINARY

Below, we describe several properties of reinforce-

ment learning, the leximin criterion for multi-

objective problems, and shortest path problems with

Matsui, T.

Reinforcement Learning Considering Worst Case and Equality within Episodes.

DOI: 10.5220/0009178603350342

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 1, pages 335-342

ISBN: 978-989-758-395-7; ISSN: 2184-433X

335

a similar criterion quoting deﬁnitions and properties

from (Matsui et al., 2018).

2.1 Q Learning

Q-learning is a fundamental reinforcement learning

method that optimizes a policy to determine a se-

quence of states and actions in a state transition

model. It consists of set of states S, set of actions

A, observed reward/cost values for actions, evaluation

values Q(s, a) for each pair of state s ∈ S and action

a ∈ A, and parameters for learning. When action a is

performed in state s, it causes a state transition with

a corresponding reward/cost value based on an envi-

ronment whose optimal policy should be mapped to

Q-values. For the minimization problem, standard Q-

learning is represented as follows

Q(s, a) ← (1 − α)Q(s, a) + α(c + γ min

Q(s

, a

)) ,

(1)

where s and a are the current state and action, s

and

are the next state and action, and c is a cost value

for action a in state s. α and γ are the parameters

of the learning and discount rates. With action selec-

tions based on an exploration strategy, Q-values are

iteratively updated and propagated in the manner of

asynchronous dynamic programming.

Online search algorithms, including the Learning

Real-time A* algorithm (Barto et al., 1995), that per-

form asynchronous dynamic programming for short-

est path problems are a base of reinforcement learning

algorithms. The algorithms are also designed to per-

form exploration and exploitation to learn the optimal

shortest path on a graph. Here, an agent repeats tours

from a start vertex to a goal vertex of the graph with

learning and exploration rules.

2.2 Criteria Considering Worst-case

and Equality

Since we focus on a class of multi-objective optimiza-

tion problems, we describe several related concepts

below.

Deﬁnition 1 (Multi-objective optimization problem).

A multi-objective optimization problem is deﬁned with

hX, D, Fi. X is a set of variables, D is a set of domains

of variables, and F is a set of objective functions.

Variable x

∈ X takes value from ﬁnite and discrete set

∈ D. For set of variables X

⊆ X, function f

∈ F

is deﬁned as f

i,1

, · ·· , x

i,k

) : D

i,1

× ··· × D

i,k

→ N,

where x

i,1

, · ·· , x

i,k

∈ X

. f

i,1

, · ·· , x

i,k

) is simply de-

noted by f

). The goal of the problem is to simulta-

neously optimize the objective functions under a cri-

terion.

A combination of the values of the objective func-

tions is represented as an objective vector.

Deﬁnition 2 (Objective vector). Objective vector v

is deﬁned as [v

, · ·· , v

]. For assignment A to the

variables in X

, v

is deﬁned as v

= f

↓X

Since the goal cannot be achieved because of

trade-offs between the objectives in general cases, a

Pareto optimal solution is selected based on several

criteria (Sen, 1997; Marler and Arora, 2004).

Leximin is deﬁned as the dictionary order on ob-

jective vectors whose values are sorted in ascending

order (Bouveret and Lema

ıtre, 2009; Greco and Scar-

cello, 2013; Matsui et al., 2014; Matsui et al., 2015).

Deﬁnition 3 (Sorted-objective vector). The values of

sorted-objective vector v are sorted in ascending or-

der.

Deﬁnition 4 (Leximin). Let v = [v

, · ·· , v

] and v

, · ·· , v

] denote the sorted-objective vectors whose

length is K. The order relation, denoted with ≺

leximin

is deﬁned as follows: v ≺

leximin

if and only if

∃t, ∀t

< t, v

= v

∧ v

< v

Since leximin is a criterion that repeats the com-

parison between the minimum values in the vectors,

it improves the worst-case values. This maximiza-

tion also relatively improves the fairness and ensures

Pareto optimality.

The addition of two sorted-objective vectors is de-

ﬁned with concatenation and resorting.

Deﬁnition 5 (Addition of sorted-objective vec-

tors). Let v and v

denote vectors [v

, · ·· , v

] and

, · ·· , v

], respectively. The addition of two vectors,

v ⊕ v

, is represented as v

= [v

, · ··v

K+K

], where v

consists of all the values in v and v

. In addition, the

values in v

are sorted in ascending order.

For the addition of sorted-objective vectors, the

following invariance exists that enables dynamic pro-

gramming to solve optimization problems with the

leximin (Matsui et al., 2014).

Proposition 1 (Invariance of leximin on addition).

Let v and v

denote sorted-objective vectors of the

same length. In addition, v

denotes another sorted-

objective vector. If v ≺

leximin

, then v ⊕ v

≺

leximin

⊕ v

Sorted objective vectors and related operations

can be performed with a representation of a sorted his-

togram or a run-length encoding that is a vector of the

sorted pairs of an objective value and the count of the

value (Matsui et al., 2014; Matsui et al., 2015).

To evaluate the inequality among different-size

populations, we employ the Theil index, a well-

known measurement of inequality.

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

336

Deﬁnition 6 (Theil index). For n objectives, Theil in-

dex T is deﬁned as

T =

∑

¯v

log

¯v

(2)

where v

is the income or cost value of an objective

and ¯v is the mean utility value for all the objectives.

The Theil index takes a value in [0, log n]. When

all utilities or cost values are identical, the Theil index

value is zero.

2.3 Application to Shortest Path

Problems

The concept of leximin has been applied to shortest

path problems (Matsui et al., 2018). The original

problem is a minimization problem for the total cost

values of edges in paths on a graph. In the previous

work, the criterion was replaced by a criterion simi-

lar to leximin to improve the worst-case cost values

and fairness among edges. Since shortest path prob-

lems are minimization problems, the maximization

on leximin is replaced by the minimization of similar

criteria called leximax with sorted-objective vectors

whose value ordering is inverted.

Deﬁnition 7 (Descending sorted-objective vector).

The values of a descending sorted-objective vector

are sorted in descending order.

Deﬁnition 8 (Leximax). Let v = [v

, · ·· , v

] and

= [v

, · ·· , v

] denote descending objective vectors

whose lengths are K. The order relation, denoted with

≺

leximax

, is deﬁned as follows. v ≺

leximax

if and only

if ∃t, ∀t

< t, v

= v

∧ v

< v

The addition of two descending sorted-objective

vectors is deﬁned similarly to the leximin.

In route optimization problems, the paths and

corresponding sorted-objective vectors with different

lengths must be compared. For this comparison, lexi-

max is extended to variable-length leximax, vleximax.

Deﬁnition 9 (Vleximax). Let v = [v

, · ·· , v

] and

= [v

, · ·· , v

] denote descending sorted-objective

vectors whose lengths are K and K

, respectively. For

K = K

, ≺

vleximax

is the same as ≺

leximax

. In other

cases, zero values are appended to one of the vectors

so that both vectors have the same number of values.

Then, the vectors are compared based on ≺

leximax

This comparison is intuitively based on two mod-

iﬁed vectors that have the same sufﬁcient length by

padding blanks with zeros. Such padding values can

be omitted in actual computation. Moreover, the vec-

tor can be represented with a histogram or a run-

length encoding with sorted objective values when the

cost values are a relatively small set of discrete values.

Addition and comparison of the vectors are also per-

formed on the histograms.

With vleximax, path-ﬁnding methods based on

dynamic programming including the Dijkstra algo-

rithm and the A* algorithm (Hart and Raphael, 1968;

Hart and Raphael, 1972; Russell and Norvig, 2003)

have been naturally extended. On the other hand, it

has been shown that the extension of the Learning

Real-time A* algorithm (Barto et al., 1995) is not

straightforward, and a heuristic approach to mitigate

the problem has been proposed (Matsui et al., 2018).

3 APPLYING

LEXIMIN/LEXIMAX TO

Q-LEARNING

We investigated the lexmin/leximax criterion with Q-

learning. The Q-learning can be considered an exten-

sion of the Learning Real-time A* algorithm, the cri-

terion is similarly applied. Below, we address several

issues in the case of reinforcement learning.

Similar to the distance values of the shortest path

problems with vleximax, we focus on the class of re-

inforcement learning problems where the cost or re-

ward values take a few discrete values. We mainly

address minimization problems where cost values are

deﬁned for each state. Moreover, we assume that

there are a start state and a goal state that ensure

an optimal episode from the start state to the goal

state. Since one of our goals is the equalization of

cost/reward values within episodes, an agent learns

the policy based on complete observation.

3.1 Representation of Sorted-objective

Vector

For shortest path problems with vleximax, differ-

ent lengths of sorted-objective vectors are employed.

In actual implementation, the sorted-objective vec-

tor can be represented as a histogram or run-length

encoded data to reduce its size and computational

cost. However, with Q-learning, there is the issue

of weighted average among the different lengths of

sorted-objective vectors. The original representation

of the different lengths of vectors cannot be employed

to average any two vectors. Therefore, only the his-

togram representation can be extended to aggregate

two vectors with the weight values. As a result, the

deﬁnition of the histograms must be modiﬁed so that

they take real values. While such a representation is

not a histogram, we call it a real-valued histogram.

Reinforcement Learning Considering Worst Case and Equality within Episodes

337

Deﬁnition 10 (Real-valued histogram and opera-

tions). A real-valued histogram is an extended rep-

resentation of a histogram of discrete values, where

a count value for a discrete value to be counted can

take a real value. Addition v

= v ⊕ v

of two real-

valued histograms v and v

is deﬁned as: v

= v

+ v

for each i

value of the real-valued histograms. Addi-

tion v

= i + v

of a discrete value i and a real-valued

histogram v

that contains the count of i is deﬁned

as: v

= v

+ 1 and v

= v

for each j

value, where

i 6= j. Product v

= wv

of a real value w and a real-

valued histogram v

is deﬁned as: v

= w · v

for each

value.

The comparison of vleximax with histogram rep-

resentation can be deﬁned for the count values sim-

ilarly to the case of integer count values. With the

above operations, the weighted average v

= wv ⊕

(1−w)v of two real-valued histograms is represented.

Proposition 2 (Weighted average of real-valued his-

tograms). A weighted average of two real-valued his-

tograms is an intermediate real-valued histogram of

the two real-valued histograms in the ordering of

vleximax.

Proof. The weighed average of two real-valued his-

tograms has weighted average values that are sepa-

rately aggregated for count values corresponding to

discrete values to be counted. Therefore, a count

value of each discrete value to be counted is between

the count values of the same discrete value in the

two real-valued histograms. Since vleximax com-

pares count values from the maximum discrete val-

ues, the aggregated real-valued histogram is between

two real-valued histograms in the ordering of vlexi-

max.

The above weighted average is actually a statis-

tical aggregation of populations regarding individual

discrete cost values. Other types of aggregation of

vectors can be available if such aggregation opera-

tions satisfy a similar property.

With the operators for real-valued histograms is

the Q-learning is represented as follows:

Q(s, a) ←(1 − α)Q(s, a)⊕

α(c + γ min

vleximax

Q(s

, a

)) ,

(3)

where Q-values are replaced by real-valued his-

tograms Q(s, a). We call these Q-histograms.

For maximization problems, the rule can basically

be replaced with rewards and a maximization operator

on ‘vleximin’ that compares real-valued histograms

whose discrete values are sorted in ascending order.

However, an applicable class of maximization prob-

lems can differ from those of minimization problems

similar to the cases of the original Q-learning.

3.2 Parameters for Learning and

Exploration/Exploitation

Although the settings of parameters for learning

and exploration/exploitation resemble the original Q-

learning with summation, part of settings affects the

case of real-valued histograms and vleximax. The

learning rate α can be set to an arbitrary value for de-

terministic state transition cases, while the values less

than one might cause a signiﬁcant delay of the con-

vergence for real-valued histograms. The settings are

related to classes of problems as shown in the follow-

ing sections.

In the case of Q-learning for minimizing prob-

lems that are similar to shortest path problems, the

discount rate γ should be set to one because the Q-

values/histograms are aggregated to capture the costs

for a whole episode. Therefore, the limitation of fu-

ture information will decrease the accuracy of policies

in both cases with the original summation values and

the real-valued histograms.

Appropriate exploitation and exploration strate-

gies and parameters such as the epsilon-greedy

method can be used.

3.3 Acyclic State Transition Cases

Here, we consider simple cases where the state tran-

sition is acyclic and deterministic. A state transi-

tion space of this class of problems can be repre-

sented with a directed acyclic graph whose vertexes

and edges represent states and actions. In addition,

we address the case where there are a start sate and a

goal state such that there are paths between two states.

Since an episode consists of a sequence of differ-

ent state-action pairs, the propagation of Q-learning

from the goal state to the start state is eventually

achieved. Therefore, the Q-learning is correctly

works with vleximax.

Like vleximax, both minimization and maximiza-

tion problems can be learned with Q-learning meth-

ods with summation and vleximax/vleximin criteria.

In this case, the initial Q-values/histograms can be set

with arbitrary values including zero, while it might

affect the convergence of the Q-values/histograms.

3.4 Cyclic State Transition Cases

Next, we consider the cases where state transition can

be cyclic. We also address the case where there are

a start sate and a goal state such that there are paths

between two states. Although the original Q-learning

with summation is applicable without modiﬁcations,

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

338

the case of Q-histograms and vleximax requires a few

considerations.

With the Learning Real-time A* algorithm for

shortest path problems, minimization with vleximax

is problematic because it is driven with lower-bound

cost values and emphasizes cyclic paths that resemble

negative cycles (Matsui et al., 2018). This contrasts

with the minimization with the summation that cor-

rectly works with both upper and lower bound cost

values. Q-learning has the similar issue.

A simple way to perform the learning based on

upper bound cost values is to set the initial values of

the Q-histograms at a sufﬁciently large upper bound

value similar to the Dijkstra method. Namely, the

count values of the Q-histograms are set to a sufﬁ-

ciently large value considering the convergence time

of the Q-histograms. Since this is not a complete way,

the correct propagation of learning from the goal state

must be assured by the setting of parameters and ex-

plorations.

With algorithms such as the Learning Real-time

A* algorithm, both of learning and exploration rules

are driven based on the lower-bound cost values.

Therefore, the learning has been modiﬁed to episode-

based learning with a heuristic exploration strat-

egy. On the other hand, the Q-learning is basically

performed with random-walk-based exploration and

there might be opportunities to ﬁnd the goal state. The

random walk based algorithm can be available for rel-

atively small problems, while the length of explored

episodes might be signiﬁcantly longer.

In the case of cyclic state transition, the deﬁni-

tion of the maximization problem is not straightfor-

ward for the real-valued histogram and vleximax. Al-

though minimization problems with summation sim-

ilar to path-ﬁnding problems can be relatively eas-

ily replaced by maximization problems with potential

ﬁelds where only the goal states have rewards, this

differs from our aim of equalizing cost/reward values

in an episode.

3.5 Stochastic Cases

When the state transition is stochastic, the solution

quality of an episode generally decreases. Since min-

imization with vleximax aims the equalization of fu-

ture cost/reward values, the noise is serious. In this

case, the weighted average of Q-histograms might

confuse the learning, since it separately aggregate the

count of each discrete cost value.

Therefore, in relatively noisy environments, the

aggregated Q-histograms cannot adequately empha-

size the probabilistically best episode. In such

cases the minimization with vleximax tends toward

1 2 3

4 5 6

7 8 9

1 2 3

4 5 6

7 8 9

DAG CYC

Figure 1: Problems (3 × 3).

nonsense and the original Q-learning with summa-

tion reduces both the maximum and summation of

cost/reward values. While the limitation is substan-

tial for our problem settings, the Q-learning still work

if the result of statistic aggregation can hold the

episodes in environments with little noise.

3.6 Properties of Solution Method

Since the proposed approach inherits a major part

form the shortest path ﬁnding with vleximax shown

in (Matsui et al., 2018), it can be optimal as vleximax

in the case of deterministic and acyclic state transi-

tion. The correctness depends on an exploration and

the learning ratio that ensure the propagation of learn-

ing from the goal state to the start state. Similar prop-

erty holds in the case case of minimization problems

with deterministic and cyclic state transition.

The weighted average of the real-valued his-

togram is reasonable in the meaning that it is an in-

termediate real-valued histogram of the original ones.

While it converges to (near) optimal histogram in de-

terministic transition cases with appropriate explo-

ration and learning, in stochastic transition cases, a

weighted average of individual count values might be

inaccurate.

The computational and memory cost for the ad-

dition, weighted average and vleximax of real-valued

histograms is greater than those of scalar cost values.

However, it linearly grows with the number of dis-

crete cost values to be counted. Therefore, it is ap-

plicable to histograms with relatively small range of

discrete cost values.

4 EVALUATION

4.1 Problem Settings

We experimentally evaluated the proposed method

with fundamental benchmark problems based on the

w × h lattice directed graphs shown in Figure 1. Ver-

texes and edges of the graphs represent states and

transitions corresponding to actions.

Reinforcement Learning Considering Worst Case and Equality within Episodes

339

The following two types of state transition models

are employed.

• DAG: State transitions are acyclic. To increase

different episodes, diagonal-directed edges are

added.

• CYC: State transitions are cyclic.

As the initial value of Q-values/histograms, we em-

ployed 100 for both DAG and CYC. In addition, two

cases of transitions are considered:

• DET: State transitions are deterministic. There-

fore, an action and a state transition exactly corre-

spond to a directed edge.

• NDT: State transitions are non-deterministic.

Each action a is successfully performed with

probability p

. In this case, the state transition

is the same as DET. Otherwise, a state transition

corresponding to one of the other actions is ran-

domly performed with uniform distribution. We

randomly set p

of action a from [p

⊥

, 1] with uni-

form distribution.

We set the start state and goal state to the left-top

and right-bottom states. Each state except the start

state gives a cost value. The cost value of each edge

was randomly set from the integer values in [1, c

]

based on uniform distribution, where c

was 5 or 10.

We performed minimization methods with the fol-

lowing two criteria.

• SUM: Minimization of summation for scalar cost

values.

• LXM: Minimization with vleximax for real-

valued histograms of cost values.

We varied learning rate α and discount rate γ. To

eliminate the inﬂuence of heuristic exploration, ran-

dom walk was performed for learning. As the ex-

ploitation of learned Q tables, episodes that perform a

sequence consisting of each best action in each state

were evaluated. In the case of NDT, 100 episodes

were averaged for evaluation.

Each episode was performed for at most 2000

steps. In each trial, at most 1,000,000 episodes were

performed. For each setting of problems results over

ten instances were averaged. The experiment was per-

formed on a computer with a Core i7-3930K CPU

(3.20 GHz), 16-GB memory, Linux 2.6.32, and g++

(GCC) 4.4.7.

4.2 Results

Table 1 shows the results of DAG, DET, 10 × 10 grid,

= 10, and γ = 1. Here, the statistic length of

objective vector that is calculated from a real-valued

Table 1: DAG, DET, 10 × 10, c

= 10, γ = 1.

alg. α len. sum. max. theil

SUM 0.25 10.5 37.3 8.1 0.191

0.5 10.8 37.3 8 0.189

1 10.8 37.3 8 0.189

LXM 0.25 11.4 44.7 7.4 0.128

0.5 11.5 41.3 7.3 0.142

1 11.6 42.2 7.3 0.135

Table 2: DAG, DET, 10 × 10, c

= 10, γ = 0.5.

alg. α len. sum. max. theil

SUM 0.25 13.6 44.8 8 0.204

0.5 13.6 44.8 8 0.204

1 13.6 44.8 8 0.204

LXM 0.25 15.1 58.4 7.4 0.127

0.5 15.9 60.4 7.3 0.121

1 16 60.1 7.3 0.120

Table 3: DAG, DET, 20 × 20, c

= 10, γ = 1.

alg. α len. sum. max. theil

SUM 0.25 23.6 73.8 8.5 0.216

0.5 23.8 73.8 8.6 0.212

1 23.8 73.8 8.6 0.212

LXM 0.25 22.3 100.1 8.2 0.151

0.5 24.8 82.8 7.3 0.151

1 25.7 84.3 7.1 0.149

Table 4: DAG, DET, 10 × 10, c

= 5, γ = 1.

alg. α len. sum. max. theil

SUM 0.25 10.4 21.1 4.3 0.143

0.5 10.7 21.1 4.2 0.137

1 10.7 21.1 4.2 0.137

LXM 0.25 11.2 22.4 4 0.117

0.5 10.8 22.7 4 0.112

1 11.2 22.4 4 0.117

histogram (len.), the total cost (sum.), the maximum

cost (max.), the Theil index (theil) are evaluated. On

average, SUM decreased the total cost value, while

LXM decreased the maximum cost and the Theil in-

dex. Due to a trade off, the length and the summation

in LXM are grater than SUM. While different learn-

ing rates affected the convergence, the results resem-

ble in this problem setting.

Table 2 shows the results of DAG, DET, 10 × 10

grid, c

= 10, and γ = 0.5. In this case, the accuracy

of both SUM and LXM decreased as compared to that

of γ = 1, since the problem resembles shortest path

problems as mentioned in Section 3.2. Table 3 shows

the results of DAG, DET, 20 × 20 grid, c

= 10, and

γ = 1. The results resemble the case of 10 × 10 prob-

lems, while the cost values and the length of policies

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

340

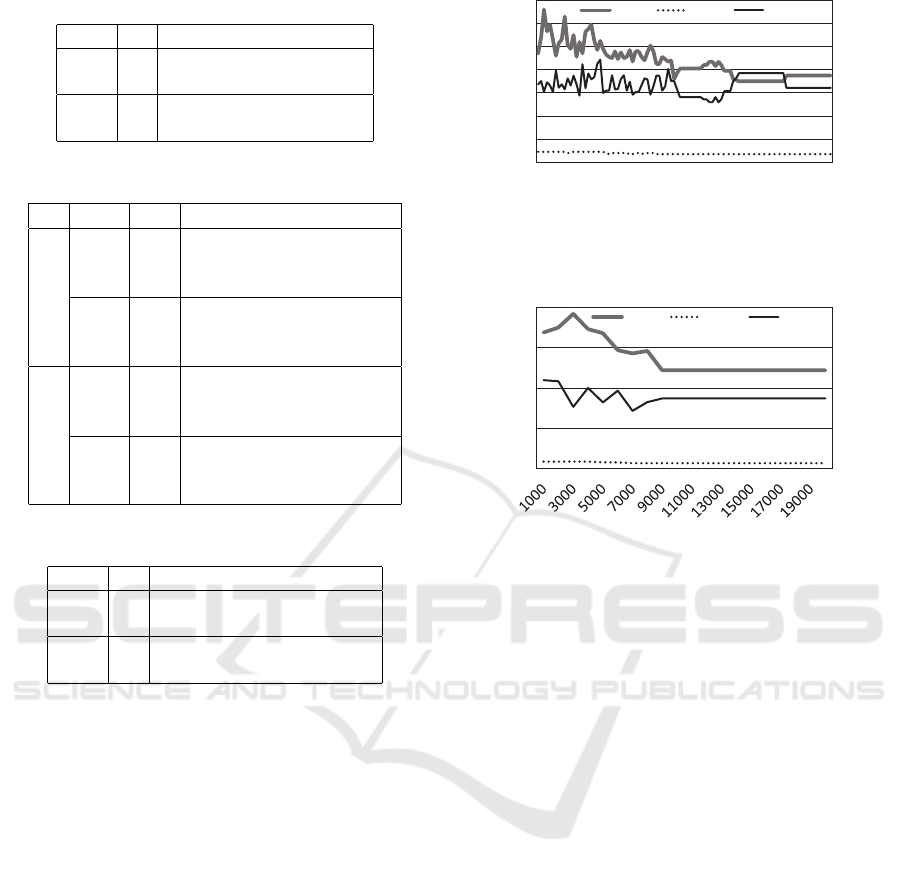
Table 5: CYC, DET, 5 × 5, c

= 10, γ = 1.

alg. α len. sum. max. theil

SUM 0.5 8 29 8.2 0.227

1 8 29 8.2 0.227

LXM 0.5 8 30.1 7.8 0.198

1 8 30.1 7.8 0.198

Table 6: DAG, NDT, 10 × 10, c

= 10, γ = 1.

⊥

alg. α len. sum. max. theil

0.7 SUM 0.25 11.7 44.8 8.62 0.202

0.5 11.6 45.8 8.52 0.189

1 12.6 51.3 8.69 0.189

LXM 0.25 13.9 67.3 8.81 0.146

0.5 13.9 67.8 8.92 0.155

1 13.5 57.6 8.70 0.149

0.9 SUM 0.25 11.0 40.0 8.28 0.187

0.5 10.8 39.9 8.10 0.195

1 11.7 44.2 8.25 0.181

LXM 0.25 14.0 68.4 8.75 0.157

0.5 14.3 71.0 8.82 0.143

1 12.6 48.0 7.99 0.146

Table 7: CYC, NDT, p

⊥

= 0.95, 5 × 5, c

= 10, γ = 1.

alg. α len. sum. max. theil

SUM 0.5 8.2 30.2 8.142 0.215

1 31.8 166.1 8.137 0.230

LXM

1 8.5 32.5 7.846 0.200

are relatively large for both methods. As shown in

Table 4, where the range of cost values is [1, 5], the

narrow range of cost values decreases the opportuni-

ties of differences between SUM and LXM.

Table 5 shows the results of CYC, DET, 5×5 grid,

= 10, and γ = 1. Here, we had to set the ini-

tial value of Q-histograms to an upper bound value of

100, since the initial value of zero results in incorrect

cyclic episodes in the case of LXM, as mentioned in

Section 3.4. Indeed, with zero initial values, resulting

episodes emphasized incorrect cyclic paths. With the

appropriate upper-bound values, the results resemble

for the cases of DAG. In the cyclic case, the conver-

gence of LXM takes a number of episodes with the

learning rates less than one, while it converged in rel-

atively smaller number of episodes with the learning

rate of one even in 20 × 20 problems.

Table 6 shows the results of DAG, NDT, 10 × 10

grid, c

= 10, and γ = 1. In the cases of non-

deterministic state transitions, the accuracy of vlex-

imax signiﬁcantly decreased. As shown in the case

of p

⊥

= 0.7, with high randomness of state transi-

tion, LXM cannot overcome SUM in any metrics ex-

0.1

0.2

0.3

0.4

100

120

140

1000

8000

15000

22000

29000

36000

43000

50000

57000

64000

71000

78000

85000

92000

99000

theil

cost

Episode

sum. max. theil

Figure 2: DAG, DET, 20 × 20, c

= 10, α = 0.5, γ = 1,

LXM.

0.1

0.2

0.3

0.4

100

150

200

theil

cost

Episode

sum. max. theil

Figure 3: CYC, DET, 20 × 20, c

= 10, α = 0.5, γ = 1,

LXM.

cept the Theil index. Since this is a substantial is-

sue of problem deﬁnition, use of vleximax should be

determined considering the opportunities of the real-

valued histograms capturing information within each

episode. We found that LXM with the learning rate

of one is better in these cases as shown in the case of

⊥

= 0.9. This reveals the difﬁculty in the statistic

aggregation of objective vectors. Table 7 shows the

cases of CYC, NDT, p

⊥

= 0.95, 5 × 5, c

= 10, and

γ = 1. Although the convergence of LXM was severe

in most problem instances, the converged results re-

semble the cases of DAG and NDT.

Figures 2 and 3 show examples of anytime curves

of learning for LXM in DET. The optimal policies

are iteratively evaluated based on learned Q tables.

The accuracy gradually improved with the progress

of learning.

The averaged computational times including

statistic operations for evaluation were 0.936 and

1.645 seconds for SUM and LXM in a DAG, 20 × 20

grid setting and 100,000 episodes. For the CYC,

20 × 20 grid, it took 39.782 and 74.359 seconds. The

above time of LXM for CYC contains the anytime

evaluation in the worst-case of cyclic episodes up to

2000 steps.

Reinforcement Learning Considering Worst Case and Equality within Episodes

341

5 DISCUSSION

Since the proposed approach resembles an extension

of shortest path problems, it can be applied to the

class of similar problems in the context of reinforce-

ment learning including the case of positive rewards

on acyclic state transition. In the other cases based on

a potential ﬁeld, more consideration is necessary to

model such problems.

A shown in (Matsui, 2019), applying the idea

of leximin/leximax to optimization of joint policies

among multiple agents so that the equality of indi-

vidual agents is improved is difﬁcult because the ag-

gregation of sorted-objective vectors cannot be well

decomposed in a direction of episodes. On the other

hand, the class of problems in this study is relatively

better, since the decomposition of a real-valued his-

togram is based on dynamic programming. However,

more investigations are necessary to discuss whether

this approach can appropriately ﬁt some class of mul-

tiagent or multi-objective problems.

Vleximax is based on the assumption that predic-

tion of future optimal episodes is possible. Therefore,

it cannot be employed in highly stochastic problems.

On the other hand, where statistically optimal policy

can be calculated with real-valued histograms, there

may be opportunities to improve policies with vlexi-

max.

We employed a simple deﬁnition of the weighted

average of real-valued histograms with scalar weight

values. It may be possibile to use weight vectors to

emphasize part of the discrete cost values. In addition,

other aggregation operators that differently generate

a histogram from the original two histograms could

affect solution quality.

6 CONCLUSIONS

We investigated applying a leximin based criterion to

the Q-learning method to consider the worst-case and

equality among individual cost/reward values in an

episode. The experimental results show that the crite-

rion is effective in several cases of problems, while

more considerations are necessary to employ it to