
A Study of Common Concerns Inhibiting Teacher Enactment of
Computational Thinking into Project-based Mathematics and Career
Technical Education
Subhrajit Majumder
1,*
, Kiyan Khaloozadeh
1
, Charlene M. Czerniak
2
, Jared Oluoch
3
,
Tod Shockey
4
, Ahmad Javaid
1
, Gale Mentzer
5
, Ryan Ducket
5
and Thehazhnan Ponnaiyan
6
1
Department of Electrical Engineering & Computer Science, University of Toledo,
2801 W Bancroft Street, Toledo, OH U.S.A.
2
College of Engineering, University of Toledo, 2801 W Bancroft Street, Toledo, OH, U.S.A.
3
Department of Engineering Technology, University of Toledo, 2801 W Bancroft Street, Toledo, OH, U.S.A.
4
Department of Teacher Education, University of Toledo, 2801 W Bancroft Street, Toledo, OH, U.S.A.
5
Acumen Research and Evaluation, 1811 N Reynolds Rd, Toledo OH, 43615, U.S.A.
6
Department of Chemical Engineering, University of Toledo, 2801 W Bancroft Street, Toledo, OH, USA
Keywords: MATH, STEM, PBL, CTE, CBAM.
Abstract: Recent studies have shown that US high school students are not as prolific as other countries in terms of their
performance in mathematics. One of the most effective solutions can be a change in the way mathematics
subjects is taught in high school. The NSF-funded “Understanding How Integrated Computational Thinking,
Engineering Design, and Mathematics Can Help Students Solve Scientific and Technical Problems in Career
Technical Education (INITIATE) project is a collaboration of The University of Toledo and high schools in
Toledo that aims to improve mathematics teaching. Project-based learning (PBL) and integrating math with
career technology education (CTE) have been established as efficient ways to improve high school students’
understanding of mathematics. Nevertheless, implementation of new ways of teaching is not always easy for
the teachers, and many factors may inhibit the teachers from implementing PBL methods. This research
analyzes common concerns teachers experienced regarding enacting new teaching methodologies in their
classroom. The Stages of Concern Questionnaire (SoCQ) was used to measure the teachers’ perceptions of
and comfort with implementing computational thinking (CT) concepts PBL lessons. Possible relationships
between teachers’ SoCQ CBAM score and other variables such as their understanding of PBL and CTE are
examined and discussed.
1 INTRODUCTION
The importance of mathematics preparation for
students pursuing higher education degrees is well
documented. Researchers at UCLA (2019) have
found that 60% of students entering community
colleges in the United States are not eligible for
college level mathematics courses. Based on
placement test results, these students arrive to
community colleges enrolling in remedial
mathematics courses. Enrolling in remedial
mathematics coursework increases time to degree,
which can lead to changes in degree pursuit
*
This project is funded by the National Science Foundation
Grant Number 1741784.
(WOLPERT, 2018). The Bureau of Labor Statistics
(Employment in STEM occupations : U.S. Bureau of
Labor Statistics, n.d.) reports that Science,
Technology, Engineering, and Mathematics (STEM)
employment rates are low when compared to overall
employment in the United States. One finding that
may contribute to a lack of engagement in
mathematics by students in secondary school may be
mathematics anxiety.
According to Maloney and Beilock, mathematics
anxiety may also be a product of poor mathematics
skills due to a lack of mathematical practice, which
may lead to a lack of conceptual understanding
(Beilock & Maloney, 2015). Mathematics anxiety is
Majumder, S., Khaloozadeh, K., Czerniak, C., Oluoch, J., Shockey, T., Javaid, A., Mentzer, G., Ducket, R. and Ponnaiyan, T.
A Study of Common Concerns Inhibiting Teacher Enactment of Computational Thinking into Project-based Mathematics and Career Technical Education.
DOI: 10.5220/0009337403410349
In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 341-349
ISBN: 978-989-758-417-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
341

being experienced by many learners. Anxiety for too
many students is expressed as “that feeling of fear,
apprehension, and helplessness when tackling a math
problem” (TRAN, n.d.). Tran citing the work of
Brooks (2014) discusses the possibility of turning
“anxiety into excitement”(Brooks, 2013). Brooks
(2014) researched how anxiety and excitement are
linked to increased heart rates but have different
psychological effects. Excitement, according to
Brooks is related to “I can do something” while
anxiety can lead to a “threat mindset.” Prior to
presenting a difficult mathematics problem,
participants in Brooks’ study were shown the
message “try to get excited.” This message resulted in
improved performance over the messages of “try to
remain calm” or “please wait a few minutes.”
The UCLA group (2019) reported that one
difficulty for students is a lack of a deep
understanding of the mathematics they study. This
lack of understanding may be attributed to the
memorization of mathematical rules and procedures
according to the group(WOLPERT, 2018). Paulos
(1991) put this in perspective:
Imagine that 90 percent of every
course in English up until college was
devoted to grammar and the diagramming
of sentences. Would graduates have any
feeling for literature? Or let’s consider a
conservatory devoting around 90 percent
of its effort to only practicing of the
scales. Would this way be good enough
for the students to develop understanding
or appropriate appreciation of music?
Obviously, the answer is no. In fact, this
gives proper allowances for the
hyperbole. This describes what frequently
occurs in our mathematics classes.
Mathematics is identified with a rote
recitation of facts and a blind carrying out
of procedures. (p. 52)(Paulos, n.d.).
Schools across the world are beginning to address this
lack of deep conceptual understanding according to
(P. Lisette et al., 2012). Addressing conceptual
understanding supports students to solve new
mathematical problems and to make connections
within mathematical concepts (Macmath et al., 2009).
This paper addresses a professional development
program that partners secondary school mathematics
teachers with university engineers, science educators,
and mathematics educators. Through this partnership
we are striving toward exciting mathematics
classrooms where teachers engage students in new
mathematical problems, the exploration of
connections within mathematics and mathematics to
other subject areas, through the study of autonomous
vehicles.
2 ISSUES WITH HOW
TEACHERS TEACH
Many teachers across the globe are going through
professional development with the goal of better way
of teaching and these are being proved successful. For
example, most teachers with this expertise cover
around 40 problems in a day through various types of
games, drills, or written work whereas amateur
teachers cover around 6-7 problems only (Wilson et
al., 2005).
2.1 PBL as a Promising Approach
According to several research studies, problem-based
learning (PBL) is considered to be a compelling
possibility to enhance students’ ability to perceive
and solve mathematical problems (Tarmizi et al.,
2010). Through PBL, students learn to develop their
critical thinking and, as a result, create a foundation
for the application of skills to new situations. Authors
in (Han et al., 2015) have investigated whether
participating in STEM PBL activities effected
students who had varied performance levels and to
what extent students’ individual factors influenced
their mathematics achievement. Since STEM PBL
embodiment in schools has been a critical challenge,
the effect of STEM PBL on various factors should be
examined. Teachers from 3 highs schools participated
in sustained professional development training
conducted by a STEM centre based in a Southwestern
University. They were asked to develop STEM based
PBL lesson plans once in every 6 weeks for a period
of 3 years(Han et al., 2015). 836 high school students
participated in Texas Assessment of Knowledge and
Skills (TAKS) test at least in the initial year. The
scores were analysed along with demographic
information by hierarchical linear modelling to
project the longitudinal study. The results show that
student achievements in mathematics by both
demographic backgrounds and performance levels
were influenced by STEM PBL instruction. Over the
3 years of this experiment, the students with low
performing skills showed significantly better
improvement than high and middle performing
students.
Another promising way is integration of Math in
CTE. Despite the fact the combination is not a
CSEDU 2020 - 12th International Conference on Computer Supported Education
342

curriculum, this strategy has been proved successful
at several high schools as this led to increased
academic engagement and achievement for students
(Newmann Editor, n.d.). Invoking PBL, putting Math
and CTE together and other established promising
techniques could have eradicated the whole issue of
“high school students lagging in Mathematics” by
their own. Except there is a major concern which
causes several other significant obstacles for this
prosperous journey.
2.2 Issues Related to Making Change
in Classrooms
As interaction with students in a classroom is the
major factor for them to learn, changes in the way of
teaching is one of the major steps. Students must find
fun in their studies to improve their ability to solve
mathematical problems and it is teachers’
responsibility to make learning interesting and fun for
the students. Although there might be no teacher who
will not value collaboration, creativity and curiosity
in their classrooms, many classes are devoid of these
very traits (Herrmann, 2017). From the past
experiments it is given that the results of
experimenting changes in high school curriculums
are equivocal.
Aguirre and Speer adopted an inclusive view of
beliefs as “conceptions, personal ideologies, world
views and values that shape practice and orient
knowledge”(Aguirre & Speer, 1999). Two important
aspects of beliefs get highlighted by this view which
receive general agreement among researchers and are
relevant to the current study. First is the conviction
that beliefs and behaviors are inherently linked (Di
Martino & Zan, 2011), (Forgasz & Leder, 2008).
While Ernest (Ernest, 1989) and Furinghetti and
Morselli in (Furinghetti & Morselli, 2011) consider
beliefs to be the main regulators of teachers’
practices, others acknowledge the general influence
they have on teachers’ pedagogical decision-making
(Goldin, 2009). Second is the relationship between
knowledge and beliefs. As teachers’ beliefs play a
significant role in conducting their practices suggests
that their beliefs act as subjective knowledge;
“knowledge” that the teachers believe to be true but
actually it is not (Beswick, 2011). Their beliefs play
one of the most significant roles in their classrooms.
Hence, teachers’ beliefs are considered to be the
fundamental factor to the investigations of teaching
and learning mathematics. While many
categorizations of beliefs exist in the literature, they
can be broadly grouped according to beliefs about the
discipline, its teaching and student learning (Cross,
2009). Often researchers who study teachers’ beliefs
focus on a cluster of related beliefs, such as their
beliefs about teaching proof (Furinghetti & Morselli,
2011). In (Bobis et al., 2016) teachers’ mathematical
beliefs about student engagement relating to the
discipline of mathematics were examined,
mathematics teaching and learning, and about
themselves as teachers and learners of mathematics.
As far as we are aware, there are few studies that
focus on the priority the teacher places on the
intervention in relation to his/her job as a teacher.
2.3 Common Reasons Change Does Not
Happen in Classrooms
“Taking a new step, uttering a new world, is what
people fear most”-Fyodor Dostoevsky. People get
accustomed to things over time, similarly teachers are
also accustomed to orthodox curriculum standards
and due to normal human behaviour adapting a
change in those might cause hiccups. Some states
claim the possibility of Common Core State
Standards (About the Standards | Common Core State
Standards Initiative, n.d.) eliminate the need for
students to undergo remedial courses upon admission
to postsecondary institutions within the system. This
claim can stand as an excuse to bypass these
standards. However, there are some states which try
to update their curriculum standards to help students
improve their skills for their career. In this the authors
have experimented work-based learning experience
to improve English and Mathskills of physically
challenged students (Cease-Cook et al., 2015).
2.4 Concerns Teachers Have
At the time of implementing those changes in
classrooms, a major issue comes into play: teachers’
beliefs (Handal & Herrington, 2003). They rely on
their beliefs more than on going trend in pedagogy.
Herrman, (Herrmann, 2017) presented possible
resistances to changes for teachers: A traditional
sense of one’s own competence, the comfort of
predictability, and familiar successes. When a teacher
is asked to apply changes in their classroom, it also
changes the way they see themselves. They face fear
to go out of their comfort zones where they lack
confidence. Also, when teachers make some
innovative moves, success is not guaranteed. They
will face failure inevitably as not every experiment
will be successful. Last but not the least, the author
also pointed out how asking teachers to leave their
comfortable lesson plans behind for a new
environment in which the students may struggle may
A Study of Common Concerns Inhibiting Teacher Enactment of Computational Thinking into Project-based Mathematics and Career
Technical Education
343

create hindrance. The change in attitudes of 29 self-
selected middle and high school teachers towards
interdisciplinary teaching is described in (Al Salami
et al., 2017). The teachers went through a profession
Development (PD) and delivered interdisciplinary
teaching for 12-15 week. Over these weeks they
designed problem units which spanned multiple
STEM subjects. Quasi-experimental pilot study had
been made by the researchers. This study used several
survey methods and implemented a single group pre-
test and post-test design from the data collected at two
intervals; first one was done at the time of PD
workshop and the later one was conducted after the
completion of the teaching unit which emphasized a
long-term engineering design problem. The goals of
this research were:
Assess the changes in attitudes to
interdisciplinary teaching, attitudes to
teamwork, teaching satisfaction, and
resistance to change.
Explore relationships among these
changes.
Describe the variation in these changes
across teachers’ gender, school level,
discipline taught, and education level.
2.5 Concerns-Based Adoption Model
(CBAM) as an Approach for
Identifying and Remedying
Concerns
Human relation in curriculum change has proved its
value for individuals and groups interested in the
improvement of education (Benne & Muntyan, n.d.).
Charalambous et.al (Charalambous & Philippou,
2010) have analysed data collected from 151
elementary mathematics teachers. They examined
how teachers’ beliefs and efficacy beliefs come into
play when mandatory changes occur in traditional
mathematic curriculums. Some researchers have
utilized anecdote circles, storytelling via moderated
group discussions, to investigate teachers’ needs
related to developing and implementing authentic,
interdisciplinary PBL activities in an urban, public
STEM high school (deChambeau & Ramlo, 2017).
The experiences and viewpoints of teachers towards
this approach were explored within three broad
themes: assessment; coaching and training; and
authentic learning. These analysis delivers insights
for implementing PBL, improving teaching and
learning best practices in a school.
The integration of STEM subjects offers students
opportunities to solve real-world problems in real-
world-like situations (Tsupros et al., n.d.) where
knowledge is used as a tool to solve problems rather
than a body of facts or procedures to be learned with
little contextual significance (Herschbach, 2011).
Despite the growing emphasis on and demonstrated
importance of integration in STEM education,
teachers and teacher educators are not typically
trained to work in areas that rely on the integration of
multiple disciplines. Thus, teachers have not likely
experienced integration themselves and are not well
prepared to engage students in the cross-disciplinary
learning called for by the latest national standards
documents in math and science, such as the Next
Generation Science Standards (Krajcik et al., 2014)
and Common Core State Standards for Mathematics
(Branding Guidelines | Common Core State
Standards Initiative, n.d.). STEM teachers may face
several challenges when they attempt to integrate
content from different disciplines. These challenges
include (a) knowledge of disciplinary specific
differences between subject areas (Lederman &
Lederman, 2014), (b) a lack of breadth in their own
content knowledge needed for teaching (Loewenberg
Ball et al., 2008) in multiple subject areas, and (c) the
contextual challenges of co-planning and/or co-
teaching across disciplinary boundaries (Berlin &
White, 2010), (Frykholm & Glasson, 2005).
This project (INITIATE) combines multiple
theories (the fusion of activity theory, social
constructivist learning theory, and project-based
learning) to form its conceptual framework or
approach to address this concern. For the guidance of
professional development using problem-based
learning to make grade 9-12 science teachers capable
to integrate Computational Thinking into their
teaching, this project uses the conceptual framework
of Concerns-Based Adoption Model (CBAM).
Activities will use smart vehicles as a mechanism to
engage mathematics teachers in Career Technical
Education, alongside with 9-12 students to better
understand why and how to embed computational
thinking in their curriculum. The program should
contribute meaningfully to the understanding of
effective characteristics of professional development.
Funded by the STEM Computing program, this
project seeks to address emerging challenges in
computational STEM areas. The project integrated
computational thinking with computing activities
within disciplinary STEM teaching and learning in
early childhood education through high school (preK-
12).
CSEDU 2020 - 12th International Conference on Computer Supported Education
344
3 METHODOLOGY
We have used several instruments and tools such as
Teacher Lesson Plans, Teacher concerns with
enactment of CT, Focus Group Interviews, etc to
create the CBAM model for the participating
teachers.
When an innovative idea is introduced to a group
of people, the initiative demands not only the
provision of materials, resources, and training; the
understanding of how each person will react to the
new initiative with different attitudes and beliefs is
also vital. “The instrument which is used to evaluate
the efficacy of the Understanding by Design
instructional framework for the implementation plan
is called Concerns Based Adoption Model (CBAM)”
(Hall Richard C Wallace & William Dossett, 1973).
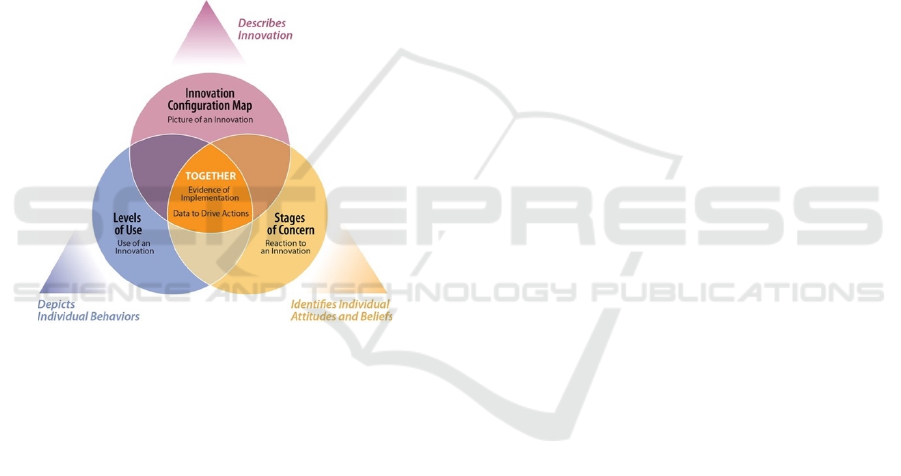
Figure 1: CBAM Model (Concerns-Based Adoption Model
(CBAM), n.d.).
This model provides techniques and tools for
accessing and facilitating the implementation of new
ideas, innovations and reform initiatives (Concerns-
Based Adoption Model (CBAM), n.d.). CBAM can be
divided into three diagnostic dimensions as follows:
Innovation Configuration:
Innovation Configuration allows the teacher to
provide feedback on the implementation of
different types of innovation in the classroom.
The teachers could as well realize what
adjustments could be made to their teaching
behaviour to decrease the difficulty level of the
content (Hall & Hord, n.d.). This allows
evaluators to monitor the results obtained from
the teachers to use an innovation appropriately
in the future.
Stages of Concern:
The Stages of Concerns (SoC) process, which
includes a questionnaire, interview, and open-
ended statements, enables leaders to identify
staff members’ attitudes and beliefs toward a
new program or initiative. With this
knowledge, leaders can take actions to address
individuals’ specific concerns. The SoC items
discussed in this work are as follows:
o Unconcerned: “I have heard about this
but don’t have time to put effort in it.”
o Informational: “This looks promising,
maybe I would like to read about it to
know better.”
o Personal: “The changes I have to make
in my daily schedule is making me
concerned.”
o Management: I am concerned about how
much effort it is going to consume to
become a hit.”
o Consequence: “If I successfully make
this project run, how it is going to affect
my students.”
o Collaboration: “I would like to share
these ideas with others also.”
o Refocusing: “Maybe this approach will
give better results than the proposed
one.”
Levels of Use:
Levels of Use (LoU) analyzes teacher
behaviors from the start of making changes in
their classroom. It indicates the magnitude and
amount of change as the teachers go through
with their teaching transition (Horsley &
Susan, 1998). Each level of the transition is
identifiable by a key decision point and its own
behavioural characteristics (Powell-Griner et
al., 1997).
In this work, we have looked into the stages of
concern encountered by the teachers from this
INITIATE project. As teachers hold the prime
deciding factor for any changes tried to make in
instructional planning and content, their behaviour
analysis must be the first step. How they react to this
change in their classroom, are they comfortable with
this new way of teaching or do the accustomed ways
seem more worthwhile to them-these are among those
vitals questions which have to be answered before
moving forward.
A Study of Common Concerns Inhibiting Teacher Enactment of Computational Thinking into Project-based Mathematics and Career
Technical Education
345

4 RESULTS
Sixteen participant teachers completed the first and
second administration of the SoCQ (one teacher had
difficulty accessing the survey and did not complete
it). As a reminder, SoCQ is divided into three major
constructs: concern about impact, concern about the
task of implementing (logistics), and concern about
self (self-efficacy). Respondents are given a series of
statements and are asked, using a 7-point scale to
indicate their level of agreement with the statement.
Anchors within the scale are:
7 = true most of the time
4 = true some of the time
1 = not true at all at this time
0 = this statement is not relevant to me
A score of 0 indicates that the innovation is not a high
priority to the respondent. There are six stages of
concern and they are illustrated in Figure 2.
Figure 2: Stages of Concern Scales.
The stages are developmental in that one progress
from the lowest “step” to the highest as he/she
becomes more comfortable implementing the
innovation.
Figure 2 illustrates the group distribution of the
2019-20 cohort. The first administration was
completed on the first day of the Summer Institute
and the second administration was in January 2020—
approximately 6 months after completing the Institute
and after (in most cases) implementing a lesson that
based upon Summer Institute content.
Figure 3: Group Distribution of the cohort 2019-2020.
Notice that the post scores show the group moving
lower on the Informational and Personal scales
(interest in the INITIATE model but not quite sure it
was relevant to their teaching and need for more
information regarding the specifics of the innovation
before being willing to implement, respectively) and
slightly higher on the unrelated category suggesting
that they have gained some information needed to
implement the lessons but in some cases this
information has moved them to a position where they
feel the INITIATE teaching strategies are not relevant
to what they do in the classroom. The remaining four
categories have remained relatively similar on pre and
post testing. The low score for Consequences
indicates that the teachers as a group do not have
concerns as to how the innovation might affect the
students, particularly adversely. Similarly, the low
score on the Refocusing scale suggests that the
teachers have little interest in refining and adjusting
the INITIATE teaching approach to better serve
students and make it more useable by other teachers.
Overall, the main conclusion that can be drawn is that
the teachers’ concerns about implementing
INITIATE teaching strategies has not changed much
over the past six months.
Individual change can provide insight as to how
teacher concerns might be addressed to help them
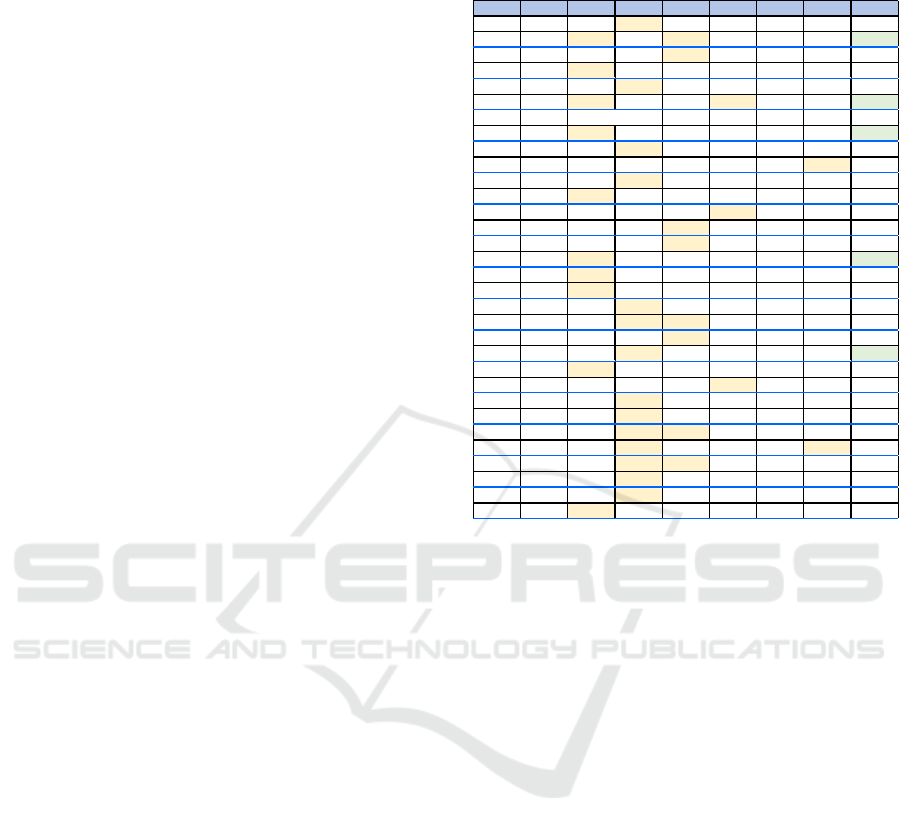
better embrace the innovation. Table 1 (next page)
illustrates the individual percentile scores for the
Stages on pre and posttest. Cells highlighted in
yellow indicate the highest percentile for each testing
occasion per individual. As recommended by the
Stages of Concern Instrument Manual, when another
stage score is within one or two percentile points of
CSEDU 2020 - 12th International Conference on Computer Supported Education
346
the highest score, both scores have been highlighted.
Concerning the adoption of an innovation, the typical
non-user profile will have high scores for Stages 0 –
2 and low scores for 4 -6. The typical user will have
the highest score at Stage 3 or above. Stage numbers
represent the following stages:
0 = unconcerne
d
1 = Informational
2 = Personal 3 = Mana
g
ement
4 = Consequence 5 = Collaboration
6 = Refocusin
g
As expected, nearly all the teachers scored as
nonusers on the pretest (one scored in the 3
rd
category). Of the cohort, five were CTE teachers, one
was a special education teacher, and the remaining
were math teachers. Two teachers (24 and 28) scored
in the Unconcerned category indicating they felt the
innovation was not a priority. The one (ID 20) who
scored as a user, was a math teacher. On the posttest,
3 remained nonusers, one (20) slipped from user to
nonuser (most likely due to preconceptions prior to
the Institute), two were split between user and
nonuser status (16 and 30), and two progressed to
users (18 and 28). Eight teachers scored in the
Unconcerned category. This category does not
indicate whether the teacher is actually a user of the
innovation but rather indicates that the innovation is
low in priority when compared to other tasks
associated with teaching. Of the eight, seven moved
from a higher category on the pretest to Unconcerned
on the posttest. One (16) was split between
Management (concern with time and facility
management and how the teaching strategies might fit
into the class period) and Unconcerned. This suggests
that 16 wants to implement INITIATE strategies but
is concerned about managing it especially
considering other teaching responsibilities.
Respondent 30 was split between Refocusing and
Information suggesting that this teacher has ideas of
ways to modify the innovation but still needs more
information about how it works.
A
higher score for Stage 6 than for Stages 4 and/or
5 indicates that the respondent has ideas that have
more merit than the proposed innovation. Scores
highlighted on the posttest in Stage 6 in light green
are such occasions. Five teachers fell into this
category.
Table 1: individual percentile scores for the Stages on pre
and posttest.
Looking at the individual scores as a whole, it appears that
many of the teachers feel INITIATE teaching strategies are
not a priority and, most likely, they are targeting the
implementation of the lessons they developed using the
self-driving model cars. In addition, several still feel the
need for more information regarding how to implement the
strategies/lessons. Others, those who ranked at the Personal
level, may have doubts as to whether they are able to
implement the lessons correctly.
Delving more into what kinds of information the
teachers need as well as their reservations about
implementing the lessons could provide insight as to the
direction of future teacher support sessions. There has been
some difficulty with the technical aspects of using the cars
and that may be contributing to the doubt some teachers
have. Exploring that as well as other types of support that
could be useful may alleviate teacher concerns.
5 FUTURE WORK AND
CONCLUSION
In this study, the behavioral changes of high school
teachers integrating PBL and Curriculum Technical
Education (CTE) in their lesson plans are analyzed
and assessed using CBAM scoring system.
INITIATE is a National Science Foundation (NSF)
program about Autonomous Vehicles that utilizes
CTE and PBL in its lesson plans, integrating these
concepts in high schools teaching curriculums. The
ID 0123456
10Pre 48756323 919 9
Post 48 45 48 34 13 22 26
11Pre 146667473828 9
Post 99 51 57 65 44 28 38
16Pre 61665923214017
Post 94 34 25 94 3 5 20
17 Pre No pretest data
Post 75 34 28 47 5 9 14
18Pre 149076432452 9
Post 14 60 45 23 8 68 14
19Pre 145139271322 9
Post 31 27 28 15 9 9 9
20Pre 81697685244460
Post 22 93 80 30 59 25 11
21Pre 55697869637252
Post 91 60 59 65 38 31 52
24Pre 99666730116417
Post 87 60 59 60 11 68 17
25Pre 31787634165547
Post 81 96 97 30 21 93 52
27Pre 487578271359 3
Post 40 57 21 30 8 22 26
28Pre 99604834 3 7 9
Post 91 37 55 95 54 55 30
29Pre 40696730213620
Post 14 43 41 15 8 22 9
30 Pre 7 54 55 39 13 25 9
Post 55 60 35 34 5 59 2
31 Pre 7 75 76 11 7 25 9
Post 14 27 25 15 11 16 9
32Pre 40976369387247
Post 75 45 45 30 21 52 38
A Study of Common Concerns Inhibiting Teacher Enactment of Computational Thinking into Project-based Mathematics and Career
Technical Education
347

Stages of Concern Questionnaire (SoCQ) was used to
measure the teachers’ perceptions of and comfort
with implementing computational thinking (CT)
concepts PBL lessons. Based on the observations
gained from the teacher implementation of the lesson
plans, the pre cohort and post cohort results follow the
expected behavioral line in the given graphs.
Furthermore, the use of technology and integrating it
into the lesson plans does indeed bring benefits, but it
also causes problems of its own that hinder the use of
PBL and CTE concepts in high schools. For instance,
if halts occur to the technology, it will require special
assistance to fix the errors and it also can cause large
delays while teaching the lesson. The initial lessons
implementing PBL and CTE topics can be monitored
to make sure that they are on the right track. Also, a
designated tech-savvy person could always be placed
in the classroom for assistance with any problem.
REFERENCES
About the Standards | Common Core State Standards
Initiative. (n.d.). Retrieved October 26, 2019, from
http://www.corestandards.org/about-the-standards/
Aguirre, J., & Speer, N. M. (1999). Examining the
relationship between beliefs and goals in teacher
practice. Journal of Mathematical Behavior, 18(3),
327–356. https://doi.org/10.1016/s0732-
3123(99)00034-6
Al Salami, M. K., Makela, C. J., & de Miranda, M. A.
(2017). Assessing changes in teachers’ attitudes toward
interdisciplinary STEM teaching. International Journal
of Technology and Design Education, 27(1), 63–88.
https://doi.org/10.1007/s10798-015-9341-0
Beilock, S. L., & Maloney, E. A. (2015). Math Anxiety.
Policy Insights from the Behavioral and Brain
Sciences, 2(1), 4–12. https://doi.org/10.1177/
2372732215601438
Benne, K. D., & Muntyan, B. (n.d.). Human relations in
curriculum change dryden press professional books in
education human relations in curriculum change.
Berlin, D. F., & White, A. L. (2010). Preservice
mathematics and science teachers in an integrated
teacher preparation program for grades 7-12: A 3-year
study of attitudes and perceptions related to integration.
International Journal of Science and Mathematics
Education, 8(1), 97–115. https://doi.org/10.1007/
s10763-009-9164-0
Beswick, K. (2011). Knowledge/Beliefs and their
relationship to emotion.
Bobis, J., Way, J., Anderson, J., & Martin, A. J. (2016).
Challenging teacher beliefs about student engagement
in mathematics. Journal of Mathematics Teacher
Education, 19(1), 33–55. https://doi.org/10.1007/
s10857-015-9300-4
Branding Guidelines | Common Core State Standards
Initiative. (n.d.). Retrieved February 27, 2020, from
http://www.corestandards.org/about-the-
standards/branding-guidelines/
Brooks, A. W. (2013). Get Excited: Reappraising Pre-
Performance Anxiety as Excitement. https://doi.org/
10.1037/a0035325
Cease-Cook, J., Fowler, C., & Test, D. W. (2015).
Strategies for Creating Work-Based Learning
Experiences in Schools for Secondary Students With
Disabilities. TEACHING Exceptional Children, 47(6),
352–358. https://doi.org/10.1177/0040059915580033
Charalambous, C. Y., & Philippou, G. N. (2010). Teachers’
concerns and efficacy beliefs about implementing a
mathematics curriculum reform: Integrating two lines
of inquiry. Educational Studies in Mathematics, 75(1),
1–21. https://doi.org/10.1007/s10649-010-9238-5
Concerns-Based Adoption Model (CBAM). (n.d.).
Retrieved February 27, 2020, from http://
www.sedl.org/cbam/
Cross, S. (2009). Adult Teaching and Learning: Developing
Your Practice - Sue Cross - Google Books.
https://books.google.com/books?hl=en&lr=&id=PAB
FBgAAQBAJ&oi=fnd&pg=PP1&dq=Cross+2009+tea
ching+and+student+learning&ots=hhKnIi-PQ0&sig=-
2_piMlr7_3Kf4iNNW1rKBkX5ow#v=onepage&q=Cr
oss 2009 teaching and student learning&f=false
deChambeau, A. L., & Ramlo, S. E. (2017). Stem high
school teachers’ views of implementing PBL: An
investigation using anecdote circles. Interdisciplinary
Journal of Problem-Based Learning, 11(1). https://
doi.org/10.7771/1541-5015.1566
Desilver, D. (n.d.). U.S. academic achievement lags that of
many other countries | Pew Research Center. Retrieved
February 26, 2020, from https://www.pewresearch.org/
fact-tank/2017/02/15/u-s-students-internationally-
math-science/
Di Martino, P., & Zan, R. (2011). Attitude towards
mathematics: A bridge between beliefs and emotions.
ZDM - International Journal on Mathematics
Education, 43(4), 471–482. https://doi.org/10.1007/
s11858-011-0309-6
Employment in STEM occupations : U.S. Bureau of Labor
Statistics. (n.d.). Retrieved February 26, 2020, from
https://www.bls.gov/emp/tables/stem-employment.htm
Ernest, P. (1989). The Knowledge, Beliefs and Attitudes of
the Mathematics Teacher: a model. Journal of
Education for Teaching, 15(1), 13–33. https://doi.org/
10.1080/0260747890150102
Forgasz, H., & Leder, G. (2008). Beliefs about mathematics
and mathematics teaching | Request PDF.
https://www.researchgate.net/publication/288945467_
Beliefs_about_mathematics_and_mathematics_teachin
g
Frykholm, J., & Glasson, G. (2005). Connecting Science
and Mathematics Instruction: Pedagogical Context
Knowledge for Teachers. School Science and
Mathematics, 105(3), 127–141. https://doi.org/
10.1111/j.1949-8594.2005.tb18047.x
CSEDU 2020 - 12th International Conference on Computer Supported Education
348

Furinghetti, F., & Morselli, F. (2011). Beliefs and beyond:
Hows and whys in the teaching of proof. ZDM -
International Journal on Mathematics Education,
43(4), 587–599. https://doi.org/10.1007/s11858-011-
0316-7
Goldin, C. D. (2009). The Race between Education and
Technology - Claudia Dale Goldin, Lawrence F. Katz -
Google Books. https://books.google.com/
books?hl=en&lr=&id=yGlCFqnakCoC&oi=fnd&pg=P
R5&dq=Goldin+et+al.+2009&ots=HtGnUpOOMV&s
ig=4UxD69rIdbEJGLFm1384YrY93RE#v=onepage&
q=Goldin et al. 2009&f=false
Hall, G. E., & Hord, S. M. (n.d.). Implementing Change:
Patterns, Principles, and Potholes. Retrieved February
27, 2020, from www.mathedleadership.org
Hall Richard C Wallace, G. E., & William Dossett, J. F.
(1973). A developmental conceptualization of the
adoption process within educational institutions this
document has been repro ouced exactly as received
from the person or organization origin ating it points of
view or opinions stated do not necessarily repre sent
official national institute of education position or policy
ill) research and development center for teacher
education.
Han, S., Capraro, R., & Capraro, M. M. (2015). How
science, technology, engineering, and mathematics
(stem) project-based learning (pbl) affects high, middle,
and low achievers differently: the impact of student
factors on achievement. International Journal of
Science and Mathematics Education, 13(5), 1089–
1113. https://doi.org/10.1007/s10763-014-9526-0
Handal, B., & Herrington, A. (2003). Mathematics
teachers’ beliefs and curriculum reform. Mathematics
Education Research Journal, 15(1), 59–69.
https://doi.org/10.1007/BF03217369
Herrmann, Z. (2017). The Challenge of Change | Harvard
Graduate School of Education. https://www.gse.
harvard.edu/uk/blog/challenge-change
Herschbach, D. R. (2011). ERIC - EJ952045 - The STEM
Initiative: Constraints and Challenges, Journal of
sTEm Teacher Education, 2011. https://eric.ed.gov/
?id=EJ952045
Horsley, D., & Susan, L.-H. (1998). ERIC - EJ586914 -
CBAM Brings Order to the Tornado of Change.,
Journal of Staff Development, 1998. https://eric.ed.gov/
?id=EJ586914
Krajcik, J., Codere, S., Dahsah, C., Bayer, R., & Mun, K.
(2014). Planning Instruction to Meet the Intent of the
Next Generation Science Standards. Journal of Science
Teacher Education, 25(2), 157–175. https://doi.org/
10.1007/s10972-014-9383-2
Lederman, N. G., & Lederman, J. S. (2014). The Next
Generation Science Standards: Implications for
Preservice and Inservice Science Teacher Education. In
Journal of Science Teacher Education (Vol. 25, Issue
2, pp. 141–143). Kluwer Academic Publishers.
https://doi.org/10.1007/s10972-014-9382-3
Loewenberg Ball, D., Thames, M. H., & Phelps, G. (2008).
Content knowledge for teaching: What makes it
special? In Journal of Teacher Education
(Vol. 59,
Issue 5, pp. 389–407). https://doi.org/10.1177/
0022487108324554
Macmath, S., Wallace, J., & Chi, X. (2009). Problem-Based
Learning in Mathematics - A tool for Developing
Students’ Conceptual Knowledge.
Newmann Editor, F. M. (n.d.). Student Engagement and
Achievement in American Secondary Schools.
P. Lisette, Hamilton, L. S., Stecher, B. M., & Yuan, K.
(2012). Standards-Based Accountability in the United
States:: Lessons Learned and Future Directions*.
Education Inquiry, 3(2), 149–170. https://doi.org/
10.3402/edui.v3i2.22025
Paulos, J. A. (n.d.). Beyond Numeracy: Ruminations of a
Numbers Man - John Allen Paulos - Google Books.
Retrieved February 26, 2020, from
https://books.google.com/books?hl=en&lr=&id=D8K
GDwAAQBAJ&oi=fnd&pg=PR11&dq=Paulos,+J.+A
.+(1991).+Beyond+numeracy.+Vintage+Books,+NY.
+&ots=q6odDIaILC&sig=EN3r2NM3JoWQfdVhTda
hKQ6-Log#v=onepage&q&f=false
Powell-Griner, E., Anderson, J. E., & Murphy, W. (1997).
State-and sex-specific prevalence of selected
characteristics--behavioral risk factor surveillance
system, 1994 and 1995. MMWR. CDC Surveillance
Summaries : Morbidity and Mortality Weekly Report.
CDC Surveillance Summaries / Centers for Disease
Control, 46(3), 1–31.
Tarmizi, R. A., Tarmizi, M. A. A., Lojinin, N. I., &
Mokhtar, M. Z. (2010). Problem-based learning:
engaging students in acquisition of mathematical
competency. Procedia - Social and Behavioral
Sciences, 2(2), 4683–4688. https://doi.org/10.1016/
j.sbspro.2010.03.750
TRAN, C. (n.d.). Research-Based Solutions to Address
Math Anxiety. Retrieved February 26, 2020, from
https://blog.mindresearch.org/blog/math-anxiety
Trends in International Mathematics and Science Study
(TIMSS) - Overview. (n.d.). Retrieved November 19,
2019, from https://nces.ed.gov/TIMSS/
Tsupros, N., Kohler, R., & Hallinan, J. (n.d.). STEM
Education in Southwestern Pennsylvania Report of a
project to identify the missing components.
Turner, J. C., Warzon, K. B., & Christensen, A. (2011).
Motivating Mathematics Learning. American
Educational Research Journal, 48(3), 718–762.
https://doi.org/10.3102/0002831210385103
Wilson, P. S., Cooney, T. J., & Stinson, D. W. (2005). What
constitutes good mathematics teaching and how it
develops: Nine high school teachers’ perspectives.
Journal of Mathematics Teacher Education, 8(2), 83–
111. https://doi.org/10.1007/s10857-005-4796-7
WOLPERT, S. (2018). Why so many U.S. students aren’t
learning math | UCLA. http://newsroom.ucla.edu/
stories/why-so-many-u-s-students-arent-learning-math
A Study of Common Concerns Inhibiting Teacher Enactment of Computational Thinking into Project-based Mathematics and Career
Technical Education
349
