
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery
Problem
Maram Hasan and Rajdeep Niyogi
Department of Computer Science and Engineering, Indian Institute of Technology Roorkee, Uttarakhand, India
Keywords:
Horizontal Collaboration, Multi-Agent System, Logistics, Last Mile Delivery Problem, Egalitarianism.
Abstract:
e-Commerce has become a primary part of any country’s economy, and seeking maximum efficiency and level
of service is an essential concern for any corporation in order to stay in business. Logistics has a significant
impact on the efficiency of online transactions, especially with the increasingly competitive domain with min-
imal profit margin-left. Thus, the collaboration between many logistics service providers (LSPs) at different
levels has become a desirable approach to reduce the overall costs and increase the utilization level of their
resources. In this work, we propose a domain-independent multi-agent framework that allows different LSPs
to plan their operations jointly. The system considers the individual satisfaction of LSPs and their profits in an
egalitarian manner while trying to achieve an overall benefit. We use different search strategies for every agent
as the underlying solving method, and investigate to what level taking the personal interest of participants will
affect the overall shared/ common goal.
1 INTRODUCTION
e-Commerce has grown remarkably over a short pe-
riod of time and become an essential part of the in-
dustry (Chatterjee et al., 2016). In order to guarantee
the success of an enterprise, companies need to pre-
serve their reputation and trust of their customers and
increase the quality of service they provide. In this
matter logistics, or what is called the Last Mile Deliv-
ery LMD, plays the most significant role as it refers to
the last step in the supply chain (Holdorf and Haasis,
2014), in which the items are carried from the ful-
fillment centers to the customers within the specified
delivery period. It forms the most important stage in
the purchase process as it adds up nearly to 30% of
the total cost. Thus, making this stage most effective
is a critical issue in e-commerce transactions (Chinh
et al., 2016).
Recently, all aspects of what is expected from lo-
gistics have changed, the competition became high,
and profit margins declined to a deficient level. This
urged many companies and carriers to collaborate
on different levels and form partnerships in order to
manage the transportation of their goods effectively
(Ouhader and El Kyal, 2017); horizontal collabora-
tion is a form of collaboration between parties that
belong to the same level of the supply chain (all car-
riers or all suppliers). Collaborative routing helps to
reduce the overall transport costs and to increase the
customer satisfaction and utilization level of the lo-
gistics and human resources. Hence, it provides bet-
ter performance from an economic and environmen-
tal perspective. For example, the collaboration be-
tween different LSPs can save them millions out of
the total travel costs by sharing the logistics resources
and thereby solving the empty load problem caused
by the large number of vehicles that travel long dis-
tances underutilized (Chinh et al., 2016). This, in
turn, reduces congestion levels on the roads, the pos-
sibility of accidents and harmful emissions, respec-
tively (Ouhader and El Kyal, 2017). Figure.1a shows
an example of independent routing of two LSPs in
LMD where every LSP has one deposit. Meanwhile,
Figure.1b shows a collaborative routing that utilizes
the resources of each LSP to deliver the packages of
all collaborators. It leads to overall shorter trips and
lower costs.
As the transportation field is dynamic, complex
and consists of many features and constraints, it
makes the agent-based paradigm a quite suitable and
exciting research method to solve famous problems
in this field (Martin et al., 2016). Multi-agent frame-
works are powerful in modeling complex problems
of distributed nature and can efficiently represent the
complicated relationship among the entities in an in-
dependent and autonomous way (Czarnowski et al.,
498
Hasan, M. and Niyogi, R.
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery Problem.
DOI: 10.5220/0009349004980505
In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 498-505
ISBN: 978-989-758-423-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) Individual Routing (b) Collaborative Routing
Figure 1: Last mile delivery scenario of two LSPs.
2013). A multi-agent system consists of a set of en-
tities (agents) that interact with each other in some
environment through predefined means of commu-
nication in order to accomplish some given goal(s)
(Czarnowski et al., 2013). Agent-based paradigm in-
creases the computational power and speeds up the
performance as it enables parallel task executions; co-
operation among the agents allows efficiency, reliabil-
ity, and robustness. Thus, it is ideal for solving differ-
ent complex optimization problems such as our last
mile delivery problem.
Since most researches on horizontal collaboration
focused solely on utilitarianism, which mainly gives
importance to overall benefit (Cruijssen et al., 2007),
(Lahyani et al., 2015), and since real-life collabo-
rators mostly care about their profits and interests
rather than the overall goal, our main contribution is
to consider the satisfaction of individual participants
in an equal manner and to investigate how this affects
the global goal of reducing costs. For this purpose,
we propose a domain-independent multi-agent frame-
work in which each LSP agent represents a collabo-
rator and manages a different search strategy to solve
the LMD problem from its perspective while cooper-
ating with other agents to combine and improve solu-
tions of all agents. This paper is organized as follows;
Section II presents a literature review of collabora-
tive and multi-agent approaches to the problem of last
mile delivery. Section III presents problem formation
while Section IV explains the proposed framework.
Section V discusses the results obtained; Section VI
states the conclusion reached.
2 LITERATURE REVIEW
LMD can be considered as a Vehicle Routing Prob-
lem (VRP), which is a significant NP-hard that was
first introduced in 1959 (Lahyani et al., 2015). It is
concerned with finding the most cost-effective set of
routes starting from a single distribution center to dif-
ferent customers spreading on a large geographic area
while satisfying constraints (Kumar and Panneersel-
vam, 2012). Different versions of the problem were
proposed in the literature under various complexities
and constraints; (Kumar and Panneerselvam, 2012)
and (Lahyani et al., 2015) present helpful surveys.
Various methods have been proposed by researchers
to solve the problem, starting with exact methods
(Mingozzi et al., 2013), and heuristics and meta-
heuristics that find near-optimal solutions (Clarke and
Wright, 1964) to hybrid meta-heuristics such as hy-
bridized genetic algorithm (Cattaruzza et al., 2014).
2.1 Horizontal Collaboration
With the increasing market demands and high cus-
tomer expectations, horizontal collaborative routing
has been studied to provide efficient routing with
lower total operational costs (Chinh et al., 2016). Dif-
ferent methods were presented through time starting
with centralized approaches where a centralized en-
tity solves the optimization problem on behalf of col-
laborating LSPs with different levels of coordination
(Chinh et al., 2016). However, in most cases, there
is less willing of different participants to share their
full customers’ details with a central authority; thus
decentralized approach was presented in the litera-
ture to provide more compatibility with these privacy
concerns such as request exchange and auction-based
methods. The work (Wang and Kopfer, 2015) pro-
posed two distributed request exchange mechanisms
to solve the dynamic routing problems to provided
stable performance. While in (Wang and Kopfer,
2014), a route-based exchange mechanism between
collaborating LSPs that do their own planning in-
dependently and then send the planned routs to a
groupage system (GS) which regenerates routes to
reduce the overall costs. Meanwhile, auction-based
trading is presented in (Dai and Chen, 2011) to al-
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery Problem
499

low the participating LSPs to negotiate and express
their preference and the profit margin in a multi-round
fashion. Another auction-based clustering method
was proposed in (Schwind et al., 2009), where a re-
quest is exported based on its cost-reduction prob-
ability using a convex hull method with a distance-
based cost estimator. Meanwhile, our proposed
method is decentralized and allows LSPs to jointly
plan their pre-defined outsourcing requests and con-
tinuously exchange existing solutions between com-
puting agents to improve the final solution.
As the works mentioned above considered achieving
a global goal of reducing overall cost, other work
in (Zhou et al., 2013) focuses on load balancing in
terms of the tour distance among the moving vehicle
as a global goal; wherein (Schwarze and Voß, 2013),
they examined effective resource utilization using a
minmax model to minimize the maximal vehicle trip
length. In our work, we consider the satisfaction of in-
dividual participants in an equal manner while achiev-
ing total cost reduction.
2.2 Agent-based Approaches
Agent-based systems have contributed to collabora-
tive routing solving because of its autonomous, dis-
tributed characteristics and its native support for a dy-
namic environment (Czarnowski et al., 2013). Several
domain-specific multi-agent architectures were pro-
posed in the literature, such as in (Baykaso
˘
glu and
Kaplano
˘
glu, 2015), where the architecture of three
types of agents (order, truck, dispatcher) was pro-
posed to obtain effective scheduling under dynamic
environment’s conditions through negotiation. Also,
in (Kalina et al., 2015), they provided a multi-agent
system consists of a set of customer agents, route
agents, and a central planner. The planner used a lo-
cal heuristic search to solve the routing problem with
time windows. In contraction, our work will not be
dedicated only to LMD domain as our agents will
be optimizing agents that able to work on any opti-
mization problem. An example of earlier population-
based, cooperative multi-agent system was proposed
in (Barbucha, 2014); where a multi-phase execution
is carried out and different search meta-heuristics
are executed at each phase simultaneously while ex-
changing information about the agents’ states and per-
formance at the end of each phase. In (Martin et al.,
2016), they proposed a general multi-agent approach
where agents periodically exchange parts of their so-
lutions that have potentials to be good edges to guide
the search of other agents in a valuable direction.
Also, the work (Chatterjee et al., 2016) included pub-
lic transportation system in their multi-agent frame-
work to plan small-size orders delivery in aim to re-
duce costs and co
2
emissions.
The work in (Barbucha, 2012) used different syn-
chronization modes in their proposed multi-agent sys-
tem, and used a learning mechanism to adapt the be-
havior of the agents to new states of the environment
while solving the optimization problem. Meanwhile,
the work (Souza et al., 2012) used particle swarm op-
timization (PSO), where each particle is considered
as autonomous agents and represented as a solution
in the search space. Otherwise, our proposed multi-
agent framework consists of a group of optimization
agents exploring different areas of the search space
simultaneously, producing a higher level of diversity
and mature solutions.
Although collaborative routing has been studied
in past years, there are fewer studies in the literature
as far as we know that use a multi-agent paradigm
to solve a multi-deposit VRP version that considers
the personal interests of participants in an equal man-
ner along with a global goal. The main contributions
are as follows; we implement a multi-agent frame-
work that supports the collaboration between differ-
ent LSPs to serve their customers jointly. Our frame-
work is domain-independent, which can be used to
solve any optimization problem in contrast to (Bayka-
so
˘
glu and Kaplano
˘
glu, 2015), (Kalina et al., 2015).
Agents will regularly exchange the best solutions
among themselves to combine and improve the solu-
tions.
3 PROBLEM DEFINITION
Last Mile Delivery Problem can be presented as a ve-
hicle routing problem. It aims to create a set of paths
to satisfy the delivery of n packages, from distribu-
tion center (s) to specified delivery locations satis-
fying some constraints ex. capacity and time, while
minimizing a cost function. Each Logistic Service
Provider LSP has a set of distribution centers DCs
which contains numerous different-size packages to
be distributed to many geographically scattered cus-
tomers within a city. Each package has a weight de-
mand Dem
j
. A distribution center has a set of vehi-
cles V used to complete the delivery tasks, each of
these vehicles v ∈ V has a capacity Q
i
that specify the
maximum load a vehicle can carry at once.
Here we present the notations of the problem;
given a undirected graph G=< V,E >, the set of ver-
tices V represents the customers, and the set of edges
E determines the existence of a direct road between
the adjacent customers; D: set of distribution cen-
ters D = {1, 2,3,... ,m}; C: set of customers C =
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
500

{1,2, 3,. .., n}; K is the total count of vehicles exist-
ing in all of the distribution center.
V
DC
:
sets of vehicles presented in the distri-
bution center DC.
d
i j
:
euclidean distance between customer i
& j.
MaxDis
i
:
maximum length of a tour a vehicle
can do.
y
k
i j
:
current weight of vehicle k while
traversing from customer i to j.
t
k
i j
:
time consumed by the vehicle k to tra-
verse from customer i to j.
[ET
i
,LT
i
] : time window of package i.
ET
i
:
earliest time at which a package i can
be delivered to its owner.
LT
i
:
latest time at which a package i is al-
lowed to be delivered to its owner.
Sk
i
:
service time needed to deliver the
package to the customer i by the ve-
hicle k.
A
i
: arrival time to customer i.
D
i
: leaving time from the customer i.
FC
v
: fixed cost of the vehicle v.
VarC
v
:
variable cost of a vehicle v within a
distance unit (ex: power supply cost).
x
mk
i j
represent a decision variable.
x
mk
i j
=
1, if a vehicle m of a distribution center k
can travel directly from i to j.
0, otherwise
(1)
3.1 The Objective Function
1. Minimize the cost of the tour
∑
k∈V
m
∑
j∈D∪C
∑
i∈D∪C
FC
k
∗ x
mk
i j
+
∑
k∈V
m
∑
j∈D∪C
∑
i∈D∪C
d
i j
∗ x
mk
i j
∗VarC
k
(2)
Subject to these constraints:
(a) Maximum Distance Constraint: the length of
the tour taken by a vehicle can not exceed the
maximum length tour that is specified for it
(due to the fuel or energy supply)
∑
j∈D∪C
∑
i∈D∪C
d
i j
∗ x
mk
i j
≤ MaxDis
k
(k ∈ V
DC
,m ∈ D)
(3)
(b) Capacity Constraints:
the load of any vehicle k traversing from a cus-
tomer i to j can not exceed the maximum capac-
ity of that vehicle.
0 ≤ y
k
i j
≤ Q
k
(k ∈ V
m
,m ∈ D,i, j ∈ C) (4)
(c) Time Constraints: each customer’s package i is
usually attached with a time window [ET
i
,LT
i
]
that specify the time period in which the cus-
tomer i is expecting to receive his package, not
before the earliest time ET
i
or after the latest
time LT
i
. We can conclude with it the follow-
ing information The arrival time A
j
to customer
j from i.
A
j
= D
i
+t
k
i j
(5)
The departure time D
i
from customer i
D
i
= A
i
+ S
k
i
(6)
We should attain the following constraints
ET
i
≤ A
i
≤ LT
i
∀(i ∈ C,k ∈ V
DC
)
ET
i
≤ S
k
i
+ A
i
≤ LT
i
∀(i ∈ C,k ∈ V
DC
)
A
j
≤ LT
j
+ S
k
j
∀( j ∈ C,k ∈ V
DC
) (7)
(d) Precedence Constraints: in case of multi de-
posit scenarios, we need to guarantee that a cus-
tomer will not be visited before his provider:
D
s
≤ D
d
(s ∈ D,d ∈ C) (8)
(e) Each customer can be served by single vehicle
only
∑
m∈D
∑
k∈V
m
∑
i∈D∪C
x
mk
i j
= 1 ∀ j ∈ C (9)
(f) The tour of each vehicle must start from a dis-
tribution center and finish at the same center.
∑
i∈D∪C
x
mk
i j
= 1 ∀ ( j,m ∈ C,k ∈ V
m
) (10)
(g) Path Contentiousness: every vehicle must leave
a customer location only after reaching and
serving that customer.
∑
i∈D∪C
x
mk
iq
=
∑
j∈D∪C
x
mk
q j
∀ ( q ∈ D∪C, m ∈ D,
k ∈ V
m
) (11)
2. Penalty for the Undelivered Packages: it is re-
quired that all packages get delivered, we use a
penalty for undelivered packages. We express the
penalty through the package’s priority prio(m).
∑
prio(m) ∀ (m not delivered successfully )
(12)
So, the final objective function is to minimize
α ∗
∑
k∈V
m
∑
j∈D∪C
∑
i∈D∪C
FC
k
∗ x
mk
i j
+
∑
k∈V
m
∑
j∈D∪C
∑
i∈D∪C
d
i j
∗ x
mk
i j
∗VarC
k
+ β ∗
∑
prio(m) ∀ (m not delivered ) (13)
Where α, β, are weight constants to weightage the
function’s value are in the overall objective func-
tion.
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery Problem
501
4 PROPOSED MULTI-AGENT
FRAMEWORK
Multi-agent approach provides speedup and compu-
tation efficiency as it supports exploring different
areas of the search space simultaneously, produc-
ing a higher level of diversity and mature solutions
(Czarnowski et al., 2013).
One of the important multi-agent paradigms is A-
Team (Asynchronous Team) that was first proposed
in (Talukdar et al., 2003) that describes a set of asyn-
chronous independent software agents that communi-
cate to jointly solve complex problems that can not be
solved by single agent alone. A central memory stores
a population of initial solutions that will be continu-
ously modified by the software agents.
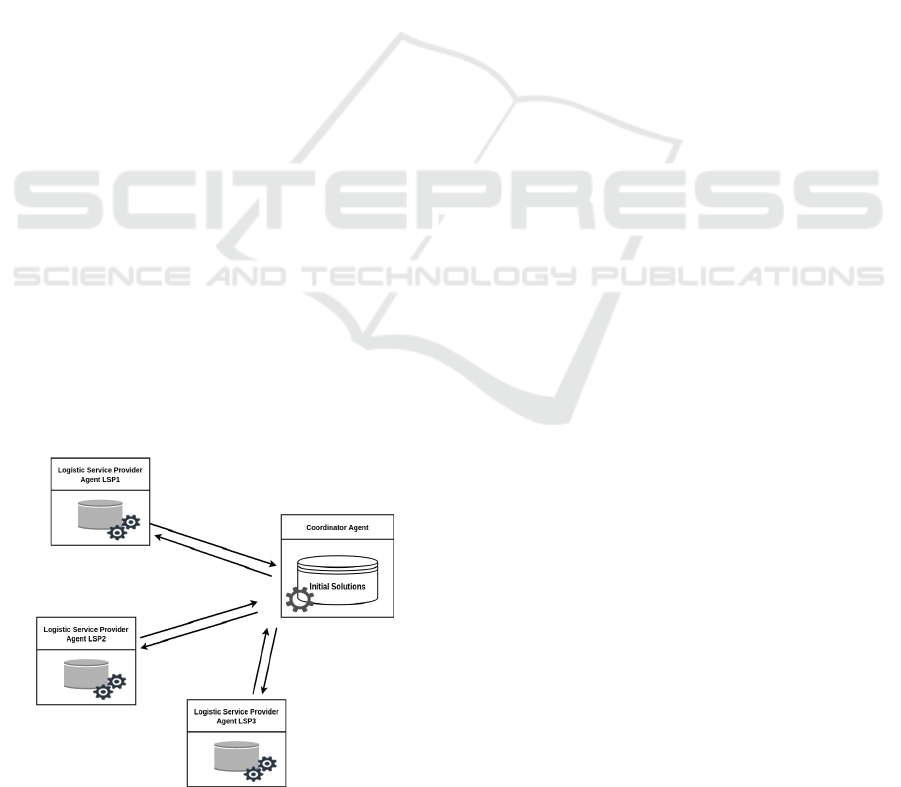
We will build the proposed distributed framework
based on A-Team architecture. It consists of two
types of agents, computing agents, each of which
represents a logistic service provider and can run
on any machine, and a coordinator agent, which
is responsible for maintaining the central memory,
and managing the communication between comput-
ing agents. Figure.2 shows the architecture of our
proposed framework. Now we discuss the types of
agents included.
4.1 Types of Agents
1. The Coordinator Agent:
It is a single agent in the proposed architecture
that manages a pool of initial valid solutions to the
collaborative problem. It receives requests from
every participating LSP agent to send it a subset
of the available solutions to use it as initial solu-
tions in its computation method. The coordinator
agent is considered a synchronizing entity in the
Figure 2: A-Team based multi-agent framework for LMD
problem.
system since it manages the communication be-
tween different LSPs agents and is kept up to date
about their latest status through message passing.
2. Logistic Service Provider Agent LSP:
Each logistic provider is represented in the
problem-solving process by an LSP agent that op-
erates on their behalf. The LSP agents do not in-
teract together directly; they exchange informa-
tion about their state and found solutions through
the coordinator agent. In this work, every LSP
agent runs a meta-heuristic strategy that is dif-
ferent from the other agents and solves the given
problem instance from its perspective and accord-
ing to its personal priorities and goals, such as fol-
lowing potential SLA agreement. LSP agent finds
the best solution and delivers it to the coordina-
tor agent to be evaluated and possibly added to
its pool of solutions replacing the worse existing
solutions there. The coordinator may then resend
the solution to other LSP agents in the next com-
putation round in order to redirect their search to
a potentially better region.
4.2 Communication between Agents
1. 2-way Handshake:
Before starting the computations, every LSP
agent registers itself with the coordinator to en-
able sending and receiving computation messages
from the coordinator. This process starts with a
SUBSCRIBE message sent by LSP agent to the
coordinator, indicating that it is ready to partici-
pate in the computation and start its tasks. Then,
the coordinator registers the LSP in the coali-
tion and sends back a CONFIRM message to
the LSP agent so it can be prepared to the next
phase, the message contains the expected num-
ber of computation rounds that every LSP shall
execute. Once the coordinator agent successfully
receives the SUBSCRIBE message from all ex-
pected LSPs agents, the computation rounds start.
Figure 3 shows the sequence of messages between
the agents in the handshake phase.
2. Computation Messages:
After all LSPs have registered with the coordina-
tor, the coordinator initializes a collection of ran-
dom feasible solutions to the collaborative prob-
lem. Periodically, every LSP agent sends a RE-
QUEST message to the coordinator asking for a
subset of the solutions from its pool, so the agent
uses it as initial solutions in its solving method.
The coordinator reply with an INFORM message
containing a random subset of solutions. After
receiving the initial solutions by the LSP agent,
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
502

Figure 3: Message exchange between different agents in the
2-way Handshake stage.
it starts running its search strategy to find the
best possible solution. When the search ends, the
LSP agent sends the best solution as an INFORM
message to the coordinator, which in turn com-
pares the solution’s quality, in terms of overall
cost-minimizing, to the existing solutions in the
pool. If its quality is better, the new solution is
added to the pool, replacing a less quality solu-
tion. Figure.4 shows messages exchange between
the agents in the computation phase.
4.3 Search Strategies
Different search strategies for every agent are carried
out in the proposed approach. Each LSP agent uses an
adaptive large neighborhood search method (ALNS)
as the underlying search method (Pisinger and Ropke,
2007). ALNS is a local search that is based on ruin
and recreate principle that was proposed in(Schrimpf
et al., 2000). It uses optimization techniques like
threshold accepting and simulated annealing to par-
tially destroy and repair the solutions. There are sev-
eral strategies for the ruin phase, namely, radial ruin,
random ruin, and cluster ruin (Pisinger and Ropke,
2007). A feasible solution is obtained by excluding a
set of customers. In the recreate phase, all excluded
customers are reintroduced to the solution wisely to
minimize their effect on the complete solution. Some
of the most widely used techniques are greedy and re-
gret insertion methods.
4.4 Gain Assignment
In real-life collaboration, participants of any coali-
tion mostly care about their profits and interests rather
than the overall gain. Therefore it is crucial to esti-
mate the individual gain for every participant in the
Figure 4: Messages exchange between different agents in
the computation phase.
coalition. In this paper, we will use two gain assign-
ment methods. The first method is the Shapley value,
which is a concept that was first presented in coopera-
tive game theory as one way to distribute the total gain
of a coalition N among the participants in a fair man-
ner. It captures the marginal contribution made by a
participant i over all permutation S ⊆ N (Ouhader and
El Kyal, 2017).
φ
N
(i) =
1
N!
∑
S⊆N\{i}
k ∗ (cost(S ∪ i) − cost(S)) (14)
Another method is a proportional method, a demand-
based proportional gain assignment that depends on
the demands of the participant served by the coalition.
Let cost(s) be the cost of the best solution found by
given coalition s. Then, the proportional assignment
of the participate i is given as :
cost(i) = ϕ
i
∗ cost(s) (15)
where ϕ
i
is the demand-based factor.
We explore two collaborative scenarios. First, we
consider a full collaboration level where the goal is
to achieve the minimum cost possible.
Table 1: Characteristics of participating LSPs and the costs
of non-collaborative routing.
No.of
orders
No. of
vehicles
Dem-
ands
Individual
routing
Cost
No. of
vehicle
LSP1 82 13 3591 2469.3 9
LSP2 90 13 4478 2644.4 10
LSP3 77 13 4037 2467.6 9
Total 249 39 12106 7581.3 28
Whereas in the second scenario, personalized collabo-
ration is considered as every LSP agent works accord-
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery Problem
503

Table 2: Cost reduction in collaborative scenarios and the satisfaction level of the participants.
Best solution Overall reduction Individual satisfaction
Cost
No. of
vehicle
Cost
No. of
vehicle
LSP1 LSP2 LSP3
Full collaboration 4142.1 26 45.3% 7.1% 5.0 6.0 5.5
Personalized collaboration 4588.9 26 39.5% 7.1% 5.67 5.7 5.4
Table 3: The routing cost allocation of LSPs under collaborative scenarios.
Best solution Cost share / Shapley value Proportional cost
Total cost
No. of
vehicle
LSP1 LSP2 LSP3 LSP1 LSP2 LSP3
Full collaboration 4142.1 26 1312.0 1419.7 1410 1228.6 1532.1 1381.2
Personalized collaboration 4588.9 26 1465.1 1539.6 1577.5 1361.2 1697.4 1530.2
ing to its personal goals while minimizing the over-
all cost. We take, as an example of LSP’s personal
goal, its desire to serve its own packages first before
the others. To measure the satisfaction level of every
participant, we use the average index of its packages’
delivery in the found routes. The smaller the value
is, it indicates that its packages are often delivered in
the early stage with a minimum value of 1 when its
packages are delivered first by every vehicle.
5 EXPERIMENTS AND RESULTS
To implement our proposed architecture, we used
JADE framework (Java Agent DEvelopment), which
supports FIPA specifications. We created a system
consisting of one coordinator agent and three LSP
agents representing three different logistics service
providers in the industry. In our experiment, ALNS
algorithm is used as the primary method, along with
different ruin and recreate strategies for every LSP
agent. LSP1 agent uses ALNS with random ruin strat-
egy and regret/best insertion, LSP2 agent uses radial
ruin strategy, and regret insertion, while LSP3 uses
cluster ruin strategy and regret/best insertion. The co-
ordinator agent maintains a pool of 20 initial solutions
which will be continuously updated. We consider
a multi-depot vehicle routing problem MDVRP; we
use a dataset derived from famous Cordeau datasets
(Cordeau et al., 1997) with few adjustments to fit
the collaborative scenario. We will evaluate the pro-
posed approach based on its performance in solving
this problem.
Table.1 shows the characteristics of partici-
pating LSPs and the cost and vehicles needed for
their individual routing, where every LSP uses its
resources to serve its own customers only with
no collaboration. Table.2 shows the cost of the
best solution for collaborative routing scenarios
using our proposed framework. We calculate the
overall cost reduction of collective routing as the
marginal percentage of (Total Cost
no_collaboration
−
Total Cost
collaboration
)/ Total Cost
no_collaboration
∗
100. Thus, we found that full collaboration between
LSPs reduced the total costs of a margin of 45%
with an almost varied level of satisfaction for the
participants in terms of the average index of delivered
packages since the overall cost reduction was the
only goal. In the second scenario, when considering
personal goals and interests, a decrease in total sav-
ings is observed compared to the first scenario, along
with an increase in participants’ satisfaction levels to
almost equal value as every agent works to achieve its
personal goal first. Table.3 shows the cost allocation
for every participant LSP in both collaboration
scenarios calculated by methods mentioned in Eq.14
and Eq.15 respectively. The overall results show that
participants’ satisfaction levels can be increased by
tolerating some loss in profits.
6 CONCLUSIONS
We have presented a multi-agent framework that sup-
ports the collaboration between different LSPs in
the logistics level serving their customers jointly.
The proposed framework is domain-independent and
can be used for different cooperation scenarios in
problem-solving. Furthermore, it is computationally
efficient and scales to large size problems as it ex-
ploits exploring different areas of the search space si-
multaneously, and produce diverse and mature solu-
tions. When the overall benefit is prioritized, some
unintended biases to one of the participants may hap-
pen, and that will affect the trust in the coalition.
Therefore, we examined when participants work to
achieve objectives according to their preferences in-
stead of focusing on the unified objective. We no-
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
504

ticed that collaboration could achieve a cost reduction
of near 45% compared with individual routing, along
with different satisfaction levels. However, when per-
sonalized goals are considered, the overall saving is
comparatively reduced, but better levels of satisfac-
tion are obtained. Therefore, considering the egali-
tarian approach that guarantees an equal level of ser-
vice and satisfaction may encourage different LSPs to
work towards further collaboration on several levels.
REFERENCES
Barbucha, D. (2012). Search modes for the cooperative
multi-agent system solving the vehicle routing prob-
lem. Neurocomputing, 88:13–23.
Barbucha, D. (2014). A cooperative population learning
algorithm for vehicle routing problem with time win-
dows. Neurocomputing, 146:210–229.
Baykaso
˘
glu, A. and Kaplano
˘
glu, V. (2015). An applica-
tion oriented multi-agent based approach to dynamic
load/truck planning. Expert Systems with Applica-
tions, 42(15-16):6008–6025.
Cattaruzza, D., Absi, N., Feillet, D., and Vidal, T. (2014).
A memetic algorithm for the multi trip vehicle routing
problem. European Journal of Operational Research,
236(3):833–848.
Chatterjee, R., Greulich, C., and Edelkamp, S. (2016). Op-
timizing last mile delivery using public transport with
multi-agent based control. In 2016 IEEE 41st Confer-
ence on Local Computer Networks Workshops (LCN
Workshops), pages 205–212. IEEE.
Chinh, N. Q., Kim, H. C., Siwei, J., and NengSheng, Z.
(2016). Collaborative vehicle routing problem for ur-
ban last-mile logistics. In 2016 IEEE International
Conference on Systems, Man, and Cybernetics (SMC),
pages 001531–001536. IEEE.
Clarke, G. and Wright, J. W. (1964). Scheduling of vehicles
from a central depot to a number of delivery points.
Operations research, 12(4):568–581.
Cordeau, J.-F., Gendreau, M., and Laporte, G. (1997). A
tabu search heuristic for periodic and multi-depot ve-
hicle routing problems. Networks: An International
Journal, 30(2):105–119.
Cruijssen, F., Bräysy, O., Dullaert, W., Fleuren, H., and Sa-
lomon, M. (2007). Joint route planning under vary-
ing market conditions. International Journal of Physi-
cal Distribution & Logistics Management, 37(4):287–
304.
Czarnowski, I., J˛edrzejowicz, P., and Kacprzyk, J. (2013).
Agent-based optimization. Springer.
Dai, B. and Chen, H. (2011). A multi-agent and auction-
based framework and approach for carrier collabora-
tion. Logistics Research, 3(2-3):101–120.
Holdorf, S. and Haasis, H.-D. (2014). Last mile deliv-
ery concepts in e-commerce an empirical approach.
In The 8th International Conference on Software,
Knowledge, Information Management and Applica-
tions (SKIMA 2014), pages 1–6. IEEE.
Kalina, P., Vok
ˇ
rínek, J., and Ma
ˇ
rík, V. (2015). Agents
toward vehicle routing problem with time win-
dows. Journal of Intelligent Transportation Systems,
19(1):3–17.
Kumar, S. N. and Panneerselvam, R. (2012). A survey on
the vehicle routing problem and its variants. Intelli-
gent Information Management, 4(03):66.
Lahyani, R., Khemakhem, M., and Semet, F. (2015). Rich
vehicle routing problems: From a taxonomy to a def-
inition. European Journal of Operational Research,
241(1):1–14.
Martin, S., Ouelhadj, D., Beullens, P., Ozcan, E., Juan,
A. A., and Burke, E. K. (2016). A multi-agent based
cooperative approach to scheduling and routing. Eu-
ropean Journal of Operational Research, 254(1):169–
178.
Mingozzi, A., Roberti, R., and Toth, P. (2013). An exact
algorithm for the multitrip vehicle routing problem.
INFORMS Journal on Computing, 25(2):193–207.
Ouhader, H. and El Kyal, M. (2017). Combining facil-
ity location and routing decisions in sustainable ur-
ban freight distribution under horizontal collabora-
tion: how can shippers be benefited? Mathematical
Problems in Engineering, 2017.
Pisinger, D. and Ropke, S. (2007). A general heuristic for
vehicle routing problems. Computers & Operations
Research, 34(8):2403–2435.
Schrimpf, G., Schneider, J., Stamm-Wilbrandt, H., and
Dueck, G. (2000). Record breaking optimization re-
sults using the ruin and recreate principle. Journal of
Computational Physics, 159(2):139–171.
Schwarze, S. and Voß, S. (2013). Improved load balancing
and resource utilization for the skill vehicle routing
problem. Optimization Letters, 7(8):1805–1823.
Schwind, M., Gujo, O., and Vykoukal, J. (2009). A com-
binatorial intra-enterprise exchange for logistics ser-
vices. Information Systems and E-business Manage-
ment, 7(4):447–471.
Souza, G. R., Goldbarg, E. F., Goldbarg, M. C., and Canuto,
A. M. (2012). A multiagent approach for metaheuris-
tics hybridization applied to the traveling salesman
problem. In 2012 Brazilian Symposium on Neural
Networks, pages 208–213. IEEE.
Talukdar, S., Murthy, S., and Akkiraju, R. (2003). Asyn-
chronous teams. In Handbook of Metaheuristics,
pages 537–556. Springer.
Wang, X. and Kopfer, H. (2014). Collaborative transporta-
tion planning of less-than-truckload freight. OR Spec-
trum, 36(2):357–380.
Wang, X. and Kopfer, H. (2015). Rolling horizon planning
for a dynamic collaborative routing problem with full-
truckload pickup and delivery requests. Flexible Ser-
vices and Manufacturing Journal, 27(4):509–533.
Zhou, W., Song, T., He, F., and Liu, X. (2013). Multiobjec-
tive vehicle routing problem with route balance based
on genetic algorithm. Discrete Dynamics in Nature
and Society, 2013.
A Meta-heuristic based Multi-Agent Approach for Last Mile Delivery Problem
505
