
Solution of a Practical Pallet Building Problem with Visibility and
Contiguity Constraints
Manuel Iori
2
, Marco Locatelli
1
, Mayron C. O. Moreira
3
and Tiago Silveira
1
1
Department of Engineering and Architecture, University of Parma, Parma, Italy
2
Department of Engineering and Architecture, University of Modena and Reggio Emilia, Reggio Emilia, Italy
3
Department of Computer Science, Federal University of Lavras, Lavras, Brazil
Keywords:
3D Packing, Practical Constraints, Contiguity, Visibility, Constructive Heuristics, Real-world Instances.
Abstract:
We study a pallet building problem that originates from a case study at a company that produces pallet building
robotized systems. The problem takes into account well known constraints, such as rotation and stackability,
and we introduce two practical constraints named visibility and contiguity between items of the same type.
We formalize the problem and propose heuristic algorithms to solve it, using a strategy that first creates 2D
layers and, then, creates the final 3D pallets. The proposed heuristic is based mainly on the Extreme Points
heuristic, that is tailored to choose feasible positions to pack items during the construction of the solution.
Besides that, we adapt our proposed heuristic using other basic heuristics from the literature, considering
different constraints. The performance of the algorithms is assessed through extensive computational tests on
real-world instances, and the obtained results show the proposed heuristics are able to create compact packing
in a very short time.
1 INTRODUCTION
We study the problem of loading a given set of items
into one or more pallets, so as to minimize the num-
ber of pallets used. The problem originates from a
real-world robotized application and is thus subject to
some non-trivial operational constraints. Items should
be packed into layers, that must then be piled one over
the other while respecting given stackability rules. In
addition, items are grouped into families, and, to fa-
cilitate loading/unloading operations, items from the
same family packed into the same layer should be
contiguous one with the other.
The problem we face lies in the field of Cutting
and Packing (C&P), one of the most widely studied
areas of Operations Research (Scheithauer, 2018; Iori
et al., 2019; Bortfeldt and W
¨
ascher, 2013; Crainic
et al., 2012; Hopper and Turton, 1998). In cutting
problems, a set of stock units has to be cut to pro-
duce smaller items, while in packing problems, a set
of items has to be packed into one or more contain-
ers. These problems have attracted the attention of re-
searchers both for their practical and theoretical inter-
est. Some practical applications involve the produc-
tion of materials that come in panels (such as wood or
glass), the optimization of layouts (as in industry or
newspaper paging), and the loading and subsequent
transportation of items employing containers, to men-
tion a few. Most C&P problems are associated with
mass-production operations in a company. Therefore,
improvements in the time performance of the process
as well as reduction in the material wasted are directly
related to the application of efficient methods. Previ-
ously, C&P tasks were usually made by skilled ex-
perts, but this has been changing over the years by
automated-packing (robotized) systems, as is the case
for the problem we face in this work.
Several interesting surveys and books have been
published in recent years to try to review the fast-
growing C&P literature, see, e.g., (Crainic et al.,
2012), (Lodi et al., 2014), (Silva et al., 2016) and
(Scheithauer, 2018). A typology of C&P problems
has been proposed by (W
¨
ascher et al., 2007). Later,
(Bortfeldt and W
¨
ascher, 2013) extended the paper of
(W
¨
ascher et al., 2007), considering the area of con-
tainer loading and its main constraints. They noted
that “the space available for packing above a pallet
might be interpreted as a container, too”, so they dis-
cussed constraints that can arise either when loading
a container or a pallet. Indeed, apart from container-
related constraints (such as weight limit and distri-
bution), they also discussed item-related constraints
Iori, M., Locatelli, M., Moreira, M. and Silveira, T.
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints.
DOI: 10.5220/0009351703270338
In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 327-338
ISBN: 978-989-758-423-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
327

(as loading priorities, orientation, and stacking) that
can be useful for pallets. The authors also considered
cargo-related constraints, positioning constraints, and
other load-related constraints that may appear dur-
ing transportation, see also (Iori and Martello, 2010);
(Iori and Martello, 2013), such as vertical and hori-
zontal stability.
The problem we face includes many of such con-
straints (as outlined in detail next in Section 2). In
particular, we highlight the contiguity among items
that belong to the same family. The concept of conti-
guity has already been addressed in the C&P literature
(Terno et al., 2000; Scheithauer and Sommerweiβ,
1998), although we could not find a univocal and for-
mal description, probably because it was included in
heuristic algorithms.
The pallet building problem that we study in this
paper is NP-hard, because it is a specific case of the
Bin Packing Problem, which is known to be NP-hard
(Martello et al., 2000). In addition, it needs to be
solved fast because it is frequently encountered at the
operational level during the everyday working activ-
ity of a robotized packing system. For these reasons,
we found it necessary to adopt heuristic solution al-
gorithms. We derived these algorithms from the most
successful and recent C&P studies, by embedding in
them in a tailored way the additional operational con-
straints of the problem at hand.
Our main contributions can be sketched as fol-
lows: an interesting problem that derives from a real-
world industrial application is presented; a concise lit-
erature review is provided; the concept of contiguity
of items, that is very useful in practice during load-
ing/unloading operations but has never been formally
treated in the literature, is discussed in detail; exten-
sive computational tests on instances derived from the
real-world case study are given.
The remainder of the paper is organized in five fur-
ther sections. Section 2 provides a formal description
of the problem. Section 3 briefly reviews the related
literature. Section 4 presents the heuristic algorithms
that we implemented. Section 5 gives the outcome of
extensive computational tests. Conclusions and some
future research directions are given in Section 6.
2 PROBLEM DESCRIPTION
We are given an arbitrarily large set R = {1, 2,.. . , m}
of identical pallets. Each pallet has a two-dimensional
loading surface of width W ∈ Z
∗
+
and length L ∈
Z
∗
+
, which can be used to load items up to a max-
imum height H ∈ Z
∗
+
. We are also given a set I =
{1,2, . . ., n} of 3D rectangular item types, where each
item type i ∈ I contains b
i
identical items, each hav-
ing width w
i
∈ Z
∗
+
, length l
i
∈ Z
∗
+
, and height h
i
∈ Z
∗
+
,
such that w
i
≤ W , l
i
≤ L, and h
i
≤ H.
Item types are partitioned in input into a set F
of families as follows. Each item type i belongs to
a given family f
i
∈ F, which is defined as a set of
item types having similar height and weight. About
this concept, as we are interested just in the packing
problem, it is enough to take into account only the ge-
ometric characteristics of the items, since they have
the same final destination.
Items belonging to the same family can be used
to form layers. Each layer is a 2D packing of items
whose total width does not exceed W , and whose total
length does not exceed L. In general, we consider
three types of layers:
• single-item type layers are formed by a unique
type of items;
• single-family layers are formed by different item
types, but all belonging to the same family;
• residual layers are formed by a combination of
items of different families or, alternatively, by
items belonging to the same family but with oc-
cupation lower than a pre-defined threshold.
Let us call a group a set of items having the same
item type and being loaded in the same layer. Pack-
ings of items in a layer should fulfill two operational
constraints that concern groups and are aimed at eas-
ing unloading operations when the pallet is delivered:
• the contiguity constraint imposes that all items
in a group are packed contiguously one with the
other, that is, each of them is ‘close enough’ to
one of the other items of the same group;
• the visibility constraint requires that at least one
item per group is packed with one of its edges
‘close enough’ to the border of the layer, so be-
ing visible by the outside;
Single-item type layers and family layers can be used
in a 3D packing to support other layers that are packed
on top of them. For this purpose, we establish two
additional conditions:
• a stackability constraint imposes that heavy items
can not be on top of fragile ones. Formally, each
family f ∈ F is assigned with a level of resistance
ρ
f
, with small values indicating fragile items and
large values indicating heavy ones. Items belong-
ing to family f cannot be put below items belong-
ing to family g if ρ
f
< ρ
g
;
• a layer can be used to support other layers only
if its total area loaded with items reaches a mini-
mum fraction of α of the total loading surface W L.
Parameter 0 < α < 1 is called fill-factor. A layer
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
328

with loaded area lower than αW L can still be used
to build a pallet, but can only be the topmost layer.
We call this the minimum supporting area con-
straint.
The aim of the pallet building problem (PBP) that we
face is to load all items into the minimum number of
pallets, by ensuring that the following constraints are
satisfied:
• all items should be packed in layers by satisfying
grouping and visibility constraints;
• single-item type and single-family layers can be
used to support other layers on top of them as long
as support and fill-factor constraints are satisfied;
• at most one residual layer can be used per pallet,
and, in such a case, it must be placed at the top of
the load;
• the total height of the layers in any pallet should
not exceed H.
Note that we use the term pallet building, instead of
pallet loading, to avoid confusion with the more fa-
mous pallet loading problem (PLP), which calls for
packing a set of two-dimensional rectangular items
without overlapping and by allowing a 90
◦
rotation
into a two-dimensional bin. We refer the reader in-
terested in the PLP to (Silva et al., 2016) for a recent
survey and to (Delorme et al., 2017) for a state-of-the-
art computational analysis.
3 BRIEF LITERATURE REVIEW
The PBP emerges as a variant of the Container
Loading Problem (CLP), which has received a good
amount of attention in the last years. (Bortfeldt and
W
¨
ascher, 2013) presented a comprehensive survey of
the main constraints used in the literature. They ver-
ified that heuristic approaches are more frequently
used than exact and approximation-guarantee algo-
rithms. (Silva et al., 2016) considered the PLP. They
proposed a broad analysis of the solution methods and
some aspects concerning computational complexity,
upper bounds, and data sets most used in numeri-
cal experiments. (Crainic et al., 2012) presented a
survey about 2D and 3D Orthogonal Packing Prob-
lems, focusing on data structures for the packing rep-
resentation and the item-positioning rules. Concern-
ing criteria to place items, they highlighted: (i) in-
terval graphs (Fekete and Schepers, 1997), to rep-
resent the overlap between items; (ii) corner points
(Martello et al., 2000), that describe feasible places to
pack an item in a partial solution; and (iii) extreme
points (Crainic et al., 2008), that increase the amount
of feasible regions on the partial packing of the corner
points. Recently, (Iori et al., 2019) proposed a sur-
vey on variants of 2D packing problems, considering
techniques to represent and handle items, relaxation
methods, as well as exact and heuristic approaches.
We also refer to (W
¨
ascher et al., 2007) for a catego-
rized typology of 2D packing problems.
The PBP can be separated into two subsequent de-
cisions: the first one consists in creating 2D layers,
while the second one involves staking layers to form
pallets and thus considers the 3D characteristics. In
the following, we discuss some relevant approaches
for 2D and 3D, respectively.
For what concerns heuristics for 2D problems,
(Chazelle, 1983) described an efficient way to imple-
ment the famous bottom-left heuristic, which packs
the items, one at a time in a given order, in the lowest-
most and left-most position. (Burke et al., 2004) pre-
sented a new placement heuristic, called best-fit, for
a 2D cutting problem, allowing non-guillotine pack-
ings and rotations of 90 degrees. This technique uses
a dynamic search based on the “niches”, which are
the available bottom-most gaps for an item in the par-
tial packing. In terms of metaheuristics, (Alvarez-
Valdes et al., 2008) developed a GRASP for the 2D
strip packing problem, which is the problem of pack-
ing items into a strip of a given width by minimizing
the used height. In the constructive phase, the items
are placed into rectangles following specific criteria.
A new rule attempts to foresee the future effect of the
tallest object in the final solution to avoid spikes. The
local search iteratively destroys and rebuilds portions
of the current solution. Extensive computational ex-
periments attested the effectiveness of the proposed
strategy. (Imahori and Yagiura, 2010) improved the
technique proposed by (Burke et al., 2004) by pre-
senting a quicker implementation based on a balanced
binary search tree and a priority heap with a doubly-
linked list. (Leung et al., 2011) presented a com-
plete set of techniques to deal with the 2D strip pack-
ing problem. They use the so-called “skyline” ap-
proach in conjunction with greedy local search, a sim-
ulated annealing metaheuristic, and a multi-start di-
versification strategy. We also mention the so-called
G4-Heuristic, developed by (Scheithauer and Terno,
1996) for the PLP.
For what concerns 3D problems, (Haessler and
Talbot, 1990) addressed a real CLP involving some
practical constraints. They proposed an integer pro-
gramming formulation and a heuristic algorithm.
(Bischoff and Ratcliff, 1995) presented two heuris-
tics for the CLP: the first one produces loading pat-
terns with a high degree of stability; the second one
considers a multi-drop situation in which a Last-In-
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints
329

First-Out constraint is imposed on the cargo. (Terno
et al., 2000) proposed the parallel generalized layer-
wise loading approach (PGL-approach) for the CLP.
The constraints they consider are: (i) weight capac-
ity; (ii) placement (some items cannot be inserted
over the others); (iii) splitting (items of the same type
should be loaded in a minimum number of contain-
ers); (iv) connectivity; and (v) stability. Using a com-
plex branch-and-bound algorithm, the authors show
a certain degree of competitiveness compared with
classical solutions reported in the literature. (Bort-
feldt and Gehring, 2001) proposed a hybrid genetic al-
gorithm to solve the CLP with a single container and a
strongly heterogeneous set of boxes, considering ori-
entation, stability, stacking, weight, and balance. The
results showed a better efficiency with more signif-
icant heterogeneity of the box sets. (Egeblad et al.,
2010) addressed the CLP for one container (in the
knapsack version), using irregular shaped items, and
taking a stability constraint into account. They per-
formed tests on randomly generated instances, and on
real-world instances deriving from a prominent Eu-
ropean furniture producer. (J
´
ozefowska et al., 2018)
study the CLP considering rotation, stackability, and
stability constraints. They considered a case study
arising from a household equipment factory. They
proposed a best fit heuristic based on the idea of wall-
building over available space.
The work that most resembles ours is the one by
(Alonso et al., 2016), who presented a real exam-
ple originating from a logistics company required to
load products into pallets (pallet building) and then
load the created pallets into trucks (truck loading),
by considering several practical constraints. For the
pallet building, they incorporated orientation, sup-
port, priority, and stackability constraints. Regard-
ing the truck loading, they adopted restrictions due
to priority among pallets, stability, and stackability.
They proposed a GRASP algorithm using a construc-
tive phase, a randomized strategy to diversify the so-
lutions, and an improvement phase. The efficiency
of their GRASP was analyzed by comparing it with
lower bounding procedures, showing good results.
The study was later extended by (Alonso et al., 2017)
and (Alonso et al., 2019), who focused on the devel-
opment of mathematical models for the case of mul-
tiple container loading, addressing a number of addi-
tional practical constraints such as vertical and hori-
zontal stability, multi-drop, and load balance.
4 SOLUTION ALGORITHMS
This section presents the 2-step heuristic that we de-
veloped to solve the PBP with visibility and contigu-
ity constraints, which we call Extreme Points Modi-
fied Heuristic (EPMH). EPMH produces feasible so-
lutions by dividing the problem into two parts. First,
we create layers to deal with individual items sepa-
rately. This phase forces the presence of packing, vis-
ibility, and contiguity constraints through a process
guided by an evaluation function. Second, the pal-
let generation step tries to minimize the quantity of
pallets using a greedy strategy. Next, we particularly
focus in the description of the first step (layers cre-
ation), as the second step (pallets creation) is based
on a quite standard algorithm.
4.1 Creating Layers
All 2D layers are created by taking into account only
the l
i
and w
i
dimensions of item i ∈ I. The following
concepts are related to the heuristic proposed.
Contiguity. Two items of the same type cannot be
placed far apart in a layer because of the contiguity
constraint. For this purpose, we establish the max-
imum euclidian distance that can separate the two
items without violating the constraint as follows.
Let ` be the smallest edge length among all items
in I. Let also G ⊆ I be a generic subset of items of
the same type packed into a layer. Then, two items
i, j ∈ G satisfy the contiguity constraint if the smallest
euclidian distance between the edges of i and the
edges of j is strictly lower than `. Roughly speaking,
in this way we guarantee that no other item can fit
between i and j. Therefore, the contiguity constraint
for a generic layer r is met if, for each group G
packed in r, any item in G meets the minimum
required euclidean distance from at least another item
in G, and there are no separated sub-groups of G (i.e.,
subgroups whose distance is ` or more).
Visibility. Similarly to what we stated for the conti-
guity, we say that a group is visible from the outside
if for at least one item in the group, the euclidean
distance between its edges and the borders of the
layer is strictly lower than `.
Item Positioning. To find the position of an item in
a layer, we use an adaptation of the Extreme Points
Heuristic (EPH) proposed by (Crainic et al., 2008).
Originally, EPH was described for 3D packings. As
we need to deal with just a 2D layer, we limit our de-
scription here to this simpler case. To this aim, let
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
330
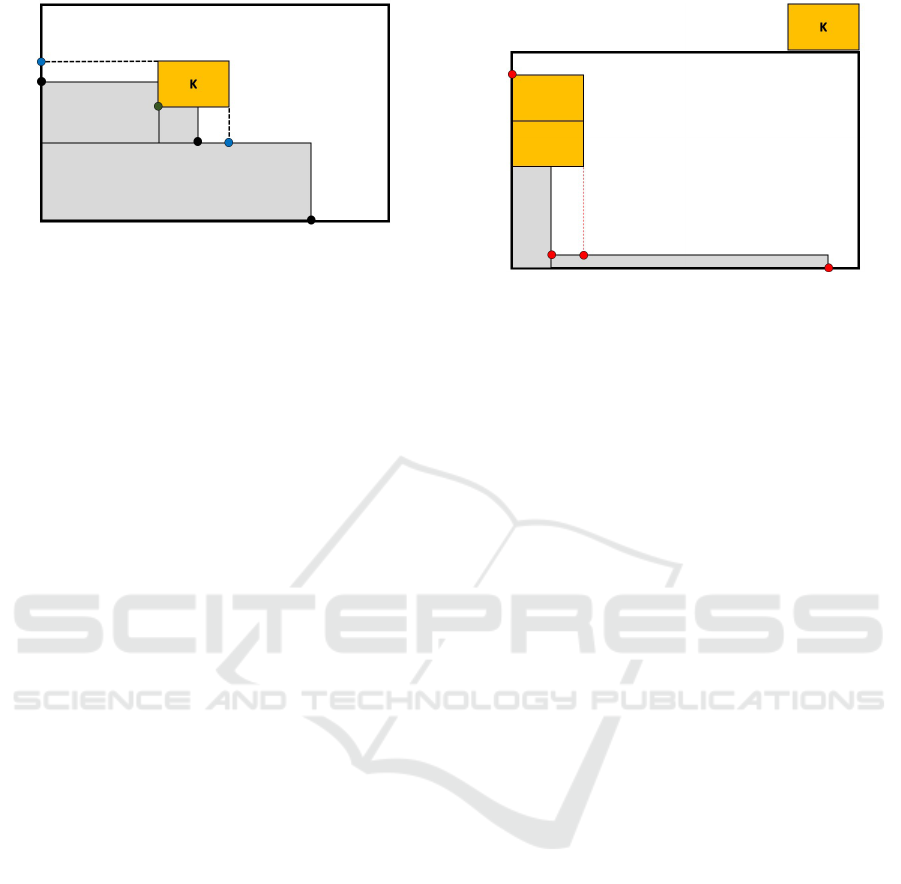
Figure 1: Extreme points: black and green points form the
current set E; the green point is chosen to pack item k (and
is then removed); blue points are the new extreme points
added to E after packing k.
us consider that the 2D layer under construction is
placed in the positive quadrant of the cartesian sys-
tem, with width parallel to the x-axis, length parallel
to the y-axis, and bottom-left corner located in the ori-
gin of the axes.
EPH works with the concept of extreme points.
An extreme point e is a point in the 2D space, where
an item k ∈ I can be packed by taking into account a
partial packing solution built so far. For the sake of
clarity, packing an item k in an extreme point e means
packing the bottom-left corner of k in e.
In EPH, the items are packed one at a time in the
layer, by considering a set E of available extreme
points. The set is initialized with the origin point
(0,0). Then, each time a new item is packed, the set is
updated by removing the point used for the packing of
the item, and possibly inserting new extreme points.
These new extreme points are obtained by computing
the projection of k over the partial packing solution
under construction, considering the two axes.
For the x-axis, EPH horizontally projects the top
edge of item k to its left, until the projection touches a
previously packed item or the left border of the layer
(i.e., the y-axis). This is the first extreme point that
is possibly created. For the y-axis, instead, EPH con-
siders the right edge of item k and vertically projects
it towards the bottom until the projection reaches a
previously packed item or the bottom border of the
layer. This is the second extreme point possibly cre-
ated. These two points are added to E if they were
not already included in it. Figure 1 depicts an exam-
ple with a set E formed by green and black points.
The green point is selected for the packing of item k
and is thus removed from E. The blue points are the
new extreme points added to E after the packing of k.
An extreme point e can be either feasible or infeasible
for the packing of the next item k, depending on the
fact that such packing meets all required constraints.
In addition to what we described so far, please also
note that, besides the projections from k, it is manda-
Figure 2: A case where the EPH generates only extreme
points that are infeasible for the PBP with visibility and con-
tiguity constraints. Packing the next item k is impossible, so
the current layer is closed and a new one is opened.
tory to verify all projections from i ∈ I that lie on k.
This step, that we name past projections, is needed to
find new extreme points not yet available. We execute
it right after having computed the projections from k.
The original EPH solves pure 2D packing prob-
lems, so we need to include a set of changes to be
able to solve the more complex PBP with visibility
and contiguity constraints. The first modification we
apply consists in increasing the search space inside a
layer. The EPH creates only two new extreme points
at a time, whereas visibility and contiguity constraints
narrow the search space. As a consequence, a layer
could be closed even when its occupation is low, be-
cause set E does not contain any feasible extreme
point. Figure 2 shows an example where this situa-
tion occurs, since none of the current feasible extreme
points fulfills the contiguity constraints.
To overcome this limitation, we included some
new extreme points, considering two cases: contigu-
ity and visibility. In the first case, the extreme points
are included around item k (the last item packed), to
allow the contiguity with the next items of the same
type. Basically, four new points are added: the k top-
left and bottom-right corners allow the top and right
connections, respectively, and the points on the left
and below k enable the left and bottom connections,
respectively. Figure 3 shows the new extreme points
for the contiguity case.
Extreme points regarding the visibility case are in-
cluded close to the top and right layer borders, when
item k has a different type from the previously packed
items, and there is no point in E that allows k to meet
the contiguity with the layer and the packing con-
straints. In this case, two new points are added: from
right to left relative to layer, we take the first feasible
point that meets the contiguity to the top layer border.
Also, from top to bottom relative to layer, we consider
the first feasible point that meets the contiguity to the
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints
331

Figure 3: New extreme points created for contiguity: after
packing k in the green point (which is then removed from
the current set E), four extreme points (represented in blue)
are added.
right layer border. Figure 4 shows the new extreme
points for this case.
The second modification is related to heuristic
efficiency. Current extreme points are directly linked
to the visibility and contiguity constraints. Note
that these points can be enabled according to item
k and its current item group in the partial solution.
Thus, we work with two extreme points sets: feasible
extreme points, E
f
, and infeasible extreme points,
E
i
, representing, respectively, points that meet or
do not meet the visibility and contiguity constraints
for item k. Therefore, before adding k to the partial
solution, we first update these two sets, and only after
this is done we check if k overlaps with previously
packed items. Note that these two sets are relative
to the current configuration and after the addition of
the new items infeasible points may become feasible
and viceversa. The benefit of using these sets is that
we avoid checking the overlapping constraint for all
extreme points, increasing the heuristic efficiency.
An example of sets E
f
and E
i
is provided in Figure 5.
Evaluation Functions. Given a set E
f
for the next
item k that meets the packing constraints, we should
choose which point results in the best packing. To
this aim, we propose the following fitness evaluation
functions:
• LOWER X: finds the point that has the minimum
x value among all feasible points;
• LOWER Y: finds the point that has the minimum
y value among all feasible points;
• BOUNDING BOX: calculates the bounding box
area – minimum rectangle area that covers a set
of items – with k, and finds the point which mini-
mizes the area among all bounding boxes;
• BOUDING SQUARE: same as above but with
squares instead of boxes;
Figure 4: New extreme points created for visibility: pre-
vious extreme points that do not meet visibility and the
packing constraints are shown in red; new feasible extreme
points that meet these constraints are shown in blue.
• SIMPLE CONTACTS: calculates the number of
contacts – a contact between two items happens
when they meet the contiguity previously de-
scribed in this Section, i.e., when their distance
is lower than ` – with k, and finds the point which
maximizes this number;
• COMPLEX CONTACTS: similar to the previous
one, but the number of contacts is switched by
the contact length – the euclidian distance of edge
overlap between different items – among the items
that meet the contiguity with k. It finds the point
which maximizes this value;
• DISTANCE SUM: calculates the distance sum
among the center of gravity of each packed item
with the center of gravity of k, and finds the point
which minimizes this sum;
• CENTER OF GRAVITY: evaluates the distance
between the center of gravity of the partial pack-
ing and the center of gravity of k, and finds the
point that minimizes this distance.
Figure 6 shows a graphical example for each fitness
evaluation function proposed.
The fitness of a new item k is calculated from the
partial packing in the layer using a specific group of
items, formed by some or the whole set of their items.
To form these groups, we proposed the following
strategy: when k is the first item of a specific type in
the partial solution, the fitness is calculated consider-
ing the group formed by all items in the layer. When
there is at least one item of the same type of k, the
fitness is calculated by considering the group formed
by the items of this specific type.
Layer Creation and Classification. The main idea of
EPMH is to create as many single-item and single-
family layers as possible. This is because the residual
layers have to be inserted at the top of pallets, at most
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
332
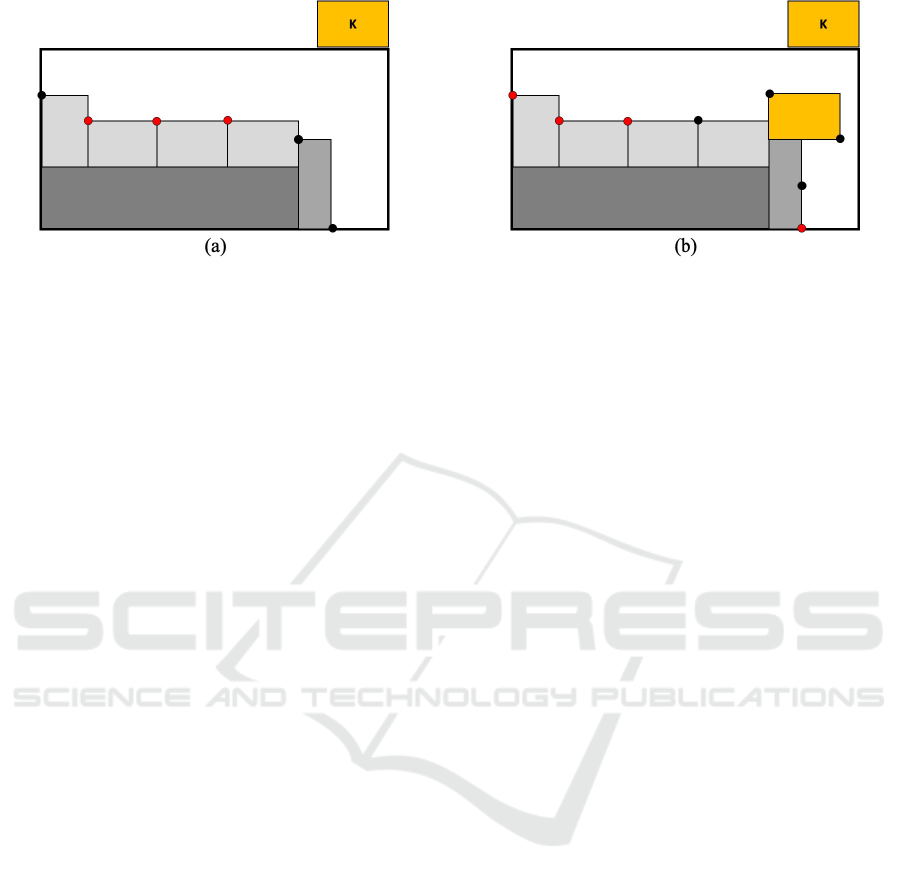
Figure 5: Partial solutions and their feasible (black) and infeasible (red) extreme points for the next item k: representation of
the extreme points that meet the (a) boundary, and (b) contiguity constraints.
one residual layer per pallet, so their number should
be as small as possible. The layer generation that we
adopted follows this rationale as follows.
In the first step, we sort the family items by non-
increasing value of stackability. Within each fam-
ily, item types are sorted by non-increasing value of
height. Using this order, EPMH tries to generate
single-item layers by packing items one at a time ac-
cording to the concepts described before in this sec-
tion. If the packing obtained with a single item type
meets the fill-factor constraint but it is not enough to
fill up the layer yet, EPMH tries adding more items of
the same family to generate a single-family layer.
When the sum of all items of a specific family is
less than the required percentage to meet the fill factor
constraint, the remaining items are put in a residual
item list. A particular case occurs when the sum of
all items of some type has enough area to meet the fill
factor constraint, but the current solution found by the
packing heuristic creates a packing that does not meet
that constraint. In this case, the heuristic removes all
items of this layer, putting them in the residual item
list. At the end of the process, after all families have
been analyzed, the items of the residual list will be
packed in remaining layers, thus forming residual lay-
ers. The classification of a layer is made after it is
closed, analyzing its occupation, the families and the
item types that are included in it.
4.2 Creating Pallets
After all items have been packed into layers, we need
to put layers together into the minimum number of
pallets. To this aim, we propose a simple greedy
heuristic. The height of each layer is calculated as
the height of the highest item in the layer. Simi-
larly, the stackability of a layer is computed as the
maximum stackability value among the items in the
layer. Single-item, single-family and residual layers
are sorted according to non-increasing stackability,
breaking ties by non-increasing height, and this order
is used throughout the algorithm.
Since residual layers need to be packed in sepa-
rated pallets, the greedy heuristic starts by choosing
the first residual layer, if any, in the order, and using
it to initialize a pallet. Then, it fills the current pal-
let with single-item layers, one at a time in the order,
by respecting stackability and maximum height con-
straint. If the current pallet has still unused height but
no more single-item layer can enter it, the heuristic
attempts filling the pallet with single-family layers.
Also in this case, the layers are scanned according to
the above order. The process is repeated until no more
layer can enter the pallet. The process is repeated un-
til all layers are packed into pallets.
This greedy heuristic allows us to have a feasible
PBP solution in quick time. We used it as a basis for
evaluating our new EPMH under several fitness func-
tions as well as existing heuristic in the literature (that
do not consider contiguity and visibility constraints),
as shown in the next section.
5 COMPUTATIONAL RESULTS
In this section, we present the details of the instances
that we adopted for our tests and then show the com-
putational results that we achieved. All experiments
have been conducted on a PC Intel Core i5 Dual-Core
1.8GHz CPU, 8GB RAM, macOS Catalina Operat-
ing System. The algorithms have been implemented
in Java (Oracle
R
JDK 8). Due to its deterministic na-
ture, each heuristic was run only once. Because of
the high number of instances addressed, in the fol-
lowing we mostly report average results for groups of
instances.
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints
333
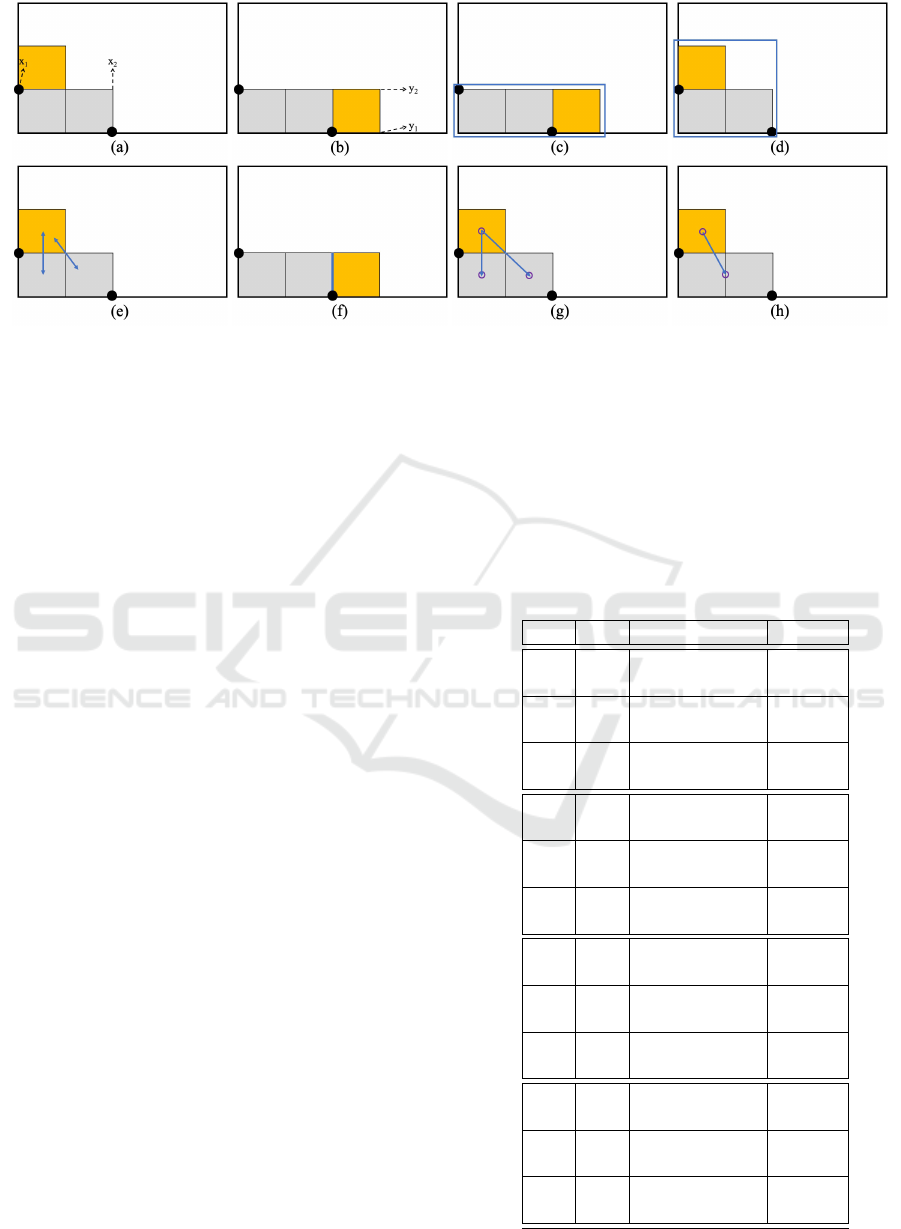
Figure 6: Fitness evaluation functions of feasible extreme points, considering a new yellow item: (a) Lower X; (b) Lower Y;
(c) Bounding Box; (d) Bounding Square; (e) Simple Contacts; (f) Complex Contacts; (g) Distance Sum; (h) Center of Gravity.
5.1 Instances
The results were obtained from a real-world database
provided by an Italian company. We randomly se-
lected 24 instances, that are separated into 4 groups,
each containing 6 instances, characterized by differ-
ent intervals in the number of distinct items: from 17
to 32; from 33 to 48; from 49 to 64; and from 65 to
80. The average number of items for each instance
is approximately 690. Table 1 summarizes the details
of the instances, reporting the instance id number, the
number of items, the number of families, and the max-
imum number of items per type. For all instances, the
fill factor was set to 75%, and the container dimen-
sions were set to 1500, 1250, and 1050 for height,
width, and length, respectively. We tested a number
of configuration, including rotation of 90 degrees of
the items allowed or not.
5.2 Evaluation
We solved the proposed instances with three algo-
rithms. The first one is the basic EPH described in
Section 4, and the second is the constructive heuris-
tic based on skylines and proposed by (Leung et al.,
2011), named SLH in the following. These two meth-
ods are taken from the literature and do not take into
account contiguity and visibility of the items. The
third method is the newly-proposed EPMH method,
attempted with the different evaluation functions dis-
cussed in the previous section. All such methods are
adopted to generate 2D layers, which are then put to-
gether into pallets by the greedy heuristic of Section
4.2. In this way, we can evaluate all methods in a
consistent way and understand which one is more ef-
fective for the layer generation.
The computational results that we obtained are
summarized in Table 2. Each row in the table pro-
vides average results for a given algorithm on the
24 attempted instances. We tested the two heuristics
from the literature, namely EPH and SLH, with (R)
and without (-) rotation. We then tested EPMH with 8
different evaluation functions, attempting 4 different
Table 1: Instances settings.
ID n N. of families Max b
i
01
20
4 208
02 12 122
03
23
4 70
04 13 35
05
29
6 60
06 15 390
07
34
7 142
08 17 158
09
37
6 63
10 17 95
11
48
9 123
12 18 182
13
59
10 53
14 19 87
15
64
11 57
16 19 64
17
61
10 26
18 19 166
19
75
16 62
20 20 79
21
79
17 79
22 21 128
23
66
13 70
24 19 98
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
334

Table 2: Computational results (average results on 24 instances on each line).
Algorithm Constraint
N. of
pallets
N. of
layers
2D fill
factor
Single-
item
layers
Single-
family
layers
Residual
layers
Max. percent.
of residual
layers
N. of
non-contiguous
items
N. of
non-contiguous
layers
N. of
non-visible
items
N. of
non-visible
layers
Time(secs)
.
EPH
R 24.75 43.46 0.82 14.46 9.13 19.88 76.36% 12.17 10.13 4.17 3.25 0.023
- 25.58 43.04 0.82 12.83 8.50 21.71 74.07% 4.75 3.88 5.42 4.33 0.026
SLH
R 22.83 42.17 0.84 16.75 7.17 18.25 73.08% 4.38 3.58 4.75 3.58 0.009
- 27.58 45.25 0.78 14.79 6.00 24.46 77.19% 5.67 4.54 7.00 5.17 0.011
EPMH –
LOWER X
R/B 22.83 42.00 0.84 14.42 9.38 18.21 73.08% 0 0 0 0 0.161
R/- 22.79 42.04 0.84 14.38 9.46 18.21 71.70% 0 0 2.92 2.42 0.068
-/B 25.88 43.29 0.81 12.83 8.46 22.00 74.07% 0 0 0 0 0.102
-/- 25.58 43.17 0.82 12.83 8.67 21.67 72.22% 0 0 3.71 2.67 0.068
EPMH –
LOWER Y
R/B 23.00 41.88 0.85 14.33 8.88 18.67 73.08% 0 0 0 0 0.137
R/- 22.83 41.75 0.85 14.33 9.00 18.42 73.08% 0 0 4.42 3.33 0.079
-/B 26.17 43.25 0.81 12.83 7.96 22.46 75.93% 0 0 0 0 0.108
-/- 25.96 43.13 0.82 12.83 8.21 22.08 74.07% 0 0 4.67 3.46 0.077
EPMH –
BOUNDING
BOX
R/B 14.46 41.00 0.86 21.79 11.58 7.63 66.67% 0 0 0 0 0.104
R/- 14.00 40.83 0.86 21.79 12.00 7.04 66.67% 0 0 6.08 3.96 0.070
-/B 26.17 43.25 0.81 12.83 7.79 22.63 75.47% 0 0 0 0 0.112
-/- 25.67 42.92 0.82 12.83 8.04 22.04 75.93% 0 0 5.38 3.79 0.068
EPMH –
BOUNDING
SQUARE
R/B 23.00 42.38 0.83 14.00 10.29 18.08 70.00% 0 0 0 0 0.110
R/- 23.50 42.42 0.83 14.04 9.63 18.75 72.55% 0 0 5.13 3.83 0.081
-/B 25.88 43.17 0.81 12.83 8.17 22.17 77.78% 0 0 0 0 0.106
-/- 25.96 43.08 0.82 12.83 7.92 22.33 74.07% 0 0 5.08 3.54 0.067
EPMH –
SIMPLE
CONTACTS
R/B 23.13 42.21 0.84 14.21 9.46 18.54 73.08% 0 0 0 0 0.110
R/- 23.33 42.29 0.84 14.21 9.29 18.79 74.51% 0 0 5.54 4.04 0.077
-/B 26.13 43.38 0.81 12.83 8.13 22.42 75.93% 0 0 0 0 0.119
-/- 26.04 43.38 0.81 12.83 8.38 22.17 75.93% 0 0 4.67 3.38 0.126
EPMH –
COMPLEX
CONTACTS
R/B 19.75 42.08 0.84 16.58 11.13 14.38 61.46% 0 0 0 0 0.110
R/- 20.50 41.88 0.84 16.58 9.96 15.33 62.50% 0 0 6.58 4.54 0.086
-/B 26.33 43.29 0.82 12.83 7.83 22.63 78.18% 0 0 0 0 0.116
-/- 26.21 43.29 0.82 12.83 8.08 22.38 75.93% 0 0 6.04 4.21 0.076
EPMH –
CENTER OF
GRAVITY
R/B 23.08 42.46 0.83 14.00 10.21 18.25 64.71% 0 0 0 0 0.129
R/- 23.88 42.29 0.83 14.00 8.88 19.42 71.15% 0 0 6.75 4.67 0.080
-/B 26.38 43.33 0.81 12.88 7.63 22.83 75.93% 0 0 0 0 0.100
-/- 26.67 43.17 0.82 12.88 7.33 22.96 75.93% 0 0 6.63 4.67 0.068
EPMH –
DISTANCE
SUM
R/B 23.17 42.38 0.83 14.04 10.04 18.29 66.67% 0 0 0 0 0.122
R/- 23.71 42.25 0.84 14.04 9.29 18.92 71.15% 0 0 6.88 4.67 0.080
-/B 26.42 43.42 0.81 12.88 7.79 22.75 76.36% 0 0 0 0 0.125
-/- 26.50 43.25 0.81 12.88 7.25 23.13 75.93% 0 0 6.79 4.46 0.070
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints
335

configurations: R/B stands for 90 degrees rotation al-
lowed and visibility constraint imposed; R/- stands
for rotation allowed and no visibility constraint im-
posed; -/B stands for no rotation allowed and visibil-
ity constraint imposed; and -/- stands for no rotation-
allowed but also no visibility constraint imposed. In
all cases, the EPMH meets the contiguity constraint
among items in the same group. In this way, we pro-
vide information on 240 solutions obtained, 10 for
each of the 24 instances.
The information on algorithm and constraint con-
figuration is contained in the first two columns. In the
six successive columns, we report, respectively, the
total number of pallets and layers created in the solu-
tion, the average fill factor considering the 2D space
of all layers, as well as the average number of single-
item, single-family and residual layers. Then we re-
port, in five additional columns, the maximum per-
centage of residual layers found among the instances
(worst case result), the average number of items not
satisfying the contiguity or the visibility constraint,
the average number of layers for which at least an
item does not meet the contiguity or the visibility con-
straint. The last column reports the computational
time in seconds. To facilitate the analysis of the re-
sults, we highlight in bold the best average values for
each column and constraint configuration.
Let us focus first on the performance of EPH and
SLH. From Table 2, we can notice that disregarding
rotation of the items has a considerable effect in the
solution cost, with an important increase in the num-
ber of single-family and single-item layers, as well as
a decrease in the number of residual layers. Between
these two algorithms, SLH has a slightly better per-
formance. This happens because the skyline structure
is an efficient structure that allows one to analyze only
a small part of the search space. However, this heuris-
tic has also the disadvantage of forming empty holes
depending on the sequence of the input items. We can
also notice that the average 2D fill factor achieved is
quite stable around 80%.
Now, let us consider the results obtained by the 8
attempted EPMH configurations. Also in this case,
rotation has a relevant impact on the solution cost. As
regards to the visibility constraint, we can notice a
slight difference in the number of layers, considering
both meeting rotation constraint and not. Concerning
the runtime, the visibility constraint has a more signif-
icant influence than the rotation constraint. Compar-
ing the results obtained by the proposed fitness eval-
uation functions, the Bounding Box function found
the best average results, at least for the configurations
R/B and R/-. The best average results for the con-
figurations -/B and -/- were instead achieved by the
Figure 7: Layers for the PBP instance 2, formed by 9 single-
item layers (layer border in blue), 1 single-family layer
(layer border in gray), and 6 residual layers (layer border
in red). Solution obtained by using the Bounding Box fit-
ness evaluation function.
Lower X function. For what concerns the number of
residual layers, the values found by the EPMH with
Bounding Box were considerably smaller than those
obtained with other functions. All computational ef-
forts were very low, always requiring less than 0.2
second on average. This is a very important detail for
future research as we can expect to create more com-
plex algorithms, maybe based on iterated executions
of the proposed heuristics, without incurring in large
computational efforts.
An example of a solution obtained for instance 2 is
provided in Figure 7. We can notice 9 single-item lay-
ers, 1 single-family layer and 6 residual layers. The
layers sum up to a total of 9 pallets.
6 CONCLUSIONS
In this paper, we studied a pallet building problem
with item rotations and practical constraints involving
visibility and contiguity. We proposed a 2-step con-
structive heuristic that enlarges the well-known ex-
treme points heuristic from the literature. In a first
step, we generate 2D layers by considering a larger
set of extreme points (candidate locations for pack-
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
336

ing) that are useful to model contiguity and visibility
requirements. In the second step, we used the cre-
ated 2D layers to build 3D pallets by using a sim-
ple greedy strategy. Extensive computational exper-
iments on real-world instances proved the effective-
ness of the proposed heuristic.
To evaluate the extreme points, we proposed sev-
eral fitness evaluation functions, and found that the
one based on the concept of Bounding Box gave bet-
ter results than the other ones on average. We also
analyzed the influence of some constraints (e.g., rota-
tion and visibility) when tailoring our heuristic to ba-
sic 2D packing heuristics from the literature, gaining
interesting insights in the difficulty of the real-world
instances that we tested.
As future work, we intend to develop metaheuris-
tic algorithms to try to enhance the quality of the solu-
tions that we generated so far. We also intend to pro-
pose formal mathematical models to express the con-
cept of contiguity and visibility of items, thus filling a
gap in the existing literature. We are also interested in
studying a more complex problem that joins together
the pallet building problem with the vehicle routing
problem, so as to consider the location of pallets into
trucks and their delivery to the clients that required
them. In this case, we should extend the concept of
family, not only relying on the geometric characteris-
tics of the items, but adding new criteria of separation,
in order to help both problems (packing and delivery)
to increase the quality of the final optimization.
ACKNOWLEDGEMENTS
We thank the University of Parma and the University
of Modena and Reggio Emilia (Italy) for the financial
support to this work.
REFERENCES
Alonso, M., Alvarez-Valdes, R., Iori, M., and Parre
˜
no,
F. (2019). Mathematical models for multi container
loading problems with practical constraints. Comput-
ers & Industrial Engineering, pages 722–733.
Alonso, M., Alvarez-Valdes, R., Iori, M., Parre
˜
no, F., and
Tamarit, J. (2017). Mathematical models for multi
container loading problems. OMEGA 66, pages 106–
117.
Alonso, M., Alvarez-Valdes, R., Parre
˜
no, F., and Tamarit, J.
(2016). Algorithms for pallet building and truck load-
ing in an interdepot transportation problem. Mathe-
matical Problems in Engineering, page 11.
Alvarez-Valdes, R., Parre
˜
no, F., and Tamarit, J. (2008). Re-
active GRASP for the strip-packing problem. Com-
puters & Operations Research, 35:1065–1083.
Bischoff, E. and Ratcliff, M. (1995). Issues in the devel-
opment of approaches to container loading. Omega,
23:377–390.
Bortfeldt, A. and Gehring, H. (2001). A hybrid genetic al-
gorithm for the container loading problem. European
Journal of Operational Research, 131:143–161.
Bortfeldt, A. and W
¨
ascher, G. (2013). Constraints in con-
tainer loading – a state-of-the-art review. European
Journal of Operational Research, 229:1–20.
Burke, E., Kendall, G., and Whitwell, G. (2004). A New
Placement Heuristic for the Orthogonal Stock-Cutting
Problem. Operations Research, 52:655–671.
Chazelle, B. (1983). The Bottomn-Left Bin-Packing
Heuristic: An Efficient Implementation. IEEE Trans-
actions on Computers, C-32:697–707.
Crainic, T., Perboli, G., and Tadei, R. (2008). Extreme
point-based heuristics for three-dimensional bin pack-
ing. INFORMS J. on Computing, 20:368–384.
Crainic, T., Perboli, G., and Tadei, R. (2012). Recent Ad-
vances in Multi-Dimensional Packing Problems. In
Volosencu, C., editor, New Technologies – Trends, In-
novations and Research. IntechOpen, Rijeka.
Delorme, M., Iori, M., and Martello, S. (2017). Logic
based benders’ decomposition for orthogonal stock
cutting problems. Computers & Operations Research,
78:290–298.
Egeblad, J., Garavelli, C., Lisi, S., and Pisinger, D. (2010).
Heuristics for container loading of furniture. Euro-
pean Journal of Operational Research, 200:881–892.
Fekete, S. and Schepers, J. (1997). A new exact algorithm
for general orthogonal d-dimensional knapsack prob-
lems. In Algorithms — ESA ’97, pages 144–156.
Haessler, R. and Talbot, F. (1990). Load planning for ship-
ments of low density products. European Journal of
Operational Research, 44:289–299.
Hopper, E. and Turton, B. (1998). Application of Genetic
Algorithms to Packing Problems – A Review. In Soft
Computing in Engineering Design and Manufactur-
ing, pages 279–288.
Imahori, S. and Yagiura, M. (2010). The best-fit heuristic
for the rectangular strip packing problem: An efficient
implementation and the worst-case approximation ra-
tio. Computers & Operations Research, 37:325–333.
Iori, M., Lima, V., Martello, S., Miyazawa, F., and Monaci,
M. (2019). Two-dimensional cutting and packing:
Problems and solution techniques. Technical report,
University of Bologna.
Iori, M. and Martello, S. (2010). Routing problems with
loading constraints. TOP, 18:4–27.
Iori, M. and Martello, S. (2013). An annotated bibliography
of combined routing and loading problems. Yugoslav
Journal of Operations Research, 23:311–326.
J
´
ozefowska, J., Pawlak, G., Pesch, E., Morze, M., and
Kowalski, D. (2018). Fast truck-packing of 3d boxes.
Engineering Management in Production and Services,
10:29–40.
Leung, S., Zhang, D., and Sim, K. (2011). A two-stage
intelligent search algorithm for the two-dimensional
strip packing problem. European Journal of Opera-
tional Research, 215:57–69.
Solution of a Practical Pallet Building Problem with Visibility and Contiguity Constraints
337

Lodi, A., Martello, S., Monaci, M., and Vigo, D. (2014).
Two-Dimensional Bin Packing Problems, pages 107–
129. John Wiley & Sons, Ltd.
Martello, S., Pisinger, D., and Vigo, D. (2000). The three-
dimensional bin packing problem. Operations Re-
search, 48:256–267.
Scheithauer, G. (2018). Introduction to Cutting and Packing
Optimization. Springer International Publishing.
Scheithauer, G. and Sommerweiβ, U. (1998). 4-block
heuristic for the rectangle packing problem. European
Journal of Operational Research, 108(3):509–526.
Scheithauer, G. and Terno, J. (1996). The G4-Heuristic for
the Pallet Loading Problem. The Journal of the Oper-
ational Research Society, 47:511–522.
Silva, E., Oliveira, J., and W
¨
ascher, G. (2016). The pallet
loading problem: a review of solution methods and
computational experiments. International Transac-
tions in Operational Research, 23:147–172.
Terno, J., Scheithauer, G., Sommerweiβ, U., and Riehme,
J. (2000). An efficient approach for the multi-pallet
loading problem. European Journal of Operational
Research, 123:372–381.
W
¨
ascher, G., Hauβner, H., and Schumann, H. (2007).
An improved typology of cutting and packing prob-
lems. European Journal of Operational Research,
183:1109–1130.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
338
