A Data Driven Approach to Derive Trafﬁc Intersection Geography using

High Resolution Controller Logs

Dhruv Mahajan, Tania Banerjee, Yashaswi Karnati, An. Rangarajan and Sanjay Ranka

Department of Computer and Information Science and Engineering, University of Florida, Gainesville, FL, U.S.A.

Keywords:

Loop Detectors Systems, ATSPM, Controller Logs, Detector Mappings, Detector Conﬁguration, Data Mining.

Abstract:

Current trafﬁc signal controllers are capable of recording events (signal events; vehicle arrival and departure)

at very high resolutions (usually, 10Hz). The high resolution data rates enable the computation and study of

various (granular) measures of effectiveness. However, without knowing the location of speciﬁc detectors on

an intersection and the phases they are mapped to, a number of measures of effectiveness (of signal perfor-

mance) cannot be evaluated. These mappings may not be available or up to date for many practical reasons

(e.g., old infrastructure, mappings not machine readable, maintenance or addition of new lanes, etc.). In this

paper, we develop an inference engine to map detectors to phases and distinguish between the stop bar and

advance detectors, or in other words, infer the location of the loop detectors with reference to the intersection.

1 INTRODUCTION

Trafﬁc signals are crucial in managing vehicular and

pedestrian trafﬁc at an intersection where two or more

road segments meet. The new generation of sig-

nal controllers, based on the latest Advanced Trans-

portation Controller (ATC) (Intelligent Transport Sys-

tems, 2009) standards, are capable of recording signal

events as well as vehicle arrival and departure events

at a very high resolution (10Hz). As a result of the

high resolution data rates, it is now possible to com-

pute signal performance metrics such as arrivals on

red, arrivals on green, and platooning ratios on a cy-

cle by cycle or sub cycle basis (U.S. Department of

Transportation, 2013). A standard 4-way intersection

with actuated or semi-actuated control, as shown in

Figure 2, has eight phases (or directions of vehicular

movement) and 4 ways to approach the intersection

given by Figure 1. Each approach usually has multi-

ple lanes and can have one or two permitted phases.

There may be more than one vehicle detector on each

lane. There are usually many detectors (e.g. stop bar

detectors and advanced detectors) at an intersection,

with more than one detector per lane. These can be of

different types, however most detectors (at the very

least) report vehicle arrivals and departures. Given

a detector identiﬁer in the log ﬁle, it is essential to

know where the detector is located in the intersection

to make meaningful observations about trafﬁc behav-

ior and the performance of the intersection. Thus, for

effective computation of performance measures, we

need to have detector to phase mappings. The phase

represents the direction of trafﬁc movement on an in-

tersection. Additionally, we would like the mappings

indicate the location of a detector, such as advanced

or stop-bar.

Figure 1: Phase Diagram Showing Vehicular & Pedestrian

Movement at a Four Way Intersections. The Solid Gray Ar-

rows Show Vehicle Movements (or phases). (U.S. Depart-

ment of Transportation, 2008).

In many practical situations, these mappings are

missing (e.g., the infrastructure was built decades ago

and the mappings are not available in a machine-

readable form) or incorrect (e.g., during maintenance

or addition of new lanes, the contractor forgot to up-

date the mappings). The absence of a detector to

phase mapping limits the value of the high-resolution

controller logs. This problem is further detailed in

Section 2.

Our goal in this paper is to ﬁnd the best map-

ping of detectors to phases and to classify detectors

Mahajan, D., Banerjee, T., Karnati, Y., Rangarajan, A. and Ranka, S.

A Data Driven Approach to Derive Trafﬁc Intersection Geography using High Resolution Controller Logs.

DOI: 10.5220/0009355402030210

In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), pages 203-210

ISBN: 978-989-758-419-0

203

Figure 2: Example of a Standard 4 Way Intersection (I).

as stop-bar detectors or advance detectors based only

on events in the high-resolution controller logs. These

events include a change in the signaling state (for ex-

ample, green, yellow, or red for vehicles, and walk,

ﬂashing do not walk, and do not walk for pedestrians)

and a change in the detector state (based on whether

the detection area is occupied or not).

Our algorithms are based on the following overar-

ching intuition:

1. During normal trafﬁc conditions, the trafﬁc pass-

ing a detector when the corresponding phase is

green will be higher than the other detectors.

2. During very low trafﬁc conditions, the sequence

of timestamps of vehicle arrivals and departures

can be used to separate advance detectors from

stop bar detectors.

Our goal is to develop automated machine-learning

methods that derive these mappings using several

months of loop detector data. This required us to de-

velop the following novel approaches:

1. Automatically decomposing data streams into cy-

cles and cluster these cycles based on similar

phase timing patterns. This is necessary because

combining data across multiple, distinct types of

patterns can lead to lower discrimination between

green versus red behavior. For this purpose, we

developed frequent pattern mining based on n-

grams and then applied clustering algorithms to

derive clusters of similar cycles.

2. For really low volume cycles (e.g., during night-

time), when only one vehicle is potentially

present, the time of arrival and departure along

with signal timing data can be used to derive or-

dering of detectors. We develop algorithms that

can leverage this information across multiple such

cycles.

3. For low to medium volume cycles, we developed

algorithms that can use green versus red depar-

ture information to derive a small subset of feasi-

ble phases for each detector. We then use frequent

set mining within a given cycle cluster to derive a

consistent mapping for that cluster.

4. We have developed algorithms to combine detec-

tor mappings derived for each cluster of similar

cycles to arrive at the overall mapping and the de-

tector type.

Since some non-conﬂicting phases are synchro-

nized, it may be infeasible to narrow down the map-

ping of a detector to one particular phase. Hence,

to quantify the quality of mapping, we compute the

prediction factor, which is the ratio of the number of

detector-to-phase assignments obtained using our al-

gorithms to the number of the actual detector-to-phase

assignments. Ideally, the prediction factor should be

1. We applied our algorithms to 10 intersections on an

arterial and found that the prediction factor was 1.3.

For this set of 10 intersections, our prediction coin-

cided with the available mappings, and we were able

to map some more detectors unambiguously to one

phase.

Figure 3 shows the overall ﬂow diagram for our

inference engine. The problems of developing an

inference engine for detector locations (i.e., the ap-

proach or phase they belong to) and types from high-

resolution controller logs may be divided into three

parts. The ﬁrst part is to map the detectors to phases.

The second part is to classify the detectors as stop bar

or advance detectors, using the controller logs. The

last part is to use the inference engine to validate and

update any known detector mappings. These three

steps are described in Section 3, Section 4, and Sec-

tion 5 respectively. Section 5 also presents the results

obtained from several intersections, and the conclu-

sions are presented in Section 6.

2 RELATED WORK

Trafﬁc data that accurately reﬂect real-time trafﬁc net-

work conditions plays a very important role in im-

proving trafﬁc efﬁciency in Intelligent Transportation

Systems (ITS) (Martin, 2013). The implementation

and uses of an inductive loop detector system have

been described in detail by Pursula et al. in (Pur-

sula and Kosonen, 1989). Several measures of ef-

fectiveness used in recent times are heavily depen-

dent on phase-speciﬁc trafﬁc analysis. Purdue Coor-

dination Diagrams (PCDs), arrivals on green (AOG)

versus those on red (AOR), and other such measures

(U.S. Department of Transportation, 2008; Day et al.,

2014) need to precisely record the phase and loca-

tion corresponding to vehicle arrivals. Yogesh et al.

(Yogesh et al., 2018) also aim to improve the per-

formance and efﬁciency of signalized intersections by

proposing an improved design and signal processing

algorithm to facilitate lane-by-lane detection in seri-

ally connected loop detectors. Lu et al. (Lu et al.,

2008) propose ways to detect fault(s) in loop detection

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

204

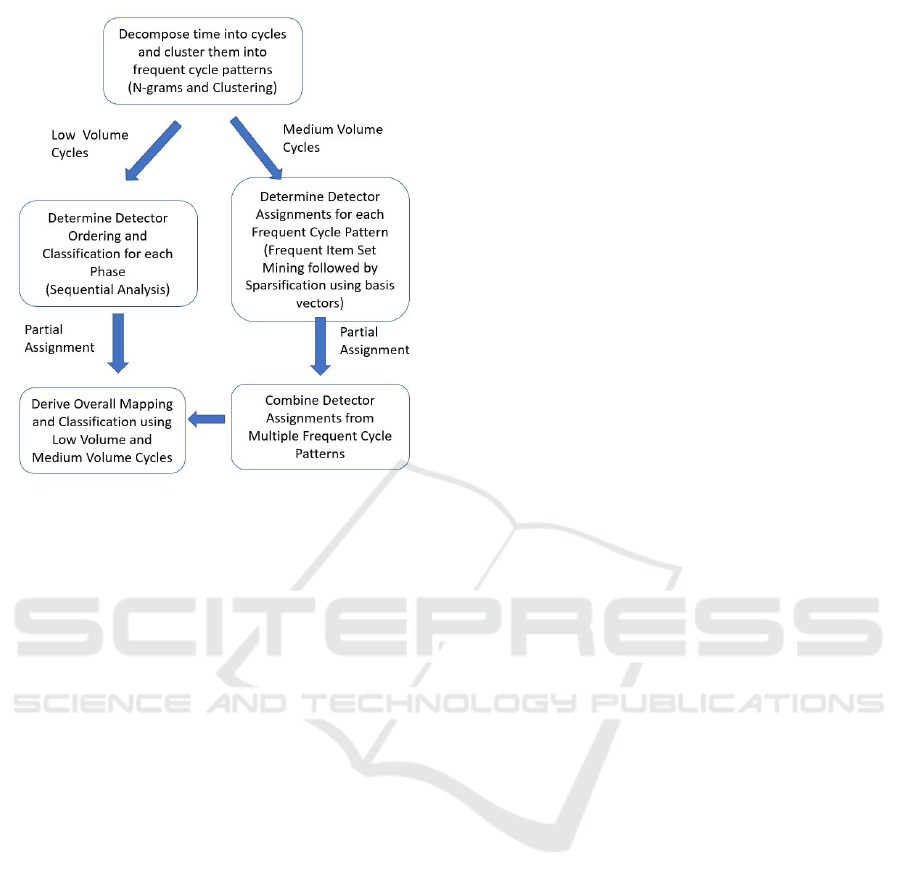
Figure 3: Flow Diagram for Our Methodology. We Sepa-

rate out the Low Volume and Medium Volume Data from

the Logs. The Medium Volume Data Is Used to for Partial

Assignments, and Low Volume Data Is Used to Distinguish

between Stop Bar and Advance Detectors, Enable Ordering

of Detectors.

systems and algorithms to temporarily correct/cleanse

(impute) faulty detector data with similar motivations.

Importance of Detector Mappings. To measure

performance of a signalized intersection in a mean-

ingful manner or effect substantial performance im-

provements, it is critical to have vehicle detection

sensors deployed. Another prerequisite for comput-

ing most performance measures in a semi-automated

manner or fully automated manner is to have high ﬁ-

delity (or resolution) data logging solutions deployed

for all signal controllers. For correctly interpreting

this high resolution data gathered at trafﬁc intersec-

tions and computing performance measures at inter-

sections, certain secondary set of data/information is

needed. The most critical requirement for interpret-

ing the high-resolution detector event data logged in

a controller is the detector mapping information. This

is outlined in (Day et al., 2016)

”Since any detector event must be understood

as a vehicle arriving at some right-of-way and

distance at the intersection, and any phase

event must be understood as an interval of

time elapsed for some movement, the detector

mapping process is the critical step in guiding

how signal output states and vehicle arrivals

are to be interpreted relative to each other.”

Hence, the focus of this research is on deriving or up-

dating these mapping using only the high resolution

event logs that have already been collected.

3 DETECTOR TO PHASE

MAPPING

Figure 2 shows the details of the intersection we use

for demonstrating our methodology throughout the

rest of the paper. This intersection is referred to as

intersection I.

We represent the mapping of detector to phases in

the form of a matrix, where the rows are the phases

and the columns are the detectors. A matrix element

is either zero, if the corresponding detector does not

belong to the corresponding phase, or 1 if that detec-

tor may belong to that phase. Without any informa-

tion, all the entries in the matrix are 1, i.e., this corre-

sponds to a situation where a detector may belong to

any phase. Applying our algorithms, we sparsify this

matrix. Table 6 shows the ﬁnal state of the matrix.

Each phase may have multiple detectors, hence there

would be many 1s in each row . However, usually,

there should be only a few 1s or a single 1 per column

because a detector often belongs to only one phase. If

non-conﬂicting phases always start and end together,

then it may not be possible to assign a detector to only

one of these non-conﬂicting phases.

A signal cycle is deﬁned as ”the total time to

complete one sequence of signalization for all move-

ments at an intersection. In an actuated controller

unit, the cycle is a complete sequence of all signal

indications.” (U.S. Department of Transportation,

2008). As a ﬁrst step, we automatically decompose

data streams into cycles and cluster these cycles based

on similar phase timing patterns. This is necessary be-

cause combining data across multiple different types

of patterns can lead to lower discrimination between

green versus red behavior. For this purpose, we de-

velop frequent pattern mining on n-grams and use the

results for clustering. In the following, we ﬁrst de-

scribe how a single cycle is processed and then how

we extend it to multiple cycles.

3.1 Cycle Identiﬁcation and Clustering

The ﬁrst step in our methodology is to identify the

cycles and cluster the signal cycles. We create a rep-

resentation of the SPaT data by writing out the phase

or groups of phases that are green at any given time.

For example, if the phases 2 and 5 receive green time

simultaneously, followed by the phases 2 and 6; 4 &

8; 3 & 7; and 1 & 5, we represent these changes as

A Data Driven Approach to Derive Trafﬁc Intersection Geography using High Resolution Controller Logs

205

Table 1: Most Frequent 6-Grams Found in the SPAT Mes-

sages from a Controller. These Correspond to the Predomi-

nant Signal Timing Plans Deployed at This Controller.

a sequence such as: ’2,5’, ’2,6’, ’4,8’, ’3,7’, ’1,5’,

and so on. After creating a representation of the SPaT

data in this manner, we identify cycles by computing

n-grams.

Originally used in the ﬁeld of computational lin-

guistics and probability, n-grams are a continuous se-

quence of n elements in a text. We ﬁnd n-grams in

our SPaT representation to automatically detect signal

timing patterns. For example, a repeated sequence of

a 6-gram: (’2,5’, ’2,6’, ’4,8’, ’3,7’, ’1,5’, ’1,6’) indi-

cates this as the most dominant signal timing pattern.

Figure 6 shows examples of n-grams in SPaT data.

Table 1 presents the most frequent 6-grams, or timing

patterns, for the intersection in Figure 2.

3.2 Deriving Detector Assignments

We consider cycles from time periods with moderate

trafﬁc activity. This is done by ﬁltering out periods of

very low (e.g., night time) and very high (e.g., rush

hour) trafﬁc. The rationale for doing this is that if

there is little trafﬁc, the detectors would not be acti-

vated, and on the other hand, if there are many ve-

hicles at the intersection, then most detectors will be

activated too frequently, which may make the differ-

ences in activation counts less perceptible.

Our approach is based on the fundamental obser-

vation that the number of vehicle departures reported

on a lane will be more when the corresponding phase

is green or yellow as compared to the number of de-

partures when that phase is red. Thus, for example,

by assigning a positive vote to each vehicle departure

when phase 2 is green and by assigning a negative

vote to each vehicle departure when phase 2 is red, it

is expected that by the end of the signal cycle, all de-

tectors which actually belong to phase 2 will be left

with an overall positive voting score.

This scheme may be unable to disambiguate two

phases that are non-conﬂicting and are served simul-

taneously. For example, if phases 2 and 6 are served

simultaneously at all times, it will be virtually impos-

sible to assign detectors speciﬁcally to 2 or 6. Instead,

we will have a set of detectors that may belong to ei-

ther 2 or 6. If the timing plan is such that during some

part of the day the non-conﬂicting phases are served

separately, then it is possible to disambiguate these

detector mappings by considering the number of de-

parture votes over these special signal timing patterns.

A visualization of the number of departures for mul-

tiple cycles is presented in Figure 4 where certain de-

tectors report departures only when phase 2 is green.

This can be seen as an indication that those detectors

may be assigned to phase 2.

For each cluster of cycles, we compute the union

of the results obtained from the cycles belonging to

the same cluster. This effectively gives all the phases

a detector can be mapped to based on cycles with sim-

ilar behavior. Next, we take an intersection of the re-

sults from different clusters, to arrive at the ﬁnal as-

signment of detectors to phases. This is because each

cluster corresponds to a potentially different combi-

nation of phases.

The details of each of these steps are presented

below.

Inference using a Single Cycle: A basis vector for

each phase is created during a cycle. The basis vector

is an array of numbers that are either +1 or -1, de-

pending respectively on whether the phase was active

or not during a time interval. Algorithm 1 presents

a method to infer partial detector-to-phase mappings

(or partial sparsiﬁcation) using a single cycle. If we

aggregate the events to a resolution of 5 seconds and

we are analyzing a signal cycle of length 35 seconds,

then, a basis vector, b1 for phase 2 would have 7

entries, given by, for example, [-1,-1,-1,+1,+1,-1,-1].

This representation shows that phase 2 was active be-

tween seconds 20 through 30 and inactive for the rest

of the time. Figure 5 is a visual representation of

how the scores for each detector are computed. Algo-

rithm 1 is a description of the same and is the ﬁrst step

in the sparsiﬁcation process. The inference from one

cycle may have problems if two phases were served

simultaneously. For example, if phases 2 and 6 are

served simultaneously and detectors d2 and d6 belong

to phases 2 and 6 respectively, they are both identiﬁed

as potentially belonging to phase 2 or 6.

Inference from a Single Cluster: Any inference

from a single cycle is subject to errors. This is be-

cause trafﬁc in a single cycle may be abnormally high

in a given phase or direction. Combining these re-

sults across multiple cycles has the beneﬁt of reduc-

ing this error, especially if the results are consistent

across multiple cycles.

For combining across multiple cycles, it is useful

to cluster cycles with similar ordering of phases and

then combining the results within each cluster sepa-

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

206

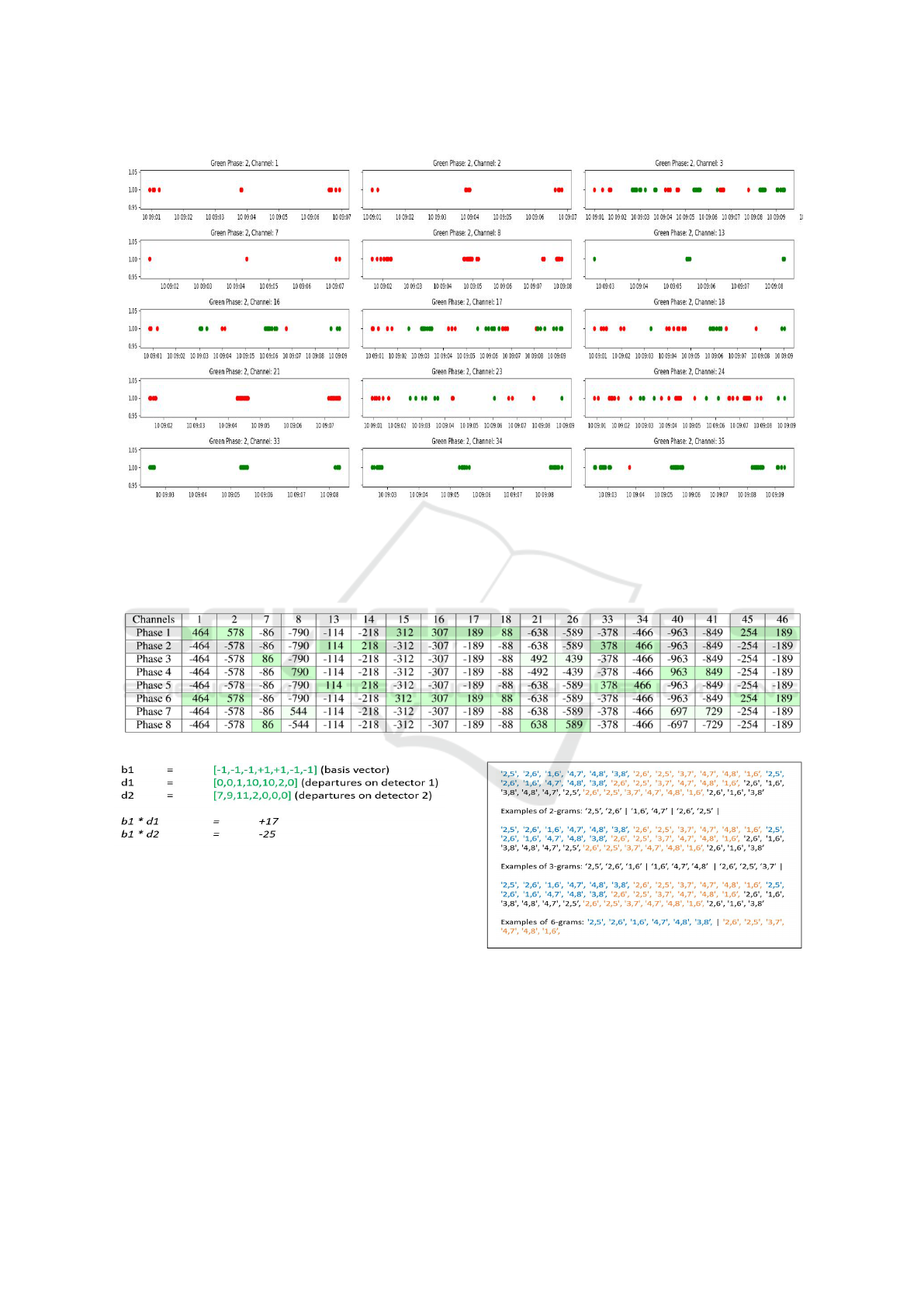
Figure 4: A Visualization of Departures Reported by Some Detectors of Intersection I for Multiple Cycles. Certain Detectors

Report Departures Only When Phase 2 Is Green. This Is a Strong Signal That These Detectors Belong to Phase 2.

Table 2: Partial Assignment Matrix Based on Pattern 1. This Assignment Matrix Is Derived from Pattern 1 in Table 1.

Detectors (Columns) Are Assigned Tentative Phases Based on the Number of Departures on Green vs. Red. But, It Is

Difﬁcult to Distinguish between Phases That Were Green Together, E.G., Phases 1 and 6.

Figure 5: An Example of Computing Scores for Each De-

tector. Based on the Dot Product, That d2 Does Not Belong

to Phase 2 Whereas d1 May Belong to Phase 2.

rately. This process is explained using the most popu-

lar patterns Pattern 1 and Pattern 2 from Table 1. For

two cycles that have same pattern, we take a set union

of the results for these two cycles. The rationale for

taking a union is that the assignments may be slightly

different for the two cycles based on speciﬁc trafﬁc

conditions during the occurrence of these cycles. For

example, in one case the volume of trafﬁc may be low,

resulting in the mapping of fewer detectors. Tables 2

and 3 show the detector to phase mappings obtained

from Pattern1 and Pattern2, respectively, by apply-

ing the union operation on all cycles with the same

Figure 6: 2,3 and 6-Grams in the SPAT Data. We Use This

Approach to Infer Signal Timing Plans from SPAT Mes-

sages.

pattern. Tables 4 and 5 show these mappings for the

Pattern1 and Pattern2, respectively.

Inference from Multiple Clusters: For two or more

clusters consisting of cycles with different patterns,

we take a set intersection of the assignment matrix

A Data Driven Approach to Derive Trafﬁc Intersection Geography using High Resolution Controller Logs

207

Table 3: Partial Assignment Matrix Based on Pattern 2. This Assignment Matrix Is Derived from Pattern 2 in Table 1. We

Combine the Results from Pattern 1 (Table 2) and Pattern 2 in Figure 7 to Get Better Mappings.

Algorithm 1: Map Detectors Using One Signal Cycle.

function MAPDETECTORS(LogsData , x, y)

Require: LogsData - High resolution controller logs of

the intersection being studied.

x - Intersection ID y - Time window of one observation

for every time window z do

Select cycles with moderate volumes.

Create basis vectors for each phase (bx).

Create departure vectors for each detector (dy).

Compute the vector dot product of each basis vec-

tor, bx with each departure vector dy.

Select the ones with the highest results for the par-

tial assignment matrix.

end for

end function

derived for each cluster in the previous step. For ex-

ample, using the results from Tables 4 and 5, we are

able to further disambiguate the overlapping assign-

ments. Here, detectors 21 and 26, are assigned to

phase 8 in Table 2 because the score for Phase 8 is

higher than the score for Phase 3. And the same de-

tectors are assigned to phases 4 and 8 in Table 3. Tak-

ing an intersection, we assign these detectors to phase

8. Next, detectors 1 and 2 can be assigned to both

Phase 1 and Phase 6. This is because they have the

exact same scores in Tables 2 and 3. Thus, apply-

ing a combination of the set union (within a cluster)

and intersection operations (across multiple clusters),

we arrive at the ﬁnal assignment results shown in Fig-

ure 7. Algorithm 2 presents the overall algorithm.

Table 4: Partial Mapping Deduced Using Only Pattern 1.

This Is a Transactional Representation of the Results Pre-

sented in Table 2.

Detector Number Possible Phases

13,14 Phase 2 or Phase 5

1,2 Phase 6 or Phase 1

21,26 Phase 8

8,40,41 Phase 4 or Phase 7

Table 5: Partial Mapping Deduced Using Only Pattern 2.

This Is a Transactional Representation of the Results Pre-

sented in Table 3.

Detector Number Possible Phases

13,14 Phase 2 or Phase 5

1,2 Phase 6 or Phase 1

7 Phase 3 or Phase 7

21,26 Phase 4 or Phase 8

Figure 7: We Use the Set Intersection Operation to Com-

bine the Partial Mappings Derived Using Data from Differ-

ent Timing Patterns.

4 CLASSIFYING DETECTORS

We use low volume cycles to infer the relative loca-

tions of the detectors from the stop bar. For example,

a single car arriving at an intersection would trigger

the detectors in order. We ﬁlter out signal cycles with

only n (n=3) reported departures within a short dura-

tion of time. We choose the number three because

Algorithm 2: Map Detectors Using Multiple Signal Cycles.

function MAPDETECTORS(Mx , Patterns)

Require: Mx - Collection of Partial Assignment matrices

obtained using only one pattern.

Patterns - The collection of signal timing pattern corre-

sponding to the mapping

for each phase p (varying 1 to 8) do

Take an intersection of the results from each as-

signment matrix.

Obtain the ﬁnal assignment matrix.

Use the low volume data to order the detec-

tors(stop bar vs advance).

end for

end function

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

208

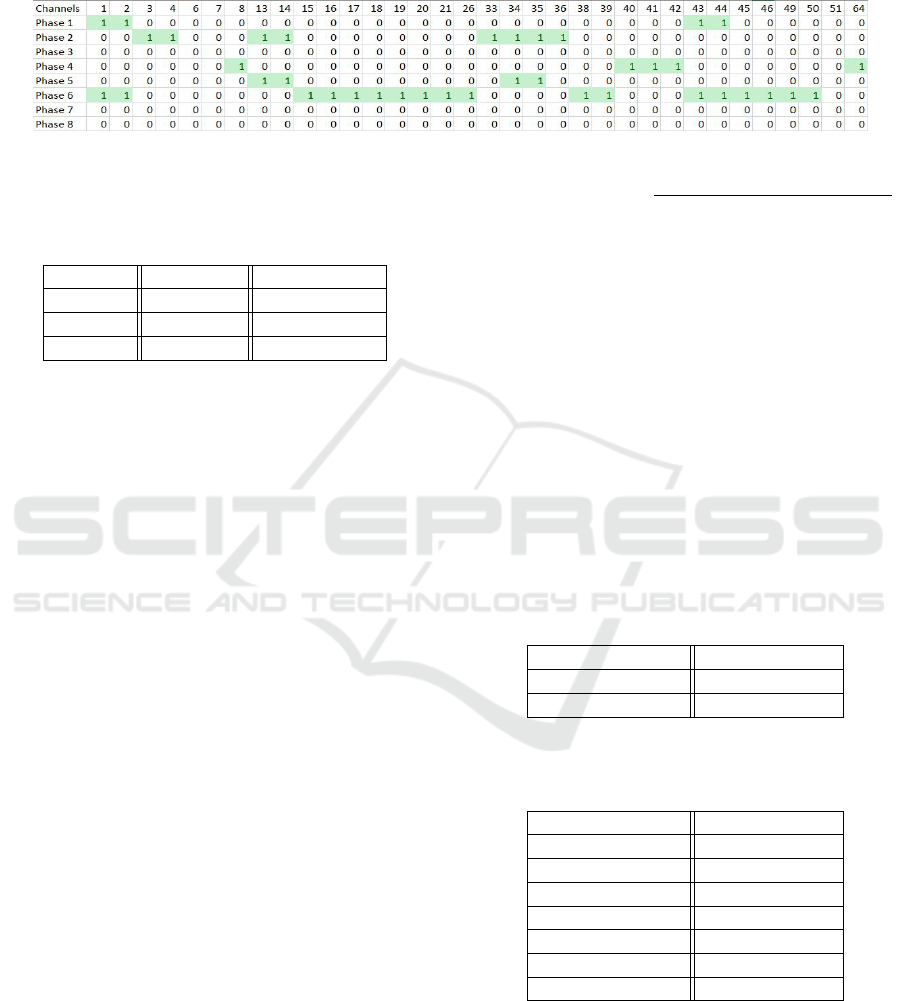
Table 6: Final Mapping or Assignment Matrix Deduced Using a Combination of Pattern 1 and Pattern 2. We Start with the

Assumption That Every Detector May Be Assigned to Any Phase. Hence, We Assume That All the Cells in the Assignment

Matrix Are Green. Techniques Presented in This Paper Can Be Used to Sparsify the Initial Matrix and Arrive at This Final

Mapping Where Green Cells Represent Likely Assignment.

Table 7: Frequent Item Sets Observed Using Very Low Vol-

ume Observation Periods. These Results Are in Agreement

with the Results Presented in Table 6. They Also Help Us

Distinguish between Stop Bar and Advance Detectors.

Item Set Frequency Green Phases

6,4,36 35 Phase 2 and 6

17,15,45 26 Phase 2 and 6

18,16,46 23 Phase 2 and 6

a single vehicle can cross a maximum of three detec-

tors while crossing the intersection. Next, we com-

pute the most frequently occurring ordered item sets

of detectors that report departures during these peri-

ods. For example, if detector 6 reports a departure

and that is followed by a departure event on detec-

tors 4 and 35. If this particular order of events is ob-

served with a high frequency, we can use these ob-

servations to order the three detectors. We could only

derive potential orderings for Phases 2 and 6 using

this technique. Table 7 presents the results for the or-

der derived using time periods with low volumes for

intersection ID 1995.

5 VERIFICATION

Assume that a (partial) mapping is available for an in-

tersection. The approach described above can be used

to determine a sparse assignment matrix of detector-

to-phase mapping. If this mapping is conﬂicts with

the mapping provided, then the derived mapping can

be effectively used to provide suitable corrections.

We applied our algorithm for a set of 10 intersections

in Seminole County. This corridor was selected to

test our algorithms because all the controllers on this

corridor are ATC compliant and detector-to-phase as-

signment was available for all of them. It was found

that the actual assignments are a subset of our predic-

tions. However, due to the problem presented by syn-

chronized phases, the model might make more than

one assignment prediction. To quantity this, we de-

ﬁne the following metric:

Prediction Factor =

No o f assignments suggested

No o f actual assignments

(1)

On this corridor of 10 intersections, we made (on

average) 1.3 predictions of assignment instead of 1,

hence our Prediction Factor was 1.3.

Our techniques can also be used to update previ-

ously known mappings to generate a more complete

picture or validate and update out-of-date mappings.

For example, for one of the signals the previously

known mappings are presented in Table 8. It can

be observed that we started with partial information

for Phases 2 and 6 and no information for the other

phases. The derived detector mappings are presented

in Table 9. Note that for Phases 2 and 6, the map-

pings are ordered, i.e., it was deduced that detectors

2, 3 and 11, 12 are advance detectors whereas the oth-

ers are stop bar detectors.

Table 8: Known Mapping for an Intersection. This Can Be

Contrasted with the Final State in Table 9.

Detector Number Possible Phases

2,3 Phase 2

11,12 Phase 6

Table 9: Final Mapping Deduced Using a Combination of

All Techniques in This Paper. We Validate the Known Map-

pings in Table 8 and Update Them at the Same Time.

Detector Number Possible Phases

1 Phase 1

2,3,26,27 Phase 2

29 Phase 3

7 Phase 5

11,12,13,14 Phase 6

15 Phase 7

16,17 Phase 8

6 CONCLUSIONS

We have proposed a framework to derive loop de-

tector mappings if none or only partial mappings are

A Data Driven Approach to Derive Trafﬁc Intersection Geography using High Resolution Controller Logs

209

available. We also presented a way to identify top-bar

and advance detectors on the same lane. Our main

contributions are as follows:

1. We have developed novel algorithms for automati-

cally decomposing data streams into cycles and to

cluster these cycles based on similar phase-timing

patterns. For this purpose, we developed frequent

pattern-mining bases on n-grams and then applied

clustering algorithms.

2. For really low volume cycles (e.g., during night-

time), when only one vehicle is potentially

present, the time of arrival and departure along

with signal timing data can be used to derive or-

dering of detectors. We develop algorithms that

can leverage this information across multiple such

cycles.

3. For low to medium volume cycles, we developed

algorithms that can use green versus red departure

information to derive a small subset of phases for

each detector. We then use frequent set mining

within a given cycle cluster to derive a consistent

mapping for that cluster.

There are several avenues for improving the work

presented in this paper. In the intersection deﬁned in

Section 3, we note that for the timing plans deployed,

phases 1, 6 and 2, 5 are partially synchronized. In

some cases, it may be possible to compute and de-

ploy a customized timing plan for a short period of

time (non-peak hour, to minimize impact on Quality

of Service) where phases 1 and 5 are synchronized.

These customized basis vectors (signal-timing plans)

can help us reduce the Prediction Factor (Step 2, Fig-

ure 7). We also plan to treat permissive left and right

turn lanes differently in the future.

ACKNOWLEDGEMENTS

This work was supported by NSF CNS 1922782,

by the Florida Dept. of Transportation (FDOT) and

FDOT District 5. The opinions, ﬁndings and conclu-

sions expressed in this publication are those of the au-

thor(s) and not necessarily those of the FDOT or the

National Science Foundation.

REFERENCES

Day, C., Bullock, D., Li, H., Remias, S., Hainen, A.,

Freije, R., Stevens, A., Sturdevant, J., and Brennan, T.

(2014). Performance Measures for Trafﬁc Signal Sys-

tems: An Outcome-Oriented Approach. Purdue Uni-

versity, West Lafayette, Indiana.

Day, C. M., Bullock, D. M., Li, H., Lavrenz, S., Smith,

W. B., and Sturdevant, J. R. (2016). Integrating traf-

ﬁc signal performance measures into agency business

processes. Joint Transportation Research Program.

Intelligent Transport Systems, U.S. Department of Trans-

portation, F. H. A. (2009). Ite advanced transporta-

tion controller (atc) family of standards. https://www.

standards.its.dot.gov/Factsheets/Factsheet/14. (Ac-

cessed on 7/20/2019).

Lu, X.-Y., Varaiya, P., Horowitz, R., and Palen, J. (2008).

Faulty loop data analysis/correction and loop fault de-

tection. In 15th World Congress on Intelligent Trans-

port Systems, pages 12–24.

Martin, Peter T; Feng, Y. W. X. (2013). Detector technol-

ogy evaluation. https://digitallibrary.utah.gov/awweb/

awarchive?item=30285. (Accessed on 7/20/2019).

Pursula, M. and Kosonen, I. (1989). Microprocessor and

pc-based vehicle classiﬁcation equipments using in-

duction loops. In Second International Conference on

Road Trafﬁc Monitoring, 1989., pages 24–28.

U.S. Department of Transportation, F. H. A. (2008). Traf-

ﬁc signal timing manual. https://ops.fhwa.dot.gov/

publications/fhwahop08024/index.htm. (Accessed on

7/20/2019).

U.S. Department of Transportation, F. H. A. (2013). Mea-

sures of effectiveness and validation guidance for

adaptive signal control technologies. https://ops.fhwa.

dot.gov/publications/fhwahop13031/index.htm. (Ac-

cessed on 7/20/2019).

Yogesh, G. K. V., Sharma, A., and Vanajakshi, L.

(2018). An improved inductive loop detector de-

sign for efﬁcient trafﬁc signal operations and leaner

space requirements. Transportation Research Record,

2672(18):143–153.

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

210